2 Discussion of the slip velocity due to diffusiophoresis

The diffuse layer of solute molecules/ions residing adjacent to a particle surface is the region where the diffusive solute flux due to gradients in chemical concentration balances the flux due to an intermolecular potential $\unicode[STIX]{x1D719}$ describing short-range interactions between the particle and solute molecules/ions. The thickness of the diffuse layer (Anderson, Lowell & Prieve Reference Anderson, Lowell and Prieve1982; Israelachvili Reference Israelachvili2011), denoted by $L$ , is the typical length scale over which $\unicode[STIX]{x1D719}$ decays away from the surface. For ions, the diffuse layer is referred to as the electric double layer, $\unicode[STIX]{x1D719}$ is the electrostatic potential and $L=\unicode[STIX]{x1D706}_{D}$ , the Debye layer thickness. In a $z:z$ electrolyte solution ( $z$ is the ion valence) with a solute concentration $c$ and dielectric constant $\unicode[STIX]{x1D716}$ , the Debye layer thickness is (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984)

(2.1) $$\begin{eqnarray}\unicode[STIX]{x1D706}_{D}=\sqrt{\frac{\unicode[STIX]{x1D716}k_{B}T}{2z^{2}e^{2}c}},\end{eqnarray}$$

where $e$ is the electric charge, $k_{B}$ is the Boltzmann constant and $T$ is the absolute temperature.

When the diffuse layer thickness $L$ is much smaller than the radius of a spherical particle $a$ , a slip velocity, at the outer boundary of the diffuse layer, can be assumed on the particle due to diffusiophoresis. For non-electrolytes, this slip velocity $\boldsymbol{v}$ at position $\boldsymbol{x}$ is solely determined by chemiphoresis, or pressure gradients established by osmotic effects, which is (Derjaguin et al. Reference Derjaguin, Sidorenkov, Zubashchenkov and Kiseleva1947; Anderson Reference Anderson1989; Michelin & Lauga Reference Michelin and Lauga2014; Mozaffari et al. Reference Mozaffari, Sharifi-Mood, Koplik and Maldarelli2016)

(2.2) $$\begin{eqnarray}\boldsymbol{v}_{s}(\boldsymbol{x})=-\frac{k_{B}TL^{2}}{\unicode[STIX]{x1D707}}\int _{0}^{\infty }y\left[\exp \left(-\frac{\unicode[STIX]{x1D719}(y)}{k_{B}T}\right)-1\right]\,\text{d}y\unicode[STIX]{x1D735}_{s}c,\end{eqnarray}$$

where $\unicode[STIX]{x1D707}$ is the fluid viscosity, $\unicode[STIX]{x1D735}_{s}$ is the gradient operator along the surface and $c$ is the solute concentration field at the outer boundary of the diffuse layer. Here, the dimensionless coordinate $y=(r_{n}-a)/L$ is normal to the surface, where $r_{n}$ is the normal coordinate. The potential distribution $\unicode[STIX]{x1D719}(y)$ is determined by interactions of the solute with the surface. For electrolytes, the slip velocity is (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984)

(2.3) $$\begin{eqnarray}\boldsymbol{v}_{s}(\boldsymbol{x})=-\frac{k_{B}TL^{2}}{\unicode[STIX]{x1D707}}\left[-2\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}+\frac{4k_{B}T}{ze}\ln \left(1-\unicode[STIX]{x1D6FE}^{2}\right)\right]\unicode[STIX]{x1D735}_{s}c,\end{eqnarray}$$

with

(2.4a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\frac{D_{+}-D_{-}}{D_{+}+D_{-}}\quad \text{and}\quad \unicode[STIX]{x1D6FE}=\tanh \left(\frac{ze\unicode[STIX]{x1D701}}{k_{B}T}\right),\end{eqnarray}$$

where $D_{+}$ ( $D_{-}$ ) is the diffusivity of the cations (anions) and $\unicode[STIX]{x1D701}$ is the zeta potential of the particle. We note that the second term in (2.3) is just an explicit form of (2.2), when $\unicode[STIX]{x1D719}$ is the electrostatic potential, while the first term in (2.3) is due to electrophoresis (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984); the difference in diffusivities of the cations and anions ( $\unicode[STIX]{x1D6FD}\neq 0$ ) generates an electric field when there is a concentration gradient, and the electric field moves the particle. Therefore, diffusiophoresis in an electrolyte solution consists of both chemiphoretic and electrophoretic contributions (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984; Anderson Reference Anderson1989).

Many papers (Golestanian et al. Reference Golestanian, Liverpool and Ajdari2007; Michelin & Lauga Reference Michelin and Lauga2014, Reference Michelin and Lauga2015; Schnitzer & Yariv Reference Schnitzer and Yariv2015; Mozaffari et al. Reference Mozaffari, Sharifi-Mood, Koplik and Maldarelli2016; Yariv Reference Yariv2016) in the study of diffusiophoresis use the slip velocity

(2.5) $$\begin{eqnarray}\boldsymbol{v}_{s}(\boldsymbol{x})=b\unicode[STIX]{x1D735}_{s}c,\end{eqnarray}$$

by assuming that the diffuse layer thickness $L$ and so

(2.6) $$\begin{eqnarray}b=-\frac{k_{B}TL^{2}}{\unicode[STIX]{x1D707}}\int _{0}^{\infty }y\left[\exp \left(-\frac{\unicode[STIX]{x1D719}(y)}{k_{B}T}\right)-1\right]\,\text{d}y\end{eqnarray}$$

are constants. The form of the slip velocity (2.5) together with (2.6) was first derived by Derjaguin et al. (Reference Derjaguin, Sidorenkov, Zubashchenkov and Kiseleva1947) for flat-plane geometry and was shown to be true at leading order in $L/a$ for a spherical particle by Anderson et al. (Reference Anderson, Lowell and Prieve1982), where $L$ is defined as the range of the solute–particle interaction. We note that the typical $L$ for many intermolecular potentials $\unicode[STIX]{x1D719}$ also depends on the local solute concentration $c$ . For example, $L$ for electrostatic interactions is just the Debye length, i.e.

(2.7) $$\begin{eqnarray}L=\unicode[STIX]{x1D706}_{D}\propto c^{-1/2},\end{eqnarray}$$

as given in (2.1). As a result, the prefactor $b$ in (2.5) is not a constant but a function of $c$ . An appropriate form of the slip velocity for diffusiophoresis in electrolyte solutions, by taking the variation of $L$ along the particle surface into account, is (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984; Anderson Reference Anderson1989)

(2.8) $$\begin{eqnarray}\boldsymbol{v}_{s}(\boldsymbol{x})=\unicode[STIX]{x1D712}\unicode[STIX]{x1D735}_{s}\ln c,\end{eqnarray}$$

in which

(2.9) $$\begin{eqnarray}\unicode[STIX]{x1D712}=-\frac{\unicode[STIX]{x1D716}(k_{B}T)^{2}}{2\unicode[STIX]{x1D707}(ze)^{2}}\left[-2\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D701}+\frac{4k_{B}T}{ze}\ln (1-\unicode[STIX]{x1D6FE}^{2})\right]\end{eqnarray}$$

is constant. Here, $\unicode[STIX]{x1D712}$ is referred to as the particle mobility.

It has been found experimentally that the autophoretic speeds of Pt/insulator (Ebbens et al. Reference Ebbens, Gregory, Dunderdale, Howse, Ibrahim, Liverpool and Golestanian2014) and Pt/Au (Paxton et al. Reference Paxton, Baker, Kline, Wang, Mallouk and Sen2006; Moran & Posner Reference Moran and Posner2014) Janus particles can be significantly decreased by adding a small amount of salt, which can be mainly explained by the combination of two mechanisms. The first is that the addition of salt changes the surface chemical reactions (Ebbens et al. Reference Ebbens, Gregory, Dunderdale, Howse, Ibrahim, Liverpool and Golestanian2014) and the second is that the autophoretic speed is proportional to the inverse of the conductivity $S$ of the bulk solution (Paxton et al. Reference Paxton, Baker, Kline, Wang, Mallouk and Sen2006; Moran & Posner Reference Moran and Posner2014). Since $S^{-1}\propto \unicode[STIX]{x1D706}_{D}^{2}$ with $\unicode[STIX]{x1D706}_{D}$ the Debye length, the autophoretic speed should be proportional to $\unicode[STIX]{x1D706}_{D}^{2}$ , which agrees with the slip velocity expressions (2.3), (2.8) and (2.9).

Within the diffuse layer, there are mainly five types of interactions driving the flow: solute/solute, solute/solvent, solute/colloid, solvent/solvent and solvent/colloid interactions. In electrolyte diffusiophoresis, only the electrostatic interactions associated with solute/solute and solute/colloid interactions are considered (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984), which results in the diffuse layer thickness $L\sim c^{-1/2}$ . However, in classical non-electrolyte diffusiophoresis, only solute/colloid and solvent/colloid interactions are considered and the solute/solute interaction is neglected by assuming dilute solutions, which makes $L$ independent of $c$ (Sharifi-Mood et al. Reference Sharifi-Mood, Koplik and Maldarelli2013). In the general case, $L$ will depend on the solute concentration, solvent and colloid properties and therefore also on the relative strengths of the different interactions, although we note that the dependence of $L$ on $c$ may be a higher-order effect for non-electrolyte diffusiophoresis.

We note that both (2.2) and (2.3) are derived by assuming local equilibrium within the diffuse layer, i.e. there is no desorption or adsorption flux. However, it has been shown that the effect of a non-zero diffusive flux within the diffuse layer on the slip velocity is only $O(L/a)$ for $L/a\ll 1$ for both ionic autophoresis (Rubinstein & Zaltzman Reference Rubinstein and Zaltzman2001; Zaltzman & Rubinstein Reference Zaltzman and Rubinstein2007) and non-ionic autophoresis (Sabass & Seifert Reference Sabass and Seifert2012; Sharifi-Mood et al. Reference Sharifi-Mood, Koplik and Maldarelli2013; Michelin & Lauga Reference Michelin and Lauga2014; Shklyaev et al. Reference Shklyaev, Brady and Córdova-Figueroa2014). Therefore, (2.2) and (2.3) are still valid to leading order when $L/a\ll 1$ . We demonstrate this idea, i.e. that the solute flux does not change the leading-order expression of the slip velocity, in appendix A.

3 Reciprocal theorem

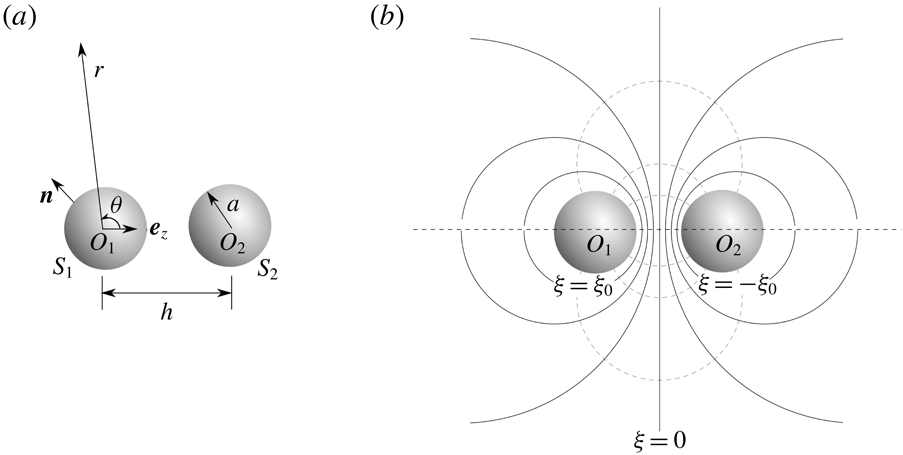
In this section, we assume that the slip velocity distribution (2.8) is known on the surfaces of the particles, which here are assumed to be two spheres of equal radius. Then, we will show that accounting for hydrodynamic interactions, the velocities of the two spheres in a Stokes flow can be computed through the reciprocal theorem.

Consider two spherical particles $O_{1}$ and $O_{2}$ , each with radius $a$ , which are steadily adsorbing ions from or desorbing ions into an unbounded electrolyte solution, as shown in figure 1. The particle surfaces are denoted by $S_{1}$ and $S_{2}$ , respectively. A spherical coordinate system is fixed onto the centre of $O_{1}$ . We want to study the interaction of the two particles due to the asymmetric solute concentration field that is established.

The translation velocities of the two particles are denoted as $\boldsymbol{v}_{p,1}$ and $\boldsymbol{v}_{p,2}$ , respectively. Then, the fluid velocity on the particle surfaces can be written as

(3.1a ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{v}_{1}(\boldsymbol{x})=\boldsymbol{v}_{p,1}+\boldsymbol{v}_{s,1}(\boldsymbol{x}), & \displaystyle\end{eqnarray}$$

(3.1b ) $$\begin{eqnarray}\displaystyle & \displaystyle \text{and}\quad \boldsymbol{v}_{2}(\boldsymbol{x})=\boldsymbol{v}_{p,2}+\boldsymbol{v}_{s,2}(\boldsymbol{x}), & \displaystyle\end{eqnarray}$$

$\boldsymbol{v}_{s,i}$

$i=1,2$

$i$

(3.2) $$\begin{eqnarray}\boldsymbol{v}_{s,i}=\unicode[STIX]{x1D712}_{i}\unicode[STIX]{x1D735}_{s}\ln c,\end{eqnarray}$$

where $\unicode[STIX]{x1D712}_{i}$ is constant when the surface charge (or the zeta potential) is uniform on the particles, and $c$ is the concentration field, which can vary along the surface. The final goal is to calculate $\boldsymbol{v}_{p,i}$ for a concentration field determined by the two particles.

The typical diffusiophoretic speed of colloids $(a\approx 1~\unicode[STIX]{x03BC}\text{m})$ in an aqueous solution is of the order of $1~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ (Palacci et al. Reference Palacci, Abécassis, Cottin-Bizonne, Ybert and Bocquet2010; Shin et al. Reference Shin, Um, Sabass, Ault, Rahimi, Warren and Stone2016). Therefore, the particle-scale Reynolds number $Re=O(10^{-6})$ and the flow field is governed by the Stokes equations, assuming incompressible flow, i.e.

(3.3a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748}=\mathbf{0}, & \displaystyle\end{eqnarray}$$

(3.3b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D748}$

$\boldsymbol{v}$

(3.4) $$\begin{eqnarray}\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\boldsymbol{v}\,\text{d}S=\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\,\text{d}S,\end{eqnarray}$$

where $\boldsymbol{v}^{\prime }$ and $\unicode[STIX]{x1D748}^{\prime }$ , respectively, are the velocity and stress fields for a model problem with different boundary conditions on the boundary surfaces $S$ , including the surfaces $S_{i}$ of particle $i=1,2$ . The domain of integration for (3.4) is $S=S_{1}+S_{2}+S_{\infty }$ , where $S_{\infty }$ is a surface at infinity enclosing both particles and the normal vector $\boldsymbol{n}$ points away from the particle into the fluid, as shown in figure 1(a).

In the sections below, we choose our model problem as two uncharged particles translating either towards each other or at the same velocity. In either case, $\boldsymbol{v}^{\prime }$ is constant and can be taken out of the integral in (3.4), and the integral $\int \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\,\text{d}S$ is the hydrodynamic force on the particles and their electric double layers, which is zero (Prieve et al. Reference Prieve, Anderson, Ebel and Lowell1984). Therefore, we have (Stone & Samuel Reference Stone and Samuel1996)

(3.5) $$\begin{eqnarray}\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\boldsymbol{v}\,\text{d}S=\int _{S}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }\,\text{d}S=\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\int \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\,\text{d}S=0.\end{eqnarray}$$

Substituting (3.2) and (3.1) into (3.5), we have

(3.6) $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \boldsymbol{v}_{p,1}\boldsymbol{\cdot }\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\,\text{d}S+\boldsymbol{v}_{p,2}\boldsymbol{\cdot }\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\,\text{d}S+\unicode[STIX]{x1D712}_{1}\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D712}_{2}\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S.\end{eqnarray}$$

In deriving (3.6), we use the fact that the surface integral at infinity is zero because the integrand decays sufficiently fast to a fluid at rest. Now we consider two special cases: (i) $\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{2}$ and (ii) $\unicode[STIX]{x1D712}_{1}=-\unicode[STIX]{x1D712}_{2}$ . Then, for arbitrary mobilities $\unicode[STIX]{x1D712}_{1}$ and $\unicode[STIX]{x1D712}_{2}$ , the velocity of each particle $\boldsymbol{v}_{p,i}$ is a linear combination of these two special cases.

Figure 1. Model set-up. (a) Two spheres $O_{1}$ and $O_{2}$ each with radius $a$ are suspended in an infinite fluid field with an initial separation distance between the centres $h$ . Their surfaces are labelled by $S_{1}$ and $S_{2}$ , respectively, with the unit normal denoted by $\boldsymbol{n}$ . A spherical coordinate system is fixed at $O_{1}$ and $\boldsymbol{e}_{z}$ is a unit vector directed from $O_{1}$ to  $O_{2}$ . (b) The bi-spherical coordinate system represented by (6.1). The solid (dashed) lines indicate the surfaces of constant $\unicode[STIX]{x1D709}$ ( $\unicode[STIX]{x1D702}$ ) and $\unicode[STIX]{x1D709}=\pm \unicode[STIX]{x1D709}_{0}$ represents the surfaces $S_{1}$ and $S_{2}$ , respectively.

3.1 Case (i): $\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{2}$

We choose a low-Reynolds-number model problem (i) as two uncharged particles translating towards each other at velocity $\boldsymbol{v}_{a}^{\prime }$ . This problem is identical to a single sphere translating towards a symmetry plane and has a well-known solution (Brenner Reference Brenner1961). Also, due to symmetry of the concentration field for the two particles adsorbing/desorbing ionic solute, we have $\boldsymbol{v}_{p,1}=-\boldsymbol{v}_{p,2}$ and

(3.7a ) $$\begin{eqnarray}\displaystyle & \displaystyle \int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\,\text{d}S=-\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\,\text{d}S, & \displaystyle\end{eqnarray}$$

(3.7b ) $$\begin{eqnarray}\displaystyle & \displaystyle \int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S=\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D748}_{a}^{\prime }$ is the stress field for model problem (i). By defining the hydrodynamic force $\boldsymbol{f}_{H,a}^{\prime }=\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\,\text{d}S$ , with (3.7), equation (3.6) becomes

(3.8) $$\begin{eqnarray}\boldsymbol{v}_{p,1}\boldsymbol{\cdot }\boldsymbol{f}_{H,a}^{\prime }=-\unicode[STIX]{x1D712}_{1}\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S.\end{eqnarray}$$

Because of the symmetry of the two-sphere configuration, $\boldsymbol{v}_{p,1}$ is parallel to $\boldsymbol{f}_{H,a}^{\prime }$ , and we have

(3.9) $$\begin{eqnarray}\boldsymbol{v}_{p,1}=-\boldsymbol{v}_{p,2}=\unicode[STIX]{x1D712}_{1}\boldsymbol{v}_{+}=-\frac{\unicode[STIX]{x1D712}_{1}}{|\boldsymbol{f}_{H,a}^{\prime }|^{2}}\boldsymbol{f}_{H,a}^{\prime }\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{a}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S,\end{eqnarray}$$

which serves to define $\boldsymbol{v}_{+}$ .

3.2 Case (ii): $\unicode[STIX]{x1D712}_{1}=-\unicode[STIX]{x1D712}_{2}$

We choose a model problem (ii) as two uncharged particles translating at the same velocity $\boldsymbol{v}_{b}^{\prime }$ in a Stokes flow, for which the flow field is given by Stimson & Jeffery (Reference Stimson and Jeffery1926). Similarly, due to symmetry, we have $\boldsymbol{v}_{p,1}=\boldsymbol{v}_{p,2}$ and

(3.10a ) $$\begin{eqnarray}\displaystyle & \displaystyle \int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\,\text{d}S=\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\,\text{d}S, & \displaystyle\end{eqnarray}$$

(3.10b ) $$\begin{eqnarray}\displaystyle & \displaystyle \int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S=-\int _{S_{2}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D748}_{b}^{\prime }$ is the stress field for model problem (ii). Similar to the steps in § 3.1, by defining $\boldsymbol{f}_{H,b}^{\prime }=\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\,\text{d}S$ , with (3.10), equation (3.6) then becomes

(3.11) $$\begin{eqnarray}\boldsymbol{v}_{p,1}\boldsymbol{\cdot }\boldsymbol{f}_{H,b}^{\prime }=-\unicode[STIX]{x1D712}_{1}\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S,\end{eqnarray}$$

i.e.

(3.12) $$\begin{eqnarray}\boldsymbol{v}_{p,1}=\boldsymbol{v}_{p,2}=\unicode[STIX]{x1D712}_{1}\boldsymbol{v}_{-}=-\frac{\unicode[STIX]{x1D712}_{1}}{|\boldsymbol{f}_{H,b}^{\prime }|^{2}}\boldsymbol{f}_{H,b}^{\prime }\int _{S_{1}}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}_{b}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\ln c\,\text{d}S,\end{eqnarray}$$

which defines $\boldsymbol{v}_{-}$ .

3.3 Arbitrary $\unicode[STIX]{x1D712}_{1}$ and $\unicode[STIX]{x1D712}_{2}$

For arbitrary constant values of $\unicode[STIX]{x1D712}_{1}$ and $\unicode[STIX]{x1D712}_{2}$ , we use the decomposition

(3.13a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D712}_{1}=\frac{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}{2}+\frac{\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}}{2}, & \displaystyle\end{eqnarray}$$

(3.13b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D712}_{2}=\frac{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}{2}-\frac{\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}}{2}, & \displaystyle\end{eqnarray}$$

together with (3.9) and (3.12). Thus, we have

(3.14a ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{v}_{p,1}=\frac{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}{2}\boldsymbol{v}_{+}+\frac{\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}}{2}\boldsymbol{v}_{-}, & \displaystyle\end{eqnarray}$$

(3.14b ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{v}_{p,2}=-\frac{\unicode[STIX]{x1D712}_{1}+\unicode[STIX]{x1D712}_{2}}{2}\boldsymbol{v}_{+}+\frac{\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}}{2}\boldsymbol{v}_{-}, & \displaystyle\end{eqnarray}$$

where $\boldsymbol{v}_{+}$ and $\boldsymbol{v}_{-}$ are determined by $\unicode[STIX]{x1D735}_{s}\ln c$ and the geometry, i.e.  $\unicode[STIX]{x1D748}_{a}^{\prime }$ and $\unicode[STIX]{x1D748}_{b}^{\prime }$ . Now, for a spherical particle in an axisymmetric configuration it suffices to determine the concentration field $c(r,\unicode[STIX]{x1D703},t)$ after which $\boldsymbol{v}_{-}$ and $\boldsymbol{v}_{+}$ follow, respectively, from (3.9) and (3.12). Note that the linear superposition in (3.14) is only valid when the governing equations and corresponding boundary conditions for both the velocity and concentration fields are linear. The Stokes equations are linear for the velocity field, and conditions for the linearity of the equations governing the concentration field will be discussed with (4.1) and (4.2) in the next section.

4 Concentration field: governing equations and boundary conditions

The typical diffusiophoretic velocity is $u\approx 1~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ (Palacci et al. Reference Palacci, Abécassis, Cottin-Bizonne, Ybert and Bocquet2010; Shin et al. Reference Shin, Um, Sabass, Ault, Rahimi, Warren and Stone2016) and the typical diffusivity for ions is $D\approx 10^{-9}~\text{m}^{2}~\text{s}^{-1}$ (Bird, Stewart & Lightfoot Reference Bird, Stewart and Lightfoot1960). For particles with radius $a\approx 1~\unicode[STIX]{x03BC}\text{m}$ , the Péclet number $Pe=au/D\approx 10^{-3}\ll 1$ . Thus, we can neglect the advection of ions when considering the transport of solute. Assuming that $c$ adjusts quasi-statically to changes in geometry, the governing equation and boundary conditions for the concentration field are

(4.1) $$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}c=0.\end{eqnarray}$$

Since the emphasis of this paper is on the effects of a slip velocity, we assume the sorption kinetics satisfies the zero-order model, i.e. the sorption flux $j$ is constant. We note that it is straightforward to generalize the uniform-flux model by considering any axisymmetric flux profile over the particle surface, which can be achieved by decomposing the flux distribution into a series of Legendre polynomials (Tătulea-Codrean & Lauga Reference Tătulea-Codrean and Lauga2018). It can be shown that at the outer boundary of the diffuse layer, the diffusive flux satisfies (Yariv Reference Yariv2011; Michelin & Lauga Reference Michelin and Lauga2014)

(4.2) $$\begin{eqnarray}-D\frac{\unicode[STIX]{x2202}c}{\unicode[STIX]{x2202}r}=j\quad \text{at }S_{1}\text{ and }S_{2},\end{eqnarray}$$

where the diffusion coefficient in (4.2) is

(4.3) $$\begin{eqnarray}D=\frac{2D_{+}D_{-}}{D_{+}+D_{-}}.\end{eqnarray}$$

Recall that $D_{+}$ and $D_{-}$ are the diffusivity of cations and anions, respectively. Equation (4.2) serves as the boundary condition for the concentration field at the particle surface in the limit $L\ll a$ . We note that $j$ can be either positive or negative, corresponding to desorption or adsorption of solute, respectively. The boundary condition (4.2) can also be used for surface chemical reactions (e.g. catalysts) satisfying Michaelis–Menten kinetics when the reactant concentration is large (Michaelis & Menten Reference Michaelis and Menten1913; Johnson & Goody Reference Johnson and Goody2011), or any kinetics satisfying a zero-order model (Dash et al. Reference Dash, Murth, Nath and Chowdhury2010). It is convenient to define an unperturbed concentration of ions $c_{\infty }$ and an excess concentration $c_{e}=c-c_{\infty }$ , which is positive for desorption and negative for adsorption of solutes. Then (4.2) becomes

(4.4) $$\begin{eqnarray}D\frac{\unicode[STIX]{x2202}c_{e}}{\unicode[STIX]{x2202}r}=-j.\end{eqnarray}$$

Based on (4.4), we define $\unicode[STIX]{x0394}c=ja/D$ as the typical scale for $c_{e}$ . In electrolyte solutions, using (2.6), $\boldsymbol{v}_{s}\propto \unicode[STIX]{x1D735}_{s}c$ , instead of (2.8), $\boldsymbol{v}_{s}\propto \unicode[STIX]{x1D735}_{s}\ln c$ , leads to errors of order $\unicode[STIX]{x0394}c/c_{\infty }$ . As a result, we will show the asymmetric effects of adsorption and desorption and the saturation of the autophoretic velocity for large adsorption fluxes ( $j$ ). In the following analysis, we first calculate the autophoresis of two adsorbing/desorbing particles asymptotically when they are far apart ( $h\gg a$ ), then for arbitrary distances $h>2a$ in bi-spherical coordinates.

It is straightforward to non-dimensionalize the excess concentration field by $ja/D$ . The typical length scale is $a$ and, from (2.8), the typical velocity is $\unicode[STIX]{x1D712}_{1}/a$ . Then we can non-dimensionalize forces by $\unicode[STIX]{x1D707}\unicode[STIX]{x1D712}_{1}$ and stresses by $\unicode[STIX]{x1D707}\unicode[STIX]{x1D712}_{1}/a^{2}$ . We introduce dimensionless variables

(4.5) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle C=\frac{c}{c_{\infty }},\quad C_{e}=\frac{Dc_{e}}{ja},\quad R=\frac{r}{a},\quad H=\frac{h}{a},\\ \displaystyle J=\frac{\unicode[STIX]{x0394}c}{c_{\infty }}=\frac{ja}{c_{\infty }D},\quad \boldsymbol{U}=\frac{a\boldsymbol{u}}{\unicode[STIX]{x1D712}_{1}},\quad \boldsymbol{F}=\frac{\boldsymbol{f}}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D712}_{1}},\quad \unicode[STIX]{x1D72E}=\frac{a^{2}\unicode[STIX]{x1D748}}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D712}_{1}}.\end{array}\right\}\end{eqnarray}$$

We note that the background concentration $c_{\infty }$ and the excess concentration $c_{e}$ are scaled differently in (4.5), by a factor of $J$ ; therefore, the dimensionless concentration field can be written as

(4.6) $$\begin{eqnarray}C=1+JC_{e}.\end{eqnarray}$$

The corresponding non-dimensional equation for the concentration distribution is

(4.7) $$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}C_{e}=0\end{eqnarray}$$

with boundary conditions

(4.8a ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}C_{e}}{\unicode[STIX]{x2202}n}=-1\quad \text{at }S_{1}\text{ and }S_{2}, & \displaystyle\end{eqnarray}$$

(4.8b ) $$\begin{eqnarray}\displaystyle & \displaystyle C_{e}=0\quad \text{as }R\rightarrow \infty . & \displaystyle\end{eqnarray}$$

5 Asymptotic analysis: $H\gg 1$

In this section, we calculate the autophoretic particle velocity for the asymptotic case of large separation distance, i.e. when $H=h/a\gg 1$ , and use the method of reflections to solve for the concentration field. The presence of the second particle breaks the symmetry and induces translation of the particles. We use a spherical coordinate system centred on sphere $O_{1}$ , as shown in figure 1(a). In the absence of sphere $O_{2}$ , the excess concentration field, which satisfies (4.7) to (4.8b ), is

(5.1) $$\begin{eqnarray}C_{e1}^{(0)}(\boldsymbol{R})=\frac{1}{R},\end{eqnarray}$$

where $\boldsymbol{R}$ is the dimensionless position vector and the superscript ‘ $(n)$ ’ indicates the solution under the $n$ th reflection. Similarly, the excess concentration induced by sphere $O_{2}$ in the absence of $O_{1}$ is

(5.2) $$\begin{eqnarray}C_{e2}^{(0)}=\frac{1}{|\boldsymbol{R}-H\boldsymbol{e}_{z}|}=\frac{1}{H}+\frac{\boldsymbol{e}_{z}\boldsymbol{\cdot }\boldsymbol{R}}{H^{2}}+O(H^{-3}),\end{eqnarray}$$

where $\boldsymbol{e}_{z}$ is the unit vector pointing from $O_{1}$ to $O_{2}$ , as shown in figure 1(a), and we assume $H\gg 1$ . The reflection of the field $C_{e2}$ due to the presence of $O_{1}$ , denoted by $C_{e2}^{(1)}$ , is

(5.3) $$\begin{eqnarray}C_{e2}^{(1)}=\frac{\boldsymbol{e}_{z}\boldsymbol{\cdot }\boldsymbol{R}}{2H^{2}R^{3}}+O(H^{-3}).\end{eqnarray}$$

Thus, the dimensionless concentration field in the vicinity of the sphere $O_{1}$ (i.e.  $R=O(1)$ ) is

(5.4) $$\begin{eqnarray}C(\boldsymbol{R})=1+JC_{e}=1+J\left(\frac{1}{R}+\frac{1}{H}\right)+\frac{J}{H^{2}}\left(1+\frac{1}{2R^{3}}\right)\boldsymbol{e}_{z}\boldsymbol{\cdot }\boldsymbol{R}+O(H^{-3}).\end{eqnarray}$$

Note that the scalings of $C_{e}$ and $C$ are different by a factor of $J$ in (4.5). By symmetry, the surface integral of the slip velocity on sphere $O_{1}$ is

(5.5) $$\begin{eqnarray}\int _{S_{1}}\unicode[STIX]{x1D735}_{s}\ln C\,\text{d}S=\frac{4\unicode[STIX]{x03C0}J}{(1+J)H^{2}}\boldsymbol{e}_{z}+O(H^{-3}).\end{eqnarray}$$

At leading order for $H\gg 1$ , the stress distributions on the particle surfaces of both model problems (i) and (ii) are the same as that of a single sphere translating through an unbounded fluid under a (dimensionless) hydrodynamic force $\boldsymbol{F}^{\prime }$ . A well-known result for this problem is (Leal Reference Leal2007)

(5.6) $$\begin{eqnarray}4\unicode[STIX]{x03C0}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D72E}^{\prime }=\boldsymbol{F}^{\prime },\end{eqnarray}$$

where $\unicode[STIX]{x1D72E}^{\prime }$ is the constant surface stress vector on the sphere surface. Therefore, based on the reciprocal theorem (3.8) and (5.5), the velocity of particle 1 is

(5.7) $$\begin{eqnarray}\boldsymbol{U}_{p,1}=-\frac{J}{(1+J)H^{2}}\boldsymbol{e}_{z},\end{eqnarray}$$

where we only keep the leading-order $O(H^{-2})$ terms. We notice that a similar asymptotic analysis for non-electrolyte autophoresis was given by Yariv (Reference Yariv2016), who adopted the formula of slip velocity (2.5) to obtain

(5.8) $$\begin{eqnarray}\boldsymbol{U}_{p,1}^{ne}=-\frac{J}{H^{2}}\boldsymbol{e}_{z}.\end{eqnarray}$$

This result can be obtained from (5.7) in the limit $|J|\ll 1$ . A comparison of these two velocities is plotted in figure 2.

Figure 2. Asymptotic results based on (5.7) and (5.8) for the autophoretic velocity, plotted as $UH^{2}$ , as functions of $J$ . The dashed line $UH^{2}=-1$ is the lower limit of (5.7) and the open circles are theoretical results calculated by numerical integration of (6.10). Here $H=10$ for all the curves plotted.

The non-electrolyte result (5.8) will increase without bound when $J=ja/Dc_{\infty }\rightarrow \infty$ , because (2.5) leads to the largest deviation in this limit, as discussed at the end of § 4. On the other hand, the autophoretic velocities produced by desorption fluxes ( $J>0$ ) in electrolyte solutions are bounded by $H^{-2}$ , as shown in figure 2. For adsorption fluxes $J<0$ , figure 2 shows that the autophoretic velocity will grow superlinearly and diverges as $J\rightarrow -1$ , because the concentration field at the particle surfaces $C\rightarrow 0$ as $J\rightarrow -1$ , which results in a large slip velocity $\unicode[STIX]{x1D735}\ln C\rightarrow \infty$ . As shown in figure 2, our theoretical results from numerical integration of (6.10) in § 6 are in good agreement with the asymptotic results except for near $J\rightarrow -1$ where the autophoretic velocity diverges and higher-order corrections in (5.5) are no longer negligible. Since our analysis is based on the assumption of a thin Debye layer, our results are valid for $\unicode[STIX]{x1D706}_{D}/a\ll 1$ . When the two particles are far apart ( $H\gg 1$ ), with (2.1), (4.5) and (5.4), the thin-Debye-layer criterion with sorption fluxes becomes

(5.9) $$\begin{eqnarray}\left(\frac{\unicode[STIX]{x1D706}_{D\infty }}{a}\right)^{2}\ll 1+J,\end{eqnarray}$$

where

(5.10) $$\begin{eqnarray}\unicode[STIX]{x1D706}_{D\infty }=\sqrt{\frac{\unicode[STIX]{x1D716}k_{B}T}{2z^{2}e^{2}c_{\infty }}}\end{eqnarray}$$

is the unperturbed Debye length. Therefore, $J>-1$ must be satisfied for adsorption fluxes because the solute concentration cannot be negative near the particles. For a typical system with $\unicode[STIX]{x1D706}_{D\infty }=10$  nm and $a=1~\unicode[STIX]{x03BC}\text{m}$ , the thin-Debye-layer criterion (5.10) requires that $1+J\gg 10^{-8}$ , which means that the thin-Debye-layer assumption can still hold as $J\rightarrow -1$ when the particles are far apart. The analysis in appendix A gives an upper limit of $J$ in (A 6). For the same system ( $\unicode[STIX]{x1D706}_{D\infty }=10~\text{nm}$ and $a=1~\unicode[STIX]{x03BC}\text{m}$ ), (A 6) requires that $J\ll 10^{4}$ . Typical values of desorption flux $j$ measured in experiments are around $7\times 10^{-6}-4\times 10^{-2}~\text{mol}~(\text{m}^{2}~\text{s})^{-1}$ (Paxton et al. Reference Paxton, Sen and Mallouk2005; Howse et al. Reference Howse, Jones, Ryan, Gough, Vafabakhsh and Golestanian2007; Sen et al. Reference Sen, Ibele, Hong and Velegol2009; Wang et al. Reference Wang, Chiang, Velegol and Mallouk2013; Brown & Poon Reference Brown and Poon2014), for particles with radius $a=1~\unicode[STIX]{x03BC}\text{m}$ in an electrolyte solution with background concentration $c_{\infty }=0.1~\text{mM}$ and diffusion coefficient $D=1\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$ . The concomitant range of $J$ is between $7\times 10^{-2}$ and $4\times 10^{2}$ , where the theory for non-ionic solvents severely over- or under-predicts the phoretic motion (e.g. see figure 2), whereas our theory should be applicable to many experiments with large $J$ .

We note that when the flux $J$ is large, steric effects may be significant due to a high solute concentration (Kilic et al. Reference Kilic, Bazant and Ajdari2007). For non-desorbing particles, the ionic steric effects can be characterized by the packing parameter $\unicode[STIX]{x1D708}=2d_{ion}^{3}c_{\infty }$ (Kilic et al. Reference Kilic, Bazant and Ajdari2007; Figliuzzi et al. Reference Figliuzzi, Chan, Moran and Buie2014), with $d_{ion}$ the ionic diameter and $c_{\infty }$ the bulk solution concentration far away from the particle. For particles with a desorption flux $j$ , we replace $c_{\infty }$ with $c_{\infty }+ja/D$ to estimate the effects of the flux on the background concentration, so the packing parameter for desorbing particles can be written as $\unicode[STIX]{x1D708}^{\prime }=2d_{ion}^{3}c_{\infty }(1+J)$ . Steric effects can be neglected when $\unicode[STIX]{x1D708}^{\prime }\ll 1$ . The typical value of $d_{ion}$ for potassium, sodium and chloride ions is ${\approx}$ 1 Å (Mancinelli et al. Reference Mancinelli, Botti, Bruni, Ricci and Soper2007). For a typical background concentration $c_{\infty }=0.1~\text{M}$ , we have $d_{ion}^{3}c_{\infty }\approx 6\times 10^{-5}$ . Therefore, steric effects can be neglected when $J\ll 10^{4}$ . We remark that this limit is greater than those typically realized in experiments, as discussed above.

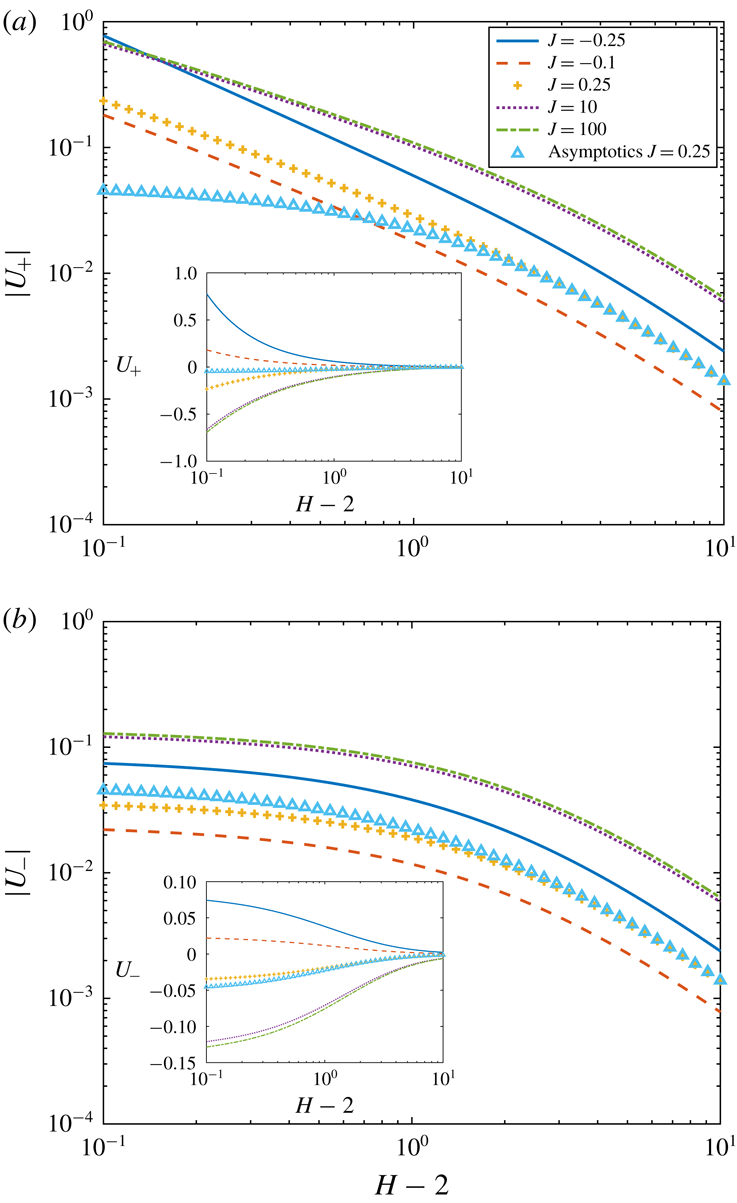
Moreover, the expression (5.8) predicts that the effects of adsorption and desorption fluxes $J$ are symmetric to the autophoresis, with only a difference of sign. However, this is not true for an electrolyte solution when $\boldsymbol{v}_{s}\propto \unicode[STIX]{x1D735}_{s}\ln c$ and the resultant autophoretic velocity (5.7) shows that an adsorption flux $J<0$ is more effective in creating stronger autophoresis because it decreases the mean concentration around the particles. We note that the results of Yariv (Reference Yariv2016) are recovered as a limit of our theory for $|J|\ll 1$ . The asymmetric contributions of desorption and adsorption fluxes will also be illustrated in figure 3 in the next section, where we provide an analysis for an arbitrary separation distance $H$ .

Figure 3. Dependence of (a) $|U_{+}|$ and (b) $|U_{-}|$ on $H-2$ for different sorption flux $J$ . Insets show values of (a) $U_{+}$ and (b) $U_{-}$ . The asymptotic result for $J=0.25$ is determined according to (5.7) and the other curves are theoretical results obtained by numerical calculation of (6.10).

6 General case: an arbitrary distance $H$

Laplace’s equation (4.7) in an unbounded fluid with two identical spherical boundaries can be solved in a bi-spherical coordinate system (Jeffery Reference Jeffery1912) and is well known. By defining $\unicode[STIX]{x1D709}_{0}=\text{arccosh}(H/2)$ , which establishes the separation distance, the transformation from the cylindrical coordinate system ( $R$ , $Z$ , $\unicode[STIX]{x1D719}$ ) to the bi-spherical coordinate system ( $\unicode[STIX]{x1D709}$ , $\unicode[STIX]{x1D702}$ , $\unicode[STIX]{x1D719}$ ) is given by

(6.1a,b ) $$\begin{eqnarray}R=\frac{\sinh \unicode[STIX]{x1D709}_{0}\sin \unicode[STIX]{x1D702}}{\cosh \unicode[STIX]{x1D709}-\cos \unicode[STIX]{x1D702}},\quad Z=\frac{\sinh \unicode[STIX]{x1D709}_{0}\sinh \unicode[STIX]{x1D709}}{\cosh \unicode[STIX]{x1D709}-\cos \unicode[STIX]{x1D702}}.\end{eqnarray}$$

The particle surfaces $S_{1}$ and $S_{2}$ can be described by $\unicode[STIX]{x1D709}=\pm \unicode[STIX]{x1D709}_{0}$ in this coordinate system, as shown in figure 1(b). By further changing variable $\unicode[STIX]{x1D70F}=\cos \unicode[STIX]{x1D702}$ , the solution to the Laplace equation (4.7) in bi-spherical coordinates is (Jeffery Reference Jeffery1912; Michelin & Lauga Reference Michelin and Lauga2015)

(6.2) $$\begin{eqnarray}C_{e}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})=(\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})^{1/2}\mathop{\sum }_{n=0}^{\infty }f_{n}(\unicode[STIX]{x1D709})P_{n}(\unicode[STIX]{x1D70F}),\end{eqnarray}$$

where $P_{n}$ is the Legendre polynomial of degree $n$ and

(6.3) $$\begin{eqnarray}f_{n}(\unicode[STIX]{x1D709})=2\unicode[STIX]{x1D6FE}_{n}\text{e}^{-(n+1/2)\unicode[STIX]{x1D709}_{0}}\cosh (n+{\textstyle \frac{1}{2}})\unicode[STIX]{x1D709},\end{eqnarray}$$

in which $\unicode[STIX]{x1D6FE}_{n}$ are constant. The coefficients $\unicode[STIX]{x1D6FE}_{n}$ can be further determined by the boundary conditions (4.8a )

(6.4) $$\begin{eqnarray}\frac{(\cosh \unicode[STIX]{x1D709}-\unicode[STIX]{x1D70F})}{\sinh \unicode[STIX]{x1D709}_{0}}\frac{\unicode[STIX]{x2202}C_{e}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=1\quad \text{at }\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0}.\end{eqnarray}$$

Due to symmetry, using the flux boundary condition on $S_{1}$ is sufficient to determine the concentration field. Equation (6.4) can be written explicitly as

(6.5) $$\begin{eqnarray}\frac{\sinh \unicode[STIX]{x1D709}_{0}}{2\sinh \unicode[STIX]{x1D709}_{0}}C_{e}+\frac{(\cosh \unicode[STIX]{x1D709}_{0}-\unicode[STIX]{x1D70F})^{3/2}}{\sinh \unicode[STIX]{x1D709}_{0}}\mathop{\sum }_{n=0}^{\infty }\frac{\text{d}f_{n}}{\text{d}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{0})P_{n}(\unicode[STIX]{x1D70F})=1,\end{eqnarray}$$

which after substituting for $C_{e}$ with (6.2) yields

(6.6) $$\begin{eqnarray}\mathop{\sum }_{n=0}^{\infty }\left[\frac{\sinh \unicode[STIX]{x1D709}_{0}}{2\sinh \unicode[STIX]{x1D709}_{0}}f_{n}(\unicode[STIX]{x1D709}_{0})+\frac{\cosh \unicode[STIX]{x1D709}_{0}-\unicode[STIX]{x1D70F}}{\sinh \unicode[STIX]{x1D709}_{0}}\,\frac{\text{d}f_{n}}{\text{d}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{0})\right]P_{n}(\unicode[STIX]{x1D70F})=(\cosh \unicode[STIX]{x1D709}_{0}-\unicode[STIX]{x1D70F})^{-1/2}.\end{eqnarray}$$

Using the properties of Legendre polynomials listed in appendix B, we have

(6.7) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}f_{n}(\unicode[STIX]{x1D709}_{0})+\frac{\text{d}f_{n}}{\text{d}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{0})\coth \unicode[STIX]{x1D709}_{0}-\frac{1}{\sinh \unicode[STIX]{x1D709}_{0}}\left[\frac{n+1}{2n+3}\,\frac{\text{d}f_{n+1}}{\text{d}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{0})+\frac{n}{2n-1}\,\frac{\text{d}f_{n-1}}{\text{d}\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D709}_{0})\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\sqrt{2}\text{e}^{-(n+1/2)\unicode[STIX]{x1D709}_{0}}.\end{eqnarray}$$

Substituting (6.3) into (6.7), we obtain a recursion relation for the coefficients $\unicode[STIX]{x1D6FE}_{n}$ :

(6.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{n+1} & = & \displaystyle \frac{\text{e}^{\unicode[STIX]{x1D709}_{0}}}{(n+1)\sinh (n+\frac{3}{2})\unicode[STIX]{x1D709}_{0}}\left\{\left[\sinh \unicode[STIX]{x1D709}_{0}\cosh \left(n+\frac{1}{2}\right)\unicode[STIX]{x1D709}_{0}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(2n+1)\cosh \unicode[STIX]{x1D709}_{0}\sinh \left(n+\frac{1}{2}\right)\unicode[STIX]{x1D709}_{0}\right]\unicode[STIX]{x1D6FE}_{n}\nonumber\\ \displaystyle & & \displaystyle -\left.n\text{e}^{\unicode[STIX]{x1D709}_{0}}\unicode[STIX]{x1D6FE}_{n-1}\sinh \left(n-\frac{1}{2}\right)\unicode[STIX]{x1D709}_{0}-\sqrt{2}\sinh \unicode[STIX]{x1D709}_{0}\right\}.\end{eqnarray}$$

We solve the linear system (6.8) numerically for the coefficients $\unicode[STIX]{x1D6FE}_{n}$ .

For both model problems (i) and (ii), the normal stress can be written as (Rallabandi, Hilgenfeldt & Stone Reference Rallabandi, Hilgenfeldt and Stone2017)

(6.9) $$\begin{eqnarray}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D72E}=-P^{\prime }\boldsymbol{n}+\unicode[STIX]{x1D6FA}^{\prime }\boldsymbol{s},\end{eqnarray}$$

where $\boldsymbol{s}$ is the unit tangent vector on the sphere, $P^{\prime }$ is the pressure and $\unicode[STIX]{x1D6FA}^{\prime }$ is the vorticity. Based on (3.9) and (3.12), by defining the mobility ratio $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D712}_{2}/\unicode[STIX]{x1D712}_{1}$ , we find that the velocities of particle 1 for the cases $\unicode[STIX]{x1D6FC}=\pm 1$ are

(6.10a ) $$\begin{eqnarray}\displaystyle & \displaystyle U_{+}=-2\unicode[STIX]{x03C0}F_{H,a}^{-1}\int _{-1}^{1}R(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6FA}_{a}^{\prime }(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})\frac{J}{1+JC_{e}(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})}\frac{\unicode[STIX]{x2202}C_{e}(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F}, & \displaystyle\end{eqnarray}$$

(6.10b ) $$\begin{eqnarray}\displaystyle & \displaystyle U_{-}=-2\unicode[STIX]{x03C0}F_{H,b}^{-1}\int _{-1}^{1}R(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6FA}_{b}^{\prime }(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})\frac{J}{1+JC_{e}(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})}\frac{\unicode[STIX]{x2202}C_{e}(\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D70F})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F}, & \displaystyle\end{eqnarray}$$

$F_{H}$

$a$

$b$

$F_{H,a}$

$F_{H,b}$

$\unicode[STIX]{x1D6FA}_{a}^{\prime }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$

$\unicode[STIX]{x1D6FA}_{b}^{\prime }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F})$

$\unicode[STIX]{x1D6FC}$

(6.11a ) $$\begin{eqnarray}\displaystyle & \displaystyle U_{p,1}=\frac{(1+\unicode[STIX]{x1D6FC})}{2}U_{+}+\frac{(1-\unicode[STIX]{x1D6FC})}{2}U_{-}, & \displaystyle\end{eqnarray}$$

(6.11b ) $$\begin{eqnarray}\displaystyle & \displaystyle U_{p,2}=-\frac{(1+\unicode[STIX]{x1D6FC})}{2}U_{+}+\frac{(1-\unicode[STIX]{x1D6FC})}{2}U_{-}, & \displaystyle\end{eqnarray}$$

We compute the integrals in (6.10) numerically using (6.2), (6.3) and coefficients $\unicode[STIX]{x1D6FE}_{n}$ obtained from (6.8). The dependence of solute fluxes $J$ on the autophoretic speeds is shown and compared with the asymptotic solution (5.7) in figure 3. We find that the magnitude of the autophoretic velocity induced by adsorption fluxes, i.e.  $J<0$ , is stronger than that induced by desorption fluxes, since adsorption fluxes result in a smaller concentration field and increase $\unicode[STIX]{x1D735}\ln C$ . In figure 3, as $J$ increases, the autophoretic speeds converge to a finite value as opposed to diverging; since the slip velocity is proportional to $\unicode[STIX]{x1D735}_{s}\ln C$ , increasing $J$ will increase both $\unicode[STIX]{x1D735}C$ and $C$ and consequently the slip velocity will converge to a finite value as $J\rightarrow \infty$ . The boundedness of autophoretic speeds with respect to $J$ is consistent with the asymptotic result (5.7). For the large fluxes in self-propelling systems with ion adsorption or desorption, the phoretic velocity does not depend linearly on the flux. There is a saturation for desoprtion and a superlinear increase of velocity with adsorption flux.

7 Concluding remarks

In this paper, we have shown that the typical thickness $L$ over which the intermolecular potential decays away from the particle surface is generally not constant but depends on the local concentration field along the particle surface. We review different expressions of diffusiophoretic slip velocities in electrolyte and non-electrolyte solutions and find that when the sorption fluxes are large enough to modify the solute concentration, i.e.  $J=ja/c_{\infty }D$ is $O(1)$ or greater, and consequently the interaction layer on particle surfaces, the assumption of a slip velocity $\boldsymbol{v}_{s}\propto \unicode[STIX]{x1D735}_{s}c$ will lead to significant errors. For autophoresis of two particles in an electrolyte solution with $\boldsymbol{v}_{s}\propto \unicode[STIX]{x1D735}_{s}\ln c$ , we show, both asymptotically and analytically, that the phoretic velocities due to adsorption and desorption are asymmetric, in the sense that not only are the directions opposite, but also the trends for increasing adsorption and desorption fluxes are different. For particles desorbing ionic solute, the phoretic velocity saturates with increasing desorption fluxes. On the other hand, the magnitude of the autophoretic velocity for two identical particles that adsorb solutes grows superlinearly with adsorption flux. These conclusions are in contrast with the symmetric results of autophoresis in a non-electrolyte solution reported in Michelin & Lauga (Reference Michelin and Lauga2014) and Yariv (Reference Yariv2016); however, their calculations can be recovered by our analysis for weak fluxes. Our theory can also be applied in dissolution/precipitation and desorption/adsorption processes where the boundary conditions of solute fluxes can be approximated as constant, which lays the foundation of understanding the collective autophoretic behaviour in chemically active and ionic many-particle systems (e.g. Papavassiliou & Alexander Reference Papavassiliou and Alexander2015; Varma, Montenegro-Johnson & Michelin Reference Varma, Montenegro-Johnson and Michelin2018; Rallabandi, Yang & Stone Reference Rallabandi, Yang and Stone2019).