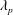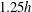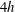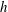1 Introduction
As urbanization continues to advance, our cities are faced with significant challenges related to air quality. These challenges are exacerbated by the complexity of the urban geometry and the dynamic processes that take place within the urban canopy and above within the atmospheric boundary layer. The urban boundary layer contains coherent structures such as large-scale turbulent organized structures of either high or low momentum that form above the roughness in the inertial layer from groups of hairpin vortices (Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000). Within the roughness sublayer, shear layers form along the top of the upstream roughness elements and contain small-scale structures induced by the presence of the roughness (Coceal et al. Reference Coceal, Dobre, Thomas and Belcher2007). These turbulent structures and the intermittent exchanges they produce govern the transport of heat, momentum and pollution in the urban canopy and understanding these turbulent structures and how they interact is crucial to addressing the challenges facing our cities today.
In smooth-wall boundary layers, in addition to the superposition mechanism of the large scales onto the near-wall flow (Townsend Reference Townsend1976), a nonlinear mechanism of amplitude modulation has been recently shown to exist between the large-scale structures in the inertial layer and the small scales close to the wall (Hutchins & Marusic Reference Hutchins and Marusic2007; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009, Reference Mathis, Hutchins and Marusic2011b ; Mathis et al. Reference Mathis, Marusic, Hutchins and Sreenivasan2011c ; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2011; Inoue et al. Reference Inoue, Mathis, Marusic and Pullin2012). As large-scale regions of high (low) momentum pass over the small scales close to the wall the small scales are amplified (suppressed) (Mathis et al. Reference Mathis, Hutchins and Marusic2009). This mechanism was first observed experimentally by Rao, Narasimha & Narayanan (Reference Rao, Narasimha and Narayanan1971) who noted a strong nonlinear coupling between the inner and outer layer in the smooth-wall boundary layer. More recently, amplitude modulation has been shown to increase with increasing Reynolds number as large-scale structures become more intense thereby contributing more to the turbulent interactions (Mathis et al. Reference Mathis, Hutchins and Marusic2009). Furthermore, all three components of velocity have been shown to be modulated by the large scales in a similar manner (Talluru et al. Reference Talluru, Baidya, Hutchins and Marusic2014). The near-wall evolution of the amplitude modulation has been found to show strong similarities with the skewness profile of the streamwise velocity component (Mathis et al. Reference Mathis, Hutchins and Marusic2009). This resemblance was found to be due to one component of the scale-decomposed skewness (see § 4.3 for more details), which proved to be a good diagnostic quantity to study the presence of amplitude modulation (Mathis et al. Reference Mathis, Marusic, Hutchins and Sreenivasan2011c ; Duvvuri & McKeon Reference Duvvuri and McKeon2015). It should be noted that strong correlation between large-scale structures and small-scale amplification or suppression does not imply that the large scales actively modulate the small scales. However, some recent studies, such as Duvvuri & McKeon (Reference Duvvuri and McKeon2015), have found evidence that support this causality.
Amplitude modulation has also been confirmed to exist using direct numerical simulation (DNS) in a d-type two-dimensional (2-D) bar-roughened wall with plan area packing density
$\unicode[STIX]{x1D706}_{p}=12.5\,\%$
(the ratio between the area of the surface occupied by the roughness elements and the total surface area) (Nadeem et al.
Reference Nadeem, Lee, Lee and Sung2015), using large eddy simulation (LES) of a staggered cube array with
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and homogenous roughness (Anderson Reference Anderson2016) and experimentally in a sand-roughened wall (Squire et al.
Reference Squire, Morill-Winter, Hutchins, Schultz, Klewicki and Marusic2016) and rod-roughened wall (Talluru et al.
Reference Talluru, Baidya, Hutchins and Marusic2014). In each of these cases the amplitude modulation was modified compared to the smooth-wall flow configuration, but the nature of the mechanism remained the same. The amplitude modulation was shown to be stronger in rough-wall flows compared to smooth-wall boundary layers, the presence of the roughness causing a wall-normal shift of the peak spectral energy of the near-wall small scales resulting in a modification of the amplitude modulation behaviour in both the near-wall and outer-wall regions (Talluru et al.
Reference Talluru, Baidya, Hutchins and Marusic2014; Anderson Reference Anderson2016). This modification was shown to cause the large-scale structures of the outer layer to interact with both the near-wall small scales and small scales away from the wall (Nadeem et al.
Reference Nadeem, Lee, Lee and Sung2015). When investigating the influence of buoyancy effect using LES Salesky & Anderson (Reference Salesky and Anderson2018) found that an increase in convection resulted in an increase in the angle of inclination of near-surface large-scale structures. This in turn causes a shift in the location of the outer peak of the streamwise velocity spectra until the energy is concentrated in a single peak. Although the modulation is shown to decrease as the large-scale structures change from streamwise to vertically dominated the modulation is still present over all cases studied. Awasthi & Anderson (Reference Awasthi and Anderson2018), who studied amplitude modulation in the flow over roughness with spanwise heterogeneity, found that the outer peak was present in upwelling zones but not present in downwelling zones where structures were steeper and shorter.
Evidence from experiments performed in a boundary layer developing over a rough wall consisting of staggered cubes with
$\unicode[STIX]{x1D706}_{p}=25\,\%$
confirmed the existence of a nonlinear interaction between the most energetic large-scale structures present above the canopy and the small-scale structures induced by the presence of the roughness (Blackman & Perret Reference Blackman and Perret2016). The analysis of the spatio-temporal modulation coefficient confirmed the existence of a mechanism similar to amplitude modulation and demonstrated that the large-scale momentum regions influence the small scales within the roughness sublayer after a time delay, agreeing with the results of Anderson (Reference Anderson2016). Further evidence of amplitude modulation within this staggered cube roughness configuration was found by Basley, Perret & Mathis (Reference Basley, Perret and Mathis2018) through investigation of the characteristics of the amplitude modulation coefficient of the three velocity components and the turbulent kinetic energy in a wall-parallel plane located in the roughness sublayer (i.e. just above the top of the roughness elements). Recently, using triple decomposition of the kinetic energy budget in a boundary layer developing over staggered cubes with
$\unicode[STIX]{x1D706}_{p}=25\,\%$
this nonlinear relationship was linked to an instantaneous exchange of energy between the large-scale momentum regions and the small scales close to the roughness (Blackman, Perret & Calmet Reference Blackman, Perret and Calmet2018). Finally, investigation of this nonlinear relationship has been expanded to the study of street canyon flows using six rough-wall boundary-layer configurations consisting of three upstream roughness geometries (cubes or 2-D bars with different streamwise spacing) and two street canyon aspect ratios (Blackman, Perret & Savory Reference Blackman, Perret and Savory2017). Although a modification of the nonlinear relationship exists close to the top of the roughness elements between 3-D and 2-D roughnesses, the nonlinear mechanism similar to amplitude modulation was confirmed to exist in all of the configurations.
The study of amplitude modulation in the smooth-wall boundary layer has led to the development of a predictive model for the near-wall fluctuations using a large-scale boundary-layer signal (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011a ). The application of this predictive model has been expanded to a rough wall consisting of sand roughness (Squire et al. Reference Squire, Morill-Winter, Hutchins, Schultz, Klewicki and Marusic2016) and has recently been improved using spectral linear stochastic estimation (SLSE) (Baars, Hutchins & Marusic Reference Baars, Hutchins and Marusic2016a ). Compared to the smooth-wall boundary layer, the linear interaction or superposition mechanism in the rough wall was found to be weaker while the amplitude modulation was found to be stronger. This suggests that roughness elements generate small scales that contribute significantly to the amplitude modulation (Squire et al. Reference Squire, Morill-Winter, Hutchins, Schultz, Klewicki and Marusic2016) agreeing with the results of Talluru et al. (Reference Talluru, Baidya, Hutchins and Marusic2014) and Anderson (Reference Anderson2016).
In the context of atmospheric flows developing over the urban canopies, the effect of the roughness configuration used to generate a rough-wall boundary layer on the mean flow characteristics and turbulence statistics has been studied extensively (Macdonald, Griffiths & Hall Reference Macdonald, Griffiths and Hall1998; Cheng & Castro Reference Cheng and Castro2002; Takimoto et al.
Reference Takimoto, Inagaki, Kanda, Sato and Michioka2013; Blackman, Perret & Savory Reference Blackman, Perret and Savory2015). Other work has used two-point statistics and correlations to investigate the characteristics of turbulent events such as sweeps and ejections that occur within the shear layer (Takimoto et al.
Reference Takimoto, Inagaki, Kanda, Sato and Michioka2013). Recently, Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) studied the influence of canopy flow regime and Reynolds number on the characteristics of the scale-decomposed velocity fluctuations using staggered cube arrays with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 %. The roughness configurations were classified using the flow regimes identified by Grimmond & Oke (Reference Grimmond and Oke1999) as isolated wake flow (6.25 %), wake-interference flow (25 %) and skimming flow (44.4 %). Through spectral analysis and scale decomposition dynamical similarities were found between the canopy configurations. The Reynolds number was shown to have a negligible effect on the characteristics of the large-scale fluctuations. However, the skimming flow regime was shown to result in near-canopy large scales that contributed more to the variance suggesting that a stronger correlation exists between the inertial layer and the roughness sublayer as the canopy flow becomes less important. The above classification has recently been investigated by Basley, Perret and Mathis (Reference Basley, Perret and Mathis2019) who performed a particle image velocimetry (PIV)-based investigation of the same three canopy configurations as Perret et al. (Reference Perret, Basley, Mathis and Piquet2019). Using data acquired in two horizontal planes, they focused on the characteristics of the coherent structures existing in the roughness sublayer and the logarithmic region. They evidenced that, closer to the canopy, the features of those participating to wall-normal exchange of momentum were dependent on the roughness array configuration. They appeared to be more or less free to develop for the sparsest configurations while constrained in the densest case. It was shown that this apparent confinement of the flow is not gradual with
$\unicode[STIX]{x1D706}_{p}$
. Their results indeed suggest that there exists a threshold in
$\unicode[STIX]{x1D706}_{p}$
above which the canopy-generated shear layers cannot develop freely (i.e. in the skimming flow regime).
The present work focuses on the interaction between the most energetic scales populating the outer layer and those from the roughness sublayer, just above the top of the canopy. A predictive model similar to that developed by Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
) for smooth-wall flows is employed to enable the quantification of both the superimposition and the modulation mechanisms when the wall geometry is strongly modified. Although this type of model has been applied successfully in boundary layers over smooth walls and homogeneous rough walls, it has not yet been applied to an urban-type rough-wall boundary layer. Furthermore, previous work has shown a non-negligible influence of the canopy configuration on the nonlinear interactions (Blackman et al.
Reference Blackman, Perret and Savory2017) and the characteristics of the near-canopy large scales (Perret et al.
Reference Perret, Basley, Mathis and Piquet2019). Here, three rough-wall boundary layers developing over arrays of cubical roughness elements with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 % will be used to investigate (i) through scale decomposition of the streamwise velocity component the influence of the canopy flow regime on the interaction between the most energetic scales existing in the outer layer and near the canopy, (ii) the impact of varying both the Reynolds number and the canopy configuration on the predictive model characteristics and (iii) whether the predictive model in its current form can be used in an urban-type boundary layer.
The following sections outline the methodologies used in the present work including the predictive model (§ 2) and experimental details (§ 3). The results and discussion, including the influence of both the plan area packing density and the Reynolds number on the characteristics of the model coefficients and universal signal, which is the signal that exists in the absence of large-scale influence, are presented in § 4. A validation of the predictive model is also presented using combinations of data from the six configurations. The last section (§ 5) is devoted to the conclusions.
2 The predictive model
The predictive model, developed by Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
) and shown in (2.1), has the ability to predict the statistics of the fluctuating streamwise velocity component in the inner region from an outer region input. Here,
$u_{p}^{+}$
is the predicted statistically representative streamwise fluctuating velocity signal and
$u_{oL}^{+}$
is the filtered outer-layer large-scale streamwise fluctuating velocity signal and the only input into the model. The signal
$u^{\ast }$
is the universal time series that corresponds to a small-scale signal that would exist if there were no large-scale influence. The superscript
$+$
denotes normalizations of the velocity fluctuations using the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
, the distance using
$\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
, and the time using
$\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}$
. The universal signal,
$u^{\ast }$
, and coefficients
$\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D703}_{L}$
are determined using a calibration method involving two-point measurements of the streamwise velocity fluctuations. The predicted signal,
$u_{p}^{+}$
, the large-scale outer-layer signal,
$u_{oL}^{+}$
, and the universal signal,
$u^{\ast }$
, are all time series as a function of
$z^{+}$
while coefficients
$\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D703}_{L}$
are all functions of
$z^{+}$
.
$$\begin{eqnarray}\displaystyle u_{p}^{+}(z^{+})=u^{\ast }(1+\unicode[STIX]{x1D6FD}u_{oL}^{+}(z_{o}^{+},\unicode[STIX]{x1D703}_{L}))+\unicode[STIX]{x1D6FC}u_{oL}^{+}(z_{o}^{+},\unicode[STIX]{x1D703}_{L}). & & \displaystyle\end{eqnarray}$$
The model consists of two parts. The first term of the right-hand side of (2.1) describes the amplitude modulation by the large-scale outer-layer structures on the small scales close to the roughness, while the second term models the superposition of these large-scale structures. To account for the inclination angle of the large-scale structures (
$\unicode[STIX]{x1D703}_{L}$
) a time lag, which corresponds to the shift in the maximum correlation between the outer- and inner-layer large-scale signals, is used. For further information regarding this model the reader is referred to the work of Mathis et al. (Reference Mathis, Hutchins and Marusic2009) and Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
). Recently, an alternative approach to this model has been proposed by Baars et al. (Reference Baars, Hutchins and Marusic2016a
) who rewrite the model as
$$\begin{eqnarray}\displaystyle u_{p}^{+}=u^{\ast }(1+\unicode[STIX]{x1D6E4}u_{L}^{+})+u_{L}^{+}, & & \displaystyle\end{eqnarray}$$
where the coefficient
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}$
and
$u_{L}^{+}=\unicode[STIX]{x1D6FC}u_{oL}^{+}(z_{o}^{+},\unicode[STIX]{x1D703}_{L})$
represents the superposition effect of the outer large scales felt at a wall-normal location
$z^{+}$
within the near canopy. Baars et al. (Reference Baars, Hutchins and Marusic2016a
) propose a refined procedure for obtaining this superposition component,
$u_{L}^{+}$
, based on a SLSE, which is applied here. A brief explanation of the method is presented below and the reader is referred to Baars et al. (Reference Baars, Hutchins and Marusic2016a
) and Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) for further information.
The present two-point measurements are first used to determine the linear coherent spectrum (LCS) between an outer-layer signal and an inner-layer signal (2.3), which represents the maximum correlation coefficient for each Fourier scale.
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}^{2}(f^{+})=\frac{\Vert \langle U_{o}(f^{+})\overline{\overline{U(f^{+})}}\rangle \Vert ^{2}}{\langle {\Vert U_{o}(f^{+})\Vert }^{2}\rangle \langle \Vert U(f^{+})\Vert ^{2}\rangle }. & & \displaystyle\end{eqnarray}$$
Here,
$U(f^{+})$
is the Fourier transform of
$u$
at frequency
$f^{+}$
,
$U_{o}(f^{+})$
is the Fourier transform of the outer-layer signal
$u_{o}$
,
$\Vert ~\Vert$
denotes the modulus,
$\langle \rangle$
denotes ensemble averaging and
$\overline{\overline{(~)}}$
denotes the complex conjugate. Thus, the LCS represents the correlation between streamwise velocity components at two wall-normal locations for a particular frequency. The spectral coherence obtained for each of the six configurations studied here are shown in figure 9 of Perret et al. (Reference Perret, Basley, Mathis and Piquet2019).
As in Baars et al. (Reference Baars, Hutchins and Marusic2016a
) the existence of a non-negligible coherence between velocities at two different wall-normal locations at certain frequencies allows for the scale decomposition of the velocity signal into
$u_{L}^{+}$
which is the portion of the signal correlated with the outer-layer signal (large scales) and
$u_{S}^{+}$
which is the portion uncorrelated with the outer-layer signal (small scales). A spectral linear stochastic estimation based on the cross-spectrum between the outer-layer signal,
$u_{o}^{+}$
, and
$u^{+}$
is used to derive a transfer function that is then used to extract
$u_{L}^{+}$
from
$u_{o}^{+}$
(Baars et al.
Reference Baars, Hutchins and Marusic2016a
),
$$\begin{eqnarray}\displaystyle U_{L}(f^{+})=H_{L}(f^{+})U_{o}(f^{+}), & & \displaystyle\end{eqnarray}$$
where
$H_{L}$
is the transfer kernel which accounts for the correlation between
$u^{+}$
and
$u_{o}^{+}$
at each frequency. This transfer function kernel is computed by using the synchronized inner-layer and outer-layer data and the following equation:
$$\begin{eqnarray}\displaystyle H_{L}(f^{+})=\frac{\langle U(f^{+})\overline{\overline{U_{o}(f^{+})}}\rangle }{\langle U_{o}(f^{+})\overline{\overline{U_{o}(f^{+})}}\rangle }. & & \displaystyle\end{eqnarray}$$
The transfer kernel is therefore the ratio between the cross-spectrum of
$u^{+}$
and
$u_{o}^{+}$
and the auto-spectrum of
$u_{o}^{+}$
. For further details see Perret et al. (Reference Perret, Basley, Mathis and Piquet2019). Beyond a certain frequency,
$f_{th}^{+}$
, coherence will no longer exist between the two signals. However, due to the presence of noise a non-physical but non-negligible value of
$\Vert H_{L}(f^{+})\Vert$
at frequencies greater than
$f_{th}^{+}$
can exist. To avoid errors in the estimated signal,
$u_{L}^{+}$
, from these non-physical values the transfer function is set to zero at frequencies above
$f_{th}^{+}$
. As in Baars et al. (Reference Baars, Hutchins and Marusic2016a
) the frequency threshold
$f_{th}^{+}$
is determined as the frequency at which the coherence
$\unicode[STIX]{x1D6FE}^{2}(f^{+})$
falls below 0.05. The transfer kernel is also smoothed to avoid further errors from noise. The transfer kernel is then applied to
$u_{o}^{+}$
in the spectral domain using (2.4). The inverse Fourier transform of the
$U_{L}(f^{+})$
signal then gives
$u_{L}^{+}(t^{+})$
.
Applying the SLSE method described above to each of the wall-normal locations (
$z$
), the new model becomes
$$\begin{eqnarray}\displaystyle u_{p}^{+}(z^{+},t^{+})=u^{\ast }(z^{+},t^{+})(1+\unicode[STIX]{x1D6E4}(z^{+})u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a}))+u_{L}^{+}(z^{+},t^{+}), & & \displaystyle\end{eqnarray}$$
where
$u_{L}^{+}(z^{+},t^{+})$
is obtained using
$$\begin{eqnarray}\displaystyle u_{L}^{+}(z^{+},t^{+})={\mathcal{F}}^{-1}[H_{L}(z^{+},f^{+}){\mathcal{F}}(u_{o}^{+}(z_{o}^{+},t^{+}))], & & \displaystyle\end{eqnarray}$$
where
${\mathcal{F}}$
and
${\mathcal{F}}^{-1}$
denote the direct and inverse Fourier transform operators, respectively. The model input is a measurement of the streamwise velocity fluctuations from the outer layer,
$u_{o}^{+}(z_{o}^{+},t^{+})$
, and a kernel
$H_{L}(z^{+},f^{+})$
. Once
$u_{L}^{+}$
has been determined the model shown in (2.6) is used to obtain the predicted signal. For this, a universal signal,
$u^{\ast }$
, and a coefficient,
$\unicode[STIX]{x1D6E4}$
, both location dependent, are required. A phase shift between the local large scales
$u_{L}^{+}(z^{+},t^{+})$
and the large-scale envelope of the amplitude modulated small scales (
$(u_{S}^{+}(z^{+},t^{+}))^{2}$
in the present case) has been evidenced both in smooth- (Guala, Metzger & McKeon Reference Guala, Metzger and McKeon2011; Baars et al.
Reference Baars, Talluru, Hutchins and Marusic2015) and rough-wall boundary layers (Pathikonda & Christensen Reference Pathikonda and Christensen2017; Basley et al.
Reference Basley, Perret and Mathis2018). To account for that effect, a time shift
$\unicode[STIX]{x1D70F}_{a}$
is introduced to the new model. Its inclusion results in a refined estimation of
$u^{\ast }$
and therefore a refined predicted signal,
$u_{p}^{+}$
(Baars et al.
Reference Baars, Hutchins and Marusic2016a
). The model parameter
$\unicode[STIX]{x1D6FC}(z^{+})$
is chosen to be equal to the maximum of from the temporal cross-correlation between the outer-layer signal,
$u_{o}^{+}$
, and the large-scale signal produced from the SLSE method,
$u_{L}^{+}(z^{+})$
(Mathis et al.
Reference Mathis, Hutchins and Marusic2011a
). The model calibration is conducted using the synchronized two-point hot-wire measurements described in § 3 at each wall-normal location of measurement. To derive
$u^{\ast }$
and
$\unicode[STIX]{x1D6E4}$
the small-scale signal of the inner layer is obtained using
$$\begin{eqnarray}\displaystyle u_{S}^{+}(z^{+},t^{+})=u^{+}(z^{+},t^{+})-u_{L}^{+}(z^{+},t^{+}). & & \displaystyle\end{eqnarray}$$
This signal represents the fluctuations that are uncorrelated with the large-scale structures in the outer layer. For the calibration
$u^{+}(z^{+},t^{+})$
is equivalent to the predicted signal giving
$$\begin{eqnarray}\displaystyle u_{S}^{+}(z^{+},t^{+})=u^{\ast }(z^{+},t^{+})(1+\unicode[STIX]{x1D6E4}(z^{+})u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a})), & & \displaystyle\end{eqnarray}$$
where
$u^{\ast }$
and
$\unicode[STIX]{x1D6E4}$
are unknown. As discussed, the universal signal is the signal that exists in the absence of any influence of the large scales in the outer layer. As described by Mathis et al. (Reference Mathis, Hutchins and Marusic2009) and Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
)
$u_{S}^{+}$
does not include any superposition effect, but does include amplitude modulation effects. Therefore, to find
$u^{\ast }$
(2.10) is used where
$\unicode[STIX]{x1D6E4}$
is solved for iteratively such that
$u^{\ast }$
does not show any amplitude modulation. Here, the absence of amplitude modulation is defined using the scale-decomposed skewness as it has been previously shown by Blackman & Perret (Reference Blackman and Perret2016) that the nonlinear term
$\overline{u_{L}^{+}u_{S}^{+2}}$
is directly related to amplitude modulation. Therefore
$u^{\ast }$
constitutes no amplitude modulation when
$$\begin{eqnarray}\displaystyle \overline{u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a})u^{\ast 2}}=\overline{u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a})\left(\frac{u_{S}^{+}(z^{+},t^{+})}{1+\unicode[STIX]{x1D6E4}(z^{+})u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a})}\right)^{2}}=0. & & \displaystyle\end{eqnarray}$$
For every wall-normal measurement location, equation (2.10) is solved iteratively to obtain
$\unicode[STIX]{x1D6E4}(z^{+})$
where
$u^{\ast }$
is minimally modulated by
$u_{L}^{+}(z^{+},t^{+}-\unicode[STIX]{x1D70F}_{a})$
. The signal
$u^{\ast }$
is then computed using the coefficient
$\unicode[STIX]{x1D6E4}$
, and
$\unicode[STIX]{x1D6FD}$
is determined from the relation
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}$
. Finally, the predicted signal,
$u_{p}^{+}$
, is estimated using (2.6). For further details, the reader is referred to Mathis et al. (Reference Mathis, Hutchins and Marusic2009), Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
) and Baars et al. (Reference Baars, Hutchins and Marusic2016a
).
3 Experimental details
The experiments were conducted in a boundary-layer wind tunnel with working section dimensions of 2 m (width)
$\times$
2 m (height)
$\times$
24 m (length) and a 5:1 inlet ratio contraction in the Laboratoire de recherche en Hydrodynamique, Energétique et Environnement Atmosphérique at Ecole Centrale de Nantes. The empty wind tunnel has a free-stream turbulence intensity of 0.5 % with spanwise uniformity to within
$\pm$
5 % (Savory, Perret & Rivet Reference Savory, Perret and Rivet2013). To reproduce the lower part of the atmospheric boundary layer five 800 mm vertical tapered spires were used immediately downstream of the contraction to initiate the boundary-layer development and were followed by a 200 mm high solid fence located 750 mm downstream of the spires. These turbulence generators were then followed by a 22 m fetch of staggered cube roughness elements with height of
$h=50$
mm. For further details related to the wind tunnel facility and set-up the reader is referred to Perret et al. (Reference Perret, Basley, Mathis and Piquet2019). Three different staggered cube configurations were studied consisting of plan area packing densities,
$\unicode[STIX]{x1D706}_{p}$
, of 6.25 %, 25 % or 44.4 % (figure 1). Finally, the experiments were performed at two nominal free-stream velocities
$U_{e}$
of 5.7 and
$8.8~\text{m}~\text{s}^{-1}$
, resulting in a total of six flow configurations.
Figure 1. Investigated canopy configurations with (a)
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, (b)
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and (c)
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
where the red cross (red
$\times$
) is the hot-wire measurement location.
Figure 2. HWA measurement set-up showing the two-probe arrangement.
Flow measurements were conducted 19.5 m downstream of the wind tunnel inlet along a wall-normal profile across the boundary layer using hot-wire anemometers (HWA). Two HWA probes were used simultaneously in order to investigate the relationship between the lower part of the boundary layer and the logarithmic region (figure 2). The first was a fixed HWA probe at a wall-normal location of
$z/h=5$
(i.e. within the inertial layer) while the second probe was positioned at 13 different wall-normal locations in the lower part of the boundary layer between
$z/h=1.25$
and
$z/h=4$
. The wall-normal location of the reference probe at
$z/h=5$
has been chosen based on previous studies (Perret & Rivet Reference Perret and Rivet2013; Blackman & Perret Reference Blackman and Perret2016; Basley et al.
Reference Basley, Perret and Mathis2018), performed in the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
cube array, in which the focus was to analyse scale interactions between the canopy flow and the overlying boundary layer in order to highlight the existence of a nonlinear amplitude modulation mechanism as previously evidenced by Mathis et al. (Reference Mathis, Hutchins and Marusic2009) in smooth-wall boundary layers. It has been shown that the amplitude modulation mechanism is effectively detected in urban surface layer with a reference point located in the range
$3h{-}5h$
. This ensures that the reference point is out of the roughness sublayer (RSL) (the targeted flow) and well within the logarithmic layer (in the constant flux region). This mild sensitivity regarding the choice of the reference wall-normal location is in agreement with the findings of Mathis et al. (Reference Mathis, Hutchins and Marusic2009). Accuracy of the single hot-wire measurements in this region of the flow was assessed by Perret & Rivet (Reference Perret and Rivet2018) using a combination of stereoscopic PIV and the concept of convective cooling velocities. Measurements of the streamwise velocity component using a single hot-wire showed good accuracy with a relative error of the variance always below 5 %. This was further confirmed by the comparison between results obtained via laser Doppler anemometry (LDA) and HWA performed by Herpin et al. (Reference Herpin, Perret, Mathis, Tanguy and Lasserre2018). Two Disa 55M01 electronics associated with Dantec 55P11
$5~\unicode[STIX]{x03BC}\text{m}$
single HWA probes with a wire length of 1.25 mm were used with overheat ratio set to 1.8. The HWA measurements were conducted at a frequency of 10 kHz for a period of 24 000
$\unicode[STIX]{x1D6FF}/U_{e}$
. The signals were treated with an eighth-order anti-aliasing linear phase elliptic low-pass filter prior to digitization. Calibration was performed at the beginning of each measurement set by placing the probes in the free-stream flow. The calibration procedure is based on King’s law and accounts for temperature correction using the method proposed by Hultmark & Smits (Reference Hultmark and Smits2010). For further details including the relative error of the mean, variance, third-order and fourth-order statistics, as well as the statistical error of convergence, refer to Perret et al. (Reference Perret, Basley, Mathis and Piquet2019). A detailed comparison between the present
$\unicode[STIX]{x1D706}_{p}=25\,\%$
flow configuration and similar configurations from the literature was completed by Perret & Rivet (Reference Perret and Rivet2018), including a comparison of the standard deviation of the three velocity components and Reynolds shear stress from Reynolds & Castro (Reference Reynolds and Castro2008). They also compared the wall-normal distribution of Q1, Q2, Q3 and Q4 events to the DNS of Coceal et al. (Reference Coceal, Dobre, Thomas and Belcher2007), confirming that the present flow shows the correct flow structure. Further comparison between the literature and measurements performed via PIV, HWA and LDA can be found in Herpin et al. (Reference Herpin, Perret, Mathis, Tanguy and Lasserre2018).
4 Results
4.1 Boundary-layer characteristics
Table 1 lists the main characteristics of the investigated boundary layers. The logarithmic-law parameter aerodynamic roughness length,
$z_{0}$
, was determined by fitting the vertical streamwise velocity profile to the logarithmic law (Perret et al.
Reference Perret, Basley, Mathis and Piquet2019). As described by Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) the zero-plane displacement height,
$d$
, is estimated directly from the calculation of the moment of pressure forces on the roughness elements while the friction velocity,
$u_{\unicode[STIX]{x1D70F}}$
, is also estimated from the measured form drag. The independence of
$u_{\unicode[STIX]{x1D70F}}/U_{e}$
and
$z_{0}/h$
from the Reynolds number
$Re_{\unicode[STIX]{x1D70F}}$
indicates that the three flow configurations are in the fully rough regime. The boundary-layer thickness,
$\unicode[STIX]{x1D6FF}$
, shown in table 1 defines the wall-normal location at which the mean velocity is equal to 99 % of the free-stream velocity
$U_{e}$
. In the measurement cross-section, for all the configurations, the non-dimensional pressure gradient
$K=(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D70C}U_{e}^{3})\,\text{d}P/\text{d}x$
along the wind tunnel was found to be below
$-2.9\times 10^{-8}$
. The aerodynamic parameters
$d$
and
$z_{0}$
can be used to classify the roughness flow regime with the model derived by Macdonald et al. (Reference Macdonald, Griffiths and Hall1998) or the data compiled by Grimmond & Oke (Reference Grimmond and Oke1999). The three canopies studied here represent the three near-wall flow regimes as defined by Grimmond & Oke (Reference Grimmond and Oke1999) where the
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
represents isolated wake flow,
$\unicode[STIX]{x1D706}_{p}=25\,\%$
represents wake-interference flow and
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
represents skimming flow (see figure 3 of Perret et al. (Reference Perret, Basley, Mathis and Piquet2019)). For further details the reader is referred to Perret et al. (Reference Perret, Basley, Mathis and Piquet2019).
Table 1. Scaling parameters. The coloured symbol chart will be used in all of the following figures.
Figure 3. Wall-normal profiles of the (a) mean, (b) variance, (c) skewness and (d) kurtosis of the streamwise velocity component. Vertical solid lines show the wall-normal location of the canopy top
$z=h$
for the three roughness configurations (being negligible when normalizing by
$\unicode[STIX]{x1D6FF}$
, variation of
$(h-d)/\unicode[STIX]{x1D6FF}$
with
$Re_{\unicode[STIX]{x1D70F}}$
is not shown).
Figure 3 shows the wall-normal profiles of the main statistical characteristics of the streamwise velocity component including mean velocity, variance, skewness and kurtosis for the six cases shown in table 1. Scaling using the roughness length and displacement height results in a collapse of the mean streamwise velocity component in regard to both canopy geometry and Reynolds number. The remaining statistics show agreement within the outer-layer scaling using the displacement height and boundary-layer thickness. However, both the variance and skewness are influenced by the canopy geometry within the inner layer close to the roughness. Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) conducted detailed scaling analysis for these six cases, but were unable to find a scaling that collapses the variance and skewness close to the wall. One salient feature of the present flow configurations put forward by these authors is the variation of the wall-normal extent of the roughness sublayer as a function of
$\unicode[STIX]{x1D706}_{p}$
. While classically defined as the region where the flow statistics are non-homogeneous in the horizontal plane, Squire et al. (Reference Squire, Morill-Winter, Hutchins, Schultz, Klewicki and Marusic2016) recently proposed defining its upper limit
$z_{RSL}$
as the lower limit of the inertial region in which the velocity variance follows a logarithmic law. Following this approach and based on the data shown in figure 3(b), Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) found that
$z_{RSL}$
varies with the roughness configuration and Reynolds number (table 1). This suggests that the densest canopy configuration prevents the canopy-induced coherent structures from developing in the wall-normal direction. This matches well with the well-recognized picture of the skimming flow regime in which a thin shear layer develops at the canopy top with very limited penetration of the flow within the canopy and is consistent with the recent results of Basley et al. (Reference Basley, Perret and Mathis2019).
4.2 Scale decomposition
In the case of the atmospheric surface layer developing over large roughness elements, the outer and inner peaks in the energy spectrum are rarely separated. The cubical obstacles induce energetic structures with typical frequencies smaller than that of the near-smooth-wall turbulence in a range closer to those attributed to the large-scale structures developing in the logarithmic and outer region. It should also be pointed out that although the outer peak is not clearly visible this does not mean that large-scale influence does not exist, but rather that scale separation is not clear and significant overlap exists between the different coherent structures interacting with each other. This has been shown by Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) and is the reason why the scale-separation method based on a two-point measurement approach is favoured here (Baars, Hutchins and Marusic Reference Baars, Hutchins and Marusic2016b
; Pathikonda & Christensen Reference Pathikonda and Christensen2017). Using the method described in § 2 the large-scale signal,
$u_{L}^{+}$
, is extracted from the raw near-wall velocity signal,
$u_{NW}^{+}$
, at each of the moving HWA probe wall-normal locations in each of the six cases using a transfer function. The modulus and phase of the transfer function for the moving probe location of
$z/h=1.25$
in each of the six cases are shown in figure 4 where it is clear that the modulus and phase of the transfer function depend on the canopy geometry, but not on the Reynolds number. In this section, the focus is on the main statistical characteristics of
$u_{L}$
and
$u_{S}$
and their contribution to the skewness, which is an indicator of the existence of amplitude modulation (Duvvuri & McKeon Reference Duvvuri and McKeon2015). A thorough analysis of the spectral content of the flow and of its large- and small-scale components has been performed by Perret et al. (Reference Perret, Basley, Mathis and Piquet2019) and Basley et al. (Reference Basley, Perret and Mathis2019) in the same flow configurations as here. These authors demonstrated the co-existence of very large-scale motions (VLSMs), large-scale motions (LSMs) and canopy-generated coherent structures whose characteristics obey different scaling laws. For the sake of conciseness, these results are not recalled here, the reader being referred to these studies.
Figure 4. (a) Modulus and (b) phase of the transfer kernel
$|H_{L}|$
at
$z/h=1.25$
for configurations with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 % at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and 49 900. The colour chart is as per table 1 for canopy configurations; solid and dashed lines correspond respectively to the low and the high Reynolds numbers.
Figure 5. Spectra of
$u^{\ast }$
(solid line) and
$u_{L}^{+}$
(dashed line) for configurations with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 % at (a)
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and (b) 49 900 at
$z/h=2.1$
. Vertical solid lines show the streamwise wavelength corresponding to the obstacle height
$\unicode[STIX]{x1D706}=h$
.
Once
$u_{L}^{+}$
is extracted using triple decomposition the small-scale signal,
$u_{S}^{+}$
, can be computed. (Triple decomposition was first introduced by Hussain (Reference Hussain1983) to decompose the instantaneous velocity field into mean, large-scale and small-scale components.) Finally,
$u^{\ast }$
is computed using the method described in § 2. The spectra of the universal and large-scale signal (figure 5) of the six cases show the differences in energy content of the two signals. No significant change occurs in the energy distribution between the different canopies and different Reynolds numbers. Finally, an increase in Reynolds number does not affect the magnitude of energy contained in the universal and large-scale signals. This last point may be tempered by the narrow range of Reynolds number used here, as it has been shown previously that the large-scale content increases as the Reynolds number increases (see Mathis et al. (Reference Mathis, Hutchins and Marusic2009, Reference Mathis, Hutchins and Marusic2011a
) among others). The statistics of the
$u^{\ast }$
signal including variance, skewness and kurtosis are compared in figure 6 with the statistics of the raw near-wall velocity signal
$u_{NW}^{+}$
,
$u_{L}^{+}$
and
$u_{S}^{+}$
showing only the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
case as an example. In all six cases (not shown here)
$u_{S}^{+}$
captures the majority of the variance in the inner layer while the large-scale contribution becomes important only in the outer layer. The skewness is shown to be almost completely captured by
$u_{S}^{+}$
with the contribution from
$u_{L}^{+}$
close to zero. The kurtosis of the raw signal is shown to be a result of both
$u_{L}^{+}$
and
$u_{S}^{+}$
with the contribution of
$u_{S}^{+}$
increasing with wall-normal distance in the outer layer. Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
) noted that the universal signal is the signal that exists in the absence of the influence of large-scale structures while
$u_{S}^{+}$
is the signal that exists in the absence of any superposition. Therefore a comparison between the
$u_{S}^{+}$
and
$u^{\ast }$
signals provides insight into the influence of the amplitude modulation on the
$u_{S}^{+}$
structures. The presence of amplitude modulation causes no influence in the variance or kurtosis as
$u_{S}^{+}$
and
$u^{\ast }$
have similar profiles. In the absence of amplitude modulation the magnitude of skewness of
$u^{\ast }$
is significantly lower throughout the boundary layer. These trends are true for each of the six configurations except in the case of the skewness of
$u^{\ast }$
. The wall-normal location at which the profile of the skewness of
$u^{\ast }$
crosses the profile of the skewness of
$u_{L}^{+}$
changes depending on the roughness configuration. In roughness configurations with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
or 25 % the
$u^{\ast }$
profile crosses the
$u_{L}^{+}$
profile at a wall-normal distance of approximately
$(z-d)/\unicode[STIX]{x1D6FF}=0.09$
while in roughness configurations with
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
this crossing occurs at
$(z-d)/\unicode[STIX]{x1D6FF}=0.05$
. As
$u^{\ast }$
is the signal that exists in the absence of influence of the large scales it should correspond to a signal from a low Reynolds number flow where large-scale influence is weak. The decrease of contribution of
$u^{\ast }$
to the skewness in the configuration with
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
is a result of increased large-scale activity. No significant differences are found between cases when varying Reynolds number as both Reynolds numbers are sufficient to generate significant large-scale activity and differ by less than a factor of two.
Figure 6. Comparison of
$u^{\ast }$
,
$u_{L}^{+}$
,
$u_{S}^{+}$
and
$u_{NW}^{+}$
statistics (a) variance, (b) skewness and (c) kurtosis for configuration with
$\unicode[STIX]{x1D706}_{p}=25\,\%$
at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
.
4.3 Influence of canopy geometry and Reynolds number
Figure 7. Triple decomposition of the skewness of the streamwise velocity component including (a)
$\overline{u_{S}^{+3}}$
, (b)
$\overline{u_{L}^{+3}}$
, (c)
$3\overline{u_{L}^{+}u_{S}^{+2}}$
and (d)
$3\overline{u_{L}^{+2}u_{S}^{+}}$
.
Skewness decomposition as shown in (4.1) has been used to investigate the nonlinear interactions between large- and small-scale structures in turbulent flows (Blackman & Perret Reference Blackman and Perret2016).
$$\begin{eqnarray}\displaystyle \overline{u^{+3}}=\overline{u_{S}^{+3}}+\overline{u_{L}^{+3}}+3\overline{u_{L}^{+}u_{S}^{+2}}+3\overline{u_{L}^{+2}u_{S}^{+}}. & & \displaystyle\end{eqnarray}$$
Here it is used to determine the influence of the canopy geometry and Reynolds number on these nonlinear interactions. Figure 7 shows the small-scale skewness, large-scale skewness and two scale-interaction terms. The influence of the canopy geometry is particularly apparent in the contribution of the small scales close to the canopy where there is a clear separation between the cases (figure 7
a). This separation is a result of the distinct canopy flow regimes in each of the cases. As mentioned, within the skimming flow regime (
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
) there is a thinner shear layer (or roughness sublayer) whereas in the isolated wake (
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
) and wake-interference (
$\unicode[STIX]{x1D706}_{p}=25\,\%$
) flow regimes the shear layer wall-normal extent is larger, increasing the importance of the small scales. Away from the canopy, in the outer layer, the influence of the canopy geometry or flow regime is not significant. Moreover, throughout the boundary layer the canopy geometry does not significantly influence the large-scale contribution or the contribution of the nonlinear term
$\overline{u_{L}^{+2}u_{S}^{+}}$
, which represents the influence of the small scales on the large scales. However, an increase in Reynolds number increases the contribution of this nonlinear term within the outer layer (figure 7
d). Finally, the nonlinear term
$\overline{u_{L}^{+}u_{S}^{+2}}$
has been shown to represent the amplitude modulation (Mathis et al.
Reference Mathis, Marusic, Hutchins and Sreenivasan2011c
; Duvvuri & McKeon Reference Duvvuri and McKeon2015). Here, it is clear that although the canopies with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
and 25 % display similar amplitude modulation, the amplitude modulation of the canopy with
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
is significantly modified at both Reynolds numbers (figure 7
c). Throughout the boundary layer, except close to the canopy, the amplitude modulation is weaker in the
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
canopy. As mentioned in § 4.1, this flow configuration has the finest roughness sublayer. This is confirmed if one considers the wall-normal location of the zero crossing of the skewness of the streamwise velocity component as the upper limit of the roughness sublayer (figure 7
a). It is also where the small-scale component
$u_{S}$
is the least energetic relative to the large scales (Perret et al.
Reference Perret, Basley, Mathis and Piquet2019). In this flow configuration, the small scales are less energetic and more confined to near the canopy top, the amplitude modulation imprint is therefore weaker than the two other cases.
The coefficients
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
of the predictive model computed for each of the cases listed in table 1 using the method in § 2 are shown in figure 8 along with the coefficient
$\unicode[STIX]{x1D6E4}$
. The roughness configuration affects the superposition coefficient,
$\unicode[STIX]{x1D6FC}$
, close to the roughness in the inner layer where differences in the flow regimes are important. However, in the outer layer the superposition is consistent in all roughness configurations. In the outer layer the influence of the roughness flow regime disappears and the large-scale structures become similar, thereby resulting in similar superposition. The amplitude modulation coefficient,
$\unicode[STIX]{x1D6FD}$
, depends on roughness configuration in the inner layer, but in the case of the roughness configuration with
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
the amplitude modulation is decreased both in the inner layer and the outer layer. This is consistent with the nonlinear term
$\overline{u_{L}^{+}u_{S}^{+2}}$
, which shows lower magnitudes of amplitude modulation in the
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
configuration. As discussed, the characteristics of the shear layer in the skimming flow regime change the characteristics of the small-scale structures and their interactions with the large-scale structures in the outer layer above. The dependence of the superposition and amplitude modulation on the roughness configuration close to the roughness is a result of changes to the dynamics of the shear layers that develop at the top of the roughness elements in the different flow regimes. Within the skimming flow regime the shear layer does not penetrate the roughness elements resulting in a thin, but strong shear layer, whereas the spacing between roughness elements in the isolated and wake-interference regimes result in a shear layer that penetrates the canopy layer increasing the vertical transfer of momentum of small-scale structures in this region (Basley et al.
Reference Basley, Perret and Mathis2019). The shear layer in the wake-interference flow regime also experiences a strong flapping phenomenon that promotes the transfer of momentum between the canopy layer (small scales) and outer layer (large scales). The results show that an increase in Reynolds number does not increase the superposition or the amplitude modulation, in contradiction to Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
), who found that increased Reynolds number increases the large-scale activity in the outer layer thereby increasing the amplitude modulation. These results should be tempered by the fact that the Reynolds numbers used here are not sufficiently separated to significantly affect the large scales and therefore the scale interactions.
Figure 8. Predictive model coefficients (a)
$\unicode[STIX]{x1D6FC}$
, (b)
$\unicode[STIX]{x1D6FD}$
and (c)
$\unicode[STIX]{x1D6E4}$
for configurations with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 % at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and 49 900.
Figure 9. Comparison of
$u^{\ast }$
statistics (a) variance, (b) skewness and (c) kurtosis, and
$u_{L}^{+}$
statistics (d) variance, (e) skewness and (f) kurtosis for configurations with
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
, 25 % and 44.4 % at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and 49 900.
The variance, skewness and kurtosis of the universal signal,
$u^{\ast }$
, and
$u_{L}^{+}$
in each of the six cases are presented in figure 9. The influence of the roughness configuration can be seen in the profiles of variance and skewness in the inner layer close to the roughness, whereas this influence becomes negligible in the profile of kurtosis. The changes in variance and skewness are a result of changes to the small-scale structures produced by the roughness. Small scales in the wake-interference flow regime have larger magnitudes of skewness and smaller magnitudes of turbulence intensity compared to the skimming flow regime. Although there is an increase in magnitude of variance of the large-scale structures in the 44.4 % configuration these changes are not limited to the region close to the roughness as in the
$u^{\ast }$
profile (figure 9
d). Excluding this slight increase in the variance the similarity of the other
$u_{L}^{+}$
profiles suggests that the very-large-scale structures in each of the cases have similar characteristics. Using the outer-layer scaling a change in Reynolds number does not affect the statistics of the universal or large-scale signals. These results have shown that the model coefficients and universal signal are significantly influenced by the canopy geometry or canopy flow regime while the large-scale structures have been shown to be similar in each of the cases. Therefore, the universal signal is not universal for all rough-wall boundary layers and the predictive model must be calibrated for each of the roughness flow regimes.
4.4 Prediction and validation
Model coefficients provided by the calibration allow for the prediction of a statistically representative signal,
$u_{p}^{+}$
, that hypothetically can be reconstructed at any Reynolds number, where the only required input is the large-scale reference signal,
$u_{L}^{+}$
. In this section, a series of tests are performed in order to assess whether the above assumption, which works well in smooth-wall boundary layer, still holds in an atmospheric boundary layer over an urban canopy. To do so, a series of tests is performed to validate and assess the capabilities of the model, in which canopy configuration and Reynolds numbers are mixed, as seen in table 2.
Figure 10. Comparison of
$u_{NW}^{+}$
and
$u_{p}^{+}$
statistics (a) variance, (b) skewness and (c) kurtosis for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
where
$u_{p}^{+}$
is determined using model coefficients calibrated at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and
$u_{L}^{+}$
at
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
(Test 1).
Table 2. Characteristics of the input (calibration parameters and large-scale signal) and output of the predictive model used for testing and validating the prediction capabilities of the model.
The capabilities of the predictive model, which has been calibrated for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
, is first tested by predicting the near-canopy signal for the same plan density at the higher Reynolds number
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
(Test 1). To do this a large-scale reference signal measured at
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
is used to run the predictive model where the universal signal and model coefficients were determined from a calibration at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
. Additionally, the large-scale reference signal must be interpolated onto the non-dimensional time scale
$t^{+}$
of the universal signal so that the time sampling of both signals is consistent. In addition, the two signals must have the same length, by clipping the longest of the two. Figure 10 shows the characteristics of the predicted signal (blue stars) compared with the characteristics of the measured near-canopy signal (black circles) up to the fourth order. Although there is some slight discrepancy between the prediction and the near-canopy signal, it is clear that the predictive model calibrated at a lower Reynolds number is able to reproduce the characteristics of the near-canopy signal at a higher Reynolds number. Finally, the spectra of the predicted signal are similar to the spectra of the measured signal as shown in figure 11. There is a slight shift in the wavelength of the spectra of the predicted signal that becomes more significant closer to the roughness. This might be due to the application of Taylor’s hypothesis which has questionable suitability close to the roughness. However, the similarity of the spectra further validates the model and suggests that the model can be calibrated at any arbitrary Reynolds number.
Figure 11. Spectra of
$u_{NW}^{+}$
and
$u_{p}^{+}$
at (a)
$z/h=1.25$
, (b)
$z/h=2.1$
and (c)
$z/h=3.2$
for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
where
$u_{p}^{+}$
is determined using model coefficients calibrated at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and
$u_{L}^{+}$
at
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
(Test 1).
Another crucial question in making a predictive model for urban canopy flow is, to what extent is the calibration dependent on the plan area packing density at which the calibration is performed? Indeed, the previous section clearly evidenced that the universal signal and model coefficients are canopy dependent. In an attempt to shed light on this, the near-canopy signal is predicted for the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
configuration using large-scale reference signals from the datasets of the
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
and 44.4 % configurations at the same Reynolds number (Test 2). To perform these predictions the calibrated model for the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration is used along with a large-scale reference signal from a configuration with a different
$\unicode[STIX]{x1D706}_{p}$
. As above, the large-scale reference signal from either the
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
or 44.4 % configuration is interpolated onto the non-dimensional time scale of the universal signal calibrated for the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration. Figure 12 shows the characteristics of the predicted signal using a large-scale reference from the
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
configuration (blue triangles),
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
configuration (red squares) and the measured near-canopy signal of the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration (black circles). The spectra of the predicted signals and measured near-canopy signal are shown at several wall-normal locations in figure 13. There is excellent agreement between the predicted signals and the near-canopy signal for the statistics up to the fourth order and the spectra in both prediction cases.
Figure 12. Comparison of
$u_{NW}^{+}$
and
$u_{p}^{+}$
statistics (a) variance, (b) skewness and (c) kurtosis for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
where
$u_{p}^{+}$
is determined using model coefficients calibrated for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$u_{L}^{+}$
from
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
or 44.4 % (Test 2).
Figure 13. Spectra of
$u_{NW}^{+}$
and
$u_{p}^{+}$
at (a)
$z/h=1.25$
, (b)
$z/h=2.1$
and (c)
$z/h=3.2$
for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
where
$u_{p}^{+}$
is determined using model coefficients calibrated for
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$u_{L}^{+}$
from
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
or 44.4 % (Test 2).
To determine the error associated with these predictions the near-canopy signal was predicted within each canopy using a large-scale reference signal from each of the other canopy configurations for the lowest wall-normal location of
$z/h=1.25$
as a test. The error for the statistics up to the fourth order was computed for each prediction using (4.2) where
$\unicode[STIX]{x1D719}_{m}$
and
$\unicode[STIX]{x1D719}_{p}$
are any statistics of the original measured and predicted signals, respectively.
$$\begin{eqnarray}\displaystyle \text{Error}=(\unicode[STIX]{x1D719}_{m}-\unicode[STIX]{x1D719}_{p})/\unicode[STIX]{x1D719}_{m}. & & \displaystyle\end{eqnarray}$$
Figure 14 shows the error averaged over the two predictions for each canopy configuration. The error is less than 3 % for all statistics and in all canopies with the largest error of 3 % for the kurtosis of the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration. This confirms that a calibrated predictive model can be used to predict the near-canopy signal using a large-scale reference measured in any other canopy configuration.
Figure 14. Error of
$u_{p}^{+}$
statistics variance, skewness and kurtosis where
$u_{p}^{+}$
is determined using model coefficients calibrated at a certain
$\unicode[STIX]{x1D706}_{p}$
and
$u_{L}^{+}$
at a different
$\unicode[STIX]{x1D706}_{p}$
both at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
.
The final validation of the model combines both the Reynolds number and
$\unicode[STIX]{x1D706}_{p}$
validation by predicting a near-canopy signal within the
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
configuration at
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
using the calibrated model at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and a large-scale reference signal from the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration at
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
(Test 3). As in the previous validation the model is able to accurately reproduce the spectra of the near-canopy signal as well as the statistics up to the fourth order (figure 15). The model is able to accurately reproduce these statistics because, as has been shown here, the characteristics of the large scales in each of the canopies are similar. However, the differences in the characteristics of the universal signal and the predictive model coefficients prevent the application of a calibrated model at one
$\unicode[STIX]{x1D706}_{p}$
to a prediction at another
$\unicode[STIX]{x1D706}_{p}$
. The model must be calibrated using measurements from a canopy with the same configuration as the targeted one.
Figure 15. Comparison of
$u_{NW}^{+}$
and
$u_{p}^{+}$
statistics (a) variance, (b) skewness and (c) kurtosis and (d) spectra at
$z/h=1.5$
for
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
where
$u_{p}^{+}$
is determined using model coefficients calibrated for
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and
$u_{L}^{+}$
from
$\unicode[STIX]{x1D706}_{p}=25\,\%$
and
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
(Test 3).
In the smooth wall special attention has been paid to conserving the phase between the universal signal and large-scale signal used to run the predictive model (Mathis et al.
Reference Mathis, Hutchins and Marusic2011a
). In these cases the large-scale reference signal used to run the predictive model was adjusted to retain the Fourier phase information of the large-scale signal used to build the universal signal. The phase information of the original large-scale signal is extracted using a Fourier transform and applied to the new large-scale reference signal. This process essentially re-synchronizes the new large-scale reference with the universal signal,
$u^{\ast }$
(Mathis et al.
Reference Mathis, Marusic, Hutchins and Sreenivasan2011c
). Here, this process was applied before performing the predictions detailed above. To determine influence of the phase shift on a prediction a test is performed using the large-scale reference signal used to build the predictive model. This signal is shifted out of phase with the universal signal and a prediction of the statistics made at each time shift (figure 16). As the phase shift increases the estimation of the variance, skewness and kurtosis worsen until they reach a plateau. The effect of the phase shift increases with increasing order of the statistic with the kurtosis showing the largest discrepancy. This suggests that conserving the phase information of the large-scale signal used to calibrate the model is important to the prediction.
Figure 16. (a) Variance, (b) skewness and (c) kurtosis of
$u_{p}^{+}$
and
$u_{NW}^{+}$
for configuration with
$\unicode[STIX]{x1D706}_{p}=25\,\%$
at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
using phase shifted large-scale reference signal at
$z/h=2.1$
(
$(z-d)/\unicode[STIX]{x1D6FF}=0.066$
).
5 Conclusion
A predictive model of the same form as that originally introduced by Mathis et al. (Reference Mathis, Hutchins and Marusic2011a
) for the smooth-wall boundary layer has been derived to investigate the scale-interaction mechanisms known to exist in the near-canopy region of boundary-layer flows developing over large roughness elements. This modelling approach allows for the identification and quantification of both the superimposition of the most energetic (large) scales from the outer layer onto the near-canopy (smaller-scale) turbulence and the amplitude modulation of the near-canopy flow by the outer-layer flow. It also enables the extraction of the portion of the near-canopy velocity that is free from any influence of the large scales. Three roughness arrays consisting of cubical roughness elements with plan area packing densities of 6.25 %, 25 % and 44.4 % (corresponding to the three flow regimes identified in such flows (Grimmond & Oke Reference Grimmond and Oke1999; Perret et al.
Reference Perret, Basley, Mathis and Piquet2019)) were studied at two free-stream velocities and used to determine the influence of both the canopy geometry and Reynolds number on the interaction between the most energetic scales from the outer layer and those in the roughness sublayer. Through analysis of the predictive model coefficients it was shown that the canopy geometry has a non-negligible influence on the scale interactions. The superposition, represented by the coefficient
$\unicode[STIX]{x1D6FC}$
, was modified in the inner layer close to the canopy top as a result of a change in the local flow regime. Furthermore, the skimming flow regime,
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
, showed lower levels of amplitude modulation (given by the model parameter
$\unicode[STIX]{x1D6FD}$
), both in the inner and outer layers when compared to configurations of isolated and wake-interference flow regime. These patterns were also visible in the statistics of the universal signal,
$u^{\ast }$
, where the variance was modified close to the roughness as a result of local canopy geometry. For the densest canopy, both the variance and skewness had lower magnitudes throughout the roughness sublayer. Investigation of the model coefficients
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
and statistics of
$u^{\ast }$
demonstrated that the Reynolds number does not significantly influence the superposition or amplitude modulation contradicting previous results in the smooth-wall boundary layer (Mathis et al.
Reference Mathis, Hutchins and Marusic2011a
). However, this is likely a result of the limited range of Reynolds numbers used here and therefore requires further investigation.
The capacity of the derived models to serve as predictive tools to model near-canopy turbulence and to generate synthetic signals which have the same statistical characteristics of the targeted flows has also been investigated. Model validation was performed in three steps. The first, consisted of a prediction of the streamwise velocity component within the roughness sublayer of the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration at the highest Reynolds number,
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
, using the model parameters calibrated at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
(Test 1). The second validation consisted of a prediction of the streamwise velocity component within the roughness sublayer of the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration using its model parameters combined with a large-scale signal from the
$\unicode[STIX]{x1D706}_{p}=6.25\,\%$
or 44.4 % configurations (Test 2). Finally, the third validation consisted of a prediction of the streamwise velocity component within the roughness sublayer of the
$\unicode[STIX]{x1D706}_{p}=44.4\,\%$
configuration at the highest Reynolds number,
$Re_{\unicode[STIX]{x1D70F}}=49\,900$
, using the model parameters calibrated at
$Re_{\unicode[STIX]{x1D70F}}=32\,400$
and a large-scale signal from the
$\unicode[STIX]{x1D706}_{p}=25\,\%$
configuration (Test 3). Each of the model validations demonstrated the suitability of the predictive model within the urban-type rough-wall boundary layer. The statistics up to the fourth order were accurately reproduced as well as the spectra. Finally, analysis of the phase between
$u^{\ast }$
and
$u_{L}^{+}$
suggests that it is important to preserve the phase between the two signals particularly in the case of higher-order statistics. It should be however emphasized that the model must be calibrated for each type of canopy flow regime.
Through this work it has been demonstrated that the nonlinear interactions within the roughness sublayer of urban-type rough-wall boundary layers can be modelled using the predictive model as proposed by Mathis et al. (Reference Mathis, Hutchins and Marusic2011a ). Although the Reynolds number was shown to have a negligible influence on the model parameters data should be obtained from higher Reynolds number rough-wall flows to expand the range studied. Another point of importance, not addressed in the present study, is the strong spatial heterogeneity of the flow within the roughness sublayer and inside the canopy. The recent experimental study by Herpin et al. (Reference Herpin, Perret, Mathis, Tanguy and Lasserre2018) on the scale superimposition in these regions has shown the spatial heterogeneity, both in the wall-normal direction and in the horizontal plane, of this mechanism. These results combined with those obtained here call for a more sophisticated model capable of accounting for the spatial heterogeneity of the flow over large roughness elements. In its present form, the statistical predictive model is a powerful tool, but the dynamic nature of the urban boundary layer and the complexity of the transport processes in the urban canopy limit the capabilities of a statistical model. Future efforts should concentrate on developing a dynamic predictive model, which would have significant potential for the urban boundary layer. Finally, urban canopies with uniform height, such as those studied here, have been shown to have characteristics that are common to other obstructed shear flow canopies (Ghisalberti Reference Ghisalberti2009). These canopies range from terrestrial vegetative canopies to submerged aquatic canopies such as coral and all have an inflection point in the profile of the shear stress. This commonality points to the need for more general approaches to the investigation of amplitude modulation in canopies.
Acknowledgements
The authors are thankful to Mr T. Piquet for his technical support and to the French National Research Agency for their funding (Urbanturb grant ANR-14-CE22-0012-01).
