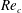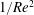1 Introduction
The general problem of motion of a light spherical particle in a rotating flow has received considerable attention since the seminal work of Thomson (Reference Thomson1873) on inviscid irrotational flows. Kelvin considered a small sphere placed in an irrotational rotating flow and predicted that the sphere will be attracted to the centre of the flow by a force which is inversely proportional to the cube of the distance from the axis of rotation.
A review of the forces involved in the motion of bubbles and rigid particles in unbounded domains at low to moderate Reynolds numbers is provided by Magnaudet (Reference Magnaudet1997). Lee & Ladd (Reference Lee and Ladd2005) use Stokesian dynamics to calculate the motion of an infinitesimally small particle in a cylinder rotating around its axis which is perpendicular to gravity. They find that the circular orbit of a particle denser than the fluid and moving with it in solid-body rotation is perturbed by outward centrifugal forces, leading to spiral trajectories that are eventually confined by the cylinder wall. The centrifugal force term used by Lee & Ladd (Reference Lee and Ladd2005) is valid only when the motion of the sphere through the surrounding fluid is much smaller than the speed of the particle, and thus their calculations of equilibrium position are difficult to justify in a physical realisation.
Lift in low Reynolds number flows was first studied theoretically by Saffman (Reference Saffman1965) and is known to be responsible for the lateral migration spheres in Poiseuille flow as reviewed by Leal (Reference Leal1980). The magnitude of the lift is proportional to the square of the radius of the sphere
![]() $a$
. Experimental work conducted by Van Nierop et al. (Reference Van Nierop, Luther, Bluemink, Magnaudet, Prosperetti and Lohse2007) concerns the motion of bubbles in a flow rotating about a horizontal axis for Reynolds number
$a$
. Experimental work conducted by Van Nierop et al. (Reference Van Nierop, Luther, Bluemink, Magnaudet, Prosperetti and Lohse2007) concerns the motion of bubbles in a flow rotating about a horizontal axis for Reynolds number
![]() $0.01<Re<500$
. For a bubble of radius
$0.01<Re<500$
. For a bubble of radius
![]() $a$
moving at speed
$a$
moving at speed
![]() $v$
through the surrounding fluid of kinematic viscosity
$v$
through the surrounding fluid of kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
, they find that at low Reynolds numbers,
$\unicode[STIX]{x1D708}$
, they find that at low Reynolds numbers,
![]() $av/\unicode[STIX]{x1D708}<10$
, the lift coefficient is always negative, i.e. the lift force on the bubble is centripetal, directed towards the axis of rotation. This contrasts with higher Reynolds numbers where the lift force on the bubble is directed outwards.
$av/\unicode[STIX]{x1D708}<10$
, the lift coefficient is always negative, i.e. the lift force on the bubble is centripetal, directed towards the axis of rotation. This contrasts with higher Reynolds numbers where the lift force on the bubble is directed outwards.
The results of a study of the motion of heavy spheres with density ratios between
![]() $1.15$
and
$1.15$
and
![]() $8.14$
in a vertical rotating cylindrical container are reported by Karanfilian & Kotas (Reference Karanfilian and Kotas1981). They explored a range of
$8.14$
in a vertical rotating cylindrical container are reported by Karanfilian & Kotas (Reference Karanfilian and Kotas1981). They explored a range of
![]() $Re$
between
$Re$
between
![]() $0.035$
and
$0.035$
and
![]() $3365$
, and found that for
$3365$
, and found that for
![]() $Re<1$
the lift coefficient is always negative, in accord with the discussion in the previous paragraph.
$Re<1$
the lift coefficient is always negative, in accord with the discussion in the previous paragraph.
Other experimental work conducted in a horizontal rotating cylinder filled with a viscous fluid focused on the motion of a single heavy sphere and the interaction between two and three spheres (Mullin et al.
Reference Mullin, Li, Del Pino and Ashmore2005). Mullin et al. find a fixed point regime where the sphere is balanced next to the wall, and a dynamical cascading regime, in which the sphere describes asymmetric orbits for
![]() $Re>1.21$
. The motion at the fixed points adjacent to the wall is studied in detail by Ashmore, Del Pino & Mullin (Reference Ashmore, Del Pino and Mullin2005) who show that cavitation is an essential component of the force balance. Yang et al. (Reference Yang, Seddon, Mullin, Del Pino and Ashmore2006) studied the effects of roughness in the interactions with the wall. The dynamical motion, including chaos, was subsequently studied in detail by Davidheiser et al. (Reference Davidheiser, Syers, Segre and Weeks2010). When many particles are added to a rotating cylinder of viscous fluid, axial segregation and pattern formation can occur (see Seiden & Thomas Reference Seiden and Thomas2011, and references therein).
$Re>1.21$
. The motion at the fixed points adjacent to the wall is studied in detail by Ashmore, Del Pino & Mullin (Reference Ashmore, Del Pino and Mullin2005) who show that cavitation is an essential component of the force balance. Yang et al. (Reference Yang, Seddon, Mullin, Del Pino and Ashmore2006) studied the effects of roughness in the interactions with the wall. The dynamical motion, including chaos, was subsequently studied in detail by Davidheiser et al. (Reference Davidheiser, Syers, Segre and Weeks2010). When many particles are added to a rotating cylinder of viscous fluid, axial segregation and pattern formation can occur (see Seiden & Thomas Reference Seiden and Thomas2011, and references therein).
The results of numerical investigations of the pedalling motion of pairs of spheres in a horizontal rotating cylinder of viscous fluid are reported by Mukundakrishnan, Hu & Ayyaswamy (Reference Mukundakrishnan, Hu and Ayyaswamy2008). They use direct numerical simulations of the incompressible Navier–Stokes equations on a finite-length horizontal rotating cylinder with
![]() $1<Re<60$
. The majority of their study is concerned with the dynamics of two particles but they also find that a single light particle has a stable fixed point, which is in accord with the theory of Coimbra & Kobayashi (Reference Coimbra and Kobayashi2002).
$1<Re<60$
. The majority of their study is concerned with the dynamics of two particles but they also find that a single light particle has a stable fixed point, which is in accord with the theory of Coimbra & Kobayashi (Reference Coimbra and Kobayashi2002).
Horizontal rotating cylinders of viscous fluid are used widely in biotechnology in applications related to tissue growth engineering. An example of this is provided by a bioreactor, where tissue can be grown in a reduced gravity environment when placed inside a rotating cylinder filled with fluid (Gao, Ayyaswamy & Ducheyne Reference Gao, Ayyaswamy and Ducheyne1996). The tissue is in the form of a near-spherical porous scaffold. It is less dense than the fluid and at a given rotation rate it is observed to sit at a fixed point which is displaced from the axis of rotation. This has practical advantages as collision between the delicate tissue and the walls of the bio-reactor can be avoided. The understanding of the dynamics of a single particle in a horizontal rotating cylinder also aids understanding of the behaviour of colloidal suspensions, specifically as a model of the manufacturing process of precision latex micro-spheres through the use of a rotating latex reactor as discussed by Roberts, Kornfeld & Fowlis (Reference Roberts, Kornfeld and Fowlis1991).
The focus of our investigation is on the fixed points for a light rigid sphere in a horizontal rotating cylinder at low Reynolds number. These fixed point observations are in good accord with a theory that we develop from the lift force expression of Gotoh (Reference Gotoh1990). We observe that a particle at a fixed point near to the centre of the cylinder becomes unstable to periodic motion as the rotation rate is reduced and the sphere approaches the wall of the cylinder. The growth rate of the oscillations is unusual as it is found to be slower than for a standard Hopf bifurcation.
The structure of the paper is as follows. In § 2 we evaluate the time-dependent forces acting on the sphere and derive an expression for the equilibrium positions. The experiment is described in § 3, followed by the experimental results in § 4 where a comparison with the results of our model is made. We draw some conclusions in § 5.
2 Equilibrium position of a sphere in a rotating viscous flow

Figure 1. Schematic of an end view of the flow domain. A cylinder of fluid (outer circle) rotates about its axis
![]() $O$
at angular velocity
$O$
at angular velocity
![]() $\unicode[STIX]{x1D6FA}$
, and a buoyant particle of radius
$\unicode[STIX]{x1D6FA}$
, and a buoyant particle of radius
![]() $a$
(inner filled circle) is held at an equilibrium position by a balance of Stokes drag
$a$
(inner filled circle) is held at an equilibrium position by a balance of Stokes drag
![]() $\boldsymbol{F}_{D}$
, centripetal forces
$\boldsymbol{F}_{D}$
, centripetal forces
![]() $\boldsymbol{F}_{C}$
, buoyancy
$\boldsymbol{F}_{C}$
, buoyancy
![]() $\boldsymbol{F}_{B}$
and lift
$\boldsymbol{F}_{B}$
and lift
![]() $\boldsymbol{F}_{L}$
.
$\boldsymbol{F}_{L}$
.
In this section, a model is described for the motion of a buoyant sphere within a cylinder rotating about its axis, which is perpendicular to gravity. This model follows the results of Candelier (Reference Candelier2008), who derived the history-dependent forces on a sphere in an unbounded rotating flow at low Reynolds number, and showed that these forces correspond to the lift and drag corrections predicted by Gotoh (Reference Gotoh1990) when the sphere is in equilibrium.
The cylinder rotates with angular velocity
![]() $\unicode[STIX]{x1D6FA}$
, and is filled with viscous fluid of density
$\unicode[STIX]{x1D6FA}$
, and is filled with viscous fluid of density
![]() $\unicode[STIX]{x1D70C}_{f}$
and dynamic viscosity
$\unicode[STIX]{x1D70C}_{f}$
and dynamic viscosity
![]() $\unicode[STIX]{x1D707}$
(figure 1). A buoyant spherical particle of radius
$\unicode[STIX]{x1D707}$
(figure 1). A buoyant spherical particle of radius
![]() $a$
and density
$a$
and density
![]() $\unicode[STIX]{x1D70C}_{s}$
is immersed in a fluid, and we assume that this sphere is small, and sufficiently far from the walls of the cylinder that hydrodynamic interactions between the particle and the walls of the cylinder can be neglected. Defining a radial coordinate system centred at the axis of the cylinder, with unit azimuthal and radial basis vectors
$\unicode[STIX]{x1D70C}_{s}$
is immersed in a fluid, and we assume that this sphere is small, and sufficiently far from the walls of the cylinder that hydrodynamic interactions between the particle and the walls of the cylinder can be neglected. Defining a radial coordinate system centred at the axis of the cylinder, with unit azimuthal and radial basis vectors
![]() $\boldsymbol{e}_{r}$
and
$\boldsymbol{e}_{r}$
and
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
, the velocity field in the absence of the sphere is solid-body rotation,
$\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
, the velocity field in the absence of the sphere is solid-body rotation,
![]() $\boldsymbol{u}=r\unicode[STIX]{x1D6FA}\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
. The location of the centre of the sphere is denoted by
$\boldsymbol{u}=r\unicode[STIX]{x1D6FA}\boldsymbol{e}_{\unicode[STIX]{x1D703}}$
. The location of the centre of the sphere is denoted by
![]() $\boldsymbol{x}$
, with radial coordinates
$\boldsymbol{x}$
, with radial coordinates
![]() $(r,\unicode[STIX]{x1D703})$
and Cartesian coordinates
$(r,\unicode[STIX]{x1D703})$
and Cartesian coordinates
![]() $(x,y)$
and the acceleration arising from gravity by
$(x,y)$
and the acceleration arising from gravity by
![]() $\boldsymbol{g}=-g(\boldsymbol{e}_{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D703}+\boldsymbol{e}_{r}\sin \unicode[STIX]{x1D703})$
. The system has three independent dimensionless groups: the density ratio
$\boldsymbol{g}=-g(\boldsymbol{e}_{\unicode[STIX]{x1D703}}\cos \unicode[STIX]{x1D703}+\boldsymbol{e}_{r}\sin \unicode[STIX]{x1D703})$
. The system has three independent dimensionless groups: the density ratio
![]() $\unicode[STIX]{x1D70C}_{s}/\unicode[STIX]{x1D70C}_{f}$
(which takes the value
$\unicode[STIX]{x1D70C}_{s}/\unicode[STIX]{x1D70C}_{f}$
(which takes the value
![]() $0.69$
in our experiments), and two Reynolds numbers, based on rotation rate and the settling velocity,
$0.69$
in our experiments), and two Reynolds numbers, based on rotation rate and the settling velocity,
where
is the rising speed of the (buoyant) sphere in quiescent fluid. The quantity
![]() $Re$
, as defined in (2.1), is often known as the Taylor number (e.g. Childress Reference Childress1964).
$Re$
, as defined in (2.1), is often known as the Taylor number (e.g. Childress Reference Childress1964).
The equation of motion for the sphere is
where
![]() $m_{p}=(4/3)\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D70C}_{s}$
is the mass of the spherical particle,
$m_{p}=(4/3)\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D70C}_{s}$
is the mass of the spherical particle,
![]() $dV$
represents the particle surface,
$dV$
represents the particle surface,
![]() $\boldsymbol{n}$
is a unit outward normal and
$\boldsymbol{n}$
is a unit outward normal and
![]() $\unicode[STIX]{x1D70E}$
is the Cauchy stress in the fluid. At infinitesimal Reynolds number, the contributions to this stress integral for a spherical particle in an unbounded domain can be described by the history, buoyancy, drag, centrifugal and added mass forces (Maxey & Riley Reference Maxey and Riley1983). Away from the Stokes flow limit, Magnaudet (Reference Magnaudet1997) reviews the forces and inertial corrections occurring at low to moderate Reynolds numbers, when the particle is also subject to a lift force. We now evaluate the contribution from each of these forces.
$\unicode[STIX]{x1D70E}$
is the Cauchy stress in the fluid. At infinitesimal Reynolds number, the contributions to this stress integral for a spherical particle in an unbounded domain can be described by the history, buoyancy, drag, centrifugal and added mass forces (Maxey & Riley Reference Maxey and Riley1983). Away from the Stokes flow limit, Magnaudet (Reference Magnaudet1997) reviews the forces and inertial corrections occurring at low to moderate Reynolds numbers, when the particle is also subject to a lift force. We now evaluate the contribution from each of these forces.
The buoyancy and Stokes drag forces are given by
and
respectively (see e.g. Batchelor Reference Batchelor1967; Maxey & Riley Reference Maxey and Riley1983). If all inertial and acceleration forces can be neglected (namely when
![]() $Re\rightarrow 0$
,
$Re\rightarrow 0$
,
![]() $Re_{p}\rightarrow 0$
,
$Re_{p}\rightarrow 0$
,
![]() $\unicode[STIX]{x1D6FA}^{2}R/g\rightarrow 0$
), then the stress on the sphere results from these two forces alone. In this limit, the radial force balance implies that any equilibrium must lie at the same vertical position as the origin.
$\unicode[STIX]{x1D6FA}^{2}R/g\rightarrow 0$
), then the stress on the sphere results from these two forces alone. In this limit, the radial force balance implies that any equilibrium must lie at the same vertical position as the origin.
The fluid acceleration generated by the rotation of the cylinder results in a radial pressure gradient, and a consequent inward-pointing radial force on the particle, given by
When a spherical particle in an unbounded parallel shear flow is subjected to a force, it experiences an additional lift force in the perpendicular direction (Segré & Silberberg Reference Segré and Silberberg1962), which cannot be explained by viscous stresses alone (Bretherton Reference Bretherton1962). For a spherical particle in a shear flow (where a Reynolds number
![]() $Re_{s}=\unicode[STIX]{x1D70C}_{f}a^{2}\dot{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D707}$
is defined from the shear rate
$Re_{s}=\unicode[STIX]{x1D70C}_{f}a^{2}\dot{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D707}$
is defined from the shear rate
![]() $\dot{\unicode[STIX]{x1D6FE}}$
), Saffman (Reference Saffman1965) calculated the strength of this lift force in the low Reynolds number regime
$\dot{\unicode[STIX]{x1D6FE}}$
), Saffman (Reference Saffman1965) calculated the strength of this lift force in the low Reynolds number regime
![]() $Re_{p}\ll Re_{s}^{1/2}\ll 1$
, showing that it scales with
$Re_{p}\ll Re_{s}^{1/2}\ll 1$
, showing that it scales with
![]() $Re_{s}^{1/2}$
.
$Re_{s}^{1/2}$
.
Saffman’s calculation of the lift force was subsequently extended by McLaughlin (Reference McLaughlin1991) to the regime in which both Reynolds numbers are much less than one, but where
![]() $Re_{p}$
is not necessarily small compared to
$Re_{p}$
is not necessarily small compared to
![]() $Re_{s}^{1/2}$
. Numerical calculation (Dandy & Dwyer Reference Dandy and Dwyer1990) indicates that the expression of Saffman (Reference Saffman1965), formally valid only in the asymptotic regime
$Re_{s}^{1/2}$
. Numerical calculation (Dandy & Dwyer Reference Dandy and Dwyer1990) indicates that the expression of Saffman (Reference Saffman1965), formally valid only in the asymptotic regime
![]() $Re_{p}\ll Re_{s}^{1/2}\ll 1$
, is nonetheless accurate if
$Re_{p}\ll Re_{s}^{1/2}\ll 1$
, is nonetheless accurate if
![]() $Re_{p}<Re_{s}^{1/2}<1$
(Mei Reference Mei1992).
$Re_{p}<Re_{s}^{1/2}<1$
(Mei Reference Mei1992).
In the case relevant to our problem, where the background flow is in solid-body rotation rather than parallel shear, Gotoh (Reference Gotoh1990) calculated the leading-order effects of inertia using a similar analysis to that of Saffman (Reference Saffman1965). At small Reynolds number (when
![]() $Re_{p}\ll Re^{1/2}\ll 1$
) and for a particle at rest, Gotoh (Reference Gotoh1990) shows that the leading-order contribution of inertia is at
$Re_{p}\ll Re^{1/2}\ll 1$
) and for a particle at rest, Gotoh (Reference Gotoh1990) shows that the leading-order contribution of inertia is at
![]() $O(Re^{1/2})$
, and takes the form
$O(Re^{1/2})$
, and takes the form
where
This expression is valid only for particles that are stationary in the laboratory frame (that is, particles that may be rotating, but for which
![]() $\text{d}\boldsymbol{x}/\text{d}t=0$
). The finite-
$\text{d}\boldsymbol{x}/\text{d}t=0$
). The finite-
![]() $Re$
adjustment (2.7) comprises both a radial lift component analogous to that found by Saffman (Reference Saffman1965) and an azimuthal component, corresponding to a modification of the Stokes drag law at small finite Reynolds number. We note that the mechanisms of lift and drag studied by Gotoh (Reference Gotoh1990) differ significantly from those that occur at high Reynolds number (Rastello et al.
Reference Rastello, Marié, Grosjean and Lance2009; Bluemink et al.
Reference Bluemink, Lohse, Prosperetti and Van Wijngaarden2010). At low Reynolds number, the lift force on a sphere in a rotating flow is directed inwards, towards the centre of rotation (Gotoh Reference Gotoh1990). Surprisingly, this is the opposite direction to the lift force in a low Reynolds number simple shear flow of the same vorticity. The explanation for this difference, given by Van Nierop et al. (Reference Van Nierop, Luther, Bluemink, Magnaudet, Prosperetti and Lohse2007), is that a sphere in a rotating base flow experiences two lift forces: an outward-directed force similar to the one occurring in simple shear flows (Saffman Reference Saffman1965), and an inward-directed force, slightly larger in magnitude, resulting from curvature of the sphere wake.
$Re$
adjustment (2.7) comprises both a radial lift component analogous to that found by Saffman (Reference Saffman1965) and an azimuthal component, corresponding to a modification of the Stokes drag law at small finite Reynolds number. We note that the mechanisms of lift and drag studied by Gotoh (Reference Gotoh1990) differ significantly from those that occur at high Reynolds number (Rastello et al.
Reference Rastello, Marié, Grosjean and Lance2009; Bluemink et al.
Reference Bluemink, Lohse, Prosperetti and Van Wijngaarden2010). At low Reynolds number, the lift force on a sphere in a rotating flow is directed inwards, towards the centre of rotation (Gotoh Reference Gotoh1990). Surprisingly, this is the opposite direction to the lift force in a low Reynolds number simple shear flow of the same vorticity. The explanation for this difference, given by Van Nierop et al. (Reference Van Nierop, Luther, Bluemink, Magnaudet, Prosperetti and Lohse2007), is that a sphere in a rotating base flow experiences two lift forces: an outward-directed force similar to the one occurring in simple shear flows (Saffman Reference Saffman1965), and an inward-directed force, slightly larger in magnitude, resulting from curvature of the sphere wake.
Candelier (Reference Candelier2008) showed that the steady lift and drag corrections obtained by Gotoh (Reference Gotoh1990) in fact arise as a special case of the time-dependent history force on the particle, in the case where the particle is stationary. This history force is not restricted to steady states, but describes the forces on a particle moving arbitrarily when
![]() $Re_{p}\ll Re^{1/2}\ll 1$
; for example, the lift and drag in the ‘centrifuging’ regime first calculated by Herron, Davis & Bretherton (Reference Herron, Davis and Bretherton1975) and the Basset–Boussinesq–Oseen force (Basset Reference Basset1888) are also captured by the history force of Candelier (Reference Candelier2008) in the appropriate regimes of particle motion. The expression for this history force is
$Re_{p}\ll Re^{1/2}\ll 1$
; for example, the lift and drag in the ‘centrifuging’ regime first calculated by Herron, Davis & Bretherton (Reference Herron, Davis and Bretherton1975) and the Basset–Boussinesq–Oseen force (Basset Reference Basset1888) are also captured by the history force of Candelier (Reference Candelier2008) in the appropriate regimes of particle motion. The expression for this history force is
where
![]() $\boldsymbol{v}_{s}=\text{d}\boldsymbol{x}/\text{d}t-\boldsymbol{u}(\boldsymbol{x})$
is the slip velocity,
$\boldsymbol{v}_{s}=\text{d}\boldsymbol{x}/\text{d}t-\boldsymbol{u}(\boldsymbol{x})$
is the slip velocity,
With the contributions to the surface integral in (2.3) calculated in (2.4), (2.5), (2.6) and (2.9), the equation of motion (2.3) then reads
We integrate (2.14) in time numerically using a second-order implicit backward differentiation formula (BDF2). The integrals in (2.9) are evaluated using a second-order trapezoidal rule, modified to account for the
![]() $1/\sqrt{t}$
singularity in the integrand. Since the history forces (2.9) involve the complete history of motion of the sphere, we must specify this motion; here we assume that the sphere is at rest for
$1/\sqrt{t}$
singularity in the integrand. Since the history forces (2.9) involve the complete history of motion of the sphere, we must specify this motion; here we assume that the sphere is at rest for
![]() $t<0$
, and starts to move at
$t<0$
, and starts to move at
![]() $t=0$
when integration of the governing equations begins. We use the result that the history force reduces to the lift force of Gotoh (Reference Gotoh1990) for a sphere at rest (i.e.
$t=0$
when integration of the governing equations begins. We use the result that the history force reduces to the lift force of Gotoh (Reference Gotoh1990) for a sphere at rest (i.e.
![]() $\boldsymbol{F}_{H}(t^{\prime })=\boldsymbol{F}_{L}(t^{\prime })$
if
$\boldsymbol{F}_{H}(t^{\prime })=\boldsymbol{F}_{L}(t^{\prime })$
if
![]() $\text{d}\boldsymbol{x}/\text{d}t=0$
for all
$\text{d}\boldsymbol{x}/\text{d}t=0$
for all
![]() $t\leqslant t^{\prime }$
) to calculate this history integral exactly for
$t\leqslant t^{\prime }$
) to calculate this history integral exactly for
![]() $t<0$
, and thus avoid numerical error due to truncation of the integral domain.
$t<0$
, and thus avoid numerical error due to truncation of the integral domain.
We use this time-dependent theory to study the existence and stability of equilibrium points. For a sphere in stationary equilibrium (2.14) reads
(since
![]() $\boldsymbol{F}_{H}$
reduces to
$\boldsymbol{F}_{H}$
reduces to
![]() $\boldsymbol{F}_{L}$
for a stationary sphere), with azimuthal and radial components
$\boldsymbol{F}_{L}$
for a stationary sphere), with azimuthal and radial components
Solving for
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D703}$
, we find the equilibrium position of the sphere to be
$\unicode[STIX]{x1D703}$
, we find the equilibrium position of the sphere to be
Since
![]() $y>0$
, the equilibrium position for a buoyant sphere lies above the origin. This arises from the requirement that the radial component of the buoyancy force
$y>0$
, the equilibrium position for a buoyant sphere lies above the origin. This arises from the requirement that the radial component of the buoyancy force
![]() $F_{B}$
is directed outwards, to balance the inward-directed lift and centrifugal forces. This differs from the prediction
$F_{B}$
is directed outwards, to balance the inward-directed lift and centrifugal forces. This differs from the prediction
![]() $y<0$
obtained from models where rotating background flow is approximated as a simple shear flow, where the Saffman (Reference Saffman1965) expression for the perpendicular component of lift is used (e.g. Coimbra & Kobayashi Reference Coimbra and Kobayashi2002; Ramirez et al.
Reference Ramirez, Lim, Coimbra and Kobayashi2003). We note that the vertical displacement of the equilibrium position is much smaller than the horizontal displacement (by an order of
$y<0$
obtained from models where rotating background flow is approximated as a simple shear flow, where the Saffman (Reference Saffman1965) expression for the perpendicular component of lift is used (e.g. Coimbra & Kobayashi Reference Coimbra and Kobayashi2002; Ramirez et al.
Reference Ramirez, Lim, Coimbra and Kobayashi2003). We note that the vertical displacement of the equilibrium position is much smaller than the horizontal displacement (by an order of
![]() $Re^{1/2}$
), and so the equilibrium points lie close to the horizontal diameter of the cylinder on a radius, which for our experimental parameters is
$Re^{1/2}$
), and so the equilibrium points lie close to the horizontal diameter of the cylinder on a radius, which for our experimental parameters is
![]() ${\lesssim}3^{\circ }$
above the central plane. The stability of these equilibrium points is discussed in § 4.
${\lesssim}3^{\circ }$
above the central plane. The stability of these equilibrium points is discussed in § 4.
3 Experiment
3.1 Experimental set-up and procedure

Figure 2. Schematic diagram of the experiment. A glass cylinder was mounted horizontally between bearings and completely filled with glycerol. A light sphere was placed inside it and the cylinder was rotated around its axis using a motor, a gear box and a smooth belt. A shaft encoder was used to measure the frequency of rotation of the cylinder.
A schematic diagram of the apparatus is given in figure 2. The apparatus comprised a precision-bored rig glass cylindrical drum of length
![]() $225.000\pm 0.005~\text{mm}$
, inner diameter
$225.000\pm 0.005~\text{mm}$
, inner diameter
![]() $120.000\pm 0.005~\text{mm}$
and with a wall thickness of
$120.000\pm 0.005~\text{mm}$
and with a wall thickness of
![]() $5.200\pm 0.005~\text{mm}$
. The cylinder was completely filled with glycerol of density
$5.200\pm 0.005~\text{mm}$
. The cylinder was completely filled with glycerol of density
![]() $\unicode[STIX]{x1D70C}_{g}=1.261~\text{g}~\text{cm}^{-3}$
and viscosity
$\unicode[STIX]{x1D70C}_{g}=1.261~\text{g}~\text{cm}^{-3}$
and viscosity
![]() $\unicode[STIX]{x1D708}=1100\pm 0.3~\text{mm}^{2}~\text{s}^{-1}$
(measured using an Ubbelohde suspended level viscometer). The experiments were performed in a temperature controlled room with a measured air temperature of
$\unicode[STIX]{x1D708}=1100\pm 0.3~\text{mm}^{2}~\text{s}^{-1}$
(measured using an Ubbelohde suspended level viscometer). The experiments were performed in a temperature controlled room with a measured air temperature of
![]() $20\pm 0.5\,^{\circ }\text{C}$
. This gave rise to an estimated temperature variation of
$20\pm 0.5\,^{\circ }\text{C}$
. This gave rise to an estimated temperature variation of
![]() $\pm 0.2\,^{\circ }\text{C}$
in the glycerol.
$\pm 0.2\,^{\circ }\text{C}$
in the glycerol.
The spheres used were polypropylene, of density
![]() $\unicode[STIX]{x1D70C}_{s}=0.87\pm 0.02~\text{g}~\text{cm}^{-3}$
and radius
$\unicode[STIX]{x1D70C}_{s}=0.87\pm 0.02~\text{g}~\text{cm}^{-3}$
and radius
![]() $a=3.15,4.76,6.32,7.05,7.90,9.50~\text{mm}\;(\pm 0.005~\text{mm})$
.
$a=3.15,4.76,6.32,7.05,7.90,9.50~\text{mm}\;(\pm 0.005~\text{mm})$
.
The cylinder was mounted on bearings on a machined steel platform with three adjustable legs, which were used to level the cylinder using an engineer’s spirit level. Careful levelling of the system was required in order to minimise buoyancy-induced drift of the sphere along the axis of the cylinder. The cylinder was rotated using a DC motor with feedback control via a 10:1 gear box, which was connected to the cylinder by a smooth belt. The speed of rotation was controlled by a commercial servo control and the rotation frequency was measured using an optical encoder, attached to the shaft of the motor, which produced 500 pulses per revolution. The pulse count was monitored using a universal counter and this was used to calibrate the rotation rate of the cylinder.
The angular velocity of the cylinder,
![]() $\unicode[STIX]{x1D6FA}=2\unicode[STIX]{x03C0}f$
, was measured by the encoder to an accuracy of 0.01 %. The maximum angular velocity used in this experiment was
$\unicode[STIX]{x1D6FA}=2\unicode[STIX]{x03C0}f$
, was measured by the encoder to an accuracy of 0.01 %. The maximum angular velocity used in this experiment was
![]() $\unicode[STIX]{x1D6FA}\approx 25~\text{rad}~\text{s}^{-1}$
giving a maximum Reynolds number
$\unicode[STIX]{x1D6FA}\approx 25~\text{rad}~\text{s}^{-1}$
giving a maximum Reynolds number
![]() $Re=a^{2}\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D708}\approx 2$
for the largest sphere. However, the majority of the experiments were performed with
$Re=a^{2}\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D708}\approx 2$
for the largest sphere. However, the majority of the experiments were performed with
![]() $0.05<Re<0.7$
.
$0.05<Re<0.7$
.
The inside of the cylinder was polished and ground, as was a 1 cm band on the outside at the ends. The end caps were machined together to ensure that, when mounted, any misalignment of the ends was minimal. The excellent agreement between the experimental results and the theory for the fixed points suggests that any secondary flows were weak.
Two time scales were considered when taking into account how long it would take the fluid to achieve solid-body rotation after the rotational velocity were modified. As described by Greenspan & Howard (Reference Greenspan and Howard1963), the viscous diffusion time is
![]() $T_{d}=R^{2}/\unicode[STIX]{x1D707}\approx 3.2~\text{s}$
, and the spin-up time is
$T_{d}=R^{2}/\unicode[STIX]{x1D707}\approx 3.2~\text{s}$
, and the spin-up time is
![]() $T_{s}=R/\sqrt{\unicode[STIX]{x1D707}\,\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FA}}\approx 1.8~\text{s}$
, for a change in rotation rate
$T_{s}=R/\sqrt{\unicode[STIX]{x1D707}\,\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FA}}\approx 1.8~\text{s}$
, for a change in rotation rate
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FA}$
. After a change of rotation rate, we waited a time much longer than
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6FA}$
. After a change of rotation rate, we waited a time much longer than
![]() $T_{d}$
and
$T_{d}$
and
![]() $T_{s}$
(at least two minutes) before making any measurements, to ensure that any transients had decayed and the fluid inside the cylinder was in solid-body rotation.
$T_{s}$
(at least two minutes) before making any measurements, to ensure that any transients had decayed and the fluid inside the cylinder was in solid-body rotation.
When the cylinder was filled with glycerol, air also entered the fluid creating bubbles. The presence of an air bubble of comparable size to the sphere produced unwanted complications in the dynamics, analogous to those found when there is more than one spherical particle in the flow; see Mullin et al. (Reference Mullin, Li, Del Pino and Ashmore2005). Hence, before each set of experiments, bubbles were removed by first rotating the cylinder at high speed so that the bubbles merged on the axis of the cylinder. The larger bubble which formed was removed by injecting degassed fluid into one of two sealable holes drilled into the end plate of the cylinder.
The cylinder was front-illuminated using two light sources, and the back lid of the cylinder was painted white to improve the contrast between the background and the dark green polypropylene sphere. Images were taken using a fast digital camera (Sony XCD-X710) and the position of the sphere was determined by a dedicated image analysis MATLAB routine. The contrast between the sphere and the white background was used to identify the position of the centre of the sphere.
4 Results
4.1 Fixed points
At the highest Reynolds numbers examined,
![]() $Re\approx 2$
, the sphere rotated on its axis about an equilibrium position close to the centre of the cylinder. As
$Re\approx 2$
, the sphere rotated on its axis about an equilibrium position close to the centre of the cylinder. As
![]() $Re$
was decreased, the sphere adopted new equilibrium positions away from the centre of the cylinder, as shown in figure 3. The sphere spun on its axis at each of the equilibrium positions with a dimensionless rotation frequency
$Re$
was decreased, the sphere adopted new equilibrium positions away from the centre of the cylinder, as shown in figure 3. The sphere spun on its axis at each of the equilibrium positions with a dimensionless rotation frequency
![]() $\unicode[STIX]{x1D714}_{r}/\unicode[STIX]{x1D6FA}\approx 1$
, as expected from the torque balance on a sphere in a rotating flow (Gotoh Reference Gotoh1990). Below a critical Reynolds number the sphere no longer stayed at a steady equilibrium point, but described a circular orbit.
$\unicode[STIX]{x1D714}_{r}/\unicode[STIX]{x1D6FA}\approx 1$
, as expected from the torque balance on a sphere in a rotating flow (Gotoh Reference Gotoh1990). Below a critical Reynolds number the sphere no longer stayed at a steady equilibrium point, but described a circular orbit.

Figure 3. Sphere of radius
![]() $a=7.90~\text{mm}$
(false-colour shaded red, online) at different Reynolds numbers. The rotational axis of the drum is marked by a dotted line and a cross where this axis meets the far wall of the drum. As
$a=7.90~\text{mm}$
(false-colour shaded red, online) at different Reynolds numbers. The rotational axis of the drum is marked by a dotted line and a cross where this axis meets the far wall of the drum. As
![]() $Re$
decreases, the horizontal displacement of sphere equilibrium position from this axis,
$Re$
decreases, the horizontal displacement of sphere equilibrium position from this axis,
![]() $x$
, moves further from the cylinder axis. (a)
$x$
, moves further from the cylinder axis. (a)
![]() $Re=1.990$
,
$Re=1.990$
,
![]() $x\approx 0~\text{mm}$
; (b)
$x\approx 0~\text{mm}$
; (b)
![]() $Re=0.792$
,
$Re=0.792$
,
![]() $x=1.8~\text{mm}$
; (c)
$x=1.8~\text{mm}$
; (c)
![]() $Re=0.332$
,
$Re=0.332$
,
![]() $x=6.25~\text{mm}$
.
$x=6.25~\text{mm}$
.

Figure 4. Horizontal displacement of the sphere as a function of Reynolds number for spheres of radii
![]() $a=9.5,7.9,7.05,6.33,4.78~\text{mm}$
. Open circles denote the centre of an orbit; filled circles indicate stationary fixed points. Each data point corresponds to the distance between the central axis of the cylinder and the centre of the sphere, averaged over 2 s (60 frames). The continuous line is the theoretical prediction for this horizontal displacement, from § 2.
$a=9.5,7.9,7.05,6.33,4.78~\text{mm}$
. Open circles denote the centre of an orbit; filled circles indicate stationary fixed points. Each data point corresponds to the distance between the central axis of the cylinder and the centre of the sphere, averaged over 2 s (60 frames). The continuous line is the theoretical prediction for this horizontal displacement, from § 2.
The equilibrium positions were measured for each diameter of sphere and the horizontal distance of this equilibrium from the cylinder axis,
![]() $x$
, is plotted as a function of
$x$
, is plotted as a function of
![]() $Re$
as figure 4. Open markers with vertical bars indicate spheres on a circular orbit, and in this case the marker denotes the position of the centre of the orbit and the height of the bar indicates the standard deviation from the average position, a measure of the amplitude of the oscillation. These positions have been normalised by
$Re$
as figure 4. Open markers with vertical bars indicate spheres on a circular orbit, and in this case the marker denotes the position of the centre of the orbit and the height of the bar indicates the standard deviation from the average position, a measure of the amplitude of the oscillation. These positions have been normalised by
![]() $Re_{p}a$
, and under this scaling the theory (2.18), plotted as a solid curve, predicts a collapse of the experimental measurements. There is generally good agreement between theoretical prediction and experimental measurement of the horizontal displacement of the equilibrium point, both in the dependence on
$Re_{p}a$
, and under this scaling the theory (2.18), plotted as a solid curve, predicts a collapse of the experimental measurements. There is generally good agreement between theoretical prediction and experimental measurement of the horizontal displacement of the equilibrium point, both in the dependence on
![]() $Re$
and the collapse with respect to
$Re$
and the collapse with respect to
![]() $Re_{p}a$
. The displacement in the vertical direction
$Re_{p}a$
. The displacement in the vertical direction
![]() $y$
is much smaller than the horizontal displacement, as predicted theoretically (2.19), but this vertical displacement is below the limits of resolution of the experiment. Although we are unable to give precise estimates for the location of the centre of the sphere we are confident that the centre was always above the central plane of the cylinder for all fixed points in accord with theory.
$y$
is much smaller than the horizontal displacement, as predicted theoretically (2.19), but this vertical displacement is below the limits of resolution of the experiment. Although we are unable to give precise estimates for the location of the centre of the sphere we are confident that the centre was always above the central plane of the cylinder for all fixed points in accord with theory.
For a wide range of parameters, including the values relevant to our experiments, numerical integration of the time-dependent model (2.14) indicates that these fixed points are stable: no orbits are predicted. This was ascertained by solving for the motion of spheres that were initially displaced from their equilibrium position. Up to a scaling factor, the trajectory obtained is independent of the size of the initial displacement of the sphere, since the model is linear in particle position and velocity. After an initial transient of duration
![]() ${\sim}1/\unicode[STIX]{x1D6FA}$
arising from the history force, the spheres are predicted to spiral towards the equilibrium point, with the distance from this point decaying exponentially in time. The mechanism driving this stable attraction to the fixed point is simply the centrifugal pressure gradient in the fluid, with the rate of approach to the fixed point modified only slightly by the history force. This behaviour is consistent with the trajectories for buoyant particles plotted in figure 5 of Candelier (Reference Candelier2008) (which are qualitatively similar to the trajectories we obtain for our experimental parameter values), in that the rate of approach to the fixed point differs only slightly in different formulations of the history force.
${\sim}1/\unicode[STIX]{x1D6FA}$
arising from the history force, the spheres are predicted to spiral towards the equilibrium point, with the distance from this point decaying exponentially in time. The mechanism driving this stable attraction to the fixed point is simply the centrifugal pressure gradient in the fluid, with the rate of approach to the fixed point modified only slightly by the history force. This behaviour is consistent with the trajectories for buoyant particles plotted in figure 5 of Candelier (Reference Candelier2008) (which are qualitatively similar to the trajectories we obtain for our experimental parameter values), in that the rate of approach to the fixed point differs only slightly in different formulations of the history force.
4.2 Oscillations
As noted in figure 4, below a critical
![]() $Re$
the spheres were observed to trace an orbit, centred around the equilibrium position predicted by the theory of § 2. This is contrary to the theoretical predictions of a stable equilibrium without a limit cycle: this discrepancy will be discussed later. The paths of these orbits for
$Re$
the spheres were observed to trace an orbit, centred around the equilibrium position predicted by the theory of § 2. This is contrary to the theoretical predictions of a stable equilibrium without a limit cycle: this discrepancy will be discussed later. The paths of these orbits for
![]() $a=7.9~\text{mm}$
are shown in figure 6(a) for a range of
$a=7.9~\text{mm}$
are shown in figure 6(a) for a range of
![]() $Re$
. Solid lines in this figure correspond to the least-squares fits of circles to the data; these circles were used to estimate the centre and radius of each orbit.
$Re$
. Solid lines in this figure correspond to the least-squares fits of circles to the data; these circles were used to estimate the centre and radius of each orbit.
The radius of each orbit is plotted as a function of
![]() $Re$
in figure 7. For all sphere sizes the orbit radius increased, as did the distance between the orbit centre and the cylinder axis, as
$Re$
in figure 7. For all sphere sizes the orbit radius increased, as did the distance between the orbit centre and the cylinder axis, as
![]() $Re$
decreased. The critical distance and Reynolds number at which the oscillation started was estimated by measuring the radius of the orbit. When the radius was smaller than 5 % of the radius of the sphere, approximately the smallest orbit that could be observed clearly, the sphere was deemed to be on a fixed point. We have chosen the critical point in this way as it enables a measure which compares the onset of the oscillations between all spheres. We observe that the sphere becomes unstable to periodic orbits when its equilibrium point is greater than
$Re$
decreased. The critical distance and Reynolds number at which the oscillation started was estimated by measuring the radius of the orbit. When the radius was smaller than 5 % of the radius of the sphere, approximately the smallest orbit that could be observed clearly, the sphere was deemed to be on a fixed point. We have chosen the critical point in this way as it enables a measure which compares the onset of the oscillations between all spheres. We observe that the sphere becomes unstable to periodic orbits when its equilibrium point is greater than
![]() ${\approx}0.7$
of the sphere radius, for a range of sphere sizes (figure 5). This corresponds to smaller spheres becoming unstable at smaller values of the critical Reynolds number
${\approx}0.7$
of the sphere radius, for a range of sphere sizes (figure 5). This corresponds to smaller spheres becoming unstable at smaller values of the critical Reynolds number
![]() $Re_{c}$
.
$Re_{c}$
.

Figure 5. Non-dimensional horizontal displacement of the sphere at the onset of instability,
![]() $x_{c}/a$
, as a function of sphere radius
$x_{c}/a$
, as a function of sphere radius
![]() $a$
.
$a$
.
In many fluid mechanics problems the onset of a simple oscillation is well described as a Hopf bifurcation in which
![]() $R\sim |Re-Re_{c}|^{1/2}$
where
$R\sim |Re-Re_{c}|^{1/2}$
where
![]() $Re_{c}$
is the critical value of
$Re_{c}$
is the critical value of
![]() $Re$
at the bifurcation point. Examples include flow past a cylinder (Sreenivasan, Strykowski & Olinger Reference Sreenivasan, Strykowski, Olinger and Ghia1987), Taylor–Couette flow (Pfister & Gerdts Reference Pfister and Gerdts1981) and Rayleigh–Bénard convection (Ecke, Zhong & Knobloch Reference Ecke, Zhong and Knobloch1992). Indeed in a study of the closely related problem of the motion of heavy spheres in a rotating horizontal cylinder of viscous fluid (Mullin et al.
Reference Mullin, Li, Del Pino and Ashmore2005), the characteristics of a simple Hopf bifurcation are also found. In the present case, when the light sphere is away from the wall the growth of the radius of the oscillation radius with decreasing
$Re$
at the bifurcation point. Examples include flow past a cylinder (Sreenivasan, Strykowski & Olinger Reference Sreenivasan, Strykowski, Olinger and Ghia1987), Taylor–Couette flow (Pfister & Gerdts Reference Pfister and Gerdts1981) and Rayleigh–Bénard convection (Ecke, Zhong & Knobloch Reference Ecke, Zhong and Knobloch1992). Indeed in a study of the closely related problem of the motion of heavy spheres in a rotating horizontal cylinder of viscous fluid (Mullin et al.
Reference Mullin, Li, Del Pino and Ashmore2005), the characteristics of a simple Hopf bifurcation are also found. In the present case, when the light sphere is away from the wall the growth of the radius of the oscillation radius with decreasing
![]() $Re$
is well fitted by
$Re$
is well fitted by
![]() $R\sim Re^{-2}$
, as demonstrated by the line of gradient
$R\sim Re^{-2}$
, as demonstrated by the line of gradient
![]() $-2$
in figure 7.
$-2$
in figure 7.

Figure 6. Orbits of a sphere with
![]() $a=7.9~\text{mm}$
at various fixed values of
$a=7.9~\text{mm}$
at various fixed values of
![]() $Re$
. Symbols are observed sphere positions, and the solid line corresponds to a circular fit for each orbit.
$Re$
. Symbols are observed sphere positions, and the solid line corresponds to a circular fit for each orbit.

Figure 7. Non-dimensional orbit radius
![]() $R/a$
, plotted against
$R/a$
, plotted against
![]() $Re$
. The grey dashed line denotes the threshold below which a sphere is assumed to lie on its equilibrium point.
$Re$
. The grey dashed line denotes the threshold below which a sphere is assumed to lie on its equilibrium point.

Figure 8. Plot of the orbits of a 12.5 mm sphere at the various given values of
![]() $Re$
, illustrating the behaviour of the orbits as they approach the side wall of the drum (solid black circle).
$Re$
, illustrating the behaviour of the orbits as they approach the side wall of the drum (solid black circle).
As
![]() $Re$
decreases, the increase of both orbit radius and displacement of the orbit centre from the cylinder axis means that the influence of the cylinder wall becomes dominant for sufficiently small
$Re$
decreases, the increase of both orbit radius and displacement of the orbit centre from the cylinder axis means that the influence of the cylinder wall becomes dominant for sufficiently small
![]() $Re$
. When
$Re$
. When
![]() $Re$
was
$Re$
was
![]() ${\lesssim}0.01$
the sphere sat at a series of fixed points adjacent to the descending wall. When
${\lesssim}0.01$
the sphere sat at a series of fixed points adjacent to the descending wall. When
![]() $Re$
was increased above
$Re$
was increased above
![]() ${\approx}0.01$
the sphere began to oscillate adjacent to the wall. Typical examples of orbits near onset can be seen in figure 8 for a 12.5 mm sphere at
${\approx}0.01$
the sphere began to oscillate adjacent to the wall. Typical examples of orbits near onset can be seen in figure 8 for a 12.5 mm sphere at
![]() $Re=0.012$
. The orbit is elliptical and the motion is localised adjacent to the cylinder wall. The radius of this oscillation was proportional to the
$Re=0.012$
. The orbit is elliptical and the motion is localised adjacent to the cylinder wall. The radius of this oscillation was proportional to the
![]() $R\sim |Re-Re_{c}|^{1/2}$
in accord with a standard Hopf bifurcation and the results of Mullin et al. (Reference Mullin, Li, Del Pino and Ashmore2005) for heavy spheres. It can also be seen in figure 8 that the orbit became more circular as
$R\sim |Re-Re_{c}|^{1/2}$
in accord with a standard Hopf bifurcation and the results of Mullin et al. (Reference Mullin, Li, Del Pino and Ashmore2005) for heavy spheres. It can also be seen in figure 8 that the orbit became more circular as
![]() $Re$
was increased and approaching the small near-perfect circular orbits close to the cylinder axis (figure 6).
$Re$
was increased and approaching the small near-perfect circular orbits close to the cylinder axis (figure 6).

Figure 9. Graph of the frequency of oscillation of spheres in the diameter range 9.5–25.0 mm plotted as a function of
![]() $Re$
. The frequencies have been made dimensionless using the rotation frequency of the cylinder.
$Re$
. The frequencies have been made dimensionless using the rotation frequency of the cylinder.
The frequency of the orbit was measured and its non-dimensional form is shown in figure 9, plotted as a function of
![]() $Re$
. The frequency ratio of the sphere to the cylinder is close to two when the sphere is near the wall and rapidly approaches one as the sphere moved towards the centre of the cylinder when
$Re$
. The frequency ratio of the sphere to the cylinder is close to two when the sphere is near the wall and rapidly approaches one as the sphere moved towards the centre of the cylinder when
![]() $Re$
was increased. As noted above, the orbit became more circular and was centred on the unstable fixed point.
$Re$
was increased. As noted above, the orbit became more circular and was centred on the unstable fixed point.
5 Discussion and conclusions
We have investigated the motion of a light sphere immersed in a rotating viscous flow at low Reynolds numbers. Our experimental results show a set of stable fixed points which are eccentric to the axis of the cylinder over a range of
![]() $Re$
. The balance of forces required for stability is explained using the buoyancy force arguments of Gotoh (Reference Gotoh1990), Magnaudet (Reference Magnaudet1997) and Candelier (Reference Candelier2008). We present results of a model for the equilibrium position of the sphere, based on these arguments, and the predictions of the equilibrium points are in excellent accord with the experiments.
$Re$
. The balance of forces required for stability is explained using the buoyancy force arguments of Gotoh (Reference Gotoh1990), Magnaudet (Reference Magnaudet1997) and Candelier (Reference Candelier2008). We present results of a model for the equilibrium position of the sphere, based on these arguments, and the predictions of the equilibrium points are in excellent accord with the experiments.
We also found experimentally that these equilibrium positions become unstable to oscillatory motion below a critical value
![]() $Re_{c}$
and the sphere follows circular orbits. The centre of the orbit is located on the fixed point predicted by the theory, but the existence of a stable orbit is not predicted by the theory, which instead predicts a stable fixed point. As
$Re_{c}$
and the sphere follows circular orbits. The centre of the orbit is located on the fixed point predicted by the theory, but the existence of a stable orbit is not predicted by the theory, which instead predicts a stable fixed point. As
![]() $Re$
decreases, the radius of the experimentally observed orbit scales initially as
$Re$
decreases, the radius of the experimentally observed orbit scales initially as
![]() $Re^{-2}$
, which is slower than the growth following a typical Hopf bifurcation.
$Re^{-2}$
, which is slower than the growth following a typical Hopf bifurcation.
Two clear possibilities exist for the difference between the stability predictions of the theory and the experimental observations. Firstly, the effect of the outer walls of the drum are neglected in the theory, but become significant in the experiments as
![]() $Re$
is decreased and the predicted equilibrium position moves away from the axis of rotation towards the drum wall. At these lower values of
$Re$
is decreased and the predicted equilibrium position moves away from the axis of rotation towards the drum wall. At these lower values of
![]() $Re$
, the experimentally observed orbits become elliptical and decrease in size, until the sphere restabilises at a stable equilibrium point adjacent to the cylinder wall. This change in stability occurs via a standard Hopf bifurcation, as reported previously for heavy spheres (Mullin et al.
Reference Mullin, Li, Del Pino and Ashmore2005). It is possible that the orbits we observe are caused by wall effects destabilising even the fixed points very close to the axis of rotation. To test this, experiments were performed in which a 100 mm long Plexiglas cylinder of radius 3 mm glued to the inner wall of the cylinder. No change to the orbits was observed, even with this large perturbation, suggesting that wall effects (and indeed any small geometrical imperfections in the experiment) are not the cause of the observed orbits.
$Re$
, the experimentally observed orbits become elliptical and decrease in size, until the sphere restabilises at a stable equilibrium point adjacent to the cylinder wall. This change in stability occurs via a standard Hopf bifurcation, as reported previously for heavy spheres (Mullin et al.
Reference Mullin, Li, Del Pino and Ashmore2005). It is possible that the orbits we observe are caused by wall effects destabilising even the fixed points very close to the axis of rotation. To test this, experiments were performed in which a 100 mm long Plexiglas cylinder of radius 3 mm glued to the inner wall of the cylinder. No change to the orbits was observed, even with this large perturbation, suggesting that wall effects (and indeed any small geometrical imperfections in the experiment) are not the cause of the observed orbits.
Secondly, the theory is formally valid only in the asymptotic limit
![]() $Re_{p}\ll Re^{1/2}\ll 1$
. In our experiments,
$Re_{p}\ll Re^{1/2}\ll 1$
. In our experiments,
![]() $Re^{1/2}<1$
is satisfied always, and
$Re^{1/2}<1$
is satisfied always, and
![]() $Re_{p}<Re^{1/2}$
is satisfied for all but three measurements of the spheres of 9.5 mm radius. We observe orbits only for smaller values of
$Re_{p}<Re^{1/2}$
is satisfied for all but three measurements of the spheres of 9.5 mm radius. We observe orbits only for smaller values of
![]() $Re$
, which suggests that while
$Re$
, which suggests that while
![]() $Re^{1/2}\ll 1$
may be satisfied, finite-
$Re^{1/2}\ll 1$
may be satisfied, finite-
![]() $Re_{p}$
effect not included in the model may act to destabilise the equilibrium points as
$Re_{p}$
effect not included in the model may act to destabilise the equilibrium points as
![]() $Re_{p}$
approaches
$Re_{p}$
approaches
![]() $Re^{1/2}$
.
$Re^{1/2}$
.
Notably, the observed dependence of orbit radius on
![]() $Re$
is not the standard
$Re$
is not the standard
![]() $R\sim |Re-Re_{c}|^{1/2}$
expected of a Hopf bifurcation, and further work is required to explain the mechanism of instability and the origins of this behaviour. A full numerical simulation of the system may shed light on these issues, but it remains a challenging problem to resolve, in three dimensions, the subtle balance of stabilising and destabilising forces acting on the sphere at finite Reynolds number.
$R\sim |Re-Re_{c}|^{1/2}$
expected of a Hopf bifurcation, and further work is required to explain the mechanism of instability and the origins of this behaviour. A full numerical simulation of the system may shed light on these issues, but it remains a challenging problem to resolve, in three dimensions, the subtle balance of stabilising and destabilising forces acting on the sphere at finite Reynolds number.
Acknowledgements
T.M. acknowledges the support of the Leverhulme Trust through an Emeritus Fellowship.