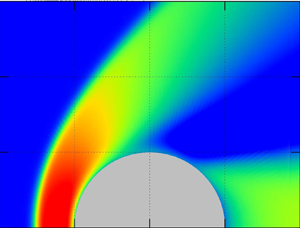
1. Introduction
A gas flow past a sphere is a fundamental problem of fluid dynamics. The solution to this problem for subsonic flows at low Reynolds numbers in the Stokes regime is well known and can be found in numerous textbooks (see e.g. Landau & Lifshitz Reference Landau and Lifshitz1989; Batchelor Reference Batchelor2000). Supersonic and hypersonic flows past a sphere in the continuum flow regime were the subject of numerous experimental and computational studies (see e.g. Nagata et al. Reference Nagata, Nonomura, Takahashi and Fukuda2016, Reference Nagata, Nonomura, Takahashi, Mizuno and Fukuda2018, Reference Nagata, Noguchi, Nonomura, Ohtani and Asai2020; Loth et al. Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021, and references therein). In this case, a supersonic flow always implies a high Reynolds number. Transonic and supersonic flows at low Reynolds numbers occur when a sphere moves with a velocity near or above the speed of sound through a low-density rarefied gas, where the mean free path of gas molecules is comparable to or larger than the sphere radius. Such flow conditions are typical at re-entry of space vehicles (Dogra, Wilmoth & Moss Reference Dogra, Wilmoth and Moss1992; Storch Reference Storch2002), impact ejecta and meteoroids (Melosh & Goldin Reference Melosh and Goldin2008), for small solid particles in two-phase flows in solid-propellant engines, jets and plumes (Carlson & Hoglund Reference Carlson and Hoglund1964; Crowe Reference Crowe1967; Nelson & Fields Reference Nelson and Fields1996; Crowe, Sommerfeld & Tsuji Reference Crowe, Sommerfeld and Tsuji1998), and in the shock layers in front of bodies moving with supersonic speed in the dusty Earth (Vasilevskii et al. Reference Vasilevskii, Osiptsov, Chirikhin and Yakovleva2001) and Martian (Papadopoulos, Tauber & Chang Reference Papadopoulos, Tauber and Chang1993; Ozawa et al. Reference Ozawa, Suzuki, Takayanagi and Fujita2011; Ching, Barnhardt & Ihme Reference Ching, Barnhardt and Ihme2021) atmospheres. These examples predetermine the practical interest to supersonic and hypersonic low-Reynolds-number flows over spheres, since the model of a spherical body is considered as the most general and common geometrical model for spacecrafts, meteoroids and dust particles. Due to the fundamental nature of this problem, the flow past a sphere can be considered as one of the benchmark problems of rarefied gas dynamics (Sharipov Reference Sharipov2012) and can be used to validate various numerical methods.
Continuum supersonic and hypersonic flows over a sphere are characterized by the formation of a bow shock wave in front of the body, a boundary layer at its surface, and flow separation that induces unsteady wakes behind the sphere. These flow features affect directly the two most important aerothermodynamic properties of a sphere, its drag force and energy transfer rate. When the gas density in the free stream or the size of a sphere gradually decreases, the effects of gas rarefaction become important. Due to gas rarefaction, the thicknesses of both bow shock wave and boundary layer increase, so that they merge smoothly into a viscous layer (Vogenitz et al. Reference Vogenitz, Bird, Broadwell and Rungaldi1968), and the degree of unsteadiness of the wake flow reduces (Dogra et al. Reference Dogra, Moss, Wilmoth and Price1994). For continuum flows past a sphere, an increase in the Mach number also reduces the degree of the wake unsteadiness (Nagata et al. Reference Nagata, Nonomura, Takahashi and Fukuda2016). In particular, three-dimensional simulations by Riahia et al. (Reference Riahia, Meldia, Favier, Serre and Goncalves2018) based on the compressible Navier–Stokes equations showed that the flow past a sphere is axisymmetric and steady at Mach number 2 and Reynolds number lower than 600. The continuum simulations and bifurcation analysis also show that the supersonic flow past a sphere remains globally stable at least for Reynolds numbers below 370 (Sansica et al. Reference Sansica, Robinet, Alizard and Goncalves2018).
In a rarefied gas, the frequency of intermolecular collisions drops, so that the assumption of local equilibrium no longer holds. Then the continuum hypothesis breaks down (Lofthouse, Boyd & Wright Reference Lofthouse, Boyd and Wright2007) and the flow cannot be described by the Navier–Stokes equations. Under such conditions, the flow regime is referred to as transitional, and the flow past a sphere can be described by mathematical models based on the Boltzmann kinetic equation (Hirschfelder, Curtiss & Bird Reference Hirschfelder, Curtiss and Bird1954; Ferziger & Kaper Reference Ferziger and Kaper1972; Cercignani Reference Cercignani1975; Sharipov Reference Sharipov2016). One of the computational methods to solve problems based on the Boltzmann equation is the direct simulation Monte Carlo (DSMC) method (Bird Reference Bird1994, Reference Bird2013). The DSMC method is a stochastic particle-based method, where the flow of a dilute gas is described by multiple simulated or modelling particles, which move and interact with each other like individual gas molecules in a real gas flow. The most important part of the DSMC method, the scheme for sampling binary collisions between simulated particles, is derived in agreement with the collision term in the Boltzmann equation. Therefore, the DSMC method is capable of providing unbiased statistical estimates for the solutions of the Boltzmann equation (Wagner Reference Wagner1992).
The DSMC method was used initially by Vogenitz et al. (Reference Vogenitz, Bird, Broadwell and Rungaldi1968) to study two-dimensional supersonic and hypersonic flows past a sphere. They considered, however, only two simulation cases, and some parameters of the computational model were not provided. A hypersonic flow of an oxygen–nitrogen mixture past a sphere was simulated by the DSMC method by Dogra et al. (Reference Dogra, Moss, Wilmoth and Price1994). A three-dimensional flow past a rotating sphere is considered by Volkov (Reference Volkov2009, Reference Volkov2011) based on the hard sphere model. The recent paper by Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) reports some results on the sphere drag based on the DSMC method without specifying the molecular model parameters. The heat transfer of a sphere was not considered in these works, with exception of papers by Volkov (Reference Volkov2009, Reference Volkov2011). Point-to-point comparison of the results obtained in these works is impossible, since the simulations were performed based on different molecular models and at different values of the Mach and Reynolds numbers. Thus the computational data on the sphere drag and heat transfer in the transitional flow regime available from literature are essentially incomplete. Moreover, none of the known DSMC-based studies addressed specifically the effects of gas species, gas–surface interaction parameters, free stream temperature and body temperature in supersonic and hypersonic transitional flows past a sphere.
In the limit of free molecular flow when the gas is highly rarefied and the intermolecular collisions can be neglected, the flow past a sphere can be obtained from a collisionless kinetic equation. The free molecular drag and energy transfer coefficients are functions of the free stream characteristics and parameters of the gas–surface interaction. For the diffuse–specular interaction (Schaaf & Chambre Reference Schaaf and Chambre1961; Kogan Reference Kogan1969; Cercignani Reference Cercignani1975; Sharipov Reference Sharipov2016), the expressions of the drag and energy transfer coefficients for a sphere are well known (Ashley Reference Ashley1949; Sauer Reference Sauer1951; Bird Reference Bird1994; Storch Reference Storch2002). However, this model contains only one parameter, which cannot describe all variety of experimental data. The model proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) contains two accommodation coefficients that allow one to describe the interaction of gas molecules with various treated and non-treated surfaces in quantitative agreement with the results of experimental measurements, and thus to account for the effect of surface state on the aerothermodynamic characteristics of bodies in rarefied gas flow. An approximate expression of the sphere drag coefficient in the free molecular flow regime based on the Cercignani–Lampis (CL) model (Cercignani & Lampis Reference Cercignani and Lampis1971) was suggested by Walker, Mehta & Koller (Reference Walker, Mehta and Koller2014) and Chernyak & Sograbi (Reference Chernyak and Sograbi2020). The CL model was applied to the gas flow past a sphere in the transitional flow regime only at small Mach numbers (Kalempa & Sharipov Reference Kalempa and Sharipov2020, Reference Kalempa and Sharipov2021). These results indicate the strong dependence of the drag and energy transfer coefficients on parameters of the CL model and surface temperature. Such a strong dependence is also expected to persist in supersonic flows in the transitional flow regime.
The sphere drag coefficient in supersonic flows was measured for the free stream Mach number up to 11 by Wegener & Ashkenas (Reference Wegener and Ashkenas1961), Kingslow & Potter (Reference Kingslow and Potter1963), Bailey & Hiatt (Reference Bailey and Hiatt1971, Reference Bailey and Hiatt1972) and Bailey (Reference Bailey1974). The known experimental data, however, correspond to the range of the free stream Reynolds number equal to or greater than 10. These experimental data, together with the approximate theoretical equations for free molecular flow, were used to design multiple semi-empirical correlations for the sphere drag coefficient in a broad range of Mach and Reynolds numbers. Among others, the correlations proposed by Henderson (Reference Henderson1976), Loth (Reference Loth2008) and Loth et al. (Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021) are used widely to predict drag force exerted on dust particles in supersonic two-phase gas–solid particle flows (see e.g. Volkov, Tsirkunov & Oesterlé Reference Volkov, Tsirkunov and Oesterlé2005; Ching et al. Reference Ching, Barnhardt and Ihme2021). Although multiple corrections were further proposed for these equations to improve the agreement with the experimental data (e.g. Walsh Reference Walsh1977; Parmar, Haselbacher & Balachandar Reference Parmar, Haselbacher and Balachandar2010; Loth et al. Reference Loth, Tyler Daspit, Jeong, Nagata and Nonomura2021), all known semi-empirical correlations for the sphere drag coefficient suffer from two drawbacks. First, they are not validated against experimental data in the transitional flow regime. Second, they do not account for the effects of gas species and parameters describing incomplete accommodation of gas molecules at the interaction with the sphere surface. The theoretical computations of high-speed flows past a sphere in the transitional flow regime can fill these gaps and provide data for the flow conditions least studied experimentally.
The effects of rarefaction and compressibility on the energy transfer of spheres in supersonic low-Reynolds-number flow were studied experimentally, among others, by Drake & Backer (Reference Drake and Backer1952), Kavanau (Reference Kavanau1955), Avleeva (Reference Avleeva1970) and Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1972). Based on the experimental results and known sphere energy transfer in free molecular flow, Sauer (Reference Sauer1951), Kavanau (Reference Kavanau1955) and Koshmarov & Svirshevskii (Reference Koshmarov and Svirshevskii1972) developed semi-empirical correlations for the sphere energy transfer coefficient applicable in broad ranges of Mach and Reynolds numbers. These equations are often used to predict energy transfer of solid particles in gas–solid particle flows (Carlson & Hoglund Reference Carlson and Hoglund1964; Volkov et al. Reference Volkov, Tsirkunov and Oesterlé2005; Ozawa et al. Reference Ozawa, Suzuki, Takayanagi and Fujita2011; Ching et al. Reference Ching, Barnhardt and Ihme2021). The known experimental data on the sphere energy transfer are even scarcer and less complete than for the sphere drag.
The flows past a sphere, as well as the sphere drag and energy transfer coefficients, in the limit of small Mach number can be calculated theoretically using the variational principles (Cercignani, Pagani & Bassanini Reference Cercignani, Pagani and Bassanini1968), direct numerical solution of the Bhatnagar–Gross–Krook and linearized Boltzmann equations (Lea & Loyalka Reference Lea and Loyalka1982; Loyalka Reference Loyalka1992; Takata, Sone & Aoki Reference Takata, Sone and Aoki1993), as well as asymptotic expansions of solutions of the Boltzmann equation (Taguchi Reference Taguchi2015). Asymptotic methods, however, are not applicable to supersonic flows, so the most reliable tool for simulations of high-speed flows past a sphere in the transitional flow regime is the DSMC method (Bird Reference Bird1994, Reference Bird2013).
The flexibility in the implementation of various models of intermolecular and gas–surface interactions is one of the fundamental advantages of the DSMC method. In the present work, the CL scattering kernel is implemented in the DSMC method in the form suggested by Lord (Reference Lord1991). As shown by Sharipov & Strapasson (Reference Sharipov and Strapasson2012a), the DSMC calculations can be performed based on arbitrary interaction potentials for monatomic gases. The use of lookup tables that determine the deflection angle for binary collisions based on the solution of classical (Sharipov & Strapasson Reference Sharipov and Strapasson2012a, Reference Sharipov and Strapasson2013) or quantum mechanical (Sharipov Reference Sharipov2018b; Dias & Sharipov Reference Dias and Sharipov2021) scattering problems allows one to perform DSMC calculations with the same computational cost as in the case of the variable hard sphere (VHS) and variable soft sphere (VSS) molecular models (Bird Reference Bird1994, Reference Bird2013). The approach based on lookup tables enables modelling interatomic collisions in the DSMC method based on arbitrary interatomic potentials, including the potentials established by ab initio (AI) calculations. The works by Sharipov (Reference Sharipov2018a,Reference Sharipovb) showed that at low temperatures, the quantum effects are significant and the lookup tables based on the classical approach lead to wrong results. According to Sharipov (Reference Sharipov2018b), DSMC calculations at any temperature based on the quantum approach require shorter computational time than those based on the classical approach. Therefore, all lookup tables used in the present work are based on quantum mechanics even when the quantum effects are not significant.
As is known, semi-empirical potentials, such as the hard spheres (HS) model and Lennard-Jones potential, are approximations that contain one or more adjustable parameters. To obtain these parameters, some experimental data, e.g. on the second virial coefficient and viscosity, are used. As a result, the parameter values vary depending on the experimental data utilized for parametrization, therefore the semi-empirical potentials have uncertainties that are hardly estimated. In contrast, the AI potentials are calculated from first physical principles, hence they are free from any adjustable parameter. In this regard, the AI potentials provide a more accurate solution to the scattering problem compared to the semi-empirical potentials such as the Lennard-Jones one. The DSMC method based on AI potentials was used successfully to study energy transfer in a rarefied gas (Strapasson & Sharipov Reference Strapasson and Sharipov2014), rarefied gas flow past a circular cylinder (Volkov & Sharipov Reference Volkov and Sharipov2017), the structure of shock waves (Sharipov & Dias Reference Sharipov and Dias2019; Dias & Sharipov Reference Dias and Sharipov2021), expansion of laser-induced plumes (Petrov et al. Reference Petrov, Ranjbar, Zhilyaev and Volkov2020), and gaseous mixture flow through an orifice (Sharipov Reference Sharipov2017). A systematic comparison of rarefied gas flows based on an AI potential with those based on VHS and VSS models performed by Wang et al. (Reference Wang, Zhang, Han, Zhang and Zhang2022) pointed out a significant error of the VHS and VSS models.
The goal of the present work is to perform high-fidelity kinetic simulations of gas flows over a sphere and to reveal the effects of the gas species, parameters of the gas–surface interaction models, free stream temperature and surface temperature on the sphere drag and energy transfer in transonic, supersonic and hypersonic flows of monatomic gases in the transitional flow regime. To this end, we perform systematic simulations of flows based on AI potentials for various noble gases at various degrees of flow rarefaction and free stream/surface temperature ratio in the range of Mach numbers from 1 to 10. The simulations are performed based on AI interatomic interaction potentials obtained by Przybytek et al. (Reference Przybytek, Cencek, Komasa, Łach, Jeziorski and Szalewicz2010), Hellmann, Bich & Vogel (Reference Hellmann, Bich and Vogel2008), Patkowski & Szalewicz (Reference Patkowski and Szalewicz2010) and Jäger et al. (Reference Jäger, Hellmann, Bich and Vogel2016), as well as the widely used HS molecular model. To study the effects of parameters of gas–surface interaction, we compare the results obtained for diffuse reflection with those based on the CL scattering kernel using the values of the tangential momentum accommodation coefficient (TMAC) and normal energy accommodation coefficient (NEAC) extracted from the experimental data available in the literature (Porodnov et al. Reference Porodnov, Suetin, Borisov and Akinshin1974; Porodnov, Kulev & Tukhvetov Reference Porodnov, Kulev and Tukhvetov1978; Semyonov, Borisov & Suetin Reference Semyonov, Borisov and Suetin1984; Trott et al. Reference Trott, Castaneda, Torczynski, Gallis and Rader2011). The calculations were done for various values of the free stream and sphere temperatures. All results are obtained in steady-state two-dimensional axisymmetric simulations, as the three-dimensional and unsteady effects due to the wake instability are known to be negligible under conditions considered here (Nagata et al. Reference Nagata, Nonomura, Takahashi and Fukuda2016; Riahia et al. Reference Riahia, Meldia, Favier, Serre and Goncalves2018; Sansica et al. Reference Sansica, Robinet, Alizard and Goncalves2018).
A special preliminary study was performed to choose the values of all numerical parameters of the DSMC method, in order to get small and controllable numerical errors of our simulations. This preliminary study is described in the supplementary material available at https://doi.org/10.1017/jfm.2022.356. It allows us to conclude, in particular, that the errors in calculations of the sphere drag and energy transfer coefficients are less than 0.5 % in the whole ranges of Mach and Reynolds numbers considered in our simulations.
Our major finding is that the differences in the drag and energy transfer coefficients between different species calculated based on AI interatomic potentials become progressively more significant with increasing Mach number. The difference reaches its maximum in the transitional flow regime, while it decreases in the limit of continuum flows. Our simulations also reveal a strong and non-obvious effect of the TMAC and NEAC on the sphere drag and energy transfer. These results suggest that the high-fidelity semi-empirical correlations for the sphere drag and energy transfer coefficients in the transitional flow regime must account for the effect of gas species and parameters of gas–surface interaction.
The rest of the paper is structured as follows. The problem formulation and definitions are presented in § 2. The gas–surface kernel and typical values of the accommodation coefficients are considered in § 3. The drag and heat transfer coefficients of a sphere in free molecular flow based on the CL scattering kernel are obtained and analysed in § 4. The main ideas of implementation of the AI potential into the DSMC method are explained in § 5. Finally, the simulation results are analysed in § 6 and summarized in § 7.
2. Statement of the problem
Consider a sphere of radius 
$R$ and temperature 
$T_w$ being at rest and immersed in a dilute monatomic gas. Far from the sphere, in the free stream, the gas at a pressure 
$p_\infty$ and temperature 
$T_\infty$ flows with constant velocity 
$U_\infty$ directed along the 
$x$-axis, as shown in figure 1. It is assumed that the stream speed 
$U_\infty$ is equal to or larger than the speed of sound. The velocity distribution function of the gas in the free stream is given by the Maxwellian
\begin{equation} f_\infty^{{ M}}({\boldsymbol v})=\frac{n_\infty}{(\sqrt{\rm \pi}v_\infty)^{3}} \exp\left[-\frac{(v_x-U_\infty)^{2}+v_y^{2}+v_z^{2}}{v_\infty^{2}}\right], \quad v_\infty=\sqrt{\frac{2{k_{{ B}}}T_\infty}{m}}, \end{equation}
where 
${\boldsymbol v}=(v_x,v_y,v_z)$ is the molecular velocity, 
$n_\infty =p_\infty /({k_{{ B}}}T_\infty )$ is the number density, 
$v_\infty$ is the most probable speed at 
$T_\infty$, 
${k_{{ B}}}=1.380649\times 10^{-23}\,{\rm J}\,{\rm K}^{-1}$ is the Boltzmann constant, and 
$m$ is the atomic mass of the gas.
Figure 1. Scheme of the flow.
Our purpose is to calculate: the integral characteristics such as the drag force acting on the sphere and energy flux on the sphere surface; the local characteristics on the sphere surface such as the pressure, friction and energy flux coefficients; and, finally, the flow field around the sphere. A wide range of the degree of gas rarefaction spanning the free molecular, transitional and near continuum flow regimes is considered. We study the effect of four factors: the interatomic gas potential of various gas species, accommodation coefficients of the gas–surface interaction model, free stream temperature 
$T_\infty$, and temperature of the sphere surface 
$T_w$. Four gas species will be considered, namely, helium, neon, argon and krypton. Each species has its own interatomic potential so that the comparison of results for different gases reveals the effect of the species on aerothermodynamic characteristics. As pointed out previously by Sharipov (Reference Sharipov2018b), two isotopes of helium, 
$^{3}$He and 
$^{4}$He, have different behaviours at low temperatures. They have the same interatomic potential, but their collision cross-sections are different. The effect of the helium isotope, therefore, is also studied in the present work by comparison of the results for 
$^{3}$He to those for 
$^{4}$He.
The main factors determining the solution to the problem in question are the Mach number 
${M\!a}$, the rarefaction parameter 
$\delta$, the ratio of the sphere temperature 
$T_w$ to the free stream temperature 
$T_\infty$, and accommodation coefficients. The Mach number is defined as
\begin{equation} {M\!a}=\frac{U_\infty}{c_s},\quad c_s=\sqrt{\gamma {k_{{ B}}}T_\infty/m}, \end{equation}
where 
$c_s$ is the speed of sound, and 
$\gamma =c_p/c_v$ is the specific energy ratio, which is 
$\gamma =5/3$ for monatomic gases. The rarefaction parameter inversely proportional to the Knudsen number is introduced as (Sharipov Reference Sharipov2016)
\begin{equation} \delta=\frac{Rp_\infty}{\mu_\infty v_\infty}, \end{equation}
where 
$\mu _\infty$ is the gas viscosity at the free stream temperature 
$T_\infty$. The Reynolds number usually defined in continuum fluid mechanics via the sphere diameter (
$2R$) is related to 
${M\!a}$ and 
$\delta$ as
\begin{equation} {Re}=\frac{2R U_\infty \rho_\infty}{\mu_\infty}= 2\sqrt{\frac{10}{3}}\, \delta \,{M\!a} , \end{equation}
where 
$\rho _\infty =m n_\infty$ is the gas mass density.
In general, the accommodation coefficient 
$\alpha$ that determines the variation of some quantity 
$\psi ({\boldsymbol v})$ associated with a single molecule at gas–surface interaction is defined as (Cercignani Reference Cercignani1975; Sharipov Reference Sharipov2016)
\begin{equation} \alpha(\psi)=J_n(\psi)/J_n^{(dif)}(\psi), \end{equation}
where 
$J_n$ is the normal flux of the quantity 
$\psi$ through a solid surface given by
\begin{equation} J_n(\psi)=\int v_n\,\psi({\boldsymbol v})\,f({\boldsymbol r},{\boldsymbol v})\,\mbox{d} {\boldsymbol v}; \end{equation}
$f=f({\boldsymbol r},{\boldsymbol v})$ is the velocity distribution function depending on the position 
${\boldsymbol r}$ and molecular velocity 
${\boldsymbol v}$, and 
$v_n$ is the normal component of 
${\boldsymbol v}$ shown in figure 1. The notation 
$J_n^{(dif)}$ means the flux 
$J_n$ at the diffuse gas–surface interaction so that 
$\alpha (\psi )=1$ for any 
$\psi$ when the interaction is diffuse. The quantities 
$\psi$ corresponding to 
$J_n^{(dif)}(\psi )=0$, such as 
$\psi =1$, should not be used in the definition (2.5). The model of gas–surface interaction used here contains two parameters: TMAC 
$\alpha _t$ defined via the tangential momentum of gaseous particles 
$\psi =mv_t$, and NEAC 
$\alpha _n$ defined via the kinetic energy determined by the velocity component normal to the surface 
$\psi =mv_n^{2}/2$. The accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$ depend on both gas species and state of the solid surface.
The calculations are performed for Mach numbers 
${M\!a}=1$, 2, 5, 10. The first value belongs to the transonic range of 
${M\!a}$, the second value corresponds to supersonic flow, the third value separates the supersonic and hypersonic flows, and the last value corresponds to hypersonic flow. Five values of the rarefaction parameter, 
$\delta =0.1$, 0.3, 1, 3, 10, 30, are considered, spanning the near free molecular, transitional and slip flow regimes. Most of the data are obtained at the free stream temperature 
$T_\infty =300$ K. To study the effect of free stream temperature, additional calculations are performed for several 
$T_\infty$ in the range from 1 K to 2000 K. The temperature of the sphere 
$T_w$ depends on many factors, including thermal properties of the sphere material and its size, and can vary in a broad range. For the flow in question, there are two characteristic temperatures: the free stream temperature 
$T_\infty$, and the stagnation temperature 
$T_s$ related to 
$T_\infty$ as
\begin{equation} T_s=T_\infty\left(1 +\frac{{M\!a}^{2}}{3}\right) \end{equation}
for monatomic gases. Occasionally, a sphere can have 
$T_\infty$ even at high 
${M\!a}$, for instance, when a supersonic flow arises abruptly in a shock tube. If a sphere is exposed to a hypersonic flow for a long time, then its temperature becomes close to 
$T_s$. To account for variability of possible thermal regimes of spheres in supersonic and hypersonic flows, the effect of the sphere temperature is studied via two limit simulations: cold sphere at 
$T_w=T_\infty$ and hot sphere 
$T_w=T_s$. In addition, the value 
$T_w=1000$ K is considered. To consider the effects of surface state for various gaseous species, several sets of the accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$ are used in the calculations.
To relate the input dimensionless parameters 
${M\!a}$ and 
$\delta$ to conditions in a real flow, the gas viscosity and its atomic mass are required. To this end, the most precise values of the viscosity obtained for the AI potentials by Cencek et al. (Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012) and Sharipov & Benites (Reference Sharipov and Benites2017, Reference Sharipov and Benites2019, Reference Sharipov and Benites2020) are used here for helium, neon, argon and krypton. As is known, the noble gases are never pure, but are composed of several isotopes (Meija et al. Reference Meija2016). The consideration of an isotope mixture as a single gas can also affect all characteristics of the flow. The calculations of viscosity and thermal conductivity for isotope mixtures of neon, argon and krypton by Sharipov & Benites (Reference Sharipov and Benites2021) pointed out that the effect of the isotope composition on the transport coefficients does not exceed 0.01 %, which is much smaller than the numerical error of the calculations reported in the present paper. Thus neon, argon and krypton are considered as single gases, with average atomic masses using the composition reported by Meija et al. (Reference Meija2016) and atomic masses of each isotope provided by Wang et al. (Reference Wang, Audi, Kondev, Huang, Naimi and Xu2017). The isotopes 
$^{3}$He and 
$^{4}$He are considered as pure gases with the corresponding atomic masses. The values of viscosity 
$\mu$ at temperature 300 K and atomic masses used here are summarized in table 1.
Table 1. Viscosity 
$\mu$ at temperature 300 K (Cencek et al. Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012; Sharipov & Benites Reference Sharipov and Benites2017, Reference Sharipov and Benites2019, Reference Sharipov and Benites2020), atomic mass 
$m$, and factor 
$G$ in (5.1) for all gases considered in the present work.
The quantities of interest can be expressed in terms of the normal stress 
$p_{n}$, shear stress 
$\tau$, and energy flux 
$J_e$ to the sphere surface calculated via the distribution function 
$f=f({\boldsymbol r},{\boldsymbol v})$ as
\begin{equation} p_{n}=\int m v_n^{2}\, f \,\mbox{d} {\boldsymbol v},\quad \tau=\int m v_n v_t\, f \,\mbox{d} {\boldsymbol v},\quad J_e=\int \frac 12m |{\boldsymbol v}|^{2} v_n\, f \,\mbox{d} {\boldsymbol v}, \end{equation}
where 
$v_n$ and 
$v_t$ are the components of the velocity 
${\boldsymbol v}$ shown in figure 1. Since the flow is axisymmetric, the quantities defined on the sphere surface (2.8a–c) depend only on the angle 
$\theta$ shown in figure 1, and are independent of the azimuthal angle. The quantities 
$p_n$, 
$\tau$ and 
$J_e$ are related to the pressure 
$C_p$, friction 
$C_f$, and energy transfer 
$C_h$ coefficients:
\begin{gather} C_p=\frac{p_{n}-p_\infty}{\rho_\infty U_\infty^{2}/2}=\frac{p_{n}-p_\infty}{p_\infty S^{2}}, \end{gather}
\begin{gather} C_f=\frac{-\tau}{\rho_\infty U_\infty^{2}/2}=\frac{-\tau}{p_\infty S^{2}}, \end{gather}
\begin{gather} C_h=\frac{-J_e}{\rho_\infty U_\infty^{3}/2} =\frac{-J_e}{ p_\infty v_\infty S^{3} }. \end{gather}
Here, 
$S$ is the speed ratio:
\begin{equation} S=\frac{U_\infty}{v_\infty}=\sqrt{\frac 56}\,{M\!a}. \end{equation} The drag force 
$F$ exerted on the sphere is given as
\begin{equation} F=2{\rm \pi} R^{2}\int_0^{\rm \pi} \left(p_n\cos\theta-\tau\sin\theta \right)\sin\theta\,\mbox{d} \theta. \end{equation}
The drag coefficient 
$C_D$ is expressed in terms of the drag force 
$F$ as
\begin{equation} C_D=\frac{F}{({\rm \pi}/2) R^{2} \rho_\infty U_\infty^{2}}=\frac{F}{{\rm \pi} R^{2} p_\infty S^{2}}, \end{equation}
which can also be rewritten in terms of 
$C_p$ and 
$C_f$ as
\begin{equation} C_D=2\int_0^{\rm \pi} \left(C_p\cos\theta+C_f\sin\theta \right)\sin\theta\,\mbox{d} \theta. \end{equation}
The average energy transferred to the sphere is defined via 
$C_h$ as
\begin{equation} C_Q=\frac{1}{2}\int_0^{\rm \pi}C_h\sin\theta \,\mbox{d} \theta. \end{equation} The local characteristics of interest, namely, number density 
$n({\boldsymbol r})$, temperature 
$T({\boldsymbol r})$ and bulk velocity 
${\boldsymbol u}({\boldsymbol r})$, are defined via the distribution function 
$f=f({\boldsymbol r},{\boldsymbol v})$ as
\begin{equation} n=\int f\,\mbox{d} {\boldsymbol v},\quad {\boldsymbol u}=\frac{1}{n}\int {\boldsymbol v} f\,\mbox{d} {\boldsymbol v},\quad T=\frac{m}{3 n{k_{{ B}}}} \int ({\boldsymbol v}-{\boldsymbol u})^{2} f \,\mbox{d} {\boldsymbol v}. \end{equation}3. Gas–surface interaction
To solve the problem in terms of the velocity distribution function 
$f({\boldsymbol r},{\boldsymbol v})$, the boundary conditions have to be imposed on the sphere surface. The distribution function 
$f({\boldsymbol r},{\boldsymbol v})$ of the particles reflected from the surface is related to that of incident particles 
$f({\boldsymbol r},{\boldsymbol v}')$ as
\begin{equation} v_n\,f({\boldsymbol r},{\boldsymbol v})={-} \int_{v_n'<0} v_n'\,R({\boldsymbol v},{\boldsymbol v}')\,f({\boldsymbol r},{\boldsymbol v}')\,\mbox{d} {\boldsymbol v}',\quad v_n>0,\end{equation}
where 
$R({\boldsymbol v},{\boldsymbol v}')$ is the scattering kernel. As was pointed out previously by Sharipov (Reference Sharipov2003a,Reference Sharipovb, Reference Sharipov2016) and Kalempa & Sharipov (Reference Kalempa and Sharipov2020, Reference Kalempa and Sharipov2021), the widely used diffuse–specular model of gas–surface interaction is not consistent from the physical viewpoint. In fact, it contains only one parameter, which varies significantly when extracted from different experiments. The kernel proposed by Cercignani & Lampis (Reference Cercignani and Lampis1971) contains two accommodation coefficients, namely, TMAC 
$\alpha _t$ and NEAC 
$\alpha _n$. Moreover, it was derived by Cercignani (Reference Cercignani1972) using a physical model of solid surface based on the Fokker–Planck equation. Thus the CL kernel given as
$$\begin{align} R({\boldsymbol v}', {\boldsymbol v})&= \frac{v_n}{{\rm \pi}^{2} \alpha_n\,\alpha_t(2-\alpha_t)v_w^{4}} \exp\left[-\frac{({\boldsymbol v}_t-(1-\alpha_t){\boldsymbol v}'_t)^{2}} {\alpha_t(2-\alpha_t)v_w^{2}}-\frac{v_n^{2}+(1-\alpha_n)v_n^{\prime 2}}{\alpha_n v_w^{2}}\right]\nonumber\\ &\quad\times \int_0^{2{\rm \pi}}\exp\left(\frac{2\sqrt{1-\alpha_n}\,v_nv_n'\cos\phi} {\alpha_n v_w^{2}}\right)\mbox{d}\phi \end{align}$$
is used in the present work. Here, 
$v_w=\sqrt {{2{k_{{ B}}}T_w}/{m}}$ is the most probable speed at the surface temperature. In the particular case when 
$\alpha _n=1$ and 
$\alpha _t=1$, the kernel (3.2) corresponds to the model of diffuse scattering.
The typical values of the accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$ published previously by Sharipov (Reference Sharipov2003a,Reference Sharipovb), Sharipov & Bertoldo (Reference Sharipov and Bertoldo2006) and Sharipov & Moldover (Reference Sharipov and Moldover2016) were extracted from experiments on Poiseuille flow reported by Porodnov et al. (Reference Porodnov, Suetin, Borisov and Akinshin1974), thermal creep by Porodnov et al. (Reference Porodnov, Kulev and Tukhvetov1978), energy transfer between two cylinders by Semyonov et al. (Reference Semyonov, Borisov and Suetin1984), and energy transfer between two parallel plates by Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011). The coefficients 
$\alpha _t$ and 
$\alpha _n$ depend on gas species, and solid surface material and its state. According to Sharipov & Moldover (Reference Sharipov and Moldover2016), the TMAC varies in the range 
$0.4\le \alpha _t\le 1$, while the NEAC varies practically in the whole range, i.e. 
$0.01\le \alpha _n\le 1$. The main trend is that the heavy gases, such as krypton, have accommodation coefficients close to 1, i.e. they are reflected diffusely from any surface. The light gases, such as helium and neon, have small accommodation coefficients for polished and clean surfaces. For instance, Sharipov & Moldover (Reference Sharipov and Moldover2016) extracted 
$\alpha _t=0.4$ and 
$\alpha _n=0.01$ using the experimental data reported by Trott et al. (Reference Trott, Castaneda, Torczynski, Gallis and Rader2011) for helium interacting with an aluminium surface treated by plasma. Using the same data for argon, the values 
$\alpha _t=0.9$ and 
$\alpha _n=0.85$ were obtained. Analysing the experimental data by Porodnov et al. (Reference Porodnov, Suetin, Borisov and Akinshin1974, Reference Porodnov, Kulev and Tukhvetov1978) and Semyonov et al. (Reference Semyonov, Borisov and Suetin1984) for helium interacting with a non-treated surface, the values 
$\alpha _t=0.9$ and 
$\alpha _n=0.1$ were extracted by Sharipov (Reference Sharipov2003a,Reference Sharipovb) and Sharipov & Bertoldo (Reference Sharipov and Bertoldo2006). Thus to consider various surface types, the calculations are performed for all gases at diffuse reflection (
$\alpha _t=1$ and 
$\alpha _n=1$), for argon assuming 
$\alpha _t=0.9$ and 
$\alpha _n=0.85$, and for helium using two sets of accommodation coefficients: (i) 
$\alpha _t=0.4$ and 
$\alpha _n=0.01$; (ii) 
$\alpha _t=0.9$ and 
$\alpha _n=0.1$. In accordance with the experimental data, only the sets of accommodation coefficients where 
$a_t > a_n$ are considered here.
4. Free molecular flow regime
The approach for calculation of aerothermodynamic coefficients of a body in a steady-state free molecular flow based on the diffuse–specular model of gas–surface interaction is well known (see e.g. Kogan Reference Kogan1969; Bird Reference Bird1994). The CL kernel was used by Chernyak & Sograbi (Reference Chernyak and Sograbi2019) and Kalempa & Sharipov (Reference Kalempa and Sharipov2020) to calculate the drag force in the case of low Mach numbers. In this section, the aerothermodynamic characteristics based on the CL kernel are calculated for arbitrary Mach number and temperature ratio 
$T_w/T_\infty$.
In the collisionless limit (
$\delta \to 0$), the distribution function of incident particles is given by the Maxwellian (2.1). The distribution function of reflected particles is obtained by substituting (2.1) into the right-hand side of the boundary conditions (3.1). Then the local quantities (2.8a–c) are computed. They can be written in a compact form using the notation
\begin{gather} \xi=S\cos\theta,\quad \eta=S\sin\theta, \end{gather}
\begin{gather} \varPsi_1(S)=\frac{{\rm e}^{{-}S^{2}}}{\sqrt{\rm \pi} S}\left(1+\frac{1}{2S^{2}}\right)+\left(1+\frac{1}{S^{2}}-\frac{1}{4S^{4}}\right)\mbox{erf}(S), \end{gather}
\begin{gather} \varPsi_2(S)= \frac{2{\rm e}^{{-}S^{2}}}{\sqrt{\rm \pi}S^{3} }+\left(\frac{2}{S^{2}}+\frac{1}{S^{4}}\right)\mbox{erf}(S), \end{gather}
where 
$\mbox {erf}(S)$ is the error function of 
$S$, and
$$\begin{align} \varPhi(\alpha_n,\xi)&=\frac{2}{{\rm \pi}^{3/2} S^{2} \alpha_n (T_w/T_\infty)}\int_0^{\infty} \int_0^{\infty} \int_0^{2{\rm \pi}} c^{2} c'\nonumber\\ &\quad \times \exp\left(-\frac{c^{2}+(1-\alpha_n)c^{\prime 2}- 2\sqrt{1-\alpha_n}\,cc'\cos\phi}{\alpha_n (T_w/T_\infty)}-(c'-\xi)^{2}\right) \mbox{d} \phi \,\mbox{d} c' \,\mbox{d} c. \end{align}$$
The last expression can be simplified in the limits 
$\alpha _n=0$ and 
$\alpha _n=1$ as
\begin{gather} \varPhi(0,\xi)=\frac{1}{S^{2}}\left[\left(\xi^{2}+\frac 12\right)(1+\mbox{erf}(\xi))+\frac{\xi {\rm e}^{-\xi^{2}}}{\sqrt{\rm \pi}}\right], \end{gather}
\begin{gather} \varPhi(1,\xi)=\frac{\sqrt{T_w/T_\infty}}{2S^{2}}\left[\sqrt{\rm \pi} \xi (1+\mbox{erf}(\xi))+{\rm e}^{-\xi^{2}}\right]. \end{gather}It can be verified that
\begin{equation} \varPhi(0,\xi)>\varPhi(1,\xi)\quad\mbox{at}\ T_w/T_\infty=1. \end{equation}Then the pressure coefficient reads
\begin{equation} C_p=\frac{1}{S^{2}}\left[\left(\xi^{2}+\frac 12\right)(1+\mbox{erf}(\xi)) +\frac{\xi {\rm e}^{-\xi^{2}}}{\sqrt{\rm \pi}}-1\right] +\varPhi(\alpha_n,\xi), \end{equation}
where the terms in the square brackets correspond to the contribution of incident particles and depend only on the speed ratio 
$S$ and the angle 
$\theta$. The last term, 
$\varPhi$, in (4.8) corresponds to the reflected particles and depends on NEAC 
$\alpha _n$, speed ratio 
$S$, temperature ratio 
$T_w/T_\infty$, and angle 
$\theta$, but it is independent of TMAC 
$\alpha _t$. The inequality (4.7) points out that the coefficient 
$C_p$ increases with decreasing NEAC 
$\alpha _n$ when 
$T_w/T_\infty =1$.
The local friction coefficient can be expressed as
\begin{equation} C_f=\frac{\alpha_t\eta}{S^{2}} \left[\xi(1+\mbox{erf}(\xi)) +\frac{{\rm e}^{-\xi^{2}}}{\sqrt{\rm \pi}}\right]. \end{equation}
As expected, it is proportional to TMAC 
$\alpha _t$ but is independent of NEAC 
$\alpha _n$ and temperature ratio 
$T_w/T_\infty$.
The drag coefficient 
$C_D$ is obtained substituting (4.8) and (4.9) into (2.15):
\begin{equation} C_D=(1+\alpha_t)\,\varPsi_1(S) +\frac{2}{S^{2}}\int_{{-}S}^{S}\xi \, \varPhi(\alpha_n,\xi) \,\mbox{d} \xi. \end{equation}
The first term on the right-hand side of this equation depends only on TMAC 
$\alpha _t$. It is largest for the diffuse reflection (
$\alpha _t=1$), and decreases with decreasing TMAC. The second term in (4.10) given by the four-fold integral depends on 
$\alpha _n$, 
$T_w/T_\infty$ and 
$S$ via (4.4). Since the function 
$\varPhi (\alpha _n,\xi )$ increases with decreasing NEAC 
$\alpha _n$ at 
$T_w/T_\infty =1$, the drag coefficient increases as well when 
$\alpha _n$ decreases.
The local energy transfer coefficient is equal to
$$\begin{gather} C_h=\frac{1}{2S^{3}}\left\{\left[\frac{{\rm e}^{-\xi^{2}}}{\sqrt{\rm \pi} }+\xi(1+\mbox{erf}(\xi))\right] \left[\alpha_n\left(\xi^{2}+\frac 32-\frac{T_w}{T_\infty}\right)\right.\right.\nonumber\\ \left.\left. {}+ \alpha_t(2-\alpha_t)\left(\eta^{2}+1-\frac{T_w}{T_\infty}\right)\right] - \frac{\alpha_n {\rm e}^{-\xi^{2}}}{2\sqrt{\rm \pi} } \right\}, \end{gather}$$
so it depends on both 
$\alpha _t$ and 
$\alpha _n$. The average energy transfer coefficient can be derived by inserting (4.11) into (2.16):
\begin{equation} {C}_Q=\frac 18\left[\alpha_n+\alpha_t(2-\alpha_t)\right] \left[\varPsi_1(S)+\left(1-\frac{T_w}{T_\infty}\right)\varPsi_2(S)\right], \end{equation}
where 
$\varPsi _1$ and 
$\varPsi _2$, given by (4.2) and (4.3), are functions of the speed ratio 
$S$ only. The expression (4.12) shows that the coefficient 
$C_Q$ reaches its maximum value for diffuse reflection (
$\alpha _t=1$ and 
$\alpha _n=1$) and decreases with decreasing either 
$\alpha _t$ or 
$\alpha _n$.
The dependence (4.12) of the energy transfer coefficient 
$C_Q$ on the accommodation coefficients and temperature ratio 
$T_w/T_\infty$ is explicit and can be understood easily. In contrast, the drag coefficient (4.10) contains the four-fold integral, therefore its dependence on the NEAC and temperature ratio is not obvious. To reveal this dependence, the numerical values of 
$C_D$ calculated via (4.10) are given in table 2 for some sets of 
$\alpha _t,\alpha _n$, and for two values of the temperature 
$T_w$: 
$T_w=T_\infty$ and 
$T_w=T_s$. The data show that the drag coefficient decreases with increasing NEAC. The effect of the ratio 
$T_w/T_\infty$ on 
$C_D$ depends on the NEAC: it is strongest at 
$\alpha _n=1$, but it becomes very weak at 
$\alpha _n\le 0.5$.
Table 2. Drag coefficient 
$C_D$ versus accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$ in free molecular flow at 
$T_w=T_\infty$ and 
$T_w=T_s$ according to (4.10).
5. Method of solution in the transitional flow regime
5.1. Computational domain and boundary conditions
The flow under consideration is axisymmetric so that the computational domain represents a cylinder of radius 
$R_d$ and length 
$2R_d$, with the sphere placed in its centre as shown in figure 2. According to the DSMC method (Bird Reference Bird1994, Reference Bird2013), the domain is divided into a regular mesh of cells with sizes 
$\Delta r$ and 
$\Delta x$ in the radial and axial directions, respectively. For the sake of simplicity, we consider 
$\Delta x=\Delta r$. The positions 
$(r,x)$ of all modelling particles, and three components of their velocities 
${\boldsymbol v}$, are stored in computer memory. The time is also discretized and advanced by a step 
$\Delta t$. Then the following procedures are realized. (i) The free motion of modelling particles during the time interval 
$\Delta t$ is simulated. Since only the radial and axial coordinates for modelling particles are saved, the azimuthal component of the velocity must be changed to compensate the azimuthal displacement of each particle. (ii) The binary interatomic collisions in accordance with the number of particles and their velocities in each cell are simulated by computing new molecular velocities. (iii) Calculations of macroscopic quantities such as the local density 
$n$, temperature 
$T$ and bulk (or gas) velocity 
${\boldsymbol u}$ are performed.
Figure 2. Scheme of computational domain.
To provide a more uniform distribution of modelling particles over the radial direction, a weight depending on the radial coordinate 
$r$ is attributed to each particle. When particles move from the 
$x$-axis to the periphery, some of them are randomly eliminated, and the weights of remaining particles are increased. If particles move from the periphery to the 
$x$-axis, then their weights are decreased and new particles are generated.
During the free motion step, some particles collide with the sphere surface. In this case, their new velocities are generated according to the CL scattering kernel (3.2). The procedure to generate velocities of reflected particles is described by Lord (Reference Lord1991) and Sharipov (Reference Sharipov2016). Some particles leave the domain during free motion, and the information about them is removed. Simultaneously, new particles are generated at the domain boundaries following the procedure described in § 4.1 of the book by Bird (Reference Bird2013), based on the free stream distribution functions (2.1). Details of the approach utilized in this work to generate new particles are provided in the supplementary material.
5.2. Intermolecular collisions
The numerical scheme by Sharipov (Reference Sharipov2018b) to simulate interatomic collisions based on AI potentials does not depend on the flow type. Here, we use the same scheme that was developed previously for simulations of shock waves (Sharipov & Dias Reference Sharipov and Dias2019; Dias & Sharipov Reference Dias and Sharipov2021) and energy and momentum transfer between two plates (Ambrus, Sharipov & Sofonea Reference Ambrus, Sharipov and Sofonea2020). During an elastic collision, the relative velocity 
${\boldsymbol g}$ changes its direction, keeping the magnitude. A calculation of the angle between relative velocities before and after a collision, i.e. the deflection angle 
$\chi$, requires significant computational effort. The main idea of the scheme proposed by Sharipov (Reference Sharipov2018b) is to calculate the lookup tables (scattering matrices) of the deflection angle. First, the differential cross-section (DCS) and total cross-section (TCS) are calculated for many values of the relative speed 
$g=|{\boldsymbol g}|$ using a quantum approach. Then a fixed number of deflection angles is calculated in the interval 
$[0,{\rm \pi} /2]$ such that these discrete angles become equiprobable. In other words, the nodes of the angle mesh are denser in a region corresponding to a larger DCS. The scattering matrices for helium and neon are given in the supplementary material to the paper by Sharipov & Dias (Reference Sharipov and Dias2019), and those for argon and krypton are given in the supplementary material to the paper by Dias & Sharipov (Reference Dias and Sharipov2021). All of them have the same structure, i.e. 900 values of the relative speed 
$g$, and 100 values of the deflection angles 
$\chi$. The tables also contain the TCS for each value of 
$g_j$. If a randomly chosen pair of modelling particles has a relative speed 
$g$, then the index 
$j$ is calculated as
\begin{equation} j= \left\lfloor \frac{\ln(1+g/G)}{\ln 1.005}+\frac 12\right\rfloor, \quad 1\le j\le 900, \end{equation}
where 
$G$ depends on the gas species and is given in table 1. Then the pair undergoes the rejection–acceptance collision test using the corresponding values of the TCS. If the collision between the considered pair of particles is accepted, then the index 
$i$ is chosen randomly from the range 
$1\le i\le 100$. The element 
$\xi _{ij}$ taken from the scattering matrix is used as 
$\cos \chi$ to calculate the post-collision velocities according to (8.32)–(8.35) from the book by Sharipov (Reference Sharipov2016).
As is known, the simplest model of the interatomic interaction, namely the HS model, does not provide a correct dependence of viscosity on gas temperature. However, it is still used widely because of some advantages such as the simplicity of its implementation and non-necessity to specify the gas species. In addition, the results of aerodynamic calculations based on the HS model can be presented in a dimensionless form that does not explicitly depend on the dimensional temperature of the free stream. Therefore, it is important to know the uncertainty of the HS model that depends on the flow type and on the input parameters determining the solution. To this end, the calculations are also performed for the HS model.
5.3. Calculation of macroscopic quantities
The approach to calculations of the macroscopic properties is described in § 8.6 of the book by Sharipov (Reference Sharipov2016) and in some papers (e.g. Sharipov Reference Sharipov2017; Sharipov & Dias Reference Sharipov and Dias2017). For the problem in question, the number density 
$n$, temperature 
$T$ and bulk velocity 
${\boldsymbol u}$ defined by (2.17a–c) are calculated following that standard procedure.
The contribution of each individual modelling particle to the stress and energy flux defined by (2.8a–c) is accounted for when the straight particle trajectory crosses the sphere surface. The corresponding procedure described below does not involve any additional approximation. The moments of the distribution function on the sphere surface (2.8a–c) are calculated via the differences of the corresponding properties between the reflected and incident fluxes. First, the angle 
$\theta$ shown in figure 1 is discretized as 
$\theta _j=(j-0.5)\,\Delta \theta$ (
$1\le j\le N_\theta$), where 
$\Delta \theta ={\rm \pi} /N_\theta$, and 
$N_\theta$ is an integer number of surface cells. Then the incident 
${\boldsymbol v}_i^{inc}$ and reflected 
${\boldsymbol v}_i^{ref}$ velocities are registered for the 
$i$th particle interacting with the surface element of area 
$\Delta A_j={\rm \pi} R^{2} \left [\cos (\theta _j-\Delta \theta /2)-\cos (\theta _i+\Delta \theta /2)\right ]$. Finally, the surface moments (2.8a–c) are calculated for each surface element as
\begin{equation} \left[\begin{array}{@{}c@{}} p_n(\theta_j)\\ \tau(\theta_j)\\ J_e(\theta_j) \end{array} \right]= \frac{m}{N_s\,\Delta t\,\Delta A_j}\sum_{i=1}^{N_j}W_i \left[ \begin{array}{@{}c@{}} v_{ni}^{ref}+v_{ni}^{inc}\\ v_{ti}^{ref}-v_{ti}^{inc} \\ \left(|{\boldsymbol v}{}^{ref}|^{2}-|{\boldsymbol v}{}^{inc}|^{2}\right)/2 \end{array}\right], \end{equation}
where 
$W_i$ is the weighting factor, i.e. the number of real particles represented by the 
$i$th model particle, 
$v_{ni}$ is the normal component of velocity of the 
$i$th particle, and 
$v_{ti}$ is its tangential component, and 
$N_j$ is the number of incident particles on the surface element 
$\Delta A_j$ during 
$N_s$ time steps needed to calculate the macroscopic quantities.
The drag force on the sphere in (2.13) is calculated via the difference of the momentum 
$mv_x$ between the reflected and incident fluxes over the whole sphere surface, i.e.
\begin{equation} F=\frac{m}{N_s\,\Delta t}\sum_{i=1}^{N_{tot}} W_i\left(v_{xi}^{ref}-v_{xi}^{inc}\right). \end{equation}
Here, 
$N_{tot}$ is the total number of particles that hit the sphere during 
$N_s$ time steps, and 
$v_{xi}$ is the 
$x$-component of velocity of the 
$i$th particle hitting the sphere.
5.4. Parameters of numerical scheme and accuracy
In the problem under consideration, the numerical error is determined by the following numerical scheme parameters: size of the computational domain 
$R_d$, size of cells 
$\Delta r$, number of modelling particles per cell 
$N_p$ in the free stream flow, time step 
$\Delta t$, number of time steps 
$N_{{steady}}$ required to establish steady-state flow, and number of time steps 
$N_s$ to calculate the macroscopic quantities. The values of these parameters were chosen to ensure that their further variations to improve the numerical accuracy do not change the drag coefficient 
$C_D$ and the average energy transfer coefficient 
$C_Q$ within 0.5 %.
The optimum value of each parameter depends on both Mach number 
${M\!a}$ and rarefaction parameter 
$\delta$. The size of the computational domain 
$R_d$ and the cell size are given in table 3. The largest size 
$R_d=30R$ corresponds to 
${M\!a}=1$ and 
$\delta =30$, while the smallest size 
$R_d=3R$ is used at 
${M\!a}=10$ and 
$\delta =30$. The cell size varies from 
$\Delta r=R/240$ used at 
${M\!a}=10$ and 
$\delta =30$, to 
$\Delta r=R/20$ used at 
$\delta =0.1$ for all values of 
${M\!a}$. The number of modelling particles is not smaller than 
$N_p=50$ in all cases. The time step varies from 
$\Delta t=0.002 R/v_\infty$ at 
$\delta =30$ to 
$\Delta t=0.005 R/v_\infty$ at 
$\delta =0.1$. Finally, the number of samples to compute the aerothermodynamic characteristics varies from 
$N_s=10^{4}$ at 
${M\!a}=10$ to 
$10^{5}$ at 
${M\!a}=1$, while the number of time steps to establish the steady-state flow is 
$N_{{steady}}=N_s/10$.
Table 3. Parameters of the numerical scheme.
Some examples of influence of the parameters 
$R_d$, 
$\Delta r$ and 
$\Delta t$ on 
$C_D$ and 
$C_Q$ are given in the supplementary material, showing the convergence of the coefficients 
$C_D$ and 
$C_Q$ when 
$R_d$ increases or when 
$\Delta r$ and 
$\Delta t$ decrease. The statistical scattering of 
$C_D$ and 
$C_Q$ estimated via their standard deviations over 
$N_s$ time steps was smaller than 0.1 %. The procedures to estimate the statistical scattering and characteristic values of the standard deviation are provided in the supplementary material. It was found that the results do not change within the statistical scattering when a double number of particles, i.e. 
$N_p=100$, is considered.
The three steps of the DSMC method – namely, free motion, intermolecular collisions and calculation of macroscopic characteristics – are elaborated independently from each other so that they can be validated separately. Since the free motion of particles and calculation of the macroscopic characteristics are independent on the intermolecular collision procedure, they are validated in the free molecular regime (
$\delta =0$). The numerical values of 
$C_D$, 
$C_Q$, 
$C_p$, 
$C_f$ and 
$C_h$ obtained by the DSMC method with the numerical scheme parameters described above, and assuming 
$\delta =0$, were compared with their analytical values given in § 4. It was verified that the disagreement is within 0.1 % for all values of TMAC 
$\alpha _t$ and NEAC 
$\alpha _n$. The intermolecular collision procedure independent of the flow configuration was the same as that used in the previous papers Sharipov (Reference Sharipov2018a), Sharipov & Dias (Reference Sharipov and Dias2019), Zhu et al. (Reference Zhu, Wu, Zhang and Sharipov2019) and Dias & Sharipov (Reference Dias and Sharipov2021). It was validated previously via calculations of viscosity and thermal conductivity by the DSMC method (Sharipov & Strapasson Reference Sharipov and Strapasson2012b) over a wide temperature range. As a result, the transport coefficients calculated by completely different methods (Cencek et al. Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012; Hellmann et al. Reference Hellmann, Bich and Vogel2008; Sharipov & Benites Reference Sharipov and Benites2017, Reference Sharipov and Benites2019, Reference Sharipov and Benites2020) and measured with high accuracy (Berg & Burton Reference Berg and Burton2013) were reproduced by the DSMC method within 0.1 %, which is smaller than the numerical error of the present results.
6. Results and discussion
6.1. Effect of gas species
First, the aerothermodynamic characteristics 
$C_D$ and 
$C_Q$ were calculated for the temperatures of the sphere 
$T_w$ and free stream 
$T_\infty$ equal to 300 K assuming diffuse scattering on the sphere surface for all considered gases, namely, helium (
$^{4}$He), neon, argon and krypton. The corresponding data together with those for the HS model are presented in table 4. The coefficients 
$C_D$ and 
$C_Q$ for 
$^{3}$He at 
$T_w=T_\infty =300$ K are the same as those for 
$^{4}$He within the numerical accuracy, so they are not reported in table 4.
Table 4. Drag 
$C_D$ and average energy transfer 
$C_Q$ coefficients versus Mach number 
${M\!a}$ and rarefaction parameter 
$\delta$ for diffuse scattering (
$\alpha _t=1$ and 
$\alpha _n=1$) at 
$T_\infty =T_w=300$ K.
As expected, the coefficients 
$C_D$ and 
$C_Q$ depend strongly on both 
${M\!a}$ and 
$\delta$. Their values for the HS model differ significantly from those for the AI potentials of all species at large values of the Mach number. In the case 
${M\!a}=10$, the relative differences of 
$C_D$ and 
$C_Q$ based on the HS model from those for krypton are 10 % and 27 %, respectively. For 
${M\!a}=1$, the relative differences become much smaller, namely, 1.3 % and 4.6 % for 
$C_D$ and 
$C_Q$, respectively.
A comparison of 
$C_D$ and 
$C_Q$ for all species calculated based on the AI potentials shows that their values for neon are systematically smaller and those for krypton are always larger in comparison with the other gases. The relative deviations of 
$C_D$ and 
$C_Q$ for neon and krypton are plotted in figure 3. These differences at 
${M\!a}=1$ do not exceed 1 % and 3 % for 
$C_D$ and 
$C_Q$, respectively. At larger Mach numbers, the relative differences reach 3 % and 7 % for 
$C_D$ and 
$C_Q$, respectively.
Figure 3. Relative deviations of coefficients (a) 
$C_D$ and (b) 
$C_Q$ for krypton from those for neon versus rarefaction parameter 
$\delta$ at diffuse scattering and 
$T_\infty =T_w=300$ K. Here, 
$\Delta C_i/C_i=(C_i^{{Kr}}-C_i^{{Ne}})/ C_i^{{Ne}}$, 
$i=D,Q$.
The fields of density 
$n/n_\infty$, temperature 
$T/T_\infty$, gas speed 
$u/U_\infty$ (
$u=|{\boldsymbol u}|$), and streamlines of neon at 
${M\!a}=2$ are shown in figure 4 for two values of the rarefaction parameter, 
$\delta =1$ and 
$\delta =30$. These are typical flow fields in the transitional (
$\delta =1$) and hydrodynamic (
$\delta =30$) flow regimes. The former is characterized by the smooth variation of all quantities 
$n/n_\infty$, 
$T/T_\infty$, 
$u/U_\infty$ and by the gas perturbed at a long distance from the sphere front surface. The latter is distinguished by the shock wave, where the macroscopic variables vary sharply from their values in the free stream to significantly different ones. In this case, a vortex arises just behind the sphere. The flow fields for other values of 
${M\!a}$ are given in the supplementary material.
6.2. Effect of free stream temperature
As is known, any dimensionless characteristics of rarefied gas obtained in term of the rarefaction parameter 
$\delta$ are independent of a reference temperature used in the definition (2.3) when the HS model is used. In fact, the viscosity based on this model is proportional to 
$T_\infty ^{1/2}$, so the rarefaction parameter is proportional to the ratio 
$p_\infty /T_\infty$, i.e. the value of 
$\delta$ is determined only by the number density 
$n_\infty$. The TCS used in the simulation of interatomic collisions is constant for the HS model. As a result, a dimensionless simulation based on the HS model does not require a specification of the gas reference temperature. The dependence of viscosity on the temperature based on the AI potentials (Cencek et al. Reference Cencek, Przybytek, Komasa, Mehl, Jeziorski and Szalewicz2012; Sharipov & Benites Reference Sharipov and Benites2017, Reference Sharipov and Benites2019, Reference Sharipov and Benites2020) is different from that for the HS model and cannot be expressed by a simple formula like 
$\mu \propto T^{\omega }$. In this case, the rarefaction parameter is necessarily determined by two variables, 
$p_\infty$ and 
$T_\infty$, but not only by their ratio. Moreover, since a TCS based on the AI potentials depends on the relative velocity (Sharipov Reference Sharipov2018b), the simulations performed for different temperatures use different values of the TCS. Therefore, a simulation can be performed when both 
$\delta$ and 
$T_\infty$ are specified. It means that one can obtain different values of the aerothermodynamic characteristics by varying the temperature 
$T_\infty$ at fixed 
$\delta$, 
${M\!a}$ and 
$T_w/T_\infty$; i.e. the free stream temperature 
$T_\infty$ affects the solution to the problem in question (Volkov & Sharipov Reference Volkov and Sharipov2017).
To reveal the effect of the free stream temperature 
$T_\infty$ on the aerothermodynamic characteristics, the coefficients 
$C_D$ and 
$C_Q$ were calculated in a wide range of 
$T_\infty$, assuming 
$T_w=T_\infty$. The corresponding results are plotted in figure 5 for the transitional flow regime at 
$\delta =1$, and for two Mach numbers 
${M\!a}=2$ and 5. The plots show that the values of 
$C_D$ and 
$C_Q$ are strongly sensitive to the free stream temperature 
$T_\infty$. In fact, both coefficients 
$C_D$ and 
$C_Q$ for all gases except 
$^{3}$He have maxima near the temperatures 
$T_\infty = 1.5$ K, 20 K, 90 K and 120 K for 
$^{4}$He, Ne, Ar and Kr, respectively. The values of 
$C_D$ and 
$C_Q$ for 
$^{3}$He gas have a minimum at 
$T_\infty =1.5$ K. The relative variations of 
$C_D$ and 
$C_Q$ due the variation of the free stream temperature 
$T_\infty$ are 8 % and 15 %, respectively. Such a dependence of the coefficients 
$C_D$ and 
$C_Q$ on 
$T_\infty$ is similar to that of the shock wave slopes reported by Dias & Sharipov (Reference Dias and Sharipov2021) for the same gases. The significant differences of 
$C_D$ and 
$C_Q$ for 
$^{4}$He from those for 
$^{3}$He at low temperatures are explained by quantum effects. Both 
$^{4}$He and 
$^{3}$He have the same potential, but the former is boson, while the latter is fermion. As a results, their cross-sections are significantly different from each other (Sharipov Reference Sharipov2018b), which leads to the different dependences of 
$C_D$ and 
$C_Q$ on 
$T_\infty$ for these two gases.
Figure 4. Fields of (a,b) density 
$n/n_\infty$, (c,d) temperature 
$T/T_\infty$, and (e, f) speed 
$u/U_\infty$, and streamlines of neon at 
${M\!a}=2$, diffuse scattering, 
$T_\infty =T_w=300$ K: (a,c,e) 
$\delta =1$; (b,d, f) 
$\delta =30$.
Figure 5. (a,c) Drag 
$C_D$ and (b,d) average energy transfer 
$C_Q$ coefficients versus free stream temperature 
$T_\infty$ at 
$\delta =1$, diffuse scattering, 
$T_w=T_\infty$.
In the cases 
${M\!a}=1$ and 10, the behaviours of 
$C_D$ and 
$C_Q$ are qualitatively the same as those shown in figure 5.
6.3. Effect of gas–surface interaction parameters
As mentioned in § 3, additional calculations were performed for helium-4 using two sets of TMAC and NEAC: (i) 
$\alpha _t=0.4$ and 
$\alpha _n=0.01$; (ii) 
$\alpha _t=0.9$ and 
$\alpha _n=0.1$. The former corresponds to a treated and polished metal surface, while the latter describes the interaction of helium with a non-treated surface. The third set, (iii) 
$\alpha _t=0.9$ and 
$\alpha _n=0.85$, considered here is specific for argon interacting with a treated metal surface.
The values of the aerothermodynamic coefficients 
$C_D$ and 
$C_Q$ for helium with sets (i) and (ii), and for argon with set (iii), are compared in figure 6 to those for argon interacting with the sphere surface diffusely. Note that when the diffuse interaction is assumed, the quantities 
$C_D$ and 
$C_Q$ of argon are very close to those of helium that are omitted in figure 6. The horizontal lines in these plots show the free molecular (
$\delta =0$) values of 
$C_D$ and 
$C_Q$ given in table 2, which help us to understand the dependence of these coefficients on 
$\alpha _t$ and 
$\alpha _n$. Both 
$C_D$ and 
$C_Q$ decrease with increasing rarefaction parameter 
$\delta$ when the Mach number and accommodation coefficients are fixed. Set (ii) leads to the largest values of the drag coefficient 
$C_D$ for all Mach numbers considered here, while set (i) corresponds to the smallest 
$C_D$ in all cases except 
${M\!a}=5$ and 
$\delta <3$. Set (iii) can both decrease and increase the drag in comparison to diffuse reflection. The reasons for this complex behaviour of 
$C_D$ as a function of the accommodation coefficients can be understood using the theoretical equations for the free molecular flow regime. According to (4.10), the formula for the drag coefficient 
$C_D$ includes two terms, where the first depends only on 
$\alpha _t$ and the second depends only on 
$\alpha _n$. The first term is proportional to 
$(1+\alpha _t)$ and decreases with decreasing TMAC 
$\alpha _t$, while the second term increases by decreasing NEAC 
$\alpha _n$ in accordance with the inequality (4.7). Both terms depend also on the speed ratio 
$S$. Thus the variation of coefficients 
$\alpha _t$ and 
$\alpha _n$ can both decrease and increase the drag coefficient depending on the Mach number. For instance, at 
${M\!a}=5$ and 
$\delta =0$, all considered sets of 
$\alpha _t$ and 
$\alpha _n$ lead to a larger drag coefficient compared to diffuse reflection. However, at 
${M\!a}=1$ and 
$\delta =0$, only set (ii) provides the drag coefficient that is larger than 
$C_D$ at diffuse reflection, while the other two sets cause a reduction of the drag.
Figure 6. (a,c,e,g) Drag 
$C_D$ and (b,d, f,h) average energy transfer 
$C_Q$ coefficients versus rarefaction parameter 
$\delta$ at 
$T_\infty =T_w=300$ K for different sets of the accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$. The horizontal lines represent the free molecular limits given by (4.10) and (4.12).
As expected, the energy transfer coefficient 
$C_Q$ is largest for diffuse reflection. This coefficient always decreases with decreasing either TMAC 
$\alpha _t$ or NEAC 
$\alpha _n$. The expression (4.12) shows that the coefficient 
$C_Q$ in the free molecular flow regime is proportional to 
$[\alpha _n+\alpha _t(2-\alpha _t)]$, which explains the largest value of 
$C_Q$ at diffuse reflection. The effect of the gas–surface interaction model becomes weaker when the rarefaction parameter 
$\delta$ increases.
The axial distributions of the density 
$n/n_\infty$, temperature 
$T/T_\infty$ and gas velocity 
$u_x/U_\infty$ along the stagnation streamline (
$x<-R$) at 
${M\!a}=1$ and 2 are depicted in figure 7. To demonstrate the effect of the gas–surface interaction parameters, the distributions of 
$^{4}$He interacting with the sphere surface diffusely are compared to those of the same gas with the accommodation coefficients 
$\alpha _t=0.4$ and 
$\alpha _n=0.01$ corresponding to a treated surface. In the case 
${M\!a}=1$, the density and temperature distributions are affected weakly by the rarefaction parameter 
$\delta$ and strongly by the gas–surface interaction parameters. The gas velocity 
$u_x/U_\infty$ changes weakly with both rarefaction parameter 
$\delta$ and accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$. The distributions demonstrate the same behaviours in the case 
${M\!a}=2$ and 
$\delta \le 1$. However, they are completely different at 
${M\!a}=2$ and 
$\delta =30$, when the quantities 
$n/n_\infty$, 
$T/T_\infty$ and 
$u_x/U_\infty$ change sharply at the point 
$x/R=-1.5$ corresponding to the shock wave position. In this case, the accommodation coefficients 
$\alpha _t$ and 
$\alpha _n$ practically do not affect the flow field. The profiles at 
${M\!a}=5$ and 10 similar to those for 
${M\!a}=2$ are given in the supplementary material.
Figure 7. Axial distributions of (a,b) density 
$n/n_\infty$, (c,d) temperature 
$T/T_\infty$, and (e, f) velocity 
$u_x/U_\infty$ at 
$T_\infty =T_w=300$ K for 
$^{4}$He: (a,c,e) 
${M\!a}=1$; (b,d, f) 
${M\!a}=2$. Solid lines indicate diffuse reflection; dashed lines indicate 
$\alpha _t=0.4$, 
$\alpha _n=0.01$.
The local pressure 
$C_p$, friction 
$C_f$, and energy transfer 
$C_h$ coefficients for 
$^{4}$He at the diffuse interaction (
$\alpha _t=1$ and 
$\alpha _n=1$), and those for the set 
$\alpha _t=0.4$ and 
$\alpha _n=0.01$, are plotted against angle 
$\theta$ in figure 8. All these coefficients are sensitive to the accommodation coefficients, rarefaction parameter and Mach number. The pressure 
$C_p$ and friction 
$C_f$ coefficients have the same qualitative behaviours as functions of 
$\theta$ for all values of 
$\delta$, 
${M\!a}$, 
$\alpha _t$ and 
$\alpha _n$, while the energy transfer coefficient 
$C_h$ differs qualitatively for diffuse (
$\alpha _t=1$, 
$\alpha _n=1$) and non-diffuse (
$\alpha _t=0.4$, 
$\alpha _n=0.01$) reflection. Curiously, the coefficient 
$C_h$ has a minimum at the stagnation point 
$\theta =0$ when 
$\delta \le 1$.
Figure 8. (a,b) Pressure 
$C_p$, (c,d) friction 
$C_f$, and (e, f) energy transfer 
$C_h$ coefficients versus angle 
$\theta$ at 
$T_\infty =T_w=300$ K for 
$^{4}$He: (a,c,e) 
${M\!a}=1$; (b,d, f) 
${M\!a}=2$. Solid lines indicate diffuse reflection; dashed lines indicate 
$\alpha _t=0.4$, 
$\alpha _n=0.01$.
6.4. Effect of the sphere temperature
To reveal the effect of 
$T_w$ on the aerothermodynamic characteristics, the calculations at 
$T_w=T_s$ and 
$T_\infty =300$ K were performed for 
$^{4}$He interacting diffusely with the sphere surface. In addition, the fixed value 
$T_w=1000$ K was considered for all Mach numbers, keeping 
$T_\infty =300$ K. In the cases 
${M\!a}=1$ and 2, the temperature 
$T_w=1000$ K is higher than 
$T_s$. This can happen when the spherical particles immersed in a gas are heated by laser radiation. In the cases 
${M\!a}=5$ and 10, the the temperature 
$T_w=1000$ K lies in between 
$T_\infty$ and 
$T_s$.
The values of 
$C_D$ and 
$C_Q$ for these two values of the sphere temperature 
$T_w$ are given in table 5. In the case 
$T_w=1000$ K, the drag coefficient is strongly affected by 
$T_w$ at 
${M\!a}=1$, while the effect of 
$T_w$ on 
$C_D$ is weak at 
${M\!a}=5$ and 10. This effect decreases with increasing the rarefaction parameter 
$\delta$ for a fixed Mach number. If 
$T_w=T_s$, then the drag coefficient at 
${M\!a}=10$ and 
$\delta =0.1$ increases 32 % in comparison with the cold sphere (
$T_w=T_\infty$) at the same 
${M\!a}$ and 
$\delta$. The difference is smaller for the smaller Mach number and becomes 4 % at 
${M\!a}=1$ and 
$\delta =0.1$. For a fixed Mach number, the influence of 
$T_w$ on the drag coefficient decreases drastically when the rarefaction parameter 
$\delta$ varies from 0.1 to 30. For instance, in the case 
${M\!a}=10$ and 
$\delta =30$, the increase of 
$C_D$ is approximately 8 % when the temperature 
$T_w$ varies from 
$T_\infty$ to 
$T_s$. According to table 2, the influence of 
$T_w$ on 
$C_D$ in the free molecular regime (
$\delta =0$) becomes weaker when the NEAC 
$\alpha _n$ changes from 1 to 0.5. Thus the effect of 
$T_w$ on 
$C_D$ is insignificant for all Mach numbers and rarefaction parameters when 
$\alpha _n\le 0.5$.
Table 5. Drag 
$C_D$ and average energy transfer 
$C_Q$ coefficients for 
$^{4}$He versus Mach number 
${M\!a}$ and rarefaction parameter 
$\delta$ at diffuse reflection (
$\alpha _t=1$ and 
$\alpha _n=1$).
The average energy transfer coefficient 
$C_Q$ is strongly sensitive to the sphere temperature 
$T_w$. It changes its sign at 
${M\!a}=1$ and 2 for all 
$\delta$ when 
$T_w=1000$ K, and at 
$\delta \ge 10$ for all 
${M\!a}$ when 
$T_w=T_s$. The decrease of 
$C_Q$ with increasing surface temperature is also predicted in the free molecular flow regime by (4.12).
The local friction coefficient 
$C_f$ is not sensitive to the surface temperature 
$T_w$, so it is not analysed here. Note that in the free molecular flow regime, the coefficient 
$C_f$ is completely independent of 
$T_w$, in accordance with (4.9). The expression (4.8) for the local pressure coefficient 
$C_p$ at 
$\delta =0$ points out its dependence on the surface temperature 
$T_w$ via the term 
$\varPhi$ given by (4.4). The local energy transfer coefficient 
$C_h$ is also affected by 
$T_w$ at 
$\delta =0$ according to (4.12). The coefficients 
$C_p$ and 
$C_h$ for 
$^{4}$He interacting diffusely with the sphere surface are plotted against angle 
$\theta$ in figure 9; the solid lines correspond to 
$T_w=300$ K, and the dashed lines correspond to 
$T_w=T_s$. The pressure coefficient 
$C_p$ is weakly sensitive to the surface temperature 
$T_w$ in the hydrodynamic flow regime at 
$\delta =30$, while it is strongly sensitive at 
$\delta =0.1$ and 
$1$ for all Mach numbers. The energy transfer coefficient 
$C_h$ is strongly sensitive to 
$T_w$ for all values of the rarefaction parameter 
$\delta$ for the small Mach number 
${M\!a}=2$. The effect of 
$T_w$ on 
$C_h$ becomes more pronounced with decreasing 
${M\!a}$. The behaviours of the coefficients 
$C_p$ and 
$C_h$ at 
${M\!a}=5$ and 10 similar to those at 
${M\!a}=2$ are given in the supplementary material.
Figure 9. (a,b) Pressure 
$C_p$ and (c,d) energy transfer coefficients 
$C_h$ versus angle 
$\theta$ for 
$^{4}$He, diffuse scattering, 
$T_\infty =300$ K: (a,c) 
${M\!a}=1$; (b,d) 
${M\!a}=2$. Solid lines indicate 
$T_w=300$ K; dashed lines indicate 
$T_w=T_s$.
To demonstrate the sphere temperature effect on the flow field, the distributions of 
$^{4}$He interacting diffusely with the cold sphere at 
$T_w=T_\infty =300$ K are compared to those for the same gas at 
$T_w=T_s$ and 
$T_\infty =300$ K in figure 10. In all situations, the sphere temperature affects strongly the temperature and density distributions near the sphere, while the gas velocity is affected weakly. In the case 
${M\!a}=2$ and 
$\delta =30$, the shock wave structure in front of the sphere is different for 
$T_w=T_s$ from that for 
$T_w=300$ K. Mainly, the increase in the sphere temperature increases the distance between the sphere surface and bow shock.
Figure 10. Axial distributions of (a,b) density 
$n/n_\infty$, (c,d) temperature 
$T/T_\infty$, and (e, f) velocity 
$u_x/U_\infty$ for 
$^{4}$He at 
$T_\infty =300$ K and diffuse scattering: (a,c,e) 
${M\!a}=1$; (b,d, f) 
${M\!a}=2$. Solid lines indicate 
$T_w=300$ K; dashed lines indicate 
$T_w=T_s$.
The effect of the sphere temperature on flows of the other gases is very similar to that for helium because of the weak influence of the gas species, which was discussed in § 6.1.
7. Conclusions
The aerothermodynamic characteristics of a sphere in transonic, supersonic and hypersonic flows were calculated by the DSMC method employing AI potentials for interatomic collisions. The calculations have been performed for the noble gases 
$^{3}$He, 
$^{4}$He, Ne, Ar and Kr over a wide range of gas rarefaction spanning the free molecular, transitional and hydrodynamic flow regimes for Mach numbers 1, 2, 5 and 10. The parameters of the numerical scheme have been chosen to provide numerical errors in the drag and energy transfer coefficients less than 0.5 %. The effects of several factors, such as gas species, free stream temperature, sphere surface temperature and accommodation coefficients, were studied. The Cercignani–Lampis kernel for gas–surface interaction was used to describe a non-diffuse reflection. The analysis of the numerical results leads to the following conclusions.
(i) The aerothermodynamic characteristics based on the AI potentials are significantly different from those based on the HS model at large values of the Mach number. The difference becomes smaller al low Mach numbers. For instance, the relative differences of the drag coefficient based on these two potentials are approximately 1.3 % and 10 % for Mach numbers 1 and 10, respectively. The relative difference of the energy transfer coefficient is almost three times larger. This conclusion is in agreement with the previous results for a gas flow past a cylinder by Volkov & Sharipov (Reference Volkov and Sharipov2017).
(ii) The comparison of the results based on AI potentials points out a small divergence of the aerothermodynamic characteristics for different gases. The drag coefficient varies within 3 % at large Mach numbers, and within 1 % for Mach number 1. The variation of the energy transfer coefficient is three-fold larger compared to that for the drag coefficient.
(iii) Both drag and energy transfer coefficients depend non-monotonically on the temperature of the free stream
$T_\infty$, assuming that the sphere temperature is equal to $T_\infty$. The variation of the drag coefficient due to the variation of $T_\infty$ is approximately 8 %, while the energy transfer coefficient varies within 15 %.(iv) The diffuse gas–surface interaction always leads to the largest value of the energy transfer coefficient in comparison to the non-diffuse reflection model. The drag coefficient can be larger or smaller when the non-diffuse reflection is used instead of the diffuse one. Such behaviour is predicted by both the DSMC calculations in the transitional flow regime and theoretical equations obtained for free molecular flow. Both coefficients are strongly sensitive to the accommodation coefficients.
(v) When the surface temperature is increased, keeping the free stream temperature constant, the drag coefficient increases. The strongest effect of the sphere temperature is observed at the highest Mach number (
${M\!a}=10$), free molecular regime ($\delta =0$), and diffuse gas–surface interaction. When the energy accommodation coefficient varies from 1 to 0.5, this effect becomes insignificant for all $\delta$ and ${M\!a}$ considered in the present work. Under the same conditions, the energy transfer coefficient decreases significantly and becomes negative in some situations.
Supplementary material
The supplementary material contains detailed information about the boundary conditions, additional information about the estimation of numerical error, additional plots of the flow field, and qualitative comparison of the present results with data published previously. The supplementary material is available at https://doi.org/10.1017/jfm.2022.356.
Funding
F.S. thanks CNPq, Brazil for the support of his research (grant no. 304831/2018-2). A.N.V. acknowledges the support of the present work by the NSF award CMMI-1554589. Computational support is provided by the Alabama Supercomputer Center and Laboratório Central de Processamento de Alto Desempenho of UFPR.
Declaration of interests
The authors report no conflict of interest.
