1 Introduction
Controlled propulsion of microscopic objects in viscous flows has recently attracted much attention for its potential biomedical applications such as drug transport and delivery (Burdick et al. Reference Burdick, Laocharoenshuk, Wheat, Posner and Wang2008; Sundararajan et al. Reference Sundararajan, Lammert, Zudans, Crespi and Sen2008; Nelson, Kaliakastos & Abbott Reference Nelson, Kaliakastos and Abbott2010) or analytical sensing in biological media (Campuzano et al. Reference Campuzano, Kagan, Orozco and Wang2011; Wu et al. Reference Wu, Kagan, Manesh, Campuzano and Wang2010). Self-propulsion in viscous flows requires temporal and spatial symmetry breaking (Purcell Reference Purcell1977; Lauga & Powers Reference Lauga and Powers2009). Based on that principle, many different mechanisms have been proposed to achieve propulsion of small rigid objects (see the reviews of Ebbens & Howse (Reference Ebbens and Howse2010), Wang et al. (Reference Wang, Duan., Ahmed, Mallouk and Sen2013)) and they generally belong to either of the two following categories.
The first and most classical group exploits an externally applied directional field, that effectively breaks the symmetry of the system at a scale much larger than the particle size, and drives the object in a specific direction. Electrophoresis (Smoluchowsky Reference Smoluchowsky1921) and diffusiophoresis (Anderson Reference Anderson1989) both fall in this first group, and result from the application of macroscopic electric or chemical gradients. The alternative approach relies on the local interaction of the particle with its close environment. Taking advantage of its own asymmetry, the particle converts locally the energy provided by a non-directional forcing field to break symmetry and self-propel.
For instance, catalytic bimetallic microrods can propel themselves (self-electrophoresis) at high velocities (up to 
$10~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$) by oxidizing hydrogen peroxide and exploiting the resulting self-generated local electric fields (see e.g. Paxton et al. Reference Paxton, Kistler, C.c., Sen, Angelo, Mallouk, Thomas, Lammert and Crespi2004, Ibele et al. Reference Ibele, Wang, Kline, Mallouk and Sen2007, Ebbens & Howse Reference Ebbens and Howse2011). For non-ionic solutes, the concentration gradient can also trigger a net motion of the particle through self-diffusiophoresis (Pavlick et al. Reference Pavlick, Sengupta, McFadden, Zhang and Sen2011, Reference Pavlick, Dey, Sirjoosingh, Benesi and Sen2013; Golestanian, Liverpool & Ajdari Reference Golestanian, Liverpool and Ajdari2007; Cordova-Figueroa & Brady Reference Cordova-Figueroa and Brady2008). Similarly, autonomous propulsion can be achieved by taking advantage of self-thermophoresis effects (Jiang, Yoshinaga & Sano Reference Jiang, Yoshinaga and Sano2010; Baraban et al. Reference Baraban, Streubel, Makarov, Han, Karnaushenko, Schmidt and Cuniberti2012; Qian et al. Reference Qian, Montiel, Bregulla, Cichos and Yang2013). Unfortunately, electrochemically and thermally based methods are not biocompatible as a result of the inherent toxicity of the involved fuels (hydrogen peroxide, hydrazine) or of the required temperature differences.
Alternatively, acoustic fields may be used to achieve autonomous motion in biofluids, which explains the increasing interest of the scientific community in this type of propulsion method. Wang et al. (Reference Wang, Castro, Hoyos and Mallouk2012) demonstrated experimentally that bimetallic rods with asymmetric shape or composition were able to self-propel with velocities up to 
$200~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ when trapped in the nodal plane of an acoustic resonator. This pioneering work was soon extended to various configurations and geometries, and self-acoustophoresis of magnetic clusters or asymmetric particles was thus reported (Sabrina et al. Reference Sabrina, Tasinkevych, Ahmed, Brooks, Olvera de la Cruz, Mallouk and Bishop2018; Ahmed et al. Reference Ahmed, Gentekos, Fink and Mallouk2014, Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016). Kaynak et al. (Reference Kaynak, Ozcelik, Nourhani, Lammert, Crespi and Huang2017) showed that bioinspired acoustic microswimmers with dedicated shapes were even able to reach velocities up to 
$1200~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$. Although the prescribed acoustic field from which self-propulsion originates is directional, self-propulsion is achieved in a plane orthogonal to the excitation and its direction is not set by the external driving in contrast, for instance, with classical electrophoretic migrations of particles along the imposed forcing.
Since the seminal work of Wang et al. (Reference Wang, Castro, Hoyos and Mallouk2012), acoustic propulsion has been repeatedly ascribed to the streaming flows self-generated by the particle’s periodic motion with respect to its fluid environment of small yet finite inertia (Riley Reference Riley1966; Nadal & Lauga Reference Nadal and Lauga2014; Collis et al. Reference Collis, Jesse, Chakraborty and Sader2017; Kaynak et al. Reference Kaynak, Ozcelik, Nourhani, Lammert, Crespi and Huang2017). To analyse the potential role of a particle’s asymmetric shape on its ability to self-propel, Nadal & Lauga (Reference Nadal and Lauga2014) first derived an integral form of the steady axial velocity of an acoustically forced near-sphere, exploiting the absence of rotation of the particle at leading order in the particle’s asymmetry as suggested by Zhang & Stone (Reference Zhang and Stone1998). Lippera et al. (Reference Lippera, Dauchot, Michelin and Benzaquen2019) recently showed, however, that this configuration did not actually yield any propulsion at leading order and that higher-order corrections in the particle’s asymmetry were necessary to obtain a rectified effect. Collis et al. (Reference Collis, Jesse, Chakraborty and Sader2017) considered the opposite case of an asymmetric (in density or shape) dumbbell of large aspect ratio, and showed that the propelling streaming flow actually arose from the inertial coupling between the viscous flows, respectively, generated by the particle’s translation and rotation, suggesting that acoustically generated rotation of the particle was just as essential as its periodic translation in order to obtain acoustic propulsion.
Inspired by this observation, we analyse here how acoustic self-propulsion of a geometrically symmetric particle (i.e. a sphere) may be achieved when its non-uniform density results in a combined translation and rotation under the effect of the acoustic forcing. We thus present the full analytical derivation of the leading-order propulsion velocity of a non-homogeneous sphere trapped at the nodal plane of a resonator. The centre of mass and centroid of the sphere do not coincide anymore, and as a result an inertial torque is imposed on the acoustically forced sphere driving a combination of translational and rotational motions. We demonstrate that spherical particles may thus self-propel thanks to a symmetry breaking in the hydrodynamic stress resulting from the inertial coupling of the viscous flows associated with the particle’s combined translation and rotation, as suggested by Collis et al. (Reference Collis, Jesse, Chakraborty and Sader2017).
The paper is organized as follows. Section 2 is devoted to the derivation of the linear translational and rotational viscous responses of a non-homogeneous sphere to the transverse acoustic forcing. The leading-order inertial propulsion velocity of such a sphere is obtained in § 3 by means of a suitable version of the Lorentz reciprocal theorem. The physical relevance of this model to experimental observations is then discussed in § 4. Finally, our main findings are summarized in § 5.
2 Acoustically forced dynamics of a sphere in a viscous fluid
2.1 Configuration and main assumptions
We consider here the dynamics of a solid sphere of radius 
$a$ and mean density 
$\unicode[STIX]{x1D70C}_{s}$ forced by a viscous periodic flow of density 
$\unicode[STIX]{x1D70C}$ and kinematic viscosity 
$\unicode[STIX]{x1D708}$. The density distribution of the solid sphere is not homogeneous, so that the centre of mass 
$G$ departs from its centroid 
$O$ (figure 1). The mass and volume of the sphere are 
$m_{s}=\unicode[STIX]{x1D70C}_{s}{\mathcal{V}}_{s}$ and 
${\mathcal{V}}_{s}=(4/3)\unicode[STIX]{x03C0}\,a^{3}$, respectively.
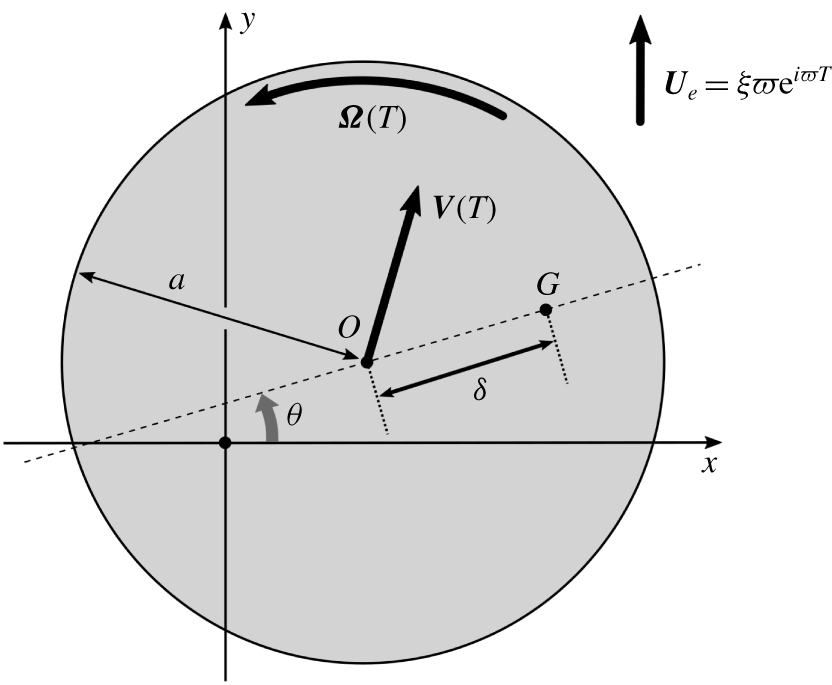
Figure 1. Oscillations of a bottom-heavy sphere forced by a uniform external oscillating flow. Here, 
$\unicode[STIX]{x1D709}$ and 
$\unicode[STIX]{x1D71B}$ are the displacement amplitude and frequency of the forcing acoustic field. The radius of the sphere is denoted by 
$a$, and 
$\unicode[STIX]{x1D6FF}$ refers to the centroid-to-centre of mass distance 
$OG$.
The forcing (acoustic) flow 
$\boldsymbol{U}_{e}$ is uniform, harmonic of frequency 
$\unicode[STIX]{x1D71B}$ and directed along the 
$y$-direction. This configuration corresponds to a sphere of size 
$a$ trapped at the pressure node of a standing acoustic wave of wave vector 
$\boldsymbol{k}=k\,\boldsymbol{e}_{y}$ in the limit 
$ka\ll 1$ (with 
$(\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z})$ are the Cartesian unit vectors). In such a case, the incident flow can be considered as locally incompressible and to depend only on 
$y$. We consider in the following that the external forcing flow is uniform and takes the simple harmonic form
$$\begin{eqnarray}\boldsymbol{U}_{e}=\hat{\boldsymbol{U}}_{\!e}\,\text{e}^{\text{i}\unicode[STIX]{x1D71B}\,T}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}\,\,\text{e}^{\text{i}\unicode[STIX]{x1D71B}\,T}\,\boldsymbol{e}_{y},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D709}$ is the amplitude of the fluid particles’ displacement in the 
$y$-direction and is assumed to be much smaller than the particle’s size 
$a$, so that 
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D709}/a\ll 1$.
The offset of the sphere’s centroid and centre of mass is characterized by 
$\unicode[STIX]{x1D739}=\mathbf{OG}=\unicode[STIX]{x1D6FF}\,\boldsymbol{d}$, where 
$\boldsymbol{d}=\cos \unicode[STIX]{x1D703}\,\boldsymbol{e}_{x}+\sin \unicode[STIX]{x1D703}\,\boldsymbol{e}_{y}$ (figure 1). The velocity of 
$O$ and 
$G$ in the laboratory reference frame are denoted by 
$\boldsymbol{V}_{O}$ and 
$\boldsymbol{V}_{G}$ and the angular velocity 
$\unicode[STIX]{x1D734}$ of the sphere is aligned with 
$z$-direction: 
$\unicode[STIX]{x1D734}=\dot{\unicode[STIX]{x1D703}}\,\boldsymbol{e}_{z}$ (i.e. we assume that the sphere’s density distribution is symmetric with respect to the 
$(Oxy)$-plane). In the following, we make the additional assumption that the velocity of the particle is periodic for the zero-mean forcing flow 
$\boldsymbol{U}_{e}(t)$ considered (note, however, that its mean value is not necessarily zero so as to allow for self-propulsion regimes).
The objective of the present section is to derive the response of the sphere to the external flow in an unsteady Stokesian framework, where inertia of the fluid is negligible, but that of the solid particle is not.
2.2 Momenta conservation
The conservation of momentum in the (Galilean) frame of reference can be written
$$\begin{eqnarray}m_{s}\,\dot{\boldsymbol{V}}_{\!G}=\boldsymbol{F}+\boldsymbol{F}_{p},\end{eqnarray}$$ where the total force experienced by the sphere is the sum of the hydrodynamic force 
$\boldsymbol{F}$ due to the relative velocity between the sphere and the surrounding fluid, and of the pressure force 
$\boldsymbol{F}_{p}=\unicode[STIX]{x1D70C}{\mathcal{V}}_{s}\,\dot{\boldsymbol{U}}_{e}$ arising from the external pressure gradient that sets the fluid in motion. Such a distinction is justified by the form of the viscous drag experienced by a solid sphere oscillating in an uniformly oscillating flow presented by Kim & Karrila (Reference Kim and Karrila2005). Note that assuming that the velocity of the particle is periodic in time immediately implies that the time average of 
$\boldsymbol{F}(t)$ is zero.
Using 
$\boldsymbol{V}_{G}=\boldsymbol{V}_{O}-\unicode[STIX]{x1D739}\times \unicode[STIX]{x1D734}$, and noting 
$\boldsymbol{V}=\boldsymbol{V}_{O}-\boldsymbol{U}_{e}$ the velocity of the sphere relative to the oscillating fluid, the previous equation can be rewritten as
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}{\mathcal{V}}_{s}\dot{\boldsymbol{V}}=m_{s}\left[(\unicode[STIX]{x1D734}\times \unicode[STIX]{x1D739})\times \unicode[STIX]{x1D734}+\,\unicode[STIX]{x1D739}\times \;\;\dot{\unicode[STIX]{x1D734}}\right]+\boldsymbol{F}+(\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}_{s}){\mathcal{V}}_{s}\dot{\boldsymbol{U}}_{e},\end{eqnarray}$$where the last term is the effective buoyancy force.
Similarly, the conservation of angular momentum can be written about the centre of mass 
$G$,
$$\begin{eqnarray}I_{G}\,\;\;\dot{\unicode[STIX]{x1D734}}=\boldsymbol{L}_{G},\end{eqnarray}$$ where 
$I_{G}$ is the moment of inertia of the sphere about the 
$(G,z)$-axis and 
$\boldsymbol{L}_{G}$ is the total torque experienced by the sphere at its centre of mass.
The sphere is rigid, thus 
$\boldsymbol{L}_{G}=\boldsymbol{L}+\boldsymbol{G}\boldsymbol{O}\times (\boldsymbol{F}+\boldsymbol{F}_{p})$, where 
$\boldsymbol{L}$ is the hydrodynamic torque about the geometric centre 
$O$, and (2.4) finally becomes
$$\begin{eqnarray}I_{G}\,\;\;\dot{\unicode[STIX]{x1D734}}=\boldsymbol{L}-\unicode[STIX]{x1D739}\times (\boldsymbol{F}+\boldsymbol{F}_{p}).\end{eqnarray}$$2.3 Dimensionless forms of the conservation laws
In the following, using 
$U_{e}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}$ and 
$\unicode[STIX]{x1D71B}^{-1}$ as reference velocity and time scales, respectively, yields the non-dimensional form of (2.3) and (2.5) (using lower-case letters for dimensionless variables)
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{v}}=\unicode[STIX]{x1D700}^{-1}\,\unicode[STIX]{x1D6FC}\,\left[(\unicode[STIX]{x1D74E}\times \boldsymbol{d})\times \unicode[STIX]{x1D74E}+\boldsymbol{d}\times \dot{\unicode[STIX]{x1D74E}}\right]+\left(\frac{3}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}}\right)\,\boldsymbol{f}+(\unicode[STIX]{x1D6FD}-1)\,\boldsymbol{f}_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\unicode[STIX]{x1D74E}}=\left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,\boldsymbol{l}-\unicode[STIX]{x1D700}\left[\left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,(\boldsymbol{d}\times \boldsymbol{f})+\left(\frac{5}{2}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{I}\right)(\boldsymbol{d}\times \boldsymbol{f}_{e})\right], & \displaystyle\end{eqnarray}$$ with 
$\boldsymbol{f}_{e}=\text{i}\,\text{e}^{\text{i}t}\,\boldsymbol{e}_{y}$ the fluctuating forcing.
In the above equations, the dimensionless moment of inertia 
$I=I_{G}/I_{0}$ is the ratio between the actual moment of inertia 
$I_{G}$ and 
$I_{0}=(2/5)~m_{s}~a^{2}$, the moment of inertia of a homogeneous sphere with the same mean density with respect to its centre. Further, 
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}/a$ is the relative geometric offset of the particle’s centre of mass and thus characterizes its non-homogeneity, 
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{s}$ is the fluid-to-solid average density ratio and 
$\unicode[STIX]{x1D706}=(a^{2}\unicode[STIX]{x1D71B}/\unicode[STIX]{x1D708})^{1/2}$ is the ratio between the radius of the sphere and the viscous penetration length (i.e. 
$\unicode[STIX]{x1D706}^{2}$ is the reduced frequency of actuation). It should be noted that the 
$\unicode[STIX]{x1D700}^{-1}$ factors are associated with the choice of characteristic velocity scale.
2.4 Harmonic response in the unsteady Stokes limit
The non-dimensional forcing field 
$\boldsymbol{f}_{e}=f_{e}\,\boldsymbol{e}_{y}$ with 
$f_{e}=\text{i}\text{e}^{\text{i}t}$ is 
$O(\unicode[STIX]{x1D700}^{0})$ and harmonic; as a result, for 
$\unicode[STIX]{x1D700}\ll 1$, the leading-order dynamics is obtained by noting that 
$v_{y}=O(1)$ while 
$v_{x}$ and 
$\unicode[STIX]{x1D703}$ are 
$O(\unicode[STIX]{x1D700})$,
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{v}_{x}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D700}^{-1}\,(\dot{\unicode[STIX]{x1D703}}^{2}+\ddot{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D703})+\left(\frac{3}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}}\right)\,f_{x}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{v}_{y}=-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D700}^{-1}\,\ddot{\unicode[STIX]{x1D703}}+\left(\frac{3}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}}\right)\,f_{y}+(\unicode[STIX]{x1D6FD}-1)\,f_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \ddot{\unicode[STIX]{x1D703}}=\left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,l-\unicode[STIX]{x1D700}\left[\left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,f_{y}+\left(\frac{5}{2}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{I}\right)\,f_{e}\right]. & \displaystyle\end{eqnarray}$$ In the unsteady Stokes limit, the total viscous force and torque on the sphere are obtained by superimposing that induced by the sphere’s translation and rotation independently. By symmetry, the force induced by the sphere’s rotation and the torque (about 
$O$) induced by the sphere’s translation are both identically zero. Therefore, considering the form of the system (2.8)–(2.10) and according to Kim & Karrila (Reference Kim and Karrila2005), one can write
$$\begin{eqnarray}\displaystyle \displaystyle v_{x}=\unicode[STIX]{x1D700}\,\hat{v}_{0,x}\,\text{e}^{2\text{i}t},\quad \displaystyle v_{y}=\hat{v}_{0,y}\,\text{e}^{\text{i}t},\quad \unicode[STIX]{x1D703}=\unicode[STIX]{x1D700}\,\hat{\unicode[STIX]{x1D703}}_{0}\,\text{e}^{\text{i}t} & & \displaystyle\end{eqnarray}$$and
$$\begin{eqnarray}\displaystyle f_{x}=-\unicode[STIX]{x1D6E5}_{2}\,v_{x},\quad f_{y}=-\unicode[STIX]{x1D6E5}_{1}\,v_{y},\quad l=-\unicode[STIX]{x1D6EC}_{1}\,\dot{\unicode[STIX]{x1D703}}, & & \displaystyle\end{eqnarray}$$ where the drag coefficients 
$\unicode[STIX]{x1D6E5}_{n}$ and 
$\unicode[STIX]{x1D6EC}_{n}$ are associated with harmonic translational or rotational motion of a sphere in unsteady viscous flows (see also § 3.4 Kim & Karrila (Reference Kim and Karrila2005))
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{n}=6\unicode[STIX]{x03C0}\left(1+\,n^{1/2}\tilde{\unicode[STIX]{x1D706}}+\frac{n\tilde{\unicode[STIX]{x1D706}}^{2}}{9}\right)\quad \text{and}\quad \unicode[STIX]{x1D6EC}_{n}=8\unicode[STIX]{x03C0}\,\frac{1+n^{1/2}\tilde{\unicode[STIX]{x1D706}}+\text{i}\,n\tilde{\unicode[STIX]{x1D706}}^{2}/3}{1+n^{1/2}\tilde{\unicode[STIX]{x1D706}}},\end{eqnarray}$$ and 
$\tilde{\unicode[STIX]{x1D706}}=\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}\,\unicode[STIX]{x1D706}$.
The leading-order dynamics (
$\hat{v}_{0,y}$, 
$\hat{\unicode[STIX]{x1D703}}_{0}$) is then obtained from the linear system
$$\begin{eqnarray}\displaystyle & \displaystyle \left[\text{i}+\left(\frac{3}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}}\right)\,\unicode[STIX]{x1D6E5}_{1}\right]\hat{v}_{0,y}-\unicode[STIX]{x1D6FC}\,\hat{\unicode[STIX]{x1D703}}_{0}=\text{i}(\unicode[STIX]{x1D6FD}-1), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,\unicode[STIX]{x1D6E5}_{1}\hat{v}_{0,y}+\left[1-\text{i}\left(\frac{15}{8\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D706}^{2}I}\right)\,\unicode[STIX]{x1D6EC}_{1}\right]\,\hat{\unicode[STIX]{x1D703}}_{0}=\text{i}\left(\frac{5}{2}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{I}\right). & \displaystyle\end{eqnarray}$$ It should be noted that the above dynamics is independent from that along the 
$x$-direction, which can be computed in a second step. The complex amplitude of the angular velocity 
$\hat{\unicode[STIX]{x1D714}}_{0}$ is then obtained using 
$\hat{\unicode[STIX]{x1D714}}_{0}=\text{i}\,\unicode[STIX]{x1D700}\,\hat{\unicode[STIX]{x1D703}}_{0}$.
From the small and large 
$\unicode[STIX]{x1D706}$ approximations of 
$\unicode[STIX]{x1D6E5}_{1}$ and 
$\unicode[STIX]{x1D6EC}_{1}$, equations (2.14)–(2.15) can be used to obtain the following useful asymptotic forms of 
$\hat{v}_{0,y}$ and 
$\hat{\unicode[STIX]{x1D703}}_{0}$:
$$\begin{eqnarray}\hat{v}_{0,y}\sim \frac{2\text{i}\unicode[STIX]{x1D706}^{2}(\unicode[STIX]{x1D6FD}-1)}{9\unicode[STIX]{x1D6FD}}\quad \text{and}\quad \hat{\unicode[STIX]{x1D703}}_{0}\sim -\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}^{2}}{6\unicode[STIX]{x1D6FD}}\quad \text{for }\unicode[STIX]{x1D706}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}\hat{v}_{0,y}\sim \frac{4I(\unicode[STIX]{x1D6FD}-1)+10\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FD}}{\displaystyle 4I+\unicode[STIX]{x1D6FD}(2I+5\unicode[STIX]{x1D6FC}^{2})}\quad \text{and}\quad \hat{\unicode[STIX]{x1D703}}_{0}\sim \frac{\displaystyle 15\text{i}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{4I+\unicode[STIX]{x1D6FD}(2I+5\unicode[STIX]{x1D6FC}^{2})}\quad \text{for }\unicode[STIX]{x1D706}\rightarrow \infty .\end{eqnarray}$$3 Acoustic propulsion of the sphere
Knowing the leading-order viscous response of the sphere to the incident acoustic field, we now proceed to explore the possibility of achieving propulsion by means of streaming effects, by accounting for the first inertial correction to the flow field following the approach of Lippera et al. (Reference Lippera, Dauchot, Michelin and Benzaquen2019).
3.1 Governing equations
By moving through the fluid, the sphere generates a flow field 
$\boldsymbol{u}(\boldsymbol{r},t)$ around itself governed by the Navier–Stokes and continuity equations, which can be written in non-dimensional form in the frame of reference moving with the fluid far from the sphere as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{2}\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+Re\,\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{eqnarray}$$ where 
$\unicode[STIX]{x1D748}$ is the non-dimensional hydrodynamic stress in the fluid due to the relative motion between the sphere and the surrounding fluid (and therefore includes a corrected pressure to account for the inertial corrections associated with the moving frame). It is recalled that, as in the previous section, all quantities are non-dimensional and 
$a$, 
$\unicode[STIX]{x1D71B}^{-1}$ and 
$\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}$ are used as reference length, time and velocity scales, respectively. In (3.1), the Reynolds number is 
$Re=\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}^{2}$ with 
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D709}/a\ll 1$. In the following we thus focus on the limit of 
$Re\ll 1$, which yields the restriction 
$\unicode[STIX]{x1D706}^{2}\ll \unicode[STIX]{x1D700}^{-1}$ for the following analysis. Note that 
$Re$ is therefore not a new independent dimensionless group so that the problem is only governed by the five parameters 
$\unicode[STIX]{x1D700}$, 
$\unicode[STIX]{x1D706}$, 
$\unicode[STIX]{x1D6FC}$, 
$\unicode[STIX]{x1D6FD}$ and 
$I$ defined in the previous section, and listed in table 1.
Table 1. List of the five independent parameters of the problem. Note that the Reynolds number 
$Re=\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}^{2}$, which is supposed to be small compared to unity, is not an independent parameter.
The flow field vanishes at infinity and satisfies the no-slip boundary condition on the moving sphere (
$|\boldsymbol{r}|=1$ in a set of axes attached to the centroid of the sphere), therefore
$$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{v}+\unicode[STIX]{x1D74E}\times \boldsymbol{r}\quad \text{for }|\boldsymbol{r}|=1,\quad \boldsymbol{u}\rightarrow 0\quad \text{for }|\boldsymbol{r}|\rightarrow \infty .\end{eqnarray}$$3.2 Expansions in power of 
$Re$ and order of the propulsion speed
The Reynolds number, 
$Re$, is a small parameter of the problem, and we now expand the velocity field 
$\boldsymbol{u}$, the hydrodynamic stress 
$\unicode[STIX]{x1D748}$, and the velocity of the sphere 
$\boldsymbol{v}$ in powers of the Reynolds number
$$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{u}^{(0)}+Re\,\boldsymbol{u}^{(1)}+\cdots \,,\quad \unicode[STIX]{x1D748}=\unicode[STIX]{x1D748}^{(0)}+Re\,\unicode[STIX]{x1D748}^{(1)}+\cdots \,,\quad \boldsymbol{v}=\boldsymbol{v}^{(0)}+Re\,\boldsymbol{v}^{(1)}+\cdots \,.\end{eqnarray}$$ We are interested in the emergence of a net propulsion of the sphere and therefore will focus on the existence of a steady component to the sphere’s velocity. Due to the linearity of the unsteady Stokes equation, such steady motions have to be generated at order 
$O(Re)$ at least, which can be written 
$\overline{\boldsymbol{v}}=Re\,\langle \boldsymbol{v}^{(1)}\rangle$, where 
$\langle \cdots \!\rangle$ refers to the time average operator over a period of oscillation. In other words, the possibly non-zero 
$O(Re)$ steady component of the speed 
$\overline{\boldsymbol{v}}$ must be induced by the steady streaming flow resulting from the self-coupling of the 
$O(1)$ (i.e. 
$Re=0$) viscous flow through the nonlinear term of the Navier–Stokes equation.
To obtain such a forcing, one could explicitly derive the steady streaming flow and integrate the corresponding hydrodynamic stress over the surface of the sphere. In order to circumvent such a cumbersome derivation, we use in the following a specific form of Lorentz reciprocal theorem suitable for the case where inertial corrections are considered (Ho & Leal Reference Ho and Leal1974; Nadal & Lauga Reference Nadal and Lauga2014; Lippera et al. Reference Lippera, Dauchot, Michelin and Benzaquen2019).
3.3 Lorentz reciprocal theorem for inertial corrections
To this end, we define the auxiliary flow and stress fields 
$(\boldsymbol{u}^{\star },\unicode[STIX]{x1D748}^{\star })$, as the unique solution of the following steady Stokes problem
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748}^{\star }=0\quad \text{and}\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}^{\star }=0,\end{eqnarray}$$with boundary conditions
$$\begin{eqnarray}\boldsymbol{u}^{\star }=\boldsymbol{v}^{\star }+\unicode[STIX]{x1D74E}^{\star }\times \boldsymbol{r}\quad \text{at }|\boldsymbol{r}|=1,\quad \boldsymbol{u}^{\star }\rightarrow 0\quad \text{for }|\boldsymbol{r}|\rightarrow \infty .\end{eqnarray}$$ Using equations (3.1) and (3.4) and denoting by 
${\mathcal{V}}$ the volume of fluid outside the sphere, one can write an instantaneous version of the Lorentz reciprocal theorem (for further details, see again Lippera et al. (Reference Lippera, Dauchot, Michelin and Benzaquen2019)) in the following form:
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{2}\int _{{\mathcal{V}}}\boldsymbol{u}^{\star }\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}\,\text{d}{\mathcal{V}}+Re\int _{{\mathcal{V}}}[\boldsymbol{u}^{\star }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}]\,\text{d}{\mathcal{V}}=\boldsymbol{f}^{\star }\boldsymbol{\cdot }\boldsymbol{v}+\boldsymbol{l}^{\star }\boldsymbol{\cdot }\unicode[STIX]{x1D74E}-\boldsymbol{v}^{\star }\boldsymbol{\cdot }\boldsymbol{f}-\unicode[STIX]{x1D74E}^{\star }\boldsymbol{\cdot }\boldsymbol{l},\end{eqnarray}$$ where 
$\boldsymbol{f}$ and 
$\boldsymbol{l}$ ( 
$\boldsymbol{f}^{\star }$ and 
$\boldsymbol{l}^{\star }$, respectively) are the hydrodynamic force and torque in 
$O$ for the real (respectively, auxiliary) problem. Because the particle is spherical, we immediately have 
$\boldsymbol{f}^{\star }=-6\unicode[STIX]{x03C0}\,\boldsymbol{v}^{\star }$ and 
$\boldsymbol{l}^{\star }=-8\unicode[STIX]{x03C0}\,\unicode[STIX]{x1D74E}^{\star }$ and (3.6) becomes
$$\begin{eqnarray}-(6\unicode[STIX]{x03C0}\boldsymbol{v}+\boldsymbol{f})\boldsymbol{\cdot }\,\boldsymbol{v}^{\star }-(8\unicode[STIX]{x03C0}\unicode[STIX]{x1D74E}+\boldsymbol{l})\boldsymbol{\cdot }\unicode[STIX]{x1D74E}^{\star }=\unicode[STIX]{x1D706}^{2}\frac{\text{d}}{\text{d}t}\left[\int _{{\mathcal{V}}}\boldsymbol{u}^{\star }\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}{\mathcal{V}}\right]+Re\int _{{\mathcal{V}}}[\boldsymbol{u}^{\star }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}]\,\text{d}{\mathcal{V}},\end{eqnarray}$$ since 
$\boldsymbol{u}^{\star }$ is time independent and 
${\mathcal{V}}$ is fixed in time. It should be noted that up until now, no assumption on the magnitude of 
$Re$ was used and the previous equation is therefore valid for any value of the Reynolds number.
Now, introducing (3.3) and the additional 
$Re$-expansions
$$\begin{eqnarray}\boldsymbol{f}=\boldsymbol{f}^{(0)}+Re\boldsymbol{f}^{(1)}+\cdots \,,\quad \boldsymbol{l}=\boldsymbol{l}^{(0)}+Re\,\boldsymbol{l}^{(1)}+\cdots\end{eqnarray}$$ for the force and torque into (3.7), and and identifying the 
$O(1)$ terms, leads to
$$\begin{eqnarray}-(6\unicode[STIX]{x03C0}\boldsymbol{v}^{(0)}+\boldsymbol{f}^{(0)})\boldsymbol{\cdot }\,\boldsymbol{v}^{\star }-(8\unicode[STIX]{x03C0}\unicode[STIX]{x1D74E}^{(0)}+\boldsymbol{l}^{(0)})\boldsymbol{\cdot }\unicode[STIX]{x1D74E}^{\star }=\unicode[STIX]{x1D706}^{2}\int _{{\mathcal{V}}}\boldsymbol{u}^{\star }\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\boldsymbol{u}^{(0)}}{\unicode[STIX]{x2202}t}\,\text{d}{\mathcal{V}}.\end{eqnarray}$$ Note that the right-hand side of (3.9) can be integrated provided assumptions on the harmonic nature of the 
$O(1)$ solution are formulated, in order to obtain the drag force and torque in unsteady Stokes flow (
$Re=0$, see § 3.4).
Considering now the 
$O(Re)$ terms in (3.7), the problem obtained at that order is structurally similar to that at 
$O(1)$ but for the emergence of an extra forcing that arises from and accounts for the effect of the streaming flow. Should a net self-propulsion occur (i.e. on average over a whole period of forcing), it would therefore be due to the streaming forcing, as anticipated. Taking the average in time of the resulting equation, one obtains
$$\begin{eqnarray}-\boldsymbol{v}^{\star }\boldsymbol{\cdot }\langle 6\unicode[STIX]{x03C0}\,\boldsymbol{v}^{(1)}+\boldsymbol{f}^{(1)}\rangle -\,\unicode[STIX]{x1D74E}^{\star }\boldsymbol{\cdot }\langle 8\unicode[STIX]{x03C0}\unicode[STIX]{x1D74E}^{(1)}+\boldsymbol{l}^{(1)}\rangle =\left\langle \int _{{\mathcal{V}}}[\boldsymbol{u}^{\star }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{(0)}\boldsymbol{\cdot }\boldsymbol{u}^{(0)}]\,\text{d}{\mathcal{V}}\right\rangle ={\mathcal{H}}.\end{eqnarray}$$ In order to derive the steady component of the propulsion speed 
$\overline{\boldsymbol{v}}=Re\,\langle \boldsymbol{v}^{(1)}\rangle$, our goal in the following lies in the computation of the right-hand side, 
${\mathcal{H}}$, of the previous equality.
3.4 Viscous drags and steady propulsion speed
Knowing the form of the viscous dynamical response of the sphere 
$(\hat{\boldsymbol{v}}_{0},\hat{\unicode[STIX]{x1D714}}_{0})$ from § 2, we are now able to derive an explicit expression of the propulsion speed 
$\bar{\boldsymbol{v}}$. We first write 
$\boldsymbol{v}^{(0)}=\hat{\boldsymbol{v}}_{0}\text{e}^{\text{i}t}$, 
$\unicode[STIX]{x1D74E}^{(0)}=\hat{\unicode[STIX]{x1D74E}}_{0}\text{e}^{\text{i}t}$, 
$\boldsymbol{u}^{(0)}=\hat{\boldsymbol{u}}_{0}\text{e}^{\text{i}t}$, 
$\boldsymbol{f}^{(0)}=\;\hat{\!\!\boldsymbol{f}}_{\!0}\text{e}^{\text{i}t}$ and 
$\boldsymbol{l}^{(0)}=\hat{\boldsymbol{l}}_{0}\text{e}^{\text{i}t}$.
In this context, the 
$O(1)$ and 
$O(Re)$ components of (3.9) and (3.10) become
$$\begin{eqnarray}\displaystyle \hspace{-24.0pt} & \displaystyle -6\unicode[STIX]{x03C0}(\hat{\boldsymbol{v}}_{0}+\;\hat{\!\!\boldsymbol{f}}_{\!0})\boldsymbol{\cdot }\boldsymbol{v}^{\star }-(8\unicode[STIX]{x03C0}\hat{\unicode[STIX]{x1D74E}}_{0}+\hat{\boldsymbol{l}}_{0})\boldsymbol{\cdot }\unicode[STIX]{x1D74E}^{\star }=\unicode[STIX]{x1D706}^{2}\int _{{\mathcal{V}}}\boldsymbol{u}^{\star }\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}_{0}}{\unicode[STIX]{x2202}t}\,\text{d}{\mathcal{V}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{-24.0pt} & \displaystyle -\boldsymbol{ v}^{\star }\boldsymbol{\cdot }\langle 6\unicode[STIX]{x03C0}\,\boldsymbol{v}^{(1)}+\boldsymbol{f}^{(1)}\rangle -\,\unicode[STIX]{x1D74E}^{\star }\boldsymbol{\cdot }\langle 8\unicode[STIX]{x03C0}\unicode[STIX]{x1D74E}^{(1)}+\boldsymbol{l}^{(1)}\rangle =\frac{1}{2}\text{Re}\left\{\int _{{\mathcal{V}}}[\boldsymbol{u}^{\star }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}_{0}^{\dagger }\boldsymbol{\cdot }\hat{\boldsymbol{u}}_{0}]\,\text{d}{\mathcal{V}}\right\}={\mathcal{H}}, & \displaystyle\end{eqnarray}$$ where 
$\text{Re}(z)$ and 
$z^{\dagger }$ stand for the real part and complex conjugate of 
$z$.
In the case of an harmonic motion, 
$\hat{\boldsymbol{u}}_{0}$ is given by
$$\begin{eqnarray}\hat{\boldsymbol{u}}_{0}=[A(r)\boldsymbol{I}+B(r)\boldsymbol{n}\boldsymbol{n}]\boldsymbol{\cdot }\hat{\boldsymbol{v}}_{0}+C(r)\,\hat{\unicode[STIX]{x1D74E}}_{0}\times \boldsymbol{n},\end{eqnarray}$$ where the exact forms for given 
$\unicode[STIX]{x1D706}$ of 
$A(r)$, 
$B(r)$ and 
$C(r)$ are recalled in appendix A (see also chapter 6 in Kim & Karrila (Reference Kim and Karrila2005)). The velocity field induced by a rectilinear steady motion of a sphere in a viscous fluid has a form similar to (3.13),
$$\begin{eqnarray}\boldsymbol{u}^{\star }=\left[A^{\star }(r)\boldsymbol{I}+B^{\star }(r)\boldsymbol{n}\boldsymbol{n}\right]\boldsymbol{\cdot }\boldsymbol{v}^{\star }+C^{\star }(r)\,\unicode[STIX]{x1D74E}^{\star }\times \boldsymbol{n},\end{eqnarray}$$ where the exact forms of 
$A^{\star }(r)$, 
$B^{\star }(r)$ and 
$C^{\star }(r)$ are also given in appendix A, and are in fact the asymptotic limits of 
$A$, 
$B$ and 
$C$ for 
$\unicode[STIX]{x1D706}\rightarrow 0$ (steady motion), respectively.
3.4.1 Order $O(1)$ – Viscous response
Successively introducing the auxiliary fields 
$(\boldsymbol{v}^{\star },\unicode[STIX]{x1D74E}^{\star })=(\boldsymbol{e}_{y},0)$ and 
$(\boldsymbol{v}^{\star },\unicode[STIX]{x1D74E}^{\star })=(0,\boldsymbol{e}_{z})$ in (3.11) provides
$$\begin{eqnarray}\;\hat{\!\!\boldsymbol{f}}_{\!0}=-[6\unicode[STIX]{x03C0}+\tilde{\unicode[STIX]{x1D706}}^{2}F(\unicode[STIX]{x1D706})]\,\hat{\boldsymbol{v}}_{0},\quad \hat{\boldsymbol{l}}_{0}=-[8\unicode[STIX]{x03C0}+\tilde{\unicode[STIX]{x1D706}}^{2}G(\unicode[STIX]{x1D706})]\,\hat{\unicode[STIX]{x1D74E}}_{0},\end{eqnarray}$$with
$$\begin{eqnarray}F(\unicode[STIX]{x1D706})=4\unicode[STIX]{x03C0}\int _{1}^{\infty }r^{2}\left[\frac{2AA^{\star }+(A+B)(A^{\star }+B^{\star })}{3}\right]\,\text{d}r,\quad G(\unicode[STIX]{x1D706})=\frac{8\unicode[STIX]{x03C0}}{3}\int _{1}^{\infty }r^{2}CC^{\star }\,\text{d}r\end{eqnarray}$$ and 
$\tilde{\unicode[STIX]{x1D706}}^{2}=\text{i}\unicode[STIX]{x1D706}^{2}$. One can note that computing the integrals on the right-hand sides of (3.16) indeed provides the classical expressions derived for the unsteady translational and rotational drag (Stokes Reference Stokes1850; Mazur & Bedeaux Reference Mazur and Bedeaux1974; Kim & Karrila Reference Kim and Karrila2005)
$$\begin{eqnarray}\;\hat{\!\!\boldsymbol{f}}_{\!0}=-6\unicode[STIX]{x03C0}\left(1+\tilde{\unicode[STIX]{x1D706}}+\frac{\tilde{\unicode[STIX]{x1D706}}^{2}}{9}\right)\hat{\boldsymbol{v}}_{0},\quad \hat{\boldsymbol{l}}_{0}=-8\unicode[STIX]{x03C0}\frac{1+\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{2}/3}{1+\tilde{\unicode[STIX]{x1D706}}}\,\hat{\unicode[STIX]{x1D74E}}_{0}.\end{eqnarray}$$3.4.2 Order $O(Re)$ – Propulsion speed
Let us turn to the leading-order mean propulsion speed 
$\overline{\boldsymbol{v}}$. Using (3.13),
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\hat{\boldsymbol{u}}_{0} & = & \displaystyle A^{\prime }\hat{\boldsymbol{v}}_{0}\boldsymbol{n}+B^{\prime }(\boldsymbol{n}\boldsymbol{\cdot }\hat{\boldsymbol{v}}_{0})\boldsymbol{n}\boldsymbol{n}\,+\,\frac{B}{r}\left\{(\boldsymbol{n}\boldsymbol{\cdot }\hat{\boldsymbol{v}}_{0})(\mathbf{I}-\boldsymbol{n}\boldsymbol{n})+\boldsymbol{n}\otimes [(\mathbf{I}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot }\hat{\boldsymbol{v}}_{0}]\right\}\nonumber\\ \displaystyle & & \displaystyle +\,C^{\prime }(\hat{\unicode[STIX]{x1D74E}}_{0}\times \boldsymbol{n})\otimes \boldsymbol{n}-\frac{C}{r}\left[\unicode[STIX]{x1D750}\boldsymbol{\cdot }\hat{\unicode[STIX]{x1D74E}}_{0}+(\hat{\unicode[STIX]{x1D74E}}_{0}\times \boldsymbol{n})\otimes \boldsymbol{n}\right],\end{eqnarray}$$ where 
$C^{\prime }=\text{d}C/\text{d}r$ and 
$(\unicode[STIX]{x1D750})_{ijk}=\unicode[STIX]{x1D716}_{ijk}$, so that 
$(\unicode[STIX]{x1D750}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}_{0})\boldsymbol{\cdot }\boldsymbol{a}=\boldsymbol{a}\times \unicode[STIX]{x1D74E}_{0}$ for any vector 
$\boldsymbol{a}$. Introducing equations (3.13), (3.14) and (3.18) in (3.12) and performing the explicit integration of its right-hand side leads to
$$\begin{eqnarray}{\mathcal{H}}=\frac{2\unicode[STIX]{x03C0}}{3}\text{Re}\bigg\{\!\left[\boldsymbol{v}^{\star }\boldsymbol{\cdot }(\hat{\unicode[STIX]{x1D74E}}_{0}\times \hat{\boldsymbol{v}}_{0}^{\dagger })\right]{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})\bigg\},\end{eqnarray}$$where the quantity
$$\begin{eqnarray}{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})=\int _{1}^{\infty }\bigg[A^{\star }\bigg(A^{\dagger }C^{\prime }+B^{\dagger }C^{\prime }+\frac{2A^{\dagger }C}{r}\bigg)+\frac{B^{\star }(A^{\dagger }-B^{\dagger })C}{r}\bigg]r^{2}\,\text{d}r\end{eqnarray}$$ is given in its fully integrated form in appendix B and its variations are indicated on figure 2. In particular, for small and large 
$\unicode[STIX]{x1D706}$, the asymptotic behaviour of 
${\mathcal{I}}$ is obtained as
$$\begin{eqnarray}{\mathcal{I}}(\unicode[STIX]{x1D706}\rightarrow 0)=-{\textstyle \frac{1}{4}},\quad {\mathcal{I}}(\unicode[STIX]{x1D706}\rightarrow \infty )=-1.\end{eqnarray}$$
Figure 2. Magnitude (a) and phase (b) of 
${\mathcal{I}}$. The bullets correspond to the direct numerical integration of (3.20).
Note that (3.19) confirms that the 
$x$-component of 
$\hat{\boldsymbol{v}}_{0}$ will have no contribution to the steady motion, as anticipated in § 2 and expected for symmetry reasons.
Now, choosing 
$\boldsymbol{v}^{\star }=\boldsymbol{e}_{x}$ and 
$\unicode[STIX]{x1D74E}^{\star }=0$ in (3.12) and (3.19), and remembering that (i) using (2.11), only the 
$y$-component of 
$\hat{\boldsymbol{v}}_{0}$ has a non-zero contribution to the mean propulsion speed, (ii) 
$\hat{\unicode[STIX]{x1D74E}}_{0}$ is along the 
$z$-axis, and (iii) 
$\langle \,\boldsymbol{f}\rangle =0$ due to the periodicity of the particle’s velocity, one obtains
$$\begin{eqnarray}\langle \boldsymbol{v}^{(1)}\rangle =\langle v^{(1)}\rangle \,\boldsymbol{e}_{x}={\textstyle \frac{1}{9}}\text{Re}[\hat{\unicode[STIX]{x1D714}}_{0}\,\hat{v}_{0,y}^{\dagger }\,{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})]\,\boldsymbol{e}_{x},\end{eqnarray}$$or equivalently, as a function of the tilt angle amplitude,
$$\begin{eqnarray}\langle \boldsymbol{v}^{(1)}\rangle =-{\textstyle \frac{1}{9}}\,\unicode[STIX]{x1D700}\,\text{Im}[\hat{\unicode[STIX]{x1D703}}_{0}\,\hat{v}_{0,y}^{\dagger }\,{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})]\,\boldsymbol{e}_{x},\end{eqnarray}$$ where 
$\text{Im}(z)$ refers to the imaginary part of 
$z$.
Note that the ratio 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}$, which is a function of the four dimensionless parameters 
$\unicode[STIX]{x1D6FC}$, 
$\unicode[STIX]{x1D6FD}$, 
$I$ and 
$\unicode[STIX]{x1D706}$, does not depend on 
$\unicode[STIX]{x1D700}$. As a result, the leading-order dimensionless mean velocity of the particle 
$\overline{\boldsymbol{v}}$ is the product of 
$\unicode[STIX]{x1D700}\,Re$ and of a dimensionless function of the four other parameters. The quantity 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}$ is plotted in 3 for 
$\unicode[STIX]{x1D6FD}=0.2$ and different combinations 
$(I,\unicode[STIX]{x1D6FC})$.
3.5 Asymptotic behaviour and reversal of the propulsion speed
As shown in figure 3, for large 
$\unicode[STIX]{x1D6FC}$ or small 
$I$, a reversal of the direction of propulsion (illustrated by the diagrams inserted in each subfigure) can be observed at a finite value 
$\unicode[STIX]{x1D706}^{\star }$ of the reduced frequency 
$\unicode[STIX]{x1D706}$. This reversal in swimming direction is not the result of the difference in behaviour of the streaming flows at low and high frequencies, and is instead entirely due to a change by a factor of 
$\unicode[STIX]{x03C0}$ in the relative phase between translation and rotation in the viscous (i.e. 
$Re=0$) response of the forced sphere.
Figure 3. Ratio 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}$ as a function of 
$\unicode[STIX]{x1D706}$ for 
$\unicode[STIX]{x1D6FD}=0.2$ and several combinations of 
$(I,\unicode[STIX]{x1D6FC})$. (a) 
$\unicode[STIX]{x1D6FC}=0.9$, 
$I=0.3,0.6,0.9$; (b) 
$I=0.3$, 
$\unicode[STIX]{x1D6FC}=0.3,0.6,0.9$. The spheres sketched in panels (a) and (b) illustrate the direction of propulsion when the centre of mass is on the right of the geometric centre (top, 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}>0$; bottom, 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}<0$).
Figure 4. Value 
$\unicode[STIX]{x1D706}^{\star }$ corresponding to a reversal of the propulsion direction plotted in the plane 
$(I,\unicode[STIX]{x1D6FC})$ for three values of 
$\unicode[STIX]{x1D6FD}$. (a) 
$\unicode[STIX]{x1D6FD}=0.05$; (b,d) 
$\unicode[STIX]{x1D6FD}=0.2$ (panel d is the same as panel b but plotted in a linear scale); (c) 
$\unicode[STIX]{x1D6FD}=0.6$. For a fixed value of 
$\unicode[STIX]{x1D6FD}$, the frontier between the reversal and the non-reversal regions is given by the equality case of (3.26) (solid red line). The cases considered in figure 3 are specified on panel (d) using white bullets. The colour bar (right) holds for all the figures. The white zones in panels (a), (b) and (c), where 
$\unicode[STIX]{x1D706}^{\star }$ is not computed, come from the practical limitation in the numerical extraction of 
$\unicode[STIX]{x1D706}^{\star }$ which tends to infinity in the vicinity of the transition (see text for further explanation).
The variations of 
$\unicode[STIX]{x1D706}^{\star }(\unicode[STIX]{x1D6FD},I,\unicode[STIX]{x1D6FC})$ are plotted in figure 4, for three different values of the density ratio 
$\unicode[STIX]{x1D6FD}$. In each case, the 
$(I,\unicode[STIX]{x1D6FC})$-plane is divided into two regions: a first one where a reversal of the direction of propulsion can be observed at finite 
$\unicode[STIX]{x1D706}$, and another one, where the direction of propulsion does not depend on 
$\unicode[STIX]{x1D706}$ (in the latter case, the sphere always propels with the light end ahead). The limit between the two regions (i.e. a criterion for existence of the reversal in swimming direction between small and large 
$\unicode[STIX]{x1D706}$) can be obtained by deriving the asymptotic behaviour of 
$\langle v^{(1)}\rangle$ at small and large 
$\unicode[STIX]{x1D706}$. Substituting the result of (2.16), (2.17) and (3.21) into (3.23), one obtains
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v^{(1)}\rangle \sim \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}^{4}(\unicode[STIX]{x1D6FD}-1)}{972\unicode[STIX]{x1D6FD}^{2}}\quad \text{for }\unicode[STIX]{x1D706}\rightarrow 0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v^{(1)}\rangle \sim \frac{10\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}[2I(\unicode[STIX]{x1D6FD}-1)+5\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FD}]}{3[4I+\unicode[STIX]{x1D6FD}(2I+5\unicode[STIX]{x1D6FC}^{2})]^{2}}\quad \text{for }\unicode[STIX]{x1D706}\rightarrow \infty . & \displaystyle\end{eqnarray}$$ A change in swimming direction between the 
$\unicode[STIX]{x1D706}\ll 1$ and 
$\unicode[STIX]{x1D706}\gg 1$ limits therefore requires 
$\unicode[STIX]{x1D6FD}-1$ and 
$2I(\unicode[STIX]{x1D6FD}-1)+5\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FD}$ to have opposite signs, or equivalently
$$\begin{eqnarray}0\leqslant \frac{2(1-\unicode[STIX]{x1D6FD})}{5\unicode[STIX]{x1D6FD}}\leqslant \frac{\unicode[STIX]{x1D6FC}^{2}}{I}.\end{eqnarray}$$ This is consistent with the results shown in figure 4 where the red line corresponds to the equality case above. The presence of a white zone in figure 4(a–c), where 
$\unicode[STIX]{x1D706}^{\star }$ is not computed, comes from the practical limitation in the numerical extraction of 
$\unicode[STIX]{x1D706}^{\star }$ which tends to infinity in the vicinity of the transition region (red line). This region would be reduced if the upper bound of the research interval in 
$\unicode[STIX]{x1D706}$ was enlarged. This has been verified for the value 
$\unicode[STIX]{x1D6FD}=0.05$, for which the white zone barely exists. Note that the reversal is only possible if 
$\unicode[STIX]{x1D6FD}\leqslant 1$ (i.e. the particle must be heavier, on average, than the fluid) and if a sufficiently large inhomogeneity exists (as measured by 
$\unicode[STIX]{x1D6FC}$).
4 Physical discussion and orders of magnitude
The dimensional form of (3.23) is
$$\begin{eqnarray}\overline{V}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}\,\overline{v}=-\frac{\unicode[STIX]{x1D709}^{3}\unicode[STIX]{x1D71B}^{2}}{9\unicode[STIX]{x1D708}}\,\text{Im}[\hat{\unicode[STIX]{x1D703}}_{0}\,\hat{v}_{0}^{\dagger }\,{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})],\end{eqnarray}$$ where it should be noted that the radius of the particle only appears through 
$\unicode[STIX]{x1D706}$ (and not in the prefactor).
Based on a mean value of the quality factor of the acoustic cavity 
$Q\sim 300$ (see Bruss (Reference Bruss2012)) and a typical displacement of the piezoelectric wall 
$\ell \sim 0.1~\text{nm}$, a maximum value for the displacement amplitude at the pressure node can be estimated as 
$\unicode[STIX]{x1D709}=2Q\ell /\unicode[STIX]{x03C0}\sim 19~\text{nm}$. For a typical particle radius 
$a=0.5~\unicode[STIX]{x03BC}\text{m}$ and forcing frequency of 
$4\,$MHz, corresponding, respectively, to 
$\unicode[STIX]{x1D700}=0.038$ and 
$\unicode[STIX]{x1D706}\simeq 2.5$, a value of 
$|\langle v^{(1)}\rangle |/\unicode[STIX]{x1D700}\sim 0.01$ is a reasonable estimate of the particle’s dimensionless velocity (see figure 3) and one obtains dimensionally
$$\begin{eqnarray}\overline{V}\sim 44~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1},\end{eqnarray}$$ which is consistent with the values reported by Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016). A quality factor of 
$10^{3}$ (upper bound measured in standard acoustic resonators, see again Bruss (Reference Bruss2012)) would have led to a propulsion velocity 
$\overline{V}\simeq 1.6\,$mm
$\,$s
$^{-1}$, which is much larger than the values reported by Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016) or Wang et al. (Reference Wang, Castro, Hoyos and Mallouk2012) (the latter reports a maximum value of 
$200~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$), but is not inconsistent with the velocities measured by Kaynak et al. (Reference Kaynak, Ozcelik, Nourhani, Lammert, Crespi and Huang2017). A quality factor of 
$10^{2}$ (lower bound measured in standard acoustic resonators) would yield 
$\overline{V}\simeq 1.6~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$.
In brief, even if the orders of magnitude of propulsion speed produced by the model are not irrelevant to the measurements, performing a quantitative comparison remains difficult because (i) the spherical geometry of our model noticeably departs from the experimental geometry depicted in Wang et al. (Reference Wang, Castro, Hoyos and Mallouk2012) and Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016) and (ii) the quality factor of the experimental acoustic cavities used by Wang et al. (Reference Wang, Castro, Hoyos and Mallouk2012) and Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016) is not known, whereas it critically impacts the estimate of the velocity.
Figure 5. (a) Ratio 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}$ as a function of 
$\unicode[STIX]{x1D6FD}$ for 
$\unicode[STIX]{x1D706}=2.5$, 
$I=0.9$ and different values of 
$\unicode[STIX]{x1D6FC}$.
The profile of the quantity 
$\langle v^{(1)}\rangle /\unicode[STIX]{x1D700}$ with respect to the density ratio 
$\unicode[STIX]{x1D6FD}$, for 
$\unicode[STIX]{x1D706}=2.5$, 
$I=0.9$ and different values of the parameter 
$\unicode[STIX]{x1D6FC}$ is plotted in figure 5. As mentioned by Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016), homogeneous rhodium rods (
$\unicode[STIX]{x1D6FD}=0.081$) were faster than heavier golden ones (
$\unicode[STIX]{x1D6FD}=0.052$), an observation which is again consistent with the values presented in the figure.
A final practical yet fundamental remark must be made regarding the zero mean value of the tilt angle. Indeed, we assumed here that the tilt angle varied periodically around the value 
$\unicode[STIX]{x1D703}=0$ in the permanent regime (no angular drift). This assumption is not a priori fully justified since the radiation pressure on a sphere has no obvious orientation effect. In contrast, a near-sphere or an ellipsoid will orient itself in such a way that, on average, its major axis would lie in the zero-pressure plane of the wave. Therefore, the present calculation can be seen as the leading-order calculation of the acoustic propulsion of a non-homogeneous near-sphere, since a slight alteration of the shape would not modify the propulsion speed obtained at leading order for a non-homogeneous sphere.
5 Conclusion
We present here a full derivation of the acoustic propulsion speed of a non-homogeneous rigid sphere. Unlike previous studies which generally rely on a numerically integrated result, the final result obtained by means of the inertial version of the Lorentz reciprocal theorem is integrated analytically. The problem is ruled by five independent dimensionless parameters: the inhomogeneity ratio or imbalance distance 
$\unicode[STIX]{x1D6FC}$; the fluid/solid density ratio 
$\unicode[STIX]{x1D6FD}$; the dimensionless moment of inertia 
$I$; the dimensionless forcing amplitude 
$\unicode[STIX]{x1D700}$; and the reduced frequency 
$\unicode[STIX]{x1D706}^{2}$. For a given density ratio 
$\unicode[STIX]{x1D6FD}\leqslant 1$, a limit value 
$\unicode[STIX]{x1D706}^{\star }$ of the parameter 
$\unicode[STIX]{x1D706}$ may exist such that propulsion takes place in different directions at low frequency (
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}^{\star }$) and high frequency (
$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}^{\star }$). A necessary and sufficient condition for the existence of a reversal in the propulsion direction for varying 
$\unicode[STIX]{x1D706}$ was obtained as 
$0\leqslant (2/5)[(1-\unicode[STIX]{x1D6FD})/\unicode[STIX]{x1D6FD}]\leqslant \unicode[STIX]{x1D6FC}^{2}/I$.
The trends of the propulsion speed as a function of 
$\unicode[STIX]{x1D706}$ as well as the possible existence of a change in propulsion direction for 
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}^{\star }$ are fully consistent with the results published by Collis et al. (Reference Collis, Jesse, Chakraborty and Sader2017). As expected, in a case where the reversal value 
$\unicode[STIX]{x1D706}^{\star }$ does exist (see figure 3), propulsion occurs at low frequency (small 
$\unicode[STIX]{x1D706}$) in the direction of the lighter part of the sphere (centre of mass behind the centroid) whereas at higher frequency (large 
$\unicode[STIX]{x1D706}$), the inhomogeneous sphere propels with the centre of mass ahead. The dependence of the propulsion speed amplitude upon the density ratio is non-monotonous and at high mean densities (typically for 
$\unicode[STIX]{x1D6FD}<0.1$), light particles propel faster than heavier ones. Yet, one should be cautious in connecting this result to the observation reported by Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016) on density effects. Indeed, Ahmed et al. (Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016) report that lighter rods propel faster than denser ones, but the rods also display a geometric asymmetry which could play a central role as well. In order to test more thoroughly the model, dedicated experiments performed using low aspect ratio solid particles with controlled density inhomogeneities would be enlightening.
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under Grant Agreement 714027 (S.M.). The authors also acknowledge insightful discussions with K. Lippera, M. Benzaquen and E. Lauga on the problem.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Definition of the coefficients $A$, $A^{\star }$, $B$, $B^{\star }$, $C$ and $C^{\star }$
The full expressions of the coefficients 
$A$, 
$B$ and 
$C$ of the unsteady harmonic Stokes flow in (3.13) are given by
$$\begin{eqnarray}\displaystyle & \displaystyle A(r)=\frac{3}{2\tilde{\unicode[STIX]{x1D706}}^{2}r^{3}}\left[(1+\tilde{\unicode[STIX]{x1D706}}r+\tilde{\unicode[STIX]{x1D706}}^{2}r^{2})\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}-1-\tilde{\unicode[STIX]{x1D706}}-\frac{\tilde{\unicode[STIX]{x1D706}}^{2}}{3}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B(r)=\frac{3}{2\tilde{\unicode[STIX]{x1D706}}^{2}r^{3}}\left[3+3\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{2}-(3+3\tilde{\unicode[STIX]{x1D706}}r+\tilde{\unicode[STIX]{x1D706}}^{2}r^{2})\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C(r)=\frac{\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}(1+\tilde{\unicode[STIX]{x1D706}}r)}{(1+\tilde{\unicode[STIX]{x1D706}})r^{2}}, & \displaystyle\end{eqnarray}$$ where 
$\tilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}$, and the corresponding coefficients 
$A^{\star }$, 
$B^{\star }$ and 
$C^{\star }$ of the auxiliary steady Stokes flow in (3.14) are given by
$$\begin{eqnarray}\displaystyle A^{\star }(r)=\frac{3}{4r}+\frac{1}{4r^{3}},\quad B^{\star }(r)=\frac{3}{4r}-\frac{3}{4r^{3}},\quad C^{\star }(r)=\frac{1}{r^{2}}\cdot & & \displaystyle\end{eqnarray}$$Appendix B. Integration of the streaming term ${\mathcal{H}}$ in the harmonic case
We note here 
$J(r)$ the integrand in the right-hand side of (3.20), namely
$$\begin{eqnarray}J(r)=\left[A^{\star }\left(A^{\dagger }C^{\prime }+B^{\dagger }C^{\prime }+\frac{2A^{\dagger }C}{r}\right)+\frac{B^{\star }(A^{\dagger }-B^{\dagger })C}{r}\right]r^{2}\end{eqnarray}$$which can be rewritten explicitly as
$$\begin{eqnarray}\displaystyle J(r) & = & \displaystyle \frac{1}{4\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}(1+\tilde{\unicode[STIX]{x1D706}})}\Bigg[\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}(\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+3\tilde{\unicode[STIX]{x1D706}}^{\dagger }+3)\left(-\frac{3\tilde{\unicode[STIX]{x1D706}}^{2}}{r^{3}}-\frac{15\tilde{\unicode[STIX]{x1D706}}}{r^{4}}+\frac{3\tilde{\unicode[STIX]{x1D706}}}{r^{6}}+\frac{3}{r^{7}}-\frac{\tilde{\unicode[STIX]{x1D706}}^{2}+15}{r^{5}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,3\text{e}^{(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })(1-r)}\Bigg(\frac{3\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }(\tilde{\unicode[STIX]{x1D706}}+2\tilde{\unicode[STIX]{x1D706}}^{\dagger })}{r^{2}}+\frac{3(\tilde{\unicode[STIX]{x1D706}}^{2}+5\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }+2\tilde{\unicode[STIX]{x1D706}}^{\dagger 2})}{r^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\tilde{\unicode[STIX]{x1D706}}^{2}\tilde{\unicode[STIX]{x1D706}}^{\dagger }-2\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+15\tilde{\unicode[STIX]{x1D706}}+15\tilde{\unicode[STIX]{x1D706}}^{\dagger }}{r^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\tilde{\unicode[STIX]{x1D706}}^{2}-3\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }-2\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+15}{r^{5}}-\frac{3(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })}{r^{6}}-\frac{3}{r^{7}}\Bigg)\Bigg].\end{eqnarray}$$ So that 
${\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}})=\int _{1}^{\infty }J(r)\,\text{d}r$ is obtained analytically as
$$\begin{eqnarray}\displaystyle {\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}}) & = & \displaystyle \frac{1}{4\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}(1+\tilde{\unicode[STIX]{x1D706}})}\Big\{(\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+3\tilde{\unicode[STIX]{x1D706}}^{\dagger }+3)\big[-3\tilde{\unicode[STIX]{x1D706}}^{2}I_{3}-15\tilde{\unicode[STIX]{x1D706}}I_{4}+3\tilde{\unicode[STIX]{x1D706}}I_{6}+3I_{7}-(\tilde{\unicode[STIX]{x1D706}}^{2}+15)I_{5}\big]\nonumber\\ \displaystyle & & \displaystyle +\,3\big[3\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }(\tilde{\unicode[STIX]{x1D706}}+2\tilde{\unicode[STIX]{x1D706}}^{\dagger })\tilde{I} _{2}+3(\tilde{\unicode[STIX]{x1D706}}^{2}+5\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }+2\tilde{\unicode[STIX]{x1D706}}^{\dagger 2})\tilde{I} _{3}\nonumber\\ \displaystyle & & \displaystyle +\,(\tilde{\unicode[STIX]{x1D706}}^{2}\tilde{\unicode[STIX]{x1D706}}^{\dagger }-2\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+15\tilde{\unicode[STIX]{x1D706}}+15\tilde{\unicode[STIX]{x1D706}}^{\dagger })\tilde{I} _{4}\nonumber\\ \displaystyle & & \displaystyle +\,(\tilde{\unicode[STIX]{x1D706}}^{2}-3\tilde{\unicode[STIX]{x1D706}}\tilde{\unicode[STIX]{x1D706}}^{\dagger }-2\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+15)\tilde{I} _{5}-3(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })\tilde{I} _{6}-3\tilde{I} _{7}\big]\!\Big\}\end{eqnarray}$$with
$$\begin{eqnarray}\displaystyle & \displaystyle I_{1}=\int _{1}^{\infty }\frac{\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}}{r}\,\text{d}r=\text{e}^{\tilde{\unicode[STIX]{x1D706}}}E_{1}(\tilde{\unicode[STIX]{x1D706}}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{I} _{1}=\int _{1}^{\infty }\frac{\text{e}^{(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })(1-r)}}{r}\,\text{d}r=\text{e}^{(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })}E_{1}(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{n}=\int _{1}^{\infty }\frac{\text{e}^{\tilde{\unicode[STIX]{x1D706}}(1-r)}}{r^{n}}\,\text{d}r=\frac{1}{n-1}(1-\tilde{\unicode[STIX]{x1D706}}I_{n-1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{I} _{n}=\int _{1}^{\infty }\frac{\text{e}^{(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })(1-r)}}{r^{n}}\,\text{d}r=\frac{1}{n-1}[1-(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })\tilde{I} _{n-1}], & \displaystyle\end{eqnarray}$$ which are well defined since 
$\tilde{\unicode[STIX]{x1D706}}$ has positive real part. In the above equation, 
$E_{1}(z)$ is the exponential integral (Abramowitz & Stegun Reference Abramowitz and Stegun1964). Using these results, one obtains 
${\mathcal{I}}$ analytically for any 
$\unicode[STIX]{x1D706}$
$$\begin{eqnarray}\displaystyle \hspace{-18.0pt}{\mathcal{I}}(\tilde{\unicode[STIX]{x1D706}}) & = & \displaystyle \frac{1}{64\tilde{\unicode[STIX]{x1D706}}^{\dagger }(1+\tilde{\unicode[STIX]{x1D706}})}\big[(\tilde{\unicode[STIX]{x1D706}}^{\dagger }+3)\tilde{\unicode[STIX]{x1D706}}^{5}-\tilde{\unicode[STIX]{x1D706}}^{\dagger }\tilde{\unicode[STIX]{x1D706}}^{4}+(2\tilde{\unicode[STIX]{x1D706}}^{\dagger }-18)\tilde{\unicode[STIX]{x1D706}}^{3}\nonumber\\ \displaystyle \hspace{-18.0pt} & & \displaystyle -\,6\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}\tilde{\unicode[STIX]{x1D706}}^{2}+(-3\tilde{\unicode[STIX]{x1D706}}^{\dagger 3}+6\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}-16\tilde{\unicode[STIX]{x1D706}}^{\dagger })\tilde{\unicode[STIX]{x1D706}}+3\tilde{\unicode[STIX]{x1D706}}^{\dagger 4}-3\tilde{\unicode[STIX]{x1D706}}^{\dagger 3}-48\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}-16\tilde{\unicode[STIX]{x1D706}}^{\dagger }\big]\nonumber\\ \displaystyle \hspace{-18.0pt} & & \displaystyle -\,\frac{\text{e}^{\tilde{\unicode[STIX]{x1D706}}}E_{1}(\tilde{\unicode[STIX]{x1D706}})}{64\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}(1+\tilde{\unicode[STIX]{x1D706}})}\big[(\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}+3\tilde{\unicode[STIX]{x1D706}}^{\dagger }+3)(\tilde{\unicode[STIX]{x1D706}}^{6}-6\tilde{\unicode[STIX]{x1D706}}^{4})\big]\nonumber\\ \displaystyle \hspace{-18.0pt} & & \displaystyle +\,\frac{3\text{e}^{\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger }}E_{1}(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })}{64\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}(1+\tilde{\unicode[STIX]{x1D706}})}(\tilde{\unicode[STIX]{x1D706}}+\tilde{\unicode[STIX]{x1D706}}^{\dagger })(\tilde{\unicode[STIX]{x1D706}}-\tilde{\unicode[STIX]{x1D706}}^{\dagger })[\tilde{\unicode[STIX]{x1D706}}^{4}-2\tilde{\unicode[STIX]{x1D706}}^{2}\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}-6\tilde{\unicode[STIX]{x1D706}}^{2}+\tilde{\unicode[STIX]{x1D706}}^{\dagger 4}-18\tilde{\unicode[STIX]{x1D706}}^{\dagger 2}].\end{eqnarray}$$ Real and imaginary parts and phase of 
${\mathcal{I}}$ are presented in figure 2. The asymptotic forms of 
${\mathcal{I}}$ at small and large 
$\unicode[STIX]{x1D706}$, equation (3.21), are obtained using the following asymptotic limits (Abramowitz & Stegun Reference Abramowitz and Stegun1964)
$$\begin{eqnarray}E_{1}(z\rightarrow 0)\sim -\ln z-\unicode[STIX]{x1D6FE},\quad E_{1}(z\rightarrow \infty )\sim \frac{\text{e}^{-z}}{z}\cdot \end{eqnarray}$$
