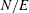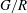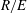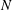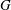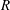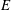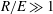1. Introduction
Thermals are observed in a wide range of atmospheric, oceanic, geophysical and industrial flows, including radioactive, volcanic and explosion clouds, and finite discharges from submerged pollutant outlets. Turbulent thermals originate from a discrete localised release of buoyancy, and entrain and mix with the surrounding environmental fluid as they rise. The loss of connection between the rising buoyant fluid and the source is one of the most striking differences between thermals and plumes. The initial momentum and circulation in a thermal are usually negligible compared with the initial buoyancy, which contrasts with the source conditions of a vortex ring, another similar structure (Turner Reference Turner1979).
The first integral models describing the motion of an inert thermal were proposed by Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956) and Turner (Reference Turner1957). Both of these studies assumed the thermal to be Boussinesq, with self-similar top-hat profiles of vertical velocity and buoyancy, and no loss of momentum or buoyancy to a wake. Morton et al. (Reference Morton, Taylor and Turner1956) assumed further that the rate of entrainment at the edge of the thermal is proportional to its volume-averaged velocity and surface area. In contrast, Turner (Reference Turner1957) described the motion of a thermal as a special case of a buoyant vortex ring. The relationship between the momentum and the circulation was that for a Hill spherical vortex, and momentum was generated by buoyancy forces. The two approaches led to similar angles of spread of the thermal. The predictions for the ultimate height reached by the thermal in density-stratified environments, where the thermal and the environment have equal densities, were also similar. The analytical solutions of the extended model of Turner (Reference Turner1960) for a vortex ring were in agreement with those of Morton et al. (Reference Morton, Taylor and Turner1956) for the case where momentum and time-dependent circulation vanished simultaneously. Despite this agreement it is important to note that Morton et al. (Reference Morton, Taylor and Turner1956) considered spherical thermals, whereas Turner (Reference Turner1957, Reference Turner1960) modelled the vortex ring with empirical shape parameters. In fact, as observed experimentally by Scorer (Reference Scorer1957), thermals have an oblate spheroidal shape. Subsequent works, such as those by Escudier & Maxworthy (Reference Escudier and Maxworthy1973) and Bush, Thurber & Blanchette (Reference Bush, Thurber and Blanchette2003), have modified the model of Morton et al. (Reference Morton, Taylor and Turner1956) to account for the non-spherical shape. Moreover, as a thermal rises, it displaces environmental fluid with it, augmenting the inertia of the thermal; this effect has been taken into account theoretically by introducing an added-mass coefficient in the models of Morton et al. (Reference Morton, Taylor and Turner1956) and Turner (Reference Turner1960) (see Saunders Reference Saunders1962; Turner Reference Turner1963b , Reference Turner1964; Wang Reference Wang1971; Escudier & Maxworthy Reference Escudier and Maxworthy1973; Beghin, Hopfinger & Britter Reference Beghin, Hopfinger and Britter1981; Thompson, Snyder & Weil Reference Thompson, Snyder and Weil2000; Bush et al. Reference Bush, Thurber and Blanchette2003).
In general, the behaviour of a thermal is dependent on the density structure in the environment (external effect) or any phenomenon inducing changes in the density inside the thermal (internal effect). The effect of environmental density stratification on the thermal dynamics has been studied extensively since the pioneering works of Morton et al. (Reference Morton, Taylor and Turner1956) and Turner (Reference Turner1957), who considered environments with uniform and linearly stratified density. A step change, a constant gradient and a combination of both were some of the vertical profiles of density explored in the experimental study of the penetration depth of thermals by Richards (Reference Richards1961), Saunders (Reference Saunders1962) and Thompson et al. (Reference Thompson, Snyder and Weil2000). Caulfield & Woods (Reference Caulfield and Woods1998) investigated thermal motion in stratified environments with a power-law buoyancy–frequency dependence with height. Other external effects influencing the flow of a thermal have also been explored theoretically and experimentally, such as the inclination of the source (Beghin et al. Reference Beghin, Hopfinger and Britter1981), turbulence in the surroundings (Turner Reference Turner1963b ) and background rotation (Helfrich Reference Helfrich1994).
Internal processes affecting the density of a thermal include phase change, chemical reaction or dissolution. These processes involve release or absorption of heat and formation of new chemical species. Thermals with internally produced buoyancy changes have been the focus of comparatively fewer studies. Thermals with chemical reaction were first studied experimentally by Turner (Reference Turner1963a ), who released a thermal of hydrochloric acid at the bottom of a tank with sodium bicarbonate. The reaction produced bubbles of carbon dioxide that increased the buoyancy of the thermal. It was observed that the thermals maintained an approximately constant angle of spread during motion, similar to that for the inert case. These reactive thermals were either accelerating or tended towards a constant velocity, depending on whether the acid was in stoichiometric excess or deficiency. Johari (Reference Johari1991) also investigated experimentally the motion of thermals with internal-buoyancy change in a uniform environment, but focused on the internal small-scale mixing and the penetration depth. Buoyancy change was obtained through the nonlinear mixing of an alcohol–glycol mixture released at the source with the water in the surrounding environment. He observed that the small-scale mixing inside thermals was not uniform, although the mixing pattern was very similar in thermals with and without buoyancy change. However, the concentration profiles were not measured.
In both the works of Turner (Reference Turner1963a ) and Johari (Reference Johari1991) quantitative results are scarce and very little information is provided regarding the initial conditions. Additionally, no attempts were made to model theoretically the effect of internal-buoyancy change on the motion of thermals, separating the effects of the reaction rate and the ability of the reaction to change buoyancy. In this work, a theoretical model for turbulent thermals with a second-order homogeneous chemical reaction is developed in § 2. Particular attention is given to the impact of non-uniform mixing inside the thermal. Analytical and numerical solutions are presented in §§ 3 and 4, and compared with results from new laboratory experiments in § 5. An application to the motion of a radioactive cloud in the atmosphere, such as that formed after the Fukushima nuclear explosions in 2011, is discussed in § 6.
2. Governing equations
2.1. Chemical reaction
We consider a discrete release of buoyant fluid
$A_{1}$
in a quiescent environment with chemical species
$A_{2}$
(figure 1). As the thermal rises, it entrains and mixes with the surrounding environmental fluid and undergoes a chemical reaction:
$$\begin{eqnarray}|{\it\nu}_{1}|A_{1}+|{\it\nu}_{2}|A_{2}\rightarrow |{\it\nu}_{3}|A_{3}+|{\it\nu}_{4}|A_{4}.\end{eqnarray}$$
Here,
${\it\nu}_{i}$
is the stoichiometric coefficient of the chemical species
$i$
involved in the reaction (positive for products and negative for reactants). The reaction is assumed to be irreversible and of second-order kinetics. The rate of change of chemical species
$i$
per unit volume of fluid in the thermal is thus
$$\begin{eqnarray}r_{i}={\it\nu}_{i}k_{r}C_{1}C_{2},\end{eqnarray}$$
where
$k_{r}$
is the kinetic constant and
$C_{i}$
is the local concentration of species
$i$
. In SI units,
$r_{i}$
is measured in
$\text{mol}~\text{m}^{-3}~\text{s}^{-1}$
,
$k_{r}$
in
$\text{mol}^{-1}~\text{m}^{3}~\text{s}^{-1}$
and
$C_{i}$
in
$\text{mol}~\text{m}^{-3}$
. The kinetic constant is considered to be independent of temperature, an assumption valid for small temperature changes.
Figure 1. Schematic of a turbulent thermal of chemical species
$A_{1}$
rising in a fluid containing species
$A_{2}$
, at four moments in time
$t_{1}{-}t_{4}$
. The thermal volume
$V$
, momentum
$M$
and buoyancy
$B$
change with time owing to external density stratification and internal chemical reaction. The position of the centre of volume of the thermal is
$z$
; the volume-averaged velocity of the thermal is
$w$
.
Chemical reactions cause variations in the energy and in the chemical composition of the system, leading to changes in the density of a thermal. For dilute systems, the variation of the density of the mixture
${\it\rho}$
with temperature
$T$
and the concentration of solutes may be assumed to be linear:
$$\begin{eqnarray}{\it\rho}={\it\rho}_{sol}\left[1-{\it\beta}_{T}(T-T_{r})+\mathop{\sum }_{i=1}^{5}K_{i}C_{i}\right].\end{eqnarray}$$
Here,
${\it\beta}_{T}$
is the coefficient of thermal expansion, defined as
${\it\beta}_{T}=(\partial {\it\rho}/\partial T)_{p}/{\it\rho}$
, and
$K_{i}$
is the solutal density-change coefficient, defined as
$K_{i}=(\partial {\it\rho}/\partial C_{i})_{p,T}/{\it\rho}$
. The subscripts
$sol$
and
$r$
refer to the solvent and a reference state usually taken to be that of the environment at the source level. The environment has uniform concentration of
$A_{2}$
, but may be stratified in density due to the presence of a chemically inert component,
$A_{5}$
; the concentrations of
$A_{1}$
,
$A_{3}$
and
$A_{4}$
in the environment are negligible.
2.2. Governing equations
The thermal dynamics is modelled following the approach of Morton et al. (Reference Morton, Taylor and Turner1956), which assumes a Boussinesq flow, with self-similar profiles of velocity and buoyancy at all times. The self-similar assumption is extended here to the concentrations of chemical species,
$C_{i}$
. For second-order reaction kinetics, it is important to consider the actual distribution of the concentrations of the reactants
$A_{1}$
and
$A_{2}$
inside the thermal, since this has an impact on the overall chemical conversion and thereby on the buoyancy. We expect this distribution to depend on the relative magnitudes of the time scales for entrainment
${\it\tau}_{en}$
and for reaction
${\it\tau}_{r}$
in the thermal. When entrainment occurs on a smaller time scale than chemical reaction,
${\it\tau}_{en}/{\it\tau}_{r}\ll 1$
, we expect good mixing of
$A_{1}$
and
$A_{2}$
within the volume
$V$
of the thermal. However, for very high
${\it\tau}_{en}/{\it\tau}_{r}$
and moderately high Reynolds numbers
$Re$
, the Kolmogorov time scale for the turbulent small-scale mixing within the thermal,
${\it\tau}_{K}\sim {\it\tau}_{en}Re^{-1/2}$
, is also large compared with that for reaction. Thus, when
${\it\tau}_{en}/{\it\tau}_{r}\gg 1$
,
$A_{1}$
and
$A_{2}$
are non-uniformly distributed. In the far field, away from the source, when the volume of the thermal is much greater than the volume of
$A_{1}$
released at the source, the fluid in the thermal is essentially composed of environmental fluid containing
$A_{2}$
, with a small amount of
$A_{1}$
and reaction products. We may envisage small parcels of
$A_{1}$
, stretched and dispersed by the turbulence, surrounded by
$A_{2}$
; interdiffusion of the two chemicals occurs across the boundaries of these parcels. In this state of partial mixing, regions of fluid containing both reactants
$A_{1}$
and
$A_{2}$
are surrounded by fluid containing only reactant
$A_{2}$
. Thus, we model below a thermal with a chemically active volume,
${\it\lambda}^{3}V$
, where
$A_{1}$
and
$A_{2}$
are assumed to coexist and be well mixed, while in the remaining volume the reaction is negligible. For self-similar behaviour
${\it\lambda}$
is constant during the growth of the thermal. We expect
${\it\lambda}\sim 1$
for a slow reaction, but
${\it\lambda}<1$
for a fast one. One of the objectives of this study is to explore the dependence
${\it\lambda}({\it\tau}_{en}/{\it\tau}_{r})$
for the limits of slow and fast chemical reactions.
We consider an ideal spherical thermal of radius
$b$
with no added mass; we shall see later that this simple model predicts well the behaviour in our experiments. The volume
$V$
, the momentum
$M$
and the buoyancy
$B$
of the thermal are then respectively defined as
$$\begin{eqnarray}\displaystyle & \displaystyle V(t)=\frac{4{\rm\pi}}{3}b^{3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M(t)=\frac{4{\rm\pi}}{3}b^{3}w, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B(t)=\frac{4{\rm\pi}}{3}b^{3}g{\displaystyle \frac{{\it\rho}_{e}-{\it\rho}}{{\it\rho}_{r}}}, & \displaystyle\end{eqnarray}$$
${\it\rho}$
and
$w$
are the volume-averaged density and velocity of the fluid in the thermal respectively. The numbers of moles of chemical species of
$A_{1}$
and
$A_{2}$
in the chemically active part of the thermal,
$n_{1}$
and
$n_{2}$
, are 
$$\begin{eqnarray}\displaystyle & \displaystyle n_{1}(t)=\frac{4{\rm\pi}}{3}({\it\lambda}b)^{3}C_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{2}(t)=\frac{4{\rm\pi}}{3}({\it\lambda}b)^{3}C_{2}. & \displaystyle\end{eqnarray}$$
The evolution of the volume, momentum and buoyancy of the thermal, and the amount of chemical species in the chemically active part of the thermal are then expressed as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}V^{4/3}}{\text{d}t}=4\left(\displaystyle \frac{4}{3}\right)^{1/3}{\rm\pi}^{1/3}{\it\alpha}|M|, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}M}{\text{d}t}=B, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}B}{\text{d}t}=-N^{2}~M-g\displaystyle \frac{{\it\rho}_{sol}}{{\it\rho}_{r}}\left[\mathop{\sum }_{i}\frac{{\it\nu}_{i}}{{\it\nu}_{1}}K_{i}+\frac{{\it\beta}_{T}(-{\rm\Delta}H_{r})}{C_{p}{\it\rho}_{r}}\right]{\it\nu}_{1}k_{r}\frac{n_{1}n_{2}}{{\it\lambda}^{3}V}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}n_{1}}{\text{d}t}={\it\nu}_{1}k_{r}\displaystyle \frac{n_{1}n_{2}}{{\it\lambda}^{3}V}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}n_{2}}{\text{d}t}=3\left(\displaystyle \frac{4{\rm\pi}}{3}\right)^{1/3}{\it\lambda}^{3}{\it\alpha}C_{2_{e}}\displaystyle \frac{|M|}{V^{1/3}}-\displaystyle \frac{{\it\nu}_{2}}{{\it\nu}_{1}}k_{r}\displaystyle \frac{n_{1}n_{2}}{{\it\lambda}^{3}V}. & \displaystyle\end{eqnarray}$$
${\it\alpha}$
is the entrainment coefficient,
${\rm\Delta}H_{r}$
is the enthalpy of reaction (negative for an exothermic reaction),
$C_{p}$
is the specific heat capacity of the plume mixture and 
$$\begin{eqnarray}N=\left(-\frac{g}{{\it\rho}_{r}}\frac{\text{d}{\it\rho}_{e}}{\text{d}z}\right)^{1/2}\end{eqnarray}$$
is the buoyancy frequency of the environment. Equations (2.6c–e
) are valid in the far field away from the source, where the thermal has a chemically active volume
${\it\lambda}^{3}V$
in which
$A_{1}$
and
$A_{2}$
are well mixed; the remaining volume is composed of essentially environmental fluid. Thus, for
${\it\lambda}<1$
the thermal has non-uniform composition; the limit of
${\it\lambda}=1$
represents a thermal that is well mixed throughout its entire volume.
In a stratified environment and/or when the chemical reaction depletes the buoyancy of the thermal, the density of the thermal may become equal to that of the surrounding environment, so that
$B=0$
at some height. Subsequently, the momentum of the thermal decreases and eventually vanishes. The thermal then stops its upward motion, sinks and spreads out radially around the neutral buoyancy height. Between the times of zero buoyancy and zero momentum, the assumptions of self-similarity and constant entrainment coefficient become dubious. Therefore, the governing equations (2.6a–e
) are valid up to the neutral buoyancy level.
2.3. Dimensionless equations
The system of (2.6a–e
) may be non-dimensionalised using the following scales for volume, momentum, number of moles of
$A_{1}$
and
$A_{2}$
, time and length respectively:
$$\begin{eqnarray}\displaystyle & \displaystyle V_{s}=\frac{4}{3}\frac{|{\it\nu}_{2}|}{|{\it\nu}_{1}|}\frac{1}{{\it\lambda}^{3}}\frac{n_{1_{0}}}{C_{2_{e}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{s}=\frac{1}{3^{1/2}{\rm\pi}^{1/6}{\it\alpha}^{1/2}}\left(\frac{|{\it\nu}_{2}|}{|{\it\nu}_{1}|}\right)^{2/3}\frac{1}{{\it\lambda}^{2}}\frac{n_{1_{0}}^{2/3}}{C_{2_{e}}^{2/3}}B_{0}^{1/2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{1_{s}}=n_{1_{0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle n_{2_{s}}=\frac{|{\it\nu}_{2}|}{|{\it\nu}_{1}|}n_{1_{0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\tau}_{en}=\frac{1}{3^{1/2}{\rm\pi}^{1/6}{\it\alpha}^{1/2}}\left(\frac{|{\it\nu}_{2}|}{|{\it\nu}_{1}|}\right)^{2/3}\frac{1}{{\it\lambda}^{2}}\frac{n_{1_{0}}^{2/3}}{C_{2_{e}}^{2/3}B_{0}^{1/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{s}=\frac{1}{4{\rm\pi}^{1/3}}\left(\frac{|{\it\nu}_{2}|}{|{\it\nu}_{1}|}\right)^{1/3}\frac{1}{{\it\alpha}}\frac{n_{1_{0}}^{1/3}}{C_{2_{e}}^{1/3}}. & \displaystyle\end{eqnarray}$$
$s$
refers to the scale for each variable and 0 to the value of the variable at the release time,
$t=0$
. The time scale
${\it\tau}_{en}$
refers to the time needed for the chemically active part of the thermal to entrain an amount
$n_{2_{s}}$
of species
$A_{2}$
from the environment; here,
$n_{2_{s}}$
is the stoichiometric number of moles of chemical species
$A_{2}$
necessary to deplete the amount of
$A_{1}$
released at the source. For a well-mixed thermal, the time for entrainment of this stoichiometric quantity of
$A_{2}$
is minimum, but increases by a factor of
$1/{\it\lambda}^{2}$
if there is segregation of the chemicals. The scales
$V_{s}$
and
$M_{s}$
give an indication of the volume and momentum of the thermal at time
${\it\tau}_{en}$
. Using these scales, (2.6a–e
) reduce to 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{V}^{4/3}}{\text{d}\hat{t}}=|\hat{M}|, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{M}}{\text{d}\hat{t}}=\hat{B}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{B}}{\text{d}\hat{t}}=-\left(\displaystyle \frac{N}{E}\right)^{2}\hat{M}+\displaystyle \frac{G}{R}\displaystyle \frac{R}{E}\displaystyle \frac{\hat{n}_{1}\hat{n}_{2}}{\hat{V}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{n}_{1}}{\text{d}\hat{t}}=-\displaystyle \frac{R}{E}\displaystyle \frac{\hat{n}_{1}\hat{n}_{2}}{\hat{V}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\hat{n}_{2}}{\text{d}\hat{t}}=\displaystyle \frac{|\hat{M}|}{\hat{V}^{1/3}}-\displaystyle \frac{R}{E}\displaystyle \frac{\hat{n}_{1}\hat{n}_{2}}{\hat{V}}. & \displaystyle\end{eqnarray}$$
The groups
$E$
,
$G$
and
$R$
have units of frequency and are defined as
$$\begin{eqnarray}\displaystyle & E=\displaystyle \frac{1}{{\it\tau}_{en}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & G=\displaystyle \frac{3}{4}|{\it\nu}_{1}|k_{r}C_{2_{e}}\frac{{\it\rho}_{sol}}{{\it\rho}_{e}-{\it\rho}_{0}}\left[\mathop{\sum }_{i}\frac{{\it\nu}_{i}}{{\it\nu}_{1}}K_{i}+\frac{{\it\beta}_{T}(-{\rm\Delta}H_{r})}{C_{p}{\it\rho}_{r}}\right]C_{1_{0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & R=\displaystyle \frac{1}{{\it\tau}_{r}}=\frac{3}{4}|{\it\nu}_{1}|k_{r}C_{2_{e}}. & \displaystyle\end{eqnarray}$$
$E$
reflects the rate of entrainment of the environmental species
$A_{2}$
required stoichiometrically for the complete reaction of
$A_{1}$
released at the source;
$G$
measures the ability of the reaction to change the thermal buoyancy, being positive for a chemical reaction generating buoyancy and negative for one depleting buoyancy;
${\it\tau}_{r}$
is the time for the complete consumption of source species
$A_{1}$
when the concentration of chemical species
$A_{2}$
remains constant and equal to
$C_{2_{e}}$
in the chemically active part of the thermal, so that
$R$
reflects the rate of reaction in the thermal.
Considering the source fluid to be free of chemical species
$A_{2}$
, the initial conditions (at
$t=0$
) for (2.9a–e
) are
$$\begin{eqnarray}\hat{V}=V_{0}/V_{s},\quad \hat{M}=M_{0}/M_{s},\quad \hat{B}=1,\quad \hat{n}_{1}=1,\quad \hat{n}_{2}=0.\end{eqnarray}$$
For negligible volume and momentum release at the source, the system behaviour is fully determined by the three dimensionless groups
$N/E$
,
$G/R$
,
$R/E={\it\tau}_{en}/{\it\tau}_{r}$
. The effects of these groups on the distances travelled by the thermal until depletion of chemical species
$A_{1}$
and until depletion of its buoyancy are determined analytically and numerically in §§ 3 and 4 respectively.
3. Analytical solutions
We consider a thermal with negligible volume and momentum, and free of chemical species
$A_{2}$
, at
$\hat{t}=0$
, in the limits of slow and instantaneous chemical reaction.
Table 1. Analytical solutions for some of the properties of a reacting thermal. The rate of depletion of the source chemical species
$A_{1}$
is determined by both chemical reaction and entrainment.
3.1. Slow consumption of entrained species
$A_{2}$
When
$R/E$
is small, the chemical reaction is considerably slower than the entrainment:
$A_{1}$
and
$A_{2}$
are consumed very slowly, and the amount of
$A_{2}$
in the thermal increases due to entrainment such that
$\text{d}\hat{n}_{2}/\text{d}\hat{t}\approx |\hat{M}|/\hat{V}^{1/3}$
. For this limiting case some analytical solutions to (2.9a–e
) may be obtained and are shown in table 1. The amount of
$A_{2}$
in the thermal depends exclusively on its concentration in the environment
$C_{2_{e}}$
and on the entrained volume of external fluid, and is therefore directly proportional to the volume entrained,
$\hat{n}_{2}=4/3\hat{V}$
(as seen from (3.1) and (3.5)). The concentration of
$A_{2}$
in the thermal is equal to that in the environment and the reaction becomes pseudo-first-order with respect to species
$A_{1}$
, with the quantity of
$A_{1}$
decreasing exponentially with time (3.4). Moreover, the consumption of
$A_{1}$
depends only on
$R/E$
, and is not influenced by any change in the buoyancy of the system. In contrast, the volume, momentum and buoyancy of the thermal depend on
$R/E$
,
$N/E$
and
$G/R$
, and include both an exponential term closely related to the rate of reaction and trigonometric terms associated with the stratification of the environment (3.1)–(3.3). We note that these expressions are valid physically up to the level where the thermal spreads out radially, which excludes the oscillating behaviour of the trigonometric functions. For
$R/E=0$
, solutions (3.1)–(3.3) recover the inert-thermal behaviour described by Morton et al. (Reference Morton, Taylor and Turner1956).
3.2. Instantaneous consumption of entrained species
For large values of
$R/E$
, the rate of entrainment is considerably smaller than the rate of reaction. All
$A_{2}$
mixed into the chemically active part of the thermal is immediately depleted by reaction until
$A_{1}$
is completely consumed, i.e. until the reaction is complete. Analytical solutions to (2.9a–e
) while
$A_{1}$
is being consumed can be found by considering
$\text{d}\hat{n}_{2}/\text{d}\hat{t}\approx 0$
, so that
$|\hat{M}|/\hat{V}^{1/3}\approx R/E\hat{n}_{1}\hat{n}_{2}/\hat{V}$
. The quantity of
$A_{1}$
in the thermal at each time depends solely on the quantity of
$A_{2}$
entrained, which is related to the volume of the thermal (3.9). The volume of the thermal, (3.6), is itself affected by the buoyancy changes caused by both the reaction and environmental stratification, measured by
$N/E$
and
$G/R$
.
An implicit analytical solution for the evolution of the volume of the thermal in a uniform environment (3.10) is also obtained. For very short times, the volume of the thermal may be obtained explicitly by the series
$$\begin{eqnarray}\hat{V}^{4/3}=\frac{\hat{t}^{2}}{2}+\frac{2^{13/4}}{105}\frac{G}{R}\hat{t}^{7/2}+O(\hat{t}^{4}).\end{eqnarray}$$
For large times, an explicit solution can also be found:
$$\begin{eqnarray}\hat{V}=\left[\frac{{\it\Gamma}(2/3){\it\Gamma}(7/6)}{{\it\Gamma}(1/6){\it\Gamma}(5/3)}\right]^{6}\left[\frac{8}{21}\frac{G}{R}\right]^{3}\hat{t}^{6},\end{eqnarray}$$
where
${\it\Gamma}$
is the Gamma function. When the chemical reaction depletes the buoyancy, the thermal eventually reaches a level at which it has no momentum. Equation (3.7) provides the volume of the thermal at this level, which upon substitution into (3.10) gives the time of rise to this level,
$$\begin{eqnarray}\hat{t}_{\hat{M}=0}=\sqrt{2{\rm\pi}}\left[-\frac{21}{16}\frac{R}{G}\right]^{2/3}\frac{{\it\Gamma}(5/3)}{{\it\Gamma}(7/6)}.\end{eqnarray}$$
From a practical perspective, it is important to know whether chemical species
$A_{1}$
released at the source is completely consumed by reaction before the buoyancy of the thermal is depleted. If so, the spreading of
$A_{1}$
in the environment is confined to the growth of the thermal and the time after release at which
$A_{1}$
vanishes can be determined. For a given value of
$N/E$
, there is a critical value
$(G/R)_{crit}$
, above which reactant
$A_{1}$
is depleted before the buoyancy of the thermal reduces to zero. For instantaneous consumption of
$A_{2}$
, (3.8) and (3.9) lead to the simple analytical expression
$$\begin{eqnarray}(G/R)_{crit}=-1+\left(\frac{N}{E}\right)^{2}\left(\frac{3}{4}\right)^{4/3}.\end{eqnarray}$$
A comparison of the analytical results above with the full solutions from numerical integration of (2.9a–e ) is presented in the next section.
4. Numerical solutions
The system of ODEs (2.9a–e
) was solved numerically using Wolfram Mathematica® to explore the effects of the parameters
$N/E$
,
$G/R$
and
$R/E$
on the behaviour of a reactive thermal. The thermal is assumed to have negligible volume and momentum, and to be free of chemical species
$A_{2}$
at
$\hat{t}=0$
.
4.1. Regimes of behaviour
Depending on the magnitudes of
$N/E$
,
$G/R$
and
$R/E$
, the thermal can have buoyancy change determined by either the chemical reaction or the external density stratification. Additionally, when the thermal spreads radially into the environment at the zero-buoyancy level, chemical species
$A_{1}$
can either have already been depleted or not. We can therefore define four regimes of thermal motion, as summarised in table 2 and illustrated in figure 2(a).
Table 2. Regimes of behaviour of a reactive thermal.
Figure 2. Dependence of
$(G/R)_{crit}$
on
$N/E$
for different magnitudes of
$R/E$
. The grey lines represent
$|G/R|=(N/E)^{2}$
and enclose the region where stratification has a dominant effect on buoyancy change. (a) Illustration of the four regimes identified in table 2; (b) the thin solid line is the analytical prediction (3.14) for an instantaneous reaction.
Whether the depletion of
$A_{1}$
occurs before or after the neutral buoyancy level is established by the critical value
$(G/R)_{crit}$
, which is in general a function of
$N/E$
and
$R/E$
. Figure 2(b) presents
$(G/R)_{crit}$
as a function of
$N/E$
for different values of
$R/E$
. Results for
$R/E$
equal to 1 (thick solid black line), 10 (dashed line), 100 (large dashed line) and 10 000 (small dashed line) are shown. For a uniform environment,
$N/E=0$
,
$(G/R)_{crit}=-1$
regardless of the magnitude of
$R/E$
. For positive values of
$G/R$
, the reaction contributes to an increase in buoyancy, which thus remains positive. For
$-1<G/R<0$
, the buoyancy decreases more slowly than the amount of
$A_{1}$
in the thermal and thus
$A_{1}$
is consumed before the thermal spreads out radially. In contrast, for
$G/R<-1$
,
$A_{1}$
spreads out radially at the zero-buoyancy level. When the environment is stably stratified, the thermal always reaches a zero-buoyancy level. For each value of
$R/E$
, the parameter space for which
$A_{1}$
spreads out radially (regimes III and IV) increases as
$N/E$
increases (figure 2), since the thermal attains neutral buoyancy faster. The lines of
$(G/R)_{crit}$
shift to larger stratification levels as
$R/E$
increases, thus favouring depletion of
$A_{1}$
, as expected. For very large
$R/E$
, the reaction becomes instantaneous and the depletion of
$A_{1}$
depends exclusively on the rate of entrainment of
$A_{2}$
. Thus,
$(G/R)_{crit}$
loses its dependence on
$R/E$
and approaches the analytical solution (3.14).
The chemical reaction has a dominant impact on the buoyancy change in the thermal when
$|G/R|\;(R/E)\gg (N/E)^{2}$
(see (2.9c
)). As described in § 3, for a very fast reaction,
$R/E\hat{n}_{1}\hat{n}_{2}/\hat{V}\approx |\hat{M}|/\hat{V}^{1/3}$
, and thus chemical reaction becomes the dominant effect on the buoyancy change when
$|G/R|\gg (N/E)^{2}$
. In figure 2, the grey lines represent
$|G/R|=(N/E)^{2}$
and enclose the parameter region for which external stratification has dominant effect on the buoyancy change of a thermal (regimes II and IV), for moderate rate (
$R/E\sim 1$
) to instantaneous chemical reaction. A thermal rising in a stratified environment with a value of
$G/R$
lying outside the two grey lines has significant effects on the buoyancy arising from reaction (regimes I and III). As
$N/E$
decreases, the impact of chemical reaction on the buoyancy change becomes increasingly significant.
4.2. Effects of
$N/E$
,
$G/R$
and
$R/E$
Figures 3 and 4 depict the behaviour of thermals with slow (
$R/E=1/3$
) and instantaneous (
$R/E=10\,000$
) consumption of entrained species respectively. The dimensionless volume
$\hat{V}$
, momentum
$\hat{M}$
, buoyancy
$\hat{B}$
, amount of chemical species
$A_{1}$
,
$\hat{n}_{1}$
, amount of chemical species
$A_{2}$
,
$\hat{n}_{2}$
, velocity
${\hat{w}}$
, radius
$\hat{b}$
and vertical position of the centre of volume
$\hat{z}$
are shown. The regimes of behaviour I–IV are represented as solid, dot-dashed, dashed and dotted lines respectively. As expected, the thermal volume increases with time. The momentum increases in the initial stage of rise of the thermal but subsequently decreases due to a depletion of buoyancy caused by stratification and/or reaction. For a reaction with positive
$G/R$
, the transition from increasing to decreasing buoyancy, upon depletion of the reactant, is abrupt for a strong reaction and low stratification (solid line, figure 4) but becomes smoother as the relative influence of stratification increases. In an environment of uniform density (solid line, figure 3), once species
$A_{1}$
is depleted and reaction ceases, the buoyancy remains constant and the thermal acquires an inert-thermal behaviour with momentum increasing linearly with time, as predicted by the theory of Morton et al. (Reference Morton, Taylor and Turner1956). For
$G/R<0$
, both reaction and stratification contribute to a decrease in the buoyancy throughout the life of the thermal.
Figure 3. Behaviour of a reactive thermal with slow consumption of entrained species (
$R/E=1/3$
). Shown are the non-dimensional (a) volume, (b) momentum, (c) buoyancy, amounts of species (d)
$A_{1}$
and (e)
$A_{2}$
in the active volume of the thermal, (f) velocity, (g) radius and (h) vertical position.
Figure 4. Behaviour of a reactive thermal with instantaneous consumption of entrained species (
$R/E=10\,000$
). Shown are the non-dimensional (a) volume, (b) momentum, (c) buoyancy, amounts of species (d)
$A_{1}$
and (e)
$A_{2}$
in the active volume of the thermal, (f) velocity, (g) radius and (h) vertical position.
For a slow reaction, the regime of behaviour has an impact mainly on the evolution of the buoyancy, volume and momentum. The decrease of source reactant
$A_{1}$
is approximately exponential in time, unaffected by the regime; as mentioned before, this exponential decrease is expected since the reaction is here pseudo-first-order. Analytical solutions (3.1)–(3.5) for the volume, momentum, buoyancy and chemical species are represented in grey in figure 3. The agreement between the analytical and numerical solutions is good, particularly for low
$G/R$
. For instantaneous reaction, the regime of behaviour strongly affects the rate of consumption of chemical species
$A_{1}$
, and the amount of chemical species
$A_{2}$
in the active volume of the thermal, which remains zero while reaction is taking place and shows a steep increase after the reaction terminates. Of note here is the concave-down shape for the decrease of the amount of species
$A_{1}$
with time, arising from the second-order kinetics of the reaction. For this case of instantaneous reaction, we can compare the predictions of analytical solutions with the numerical ones only at specific times, namely the times for depletion of chemical species and buoyancy (see solutions (3.7)–(3.9)). The analytical predictions are all in agreement with the numerical results shown. For example, in both cases I and II (solid and dot-dashed lines), the volume is
$3/4$
when
$A_{1}$
is completely consumed, as expected from (3.9).
4.3. Times for neutral buoyancy and for complete consumption of
$A_{1}$
Figure 5 shows the times for neutral buoyancy (black lines) and complete reaction (grey lines) as a function of the stratification intensity
$N/E$
, for different strengths of buoyancy change induced by reaction
$G/R$
, (a) when reaction is very slow,
$R/E\approx 0$
; (b) when the rates of entrainment and reaction are balanced,
$R/E=1$
; and (c) for instantaneous reaction,
$R/E=10^{4}$
.
Figure 5. Times for neutral buoyancy (black lines) and for complete reaction (grey lines) as a function of the stratification intensity
$N/E$
, for different strengths of buoyancy change by reaction
$G/R$
. (a) Slow reaction,
$R/E\approx 0$
; (b) intermediate reaction strength,
$R/E=1$
; (c) instantaneous reaction,
$R/E=10^{4}$
.
For
$R/E\approx 0$
, the reaction is extremely slow, so the amount of
$A_{1}$
in the thermal is approximately constant. The effect of
$G/R$
is very weak, as expected, and the time for neutral buoyancy is equal to that for an inert thermal rising in a stratified environment, as predicted by Morton et al. (Reference Morton, Taylor and Turner1956). For a thermal with similar rates of entrainment and reaction,
$R/E=1$
, reactant
$A_{1}$
is depleted before the thermal spreads out radially when
$G/R$
is greater than
$(G/R)_{crit}$
(figure 2); this occurs for
$G/R=5$
and
$G/R=20$
in weakly stratified environments. The lines for complete depletion of
$A_{1}$
are nearly horizontal, demonstrating that the effect of
$N/E$
on the time when depletion occurs is negligible, in agreement with the results in figures 3 and 4(d). An increase in
$G/R$
causes the time for complete reaction to decrease, as expected. As the stratification becomes stronger, the impacts of
$G/R$
and
$N/E$
on the time for neutral buoyancy become smaller. In general, an increase in
$G/R$
allows the thermal to move for a longer time. A thermal with instantaneous consumption of
$A_{2}$
,
$R/E=10^{4}$
, exhibits two main differences in behaviour compared with one with intermediate reaction strength:
$A_{1}$
is depleted at an earlier time and the impact of
$G/R$
on the time for neutral buoyancy is slightly magnified. It is also interesting to note that when
$G/R$
is large and positive, the time for neutral buoyancy as a function of
$N/E$
has a discontinuous slope at the time when reaction terminates.
5. Comparison of experimental results with the theory
The motion of thermals has been studied in the laboratory using different release mechanisms. In Morton et al. (Reference Morton, Taylor and Turner1956), Turner (Reference Turner1957, Reference Turner1963a ) and Beghin et al. (Reference Beghin, Hopfinger and Britter1981), thermals were formed by removing a lid cover from a reservoir placed at the bottom of a tank. Turner (Reference Turner1957, Reference Turner1963a ) also released thermals by injecting the fluid directly into the bottom of the tank through a vertical nozzle. The same method was later used by Wu (Reference Wu1977) and Diez et al. (Reference Diez, Sangras, Faeth and Kwon2003). In Sanchez et al. (Reference Sanchez, Raymond, Libersky and Petschek1989), the thermal fluid was separated from the tank fluid by a thin oil film which eventually ruptured. More recently, a stretched latex membrane was used to contain the initial thermal fluid, which was subsequently broken by a needle (Hart & Dalziel Reference Hart, Dalziel and Ivey2006; Thomas, Marino & Dalziel Reference Thomas, Marino and Dalziel2008) or by heating a thin metal wire (Bond & Johari Reference Bond and Johari2005). In other experimental set-ups, heat acted as the initial source of buoyancy (Sparrow, Husar & Goldstein Reference Sparrow, Husar and Goldstein1970; Baines & Hopfinger Reference Baines and Hopfinger1984). Despite this variety of release mechanisms, the most common configuration was introduced by Scorer & Ronne (Reference Scorer and Ronne1956) and Scorer (Reference Scorer1957), where thermals of heavy fluid were released at the top of a tank, by pivoting a thin hemispherical cup about a horizontal axis. This release mechanism produced consistent results in several works, namely Woodward (Reference Woodward1959), Richards (Reference Richards1961), Saunders (Reference Saunders1962), Turner (Reference Turner1963b ), Johari (Reference Johari1991), Helfrich (Reference Helfrich1994) and Thompson et al. (Reference Thompson, Snyder and Weil2000), and was also chosen for the present study.
Experiments were performed in a clear Perspex® tank with dimensions of
$40~\text{cm}\times 40~\text{cm}\times 75~\text{cm}$
(length
$\times$
width
$\times$
depth). The tank was illuminated from the back with an LED (light-emitting diode) lightbox. A thermal was released by rotating a 10 ml hemispherical cup suspended at the top of the tank. The descending motion of the thermal was captured by a digital camera (1.3 Mpixel Nikon D300S DSLR) mounted on a tripod and at a distance of 1.3 m from the front of the tank. The shutter speed of the camera was set to
$1/100~\text{s}$
and an ISO of 200 was used to take pictures with an
$f2.8$
lens. Pictures were taken every second, for 35 s, starting at the time of release. The tank fluid had a uniform density, measured with a Anton Paar DMA density meter (with accuracy
$\pm 10^{-3}~\text{g}~\text{cm}^{-3}$
). The limiting cases of slow and instantaneous consumption of environmental reactive species
$A_{2}$
were studied. The reactive systems chosen were the reduction of methylene blue by ascorbic acid, for slow reaction, and the acid–base reaction between ammonium hydroxide and acetic acid, for very fast chemistry. Table 3 summarises the range of thermal and reaction parameters for which experiments were performed.
Table 3. Details of the initial experimental conditions.
Methylene blue has a blue–greenish colour whereas ascorbic acid is colourless. The two chemicals react with 1:1 stoichiometry to form two colourless products, leucomethylene blue and dehydroascorbic acid (Mowry & Ogren Reference Mowry and Ogren1999). Methylene blue in an aqueous solution was released as a thermal at the top of a tank containing an acidic solution of ascorbic acid. The amount of methylene blue in the thermal, at a given time, was determined from the measured intensity of blue–greenish colour in the picture, using the Beer–Lambert law (Cenedese & Dalziel Reference Cenedese and Dalziel1998). Methylene blue has a deep colour, so the initial concentration had to be smaller than
$10^{-3}$
M for changes in concentration to be noticeable over the time scale of thermal motion. Due to this low-concentration requirement, the initial buoyancy of the thermal was induced by the presence of sucrose dissolved in the methylene blue solution. The chemical reaction between methylene blue and ascorbic acid is irreversible and obeys a second-order rate law with respect to methylene blue and ascorbic acid. For experiments at
$20\,^{\circ }\text{C}$
, where only ascorbic acid is contributing to the acidity of the medium,
$k_{r}=1.0\pm 0.2~\text{M}^{-1}~\text{s}^{-1}$
(Mowry & Ogren Reference Mowry and Ogren1999). Batch experiments with methylene blue concentrations smaller than
$10^{-3}~\text{M}$
, and controlled temperature and density (sensitivities of
$0.1\,^{\circ }\text{C}$
and
$\pm 10^{-3}~\text{g}~\text{cm}^{-3}$
), indicated that the change in buoyancy due to reaction was negligible, i.e.
$G\approx 0$
.
For the reaction between acetic acid and ammonium hydroxide, safety considerations required the ammonium hydroxide to be the chemical released as a thermal and acetic acid was used as the environmental solution. A few drops of phenolphthalein indicator solution were added to the initial ammonium hydroxide solution, which turned pink. Ammonium hydroxide solutions are lighter than acetic acid, so the initial buoyancy driving the motion of the thermal was induced by the presence of sodium chloride. As the thermal descended, the pH of the thermal decreased due to entrainment and reaction with the acidic environmental solution. Consequently, the intensity of colour in the thermal reduced, and this reduction was related to the depletion of ammonium hydroxide using the Beer–Lambert law. The acid–base chemical reaction between acetic acid and ammonium hydroxide is second order and very fast, with a kinetic constant of
$k_{r}=10^{11}~\text{M}^{-1}~\text{s}^{-1}$
at
$20\,^{\circ }\text{C}$
(Someya et al.
Reference Someya, Yoshida, Tabata and Okamoto2009). Although sodium chloride is an ionic component, the ionic strength of the solution in the thermal is not expected to have a relevant effect on the kinetic constant for the concentration ranges used in this study (Steinfeld, Francisco & Hase Reference Steinfeld, Francisco and Hase1999). This reaction is practically irreversible with an equilibrium constant of neutralisation equal to
$3.2\times 10^{4}$
(Housecroft & Constable Reference Housecroft and Constable2002). The non-dimensional group
$G/R$
was estimated for each experiment based on the literature (Weast & Astle Reference Weast and Astle1979; Someya et al.
Reference Someya, Yoshida, Tabata and Okamoto2009) and is shown in table 3. The magnitude of
$G/R$
is considerably lower than that of
$R/E$
, and the effect of
$G/R$
over the time scale of thermal motion was found to be of the same order of magnitude as the turbulent fluctuations.
The conditions for
$G/R$
and
$R/E$
summarised in table 3 show that the reactive systems chosen allow us to study the effect of reaction on the chemical evolution of the thermal, but not on buoyancy. Although the laboratory programme has been constrained by safety considerations, it contributes new measurements to a field of previous data focusing on buoyancy changes in inert thermals rising in uniform and stratified environments. The experimental and theoretical results for the (a) position of the centre of volume
$\hat{z}$
, (b) radius
$\hat{b}$
and (c) amount of source reactant
$\hat{n}_{1}$
are presented in figures 6 and 7 for a moderately slow chemical reaction and an instantaneous chemical reaction respectively. For this comparison the measured entrainment coefficient of
${\it\alpha}=0.25$
was used, which is compatible with previous work (Morton et al.
Reference Morton, Taylor and Turner1956). The results shown neglect the initial injection time, when the thermal is still adjusting to a self-similar state, and fluid is lost to the wake. The experimental results for the reactive system are represented as filled circles, the inert control is shown as filled triangles and the theoretical predictions as solid lines. Different grey shades indicate different experimental conditions. The error bars shown in the figures represent the standard deviation over an ensemble of 10 repeated experiments, which includes the variation caused by the turbulence.
Figure 6. Comparison between the theoretical predictions and the experimental results for the (a) position of the centre of volume, (b) radius and (c) amount of source chemical in a thermal with moderately slow reaction (methylene blue–ascorbic acid system).
Figure 7. Comparison between the theoretical predictions and the experimental results for the (a) position of the centre of volume, (b) radius and (c) amount of source chemical in a thermal with instantaneous chemical reaction (ammonium hydroxide–acetic acid system).
We noted earlier in the theory that the parameter
${\it\lambda}$
depends on the relative magnitude of the time scales for entrainment and reaction,
$R/E={\it\tau}_{e}/{\it\tau}_{r}$
. For our laboratory thermals with moderately slow chemical reaction between methylene blue and ascorbic acid,
$R/E\sim 10^{-4}$
and
${\it\tau}_{K}/{\it\tau}_{r}\sim 10^{-6}$
; for the fast reaction between ammonium hydroxide and acetic acid,
$R/E\sim 10^{10}$
and
${\it\tau}_{K}/{\it\tau}_{r}\sim 10^{8}$
. We therefore expect good mixing over the whole thermal before reaction and
${\it\lambda}\sim 1$
for the slow reacting system. In contrast, the fast reaction should occur preferentially in the regions of the thermal with good mixing, while regions with chemical segregation remain chemically inactive, and we expect
${\it\lambda}$
to be decreased. For the moderately slow chemical reaction, the results in figure 6 show that the theoretical model predicts reasonably well the front position and the radius of the thermal, as well as the exponential depletion of reactive chemical in the thermal, assuming
${\it\lambda}=1$
. The thermals are thus very close to ideal. A larger value of
$R/E$
, associated with a faster reaction, causes a faster depletion of reactant.
For the instantaneous chemical reaction in the ammonium hydroxide–acetic acid system (figure 7), the thermal position, radius and depletion of source chemical are very successfully predicted by assuming
${\it\lambda}=0.7$
. The expected concave-down shape of the evolution of
$n_{2}$
for a second-order reaction is clear in the experimental measurements. These results suggest that the chemical reaction was not occurring uniformly in the whole volume of the thermal, although this is not visible in the photographs (figure 8
a) because of depth averaging and the on/off character of the phenolphthalein indicator (pink in the basic form and colourless in the acidic form). To demonstrate the non-uniformity of chemical activity, a new set of experiments was performed using bromocresol green as an alternative pH indicator. Bromocresol green is blue in the basic form and yellow in the acidic form. Initially, the thermal was predominantly blue with some green regions at the edges (figure 8
b). This indicates that the edge of the thermal is the first region where mixing occurs, in agreement with the observations of Scorer (Reference Scorer1957) and in contrast to those of Johari (Reference Johari1991). Later, as a result of entrainment of fluid from the rear to the centre of the thermal, a larger fraction of acidic yellow parcels appear in the centre, although green is still observed at the edges and throughout the thermal. The thermal only turned completely yellow when all of its volume had mixed and reacted. In turbulent plumes with instantaneous chemical reaction (Ülpre, Eames & Greig Reference Ülpre, Eames and Greig2013), the presence of reacted and unreacted parcels within the plume has also been observed in the laboratory but was not commented upon by the authors. The unmixed blue parcels of the thermal here, where reaction is yet to occur, appear distributed throughout the whole thermal and strongly affect chemical conversion. The parameter
${\it\lambda}$
reflects the effectiveness of mixing in the thermal. The fact that a constant value of
${\it\lambda}=0.7$
predicts well the experimental results at different times and for different experimental conditions confirms the self-similar character of the mixing in thermals.
Figure 8. Reactive thermal of ammonium hydroxide (released at the source) descending in an aqueous solution of acetic acid. The colour indicator was phenolphthalein in (a) and bromocresol blue in (b). In (b) the brightness and contrast levels of the picture were adjusted using Wolfram Mathematica®. The scale bar is 5 cm.
6. Application to radioactive clouds
Radioactive clouds arise following the detonation of nuclear weapons, and explosions in nuclear reactors and spent fuel pools. These clouds are usually composed of hydrogen, steam, air and a collection of radioactive nuclides. Radioactive nuclides decay with time releasing
${\it\beta}$
,
${\it\alpha}$
or
${\it\gamma}$
radiation particles until they form a stable nuclide. The radioactive disintegration of each nuclide
$i$
follows first-order kinetics, such that
$\text{d}n_{i}/\text{d}t=-R_{i}n_{i}$
, where
$n_{i}$
is the number of nuclides
$i$
present in the cloud and
$R_{i}$
is the radioactive decay constant of the nuclide (Stephenson Reference Stephenson1954). In addition, given that
${\it\beta}$
and
${\it\alpha}$
radiation particles can only penetrate 1 cm and 2 m in the air (Bennet & Thomson Reference Bennet and Thomson1989) respectively, they are converted into heat; the radioactive decay therefore contributes to internal generation of buoyancy within the cloud. The rate of buoyancy change in the cloud associated with nuclide
$i$
can be expressed as
$$\begin{eqnarray}G_{i}=g\frac{{\it\rho}_{solv}}{{\it\rho}_{r}}\left(\frac{{\it\beta}_{T}E_{{\it\beta}_{i}/{\it\alpha}_{i}}}{C_{p}{\it\rho}_{r}}\right)\frac{n_{i_{0}}}{B_{0}}R_{i},\end{eqnarray}$$
where
$E_{{\it\beta}_{i}/{\it\alpha}i}$
(J per particle) is the decay energy emitted by
${\it\beta}$
and
${\it\alpha}$
particles.
The model presented in § 2 can be easily extended to consider the multicomponent nature of a radioactive cloud: the balances of chemical species (2.6d,e
) are replaced by a balance statement for each nuclide, as above; the balance of buoyancy (2.6c
) now takes account of the radioactive decay of each radionuclide such that
$\text{d}B/\text{d}t=-N^{2}M+\sum _{i=1}^{n}G_{i}B_{0}/n_{i_{0}}n_{i}$
. This approach neglects a decay chain of radionuclides. The relative effect of environmental stratification and decay heat on the dynamics of a radioactive cloud is investigated below using this extended model. We note that although previous models have attempted to describe the motion of a radioactive cloud, they either considered an ad hoc linear variation of heat generation with time (Bennet & Thomson Reference Bennet and Thomson1989) or included a global heat release rate, without considering the contribution of each radionuclide (Gifford Reference Gifford1967; Badre & Grand Reference Badre and Grand1983; Smyth Reference Smyth1985).
Figure 9. Effects of the quantity of radionuclides and the time lapse between reactor shutdown and explosion on the motion of a radioactive cloud. The black line separates the parameter spaces where atmospheric stratification is dominant and where radioactive decay has an effect on cloud buoyancy. The stars represent predictions for clouds formed following the explosion of a reactor with 784 MW power.
When an accident occurs in a nuclear plant the first safety measure is shutdown of the reactors. However, radioactive elements inside each reactor continue to decay with time, releasing heat. A failure in the cooling system allows the pressure inside the reactor vessel to increase and may lead to an exposure of the fuel rods. The fuel rods contain a zircaloy material, which above a temperature of
$1200\,^{\circ }\text{C}$
reacts rapidly with steam, producing zirconium oxide and hydrogen. This hydrogen undergoes a strongly exothermic chemical reaction if in contact with the oxygen in air. This reaction leads to explosion of the reactor and the consequent release of a radioactive cloud. Such an accident occurred in the Fukushima Daiichi nuclear plant in Japan, following an earthquake in 2011 (IRSN 2012). The initial conditions for the present case study were taken as those from the Fukushima Unit 3 explosion. The initial buoyancy released in the cloud is estimated to be
$B_{0}=1.01\times 10^{6}~\text{m}^{4}~\text{s}^{-2}$
, considering the hydrogen combustion as the only source of buoyancy (Shepherd Reference Shepherd2011). The relatively low percentage of hydrogen of 10–15 % (Shepherd Reference Shepherd2011) and a release velocity of approximately
$300~\text{m}~\text{s}^{-1}$
(Breitung et al.
Reference Breitung, Chan, Dorofeev, Eder, Gelfand, Heitsch, Klein, Malliakos, Shepherd, Studer and Thibault2000; Tsuruda Reference Tsuruda2013) suggest the absence of a shock wave. The initial volume and the momentum of the cloud are estimated to be
$V_{0}=3.26\times 10^{5}~\text{m}^{3}$
and
$M_{0}=9.78\times 10^{7}~\text{m}^{4}~\text{s}^{-1}$
(Shepherd Reference Shepherd2011) respectively. These quantities have a negligible effect on the cloud compared with that of buoyancy after
$V_{0}^{2/3}/B_{0}^{1/2}\approx 5~\text{s}$
and
$M_{0}/B_{0}\approx 100~\text{s}$
of motion respectively, in agreement with observations of Tsuruda (Reference Tsuruda2013). Thus, we model the radioactive cloud as a thermal, with zero initial momentum and volume, rising in a US Standard Atmosphere (COESA 1976) at rest.
The impact of radioactive decay on the motion of the cloud depends on the magnitudes of
$G_{i}$
and
$R_{i}$
, and therefore on the identity and the amount of each radionuclide released. The collection of radionuclides released with the explosion cloud varies with the time lapse between the reactor shutdown and the explosion, as well as with the amount of fuel injected into the reactor and the strength of the explosion. The relative compositions of radionuclides released 10, 100, 1000 and 10 000 s after a reactor shutdown were published by Gupta et al. (Reference Gupta, Kellett, Nichols and Bersillon2010), while the composition of the Fukushima cloud two days after shutdown was reported by IRSN (2012).
The predicted influence of atmospheric stratification and radioactive decay on the buoyancy of the thermal, using our model, is shown in figure 9 for various time periods between reactor shutdown and explosion, and for different magnitudes of the release. The solid line is
$(N/R_{ref})^{2}=10\sum G_{i}/R_{ref}$
, and thus separates the regions of parameter space where environmental stratification has a dominant effect and where decay heat has an influence on the motion of the cloud; here, the subscript
$ref$
refers to the radionuclide with fastest decay for each time lapse. The stars show predictions for a cloud resulting from the explosion of a reactor with 784 MW power. For a large release of radionuclides in the cloud and a short time interval between reactor shutdown and explosion, the radioactive decay heat has a significant effect on the cloud motion. In contrast, if the cooling system is able to delay the explosion for sufficient time, the environmental stratification controls the change in buoyancy of the cloud. The figure indicates that in the Fukushima case, for which explosion occurred 2 days (
${\approx}250\times 10^{3}~\text{s}$
) after the shutdown of the reactor, the ambient stratification determined the motion of the nuclear cloud.
7. Conclusions
A theoretical and experimental study of single-phase thermals undergoing a second-order chemical reaction with the entrained environmental fluid was carried out. Scaling of the governing volume, momentum, buoyancy and chemical balances showed that the thermal behaviour is fully determined by three dimensionless groups: the ratio of the effects of environmental stratification and entrainment of reactive chemical species on the buoyancy of the thermal,
$N/E$
; the ratio of the ability of chemical reaction to change buoyancy and the rate of consumption of chemical species,
$G/R$
; and the relative rates of consumption of chemical species and entrainment from the environment,
$R/E$
. Analytical solutions for the limiting cases of instantaneous and very slow reactions were obtained. For intermediate cases, numerical solutions were presented. A regime diagram in
$N/E{-}G/R{-}R/E$
space was developed, defining the parametric conditions for which the chemical released at the source is depleted before or after the thermal spreads out radially, and whether environmental stratification or chemical reaction controls the buoyancy change in the thermal.
Good agreement was found between the experiments and theory for the evolution of source chemical in the thermal, for different reaction strengths
$R/E$
. Importantly, it was shown that the state of mixing in the thermal depends on the magnitude of
$R/E$
. Experimental measurements suggest that for a moderately slow chemical reaction, where the time scale for entrainment is much smaller than that for reaction, the thermal is approximately homogeneous in composition. For an instantaneous acid–base chemical reaction, where the time scale for reaction is much smaller than the entrainment time, reaction proceeds preferentially near the centre of the thermal. The regions with slower mixing reduce the rate of consumption of chemical species.
Our results were applied to the case of a radioactive cloud, such as that from the Fukushima nuclear explosions in 2011. It was shown that the heat released from radioactive decay can have a significant impact on the cloud motion when a large quantity of radionuclides is released and/or when the explosion occurs a short time after the reactor shutdown.
Acknowledgements
M.G.D. gratefully acknowledges funding from the Portuguese Foundation for Science and Technology (FCT), Portugal (grant SFRH/BD/60730/2009). We thank L. Howell and L. Tonna, final year Research Project students, for carrying out some of the experiments for the slow reaction.
