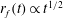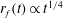1. Introduction
Interactions between fluids and elastic materials arise in a wealth of situations from everyday life, such as the clumping of fibres in a paintbrush (Boys Reference Boys1959; Bico et al. Reference Bico, Roman, Moulin and Boudaoud2004), to environmental challenges, such as the spreading of oil within the fibres of bird feathers (Duprat et al. Reference Duprat, Protiere, Beebe and Stone2012), and in the geosciences, where fluid–elastic interactions are responsible for the intrusion of magma under the Earth’s crust (Bunger & Cruden Reference Bunger and Cruden2011; Michaut Reference Michaut2011; Lister, Peng & Neufeld Reference Lister, Peng and Neufeld2013; Hewitt, Balmforth & De Bruyn Reference Hewitt, Balmforth and De Bruyn2015). The effect of fluids on compliant materials also impacts new technologies, for example, in the fabrication and failure of MEMS devices (Mastrangelo & Hsu Reference Mastrangelo and Hsu1993a ,Reference Mastrangelo and Hsu b ; Tanaka, Morigami & Atoda Reference Tanaka, Morigami and Atoda1993; Unger et al. Reference Unger, Chou, Thorsen, Scherer and Quake2000; Rogers, Someya & Huang Reference Rogers, Someya and Huang2010) and in printing processes (see, e.g, Yin & Kumar Reference Yin and Kumar2005, Reference Yin and Kumar2006). An important biological example of fluid flow on an elastic substrate is in neonatal respiratory distress syndrome, where the flow of the liquid lining the walls of the lungs can induce airway closure (see, e.g., Macklem, Proctor & Hogg Reference Macklem, Proctor and Hogg1970; Grotberg Reference Grotberg2011).
In all of these examples, the interplay between the fluid motion and the elastic material determines the system behaviour. As a result of their ubiquitous nature, these interactions have long received attention (see, e.g., Gohar Reference Gohar2001). In many cases, reduced-order models that provide insight into the dynamics are highly desirable so as to provide a better understanding of how the behaviour depends on the system parameters. Here, we are interested in simplifications that allow analytical descriptions for the case of deformation of an elastic medium as fluid is poured onto its surface. Such a situation could, for example, describe the pooling and spreading of water on a flexible roof.
It is well known that, by using the lubrication approximation for thin-film flows, it is possible to derive similarity solutions that give insight into the system behaviour for the spreading of fluid as it is poured onto a rigid surface (see, e.g., Smith Reference Smith1969; Didden & Maxworthy Reference Didden and Maxworthy1982; Huppert Reference Huppert1982; Zheng, Rongy & Stone Reference Zheng, Rongy and Stone2015). Consideration of the flow on an elastic substrate exposes a rich variety of behaviours depending on the system parameters, such as the flexibility of the material used or the rate at which fluid is injected onto the surface. For example, for the flow of fluid on an elastic beam that is clamped at one end, distinct families of asymptotic solutions can be classified mathematically depending on the operating regime (Howell, Robinson & Stone Reference Howell, Robinson and Stone2013). For a tilted elastic substrate, the coupling of gravity and elasticity gives rise to instabilities if the elastic medium is suitably flexible, offering potential strategies for promoting interfacial instabilities and mixing (see, e.g., Matar & Kumar Reference Matar and Kumar2004, Reference Matar and Kumar2007; Matar, Craster & Kumar Reference Matar, Craster and Kumar2007). In the case of fluid flow in the lung airways, Halpern & Grotberg (Reference Halpern and Grotberg1992, Reference Halpern and Grotberg1993) use fluid mechanics models to explain the mechanisms that give rise to the observed airway collapse in newborns, and show the effect of pulmonary surfactant in delaying or halting airway closure.
Despite the everyday occurrence of free-surface flows of fluids on elastic materials, the number of studies is relatively limited. Many authors instead focus on the behaviour of a constrained fluid beneath an elastic medium. These set-ups arise in, for example, the gravitational flow of magma intrusions beneath the Earth’s crust (see, e.g., Michaut Reference Michaut2011; Lister et al. Reference Lister, Peng and Neufeld2013; Hewitt et al. Reference Hewitt, Balmforth and De Bruyn2015) and in liquid blister tests where fluid is injected beneath an elastic medium, which provides information on the adhesive strength of the elastic medium (see, e.g., Chopin, Vella & Boudaoud Reference Chopin, Vella and Boudaoud2008; Lister et al. Reference Lister, Peng and Neufeld2013). The compliance of the constraining surface can also be shown to modify the flow properties, such as the well-known viscous fingers observed in Hele-Shaw cells (see, e.g., Pihler-Puzović et al. Reference Pihler-Puzović, Illien, Heil and Juel2012, Reference Pihler-Puzović, Périllat, Russell, Juel and Heil2013).
In this paper, we use lubrication theory and elasticity theory (see, e.g., Balmforth, Cawthorn & Craster Reference Balmforth, Cawthorn and Craster2010; Howell et al. Reference Howell, Robinson and Stone2013; Lister et al. Reference Lister, Peng and Neufeld2013) to form a simplified model to describe the dynamic response of a circular elastic extensible membrane pinned at its edge as fluid is injected onto its surface, as shown in figure 1. We exploit geometrical and material properties such as the thinness of the membrane and its weak bending stiffness and use asymptotic analysis to consider the behaviour in the early and late time periods to further simplify the problem. In particular, we seek similarity solutions in these regimes to describe the time-dependent spreading of the fluid, to complement those for flow on a rigid substrate (see, e.g., Huppert Reference Huppert1982) and for the fluid flow constrained by an elastic medium (see, e.g., Lister et al. Reference Lister, Peng and Neufeld2013; Hewitt et al. Reference Hewitt, Balmforth and De Bruyn2015). The resulting model is used to identify the key parameters that control the spreading behaviour. In § 2, we present a mathematical model that couples the equations for the flow of fluid on the surface with those for the deflection of an elastic membrane. In § 3, we investigate analytically the behaviour in the early and late stages of injection. In § 4, we perform a series of laboratory experiments with a range of viscous fluids and elastic membranes to test and validate our theory. In § 5, we summarize the major findings and discuss several model assumptions.
Figure 1. A viscous thin film spreads on an elastic membrane; the red thick arrows indicate the direction of spreading. Both the membrane and the liquid are exposed to the air with a reference pressure
$p_{a}$
at height
$h_{a}$
. The film thickness is denoted by
$h(r,t)$
and the membrane deformation is characterized by
$w(r,t)$
. The extent of the liquid film is described by
$r_{f}(t)$
, and the outer radius of the membrane is
$\ell$
, which is fixed with
$w(\ell )=0$
. The pressure, density and viscosity of the liquid are denoted by
$p(r,z,t)$
,
${\it\rho}$
and
${\it\mu}$
respectively, and the vertically averaged horizontal velocity is denoted by
$u(r,t)$
;
$\boldsymbol{g}$
is the gravitational constant.
2. Theoretical model
2.1. Governing equations
We study the spreading of a viscous liquid of density
${\it\rho}$
and viscosity
${\it\mu}$
over an elastic membrane of radius
$\ell$
, thickness
$d$
and Young’s modulus
$E$
, as shown in figure 1. We consider a cylindrical coordinate system
$(r,z)$
to describe the dynamics. The membrane is deflected downward by the gravitational force exerted by the liquid; the shape of the elastic membrane is denoted by
$-w(r,t)$
and the thickness of the liquid film is
$h(r,t)$
. We assume that the liquid film is long and thin so that we may apply the lubrication approximation: the flow is mainly horizontal and the vertical velocity is negligible. Neglecting the effect of surface tension, the pressure
$p(r,z,t)$
in the liquid has a hydrostatic distribution. We assume that the air has a reference pressure
$p_{a}$
at height
$h_{a}$
, and we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle p(r,z,t)=p_{a}+{\it\rho}_{a}g(h_{a}+w(r,t)-h(r,t))+{\it\rho}g(-z-w(r,t)+h(r,t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial p}{\partial r}={\rm\Delta}{\it\rho}g\frac{\partial (h-w)}{\partial r}, & \displaystyle\end{eqnarray}$$
${\rm\Delta}{\it\rho}\equiv {\it\rho}-{\it\rho}_{a}>0$
is the density difference between the liquid and the air. Following standard steps in the lubrication description of the flow, the vertically averaged horizontal velocity
$u(r,t)$
is 
$$\begin{eqnarray}u(r,t)=-\frac{h^{2}}{3{\it\mu}}\frac{\partial p}{\partial r}.\end{eqnarray}$$
The continuity equation gives an evolution for the film shape
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial (rhu)}{\partial r}=0.\end{eqnarray}$$
Substituting (2.1) and (2.2) into (2.3), we obtain
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{{\rm\Delta}{\it\rho}g}{3{\it\mu}}\frac{1}{r}\frac{\partial }{\partial r}\left[rh^{3}\frac{\partial (w-h)}{\partial r}\right]=0.\end{eqnarray}$$
For constant liquid injection of volumetric flow rate
$q$
, the global mass conservation equation gives
$$\begin{eqnarray}2{\rm\pi}\int _{0}^{r_{f}(t)}rh(r,t)\,\text{d}r=qt,\end{eqnarray}$$
where
$r_{f}(t)$
denotes the location of the propagating front of liquid (see figure 1) and
$h(r_{f}(t),t)=0$
. In fact,
$h(r,t)=0$
for
$r_{f}(t)\leqslant r\leqslant \ell$
, where
$\ell$
denotes the radius of the membrane.
In addition, we can apply a force balance on an elastic membrane of Young’s modulus
$E$
and thickness
$d$
. We neglect the weight of the membrane and the effects of surface tension and moving contact lines. When the elastic sheet is very thin, the effect of bending is negligible compared with the stretching effect (see, e.g., Landau & Lifshitz Reference Landau and Lifshitz1959; Vella, Adda-Bedia & Cerda Reference Vella, Adda-Bedia and Cerda2010; Lister et al.
Reference Lister, Peng and Neufeld2013). Thus, for
$0\leqslant r\leqslant r_{f}(t)$
, the balance of the liquid weight and membrane stretching provides
$$\begin{eqnarray}-\frac{1}{r}\frac{\partial }{\partial r}\left(r{\it\sigma}\frac{\partial w}{\partial r}\right)={\rm\Delta}{\it\rho}gh,\end{eqnarray}$$
where
${\it\sigma}(r,t)$
is the radial tension produced by stretching of the membrane (see, e.g., Jensen Reference Jensen1991; Lister et al.
Reference Lister, Peng and Neufeld2013), which satisfies
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r^{3}\frac{\partial {\it\sigma}}{\partial r}\right)=-\frac{Ed}{2}\left(\frac{\partial w}{\partial r}\right)^{2}.\end{eqnarray}$$
For
$r_{f}(t)\leqslant r\leqslant \ell$
, there exists no liquid over the membrane. The force balance on the membrane provides
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}\left(r{\it\sigma}\frac{\partial w}{\partial r}\right)=0,\end{eqnarray}$$
where
${\it\sigma}(r,t)$
and
$w(r,t)$
are also related through (2.7).
Thus, within the extent of the liquid film, i.e.
$0\leqslant r\leqslant r_{f}(t)$
, (2.4), (2.6) and (2.7) provide a coupled system for the film thickness
$h(r,t)$
, the membrane shape
$w(r,t)$
and the radial tension
${\it\sigma}(r,t)$
. Outside the extent of the liquid film, i.e.
$r_{f}(t)\leqslant r\leqslant \ell$
, (2.7) and (2.8) form a coupled system for
$w(r,t)$
and
${\it\sigma}(r,t)$
, while
$h(r,t)=0$
always holds in this region. For both regions, it is necessary to provide the appropriate initial and boundary conditions to complete the problem statement.
2.2. Initial and boundary conditions
We assume that liquid injection begins at
$t=0$
, and there is no initial stress in the membrane. Thus, for all
$r$
, the initial conditions for
$h(r,t)$
,
$w(r,t)$
and
${\it\sigma}(r,t)$
are
$$\begin{eqnarray}h(r,0)=0,\quad w(r,0)=0\quad \text{and}\quad {\it\sigma}(r,0)=0.\end{eqnarray}$$
We note that these initial conditions satisfy the quasi-steady governing equations for the membrane, i.e. (2.6)–(2.8).
Within the extent of the liquid film,
$0\leqslant r\leqslant r_{f}(t)$
, at
$r=0$
two symmetry boundary conditions apply for
$w(r,t)$
and
${\it\sigma}(r,t)$
:
$$\begin{eqnarray}\frac{\partial w}{\partial r}(0,t)=0\quad \text{and}\quad \frac{\partial {\it\sigma}}{\partial r}(0,t)=0,\end{eqnarray}$$
and also there are two boundary conditions for the thickness of the liquid
$h(r,t)$
:
$$\begin{eqnarray}h(r_{f}(t),t)=0\quad \text{and}\quad rh^{3}\left.\frac{\partial h}{\partial r}\right|_{r\rightarrow 0^{+}}=-\frac{3{\it\mu}q}{2{\rm\pi}{\rm\Delta}{\it\rho}g}.\end{eqnarray}$$
We note that the boundary condition (2.11b
) comes from an integration of (2.4) from
$r=0$
to
$r=r_{f}(t)$
, while using the global mass conservation equation (2.5) and boundary condition (2.10a
). The condition (2.11b
) can be used instead of (2.5). We also assumed that
$(w-h)$
is not too singular at the front, i.e.
$rh^{3}(\partial (w-h)/\partial r)|_{r=r_{f}(t)}=0$
.
Outside the extent of the liquid film,
$r_{f}(t)\leqslant r\leqslant \ell$
, the boundary conditions for
$w(r,t)$
and
${\it\sigma}(r,t)$
are
$$\begin{eqnarray}w(\ell ,t)=0\quad \text{and}\quad \frac{1}{Ed}\left.\left[(1-{\it\nu})r{\it\sigma}+r^{2}\frac{\partial {\it\sigma}}{\partial r}\right]\right|_{r=\ell }=0,\end{eqnarray}$$
where
${\it\nu}$
is the Poisson ratio, and we assume
${\it\nu}=1/2$
in this work. Equation (2.12b
) indicates that the horizontal displacement is zero at the outer boundary of the membrane (see, e.g., Jensen Reference Jensen1991).
The equations are second order in space, so conditions on the function and first derivative are placed at the location of the liquid front
$r_{f}(t)$
. Therefore, four more boundary conditions for
$w(r,t)$
and
${\it\sigma}(r,t)$
can be obtained by matching the solutions for
$w(r,t)$
and
$\partial w/\partial r$
from
$0\leqslant r\leqslant r_{f}(t)$
and
$r_{f}(t)\leqslant r\leqslant \ell$
:
$$\begin{eqnarray}w|_{r\rightarrow r_{f}^{-}}=w|_{r\rightarrow r_{f}^{+}}\quad \text{and}\quad \left.\frac{\partial w}{\partial r}\right|_{r\rightarrow r_{f}^{-}}=\left.\frac{\partial w}{\partial r}\right|_{r\rightarrow r_{f}^{+}},\end{eqnarray}$$
and by matching the solutions for
${\it\sigma}(r,t)$
and
$\partial {\it\sigma}/\partial r$
from both sides:
$$\begin{eqnarray}{\it\sigma}|_{r\rightarrow r_{f}^{-}}={\it\sigma}|_{r\rightarrow r_{f}^{+}}\quad \text{and}\quad \left.\frac{\partial {\it\sigma}}{\partial r}\right|_{r\rightarrow r_{f}^{-}}=\left.\frac{\partial {\it\sigma}}{\partial r}\right|_{r\rightarrow r_{f}^{+}}.\end{eqnarray}$$
2.3. Non-dimensionalization
By scaling it is possible to eliminate all of the physical variables from the differential equations. We define dimensionless variables
$T=t/t_{c}$
,
$R=r/r_{c}$
,
$H=h/h_{c}$
,
$W=w/h_{c}$
and
${\it\Sigma}={\it\sigma}/{\it\sigma}_{c}$
based on characteristic scales:
$$\begin{eqnarray}t_{c}=\left(\frac{3{\rm\pi}{\it\mu}Ed}{q{\rm\Delta}{\it\rho}^{2}g^{2}}\right)^{1/2},\quad r_{c}=\left(\frac{3{\it\mu}qE^{2}d^{2}}{8{\rm\pi}{\rm\Delta}{\it\rho}^{3}g^{3}}\right)^{1/8},\end{eqnarray}$$
$$\begin{eqnarray}h_{c}=\left(\frac{3{\it\mu}q}{2{\rm\pi}{\rm\Delta}{\it\rho}g}\right)^{1/4},\quad {\it\sigma}_{c}=\left(\frac{3{\it\mu}qE^{2}d^{2}{\rm\Delta}{\it\rho}g}{8{\rm\pi}}\right)^{1/4}.\end{eqnarray}$$
The characteristic scales in (2.15) are chosen such that the coefficients for each term of the rescaled equations (2.16) are unity. Then, within the extent of the liquid film, i.e.
$0\leqslant R\leqslant R_{f}(T)$
with
$R_{f}(T)\equiv r_{f}(t)/r_{c}$
, (2.4), (2.6) and (2.7) can be rewritten in dimensionless form:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial H}{\partial T}+\frac{1}{R}\frac{\partial }{\partial R}\left[RH^{3}\frac{\partial (W-H)}{\partial R}\right]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{R}\frac{\partial }{\partial R}\left(R{\it\Sigma}\frac{\partial W}{\partial R}\right)=-H, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{R}\frac{\partial }{\partial R}\left(R^{3}\frac{\partial {\it\Sigma}}{\partial R}\right)=-\left(\frac{\partial W}{\partial R}\right)^{2}. & \displaystyle\end{eqnarray}$$
$R_{f}(T)\leqslant R\leqslant L$
with
$L\equiv \ell /r_{c}$
, the dimensionless form of (2.8) is 
$$\begin{eqnarray}\frac{1}{R}\frac{\partial }{\partial R}\left(R{\it\Sigma}\frac{\partial W}{\partial R}\right)=0.\end{eqnarray}$$
We note that
$L$
enters the problem statement as an independent parameter, and represents the dimensionless size of the elastic membrane.
In addition, the initial and boundary conditions can be rewritten in dimensionless forms based on (2.15). Specifically, the initial conditions (2.9) become
$$\begin{eqnarray}H(R,0)=0,\quad W(R,0)=0\quad \text{and}\quad {\it\Sigma}(R,0)=0,\end{eqnarray}$$
the boundary conditions (2.10) at the centre of the membrane
$R=0$
become
$$\begin{eqnarray}\frac{\partial W}{\partial R}(0,T)=0\quad \text{and}\quad \frac{\partial {\it\Sigma}}{\partial R}(0,T)=0,\end{eqnarray}$$
and the boundary conditions for
$H(R,T)$
from (2.11) are
$$\begin{eqnarray}H(R_{f},T)=0\quad \text{and}\quad RH^{3}\left.\frac{\partial H}{\partial R}\right|_{R\rightarrow 0^{+}}=-1.\end{eqnarray}$$
The corresponding boundary conditions (2.12) at the edge of the membrane
$R=L$
are
$$\begin{eqnarray}W(L,T)=0\quad \text{and}\quad \left.\left[(1-{\it\nu}){\it\Sigma}+R\frac{\partial {\it\Sigma}}{\partial R}\right]\right|_{R=L}=0.\end{eqnarray}$$
Further, the matching conditions (2.13a,b ) can be rewritten as
$$\begin{eqnarray}W|_{R\rightarrow R_{f}^{-}}=W|_{R\rightarrow R_{f}^{+}}\quad \text{and}\quad \left.\frac{\partial W}{\partial R}\right|_{R\rightarrow R_{f}^{-}}=\left.\frac{\partial W}{\partial R}\right|_{R\rightarrow R_{f}^{+}},\end{eqnarray}$$
and the matching conditions (2.14a,b ) can be rewritten as
$$\begin{eqnarray}{\it\Sigma}|_{R\rightarrow R_{f}^{-}}={\it\Sigma}|_{R\rightarrow R_{f}^{+}}\quad \text{and}\quad \left.\frac{\partial {\it\Sigma}}{\partial R}\right|_{R\rightarrow R_{f}^{-}}=\left.\frac{\partial {\it\Sigma}}{\partial R}\right|_{R\rightarrow R_{f}^{+}}.\end{eqnarray}$$
To summarize, within the extent of the liquid film, i.e.
$0\leqslant R\leqslant R_{f}(T)$
, the governing equations are (2.16a
–
c
), while outside the extent of the liquid film, i.e.
$R_{f}(T)\leqslant R\leqslant L$
, the thickness of the liquid film is zero, and the membrane deformation
$W(R,T)$
and radial tension
${\it\Sigma}(R,T)$
are governed by a coupled system (2.16c
) and (2.17). The initial conditions are (2.18a–c
). The boundary conditions for
$H(R,T)$
are (2.20); the boundary conditions for
$W(R,T)$
and
${\it\Sigma}(R,T)$
are (2.19) at
$R=0$
, (2.21) at
$R=L$
, and the matching conditions (2.22) and (2.23) at
$R=R_{f}(T)$
.
It should be noted that, based on the scaling (2.15), (2.16a
) suggests that when
$T=O(1)$
both the unsteady and the diffusive terms are important for the dynamics of the thin liquid film. In addition, (2.16b
) indicates that when
$T=O(1)$
both the buoyancy and the stretching terms are important for the force balance on the membrane. However, the balance for the liquid film and the membrane can change in the early-time period,
$T\ll 1$
, and in the late-time period,
$T\gg 1$
, as will be discussed in § 3.
3. Early-time and late-time behaviours
In this section, we discuss the early-time (
$T\ll 1$
) and late-time (
$T\gg 1$
) approximate solutions for the shape of the air–liquid interface
$H(R,T)$
, the deformation of the membrane
$W(R,T)$
and the radial tension within the membrane
${\it\Sigma}(R,T)$
. In particular, we obtain a gravity current regime in the early-time period, when the spreading is driven by buoyancy and membrane stretching is the response to the buoyancy-controlled distribution of liquid weight; in the late-time period, we obtain a membrane stretching regime, when the flow is quasi-steady and the air–liquid interface is flat.
3.1. Early time: gravity current regime
In the early-time period, i.e.
$T\ll 1$
, the deformation of the membrane
$W(R,T)$
is much smaller than the thickness of the liquid film
$H(R,T)$
. Let us define dimensionless variables
$\hat{T}$
,
$\hat{R}$
,
${\hat{H}}$
,
${\hat{W}}$
and
$\hat{{\it\Sigma}}$
, using
${\it\epsilon}t_{c}$
,
${\it\epsilon}^{1/2}r_{c}$
,
$h_{c}$
,
${\it\epsilon}^{2/3}h_{c}$
and
${\it\epsilon}^{1/3}{\it\sigma}_{c}$
, with
${\it\epsilon}\ll 1$
. Then, within the extent of the liquid film, i.e.
$0\leqslant \hat{R}\leqslant \hat{R}_{f}$
with
$\hat{R}_{f}\equiv R_{f}/{\it\epsilon}^{1/2}$
, the governing equations (2.16) become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\hat{H}}}{\partial \hat{T}}-\frac{1}{\hat{R}}\frac{\partial }{\partial \hat{R}}\left(\hat{R}{\hat{H}}^{3}\frac{\partial {\hat{H}}}{\partial \hat{R}}\right)=O({\it\epsilon}^{2/3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\hat{R}}\frac{\partial }{\partial \hat{R}}\left(\hat{R}\hat{{\it\Sigma}}\frac{\partial {\hat{W}}}{\partial \hat{R}}\right)=-{\hat{H}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\hat{R}}\frac{\partial }{\partial \hat{R}}\left(\hat{R}^{3}\frac{\partial \hat{{\it\Sigma}}}{\partial \hat{R}}\right)=-\left(\frac{\partial {\hat{W}}}{\partial \hat{R}}\right)^{2}. & \displaystyle\end{eqnarray}$$
$\hat{R}_{f}\leqslant \hat{R}\leqslant \hat{L}$
with
$\hat{L}\equiv L/{\it\epsilon}^{1/2}$
, the governing equation (2.17) becomes 
$$\begin{eqnarray}\frac{1}{\hat{R}}\frac{\partial }{\partial \hat{R}}\left(\hat{R}\hat{{\it\Sigma}}\frac{\partial {\hat{W}}}{\partial \hat{R}}\right)=0,\end{eqnarray}$$
and we note that (3.1c ) also holds in this region.
Thus, in the limit of
$0<{\it\epsilon}\ll 1$
, the leading-order terms of (3.1a
) reduce to the well-known nonlinear diffusion equation of
${\hat{H}}(\hat{R},\hat{T})$
for the spreading of a viscous gravity current on a rigid horizontal plane (see, e.g., Smith Reference Smith1969; Barenblatt Reference Barenblatt1979; Huppert Reference Huppert1982):
$$\begin{eqnarray}\frac{\partial {\hat{H}}}{\partial \hat{T}}-\frac{1}{\hat{R}}\frac{\partial }{\partial \hat{R}}\left(\hat{R}{\hat{H}}^{3}\frac{\partial {\hat{H}}}{\partial \hat{R}}\right)=0.\end{eqnarray}$$
Together with the global mass conservation equation rescaled from (2.5),
$$\begin{eqnarray}\int _{0}^{\hat{R}_{f}(\hat{T})}\hat{R}{\hat{H}}(\hat{R},\hat{T})\,\text{d}\hat{R}=\hat{T},\end{eqnarray}$$
a self-similar solution of the first kind can be obtained for the time evolution of the interface shape
${\hat{H}}(\hat{R},\hat{T})$
with
$\hat{R}\sim \hat{T}^{1/2}$
and
${\hat{H}}\sim 1$
for constant liquid injection.
Specifically, a similarity variable can be defined as
${\it\xi}\equiv \hat{R}/\hat{T}^{1/2}$
, and the location of the liquid front is
$\hat{R}_{f}(\hat{T})={\it\xi}_{f}\hat{T}^{1/2}$
, where
${\it\xi}_{f}$
is a constant to be determined. Following standard steps, we define
$s\equiv {\it\xi}/{\it\xi}_{f}$
, and the liquid thickness can be expressed as
${\hat{H}}(\hat{R},\hat{T})={\it\xi}_{f}^{2/3}f(s)$
. Equation (3.3) is transformed to the ordinary differential equation (ODE)
$$\begin{eqnarray}(sf^{3}f^{\prime })^{\prime }+{\textstyle \frac{1}{2}}s^{2}f^{\prime }=0,\end{eqnarray}$$
where primes denote differentiation with regard to
$s$
. We note that
$f(1)=0$
, and the asymptotic behaviour of (3.5) near
$s\rightarrow 1^{-}$
can be identified as
$$\begin{eqnarray}f(s)\sim (3/2)^{1/3}(1-s)^{1/3}\quad \text{as}~s\rightarrow 1^{-},\end{eqnarray}$$
which provides the values of
$f(1-{\it\lambda})$
and
$f^{\prime }(1-{\it\lambda})$
, with
${\it\lambda}\ll 1$
, as two boundary conditions for (3.5). A shooting procedure is then used to obtain the numerical solution for
$f(s)$
, which is shown in figure 2(a). In addition, the global mass conservation equation (3.4) is transformed to
$$\begin{eqnarray}{\it\xi}_{f}=\left(\int _{0}^{1}sf(s)\,\text{d}s\right)^{-3/8},\end{eqnarray}$$
and we can determine the constant
${\it\xi}_{f}\approx 1.43$
. Further details of this self-similar solution can be found in Huppert (Reference Huppert1982).
Figure 2. Numerical solutions for the similarity functions for the film height,
$f$
, membrane shape,
$m$
, and radial tension,
$n$
, in the early-time gravity current regime. In (a),
$f(s)$
describes the shape of the air–liquid interface. Our numerical solution agrees well with the calculation of Huppert (Reference Huppert1982). In (b),
$m(s)-m(1)$
represents the shape of the stretched membrane. In (c),
$n(s)$
represents the distribution of radial tension in the membrane. As
$s_{\infty }$
increases, the numerical solutions of
$m(s)-m(1)$
and
$n(s)$
converge to the self-similar solutions, which correspond to
$s_{\infty }\rightarrow +\infty$
.
We can also seek the corresponding self-similar solutions for
${\hat{W}}(\hat{R},\hat{T})$
and
$\hat{{\it\Sigma}}(\hat{R},\hat{T})$
. In particular, we expect that
${\hat{W}}(\hat{R},\hat{T})={\it\xi}_{f}^{14/9}\hat{T}^{2/3}m(s)$
and
$\hat{{\it\Sigma}}(\hat{R},\hat{T})={\it\xi}_{f}^{10/9}\hat{T}^{1/3}n(s)$
. Then, within the extent of the liquid film, i.e.
$0\leqslant s\leqslant 1$
, (3.1b
,
c
) are transformed to
$$\begin{eqnarray}\displaystyle & \displaystyle (snm^{\prime })^{\prime }+sf=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (s^{3}n^{\prime })^{\prime }+s(m^{\prime })^{2}=0, & \displaystyle\end{eqnarray}$$
$f(s)$
is already known from solving (3.5). Outside the extent of the liquid film, the domain is
$1\leqslant s\leqslant s_{\infty }$
, where
$s_{\infty }\equiv L/({\it\xi}_{f}T^{1/2})=L/R_{f}(T)$
. In the early-time period,
$s_{\infty }\rightarrow +\infty$
as
$T\rightarrow 0^{+}$
, and (3.2) and (3.1c
) are now transformed to 
$$\begin{eqnarray}\displaystyle & \displaystyle (snm^{\prime })^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (s^{3}n^{\prime })^{\prime }+s(m^{\prime })^{2}=0. & \displaystyle\end{eqnarray}$$
$m(s)$
and
$n(s)$
from (2.19) and (2.21): 
$$\begin{eqnarray}m^{\prime }(0)=0,\quad m(s_{\infty })=0,\quad n^{\prime }(0)=0\quad \text{and}\quad [(1-{\it\nu})n(s)+sn^{\prime }(s)]|_{s=s_{\infty }}=0.\end{eqnarray}$$
We note that
$s_{\infty }$
, by definition, is time-dependent. However, in the early-time period,
$L/R_{f}\gg 1$
, so we take
$s_{\infty }\rightarrow +\infty$
. The solution of
$m^{\prime }(s)$
(or, alternatively,
$m(s)-m(1)$
for the deformation of the membrane) and
$n(s)$
for
$0\leqslant s\leqslant 1$
have negligible dependence on the value of the large number
$s_{\infty }$
. Numerical solutions of (3.8) and (3.9) for different choices of
$s_{\infty }$
are obtained for
$m(s)$
and
$n(s)$
, and we find that the influence of
$s_{\infty }$
is very small even when
$s_{\infty }=O(1)$
, as shown in figure 2(b,c).
To obtain some representative values, we set
$s_{\infty }=10$
. We note that we can use as large a value as we choose for
$s_{\infty }$
, but this must remain finite numerically. Nevertheless, we observe convergence of the solution as
$s_{\infty }$
becomes larger:
$$\begin{eqnarray}m(0)\approx 4.12\quad \text{and}\quad n(0)\approx 0.61.\end{eqnarray}$$
We can also calculate the shape of the air–liquid interface and the membrane, as shown in rescaled variables in figure 3. As an example, we have chosen the membrane size to be
$L=1$
, and we calculate the air–liquid interface and membrane deformation at two different early times,
$T=1/20$
(
$s_{\infty }\approx 3.1$
) and
$T=1/10$
(
$s_{\infty }\approx 2.2$
). It should be noted that there is a singularity as
$R\rightarrow 0$
for the air–liquid interface, where the self-similar solution fails to capture the interface shape, as discussed in Huppert (Reference Huppert1982).
Figure 3. Numerical solutions of the air–liquid interface and membrane shape in the early-time gravity current regime. We show the solutions for
$L=1$
at
$T=1/20$
(dashed-curves) and
$T=1/10$
(solid-curves) as an example. It should be noted that there is a singularity as
$R\rightarrow 0$
for the air–liquid interface, where the self-similar solution fails to capture the interface shape (Huppert Reference Huppert1982).
3.2. Late time: membrane stretching regime
In the late-time period, i.e.
$T\gg 1$
, we expect stretching of the membrane to become important. We now define dimensionless variables
$\tilde{T}$
,
$\tilde{R}$
,
$\tilde{H}$
,
$\tilde{W}$
and
$\tilde{{\it\Sigma}}$
using
${\it\epsilon}^{-1}t_{c}$
,
${\it\epsilon}^{-1/4}r_{c}$
,
${\it\epsilon}^{-1/2}h_{c}$
,
${\it\epsilon}^{-1/2}h_{c}$
and
${\it\epsilon}^{-1/2}{\it\sigma}_{c}$
, with
${\it\epsilon}\ll 1$
. Then, within the extent of the liquid film, i.e.
$0\leqslant \tilde{R}\leqslant \tilde{R}_{f}$
with
$\tilde{R}_{f}\equiv {\it\epsilon}^{1/4}R_{f}$
, the governing equations of the problem (2.16a
–
c
) become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left[\tilde{R}\tilde{H}^{3}\frac{\partial (\tilde{W}-\tilde{H})}{\partial \tilde{R}}\right]=O({\it\epsilon}^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left(\tilde{R}\tilde{{\it\Sigma}}\frac{\partial \tilde{W}}{\partial \tilde{R}}\right)=-\tilde{H}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left(\tilde{R}^{3}\frac{\partial \tilde{{\it\Sigma}}}{\partial \tilde{R}}\right)=-\left(\frac{\partial \tilde{W}}{\partial \tilde{R}}\right)^{2}. & \displaystyle\end{eqnarray}$$
$\tilde{R}_{f}\leqslant \tilde{R}\leqslant \tilde{L}$
with
$\tilde{L}\equiv {\it\epsilon}^{1/4}L$
, the governing equation (2.17) becomes 
$$\begin{eqnarray}\frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left(\tilde{R}\tilde{{\it\Sigma}}\frac{\partial \tilde{W}}{\partial \tilde{R}}\right)=0,\end{eqnarray}$$
and we note again that (3.12c ) also holds in this region. We also note that the rescaled global mass equation becomes
$$\begin{eqnarray}\int _{0}^{\tilde{R}_{f}(\tilde{T})}\tilde{R}\tilde{H}(\tilde{R},\tilde{T})\,\text{d}\tilde{R}=\tilde{T}.\end{eqnarray}$$
In this reduced set-up, time now appears only in the condition expressing the volume of fluid deposited on the membrane (3.14). As such, we may alternatively view the set-up as a steady-state configuration of a constant volume of fluid residing on a membrane, where the time variable is equated to the volume of fluid.
Equation (3.12a
) indicates that
$\tilde{W}-\tilde{H}$
is independent of
$\tilde{R}$
, so is only a function of time
$\tilde{T}$
. Physically, this indicates that the air–liquid interface is horizontal, and the location and extent of this flat interface increase with time. In particular, within the extent of the liquid film, from boundary conditions (2.20a
) and (2.22a
), we obtain
$$\begin{eqnarray}\tilde{W}(\tilde{R},\tilde{T})-\tilde{H}(\tilde{R},\tilde{T})=\tilde{W}(\tilde{R}_{f}(\tilde{T}),\tilde{T})\equiv \tilde{W}_{f}(\tilde{T}).\end{eqnarray}$$
Substituting (3.15) into (3.12b
,
c
), we obtain a coupled system of equations for the membrane deformation
$\tilde{W}(\tilde{R},\tilde{T})$
and radial tension
$\tilde{{\it\Sigma}}(\tilde{R},\tilde{T})$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left(\tilde{R}\tilde{{\it\Sigma}}\frac{\partial \tilde{W}}{\partial \tilde{R}}\right)=\tilde{W}_{f}-\tilde{W}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}\left(\tilde{R}^{3}\frac{\partial \tilde{{\it\Sigma}}}{\partial \tilde{R}}\right)=-\left(\frac{\partial \tilde{W}}{\partial \tilde{R}}\right)^{2}. & \displaystyle\end{eqnarray}$$
$\tilde{R}\sim \tilde{T}^{1/4}$
,
$\tilde{W}\sim \tilde{T}^{1/2}$
and
$\tilde{{\it\Sigma}}\sim \tilde{T}^{1/2}$
, before the edge effect of the membrane becomes important, i.e. as long as
$\tilde{L}\equiv {\it\epsilon}^{1/4}L\gg 1$
. We note again that
$L$
is an independent parameter that represents the dimensionless size of the membrane, and our scaling argument for the late-time period holds when
$1\ll T\ll L^{4}$
.
Thus, we define a similarity variable as
${\it\eta}\equiv \tilde{R}/\tilde{T}^{1/4}$
, and
${\it\eta}_{f}\equiv \tilde{R}_{f}(\tilde{T})/\tilde{T}^{1/4}$
which indicates the position of the liquid front. Following standard steps, we also write
$y\equiv {\it\eta}/{\it\eta}_{f}$
. Then, the solutions can be written as
$\tilde{W}(\tilde{R},\tilde{T})={\it\eta}_{f}^{2}\tilde{T}^{1/2}{\it\psi}(y)$
,
$\tilde{W}_{f}(\tilde{T})={\it\eta}_{f}^{2}\tilde{T}^{1/2}{\it\psi}(1)$
and
$\tilde{{\it\Sigma}}(\tilde{R},\tilde{T})={\it\eta}_{f}^{2}\tilde{T}^{1/2}{\it\phi}(y)$
. Consequently, for
$0\leqslant y\leqslant 1$
, (3.16) can be rewritten as ODEs:
$$\begin{eqnarray}\displaystyle & \displaystyle (y{\it\phi}{\it\psi}^{\prime })^{\prime }+y{\it\psi}-y{\it\psi}(1)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (y^{3}{\it\phi}^{\prime })^{\prime }+y({\it\psi}^{\prime })^{2}=0. & \displaystyle\end{eqnarray}$$
$1\leqslant y\leqslant y_{\infty }$
, where
$y_{\infty }\equiv L/({\it\eta}_{f}T^{1/4})=L/R_{f}(T)$
and we assume that
$y_{\infty }\rightarrow +\infty$
holds for large membranes, (3.13) and (3.12c
) are now transformed to 
$$\begin{eqnarray}\displaystyle & \displaystyle (y{\it\phi}{\it\psi}^{\prime })^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (y^{3}{\it\phi}^{\prime })^{\prime }+y({\it\psi}^{\prime })^{2}=0. & \displaystyle\end{eqnarray}$$
${\it\psi}(y)$
and
${\it\phi}(y)$
from (2.19) and (2.21): 
$$\begin{eqnarray}{\it\psi}^{\prime }(0)=0,\quad {\it\psi}(y_{\infty })=0,\quad {\it\phi}^{\prime }(0)=0\quad \text{and}\quad [(1-{\it\nu}){\it\phi}(y)+y{\it\phi}^{\prime }(y)]|_{y=y_{\infty }}=0.\vphantom{\sum }\end{eqnarray}$$
Meanwhile, the constant
${\it\eta}_{f}$
can be determined using the global mass conservation equation (3.14):
$$\begin{eqnarray}{\it\eta}_{f}=\left(\int _{0}^{1}y[{\it\psi}(y)-{\it\psi}(1)]\,\text{d}y\right)^{-1/4}.\end{eqnarray}$$
Again, we note that
$y_{\infty }$
, by definition, is time-dependent. However, we study the time period before the edge effect becomes important, i.e.
$L/R_{f}\gg 1$
, and we take
$y_{\infty }\rightarrow +\infty$
. We numerically solve (3.17) and (3.18) using different values of
$y_{\infty }$
, and we find that the solution of
${\it\psi}(y)$
and
${\it\phi}(y)$
has negligible dependence on
$y_{\infty }$
when
$y_{\infty }$
is large enough. In fact, our numerical solutions show that the influence of
$y_{\infty }$
is actually quite small even when
$y_{\infty }=O(1)$
, as shown in figure 4. The solutions appear to converge to the self-similar solutions that correspond to
$y_{\infty }\rightarrow +\infty$
.
Figure 4. As
$y_{\infty }$
increases, the numerical solutions of
${\it\psi}(y)$
and
${\it\phi}(y)$
converge to the self-similar solutions, which correspond to
$y_{\infty }\rightarrow +\infty$
. In (a),
${\it\psi}(y)$
represents the shape of the stretched membrane. In (b),
${\it\phi}(y)$
describes the distribution of radial stress in the membrane.
To obtain some representative values, we set
$y_{\infty }=10$
. Again, we can use as large a value as we choose for
$y_{\infty }$
. Convergence of the solution is observed as
$y_{\infty }$
becomes larger, and
$y_{\infty }=10$
is large enough to produce the representative values
$$\begin{eqnarray}{\it\psi}(0)\approx 2.329,\quad {\it\psi}(1)\approx 2.041,\quad {\it\phi}(0)\approx 0.2047\quad \text{and}\quad {\it\phi}(1)\approx 0.1561.\end{eqnarray}$$
From (3.20), we also obtain
${\it\eta}_{f}\approx 1.97$
. The representative time-dependent shapes of the air–liquid interface and stretching membrane are shown in figure 5, where we choose
$L=10$
as the membrane size, and we show profile shapes at two different late times,
$T=10$
and
$T=20$
.
Figure 5. Numerical solutions of the air–liquid interface and membrane shape in the late-time membrane stretching regime. We show the solutions for
$L=10$
at
$T=10$
(dashed-curves) and
$T=20$
(solid-curves) as an example. We note that the air–liquid interface is horizontal in the late-time period.
Figure 6. Experimental set-up: propagation of a viscous liquid above a stretching membrane. Silicone oil was injected through a syringe pump system onto a thin elastic membrane. This picture was taken from experiment no. 10 in table 1. We have adjusted the brightness and contrast of this picture to highlight the liquid pool.
4. Experimental observations
We have designed and conducted a series of bench-top experiments on viscous thin films spreading over thin elastic membranes under constant liquid injection. The experimental set-up is shown in figure 6. Before liquid injection, various thin elastic membranes were carefully glued to copper round shims with inner radius of 0.102 m and outer radius of 0.127 m. Then, the membranes were placed horizontally below a syringe needle, and silicone oils of varying viscosity were injected at a constant flow rate onto the elastic membranes through a syringe pump (Harvard Apparatus). The injection rate and the physical properties of the liquids (silicone oils: Sigma–Aldrich) and membranes (silicone rubber sheets, smooth finish: McMaster-Carr 86435K41, 9010K121) used in each experiment are listed in table 1. The thickness of the membranes was measured using a stainless steel dial calliper with a precision of 0.02 mm. The Young’s modulus for the elastic membrane was measured using Hooke’s law by recording the change of length of a rectangular piece of the material when known weights were hanging from it. We stayed in the linear regime below the limit where wrinkling occurs. The Poisson ratio was taken to be
${\it\nu}=1/2$
. We used new membranes after each experiment.
Table 1. Summary of the experimental parameters of viscous gravity currents spreading on a stretching membrane. Elastic membranes of different Young’s modulus
$E$
and thickness
$d$
were used. Silicone oils of different viscosity
${\it\mu}$
were injected at different volumetric rates
$q$
. The kinematic viscosity and its error for the silicone oils were obtained from the Sigma–Aldrich product description, and we confirmed the values from our own measurements using a rheometer (Physica MCR 301). The density of the silicone oils was
${\it\rho}\approx 970~\text{kg m}^{-3}$
. The injection rate was read from the syringe pump (Harvard Apparatus) with a
$\pm 0.35\,\%$
error, reported by the company.
The time evolution of the front location of the air–liquid interface was captured by a USB camera (IDS uEye) installed directly above the shims and membranes, with sample pictures shown in figure 7(a). The air–liquid interface could be clearly identified and remained roughly circular during the entire spreading process. The deflection of the membrane was also recorded using a second digital camera (Nikon 7100) taking pictures from the side (sample pictures shown in figure 7
b). In our experiments, we first turned on the cameras and confirmed that they were working correctly. Then, we turned on the syringe pump, and started the fluid injection process;
$t=0$
corresponds to the time when we observed the first deposition of liquid on the membrane. The experiments were found to be reproducible by comparing the time-dependent locations of the propagating front for experiments with the same parameters (not listed in table 1). For example, the difference for the frontal location was found to be less than 1 % at the half time of repeated experiments for condition no. 10. The experimental data for the front locations of the air–liquid interface and the shape of the deformed membrane were used to compare with the theoretical predictions, and verify the approximate analytical solutions and our model, which was developed in § 3.
Figure 7. Typical experimental observations: (a–f) from the top and (g–l) from the side. The pictures are captured from experiment no. 5 listed in table 1. It should be noted that the brightness and contrast of the pictures have been adjusted to provide a clearer image of the propagating liquid front and membrane deflection. Images captured at
$t=0$
s (a,g);
$t=10$
s (b,i);
$t=50$
s (c,k);
$t=200$
s (d,h);
$t=500$
s (e,j);
$t=1500$
s (f,l).
4.1. Front location
As described in § 3, from our theoretical model, we have identified a transition from an early-time gravity current regime to a late-time membrane stretching regime during the fluid injection process. In particular, in the early-time period, the gravity current model (§ 3.1) predicts that the front location of the air–liquid interface obeys
$$\begin{eqnarray}R_{f}(T)={\it\xi}_{f}T^{1/2},\quad \text{with }{\it\xi}_{f}\approx 1.43,\end{eqnarray}$$
while in the late-time period, the membrane stretching model (§ 3.2) predicts that the front propagates in the form of
$$\begin{eqnarray}R_{f}(T)={\it\eta}_{f}T^{1/4},\quad \text{with }{\it\eta}_{f}\approx 1.97.\end{eqnarray}$$
The time transition happens at
$T\approx 1$
or
$t\approx t_{c}$
, as defined in (2.15a
). The scalings in (2.15) indicate how to rescale the experimental data with varying parameters.
To clearly show the effect of individual parameters, we select representative experiments and demonstrate the effects of the liquid injection rate (figure 8 a,b), the viscosity of the injected liquid (figure 8 c,d), the thickness of the elastic membrane (figure 8 e,f) and the Young’s modulus of the membrane (figure 8 g,h). The theoretical predictions in the gravity current (GC) regime, i.e. (4.1), and membrane stretching (MS) regime, i.e. (4.2), are also shown in the subfigures of rescaled parameters based on (2.15). We have also provided error bars in the plots.
Figure 8. Time evolution of the front location in different experiments with varying liquid or membrane properties: (a,b) liquid injection rate
$(10^{-6}~\text{m}^{3}~\text{s}^{-1})$
, (c,d) liquid viscosity
$(10^{-3}~\text{m}^{2}~\text{s}^{-1})$
, (e,f) membrane thickness
$(10^{-3}~\text{m}^{-1})$
and (g,h) Young’s modulus (
$10^{6}$
Pa). Panels (b,d,f,h) are the dimensionless versions of panels (a,c,e,g). The theoretical predictions of the front location in the gravity current (GC) and membrane stretching (MS) regimes are also shown.
Data collapse has been clearly observed for all of the experimental parameters we tested. The scaling argument based on (2.15) appears to capture the spreading behaviour through the entire liquid injection period. In particular, the influence of the injection rate spans the entire injection process (figure 8 a,b), the effect of the liquid viscosity is important only in the early-time period (figure 8 c,d) and the effects of the membrane thickness and Young’s modulus become important in the late-time period (figure 8 e–h).
Finally, the data for experiments 1–19 in table 1 are plotted all together in figure 9. The raw data for
$r_{f}(t)$
are plotted versus time
$t$
in figure 9(a), and the rescaled front location
$R_{f}(T)$
and time
$T$
based on (2.15) are plotted in figure 9(b). The transition from the early-time
$R_{f}\propto T^{1/2}$
to the late-time
$R_{f}\propto T^{1/4}$
is evident.
Figure 9. Time evolution of the front location for a viscous liquid injection above a stretching membrane. Transition from an early-time gravity current regime, i.e.
$R_{f}\propto T^{1/2}$
, to a late-time membrane stretching regime, i.e.
$R_{f}\propto T^{1/4}$
, has been observed.
4.2. Membrane deformation
The time evolution of the shape of the deformed membrane was also recorded in the experiments (see figure 7
b for example). The resolution of the Nikon camera for the side-view images was
$960\times 768$
in a representative experiment. When the deformation was small, the measurement error became significant. In particular, the centre of the camera had to be precisely placed in the same horizontal place as the bottom of the copper ring, where we attached the membranes. We assume that the error is too large for a comparison with theoretical predictions in the early-time period. However, the deflection in the late-time period is large enough for us to compare with the theoretical predictions of the membrane shape.
A comparison between theory and experiment is shown in figure 10 when the vertical deflection is large enough for experimental measurements in the late-time period (
$T\gg 1$
). In this representative experiment (no. 5 in table 1), from
$T=10$
, the theoretical calculation of the membrane deformation is greater than the experimental observation; the prediction of the location of the propagating front is also greater than the experimental measurement, as indicated by the arrows (see also figure 9
b), and the late-time self-similar solution is still under development. As time progresses, the self-similar solution continues to develop, and the agreement at
$T=20$
appears to be very good in both the membrane deformation and the front location. At
$T=35$
, the theoretical calculations for the membrane deformation and front location also agree well with the experimental observations. We note that the major difference between theory and experiment for the membrane shape appears in the region near the centre, where the theory slightly overpredicts the membrane deformation. We also note that the edge effect may contribute to the deviation from the predictions of the late-time self-similar solution, where the size of the membrane is assumed to be much greater than the location of the liquid front.
Figure 10. Shape of the stretched membrane: a comparison between experimental observations and theoretical predictions at
$T=10$
(a), 20 (b) and 35 (c). After
$T=10$
, the experimental observation shows good agreement with the predictions from the membrane stretching (MS) regime discussed in § 3.2. This example is based on experiment no. 5 in table 1, where
$t_{c}\approx 43.5~\text{s}$
,
$r_{c}\approx 10.7~\text{mm}$
and
$h_{c}\approx 2.02~\text{mm}$
; the dimensionless membrane radius is
$L\approx 9.55$
. The arrows indicate the location of the propagating front from theoretical predictions (below the curves) and experiments (above the curves).
4.3. Experimental uncertainties
There are experimental errors in the measurement of time, length, and thickness and Young’s modulus of the elastic membranes. We have provided error bars in our data analyses. The error for the time measurement depends on the frame rate we set for the camera; the representative values for the frame rate are 1 s for the USB camera that provides the top view (figure 7
a) and 10 s for the Nikon camera that generates the side view (figure 7
b). We included a ruler in the images of our experiments for information on the length scale. The ruler has a precision of 1 mm, so the typical error in our measurement of length (e.g. front location
$r_{f}$
) is 1 mm. The errors in the measurements of the Young’s modulus and the thickness of the elastic membranes are reported in table 1. The error for dimensionless parameters (e.g. dimensionless time
$T$
) includes errors for both measuring the original parameters (e.g. real time
$t$
) and estimating the characteristic scales (e.g. characteristic time
$t_{c}$
). For example, for dimensionless time
$T$
, where
$T\equiv t/t_{c}$
, we use
$({\rm\Delta}T/T)^{2}\approx ({\rm\Delta}t/t)^{2}+({\rm\Delta}t_{c}/t_{c})^{2}$
, where
${\rm\Delta}T$
,
${\rm\Delta}t$
and
${\rm\Delta}t_{c}$
represent the errors for
$T$
,
$t$
and
$t_{c}$
respectively.
It should be noted that there exist other factors that can contribute to the experimental uncertainty. For example, the injection point might not be located exactly at the centre of the membrane, and the air–liquid interface may not spread in a perfectly circular manner. The effect of surface tension and the moving contact line can also contribute to the spreading process to some extent, which we comment on in § 5.3. In addition, the weight and initial tension of the elastic membranes are neglected in the mathematical model. The effect of membrane bending is also neglected in the model, the validity of which we comment on in more detail in § 5.4. However, it appears that overall the experimental observations agree well with the approximate analytical solutions in the asymptotic regimes.
5. Conclusions and discussion
5.1. Conclusions
In this paper, we studied the spreading of thin viscous films over an elastic membrane that is stretched by the weight of the liquid. A coupled system of partial differential equations was derived, using the lubrication approximation for the dynamics of the thin film, to describe the time evolution of the film thickness, membrane deflection and radial tension in the membrane. For constant liquid injection, we obtained distinct early-time and late-time self-similar regimes. In particular, in the early-time period, the dynamics is dominated by the buoyancy-driven spreading of the liquid film, and the membrane stretches to balance the buoyancy-controlled distribution of liquid weight. In the late-time period, the system is quasi-steady, the air–liquid interface is flat and membrane stretching is the dominant mechanism, which regulates the speed of the spreading front. As a result, the location of the front exhibits a transition from a
$t^{1/2}$
power law in the early-time period to a
$t^{1/4}$
power law in the late-time period. Laboratory-scale experiments have also been conducted to verify the model predictions. Our study extends the gravity current literature, and provides insight into buoyancy-driven spreading problems where the horizontal boundaries are stretchable.
5.2. Influence of injection modes
In this paper we only considered the case of a constant liquid injection rate. However, we note that the problem can be generalized to a broader range of injection modes, and various approximate analytical solutions may still be obtained, for example, for power-law or exponential injection modes. In this case, the global mass conservation equation (2.5) must be modified for the specific injection mode, as well as the boundary condition (2.11b ). The procedures are analogous to the case of constant injection, while we note that the appropriate time, length and tension scales in (2.15) are expected to be different to non-dimensionalize the differential equations, and boundary and initial conditions. As a result, the scaling laws are also expected to be different.
5.3. Influence of surface tension
We have neglected the effects of surface tension and the moving contact line in this work, as mentioned before. We note that the thickness of the liquid film is large (for example,
$h=1~\text{cm}$
) for the bulk part of the film away from the location of the propagating front, so we expect the effects of surface tension and the moving contact line to be important only in the region very close to the front. However, the global spreading rate and the shape of the bulk part of the air–liquid interface can still be estimated by the gravity current models, as reported before (see, e.g., Huppert Reference Huppert1982). In addition, the length scale of the liquid film is large (for example,
$r_{f}=5~\text{cm}$
) in this study, such that the effect of surface-tension-induced membrane wrinkling is also negligible (see, e.g., Huang et al.
Reference Huang, Juszkiewicz, de Jeu, Cerda, Emrick, Menon and Russell2007; Vella et al.
Reference Vella, Adda-Bedia and Cerda2010).
5.4. Influence of membrane bending
We have neglected the effect of membrane bending in our study. For a deflection
$w$
, the liquid pressure from membrane bending scales as
$p_{b}\sim Bw/\ell ^{4}\sim Ed^{3}w/[12(1-{\it\nu}^{2})\ell ^{4}]$
, with
$B$
denoting the bending stiffness and
${\it\nu}$
the Poisson ratio. On the other hand, the pressure from membrane stretching scales as
$p_{s}\sim {\it\sigma}w/\ell ^{2}\sim Edw^{3}/\ell ^{4}$
. Thus,
$p_{s}/p_{b}\sim 6(1-{\it\nu}^{2})w^{2}/d^{2}$
. In the early-time period, there will always exist a time range in which the membrane deflection
$w$
is small compared with the thickness of the membrane
$d$
, and hence the bending effect is important. However, this time range is very short when using the very thin membranes in our experiments. For example, in experiment no. 2, the membrane thickness is
$d\approx 0.27~\text{mm}$
; at
$t=1~\text{s}$
(
$t\approx 0.1t_{c}$
), we obtain a deflection of
$w\approx 2~\text{mm}$
(
$w\approx 2h_{c}$
) at the centre of the membrane, by which time
$p_{b}/p_{s}$
is already
${\approx}10^{-3}$
. Thus, neglecting the effect of membrane bending is a good assumption in this work.
Acknowledgements
We thank the Princeton Carbon Mitigation Initiative for support of this research. I.M.G. gratefully acknowledges support from the Royal Society through a University Research Fellowship. We also thank M. Bruna, I. Christov, M. Fontelos, Z. Li, A. Krupp, J. Neufeld, C. P. Please, R. Socolow and D. Vella for helpful conversations. We thank E. Dressaire, D. Geyer and C. Lai for discussions on the measurement of the Young’s modulus of the materials, and J. Feng, H. Kim and S. Shin for discussions on the measurement of the viscosity of the silicone oils. We also thank the three anonymous reviewers for their helpful comments and suggestions, including identification of an error in handling boundary conditions in an earlier version of the paper.
