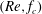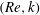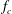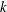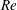1 Introduction
Shallow-water flows on a slope featuring a free surface often present an unstable motion, characterized by various types of surface waves. These waves may be complex, depending on inertia, inclination or fluid properties. If the waves that are triggered in such flows are initially quasiplane with large wavelength, farther downstream they grow in amplitude and quickly evolve towards a nonlinear regime. In this paper, an experimental study is performed to investigate the stability of such films when the fluid is shear-thinning, a relevant configuration for many geophysical flows such as debris flows or mud surge waves.
In the case of Newtonian fluids, the onset of such waves is well understood since the early linear theoretical studies of Benjamin (Reference Benjamin1957) and Yih (Reference Yih1963), who showed that the critical Reynolds number for the onset of the instabilities only depends on the slope angle, and is proportional to its cotangent. The same value is obtained with shallow-water or Orr–Sommerfeld approaches, as long as the long-wave hypothesis is used. This cotangent dependence was later confirmed experimentally by Liu, Paul & Gollub (Reference Liu, Paul and Gollub1993).
Smith (Reference Smith1990) proposed a phenomenological approach in order to understand the physical mechanisms for the long-wave instability in Newtonian thin liquid films. (i) He showed that the disturbance of the free surface is the trigger point of the shear-induced instability, which is consistent, in shallow-water models, with the existence of a kinematic wave that is exclusively governed by the conservation of mass (Kalliadasis et al. Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2011; Whitham Reference Whitham2011). (ii) He investigated the effect of the stabilizing and destabilizing terms in the growth phase of the instability, which, at the leading orders in the long-wave expansion theory, correspond to the responses of the film to the variation in momentum through dynamic waves (Kalliadasis et al. Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2011). (iii) He wrote the mass balance equation in the wave framework and showed that, at the linear threshold, the waves travel two times faster than the flow velocity at the free surface, this latter point being a key ingredient in this inertia-driven instability.
In the literature, most experimental studies on waves down an incline are based on a Newtonian fluid model (Liu et al. Reference Liu, Paul and Gollub1993; Vlachogiannis et al. Reference Vlachogiannis, Samandas, Leontidis and Bontozoglou2010; Georgantaki et al. Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011). However, in many engineering applications (coating processes in paint, paper, food, plastic, etc. industries) or geophysical phenomena (glaciers, mud and debris flows), the liquids involved present more complex rheological behaviours (Benchabane & Bekkour Reference Benchabane and Bekkour2008; Chambon, Ghemmour & Laigle Reference Chambon, Ghemmour and Laigle2009; Jouvet et al. Reference Jouvet, Picasso, Rappaz, Huss and Funk2011). In particular, the viscoplastic rheology was shown to describe quite well the global behaviour of the materials involved in debris flows (Huang & Garcia Reference Huang and Garcia1998; Chambon et al. Reference Chambon, Ghemmour and Laigle2009). Most viscoplastic liquids are not ideal Bingham liquids and have shear-thinning properties in addition to the yield stress. In this study, we chose to focus on purely shear-thinning fluids and leave the yield stress out, for the sake of simplicity. This should be seen as a first step towards understanding the physics of complex fluids. Moreover, this simplified rheology could already be sufficient to describe some real geological materials (Jeong Reference Jeong2010).
Several models are available to describe the rheology of shear-thinning fluids, among which is the power-law model. Under the shallow-water approximation, the stability of a film of a power-law fluid flowing down an inclined plane has been studied theoretically by several authors (Ng & Mei Reference Ng and Mei1994; Dandapat & Mukhopadhyay Reference Dandapat and Mukhopadhyay2001; Amaouche, Djema & Bourdache Reference Amaouche, Djema and Bourdache2009; Fernández-Nieto, Noble & Vila Reference Fernández-Nieto, Noble and Vila2010). However, this rheology yields an infinite viscosity at zero shear rate (i.e. at the surface), which demands a careful handling in theoretical computation of the critical Reynolds number (Noble & Vila Reference Noble and Vila2013). Moreover, this rheology is sometimes not physically accurate, for example in the case of polymer solutions and melts, whose viscosities always remain finite.
To solve this issue, Ruyer-Quil, Chakraborty & Dandapat (Reference Ruyer-Quil, Chakraborty and Dandapat2012) recently modified the power-law model by introducing a Newtonian plateau at low values of the shear rate, and they provided asymptotic expressions for the critical Reynolds number under the long-wave expansion.
It is possible, however, to describe such behaviour without introducing discontinuities by using a Carreau law (see § 2), and this approach is preferred by many authors, notably in the polymer and coating communities (Weinstein Reference Weinstein1990; Rodd, Dunstan & Boger Reference Rodd, Dunstan and Boger2000; Escudier et al. Reference Escudier, Gouldson, Pereira, Pinho and Poole2001; Benchabane & Bekkour Reference Benchabane and Bekkour2008). Rousset et al. (Reference Rousset, Millet, Botton and Ben Hadid2007) and Millet et al. (Reference Millet, Botton, Rousset and Ben Hadid2008) numerically studied flows of Carreau fluids down an incline. They investigated the influence of the Carreau law parameters on the modification of the stability threshold, using temporal stability analysis based on the Orr–Sommerfeld equation. Following the same approach as Smith (Reference Smith1990), they found that (i) the critical Reynolds number is lower than that for a Newtonian fluid having a viscosity equal to the zero-shear-rate viscosity of the Carreau fluid and (ii) the critical wave celerity, normalized by the surface velocity, is larger. They concluded that shear-thinning rheology has a destabilizing effect.
In contrast, on the experimental side, the literature is less abundant. The first experimental visualization record of surface waves in Newtonian falling films was the paper by Kapitza & Kapitza (Reference Kapitza and Kapitza1949). However, it was not until the work of Liu et al. (Reference Liu, Paul and Gollub1993) that the theoretical predictions of Benjamin (Reference Benjamin1957) and Yih (Reference Yih1963) were confirmed experimentally. In particular, Liu et al. (Reference Liu, Paul and Gollub1993) confirmed the convective nature of this instability, which has the practical consequence of making it extremely sensitive to external noise.
There is very little work on flows of non-Newtonian fluids down a slope, apart from three notable exceptions. First, Coussot (Reference Coussot1994) investigated the stability of mud flows down an incline. Later, Forterre & Pouliquen (Reference Forterre and Pouliquen2003) adapted the set-up of Liu et al. (Reference Liu, Paul and Gollub1993) to investigate this instability in the different, but related, context of granular flows. Finally, Chambon, Ghemmour & Naaim (Reference Chambon, Ghemmour and Naaim2014) recently developed an original experimental configuration in which a viscoplastic surge is stationary in the laboratory frame.
In this paper, we present an experimental study on the stability of gravity-driven film flows when the fluid is shear-thinning. In the next section, we will describe our experimental set-up, which is similar to the one used by Liu et al. (Reference Liu, Paul and Gollub1993). We will then present results obtained with Newtonian fluid and compare them favourably with the literature. Finally, we will present our results obtained for shear-thinning fluids, and we will compare them with models and numerical simulations.
2 Experimental set-up
2.1 Description
The experiments were carried out in an inclined channel of length
![]() $2~\text{m}$
and width
$2~\text{m}$
and width
![]() $W_{ch}=46~\text{cm}$
, in which a flowing film was perturbed upstream, and the perturbation was recorded further downstream. The channel ended in a reservoir, and with a PCM EcoMoineau™ progressing cavity pump, the fluid was pumped up to a manifold at the entrance of the channel (filters were used to tranquilize the flow). The flow rate
$W_{ch}=46~\text{cm}$
, in which a flowing film was perturbed upstream, and the perturbation was recorded further downstream. The channel ended in a reservoir, and with a PCM EcoMoineau™ progressing cavity pump, the fluid was pumped up to a manifold at the entrance of the channel (filters were used to tranquilize the flow). The flow rate
![]() $q$
was measured with a Rosemount electromagnetic flow meter. To allow optical measurements (see below), the channel base was chosen transparent (glass).
$q$
was measured with a Rosemount electromagnetic flow meter. To allow optical measurements (see below), the channel base was chosen transparent (glass).
The inclination angle of the channel,
![]() $\unicode[STIX]{x1D719}$
, was adjustable thanks to a telescopic motorized leg holding the end of the channel, from
$\unicode[STIX]{x1D719}$
, was adjustable thanks to a telescopic motorized leg holding the end of the channel, from
![]() $0^{\circ }$
up to
$0^{\circ }$
up to
![]() $15^{\circ }$
with a precision of
$15^{\circ }$
with a precision of
![]() $0.5^{\circ }$
. A sketch of the set-up is shown in figure 1.
$0.5^{\circ }$
. A sketch of the set-up is shown in figure 1.

Figure 1. Sketch of the experimental apparatus.
We chose to study primary waves in the linear regime, for which the disturbances are almost two-dimensional and sinusoidal, and their amplitude is as small as possible. To impose such perturbations with controlled frequency
![]() $f$
and amplitude
$f$
and amplitude
![]() $A$
, we used a vibration device (B&K 4809) linked to a blade plunged in the upstream manifold. This system allowed us to produce quasiplane waves with an amplitude
$A$
, we used a vibration device (B&K 4809) linked to a blade plunged in the upstream manifold. This system allowed us to produce quasiplane waves with an amplitude
![]() $A$
smaller than one millimetre, and a wavelength
$A$
smaller than one millimetre, and a wavelength
![]() $\unicode[STIX]{x1D706}$
of a few centimetres. The perturbations are sinusoidal close to the channel entrance, but as they grow downstream, they evolve into complex solitary waves. This nonlinear regime has been the subject of many other studies (see, e.g., Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), but it is not in the scope of the present study. Instead, we focused on the onset of the instability, and all our measurements were made close to the entrance manifold, i.e. still in the linear regime.
$\unicode[STIX]{x1D706}$
of a few centimetres. The perturbations are sinusoidal close to the channel entrance, but as they grow downstream, they evolve into complex solitary waves. This nonlinear regime has been the subject of many other studies (see, e.g., Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), but it is not in the scope of the present study. Instead, we focused on the onset of the instability, and all our measurements were made close to the entrance manifold, i.e. still in the linear regime.
2.2 Detection methods
We used two detection methods to monitor the propagation of the perturbation, a local one (point measurement) and a global one (surface measurement).
The local method was the same technique as used by Liu et al. (Reference Liu, Paul and Gollub1993): a laser beam was shot perpendicularly through the channel and was deflected by the liquid–air interface. A position sensitive device (PSD) recorded the laser beam position, from which the local slope of the free surface,
![]() $\text{d}h/\text{d}x$
, was inferred. To prevent the signals from being affected by non-planar effects (e.g. induced by the walls), we always made sure that we used this method at the centreline of the channel. We repeated this measurement at regularly spaced positions, and we measured the signal amplitude (by synchronous demodulation) and the phase shift with a reference signal (the vibration device generating the waves). From these measurements we were able to extract the amplitude variation and the wavelength of the surface waves.
$\text{d}h/\text{d}x$
, was inferred. To prevent the signals from being affected by non-planar effects (e.g. induced by the walls), we always made sure that we used this method at the centreline of the channel. We repeated this measurement at regularly spaced positions, and we measured the signal amplitude (by synchronous demodulation) and the phase shift with a reference signal (the vibration device generating the waves). From these measurements we were able to extract the amplitude variation and the wavelength of the surface waves.
We also used free-surface synthetic schlieren (FS-SS) to test for wave planarity. This technique, proposed by Moisy, Rabaud & Salsac (Reference Moisy, Rabaud and Salsac2009), allows an instant global measurement of the free-surface slope. A pattern of computer-generated random dots is placed under the channel, approximately
![]() $70~\text{cm}$
below the free surface. A CCD camera (resolution
$70~\text{cm}$
below the free surface. A CCD camera (resolution
![]() $1280\times 1024$
) located
$1280\times 1024$
) located
![]() $170~\text{cm}$
above it records its image. When the liquid surface is modified by the perturbation, the image is different from the original pattern, and by tracking the apparent displacement of the dots with standard PIV software (DaVis, LaVision), we are able to reconstruct the free-surface slope over a
$170~\text{cm}$
above it records its image. When the liquid surface is modified by the perturbation, the image is different from the original pattern, and by tracking the apparent displacement of the dots with standard PIV software (DaVis, LaVision), we are able to reconstruct the free-surface slope over a
![]() $40~\text{cm}$
long domain, located roughly
$40~\text{cm}$
long domain, located roughly
![]() $40~\text{cm}$
from the entrance manifold. The decay rate
$40~\text{cm}$
from the entrance manifold. The decay rate
![]() $\unicode[STIX]{x1D6FC}$
and wavenumber
$\unicode[STIX]{x1D6FC}$
and wavenumber
![]() $k$
are then determined by fitting the surface slope measurements to the analytical expression
$k$
are then determined by fitting the surface slope measurements to the analytical expression
Figure 2(a) compares the results obtained with the two techniques. The good agreement with (2.1) gives us confidence in both techniques. In practice, we mostly used the local detection, first because the linear regime is located near the channel entrance, hardly accessible to the FS-SS technique, and second because it is much simpler to use.

Figure 2. (a) Normalized surface slope versus position for the FS-SS method at a given time, and for the corresponding local measurements (60 % vol. water–glycerol solution,
![]() $\unicode[STIX]{x1D719}=1^{\circ }$
,
$\unicode[STIX]{x1D719}=1^{\circ }$
,
![]() $\mathit{Re}=23$
,
$\mathit{Re}=23$
,
![]() $f=15~\text{Hz}$
). (b) Rheological law for fluids 1, 2 and 3 (from bottom to top). Solid lines: fit with a Carreau law. Black points and rectangles: shear rates in the experiments (see § 4).
$f=15~\text{Hz}$
). (b) Rheological law for fluids 1, 2 and 3 (from bottom to top). Solid lines: fit with a Carreau law. Black points and rectangles: shear rates in the experiments (see § 4).
2.3 Fluids
A 60 % vol. water–glycerol mixture was used for its Newtonian properties, whereas mixed solutions of both carboxymethylcellulose (CMC, E466) and xanthan gum (E415) were used as shear-thinning fluids.
The rheology of the non-Newtonian fluids is well described by a four-parameter Carreau inelastic model,
where
![]() $\unicode[STIX]{x1D702}_{0}$
and
$\unicode[STIX]{x1D702}_{0}$
and
![]() $\unicode[STIX]{x1D702}_{\infty }$
are the limit Newtonian viscosities at zero and infinite shear rate respectively,
$\unicode[STIX]{x1D702}_{\infty }$
are the limit Newtonian viscosities at zero and infinite shear rate respectively,
![]() $\dot{\unicode[STIX]{x1D6FE}}_{c}$
is the critical shear rate separating the Newtonian and shear-thinning behaviours,
$\dot{\unicode[STIX]{x1D6FE}}_{c}$
is the critical shear rate separating the Newtonian and shear-thinning behaviours,
![]() $n$
is the power-law index,
$n$
is the power-law index,
![]() $\unicode[STIX]{x1D702}$
is the local viscosity and
$\unicode[STIX]{x1D702}$
is the local viscosity and
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the local shear rate.
$\dot{\unicode[STIX]{x1D6FE}}$
is the local shear rate.
A Rheomat™ RM115-A Couette rheometer (Lamy Rheology,
![]() $10~\text{mN}~\text{m}$
torque) was used for the main flow curve determination. However, because most commercial rheometers are torque-sensitive, it is very difficult to precisely determine the zero-shear-rate viscosity, yet this is crucial for the characterization of flows featuring a free surface. We then implemented an electro-capillary technique to measure, when possible, the viscosity and surface tension of the fluids at values of the shear rate as small as
$10~\text{mN}~\text{m}$
torque) was used for the main flow curve determination. However, because most commercial rheometers are torque-sensitive, it is very difficult to precisely determine the zero-shear-rate viscosity, yet this is crucial for the characterization of flows featuring a free surface. We then implemented an electro-capillary technique to measure, when possible, the viscosity and surface tension of the fluids at values of the shear rate as small as
![]() $10^{-3}~\text{s}^{-1}$
. This technique and the measurements are fully described in Allouche et al. (Reference Allouche, Botton, Henry, Millet, Usha and Ben Hadid2015). The rheological parameters for the Carreau law and physical properties such as the density
$10^{-3}~\text{s}^{-1}$
. This technique and the measurements are fully described in Allouche et al. (Reference Allouche, Botton, Henry, Millet, Usha and Ben Hadid2015). The rheological parameters for the Carreau law and physical properties such as the density
![]() $\unicode[STIX]{x1D70C}$
and the surface tension
$\unicode[STIX]{x1D70C}$
and the surface tension
![]() $\unicode[STIX]{x1D70E}$
of the three shear-thinning fluids used are displayed in table 1 and their rheograms are plotted in figure 2(b). Based on this measured zero-shear-rate viscosity, we were able to define a Reynolds number for each experiment as
$\unicode[STIX]{x1D70E}$
of the three shear-thinning fluids used are displayed in table 1 and their rheograms are plotted in figure 2(b). Based on this measured zero-shear-rate viscosity, we were able to define a Reynolds number for each experiment as
![]() $\mathit{Re}=\unicode[STIX]{x1D70C}q/W_{ch}\unicode[STIX]{x1D702}_{0}$
(Rousset et al.
Reference Rousset, Millet, Botton and Ben Hadid2007).
$\mathit{Re}=\unicode[STIX]{x1D70C}q/W_{ch}\unicode[STIX]{x1D702}_{0}$
(Rousset et al.
Reference Rousset, Millet, Botton and Ben Hadid2007).
Table 1. The mechanical properties of the fluids used in the present study: Carreau parameters, density and surface tension. Newtonian values were obtained from Takamura, Fischer & Morrow (Reference Takamura, Fischer and Morrow2012).

The first fluid used in this study was a xanthan gum solution at 0.008 wt%, whose rheology had been characterized in Allouche et al. (Reference Allouche, Botton, Henry, Millet, Usha and Ben Hadid2015) (fluid 1 in table 1). This fluid exhibits a strong shear-thinning behaviour because its critical shear rate,
![]() $\dot{\unicode[STIX]{x1D6FE}}_{c}$
, is low. For this fluid,
$\dot{\unicode[STIX]{x1D6FE}}_{c}$
, is low. For this fluid,
![]() $\dot{\unicode[STIX]{x1D6FE}}_{c}$
was reached even at very small inclination angles in our set-up. On the contrary, the shear-thinning behaviour in CMC solutions occurs later, at higher shear rates than we could reach in our set-up. We then decided to mix CMC and xanthan gum in different proportions to obtain moderate shear-thinning fluids.
$\dot{\unicode[STIX]{x1D6FE}}_{c}$
was reached even at very small inclination angles in our set-up. On the contrary, the shear-thinning behaviour in CMC solutions occurs later, at higher shear rates than we could reach in our set-up. We then decided to mix CMC and xanthan gum in different proportions to obtain moderate shear-thinning fluids.
3 Experimental test with a Newtonian fluid
In this section, we present the results obtained with a Newtonian fluid. The goal here is to compare these results with well-established results from the literature, in order to evaluate the accuracy and limits of our set-up. The measurement of the linear stability thresholds consisted of the following steps. At fixed slope
![]() $\unicode[STIX]{x1D719}$
, flow rate
$\unicode[STIX]{x1D719}$
, flow rate
![]() $q$
and frequency
$q$
and frequency
![]() $f$
, we measured the wavenumber
$f$
, we measured the wavenumber
![]() $k$
and the decay rate
$k$
and the decay rate
![]() $\unicode[STIX]{x1D6FC}$
(figure 2(a) and (2.1)). We then repeated the measurement for different frequencies (keeping
$\unicode[STIX]{x1D6FC}$
(figure 2(a) and (2.1)). We then repeated the measurement for different frequencies (keeping
![]() $q$
constant) to identify the cutoff frequency
$q$
constant) to identify the cutoff frequency
![]() $f_{c}$
where the waves neither amplify nor attenuate (
$f_{c}$
where the waves neither amplify nor attenuate (
![]() $\unicode[STIX]{x1D6FC}=0$
), i.e. the marginal conditions. We repeated the procedure for different flow rates (i.e. different
$\unicode[STIX]{x1D6FC}=0$
), i.e. the marginal conditions. We repeated the procedure for different flow rates (i.e. different
![]() $Re$
), keeping
$Re$
), keeping
![]() $\unicode[STIX]{x1D719}$
constant.
$\unicode[STIX]{x1D719}$
constant.
Figure 3(a) shows the obtained
![]() $f_{c}(Re)$
at
$f_{c}(Re)$
at
![]() $\unicode[STIX]{x1D719}=3.2^{\circ }$
. Like Liu et al. (Reference Liu, Paul and Gollub1993), we find that the cutoff frequency varies as follows:
$\unicode[STIX]{x1D719}=3.2^{\circ }$
. Like Liu et al. (Reference Liu, Paul and Gollub1993), we find that the cutoff frequency varies as follows:
From this, we could extract the critical Reynolds number, i.e. at zero frequency, by fitting (3.1) to our data. Finally, we repeated this procedure at different inclination angles, and we obtained the variation of
![]() $Re_{c}^{exp}$
with
$Re_{c}^{exp}$
with
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
It should be noted that measurements at low frequencies are very difficult: the perturbation becomes nonlinear over a distance shorter than the wavelength and generates parasitic waves (Argyriadi, Serifi & Bontozoglou Reference Argyriadi, Serifi and Bontozoglou2004). Moreover, the experiment is very sensitive to external vibrations, in particular the pump rotation speed. In practice, no measurement could be made below
![]() $f\sim 2~\text{Hz}$
.
$f\sim 2~\text{Hz}$
.

Figure 3. (a) Neutral curve in the (
![]() $Re,f_{c}$
) plane for a Newtonian water–glycerol solution at
$Re,f_{c}$
) plane for a Newtonian water–glycerol solution at
![]() $\unicode[STIX]{x1D719}=3.2^{\circ }$
. (b) Critical Reynolds number
$\unicode[STIX]{x1D719}=3.2^{\circ }$
. (b) Critical Reynolds number
![]() $Re_{c}$
as a function of the inclination angle. The crosses represent the experimental results
$Re_{c}$
as a function of the inclination angle. The crosses represent the experimental results
![]() $Re_{c}^{exp}$
for water–glycerol solutions and the solid line corresponds to the theoretical prediction
$Re_{c}^{exp}$
for water–glycerol solutions and the solid line corresponds to the theoretical prediction
![]() $Re_{c}^{th}$
for an infinite channel (Yih Reference Yih1963) (see (3.2)). (c) The ratio
$Re_{c}^{th}$
for an infinite channel (Yih Reference Yih1963) (see (3.2)). (c) The ratio
![]() $Re_{c}^{exp}/(R^{\ast }Re_{c}^{th})$
as a function of
$Re_{c}^{exp}/(R^{\ast }Re_{c}^{th})$
as a function of
![]() $\unicode[STIX]{x1D719}$
, where
$\unicode[STIX]{x1D719}$
, where
![]() $R^{\ast }$
is the correction factor of Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011).
$R^{\ast }$
is the correction factor of Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011).
We can now compare our experimental stability thresholds, shown in figure 3(b), with the theoretical curve of Yih (Reference Yih1963), given by
We find that our results are in good agreement with the theory, although there is a systematic shift of a few units above the theoretical curve. We interpret this shift as an effect of the finite width. Indeed, equation (3.2) is obtained for the case of Newtonian film flows of infinite width (Yih Reference Yih1963). Vlachogiannis et al. (Reference Vlachogiannis, Samandas, Leontidis and Bontozoglou2010) experimentally showed that the finite width of experimental channels stabilizes the liquid film and increases the critical Reynolds number, which is consistent with what we see in figure 3(b).
To further investigate the stabilizing effect of the channel width on our results, we follow the analysis by Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011). They quantified the deviation from the theory
![]() $R^{\ast }=Re_{c}^{exp}/Re_{c}^{th}$
, which they found to be governed by surface tension effects, and depend only on the Kapitsa number
$R^{\ast }=Re_{c}^{exp}/Re_{c}^{th}$
, which they found to be governed by surface tension effects, and depend only on the Kapitsa number
![]() $Ka=l_{c}^{2}/l_{v}^{2}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}^{1/3}/g^{1/3}\unicode[STIX]{x1D702}^{4/3}$
(where
$Ka=l_{c}^{2}/l_{v}^{2}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}^{1/3}/g^{1/3}\unicode[STIX]{x1D702}^{4/3}$
(where
![]() $g$
is the gravitational acceleration,
$g$
is the gravitational acceleration,
![]() $l_{c}$
is the capillary length and
$l_{c}$
is the capillary length and
![]() $l_{v}$
is the viscous length). At large
$l_{v}$
is the viscous length). At large
![]() $Ka$
, this deviation reaches a plateau that scales as
$Ka$
, this deviation reaches a plateau that scales as
![]() $R_{m}^{\ast }\sim l_{c}/W_{ch}$
, and at small
$R_{m}^{\ast }\sim l_{c}/W_{ch}$
, and at small
![]() $Ka$
,
$Ka$
,
![]() $R^{\ast }$
varies in first approximation as
$R^{\ast }$
varies in first approximation as
![]() $R^{\ast }=1+(Ka/2000)(R_{m}^{\ast }-1)$
. We use this expression to evaluate the deviation from theory, with
$R^{\ast }=1+(Ka/2000)(R_{m}^{\ast }-1)$
. We use this expression to evaluate the deviation from theory, with
![]() $R_{m}^{\ast }=1.6$
and
$R_{m}^{\ast }=1.6$
and
![]() $Ka=127$
, yielding a correction factor of
$Ka=127$
, yielding a correction factor of
![]() $R^{\ast }=1.04$
. Figure 3(c) shows the ratio
$R^{\ast }=1.04$
. Figure 3(c) shows the ratio
![]() $Re_{c}^{exp}/(R^{\ast }Re_{c}^{th})$
as a function of the inclination angle for both our data (crosses) and the data of Liu et al. (Reference Liu, Paul and Gollub1993) (diamonds). We see that the ratio does not seem to vary with
$Re_{c}^{exp}/(R^{\ast }Re_{c}^{th})$
as a function of the inclination angle for both our data (crosses) and the data of Liu et al. (Reference Liu, Paul and Gollub1993) (diamonds). We see that the ratio does not seem to vary with
![]() $\unicode[STIX]{x1D719}$
, as expected from Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011). That being said, their correction is not sufficient to fully capture the deviation from the theory, both in our case and in the case of Liu et al. (Reference Liu, Paul and Gollub1993). This observed discrepancy could be due to the parameters we used in our experiments. These parameters (large
$\unicode[STIX]{x1D719}$
, as expected from Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011). That being said, their correction is not sufficient to fully capture the deviation from the theory, both in our case and in the case of Liu et al. (Reference Liu, Paul and Gollub1993). This observed discrepancy could be due to the parameters we used in our experiments. These parameters (large
![]() $W_{ch}$
, higher viscosity and low
$W_{ch}$
, higher viscosity and low
![]() $Ka$
) are precisely in the range where
$Ka$
) are precisely in the range where
![]() $R^{\ast }$
is the hardest to evaluate. In fact, the data of Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011) are scarce in this range, and the linear fit we used to evaluate
$R^{\ast }$
is the hardest to evaluate. In fact, the data of Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011) are scarce in this range, and the linear fit we used to evaluate
![]() $R^{\ast }$
could be wrong. A possible cause could be that at high viscosity, the capillary effects might not be the dominant stabilizing mechanism anymore. In the end, we conclude that a systematic stabilizing effect of the channel width is very likely, and we will keep it in mind when dealing with the shear-thinning fluids. However, this effect is small enough so that our experiment is able to capture the correct instability behaviour of the fluids, as seen in figures 3(c) and 4(a).
$R^{\ast }$
could be wrong. A possible cause could be that at high viscosity, the capillary effects might not be the dominant stabilizing mechanism anymore. In the end, we conclude that a systematic stabilizing effect of the channel width is very likely, and we will keep it in mind when dealing with the shear-thinning fluids. However, this effect is small enough so that our experiment is able to capture the correct instability behaviour of the fluids, as seen in figures 3(c) and 4(a).

Figure 4. (a) Neutral curve in the (
![]() $Re,f_{c}$
) plane for the shear-thinning fluids. Solid line: fit from (3.1). (b) Neutral curves in the (
$Re,f_{c}$
) plane for the shear-thinning fluids. Solid line: fit from (3.1). (b) Neutral curves in the (
![]() $Re,k$
) plane. Solid lines: numerically obtained neutral curves for the fluids (for fluid 3,
$Re,k$
) plane. Solid lines: numerically obtained neutral curves for the fluids (for fluid 3,
![]() $\unicode[STIX]{x1D70E}$
was set to minimize the error in the neutral curve). Coloured areas: range of numerical results corresponding to the
$\unicode[STIX]{x1D70E}$
was set to minimize the error in the neutral curve). Coloured areas: range of numerical results corresponding to the
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}=0.5^{\circ }$
uncertainty (except for fluid 1, where
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}=0.5^{\circ }$
uncertainty (except for fluid 1, where
![]() $\unicode[STIX]{x1D719}\in [0.25^{\circ },1^{\circ }]$
). (c) Wave celerity
$\unicode[STIX]{x1D719}\in [0.25^{\circ },1^{\circ }]$
). (c) Wave celerity
![]() $c$
to surface velocity
$c$
to surface velocity
![]() $U_{0}$
ratio as a function of
$U_{0}$
ratio as a function of
![]() $\mathit{Re}$
. Coloured solid lines: numerically obtained wave celerity. The critical threshold values are reached numerically for
$\mathit{Re}$
. Coloured solid lines: numerically obtained wave celerity. The critical threshold values are reached numerically for
![]() $k\rightarrow 0$
(solid circles). Dashed line: Newtonian limit
$k\rightarrow 0$
(solid circles). Dashed line: Newtonian limit
![]() $c/U_{0}=2$
. Solid lines: power-law fluid limit
$c/U_{0}=2$
. Solid lines: power-law fluid limit
![]() $c/U_{0}=1+1/n$
.
$c/U_{0}=1+1/n$
.
4 Primary instability in the shear-thinning case
Before presenting the experimental stability measurements for shear-thinning fluids, we dedicate a few words to the numerical resolution of the Orr–Sommerfeld equation with which they will be compared. In the study of Rousset et al. (Reference Rousset, Millet, Botton and Ben Hadid2007), a steady uniform flow is considered (flow rate
![]() $q$
, channel width
$q$
, channel width
![]() $W_{ch}$
, inclination angle
$W_{ch}$
, inclination angle
![]() $\unicode[STIX]{x1D719}$
), and the linear stability equations are derived. These equations are set in dimensionless form using the characteristic scalings one would find for a Newtonian fluid of viscosity
$\unicode[STIX]{x1D719}$
), and the linear stability equations are derived. These equations are set in dimensionless form using the characteristic scalings one would find for a Newtonian fluid of viscosity
![]() $\unicode[STIX]{x1D702}_{0}$
(the zero-shear viscosity of the Carreau fluid): a length scale
$\unicode[STIX]{x1D702}_{0}$
(the zero-shear viscosity of the Carreau fluid): a length scale
![]() $d_{s}=(\unicode[STIX]{x1D702}_{0}q/\unicode[STIX]{x1D70C}gW_{ch}\sin \unicode[STIX]{x1D719})^{1/3}$
, a velocity scale
$d_{s}=(\unicode[STIX]{x1D702}_{0}q/\unicode[STIX]{x1D70C}gW_{ch}\sin \unicode[STIX]{x1D719})^{1/3}$
, a velocity scale
![]() $v_{s}=(q/W_{ch}d_{s})$
and a shear-rate scale
$v_{s}=(q/W_{ch}d_{s})$
and a shear-rate scale
![]() $\dot{\unicode[STIX]{x1D6FE}}_{s}=d_{s}/v_{s}$
. In particular, the dimensionless Carreau law is expressed as
$\dot{\unicode[STIX]{x1D6FE}}_{s}=d_{s}/v_{s}$
. In particular, the dimensionless Carreau law is expressed as
with
![]() $I=\unicode[STIX]{x1D702}_{\infty }/\unicode[STIX]{x1D702}_{0}$
,
$I=\unicode[STIX]{x1D702}_{\infty }/\unicode[STIX]{x1D702}_{0}$
,
![]() $L=q/W_{ch}\dot{\unicode[STIX]{x1D6FE}}_{c}d_{s}^{2}$
and
$L=q/W_{ch}\dot{\unicode[STIX]{x1D6FE}}_{c}d_{s}^{2}$
and
![]() $\dot{\unicode[STIX]{x1D6E4}}=\dot{\unicode[STIX]{x1D6FE}}W_{ch}d_{s}^{2}/q$
. Then, the perturbation growth rates are numerically calculated, which eventually gives the neutral curve and the critical Reynolds number. We want to emphasize that the parameter
$\dot{\unicode[STIX]{x1D6E4}}=\dot{\unicode[STIX]{x1D6FE}}W_{ch}d_{s}^{2}/q$
. Then, the perturbation growth rates are numerically calculated, which eventually gives the neutral curve and the critical Reynolds number. We want to emphasize that the parameter
![]() $L$
has an important impact on the numerical results: when
$L$
has an important impact on the numerical results: when
![]() $L$
is too large, the numerical solution becomes difficult, whereas when
$L$
is too large, the numerical solution becomes difficult, whereas when
![]() $L$
is too small, the difference from a Newtonian fluid becomes negligible. Because of this constraint, we chose to perform experiments at parameters corresponding to acceptable values of
$L$
is too small, the difference from a Newtonian fluid becomes negligible. Because of this constraint, we chose to perform experiments at parameters corresponding to acceptable values of
![]() $L$
, i.e. for which the estimated typical shear rate
$L$
, i.e. for which the estimated typical shear rate
![]() $\dot{\unicode[STIX]{x1D6FE}}_{s}$
was above the critical shear rate of the Carreau law
$\dot{\unicode[STIX]{x1D6FE}}_{s}$
was above the critical shear rate of the Carreau law
![]() $\dot{\unicode[STIX]{x1D6FE}}_{c}$
while staying of the same order of magnitude,
$\dot{\unicode[STIX]{x1D6FE}}_{c}$
while staying of the same order of magnitude,
![]() $\dot{\unicode[STIX]{x1D6FE}}_{s}\gtrsim \dot{\unicode[STIX]{x1D6FE}}_{c}$
. To achieve this, we operated each fluid at a chosen angle. Small
$\dot{\unicode[STIX]{x1D6FE}}_{s}\gtrsim \dot{\unicode[STIX]{x1D6FE}}_{c}$
. To achieve this, we operated each fluid at a chosen angle. Small
![]() $\dot{\unicode[STIX]{x1D6FE}}_{c}$
required small angles, and we chose the following values:
$\dot{\unicode[STIX]{x1D6FE}}_{c}$
required small angles, and we chose the following values:
![]() $\unicode[STIX]{x1D719}=0.5^{\circ }$
,
$\unicode[STIX]{x1D719}=0.5^{\circ }$
,
![]() $\unicode[STIX]{x1D719}=3.5^{\circ }$
and
$\unicode[STIX]{x1D719}=3.5^{\circ }$
and
![]() $\unicode[STIX]{x1D719}=6.5^{\circ }$
for fluids
$\unicode[STIX]{x1D719}=6.5^{\circ }$
for fluids
![]() $1$
,
$1$
,
![]() $2$
and
$2$
and
![]() $3$
respectively. As we can see on the rheograms of figure 2(b), the typical shear rates of our experiments satisfy our condition.
$3$
respectively. As we can see on the rheograms of figure 2(b), the typical shear rates of our experiments satisfy our condition.
Table 2. Critical Reynolds numbers found with different methods. Explanations are given in the text.

Our measurements followed the same protocol as described in the previous section: we measured the stability threshold for different flow rates in order to deduce the critical Reynolds number
![]() $Re_{c}$
. Figure 4(a) shows the experimental stability thresholds for fluids
$Re_{c}$
. Figure 4(a) shows the experimental stability thresholds for fluids
![]() $1$
,
$1$
,
![]() $2$
and
$2$
and
![]() $3$
at their inclination angles, in the
$3$
at their inclination angles, in the
![]() $(Re,f_{c})$
plane. Again, we find that the neutral frequency varies as a square root expression. We can then fit (3.1) to our data and extract a critical Reynolds number. The extracted values are given in table 2 and are found to be significantly smaller than in the Newtonian case. In figure 4(b), we present together the experimental thresholds (symbols) and the thresholds computed from the Orr–Sommerfeld equation resolution (solid lines). The computational neutral curves fit the experimental points very well and the numerically computed critical Reynolds number is very close to the one extracted from the experiments (see table 2). The Newtonian case thresholds given by (3.2) are plotted as empty stars. The theoretical thresholds obtained by Ng & Mei (Reference Ng and Mei1994) with a power-law fluid and Ruyer-Quil et al. (Reference Ruyer-Quil, Chakraborty and Dandapat2012) with a regularized power-law fluid are respectively plotted as black dots and empty diamonds.
$(Re,f_{c})$
plane. Again, we find that the neutral frequency varies as a square root expression. We can then fit (3.1) to our data and extract a critical Reynolds number. The extracted values are given in table 2 and are found to be significantly smaller than in the Newtonian case. In figure 4(b), we present together the experimental thresholds (symbols) and the thresholds computed from the Orr–Sommerfeld equation resolution (solid lines). The computational neutral curves fit the experimental points very well and the numerically computed critical Reynolds number is very close to the one extracted from the experiments (see table 2). The Newtonian case thresholds given by (3.2) are plotted as empty stars. The theoretical thresholds obtained by Ng & Mei (Reference Ng and Mei1994) with a power-law fluid and Ruyer-Quil et al. (Reference Ruyer-Quil, Chakraborty and Dandapat2012) with a regularized power-law fluid are respectively plotted as black dots and empty diamonds.
The first outcome of these results is experimental evidence of the destabilizing effect of the shear-thinning property: in all three fluids, the critical Reynolds number is lower than in the corresponding Newtonian case, and the effect is more pronounced when the shear-thinning is important, as for fluid 1. We can also state that the critical Reynolds numbers we found, both experimentally and numerically, correspond very well to the values predicted by the theory of Ruyer-Quil et al. (Reference Ruyer-Quil, Chakraborty and Dandapat2012) (long-wave expansion method for a power-law fluid regularized at low shear rates). They also correspond well to the values obtained with the model of Ng & Mei (Reference Ng and Mei1994). Finally, we want to point out that the effect of the width of the channel here is perfectly captured by the correction proposed by Georgantaki et al. (Reference Georgantaki, Vatteville, Vlachogiannis and Bontozoglou2011): for fluid 1, we have
![]() $Re_{c}/R^{\ast }=35.3$
and for fluid 2,
$Re_{c}/R^{\ast }=35.3$
and for fluid 2,
![]() $Re_{c}/R^{\ast }=11.7$
(for
$Re_{c}/R^{\ast }=11.7$
(for
![]() $Ka=306$
and
$Ka=306$
and
![]() $Ka=123$
respectively), which compare very well with the Orr–Sommerfeld values given in table 2. This is possibly due to the shear-thinning property, which makes the viscosity at the sides of the channel less important than for the corresponding Newtonian fluid.
$Ka=123$
respectively), which compare very well with the Orr–Sommerfeld values given in table 2. This is possibly due to the shear-thinning property, which makes the viscosity at the sides of the channel less important than for the corresponding Newtonian fluid.
Finally, figure 4(c) shows the wave phase speed
![]() $c=2\unicode[STIX]{x03C0}f_{c}/k$
, rescaled by the surface velocity
$c=2\unicode[STIX]{x03C0}f_{c}/k$
, rescaled by the surface velocity
![]() $U_{0}$
(
$U_{0}$
(
![]() $U_{0}$
is calculated from
$U_{0}$
is calculated from
![]() $q$
,
$q$
,
![]() $\unicode[STIX]{x1D719}$
and the rheology of the fluid). Again, we compare the measurements with the numerical results from the Orr–Sommerfeld formulation. The rescaled phase speed asymptotically reaches a maximum value at the stability threshold, i.e. for
$\unicode[STIX]{x1D719}$
and the rheology of the fluid). Again, we compare the measurements with the numerical results from the Orr–Sommerfeld formulation. The rescaled phase speed asymptotically reaches a maximum value at the stability threshold, i.e. for
![]() $k\rightarrow 0$
and
$k\rightarrow 0$
and
![]() $Re\rightarrow Re_{c}$
. As expected from Millet et al. (Reference Millet, Botton, Rousset and Ben Hadid2008), this maximum value is bounded within an interval of
$Re\rightarrow Re_{c}$
. As expected from Millet et al. (Reference Millet, Botton, Rousset and Ben Hadid2008), this maximum value is bounded within an interval of
![]() $c/U_{0}\in [2,(1+1/n)]$
, corresponding to the Newtonian and power-law limit cases of the Carreau model. It should be noted that the power-law limit is reached in the case of fluid 1 since its shear-thinning properties are much stronger.
$c/U_{0}\in [2,(1+1/n)]$
, corresponding to the Newtonian and power-law limit cases of the Carreau model. It should be noted that the power-law limit is reached in the case of fluid 1 since its shear-thinning properties are much stronger.
Presented in these axes, the experimental data are noisier than in figure 4(a,b), mostly because the scale of variation of
![]() $c/U_{0}$
is very narrow, and therefore very sensitive to the error, but also because it cumulates uncertainties present in the
$c/U_{0}$
is very narrow, and therefore very sensitive to the error, but also because it cumulates uncertainties present in the
![]() $f_{c}$
and
$f_{c}$
and
![]() $k$
independent measurements, and on the parameters to be used in the numerical evaluation of
$k$
independent measurements, and on the parameters to be used in the numerical evaluation of
![]() $U_{0}$
. However, the agreement between experiments and computations is still good.
$U_{0}$
. However, the agreement between experiments and computations is still good.
The obtained overall picture is consistent with the destabilizing effect observed in figure 4(b): the phase speed to free-surface velocity ratio
![]() $c/U_{0}$
reaches values larger than 2 (the Newtonian value) at the threshold, and is larger when the shear-thinning is more pronounced. However, despite its ability to produce the correct critical Reynolds number, the power-law rheology model is not as good at predicting the critical wave phase speed, since the derived
$c/U_{0}$
reaches values larger than 2 (the Newtonian value) at the threshold, and is larger when the shear-thinning is more pronounced. However, despite its ability to produce the correct critical Reynolds number, the power-law rheology model is not as good at predicting the critical wave phase speed, since the derived
![]() $c/U_{0}$
value does not reach the maximum value of
$c/U_{0}$
value does not reach the maximum value of
![]() $(1+1/n)$
for fluids 2 and 3.
$(1+1/n)$
for fluids 2 and 3.
5 Conclusion
In this study, stability experiments on film flows down an incline have been made for weakly to moderately shear-thinning fluids at fixed inclination angles. The results in terms of neutral curves and critical Reynolds number have been plotted in the
![]() $(Re,f_{c})$
,
$(Re,f_{c})$
,
![]() $(Re,k)$
and
$(Re,k)$
and
![]() $(Re,c/U_{0})$
planes, and are in good agreement with the numerical results obtained by either a full resolution of the generalized Orr–Sommerfeld equation or asymptotic expressions for the critical Reynolds number found in the literature under the long-wave expansion theory. Measurements of marginal wavelengths near the threshold remain difficult (
$(Re,c/U_{0})$
planes, and are in good agreement with the numerical results obtained by either a full resolution of the generalized Orr–Sommerfeld equation or asymptotic expressions for the critical Reynolds number found in the literature under the long-wave expansion theory. Measurements of marginal wavelengths near the threshold remain difficult (
![]() $f<1~\text{Hz}$
;
$f<1~\text{Hz}$
;
![]() $\unicode[STIX]{x1D706}>20~\text{cm}$
), and their uncertainties affect the results for the critical wave celerity. The probable stabilizing effect of the channel width appears to be weak in the presented experimental runs. To the best of our knowledge, this work is the first experimental measurement of the destabilizing effect induced by the shear-thinning behaviour on liquid films flowing down an inclined plane: at a given slope, the critical Reynolds number is lower and the rescaled phase speed is higher than for a Newtonian fluid.
$\unicode[STIX]{x1D706}>20~\text{cm}$
), and their uncertainties affect the results for the critical wave celerity. The probable stabilizing effect of the channel width appears to be weak in the presented experimental runs. To the best of our knowledge, this work is the first experimental measurement of the destabilizing effect induced by the shear-thinning behaviour on liquid films flowing down an inclined plane: at a given slope, the critical Reynolds number is lower and the rescaled phase speed is higher than for a Newtonian fluid.