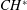1 Introduction
Turbulent combustors in gas turbine engines have been at the heart of the power and propulsion industries. However, the development of such practical devices is afflicted by large-amplitude acoustic oscillations, better known as thermoacoustic instability. These oscillations manifest as a result of the nonlinear coupling between the flame dynamics and the acoustic field in the combustor (Lieuwen & Yang Reference Lieuwen and Yang2005). Such high-amplitude oscillations are undesirable and are detrimental to the performance and the lifespan of the engine. The dynamics of the transition from stable operation to thermoacoustic instability has been the subject of intense research, as thermoacoustic instability has led to disastrous consequences such as failure of space rockets (Fisher & Rahman Reference Fisher and Rahman2009) and gas turbine power plants (Lieuwen & Yang Reference Lieuwen and Yang2005).
Thermoacoustic instability is established through an interaction of the acoustic waves in a confinement and the rate of heat released from the flame. This flame–acoustic interaction has been studied using simpler configurations by many researchers. Searby (Reference Searby1992) experimentally showed the distinct regimes of acoustic instability and corresponding flame shapes by varying the laminar flame velocity of propane–air flames propagating in a vertical tube. Detailed investigations of acoustic instability in premixed flames were performed by Searby & Rochwerger (Reference Searby and Rochwerger1991) and Bychkov (Reference Bychkov1999). The effect of external acoustic perturbation on the response of a flame front has also been studied and the stability limit of the flame was calculated numerically (Searby & Rochwerger Reference Searby and Rochwerger1991) as well as analytically (Bychkov Reference Bychkov1999). In a recent study, Wu & Law (Reference Wu and Law2009) investigated the influence of vortical disturbances on the flame and flame–acoustic coupling. The acoustic field of the confinement has been shown to modify the power-law behaviour of flame acceleration (Akkerman, Law & Bychkov Reference Akkerman, Law and Bychkov2011; Akkerman & Law Reference Akkerman and Law2013) and to trigger the parametric instability (Searby & Rochwerger Reference Searby and Rochwerger1991; Akkerman & Law Reference Akkerman and Law2016). In short, these studies explored flame–acoustic interaction either in a flame forced with external acoustic perturbation or during self-excited thermoacoustic instability; they did not discuss the transition to an impending thermoacoustic instability. On the other hand, the transition to thermoacoustic instability has become the focus of studies on combustion dynamics in recent years.
Traditionally, the onset of thermoacoustic instability was thought of as a Hopf bifurcation (Lieuwen Reference Lieuwen2002). Even though this simple description is valid for laminar systems, for turbulent systems the transition characteristics become rather complicated and a simple description of Hopf bifurcation may not suffice. Recently, studies have been conducted to explore the transition from combustion noise to thermoacoustic instability for turbulent reactive flows from the viewpoint of dynamical systems theory. Nair et al. (Reference Nair, Thampi, Karuppusamy, Gopalan and Sujith2013) suggested that combustion noise is chaotic in nature. Further, using rigorous surrogate analysis, Tony et al. (Reference Tony, Gopalakrishnan, Sreelekha and Sujith2015) reaffirmed this finding. Nevertheless, there have been studies that adopted an alternative viewpoint and described turbulent combustor as a stochastically driven system (Noiray & Schuermans Reference Noiray and Schuermans2013). Nair, Thampi & Sujith (Reference Nair, Thampi and Sujith2014) identified that the transition from combustion noise (aperiodic dynamics) to thermoacoustic instability (periodic dynamics) happens through a dynamical regime called intermittency. Intermittency in thermoacoustic systems was already brought to light by Kabiraj & Sujith (Reference Kabiraj and Sujith2012). Nair & co-workers (Nair et al. Reference Nair, Thampi, Karuppusamy, Gopalan and Sujith2013, Reference Nair, Thampi and Sujith2014; Nair & Sujith Reference Nair and Sujith2014) developed precursors for thermoacoustic instability, by examining measures that detect the presence of intermittent dynamics. Intermittency has also been observed and characterized using the concept of dynamical systems theory in different studies (Gotoda et al. Reference Gotoda, Shinoda, Kobayashi and Okuno2014; Domen et al. Reference Domen, Gotoda, Kuriyama, Okuno and Tachibana2015; Unni & Sujith Reference Unni and Sujith2015; Wilhite et al. Reference Wilhite, Dolan, Gomez, Kabiraj, Paschereit and Gutmark2016).
Most of these studies, however, explored only the temporal dynamics. The spatiotemporal interaction between the heat release rate, the flow and the acoustic field is responsible for the complex dynamics observed temporally. The spatiotemporal dynamics during the occurrence of thermoacoustic instability has been studied from the perspective of flow and flame dynamics in the past. A few studies (Keller et al. Reference Keller, Vaneveld, Korschelt, Hubbard, Ghoniem, Daily and Oppenheim1982; Zukoski & Smith Reference Zukoski and Smith1985; Poinsot et al. Reference Poinsot, Trouve, Veynante, Candel and Esposito1987) discussed the spatiotemporal variation of heat release rate and the emergence of coherent structures during the occurrence of thermoacoustic instability. Zukoski & Smith (Reference Zukoski and Smith1985) showed that, during thermoacoustic instability, large vortical structures are formed with a frequency equal to the frequency of the acoustic mode of the system. Due to these coherent vortices, large velocity fluctuations occur in the reaction zone (Smith Reference Smith1985). However, to date, studies have not focused on describing the spatiotemporal dynamics during the transition to an impending thermoacoustic instability. Here, we present the analysis of the spatiotemporal dynamics during the intermittency route to thermoacoustic instability in a turbulent combustor.
Since the energy required to drive the acoustic field is derived from the field of heat release rate, we study its spatiotemporal dynamics. The objective of this paper is to study the spatiotemporal dynamics during the intermittency route to thermoacoustic instability and describe it both qualitatively and quantitatively. To that end, we view thermoacoustic instability as a problem of synchronization between the acoustic field and the local heat release rate oscillations in the reaction zone. Synchronization, a growing field of research, stemmed from Huygens’ discovery of the phenomenon, and is defined as ‘an adjustment of rhythms of oscillating objects coupled each other’ (Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2003). Synchronization theory (Pikovsky et al. Reference Pikovsky, Rosenblum and Kurths2003) has been used to describe the phenomena in various fields such as physiology (Leon Reference Leon2001), ecology (Blasius, Amit & Lewi Reference Blasius, Amit and Lewi1999) and electrochemistry (Kiss, Vilmos & John Reference Kiss, Vilmos and John2000).
Natural and engineering systems that can be modelled as networks of oscillators coupled with each other in space and time, can be studied under the purview of synchronization. For a long time, researchers have studied the spatiotemporal dynamics and patterns exhibited by such networks of oscillators (Winfree Reference Winfree2001; Kuramoto Reference Kuramoto2012). We adopt the techniques developed for studying the pattern formation in a network of coupled oscillators so as to investigate the spatiotemporal dynamics of the reactive flow field. In a turbulent reacting flow field, the concentration of the reacting mixture at any point in space oscillates with time, not necessarily in a periodic manner (Hubbard & Dowling Reference Hubbard and Dowling1998; Sattelmayer Reference Sattelmayer2003). This results in the temporal oscillations of the reaction rate (and hence the heat release rate) at each spatial location. Having identified the oscillatory nature of heat release rate, we attempt to cast the problem in the form of a network of oscillators that engenders the use of synchronization theory. With this in mind, we turn towards reaction–diffusion systems.
A reaction–diffusion system can be considered as a congregation of a large number of identical local systems that are coupled to each other (Kuramoto Reference Kuramoto2012). For instance, in the Belousov–Zhabotinsky (BZ) reaction, a small element of the solution, isolated by some means from the bulk medium, shows a limit cycle oscillation, and the whole reaction zone can be visualized as a diffusion-coupled system of identical limit cycle oscillators (Tyson Reference Tyson1994). In a similar fashion, we consider the turbulent reactive flow field as a network of coupled oscillators even though the individual oscillatory units are inseparable. However, the individual oscillatory units cannot be assumed identical due to the inherent heterogeneity in experimental systems (Boccaletti et al. Reference Boccaletti, Kurths, Osipov, Valladares and Zhou2002) and due to the complexity of the turbulent flow field. In summary, we consider the turbulent reactive flow field as a network of coupled non-identical oscillatory units. Further, the nature of coupling between local heat release oscillations is complex in a turbulent reactive flow field.
Local heat release rate oscillations are coupled due to convective transport (Lieuwen Reference Lieuwen2012) which includes non-local and delayed coupling. Even though the former statement is qualitatively true, it is very difficult to quantify the coupling strength for each type of coupling in a complex system such as a turbulent combustor. Moreover, molecular mixing between reactants happens only through diffusion process in a combustion chamber, making the diffusive coupling significant. Finally, in a thermoacoustic system, the acoustic field acts as a global coupling. Therefore, the presence of various types of coupling makes this system complex, and hence the inverse problem of separating them is hard to solve. This complex coupling is reflected as both regions of periodicity and regions of aperiodicity, existing simultaneously.
On the other hand, convective coupling can give rise to spatial correlations in heat release rate oscillations. A spatial correlation can be estimated by removing turbulent fluctuations in forced flame dynamics (Shanbhogue et al. Reference Shanbhogue, Shin, Hemchandra, Plaks and Lieuwen2009a ; Thumuluru & Lieuwen Reference Thumuluru and Lieuwen2009). Ensemble averaging of phase-locked data fields is generally adopted to remove the turbulent fluctuations so that one can visualize the mean field clearly. However, at the onset of an impending self-excited thermoacoustic instability, removing turbulent fluctuations by averaging is not possible as, during intermittency, both periodic and aperiodic dynamics are visible, alternating in space and time in an apparently random fashion. Addressing this issue demands a rigorous study to quantify the spatial correlation at the onset of an impending thermoacoustic instability.
The other piece of the puzzle is the acoustic field in the confined chamber, which is intrinsically an oscillator. We then view thermoacoustic instability as synchronization in relative phases between the acoustic pressure and the local heat release rate oscillations in the reaction zone, albeit there is always a three-way coupling between the acoustic field, hydrodynamics (and/or air/fuel ratio fluctuation) and combustion. We have not included the hydrodynamic fluctuation or fuel/air ratio fluctuations in our study. However, establishing synchronization behaviour in the relative phase between hydrodynamic and heat release rate fluctuation can be an interesting study, as mediated by the finding of phase jitter in the location of vortices (Shanbhogue, Seelhorst & Lieuwen Reference Shanbhogue, Seelhorst and Lieuwen2009b ).
We conduct experiments on a backward facing step combustor where a bluff body is used as a flame holding device. Firstly, from the experiments performed, we obtain the two-dimensional (2D) heat release rate field within the combustor by imaging the chemiluminescence (
$CH^{\ast }$
) of the reacting flow field. Simultaneously, the unsteady pressure data is also acquired. Subsequently, for each location (i.e. the discretized locations represented by each pixel of the chemiluminescence image) in the reactive flow field, we calculate the instantaneous phase difference between the heat release rate and the acoustic pressure, obtaining an instantaneous ‘phase field’. This phase field represents the phase distribution of the reactive flow field at a particular instant of time. From the spatiotemporal analysis, we observe that the transition from combustion noise to thermoacoustic instability corresponds to a transition from asynchronous aperiodic oscillations to phase-synchronized periodic oscillations via an intermediate state, where regions of phase asynchrony of aperiodic oscillations and phase synchrony of periodic oscillations coexist simultaneously.
In the context of a system of coupled identical oscillators, as the system transits from an incoherent state to a coherent state, there could be a stable intermediate state in which coherent oscillations coexist with incoherent ones. Such a state was first found in a system of identical oscillators modelled using non-locally coupled complex Ginzburg–Landau equations (Kuramoto & Battogtokh Reference Kuramoto and Battogtokh2002). This state was further characterized and named as ‘chimera state’ by Abrams & Strogatz (Reference Abrams and Strogatz2004), for the idea resembles the Greek mythological monster, chimera, which has a lion’s head, a goat’s body and a serpent’s tail. The spatiotemporal state that we observe in our system during intermittency is similar to a chimera state. However, since the spatially extended oscillators that represent our system may not be identical, we may not strictly consider the spatiotemporal dynamics during intermittency in our system as a chimera state. A network of non-identical oscillators can exhibit various complex phenomena such as frequency locking, phase synchronization, partial synchronization and incoherence (Panaggio & Abrams Reference Panaggio and Abrams2015).
The rest of the paper is organized as follows. The details of the experimental set-up are provided in § 2. We discuss the results in § 3. In § 4, we provide the quantitative characterization of the global phase synchrony using the Kuramoto order parameter (
$R$
). Finally, the major findings are summarized in § 5.
2 Experiments
To conduct the experiments with turbulent reacting flow, we use a backward facing step combustor where a bluff body is used as a flame holding device. The same combustor was used previously by Nair & Sujith (Reference Nair and Sujith2014) and Unni & Sujith (Reference Unni and Sujith2015) for their experiments. The schematic of the combustor is provided in figure 1.
Figure 1. (a) The schematic of the laboratory-scale combustor used for this study. A piezoelectric transducer is used to measure the pressure fluctuations in the combustor. (b) A circular bluff body is used as a flame holding device. For this study, the length of the combustor was fixed at 1400 mm. A quartz window (
$400~\text{mm}\times 90~\text{mm}\times 10~\text{mm}$
) is provided to allow for optical access. The design of this combustor was adapted from Komarek & Polifke (Reference Komarek and Polifke2010).
Air required for combustion enters the settling chamber through the air inlet. The settling chamber is provided to restrict the flow fluctuations in the air inlet from entering the test section. The fuel used in the experiment is liquefied petroleum gas (LPG, 40 % Propane and 60 % Butane). The fuel is introduced to the combustion chamber using the central shaft and is injected 120 mm upstream of the bluff body through four radial injection holes of diameter 1.7 mm. The bluff body is mounted at the end of the central shaft. The bluff body is a circular disk of diameter 47 mm and a thickness of 10 mm. The combustion chamber has a square cross-section (
$90~\text{mm}\times 90~\text{mm}$
) and a length of 1400 mm. The air flow rate (
${\dot{m}}_{a}$
) and fuel flow rates (
${\dot{m}}_{f}$
) are controlled and measured using mass flow controllers (Alicat Scientific, MCR Series, 100 SLPM model for fuel flow, 2000 SLPM model for air flow; uncertainty is
$\pm$
(0.8 % of reading
$+0.2\,\%$
of full scale)). The flow conditions are maintained such that the reactive flow is turbulent (Reynolds number,
$Re=1.09\times 10^{5}$
to
$Re=2.12\times 10^{5}$
) throughout the experiments. The equivalence ratio is estimated as
$\unicode[STIX]{x1D719}=({\dot{m}}_{f}/{\dot{m}}_{a})_{actual}/({\dot{m}}_{f}/{\dot{m}}_{a})_{stoichiometry}$
. The uncertainty in the range of estimated equivalence ratios (
$\unicode[STIX]{x1D719}=1.00$
to 0.54) is
$\pm (0.032\text{ to }0.014)$
. A piezoelectric pressure transducer (PCB103B02, with a sensitivity of
$223.4~\text{mV}~\text{kPa}^{-1}$
and an uncertainty
$\pm 0.15~\text{Pa}$
) is used to measure the dynamic pressure within the combustion chamber. A spark plug (along with an 11 kV ignition transformer – National Engineering Corporation) is used to ignite the combustible air–fuel mixture. The pressure transducer is mounted on the sidewall of the combustor 20 mm away from the dump plane. A quartz window is provided in the combustor (
$400~\text{mm}\times 90~\text{mm}\times 10~\text{mm}$
) that enables optical access to the combustion chamber. High-speed images of flame dynamics (applying a
$CH^{\ast }$
filter, narrowband, peak at 432 nm, 10 nm FWHM) are captured using a Phantom v12.1 high-speed camera (pixel resolution of
$592\times 256$
; grey scale resolution of
$12~\text{bits}~\text{pixel}^{-1}$
) simultaneously with the pressure measurements. The data was acquired for 3 s at a sampling frequency of 2 kHz, using a 16-bit analog to digital conversion card (NI-6143).
3 Results and discussion
We present the time series of dynamic pressure in figure 2 to familiarize the readers with the system’s temporal dynamics. Temporally, a thermoacoustic system with turbulent reactive flow transitions from combustion noise to thermoacoustic instability via intermittency as we vary the equivalence ratio from stoichiometry to lean conditions (Nair et al. Reference Nair, Thampi and Sujith2014). The equivalence ratio is varied by changing the air flow rate, while the fuel flow rate is maintained constant. This ensures that the thermal power of the combustor remains constant across different equivalence ratios.
For higher equivalence ratios (near stoichiometric in our experiments), the time series of acoustic pressure from the thermoacoustic system exhibits low-amplitude irregular pressure fluctuations (see figure 2
a, for
$\unicode[STIX]{x1D719}=0.98$
), which is known as combustion noise (Strahle Reference Strahle1978). This state corresponds to the stable operating regime for the combustor. With decreasing
$\unicode[STIX]{x1D719}$
, the combustor exhibits a transition from combustion noise (figure 2
a) to limit cycle oscillation (for
$\unicode[STIX]{x1D719}=0.58$
in figure 2
c) via intermittency (for
$\unicode[STIX]{x1D719}=0.72$
in figure 2
b). Large-amplitude periodic pressure oscillations occur during thermoacoustic instability (figure 2
c). In contrast to combustion noise and thermoacoustic instability (limit cycle oscillations), during intermittency, bursts of high-amplitude periodic oscillations occur amidst regions of low-amplitude aperiodic fluctuations (figure 2
b). This intermittency route to thermoacoustic instability in turbulent combustors has been reported by many researchers (Gotoda et al.
Reference Gotoda, Shinoda, Kobayashi and Okuno2014; Nair Reference Nair2014; Nair et al.
Reference Nair, Thampi and Sujith2014; Domen et al.
Reference Domen, Gotoda, Kuriyama, Okuno and Tachibana2015; Wilhite et al.
Reference Wilhite, Dolan, Gomez, Kabiraj, Paschereit and Gutmark2016).
Figure 2. Time series of dynamic pressure obtained from experiments for different equivalence ratios (
$\unicode[STIX]{x1D719}$
) during (a) combustion noise (
$\unicode[STIX]{x1D719}=0.98$
), (b) intermittency (
$\unicode[STIX]{x1D719}=0.72$
) and (c) thermoacoustic instability (
$\unicode[STIX]{x1D719}=0.58$
). At an equivalence ratio of 0.98, the pressure fluctuations are aperiodic and have low amplitude. The equivalence ratio is reduced by increasing the air flow rate, keeping the fuel flow rate fixed. At an equivalence ratio of 0.72, we observe intermittency where the bursts of periodic pressure oscillations appear in an apparently random manner amongst aperiodic pressure fluctuations. On further reduction of equivalence ratio to 0.58, we observe periodic behaviour in the pressure fluctuations.
We study the spatiotemporal characteristics during the transition to thermoacoustic instability by analysing the high-speed chemiluminescence (
$CH^{\ast }$
) images of the combustion zone.
$CH^{\ast }$
intensity is considered to be a signature of the chemical reaction rate, and hence of the heat release rate from the flame (Hardalupas & Orain Reference Hardalupas and Orain2004; Guethe et al.
Reference Guethe, Guyot, Singla, Noiray and Schuermans2012). Although the phenomenon inside the turbulent reactive field is three dimensional, we analyse it in two dimensions by imaging the central plane of the combustor (mentioned as the focal plane in figure 1) with a depth of focus of
$9~\text{mm}$
(while the width of the combustor is
$90~\text{mm}$
). The intensity (
$CH^{\ast }$
) of the chemiluminescence images is then post-processed along with the unsteady pressure data in order to analyse the spatiotemporal dynamics of the reaction zone.
The unsteady pressure,
$P^{\prime }(t)$
is measured at a single point along the combustor wall. Lieuwen & Zinn (Reference Lieuwen and Zinn2000) have shown that if the length scale of the combustion zone is much less than the acoustic length scale, pressure variation across the flame is small. For the combustor used for this study, Nair (Reference Nair2014) has confirmed this experimentally. Hence we can assume that the acoustic pressure along the reaction zone is nearly uniform. Further, the chemiluminescence images represent the field of unsteady heat release rate,
$\dot{q}^{\prime }(x,y,t)$
. We then evaluate the instantaneous phase difference (henceforth called instantaneous phase) between the unsteady heat release rate,
$\dot{q}^{\prime }(x,y,t)$
and unsteady pressure,
$P^{\prime }(t)$
. Here, we write the signals,
$\dot{q}^{\prime }(x,y,t)$
and
$P^{\prime }(t)$
in terms of their amplitude and phase using Hilbert transform (Madjarova, Kadono & Toyooka Reference Madjarova, Kadono and Toyooka2003) and calculate the instantaneous phase between
$\dot{q}^{\prime }(x,y,t)$
and
$P^{\prime }(t)$
. In short, phase is defined as the difference in instantaneous phase between the acoustic pressure and the heat release rate oscillations, unlike the definition given in Lieuwen (Reference Lieuwen2001). He has shown drifting of phase in course of time, defining phase as the difference in instantaneous phase between pressure oscillations and a sinusoid having an amplitude the same as the averaged amplitude of pressure signal and frequency as the dominant frequency of the pressure signal.
For the present analysis, we calculate the instantaneous phase of a signal through Hilbert transform (HT), which is a widely used approach to calculate the instantaneous phase in synchronization literature. However, for the interpretation of the calculated quantity using HT as phase, the trajectories of the signal in the analytic plane must go around a fixed centre (Romano et al. Reference Romano, Thiel, Kurths, Kiss and Hudson2005). For an aperiodic signal with a broadband power spectrum or a non-stationary signal, it is difficult to find a unique centre of rotation in the analytic plane. Therefore, for such signals, the quantity computed using Hilbert transform, in principle, cannot strictly be interpreted as the phase of the signal. During limit cycle oscillations, there is a unique centre of rotation in the analytic plane. Therefore, we can interpret the quantity calculated using HT as phase. However, we use the phase of analytic signal computed using HT in our subsequent analysis so that we can visualize how the field of phase from HT changes during the transition from combustion noise to thermoacoustic instability. We further substantiate our results with other approaches prescribed in the literature (appendix A).
Typical instantaneous phase fields for different dynamical states are shown in figure 3. The instantaneous phase fields show interesting patterns for the different equivalence ratios during the transition to thermoacoustic instability. In figure 3(a), the phase pattern is shown for a condition where the reactive flow system produces broadband combustion noise. The grainy nature of the instantaneous phase field shows the asynchrony in the heat release rate field.
Figure 3. Typical instantaneous phase (between the heat release rate and the acoustic pressure) fields for (a) an instant during the occurrence of combustion noise at
$\unicode[STIX]{x1D719}=0.98$
, (b) at a time instant of low-amplitude aperiodic pressure oscillation during intermittency at
$\unicode[STIX]{x1D719}=0.72$
, (c) at a time instant of an intermittent burst of periodic oscillations during intermittency at
$\unicode[STIX]{x1D719}=0.72$
and (d) an instant during thermoacoustic instability at
$\unicode[STIX]{x1D719}=0.58$
. The grainy nature in (a) shows the asynchrony in the heat release rate field whereas, during the occurrence of thermoacoustic instability (d), the field of local heat release rate is nearly coherent. During intermittency (b and c), regions of synchrony and asynchrony coexist. Synchronous regions of heat release rate during high-amplitude bursts (c) are mostly ‘in phase’ (light colours) with pressure.
Due to this asynchronous behaviour of the heat release rate at different spatial locations, the overall amplitude of the acoustic pressure does not grow, and manifests as low-amplitude aperiodic oscillations in the time series of acoustic pressure (figure 2 a). This incoherence can be attributed to the presence of turbulence in the system. The inhomogeneities in the flow field caused by turbulence can cause incoherent fluctuations in the local heat release rate (Abugov & Obrezkov Reference Abugov and Obrezkov1978). The loss of spatial correlation in a flow field due to turbulence has already been observed by Chaté & Manneville (Reference Chaté and Manneville1987).
During the occurrence of intermittency, the time series of acoustic pressure shows an apparently randomly occurring alternate sequence of low-amplitude aperiodic oscillations and high-amplitude bursts of periodic oscillations (figure 2
b). To examine this phenomena, typical instantaneous phase fields at the time instant of low-amplitude aperiodic oscillations and high-amplitude bursts of periodic oscillations during intermittency are shown in figures 3(b) and 3(c), respectively. In these figures, similar to the coexistence of high-amplitude periodic and low-amplitude aperiodic pressure oscillation in time series, a few phase-synchronized regions of oscillating heat release rate coexist with regions of phase asynchrony (figures 3
b and 3
c). The difference in phase pattern during high- and low-amplitude oscillations of intermittency remains in the phase values of the synchronous regions. In synchronous regions, we find phase values between
$-\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}/2$
at the time instant of high-amplitude bursts (figure 3
c) during intermittency. We will discuss this further in connection with the Rayleigh criterion. Typical phase pattern during the occurrence of thermoacoustic instability shows that the field of local heat release rate is nearly coherent (3
d).
According to the Rayleigh criterion, driving of the acoustic field happens when the instantaneous phase between heat release rate and acoustic pressure lies between
$-\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}/2$
radians (Culick Reference Culick1987; Lieuwen & Yang Reference Lieuwen and Yang2005). In other words, the ‘in-phase’ regions (light colours in figure 3) in the instantaneous phase fields act as the sources of acoustic driving, whereas the ‘out of phase’ regions (dark colours in figure 3) act as sinks for the acoustic energy. During the occurrence of combustion noise, the instantaneous phases are incoherently distributed over the reaction zone (figure 3
a). The region of phase incoherence makes the net acoustic driving small. In other words, the net energy pumped into the acoustic field is low, and hence a coherent acoustic field is not formed during the occurrence of combustion noise. As a result, combustion noise is aperiodic and has low amplitude (figure 2
a), compared to the periodic pressure fluctuations obtained during thermoacoustic instability (figure 2
c), where the coherent regions are nearly ‘in phase’. The driving from these ‘in-phase’ coherent regions is adequate to overcome the damping from ‘out of phase’ regions, from the boundaries, and the viscous damping, leading to thermoacoustic instability (figure 3
c). Further, we note that even in the case of limit cycle oscillations (thermoacoustic instability) there are a few desynchronized patches, possibly due to the presence of turbulence. Since the Rayleigh criterion is satisfied, a positive feedback loop between the heat release rate and the pressure oscillation is established. This results in high-amplitude periodic oscillations during thermoacoustic instability.
On other hand, during intermittency, the coexistence of phase synchrony and phase asynchrony in the reaction zone is apparent. During low amplitude aperiodic pressure oscillations, the heat release zone is dominated by regions of phase asynchrony and we have large regions where
$P^{\prime }$
and
$\dot{q}^{\prime }$
are ‘out of phase’ (figure 3
b). In contrast, during bursts of periodic oscillations, the heat release zone is mostly dominated by coherent regions which are nearly ‘in phase’ (figure 3
c). When there are ‘in-phase’ coherent regions in the heat release zone, positive driving causes intermittent periodic bursts. Whereas, at other instances during intermittency, due to the presence of prevailing incoherent regions, the system starts to exhibit low-amplitude aperiodic oscillations.
Figure 4. Instantaneous phasor fields showing emergent order from phase turbulence. Distinct patterns are seen at different
$\unicode[STIX]{x1D719}$
. Typical snapshots of phasor fields are shown at arbitrarily chosen time instants. The phase asynchrony at high
$\unicode[STIX]{x1D719}$
(a,
$\unicode[STIX]{x1D719}=0.98$
) is evident from the randomly oriented phasors, whereas at sufficiently low value of
$\unicode[STIX]{x1D719}$
(c,
$\unicode[STIX]{x1D719}=0.58$
), the phasors are mostly aligned, which confirms the phase synchrony. Most interestingly, at intermediate values of
$\unicode[STIX]{x1D719}$
(b,
$\unicode[STIX]{x1D719}=0.72$
), a group of phasors are aligned and the rest are randomly oriented. This mixed spatial structure, where phase synchrony and phase asynchrony coexist, resembles a chimera state that is found prior to the emergence of order with spatial phase synchrony of a network of identical oscillators.
This transition from disorder (asynchrony) to order (synchrony) with decrease in
$\unicode[STIX]{x1D719}$
is evident in the phasor plots (figure 4), which depict the instantaneous phases with arrows. Phasor plots are drawn with the instantaneous phase between
$\dot{q}^{\prime }$
and
$P^{\prime }$
. We employ unit amplitude for all phasors as we focus only on their alignment. At high
$\unicode[STIX]{x1D719}$
(figure 4
a), the phasors are randomly oriented (incoherence) in the phasor field, indicating spatial asynchrony. This spatial asynchrony, generally known as phase turbulence (Shraiman Reference Shraiman1986), might be due to the inhomogeneity caused by hydrodynamic turbulence in the system. At sufficiently low
$\unicode[STIX]{x1D719}$
(figure 4
c), spatial phase synchrony is seen to emerge. The presence of spatial phase synchrony can be inferred from the alignment of phasors (coherence) to their neighbours. Such an emergence of an ordered state is due to the enhanced positive feedback between the reactive flow and the acoustic field.
We now turn our attention to intermediate equivalence ratios, with a view to explore the route to self-organization. In the considered system, we observe a spatial structure in the phasor plots, where the regions exhibiting phase asynchrony of aperiodic oscillations and the regions exhibiting phase synchrony of periodic oscillations coexist prior to the emergence of spatial phase synchrony (figure 4 b), resembling a chimera state. This mixed spatial structure where synchrony and asynchrony coexist is found to be the characteristic of intermittency, a chimera-like state observed in an ensemble of coupled non-identical oscillators. The situation where the global synchrony in chimera state varies in time is known as breathing chimera (Abrams et al. Reference Abrams, Mirollo, Strogatz and Wiley2008).
Figure 5. Instantaneous phasor fields during the chimera-like state are shown for different instants of time: (a)
$t=0.05~\text{s}$
, (b)
$t=0.1~\text{s}$
, (c)
$t=0.15~\text{s}$
, (d)
$t=0.2~\text{s}$
. By observing the phasor plots, it is apparent that the desynchronized regions in the chimera-like states are changing locations with time, indicating the transition from an aperiodic to a periodic state as they synchronize intermittently.
Instantaneous phasor fields during the chimera-like state are shown for different instants of time in figure 5. We observe that the regions of disordered and ordered phasors change their locations with time. Therefore, desynchronized aperiodic oscillations undergo a transition from an aperiodic to a periodic state as they synchronize intermittently.
Figure 6. Space–time plots (I) and spatial distribution (II) of instantaneous phase for a 1D field. Space,
$x$
corresponds to
$x^{\prime }{-}x^{\prime }$
shown in figure 3(c) indicating the cross-sectional line along which the time evolution of the instantaneous phase is plotted (I) for different dynamical states. The instantaneous phase corresponds to the instantaneous relative phase of the local heat release rate with respect to the dynamic pressure. Phase turbulence is clear from the grainy structure in the space–time plot (a-I) and also from the scattered instantaneous phases in the phase distribution plot (a-II) during combustion noise at high
$\unicode[STIX]{x1D719}$
. At sufficiently low
$\unicode[STIX]{x1D719}$
, the phase synchrony in the ordered state is evident in the space–time plot (c-I) and also from the instantaneous phases congregated around some particular value in the phase distribution plot (c-II) during thermoacoustic instability. At intermediate
$\unicode[STIX]{x1D719}$
, however, the coexistence of regions of phase synchrony and phase asynchrony is observed during intermittency (b-I, b-II).
Further, we present the results obtained using space–time plots and spatial distribution of instantaneous phases for a 1D field. To that end, we choose sections,
$x^{\prime }{-}x^{\prime }$
(figure 6) and
$y^{\prime }{-}y^{\prime }$
(figure 7), which are shown in figure 3(c), indicating the cross-sectional line along which the time evolution and the distribution of the instantaneous phases at a particular instant are plotted. We observe the phase asynchrony, also known as phase turbulence, during combustion noise at high
$\unicode[STIX]{x1D719}$
. Phase turbulence can be inferred from the grainy structure in the space–time plot (figures 6
a-I and 7
a-I). Phase distribution turns out to be scattered (figures 6
a-II and figure 7
a-II) during combustion noise. The asynchrony, continuing in time, leads to low-amplitude pressure fluctuations. In contrast, at low
$\unicode[STIX]{x1D719}$
, spatial phase synchrony is apparent in the space–time plot (figures 6
c-I and 7
c-I). The corresponding time series of unsteady pressure shows limit cycle oscillations during thermoacoustic instability (figure 2
c). Synchrony manifests as a dense phase distribution over the field (figures 6
c-II and 7
c-II).
It is interesting to observe concurrent regions of phase synchrony and asynchrony in the space–time plots (figures 6
b-I and 7
b-I) at intermediate
$\unicode[STIX]{x1D719}$
, resembling a chimera state. The distribution of instantaneous phases (figures 6
b-II and 7
b-II) clearly displays the coexistence of synchrony and asynchrony over the chosen 1D field. Further, the movement of synchronized or desynchronized regions over space and time is also evident from space–time plots (figures 6
b-I and 7
b-I). The phase asynchrony of aperiodic oscillations appears intermittently with time, which corresponds to low amplitude aperiodic pressure oscillations between intermittent bursts. Synchrony in the phase field of heat release rate corresponds to intermittent bursts of periodic oscillations whereas the system returns to low-amplitude aperiodic pressure fluctuations when it exhibits asynchrony in the phase field.
The coexistence of high-amplitude periodic and low-amplitude aperiodic pressure oscillations is found to be the characteristic of the temporal dynamics of intermittency prior to the onset of thermoacoustic instability (Gotoda et al. Reference Gotoda, Shinoda, Kobayashi and Okuno2014; Nair et al. Reference Nair, Thampi and Sujith2014). In the present study, we show that, when the unsteady pressure oscillations exhibit intermittency, the reaction zone exhibits a novel spatiotemporal dynamics. Here, novel spatiotemporal dynamics refers to a dynamic state where the spatially extended system exhibits simultaneous existence of regions of synchronous periodic oscillations and asynchronous aperiodic oscillations, and where the regions of synchronized oscillations at some time become desynchronized at another time and vice versa. Further, during intermittency, ‘in-phase’ synchronous patches causing an increase in acoustic driving emerge out of completely incoherent local heat release rate oscillations at apparently random intervals. Consequently, this intermittent energy transfer to the acoustic field produces bursts of periodic oscillations in the time series of acoustic pressure (figure 2 b).
Figure 7. Space–time plots (I) and spatial distribution (II) of instantaneous phase for 1D field. Space,
$y$
corresponds to
$y^{\prime }{-}y^{\prime }$
shown in figure 3(c) indicating the cross-sectional line along which the time evolution of the instantaneous phase is plotted (I) for different dynamical states. Phase turbulence is clear from the grainy structure in the space–time plot (a-I) and also from the scattered instantaneous phases in the phase distribution plot (a-II) during the combustion noise at high
$\unicode[STIX]{x1D719}$
. (c) At sufficiently low
$\unicode[STIX]{x1D719}$
, the phase synchrony in the ordered state is evident in the space–time plot (c-I) also from the instantaneous phases congregated around some particular value in the phase distribution plot (c-II) during thermoacoustic instability. At intermediate
$\unicode[STIX]{x1D719}$
, however, the coexistence of regions of phase synchrony and phase asynchrony is observed during intermittency (b-I, b-II).
We also show a type of synchronization where the dynamic characteristics of the individual oscillators in the network change from aperiodic to periodic as the network gets synchronized. Generally, it is observed that, while synchronizing, the coupled chaotic or periodic oscillators retain their respective dynamics (Pikovsky et al. Reference Pikovsky, Rosenblum and Kurths2003). In the present study, we find that patches of desynchronized aperiodic oscillations turn into patches of synchronized periodic oscillations and vice versa. Therefore, the dynamics changes from aperiodic to periodic as the heat release oscillations get synchronized intermittently with acoustic pressure.
In short, order with phase synchrony emerges from the disordered turbulent flow through a chimera-like state where regions of disordered and ordered phases are simultaneously present in the field. As this synchrony emerges, the acoustic driving increases, leading to the onset of large-amplitude oscillations that we call thermoacoustic instability.
Intermittency has also been observed in related studies (Emerson et al. Reference Emerson, O’Connor, Juniper and Lieuwen2012; Emerson, Lieuwen & Juniper Reference Emerson, Lieuwen and Juniper2016; Suresha et al. Reference Suresha, Sujith, Emerson and Lieuwen2016) which focused on the transition to global hydrodynamic instability. Further, the intermittency route to periodicity is also observed in Emerson’s study, as in our study. Therefore, we speculate that similar spatiotemporal patterns could be observed in Emerson’s work (Emerson et al. Reference Emerson, O’Connor, Juniper and Lieuwen2012, Reference Emerson, Lieuwen and Juniper2016; Suresha et al. Reference Suresha, Sujith, Emerson and Lieuwen2016). In other words, our present study could possibly be extended to study the onset of hydrodynamics instability and even more general phenomena where emergence of order from disorder occurs in turbulent flow fields in aeroelastic (Trickey, Virgin & Dowell Reference Trickey, Virgin and Dowell2002; Venkatramani et al. Reference Venkatramani, Nair, Sujith, Gupta and Sarkar2016) and aeroacoustic systems (Nair & Sujith Reference Nair and Sujith2016).
Modelling of a thermoacoustic system exhibiting such complex spatiotemporal dynamics would be really interesting. One possibility is to consider an ensemble of narrowband forced oscillators that are spatially connected (Noiray & Schuermans Reference Noiray and Schuermans2013). In this regard, a proper design of coupling will be very crucial.
4 Quantitative characterization of global synchrony
Characterization of global synchrony is needed to confirm the synchronization transition quantitatively at the onset of thermoacoustic instability. Synchronization transition, wherein the network of coupled oscillators gets eventually synchronized, is analogous to thermodynamic phase transition. Kuramoto (Reference Kuramoto2012) developed an order parameter to quantify synchronization transition. In the context of thermodynamics, an order parameter amounts to the degree of order in a system during phase transition. It varies from zero to one. To measure the global synchrony of the phase field, we calculate the Kuramoto order parameter (
$R$
) as,
$$\begin{eqnarray}R(t)=N^{-1}\left|\mathop{\sum }_{j=1}^{N}\text{e}^{\text{i}\unicode[STIX]{x1D703}_{j}(t)}\right|,\end{eqnarray}$$
where
$R(t)$
is the order parameter at time
$t$
,
$\unicode[STIX]{x1D703}_{j}(t)$
is the phase of
$j\text{th}$
oscillator (here, the spatial location in the field) at time
$t$
and
$N$
is total number of oscillators in the network. The Kuramoto order parameter is a good indicator of transition in global synchrony (Arumugam & Spano Reference Arumugam and Spano2015).
We can associate each
$\text{e}^{\text{i}\unicode[STIX]{x1D703}_{j}(t)}$
term in (4.1) to a vector lying on the unit circle in the complex plane.
$R$
, then, is a measure of the resultant of these vectors normalized with the total number of vectors. The vectors being distributed uniformly inside the circle is indicative of a disordered state and, correspondingly,
$R$
is close to zero. On the other hand, for a synchronized state, they are all aligned in one direction, leading to a value of
$R$
close to 1. In other words, a mean value of
$R(t)$
close to one implies a perfectly ordered state, while a value close to zero indicates a perfectly disordered state.
Figure 8. Time series of the Kuramoto order parameter (
$R$
), indicating the variation of global phase synchrony during (a) combustion noise, (b) intermittency and (c) thermoacoustic instability. Corresponding mean (
$\bar{R}$
) and variance (
$\unicode[STIX]{x1D70E}^{2}$
) of
$R$
are shown. The fluctuations in
$R$
are evident in all the cases examined during the transition. The increase in mean value (
$\bar{R}$
) with decrease in
$\unicode[STIX]{x1D719}$
(a–c), shows a transition from disorder to order. Maximum variance is achieved during intermittency (b), mimicking a breathing chimera. The breathing nature is also confirmed by plotting the time series of
$\cos (\unicode[STIX]{x1D703}_{j})$
at intermediate values of
$\unicode[STIX]{x1D719}$
for randomly chosen spatial locations in the combustion zone. Different colours are used for different spatial locations.
The time series of the order parameter are presented for combustion noise (figure 8
a), intermittency (figures 8
b), and thermoacoustic instability (figure 8
c). The mean (
$\bar{R}$
) and variance (
$\unicode[STIX]{x1D70E}^{2}$
) of
$R$
are also mentioned in the plot. For all the flow conditions we consider, the fluctuations in
$R$
are evident. These fluctuations are likely to be a result of turbulence in the flow. However, an increase in time-averaged
$\bar{R}$
with the increase in the control parameter (
$\unicode[STIX]{x1D719}$
) is indicative of a transition from disorder to order (figure 8). Further, in figure 9(a), the variation of
$\bar{R}$
with equivalence ratio is plotted for the entire range of investigation. Figure 9(a) shows the growth in global synchrony quantitatively at the onset of thermoacoustic instability.
Figure 9. (a) Mean (
$\bar{R}$
) and (b) variance (
$\unicode[STIX]{x1D70E}^{2}$
) of
$R$
are plotted with the equivalence ratios examined. The growth in the order parameter indicates the emergence of global synchrony at the onset of thermoacoustic instability. Higher fluctuation indicated by higher
$\unicode[STIX]{x1D70E}^{2}$
is observed during intermittency, pointing out the breathing nature of the chimera-like state.
We obtain the value of
$\bar{R}$
during thermoacoustic instability as 0.64. This is not close to 1 because of the following reasons. There exists turbulent fluctuations even in the ordered state. Further, looking at figure 4(c), one can note that even at the ordered state, all phasors in the flow field are not in the same direction. Rather, they are locally synchronized. Both these aspects result in the lower value of
$\bar{R}$
. On the other hand, the fluctuations in
$R$
, measured through variance (
$\unicode[STIX]{x1D70E}^{2}$
), tends to become lower when the system is in an ordered or disordered state (figure 9
b). However, prior to the ordered state, we observe huge fluctuations in
$R$
, which are larger by almost an order when compared to the ordered and the disordered states (figures 8
b and 9
b). These large fluctuations in the order parameter allude the breathing nature of the chimera-like states (Abrams et al.
Reference Abrams, Mirollo, Strogatz and Wiley2008). To confirm this, we also plot the time series of
$\cos (\unicode[STIX]{x1D703}_{j})$
for a few arbitrarily chosen spatial locations (locations are not shown here) in the field (figure 8
b). The phase synchrony (indicated by overlapping time series) and asynchrony (indicated by non-overlapping time series) appear at different time instants in this time series, reaffirming the breathing nature of the chimera-like state.
5 Conclusion
The spatiotemporal dynamics during the transition from combustion noise to thermoacoustic instability via intermittency in a turbulent combustor is investigated in this study. To that end, we examine the phases between acoustic pressure and local heat release rate oscillations. Combustion noise corresponds to a state of phase asynchronous aperiodic oscillations whereas phase synchronous periodic oscillations are observed during thermoacoustic instability. As this synchrony emerges, the acoustic driving increases, leading to the onset of thermoacoustic instability. Interestingly, this transition happens through an intermediate state where regions of phase asynchronous aperiodic oscillations and regions of phase synchronous periodic oscillations coexist simultaneously, similar to the chimera state observed in a network of coupled identical oscillators. We also show a type of synchronization where the dynamic characteristics of the individual oscillators in the network change from aperiodic to periodic as the network gets synchronized.
During the occurrence of a chimera-like state, the synchronous and asynchronous regions are observed to change their locations in the reaction zone, being qualitatively similar to a ‘breathing chimera’. The breathing nature of the chimera-like state is further quantified through the Kuramoto order parameter. This order parameter indicates the synchronization transition at the onset of thermoacoustic instability as the mean value of the order parameter increases. The maximum variance obtained during intermittency reaffirms the breathing nature of the chimera-like state quantitatively. We also find similar spatiotemporal dynamics during transition to thermoacoustic instability in a swirl stabilized combustor.
Acknowledgements
The authors would like to thank Office of Naval Research Global (ONRG) for the funding (grant no. N62909-14-1-N 299); Dr R. Kolar is the contract monitor from ONRG. The first author (S.M.) gratefully acknowledges the institute post-doctoral fellowship from IIT Madras. The authors gratefully acknowledge the valuable discussions with Mr A. Seshadri, Dr D. V. Senthilkumar, Dr V. K. Chandrasekar and Professor M. Lakshmanan. The authors would also like to acknowledge the help provided by Mr N. Babu, Mr Thilagraj, Mr Manikandan and Mr Syam for conducting the experiments, Dr T. Komarek and Professor W. Polifke for providing the design, which was adapted to fabricate this set-up.
Appendix A
The trajectories in the analytic plane for
$P^{\prime }$
and
$\dot{q}^{\prime }$
(for an arbitrary pixel in the chemiluminescence images) during the occurrence of combustion noise are shown in figure 10. As there is no unique centre of rotation in the analytic plane, we cannot strictly interpret the computed quantity using Hilbert transform (HT) as instantaneous phase.
During the occurrence of thermoacoustic instability, even though a single centre of rotation is found for the
$P^{\prime }$
signal, the trajectories for the
$\dot{q}^{\prime }$
signal does not go around an origin in the analytic plane (figure 11).
For such signals, Romano et al. (Reference Romano, Thiel, Kurths, Kiss and Hudson2005) proposed an approach to detect synchronization based on the recurrence of trajectories in the phase space. In this regard, the probability (
$P(\unicode[STIX]{x1D70F})$
) that a point in phase space returns to a close neighbourhood of the former point after
$\unicode[STIX]{x1D70F}$
time steps is estimated for both signals to detect synchronization. If the position of peaks for two signals match in the plot of
$P(\unicode[STIX]{x1D70F})$
versus
$\unicode[STIX]{x1D70F}$
, it indicates phase synchronization (Romano et al.
Reference Romano, Thiel, Kurths, Kiss and Hudson2005). To confirm the synchronization, we validate our results obtained through phase from HT with recurrence measure (
$P(\unicode[STIX]{x1D70F})$
). The plots for
$P(\unicode[STIX]{x1D70F})$
are shown for combustion noise (figure 12
a, corresponding to the signals shown in figure 10) and thermoacoustic instability (figure 12
b, corresponding to the signals shown in figure 11).
Figure 10. Analytic representation of (a)
$P^{\prime }$
and (b)
$\dot{q}^{\prime }$
signal during the occurrence of combustion noise. Analytic signal is obtained using Hilbert transform.
Figure 11. Analytic representation of (a)
$P^{\prime }$
and (b)
$\dot{q}^{\prime }$
signal during the occurrence of thermoacoustic instability. Analytic signal is obtained using Hilbert transform.
Figure 12. Probabilities of recurrence (
$P(\unicode[STIX]{x1D70F})$
) with the time steps (
$\unicode[STIX]{x1D70F}$
) are compared between
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals during (a) combustion noise and (b) thermoacoustic instability.
In figure 12(a), neither the position nor the height of the peaks are perfectly matching for the
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals, which confirms the asynchrony between the pressure and the heat release rate oscillations during the occurrence of combustion noise. On the other hand, the position of the peaks are matching for the
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals during thermoacoustic instability, confirming phase synchronization (figure 12
b). This validates our findings of synchronization behaviour obtained through the phase from Hilbert transform.
Further, the phase (
$\unicode[STIX]{x1D719}(t)$
) between heat release and pressure oscillation can alternatively be defined through the correlation between the
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals (Sethares Reference Sethares2007; Balasubramanian & Sujith Reference Balasubramanian and Sujith2008) as
$$\begin{eqnarray}\cos \unicode[STIX]{x1D719}(t)=\frac{\displaystyle \int _{0}^{t}P^{\prime }(t^{\prime })\dot{q}^{\prime }(t^{\prime })\,\text{d}t^{\prime }}{\displaystyle \sqrt{\int _{0}^{t}P^{\prime 2}(t^{\prime })\,\text{d}t^{\prime }}\sqrt{\int _{0}^{t}\dot{q}^{\prime 2}(t^{\prime })\,\text{d}t^{\prime }}}.\end{eqnarray}$$
This gives the cosine of angle between two vectors (here,
$P^{\prime }(t)$
and
$\dot{q}^{\prime }(t)$
), which lie in the
$N$
-dimensional space,
$\mathbb{R}^{N}$
(
$t=1,2,3,\ldots ,N$
), through the definition of inner product between them. Following the Rayleigh criterion, when
$\cos \unicode[STIX]{x1D719}(t)$
is positive (negative), there is acoustic driving (damping). In other words, when the acoustic pressure and the heat release rate interacts in phase, it contributes to the acoustic energy. We calculate the cosine of instantaneous phase between the
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals by evaluating the correlation considering a small time window of the time series as
$$\begin{eqnarray}\cos \unicode[STIX]{x1D719}(t)=\frac{\displaystyle \int _{t-w/2}^{t+w/2}P^{\prime }(t^{\prime })\dot{q}^{\prime }(t^{\prime })\,\text{d}t^{\prime }}{\displaystyle \sqrt{\int _{t-w/2}^{t+w/2}P^{\prime 2}(t^{\prime })\,\text{d}t^{\prime }}\sqrt{\int _{t-w/2}^{t+w/2}\dot{q}^{\prime 2}(t^{\prime })\,\text{d}t^{\prime }}},\end{eqnarray}$$
where
$w$
is the window length for integration (
$1/2$
cycle). First, we compare
$\cos \unicode[STIX]{x1D719}(t)$
obtained using correlation and the same calculated using Hilbert transform for
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals. Analytic representation of
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals are shown for two different cases: (1) periodic signals with a unique centre of rotation (figures 13
a) and 2) aperiodic signals without a unique centre of rotation (figure 13
b) in the analytic plane. Comparisons between
$\cos \unicode[STIX]{x1D719}(t)$
obtained using correlation and that calculated using Hilbert transform are shown in figure 13(c) for the signals with a unique centre of rotation and in figure 13(d) for signals without a unique centre of rotation.
Figure 13. Comparison between cos
$\unicode[STIX]{x1D719}(t)$
estimated using Hilbert transform and correlation is examined for the signals (c) with and (d) without a unique centre of rotation in the analytic plane. Corresponding analytic representations of the signals are shown in (a) and (b).
Figure 14. Space–time plots (I) and spatial distribution (II) of
$\cos \unicode[STIX]{x1D719}(t)$
for 1D field. Space,
$x$
corresponds to
$x^{\prime }{-}x^{\prime }$
shown in figure 3(c) indicating the cross-sectional line along which the time evolution of the
$\cos \unicode[STIX]{x1D719}(t)$
is plotted (I) for different dynamical states: (a) combustion noise, (b) intermittency and (c) thermoacoustic instability. The results obtained using
$\cos \unicode[STIX]{x1D719}(t)$
calculated from correlation are similar to those obtained using
$\unicode[STIX]{x1D719}(t)$
calculated from Hilbert transform (figure 6).
Figure 15. Space–time plots (I) and spatial distribution (II) of
$\cos \unicode[STIX]{x1D719}(t)$
for 1D field. Space,
$y$
corresponds to
$y^{\prime }{-}y^{\prime }$
shown in figure 3(c) indicating the cross-sectional line along which the time evolution of the
$\cos \unicode[STIX]{x1D719}(t)$
is plotted (I) for different dynamical states: (a) combustion noise, (b) intermittency and (c) thermoacoustic instability. The results obtained using
$\cos \unicode[STIX]{x1D719}(t)$
calculated from correlation are similar to those obtained using
$\unicode[STIX]{x1D719}(t)$
calculated from Hilbert transform (figure 7).
For periodic signals,
$\cos \unicode[STIX]{x1D719}(t)$
calculated using correlation closely matches with that estimated through HT (figure 13
a). Further, for aperiodic signals,
$\cos \unicode[STIX]{x1D719}(t)$
calculated using HT fairly follows the trend of
$\cos \unicode[STIX]{x1D719}(t)$
calculated using correlation. We further compare the spatiotemporal patterns of instantaneous phase obtained through Hilbert transform with that of
$\cos \unicode[STIX]{x1D719}(t)$
obtained by evaluating the correlation between
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals. Similar to our analysis with phase from HT (figures 6 and 7), we draw the space–time plot of
$\cos \unicode[STIX]{x1D719}(t)$
and the spatial distribution of
$\cos \unicode[STIX]{x1D719}(t)$
for a 1D field (figures 14 and 15).
Phase turbulence is clear from the grainy structure in the space–time plot (figures 14 and 15, a-I) and also from the scattered
$\cos \unicode[STIX]{x1D719}(t)$
values (figures 14 and 15, a-II) during combustion noise at high
$\unicode[STIX]{x1D719}$
. At sufficiently low
$\unicode[STIX]{x1D719}$
, the phase synchrony is evident from the presence of similar
$\cos \unicode[STIX]{x1D719}(t)$
values (close to 1, showing alignment of acoustic pressure and heat release rate oscillations) for a 1D field (figures 14 and 15, c-I) and also from the
$\cos \unicode[STIX]{x1D719}(t)$
values congregated around some particular value (figures 14 and 15, c-II) during thermoacoustic instability. At intermediate
$\unicode[STIX]{x1D719}$
, however, the coexistence of regions of phase synchrony and phase asynchrony is observed during intermittency (figures 14 and 15, b-I and b-II). In short, the results obtained using
$\cos \unicode[STIX]{x1D719}(t)$
calculated from correlation (figures 14 and 15) are similar to those obtained using
$\unicode[STIX]{x1D719}(t)$
calculated from Hilbert transform (figures 6 and 7). Further, though the cosine of the phase can be calculated, the phase itself cannot be evaluated from the correlation between the
$P^{\prime }$
and
$\dot{q}^{\prime }$
signals. Therefore, we use the phase calculated through Hilbert transform for the visualization of the spatiotemporal pattern, in figures 4 and 5.
