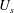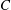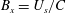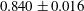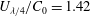1 Introduction
Water wave breaking is a dominant dynamical process of the upper ocean, inducing strong flow–turbulence–wave interactions and air–sea exchanges (Banner & Peregrine Reference Banner and Peregrine1993; Melville Reference Melville1996; Perlin & Schultz Reference Perlin and Schultz2000; Perlin, Choi & Tian Reference Perlin, Choi and Tian2013; Peirson, Walker & Banner Reference Peirson, Walker and Banner2014). Phillips (Reference Phillips1977, § 3.9) provides a very insightful characterisation of wave breaking and its historical developments at that time. The above references highlight the heightened interest in wave breaking and its consequences in the ensuing decades. However, as Holthuijsen (Reference Holthuijsen2007, p. 188) points out, ‘A complicating factor is that there is no generally accepted, precise definition of breaking’. Despite the high visibility of whitecaps at sea and wave breaking at coastlines and beaches, there remains a fundamental and long-standing gap as to how to characterise and predict the onset of wave breaking.
Historically, Stokes (Reference Stokes1880) developed his theoretical approach culminating in his steady irrotational wave of maximum steepness, beyond which breaking was assumed to occur. During subsequent decades, a number of other strategies have been proposed for determining a robust threshold for breaking of freely propagating water waves, involving geometric, kinematic and dynamic criteria. For example, Banner & Phillips (Reference Banner and Phillips1974) refined Stokes’ approach to account for the effects of wind drift, investigating its impact via the kinematic criterion in which breaking onset is linked directly to fluid at the crest point exceeding the speed of the crest. Other criteria based on a limiting fluid particle acceleration for stability of the crest point have also been proposed and investigated (e.g. Longuet-Higgins Reference Longuet-Higgins1963, appendix).
Perlin et al. (Reference Perlin, Choi and Tian2013) also describe a more recent genre of breaking onset criteria based on energy flux rates at steep crests, which appear to provide a more robust basis for quantifying breaking onset (Song & Banner Reference Song and Banner2002; Banner & Peirson Reference Banner and Peirson2007; Tian, Perlin & Choi Reference Tian, Perlin and Choi2008). A significant refinement of this approach was published very recently by Derakhti & Kirby (Reference Derakhti and Kirby2016). In this context, our perspective is that the critical transition in energy convergence rate from maximum recurrence to the weakest spilling breaking defines a breaking threshold. Above this threshold, the wave will break. Apart from this latest work, the interested reader is referred to Perlin et al. (Reference Perlin, Choi and Tian2013) for a comprehensive overview of the status of the various proposed breaking onset criteria.
In the present paper, we examine critically the threshold proposed by Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2015). Through an ensemble of boundary element numerical simulations of fully nonlinear two- and three-dimensional wave packets in deep and finite depth water, these authors proposed a breaking onset threshold based on a local threshold of wave energy flux in the crest region of a steep wave. They found that predicting the subsequent local onset of breaking can be described with reference to energy flux considerations. For nonlinear wave groups, the local energy flux vector
$\boldsymbol{F}=\boldsymbol{U}(P+\unicode[STIX]{x1D70C}gz+0.5\unicode[STIX]{x1D70C}U^{2})$
, where
$\boldsymbol{U}$
is velocity and
$U=|\boldsymbol{U}|$
,
$P$
is pressure,
$\unicode[STIX]{x1D70C}$
is the fluid density and
$z$
is the elevation, when normalised by the local energy density
$E=\unicode[STIX]{x1D70C}gz+0.5\unicode[STIX]{x1D70C}U^{2}$
, can be considered as a local energy flux velocity. At the wave surface and under the specific conditions of zero surface pressure, this local energy flux velocity reduces to the water surface particle velocity, which maximises at the wave crest point. At the wave crest point (used interchangeably with the ‘crest maximum elevation’ throughout this paper), the water surface particle velocity is denoted by
$U_{s}$
. Based on the local energy flux velocity
$(\boldsymbol{F}/E)$
and the local (horizontal) crest point speed (
$C$
), Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2015) define a new breaking onset variable
$\boldsymbol{B}=(\boldsymbol{F}/E)/C$
, which is the ratio of the local energy flux velocity and the local crest point speed. In the wave propagation direction (taken as the
$x$
direction), this reduces to
$B_{x}=(U_{s}/C)$
. They found that the onset of breaking occurs once the water surface particle speed at the wave crest point exceeds a critical proportion of the speed of the slowing crest point as it passes through the maximum of a wave group. The critical threshold was observed to be robust, for both long-crested and short-crested waves.
Using thermal image velocimetry (TIV) techniques to measure water surface particle speeds (Veron & Melville Reference Veron and Melville2001; Veron, Melville & Lenain Reference Veron, Melville and Lenain2008) at the crests of waves transitioning through a group maximum (the spatial and temporal instant at which group energy density is at a maximum), we critically examine the robustness of this breaking threshold for grouped waves in the laboratory with different group classes, spectral bandwidths and degrees of wind forcing.
To avoid the uncertainty associated with capturing wave breaking onset events with their attendant very short time scales (Duncan et al. Reference Duncan, Qiao, Philomin and Wenz1999), this present study identified the threshold for wave breaking as follows. Using the approach of Rapp & Melville (Reference Rapp and Melville1990) and Banner & Peirson (Reference Banner and Peirson2007), the rate of energy convergence at the point of initial wave breaking was systematically increased. Repeat observations of the wave groups transitioning through the point of initial breaking revealed that two conditions could be clearly defined.
Up to a certain wave paddle forcing level, dominant waves of successive groups were observed to progress through the group envelope maximum with no observable residual disturbance of the water surface. This condition was termed the maximum recurrent or maximum non-breaking threshold, and indicated a lower bound to the breaking threshold. Further slight but sufficient augmentation of paddle forcing level triggered a significant change in dominant wave behaviour at the initial break point. For each successive group, a disturbance in the wave surface was observed to occur at the same fetch, characterised by a visible bulge just ahead of the wave crest (Duncan et al. Reference Duncan, Qiao, Philomin and Wenz1999), accompanied by surface irregularity and trailing patches of capillary ripples. This condition was termed the marginal breaking condition and used to identify the upper bound of the breaking threshold. Based on this definition of the breaking threshold, this present contribution critically examines the proposal of Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2015).
As discussed above, for zero wind forcing, the energy flux criterion on the wave surface simplifies to the ratio of fluid speed to crest point speed, which gives it the character of a kinematic breaking criterion, which has been investigated by previous investigators. Although, Melville & Rapp (Reference Melville and Rapp1988) did not measure crest point speeds, they did highlight the significant changes in crest surface current structure associated with initiation of breaking. Perlin, He & Bernal (Reference Perlin, He and Bernal1996) capture velocity fields within the crest of a single wave transitioning from a pre-breaking to plunging state. Qiao & Duncan (Reference Qiao and Duncan2001) show that, at the transition to spilling breaking, the maximum water velocity in the crest of the wave shifts to the forward face of the wave. They also show a systematic increase in the maximum water velocity in the crest as a proportion of the crest point speed when expressed as a function of crest propagation distance. Oh et al. (Reference Oh, Mizutani, Suh and Hashimoto2005) found that breaking of strongly forced wind waves is observed when the crest point surface velocities are substantially less than the crest point speed. However, their observations do not distinguish whether individual waves were actually breaking. Consequently, their data do not permit a robust assessment of whether there is a systematic difference between crest water speed to crest speed ratios of non-breaking waves in comparison with those of breaking waves.
Of specific relevance to the present investigation is the incisive work of Stansell & MacFarlane (Reference Stansell and MacFarlane2002), who investigated the kinematic breaking criterion experimentally. From their measurements, they concluded that wave breaking was initiated at a ratio of crest water speed to crest point speed significantly less than unity, which is the value implied by the kinematic breaking criterion. Their findings are compared with present measurements later in this paper.
2 Experimental facilities and methods
2.1 Laboratory facilities
The experiments were conducted in the two-dimensional wind–wave tank located at UNSW Australia, Water Research Laboratory, Manly Vale. The flume was 30 m long, 0.6 m wide and 0.6 m deep with glass sidewalls and a solid floor. Waves were generated using a computer-controlled, flexible cantilevered wave paddle located at one end of the flume. A flexible reticulated polyester–urethane foam absorbent beach was installed at the other end of the tank to minimise reflections of the generated waves (figure 1). The water depth during these present experiments was 0.46 m and the waves propagating along the tank were two-dimensional.
The tank configuration was identical to that used by Banner & Peirson (Reference Banner and Peirson2007), except that a movable wind tunnel of length of 7.5 m was mounted on the tank, with the roof of the tunnel 0.5 m above the still water surface. At the upwind end of the tunnel, an adjustable honeycomb flow guide of 50 mm thickness and composed of 8 mm diameter tubes was installed to establish a uniform air flow within the wind tunnel when air was drawn through the tunnel by a fan at its downstream end. Wind intensity was controlled by varying the fan input voltage using a metered Variac. The wind speed was measured on the centreline of the tunnel approximately 4.8 m downwind of the inlet and 0.25 m above the still water level (SWL) using a pre-calibrated hot probe air velocity meter (Velocicalc model 8347).
Figure 1. Sketch of the experimental set-up (not to scale) used in the present study. The details of the dimensions and distances are given in the text.
A thermal camera (Flir T420) was mounted looking down at the centre of the wind tunnel roof to observe the tank water surface through a shuttered window 3.6 m downwind of its inlet. The movable wind tunnel could be positioned so that the camera observed the water surface at the location of the group maximum (the locations at which a repetitive wave group has its extreme amplitude). TIV was used to measure the horizontal water particle velocities at the crests of waves transitioning through the group maximum. The entire TIV system consisted of an irradiating source, a computer-controlled shutter, the thermal imaging camera and a computer controlling the system components.
Surface irradiation was provided by a pulsed
$\text{CO}_{2}$
laser (Firestar T100) mounted at the centre of the wind tunnel roof and aligned using an adjustable infrared range flat mirror. Pulses triggered by the controlling computer were timed to create a sequence of circular heat patches of approximately 4 mm diameter at locations just upstream of the group maximum location.
Surface reflections could potentially damage the thermal imaging camera used to acquire images of the moving heat patches. Consequently, the computer-controlled shutter remained closed during surface irradiation.
After irradiation, the shutter was opened and the thermal imaging camera was able to observe the water surface vertically from above, capturing 320 pixel
$\times$
240 pixel images of the surface at 30 frames per second. The physical resolution of the thermal imager was approximately 0.66 mm per pixel at the water surface, determined using calibration grids placed within the field of view.
Wave paddle amplitudes corresponding to maximum group recurrence and marginal group breaking were determined by illuminating the tunnel and observing waves through the glass walls. Wave motion was monitored by two linear arrays of capacitance wave probes mounted 50 mm in from each of the tank sidewalls. To minimise any effect of the probes on the wind flow, the wave probe signal conditioning boxes were mounted outside of the tunnel with 6 mm diameter cables connecting the boxes to the 3 mm diameter, 250 mm long probe frames.
The central probe of each set of wave probes was positioned at the same fetch as the centre of the thermal imaging area. The fetch is the horizontal distance from the wave generator to the observation point. Each probe was fitted with a 200 mm long, 0.2 mm diameter wire element. The wave data were captured using a National Instruments PCI-6225 data acquisition at 1000 Hz sample rate per channel. The probe resolution was 0.1 mm with the linearity of
$\pm 0.2~\text{mm}$
over their length.
To measure the local crest point speeds, five wave probes were installed along one tank wall with a spacing of 6 mm. Using the time series recorded by wave probes, the time of the dominant crest arrival at each wave probe was determined and thereby the crest point speed at the central probe was calculated.
To measure the geometry of the crests, seven wave probes were located at the other side of the tank with the spacing of 100 mm. The water level time series captured by the wave probes were interpolated in space to obtain the zero-crossing locations at the time of the wave group maximum and, thereby, crest geometry (figure 2). The geometric characterisations of Kjeldsen & Myrhaug (Reference Kjeldsen and Myrhaug1979), i.e. local steepness
$S_{c}$
, crest-front steepness
$\unicode[STIX]{x1D700}$
, crest-rear steepness
$\unicode[STIX]{x1D6FF}$
and vertical asymmetry
$\unicode[STIX]{x1D706}$
, were determined at the instant of the wave group maximum using the equations presented in figure 2.
Figure 2. Definitions of the local crest geometry:
$S_{c}$
is the local steepness,
$\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D6FF}$
are the crest-front and crest-rear steepness, respectively, and
$\unicode[STIX]{x1D706}$
is the vertical asymmetry parameter (Kjeldsen & Myrhaug Reference Kjeldsen and Myrhaug1979).
Fast Fourier transforms were used to obtain the single-sided wave frequency spectra, the peak frequency (
$f_{0}$
), the frequencies associated with the half-peak energy (
$f_{min}$
and
$f_{max}$
) and frequency bandwidth
$(\unicode[STIX]{x0394}f=(f_{max}-f_{min})/2)$
. The Benjamin–Feir index
$(BFI=(k_{0}^{2}\langle \unicode[STIX]{x1D702}^{2}\rangle )^{1/2}\sqrt{2}/(\unicode[STIX]{x0394}f/f_{0}))$
was used for comparison with other studies (e.g. Janssen Reference Janssen2003) where
$k_{0}$
is the characteristic wavenumber associated with the peak frequency and
$\langle \unicode[STIX]{x1D702}^{2}\rangle$
is the variance of the average surface elevation. Linear wave theory was used to calculate the corresponding wavenumber
$k_{0}$
and linear phase speed
$C_{0}$
for each wave group.
2.2 Initial wave group conditions
Concomitant crest point water particle velocities and the crest point speeds were measured for both monochromatic and group waves. To validate the TIV technique, the monochromatic waves were generated using
$$\begin{eqnarray}x_{p}(t)=A_{p}\sin (\unicode[STIX]{x1D714}_{p}t),\end{eqnarray}$$
where
$x_{p}$
is the wave paddle motion,
$A_{p}$
is proportional to the piston amplitude,
$\unicode[STIX]{x1D714}_{p}$
is the paddle angular frequency and
$t$
is time.
The wave packets generated by the paddle were selected to correspond to the cases used by Banner & Peirson (Reference Banner and Peirson2007). Both a bimodal spectrum with developing sideband instabilities (called here class 2; Benjamin & Feir Reference Benjamin and Feir1967) and chirped wave packets (class 3; Longuet-Higgins Reference Longuet-Higgins1974) were considered in the present study.
The bimodal initial spectrum was defined by two superimposed frequency components as follows:
$$\begin{eqnarray}x_{p}(t)=A_{p}\left(a_{0}\cos (\unicode[STIX]{x1D714}_{p0}t)+a_{1}\cos \left(\unicode[STIX]{x1D714}_{p1}t-\frac{\unicode[STIX]{x03C0}}{18}\right)\right),\end{eqnarray}$$
where
$a_{0}=0.473$
and
$a_{1}=0.530$
are dimensionless amplitudes corresponding to the two frequency components. For the two class 2 cases,
$\unicode[STIX]{x1D714}_{p0}$
was specified as
$9.383~\text{rad}~\text{s}^{-1}$
with
$\unicode[STIX]{x1D714}_{p1}$
taking values of
$8.043~\text{rad}~\text{s}^{-1}$
and
$8.530~\text{rad}~\text{s}^{-1}$
for
$N=3$
(C2N3) and
$N=5$
(C2N5) waves, respectively.
The chirped (class 3) wave packets were generated using
$$\begin{eqnarray}x_{p}=-0.25A_{p}\left(1+\tanh \frac{4\unicode[STIX]{x1D714}_{p}t}{N\unicode[STIX]{x03C0}}\right)\left(1-\tanh \frac{4(\unicode[STIX]{x1D714}_{p}t-2N\unicode[STIX]{x03C0})}{N\unicode[STIX]{x03C0}}\right)\sin (\unicode[STIX]{x1D714}_{p}(t-\unicode[STIX]{x1D714}_{p}C_{t2}t^{2}/2)),\end{eqnarray}$$
where
$C_{t2}$
is the chirp rate of the linear modulation. The paddle frequency
$\unicode[STIX]{x1D714}_{p}$
of
$8.18~\text{rad}~\text{s}^{-1}$
and the non-dimensional chirp rate of
$C_{t2}=0.0101$
were used for three class 3 wave packets with
$N=5$
, 7 and 9 (denoted hereafter as C3N5, C3N7 and C3N9).
2.3 Method
Prior to each experiment, the tank water surface was cleaned by generating waves for approximately 1 h at the beginning of each day. Any surface slick material was transported to the dissipating beach at the far end from the wave generator. Once the water surface had been cleaned, the wave probes were immersed into the tank for approximately 1 h to ensure that their signals were stable. The tank surface was inspected regularly to ensure that it was not contaminated with any slick material. Tank water temperatures were recorded before and after each experiment.
The threshold amplitudes for breaking for the five different wave packets described above were determined in the absence of wind. In addition, the thresholds for the C3N7 wave packet were determined with wind forcing applied.
The wind conditions were selected as a perturbation on the no-wind condition. To minimise possible wind-induced growth or attenuation effects, the wind speeds were selected to match the wave speeds as closely as possible (Mastenbroek Reference Mastenbroek1996, figure 4.5).
In each case, paddle amplitudes were incrementally increased to determine the conditions of maximum recurrence (that is, the maximum paddle amplitude at which no surface rupture was observed anywhere on the water surface) and marginal breaking (the minimum paddle amplitude at which consistent breaking was observed at the point of maximum wave group amplitude) in each case. The paddle amplitudes (
$A_{p}$
) for the different group classes and wind forcing conditions are presented in table 1. The fetches of the group maximum were carefully recorded. Group maximum fetches (and therefore the fetch of marginal breaking) increased systematically with the number of waves in each group. Once the group maximum fetch had been determined, the entire wind tunnel assembly was located over this point and measurement of the local wave characteristics and surface current proceeded. The time series of surface elevation at the location of the group maximum for maximum recurrence and marginal breaking C2N3 and C3N7 wave packets in the absence of wind as well as wind-forced C3N7 wave packets are shown in figure 3. Figure 3 shows the differences of the mean steepness at breaking onset between the two classes of waves. As can be seen, only small differences can be observed in the time water level records obtained at the location of the crest maximum elevation. As shown in the insets, the implied forward face steepnesses of the marginally breaking waves are significantly higher than their corresponding maximally recurrent waves.
Figure 3. Surface elevation time series at the location of group maximum for unforced non-breaking (- - -) and marginal breaking (——) C2N3 and C3N7 waves and wind-forced non-breaking (— ⋅ —) and marginal breaking (
$\cdots \cdots$
) C3N7U2.0 waves. C2N3 are of smaller amplitudes and the crest detail is shown by the left inset; C3N7 crest detail is shown in the right inset. Time (
$t$
) is referenced to the instant of the crest maximum elevation. Note the implied steeper forward face of the marginally breaking wave in comparison with its corresponding maximally recurrent wave and the differences of the mean steepness at breaking onset between the two classes of waves.
The measured geometric parameters for the different group classes and wind forcing conditions are summarised in table 1. Table 1 shows the averaged values obtained from each dataset, with uncertainty expressed as standard error. The degree of the asymmetry of the crest for each wave packet in the present study has been compared with the breaking threshold of Kjeldsen & Myrhaug (Reference Kjeldsen and Myrhaug1979) for different types of breaking waves in table 1. As shown in table 1, characterising wave steepness in this way does not yield a robust breaking criterion.
Table 1. Wind speed at the elevation of one quarter of the dominant wavelength above SWL (
$U_{\unicode[STIX]{x1D706}/4}$
), wave paddle amplitude at SWL (
$A_{p(SWL)}$
), the average and standard deviation of measured crest steepness (
$S_{c}$
), crest-front steepness (
$\unicode[STIX]{x1D700}$
), crest-rear steepness (
$\unicode[STIX]{x1D6FF}$
) and horizontal asymmetry parameter (
$\unicode[STIX]{x1D706}$
) for maximum recurrence and marginal breaking wave groups. The last row indicates the Kjeldsen & Myrhaug (Reference Kjeldsen and Myrhaug1979) breaking threshold for each geometric parameter.
The most challenging measurements were determining the crest surface velocities at the crest points. This required ensuring that the position of heat patches coincided with the crest maximum concomitant with group maximum occurrence. Consequently, the sequence of heat patches had to be initially positioned on the surface, allowing for their subsequent wave orbital transport to the immediately vicinity of group maximum. Trial and error was used to achieve this.
Also, the temperature of the heat patches decreased with time. This required careful minimisation of the measurement duty cycle and careful selection of those thermal image sequences in which the thermal patches remained clearly defined (figure 4).
Figure 4. Tracking the hot spot on the wave crest at the location of crest maximum elevation for three successive frames. The camera is stationary.
By differentiating the heat patch positions with time, a sequence of surface water velocities in the vicinity of the group maximum could be determined. An exemplary sequence for C3N7 in the absence of wind is shown in figure 5. In figure 5,
$X$
is the position of each point referenced to the location of crest maximum elevation (the centre of the image) and
$t$
is time, referenced to the crest maximum elevation event.
Figure 5. Surface water velocity
$(\text{m}~\text{s}^{-1})$
for marginal breaking C3N7 wave group. The arrows represent the surface water velocity;
$X_{cr\text{-}max}$
is the position of each point referenced to the location of crest maximum elevation of the transiting group.
In figure 5, the arrows show an ensemble of surface velocity measurements obtained from thermal image records obtained in the vicinity of a sequence of crest maximum elevation events for five wave groups.
To obtain a measurement of velocity localised at the time and location of a crest maximum elevation event, the synchronised thermal imagery and wave probe records were processed as follows. First, thermal patch velocities in immediate spatial proximity of the crest maximum elevation were determined at the time of the crest maximum elevation event. It was found that the duty cycle of the coupled laser–shutter–camera–wave probe system could be synchronised to achieve five velocity measurements surrounding the crest maximum elevation location at the time of the crest maximum elevation.
These five velocities were plotted as a function of distance referenced to the crest maximum elevation position as shown in figure 6. The results indicated that the maximum surface velocity coincided with the location of crest maxima in each case. A polynomial curve was fitted as shown in figure 6 to determine the maximum water velocity
$U_{s}$
.
Figure 6. Polynomial curve fitted to water surface velocities and the interpolated velocity at the crest maximum elevation for a marginal breaking C3N7 wave group. The error bars indicate the uncertainty arising from synchronisation of the TIV measurements with the wave probes. Note that the maximum velocity occurs at the wave crest point.
Owing to the framing rate, the absolute time reference of the thermal imagery can only be synchronised with the wave probes with an accuracy of
$\pm 17~\text{ms}$
. This uncertainty in synchronisation determines an uncertainty in the wave crest point velocity determined by this process. This uncertainty was evaluated using polynomial fits to the data obtained in the vicinity of crest maximum elevation events and is indicated in figure 6.
The influence of wind on the onset of wave breaking was investigated for the C3N7 case and followed an identical method. The maximum wind speed investigated was
$2.0~\text{m}~\text{s}^{-1}$
. Above this speed, the thermal patches created by the laser could no longer be clearly identified and tracked within five thermal image frames captured through a group maximum occurrence event. Measurements were also undertaken at a wind speed of
$1.4~\text{m}~\text{s}^{-1}$
to verify that any observed trends were consistent. In the absence of forced waves, the TIV technique was used to measure the water surface velocities at a fetch of 3.6 m. These water surface velocities were found to be
$0.065~\text{m}~\text{s}^{-1}$
and
$0.078~\text{m}~\text{s}^{-1}$
at the wind speeds of
$1.4~\text{m}~\text{s}^{-1}$
and
$2.0~\text{m}~\text{s}^{-1}$
, respectively.
Validation was undertaken by applying the TIV technique to monochromatic waves of modest steepness and frequency
$10.472~\text{rad}~\text{s}^{-1}$
. The water depth and the paddle amplitude for the validation case were
$d=0.23~\text{m}$
and
$A_{p}=0.0052~\text{m}$
. Measured wave characteristics were compared with linear wave theory predictions of the surface water velocity (
$u_{sL}$
) at the wave crest and crest speed (
$C_{L}$
) obtained based on the wave frequency. The comparison is presented in table 2. As shown, the measurements and linear theory agree within 1 %.
Figure 7. Local wave steepness
$S_{c}$
versus crest and surface speeds ratio at the wave crest point
$B_{x}=U_{s}/C$
for unforced waves, showing C2N3 (♢), C2N5 (✩), C3N5 (▫), C3N7 (◃) and C3N9 (○), with maximum recurrence waves (hollow symbols) and marginal breaking waves (solid symbols). Error bars indicate the standard deviation of the repeat measurement set (6–8 replicates).
Table 2. Measurements verifying the TIV technique. Using a monochromatic paddle frequency
$\unicode[STIX]{x1D714}_{p}=10.472~\text{rad}~\text{s}^{-1}$
and locally measuring
$a$
, the local wave steepness (
$ak$
), linear wave crest speed (
$C_{L}$
) and water surface velocity (
$u_{sL}$
) were estimated using linear wave theory. These are compared with the water surface velocity (
$U_{s}$
) measured using the TIV technique and crest speed (
$C$
) obtained from the wave probe records. Note that the differences between theory and measurement are less than 1 %.
3 Results and discussion
The measurements of group waves showed that the wave crest points systematically slow down as they approach their crest maximum and subsequently reaccelerate thereafter, as described by Banner et al. (Reference Banner, Barthelemy, Fedele, Allis, Benetazzo, Dias and Peirson2014).
The measured crest point speeds and crest surface water velocities at the instant of the wave group maximum are summarised in table 3 for each experimental case. Sample values at both maximum recurrence and marginal breaking define the bounds on the onset threshold and are shown in figure 7. Table 3 shows averaged values obtained from each dataset, with uncertainty expressed as standard error.
Table 3. Wind forcing (
$U_{\unicode[STIX]{x1D706}/4}/C_{0}$
) and the average and standard deviation of measured crest point speed (
$C$
), crest point water surface particle velocity (
$U_{s}$
), energy flux ratio at the crest point
$U_{s}/C$
, peak frequency (
$f_{0}$
), frequency bandwidth (
$\unicode[STIX]{x0394}f$
) and Benjamin–Feir index (
$BFI$
) for maximum recurrence and marginal breaking waves.
The results show a robust global threshold for the onset of wave breaking of
$B_{x}=U_{s}/C=0.840\pm 0.016$
. None of the recurrent groups reach the threshold, while all marginal breaking cases exceed the threshold. This threshold is robust for different types of wave groups and shows no dependence on peak spectral wavenumbers. As shown in figure 7, the characteristic local steepness levels at the threshold of breaking between the class 2 and class 3 groups are distinct.
In each case, it is the crest surface water velocity that plays the dominant role in determining the overall value of this parameter. For all wave groups, across the threshold the crest point speed remained almost unchanged between the recurrent to marginal breaking wave condition. In contrast, the surface water velocity increased significantly across the threshold.
Stansell & MacFarlane (Reference Stansell and MacFarlane2002) gathered similar data but without a direct method of measuring the surface velocity. They used particle image velocimetry to capture the near-surface velocity profiles beneath waves approaching breaking onset. Smooth extrapolations of 10 points of data gathered at 5 mm grid points below the surface were used to estimate the surface velocity.
The findings of their study support this present investigation except in one aspect. Stansell & MacFarlane (Reference Stansell and MacFarlane2002) found that for a single case of a wave (their wave 1) captured just before the onset of plunging breaking, the ratio of crest point water speed to crest point speed was 0.81. This is 5 % less than the breaking onset threshold found during this present study.
Figure 3 in Stansell & MacFarlane (Reference Stansell and MacFarlane2002) illustrates their surface velocity extrapolation technique using another experimental case (wave 3). If the two velocity measurements most proximate to the surface of wave 3 are linearly extrapolated to the surface, the estimated surface velocity would be
$1.66~\text{m}~\text{s}^{-1}$
, as opposed to the value of
$1.51~\text{m}~\text{s}^{-1}$
determined by their extrapolation technique. Consequently, an extrapolation technique using the data in closest proximity to the surface may yield values more than 10 % higher than they report. If a similar correction is applicable to their more extreme plunging case (case 1, referred to above), their data would be entirely consistent with the finding of this present investigation.
Returning to these present results, their sensitivity has also been investigated in relation to two factors: wind forcing and group bandwidth.
As shown in table 3, the degree of wind forcing has been characterised in terms of the wind speed at an elevation of one quarter of the dominant wavelength
$(U_{\unicode[STIX]{x1D706}/4})$
above the mean water surface. For wind forcing
$U_{\unicode[STIX]{x1D706}/4}/C_{0}$
less than 1.42, the determined breaking threshold remains robust as shown in figure 8.
Figure 8. Wind forcing
$U_{\unicode[STIX]{x1D706}/4}/C_{0}$
versus crest and surface speeds ratio at the crest point
$B_{x}=U_{s}/C$
for wind-forced waves, showing C3N7 (◃), C3N7U1.4 (▿) and C3N7U2.0 (▵), with maximum recurrence waves (hollow symbols) and marginal breaking waves (solid symbols). Error bars indicate the standard deviation of the repeat measurement set (6–8 replicates).
However, more careful examination of the C3N7 data presented in figure 8 and table 3 shows that, as
$U_{\unicode[STIX]{x1D706}/4}/C_{0}$
increases from zero to 1.42, there is a slight systematic increase in the threshold in
$U_{s}/C$
of approximately 2.0 %. Consequently, wind has a slightly stabilising effect on the underlying wave field.
The local energy density has no contribution from any change in the surface pressure. In view of this systematic response to wind, it is useful to review the relative contributions of the three energy flux components: pressure, elevation and water speed.
As shown in Mastenbroek (Reference Mastenbroek1996, figure 4.7), a wave of crest steepness
$S_{c}=0.48$
with
$U_{\unicode[STIX]{x1D706}}/C=2$
has an estimated wind-induced crest surface pressure perturbation less than
$15ak\unicode[STIX]{x1D70C}_{a}u_{\ast }^{2}$
, where
$ak$
is the mean wave steepness,
$\unicode[STIX]{x1D70C}_{a}$
is the density of air and
$u_{\ast }$
is the friction velocity in the air. No measurements of friction velocity were taken during this present investigation, but by referring to the similar conditions investigated by Hsu & Hsu (Reference Hsu and Hsu1983), friction velocities will remain less than
$0.08~\text{m}~\text{s}^{-1}$
. Consequently, the pressure perturbation due to the imposition of wind is estimated as less than 0.05 Pa. This is less than 0.03 % of the other contributions to the energy flux.
As shown in table 3, the imposition of wind perturbs the elevation contribution to the flux by approximately 6 % and the water speed component by over 10 %. The dominant perturbation to the flux ratio arises from changes in the crest water speed due to the wind. Perturbations by the wind-induced pressure itself are negligible.
Group bandwidth has been proposed as an important factor in determining the occurrence of extreme waves, and so we have assessed its influence on the threshold. We note that spectral bandwidth can change appreciably with fetch and therefore is not a robust means of characterising group wave fields. In the context of these experiments, spectral bandwidth changed by less than
$\pm 5\,\%$
within a distance of
$\pm 3\unicode[STIX]{x1D706}_{0}$
around the group maximum location.
As discussed earlier, the fetch to initial breaking increases as the bandwidth increases. Consequently, there is also a correlation between bandwidth and the envelope growth rate immediately prior to breaking inception (Banner & Peirson Reference Banner and Peirson2007, figure 5).
Figure 9. Benjamin–Feir index
$BFI$
versus crest and surface speeds ratio at the wave crest point
$B_{x}=U_{s}/C$
for unforced waves. The shapes are as defined in figure 7. Error bars indicate the standard deviation of the repeat measurement set (6–8 replicates).
The most systematic relationship between breaking onset threshold and spectral bandwidth that emerged from the measurements is shown in figure 9. As shown, the threshold systematically increases with the
$BFI$
. Over the range of group bandwidths considered here, the change in the threshold is only a few per cent.
4 Conclusions and recommendations
Thermal image velocimetry has been used to measure the crest surface water velocity at the crest maximum elevation of freely propagating, unsteady deep water wave groups in the laboratory. Wave crest point speeds were determined using an array of closely spaced wave gauges at the same instant as the crest point water velocity measurements.
Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2015) proposed an energy flux ratio
$B_{x}=U_{s}/C$
to define a threshold that distinguishes maximum recurrence from marginal breaking. The threshold value
$B_{x}$
was determined to be
$0.840\pm 0.016$
during this present experimental study. This present study encompassed different classes of wave groups exhibiting distinct characteristic steepnesses in the vicinity of the breaking threshold.
Increasing wind forcing from zero to
$U_{\unicode[STIX]{x1D706}/4}/C_{0}=1.42$
increased the threshold systematically by 2.0 %.
Increasing the spectral bandwidth (decreasing the Benjamin–Feir index from 0.39 to 0.31) systematically reduced of the threshold by 1.5 %.
These encouraging results motivate extension of this present work to shallow waters, three-dimensional breaking and field conditions.
Acknowledgements
Funding for this investigation was provided by the Australian Research Council under Discovery Project DP120101701. The expert technical assistance provided by Mr L. Paice and Mr R. Jenkins are gratefully acknowledged.
