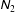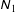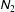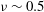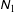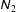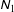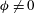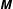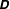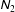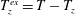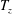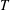1 Introduction
Granular materials, a collection of macroscopic particles, are ubiquitous in nature (avalanche, debris flows, planetary rings, etc.) and also very important in many chemical processing industries. At rest, the ‘dry’ granular materials (for which the effect of interstitial fluid can be neglected) behave like a solid, having a compressive strength but no tensile strength, and hence dubbed a ‘peculiar’ solid. On the other hand, a collection of particles can flow like a liquid as in an hour glass or behave like a gas under strong shaking (Forterre & Pouliquen Reference Forterre and Pouliquen2008; Rao & Nott Reference Rao and Nott2008). In the case of a granular gas (Goldhirsch Reference Goldhirsch2003; Brilliantov & Pöschel Reference Brilliantov and Pöschel2004), the particle collisions are inelastic, leading to the dissipation of the kinetic energy of colliding particles. The inelastic dissipation is known to be the progenitors of many interesting properties of a granular fluid, and is also responsible for the loss of ‘microscopic’ reversibility at the level of Liouville and Boltzmann equations that calls for non-standard statistical mechanics (Jenkins & Richman Reference Jenkins and Richman1985; Sela & Goldhirsch Reference Sela and Goldhirsch1998; Garzo & Dufty Reference Garzo and Dufty1999; Lutsko Reference Lutsko2005; Rongali & Alam Reference Rongali and Alam2014) to develop coarse-grained theories for flowing granular matter.
Unlike normal fluids, however, the granular fluids possess prominent non-Newtonian properties, like the normal stress differences which can be of the order of its isotropic pressure in a dilute granular gas (Walton & Braun Reference Walton and Braun1986; Campbell Reference Campbell1989; Sela & Goldhirsch Reference Sela and Goldhirsch1998; Alam & Luding Reference Alam and Luding2003a
,Reference Alam and Luding
b
, Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005; Santos, Garzo & Dufty Reference Santos, Garzo and Dufty2004; Montanero et al.
Reference Montanero, Garzo, Alam and Luding2006; Saha & Alam Reference Saha and Alam2014) in contrast to its infinitesimal magnitude in a molecular gas. Figure 1, taken from Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005), displays the variations of two normal stress differences (
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
) with the volume fraction of particles; the restitution coefficient is
$\unicode[STIX]{x1D615}_{2}$
) with the volume fraction of particles; the restitution coefficient is
![]() $e=0.9$
. The scaled first normal stress difference (
$e=0.9$
. The scaled first normal stress difference (
![]() $\unicode[STIX]{x1D615}_{1}=(\unicode[STIX]{x1D617}_{xx}-\unicode[STIX]{x1D617}_{yy})/p$
, where
$\unicode[STIX]{x1D615}_{1}=(\unicode[STIX]{x1D617}_{xx}-\unicode[STIX]{x1D617}_{yy})/p$
, where
![]() $\unicode[STIX]{x1D617}_{{\it\alpha}{\it\alpha}}$
is the diagonal component of the stress tensor along the
$\unicode[STIX]{x1D617}_{{\it\alpha}{\it\alpha}}$
is the diagonal component of the stress tensor along the
![]() ${\it\alpha}$
-direction, and
${\it\alpha}$
-direction, and
![]() $p$
is the mean pressure) is positive and maximal in the dilute limit (
$p$
is the mean pressure) is positive and maximal in the dilute limit (
![]() ${\it\nu}\rightarrow 0$
) and decreases in magnitude with increasing density. On the other hand, the second normal stress difference (
${\it\nu}\rightarrow 0$
) and decreases in magnitude with increasing density. On the other hand, the second normal stress difference (
![]() $\unicode[STIX]{x1D615}_{2}=(\unicode[STIX]{x1D617}_{yy}-\unicode[STIX]{x1D617}_{zz})/p$
) is negative in the dilute limit, increases with increasing density, becomes positive at a critical density
$\unicode[STIX]{x1D615}_{2}=(\unicode[STIX]{x1D617}_{yy}-\unicode[STIX]{x1D617}_{zz})/p$
) is negative in the dilute limit, increases with increasing density, becomes positive at a critical density
![]() ${\it\nu}_{cr}\approx 0.13$
and increases monotonically thereafter. Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) also postulated a frame-indifferent phenomenological constitutive model for granular fluids to predict the sign reversals of both first and second normal stress differences. Returning to figure 1, we can conclude that the normal stress differences must be incorporated in the theoretical modelling of a granular fluid so that the theory remains valid from the dilute to the dense limit.
${\it\nu}_{cr}\approx 0.13$
and increases monotonically thereafter. Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) also postulated a frame-indifferent phenomenological constitutive model for granular fluids to predict the sign reversals of both first and second normal stress differences. Returning to figure 1, we can conclude that the normal stress differences must be incorporated in the theoretical modelling of a granular fluid so that the theory remains valid from the dilute to the dense limit.

Figure 1. Variations of the first (
![]() $\unicode[STIX]{x1D615}_{1}$
) and second (
$\unicode[STIX]{x1D615}_{1}$
) and second (
![]() $\unicode[STIX]{x1D615}_{2}$
) normal stress differences with particle volume fraction (
$\unicode[STIX]{x1D615}_{2}$
) normal stress differences with particle volume fraction (
![]() ${\it\nu}$
) in the uniform shear flow of smooth inelastic spheres; the symbols represent the particle dynamics simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for a restitution coefficient of
${\it\nu}$
) in the uniform shear flow of smooth inelastic spheres; the symbols represent the particle dynamics simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for a restitution coefficient of
![]() $e=0.9$
. The solid lines denote the present anisotropic moment theory as discussed in §§ 5.3 and 5.5.
$e=0.9$
. The solid lines denote the present anisotropic moment theory as discussed in §§ 5.3 and 5.5.
The studies on normal stresses have a long and rich history in the area of particulate suspensions (Bagnold Reference Bagnold1954; Brady & Morris Reference Brady and Morris1997; Singh & Nott Reference Singh and Nott2003; Guazzelli & Morris Reference Guazzelli and Morris2011), with the early works being carried out in the dense regime of such systems. More recent experimental work (Boyer, Pouliquen & Guazzelli Reference Boyer, Pouliquen and Guazzelli2011; Couturier et al. Reference Couturier, Boyer, Pouliquen and Guazzelli2011) on the behaviour of normal stresses in non-Brownian suspensions has generated renewed interest to understand the non-Newtonian rheology of suspensions and dense granular media via simulation and experiment (Lerner, Düring & Wyart Reference Lerner, Düring and Wyart2012; Trulsson, Andreotti & Claudin Reference Trulsson, Andreotti and Claudin2012; Dbouk, Lobry & Lemaire Reference Dbouk, Lobry and Lemaire2013; Denn & Morris Reference Denn and Morris2014). Even after 60 years of research starting from Bagnold (Reference Bagnold1954), there remain debates about the sign of two normal stresses in the dense regime of a suspension. In any case, studying the non-Newtonian behaviour is also important since the normal stresses themselves are responsible for many interesting flow-features (e.g. rod climbing or Weissenberg effect, die swelling, secondary flows, etc.) in non-Newtonian fluids. Moreover, it is also known from the literature on polymeric fluids and suspensions that the non-Newtonian flows can support additional instability modes whose origin can solely be tied to normal stresses. From the modelling viewpoint, the presence of large normal stress differences readily calls for higher-order constitutive models even at the minimal level.
The present work is a direct descendant of our previous work (Saha & Alam Reference Saha and Alam2014) which dealt with a Grad-like (Grad Reference Grad1949) extended hydrodynamic theory for the shear flow of inelastic disks in two dimensions. It must be noted that the seminal contributions in this direction have been made by Goldreich & Tremaine (Reference Goldreich and Tremaine1978), Araki & Tremaine (Reference Araki and Tremaine1986), Jenkins & Richman (Reference Jenkins and Richman1988), Richman (Reference Richman1989), Chou & Richman (Reference Chou and Richman1998) and Lutsko (Reference Lutsko2004): all these authors solved the inelastic Boltzmann or Boltzmann–Enskog equation either numerically at finite densities, or semianalytically in the limiting case of dilute flows. Our focus is however a little different: we would like to derive analytical expressions for normal stress differences and other transport coefficients that are valid for (i) a large range of density (encompassing both the dilute and dense limits) and (ii) a small restitution coefficient (far away from the limit of elastic collisions). Towards this goal and considering the canonical set-up of homogeneous shear flow, we follow an analytical route to derive (i) an exact Burnett-order solution for all transport coefficients and (ii) the corresponding perturbation solutions at super-Burnett orders; (iii) this in turn helps to tie the origin of normal stress differences with the anisotropy of the second-moment tensor of velocity fluctuations.
This paper is organized as follows. The extended hydrodynamic theory is briefly outlined in § 2. The second-moment tensor of velocity fluctuations is constructed via a geometric analysis in terms of its eigenvalues and eigenvectors for the uniform shear flow in § 3.1; its balance equation is analysed in §§ 3.2 and 3.3. Working in a rotated coordinate frame and using a series expansion for certain integrals, the balance equation for the second moment is reduced to a set of algebraic equations as described in § 4. Two sets of analytical solutions of these algebraic equations at different orders in the perturbation parameter are derived in §§ 4.1 and 4.2. The closed-form expressions for (i) all components of the stress tensor, (ii) the shear viscosity, (iii) the pressure, (iv) two normal stress differences and (v) the source of the second-moment tensor (and the rate of collisional dissipation) are derived and validated in § 5. The origin of stress anisotropy is discussed in § 6. The conclusions and future work are given in § 7.
2 Extended hydrodynamic equations for a dense granular fluid
We consider a dense granular gas consisting of
![]() $N$
randomly moving smooth inelastic hard spheres of diameter
$N$
randomly moving smooth inelastic hard spheres of diameter
![]() ${\it\sigma}$
and mass
${\it\sigma}$
and mass
![]() $m$
. The particles loose energy upon collisions which is characterized by a single parameter
$m$
. The particles loose energy upon collisions which is characterized by a single parameter
![]() $e$
, called the coefficient of normal restitution, with
$e$
, called the coefficient of normal restitution, with
![]() $e=1$
and 0 referring to perfectly elastic and sticking collisions, respectively. For a pair of colliding smooth spheres, the tangential component of their relative velocity remains invariant but the normal component changes according to the collision rule:
$e=1$
and 0 referring to perfectly elastic and sticking collisions, respectively. For a pair of colliding smooth spheres, the tangential component of their relative velocity remains invariant but the normal component changes according to the collision rule:
![]() $(\boldsymbol{g}^{\prime }\boldsymbol{\cdot }\boldsymbol{k})=-e(\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k})$
, where
$(\boldsymbol{g}^{\prime }\boldsymbol{\cdot }\boldsymbol{k})=-e(\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k})$
, where
![]() $\boldsymbol{g}\equiv \boldsymbol{g}_{12}=\boldsymbol{c}_{1}-\boldsymbol{c}_{2}$
and
$\boldsymbol{g}\equiv \boldsymbol{g}_{12}=\boldsymbol{c}_{1}-\boldsymbol{c}_{2}$
and
![]() $\boldsymbol{g}^{\prime }=\boldsymbol{c}_{1}^{\prime }-\boldsymbol{c}_{2}^{\prime }$
are the pre- and post-collisional relative velocities, respectively,
$\boldsymbol{g}^{\prime }=\boldsymbol{c}_{1}^{\prime }-\boldsymbol{c}_{2}^{\prime }$
are the pre- and post-collisional relative velocities, respectively,
![]() $\boldsymbol{k}\equiv \boldsymbol{k}_{12}=(\boldsymbol{x}_{2}-\boldsymbol{x}_{1})/|\boldsymbol{x}_{2}-\boldsymbol{x}_{1}|$
is the unit contact vector joining the centre of sphere-1 to that of sphere-2 at collision. At the mesoscopic level, the collective behaviour of such an
$\boldsymbol{k}\equiv \boldsymbol{k}_{12}=(\boldsymbol{x}_{2}-\boldsymbol{x}_{1})/|\boldsymbol{x}_{2}-\boldsymbol{x}_{1}|$
is the unit contact vector joining the centre of sphere-1 to that of sphere-2 at collision. At the mesoscopic level, the collective behaviour of such an
![]() $N$
-particle system is well described by the evolution of the single-particle distribution function
$N$
-particle system is well described by the evolution of the single-particle distribution function
![]() $f(\boldsymbol{c},\boldsymbol{x},t)$
which, for a granular dense gas, reads as (Chapman & Cowling Reference Chapman and Cowling1970; Jenkins & Richman Reference Jenkins and Richman1985)
$f(\boldsymbol{c},\boldsymbol{x},t)$
which, for a granular dense gas, reads as (Chapman & Cowling Reference Chapman and Cowling1970; Jenkins & Richman Reference Jenkins and Richman1985)
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial }{\partial t}+\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\right)f & = & \displaystyle {\it\sigma}^{2}\int \text{d}\boldsymbol{c}_{2}\int _{\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0}\,\text{d}\boldsymbol{k}(\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,[\text{e}^{-2}f^{(2)}(\boldsymbol{c}_{1},\boldsymbol{x},\boldsymbol{c}_{2},\boldsymbol{x}-{\it\sigma}\boldsymbol{k};t)-f^{(2)}(\boldsymbol{c}_{1}^{\prime },\boldsymbol{x},\boldsymbol{c}_{2}^{\prime },\boldsymbol{x}+{\it\sigma}\boldsymbol{k};t)],\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial }{\partial t}+\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\right)f & = & \displaystyle {\it\sigma}^{2}\int \text{d}\boldsymbol{c}_{2}\int _{\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0}\,\text{d}\boldsymbol{k}(\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,[\text{e}^{-2}f^{(2)}(\boldsymbol{c}_{1},\boldsymbol{x},\boldsymbol{c}_{2},\boldsymbol{x}-{\it\sigma}\boldsymbol{k};t)-f^{(2)}(\boldsymbol{c}_{1}^{\prime },\boldsymbol{x},\boldsymbol{c}_{2}^{\prime },\boldsymbol{x}+{\it\sigma}\boldsymbol{k};t)],\qquad\end{eqnarray}$$
where
![]() $f^{(2)}$
is the two-body distribution function and
$f^{(2)}$
is the two-body distribution function and
![]() $\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0$
accounts for the constraint of impending collisions.
$\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0$
accounts for the constraint of impending collisions.
2.1 The 10-moment system
Going beyond the Navier–Stokes (NS)-order hydrodynamics of five field variables, here we will work with an ‘extended’ set of 10 hydrodynamic fields: (i) the mass density
(ii) the coarse-grained velocity
and (iii) the second-moment tensor
where
![]() $n(\boldsymbol{x},t)$
is the number density and
$n(\boldsymbol{x},t)$
is the number density and
![]() $\boldsymbol{C}\equiv \boldsymbol{c}-\boldsymbol{u}$
is the peculiar/fluctuation velocity of particles. The last hydrodynamic field (2.4) is required to account for normal stress differences (Jenkins & Richman Reference Jenkins and Richman1988; Chou & Richman Reference Chou and Richman1998; Saha & Alam Reference Saha and Alam2014) which are the primary focus of the present work. The balance equations for the mass, momentum and second moment, respectively, can be obtained by taking the appropriate moment of (2.1):
$\boldsymbol{C}\equiv \boldsymbol{c}-\boldsymbol{u}$
is the peculiar/fluctuation velocity of particles. The last hydrodynamic field (2.4) is required to account for normal stress differences (Jenkins & Richman Reference Jenkins and Richman1988; Chou & Richman Reference Chou and Richman1998; Saha & Alam Reference Saha and Alam2014) which are the primary focus of the present work. The balance equations for the mass, momentum and second moment, respectively, can be obtained by taking the appropriate moment of (2.1):
where
![]() $\unicode[STIX]{x1D64B}$
is the total stress, a second-rank tensor, given by
$\unicode[STIX]{x1D64B}$
is the total stress, a second-rank tensor, given by
![]() $\unicode[STIX]{x1D64C}$
is the flux of the second moment, a third-rank tensor, given by
$\unicode[STIX]{x1D64C}$
is the flux of the second moment, a third-rank tensor, given by
and
![]() $\boldsymbol{\aleph }$
is the collisional source of the second moment, a second-rank tensor, given by
$\boldsymbol{\aleph }$
is the collisional source of the second moment, a second-rank tensor, given by
In (2.8)–(2.9), the first and second terms refer to the corresponding kinetic and collisional contributions, respectively. The integral expression for the collisional flux term
![]() ${\it\bf\Theta}({\it\psi})$
of any particle-level property
${\it\bf\Theta}({\it\psi})$
of any particle-level property
![]() ${\it\psi}$
is given by
${\it\psi}$
is given by
 $$\begin{eqnarray}\displaystyle {\it\bf\Theta}({\it\psi}) & = & \displaystyle -\frac{{\it\sigma}^{3}}{2}\iiint _{\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0}({\it\psi}_{1}^{\prime }-{\it\psi}_{1})\boldsymbol{k}\int _{0}^{1}f^{(2)}(\boldsymbol{c}_{1},\boldsymbol{x}-{\it\omega}{\it\sigma}\boldsymbol{k},\boldsymbol{c}_{2},\boldsymbol{x}+{\it\sigma}\boldsymbol{k}-{\it\omega}{\it\sigma}\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{g})\,\text{d}{\it\omega}\,\text{d}\boldsymbol{k}\,\text{d}\boldsymbol{c}_{1}\,\text{d}\boldsymbol{c}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\bf\Theta}({\it\psi}) & = & \displaystyle -\frac{{\it\sigma}^{3}}{2}\iiint _{\boldsymbol{g}\boldsymbol{\cdot }\boldsymbol{k}>0}({\it\psi}_{1}^{\prime }-{\it\psi}_{1})\boldsymbol{k}\int _{0}^{1}f^{(2)}(\boldsymbol{c}_{1},\boldsymbol{x}-{\it\omega}{\it\sigma}\boldsymbol{k},\boldsymbol{c}_{2},\boldsymbol{x}+{\it\sigma}\boldsymbol{k}-{\it\omega}{\it\sigma}\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{g})\,\text{d}{\it\omega}\,\text{d}\boldsymbol{k}\,\text{d}\boldsymbol{c}_{1}\,\text{d}\boldsymbol{c}_{2},\end{eqnarray}$$
where
![]() ${\it\omega}$
is an integration variable (Jenkins & Richman Reference Jenkins and Richman1985), and that for the collisional source of
${\it\omega}$
is an integration variable (Jenkins & Richman Reference Jenkins and Richman1985), and that for the collisional source of
![]() ${\it\psi}$
,
${\it\psi}$
,
![]() $\boldsymbol{\aleph }({\it\psi})$
, is
$\boldsymbol{\aleph }({\it\psi})$
, is
Note that the origin of the collisional flux term (2.11) is tied to the ‘macroscopic’ nature of particles (and hence to the ‘denseness’ of the matter) and this term is zero in a dilute gas of point particles.
Defining the granular temperature as
![]() $T\equiv \unicode[STIX]{x1D614}_{{\it\alpha}{\it\alpha}}/3$
and taking the trace of (2.7), we obtain the balance equation for the granular energy
$T\equiv \unicode[STIX]{x1D614}_{{\it\alpha}{\it\alpha}}/3$
and taking the trace of (2.7), we obtain the balance equation for the granular energy
and that of the deviator of the second moment
 $$\begin{eqnarray}\displaystyle \frac{1}{2}{\it\rho}\left(\frac{\partial }{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\right)\widehat{\unicode[STIX]{x1D614}}_{{\it\alpha}{\it\beta}} & = & \displaystyle -\frac{\partial }{\partial x_{{\it\gamma}}}\left(\unicode[STIX]{x1D618}_{{\it\gamma}{\it\alpha}{\it\beta}}-\frac{2}{3}q_{{\it\gamma}}{\it\delta}_{{\it\alpha}{\it\beta}}\right)\nonumber\\ \displaystyle & & \displaystyle -\left\{\frac{1}{2}\left(\unicode[STIX]{x1D617}_{{\it\gamma}{\it\alpha}}\frac{\partial u_{{\it\beta}}}{\partial x_{{\it\gamma}}}+\unicode[STIX]{x1D617}_{{\it\gamma}{\it\beta}}\frac{\partial u_{{\it\alpha}}}{\partial x_{{\it\gamma}}}\right)-\frac{1}{3}\unicode[STIX]{x1D617}_{{\it\gamma}{\it\xi}}\frac{\partial u_{{\it\xi}}}{\partial x_{{\it\gamma}}}{\it\delta}_{{\it\alpha}{\it\beta}}\right\}+\frac{1}{2}\widehat{\aleph }_{{\it\alpha}{\it\beta}}.\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{2}{\it\rho}\left(\frac{\partial }{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\right)\widehat{\unicode[STIX]{x1D614}}_{{\it\alpha}{\it\beta}} & = & \displaystyle -\frac{\partial }{\partial x_{{\it\gamma}}}\left(\unicode[STIX]{x1D618}_{{\it\gamma}{\it\alpha}{\it\beta}}-\frac{2}{3}q_{{\it\gamma}}{\it\delta}_{{\it\alpha}{\it\beta}}\right)\nonumber\\ \displaystyle & & \displaystyle -\left\{\frac{1}{2}\left(\unicode[STIX]{x1D617}_{{\it\gamma}{\it\alpha}}\frac{\partial u_{{\it\beta}}}{\partial x_{{\it\gamma}}}+\unicode[STIX]{x1D617}_{{\it\gamma}{\it\beta}}\frac{\partial u_{{\it\alpha}}}{\partial x_{{\it\gamma}}}\right)-\frac{1}{3}\unicode[STIX]{x1D617}_{{\it\gamma}{\it\xi}}\frac{\partial u_{{\it\xi}}}{\partial x_{{\it\gamma}}}{\it\delta}_{{\it\alpha}{\it\beta}}\right\}+\frac{1}{2}\widehat{\aleph }_{{\it\alpha}{\it\beta}}.\qquad \quad\end{eqnarray}$$
In the above equations,
is the heat flux vector, and
is the rate of dissipation of kinetic energy per unit volume. The balance equations (2.5)–(2.6) and (2.13), along with constitutive relations for (2.8), (2.15) and (2.16), constitute the NS-order hydrodynamics for which the equation for the deviatoric part of the second-moment tensor (2.14) is satisfied identically.
For an extended hydrodynamic description of granular fluids, incorporating normal stress differences, the balance equation (2.7) for the full second-moment tensor along with the mass and momentum balances (2.5)–(2.6) are needed. For a closure of (2.7), the deviatoric part of the third order
![]() $\unicode[STIX]{x1D618}_{{\it\gamma}{\it\alpha}{\it\beta}}$
,
$\unicode[STIX]{x1D618}_{{\it\gamma}{\it\alpha}{\it\beta}}$
,
is assumed to be zero, leaving only its isotropic part, the heat flux vector (2.15), to be evaluated as a constitutive relation. In this paper, we specifically focus on the uniform shear flow (see § 3) for which (2.15) is zero; therefore we are left to determine constitutive relations for the stress tensor (2.8) and the source of the second moment (2.10) as discussed in §§ 3–5.
2.2 Anisotropic Gaussian distribution function and the maximum entropy principle
To evaluate (2.11) and (2.12), we adopt the molecular chaos ansatz (Chapman & Cowling Reference Chapman and Cowling1970)
that relates the two-particle distribution function as a product of two single-particle velocity distribution functions. The positional correlation is taken care of via the well-known contact radial distribution function of Carnahan & Starling (Reference Carnahan and Starling1969),
with
being the local volume fraction of particles. Finally we assume that the single-particle velocity distribution is an anisotropic Maxwellian/Gaussian
with
![]() $|\unicode[STIX]{x1D648}|=\det (\unicode[STIX]{x1D648})$
, which contains complete information about the second-moment tensor
$|\unicode[STIX]{x1D648}|=\det (\unicode[STIX]{x1D648})$
, which contains complete information about the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
. This form was originally used by Holway (Reference Holway1966) to improve certain problems in the BGK (Bhatnagar–Gross–Krook) model of gas dynamics, resulting in what is popularly known as the ‘Ellipsoidal’ BGK model. In fact it is straightforward to show that (2.21) follows from the maximum entropy principle (Jaynes Reference Jaynes1957; Holway Reference Holway1966) when an extended set of hydrodynamic fields (
$\unicode[STIX]{x1D648}$
. This form was originally used by Holway (Reference Holway1966) to improve certain problems in the BGK (Bhatnagar–Gross–Krook) model of gas dynamics, resulting in what is popularly known as the ‘Ellipsoidal’ BGK model. In fact it is straightforward to show that (2.21) follows from the maximum entropy principle (Jaynes Reference Jaynes1957; Holway Reference Holway1966) when an extended set of hydrodynamic fields (
![]() ${\it\rho}$
,
${\it\rho}$
,
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D648}$
) is assumed to hold.
$\unicode[STIX]{x1D648}$
) is assumed to hold.
While (2.21) is an appropriate leading-order distribution function for a non-equilibrium steady state, such as steady uniform shear flow (Goldreich & Tremaine Reference Goldreich and Tremaine1978; Araki & Tremaine Reference Araki and Tremaine1986; Araki Reference Araki1988; Jenkins & Richman Reference Jenkins and Richman1988; Richman Reference Richman1989; Chou & Richman Reference Chou and Richman1998; Lutsko Reference Lutsko2004; Saha & Alam Reference Saha and Alam2014), the isotropic Maxwellian/Gaussian
(i.e. (2.21) with
![]() $\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}=T{\it\delta}_{{\it\alpha}{\it\beta}}$
) holds for the rest state of a gas at equilibrium.
$\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}=T{\it\delta}_{{\it\alpha}{\it\beta}}$
) holds for the rest state of a gas at equilibrium.
3 Steady uniform shear flow and the second-moment tensor
We consider a collection of smooth inelastic spheres of mass
![]() $m$
and diameter
$m$
and diameter
![]() ${\it\sigma}$
, subjected to uniform shear flow in the (
${\it\sigma}$
, subjected to uniform shear flow in the (
![]() $x,y$
)-plane:
$x,y$
)-plane:
where
![]() $2\dot{{\it\gamma}}$
is the uniform/constant shear rate. Note that
$2\dot{{\it\gamma}}$
is the uniform/constant shear rate. Note that
![]() $x$
and
$x$
and
![]() $y$
denote flow and gradient directions, respectively, and the
$y$
denote flow and gradient directions, respectively, and the
![]() $z$
direction is perpendicular to the
$z$
direction is perpendicular to the
![]() $x$
–
$x$
–
![]() $y$
plane, see figure 2; in the following, the (
$y$
plane, see figure 2; in the following, the (
![]() $x,y$
)-plane is referred to as the shear plane, with the
$x,y$
)-plane is referred to as the shear plane, with the
![]() $z$
-direction being the vorticity direction. The velocity gradient tensor completely characterizes the uniform shear flow (USF):
$z$
-direction being the vorticity direction. The velocity gradient tensor completely characterizes the uniform shear flow (USF):
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{u}=\left[\begin{array}{@{}ccc@{}}0 & 2\dot{{\it\gamma}} & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right]\equiv \unicode[STIX]{x1D63F}+\unicode[STIX]{x1D652},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{u}=\left[\begin{array}{@{}ccc@{}}0 & 2\dot{{\it\gamma}} & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right]\equiv \unicode[STIX]{x1D63F}+\unicode[STIX]{x1D652},\end{eqnarray}$$
with the shear (
![]() $\unicode[STIX]{x1D63F}$
) and spin (
$\unicode[STIX]{x1D63F}$
) and spin (
![]() $\unicode[STIX]{x1D652}$
) tensors, respectively, given by
$\unicode[STIX]{x1D652}$
) tensors, respectively, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D63F}=\left[\begin{array}{@{}ccc@{}}0 & \dot{{\it\gamma}} & 0\\ \dot{{\it\gamma}} & 0 & 0\\ 0 & 0 & 0\end{array}\right]\quad \text{and}\quad \unicode[STIX]{x1D652}=\left[\begin{array}{@{}ccc@{}}0 & \dot{{\it\gamma}} & 0\\ -\dot{{\it\gamma}} & 0 & 0\\ 0 & 0 & 0\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63F}=\left[\begin{array}{@{}ccc@{}}0 & \dot{{\it\gamma}} & 0\\ \dot{{\it\gamma}} & 0 & 0\\ 0 & 0 & 0\end{array}\right]\quad \text{and}\quad \unicode[STIX]{x1D652}=\left[\begin{array}{@{}ccc@{}}0 & \dot{{\it\gamma}} & 0\\ -\dot{{\it\gamma}} & 0 & 0\\ 0 & 0 & 0\end{array}\right].\end{eqnarray}$$
It is straightforward to verify that
![]() $\dot{{\it\gamma}}$
,
$\dot{{\it\gamma}}$
,
![]() $-\dot{{\it\gamma}}$
and 0 are the eigenvalues of
$-\dot{{\it\gamma}}$
and 0 are the eigenvalues of
![]() $\unicode[STIX]{x1D63F}$
and the corresponding orthonormal eigenvectors are, respectively,
$\unicode[STIX]{x1D63F}$
and the corresponding orthonormal eigenvectors are, respectively,
 $$\begin{eqnarray}|\unicode[STIX]{x1D60B}_{1}\rangle =\left[\begin{array}{@{}c@{}}\cos {\displaystyle \frac{{\rm\pi}}{4}}\\ \sin {\displaystyle \frac{{\rm\pi}}{4}}\\ 0\end{array}\right],\quad |\unicode[STIX]{x1D60B}_{2}\rangle =\left[\begin{array}{@{}c@{}}-\text{sin}\,{\displaystyle \frac{{\rm\pi}}{4}}\\ \cos {\displaystyle \frac{{\rm\pi}}{4}}\\ 0\end{array}\right]\quad \text{and}\quad |\unicode[STIX]{x1D60B}_{3}\rangle =\left[\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D60B}_{1}\rangle =\left[\begin{array}{@{}c@{}}\cos {\displaystyle \frac{{\rm\pi}}{4}}\\ \sin {\displaystyle \frac{{\rm\pi}}{4}}\\ 0\end{array}\right],\quad |\unicode[STIX]{x1D60B}_{2}\rangle =\left[\begin{array}{@{}c@{}}-\text{sin}\,{\displaystyle \frac{{\rm\pi}}{4}}\\ \cos {\displaystyle \frac{{\rm\pi}}{4}}\\ 0\end{array}\right]\quad \text{and}\quad |\unicode[STIX]{x1D60B}_{3}\rangle =\left[\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right],\end{eqnarray}$$
that are sketched in figure 2. While
![]() $|\unicode[STIX]{x1D60B}_{3}\rangle$
is directed along the
$|\unicode[STIX]{x1D60B}_{3}\rangle$
is directed along the
![]() $z$
-axis, the shear-plane eigenvectors
$z$
-axis, the shear-plane eigenvectors
![]() $|\unicode[STIX]{x1D60B}_{1}\rangle$
and
$|\unicode[STIX]{x1D60B}_{1}\rangle$
and
![]() $|\unicode[STIX]{x1D60B}_{2}\rangle$
are rotated by 45° anticlockwise from the
$|\unicode[STIX]{x1D60B}_{2}\rangle$
are rotated by 45° anticlockwise from the
![]() $xy$
-axes.
$xy$
-axes.

Figure 2. Sketch of the spherical coordinate system showing the eigendirections of the shear tensor
![]() $\unicode[STIX]{x1D63F}$
and the second-moment tensor
$\unicode[STIX]{x1D63F}$
and the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
. The uniform shear flow,
$\unicode[STIX]{x1D648}$
. The uniform shear flow,
![]() $\boldsymbol{u}=(2\dot{{\it\gamma}}y,0,0)$
, is directed along the
$\boldsymbol{u}=(2\dot{{\it\gamma}}y,0,0)$
, is directed along the
![]() $x$
-direction, with the velocity gradient along the
$x$
-direction, with the velocity gradient along the
![]() $y$
-direction and the mean vorticity along the
$y$
-direction and the mean vorticity along the
![]() $z$
-direction.
$z$
-direction.
3.1 Construction of the second-moment tensor from its eigenvectors
Recalling that the granular temperature
![]() $T=\unicode[STIX]{x1D614}_{{\it\alpha}{\it\alpha}}/3$
is the isotropic measure of the second-moment tensor
$T=\unicode[STIX]{x1D614}_{{\it\alpha}{\it\alpha}}/3$
is the isotropic measure of the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
, we can decompose
$\unicode[STIX]{x1D648}$
, we can decompose
![]() $\unicode[STIX]{x1D648}$
into an isotropic tensor and a traceless deviatoric tensor:
$\unicode[STIX]{x1D648}$
into an isotropic tensor and a traceless deviatoric tensor:
where
![]() $\widehat{\unicode[STIX]{x1D648}}/T$
is the dimensionless counterpart of its deviatoric/traceless tensor whose eigenvalues
$\widehat{\unicode[STIX]{x1D648}}/T$
is the dimensionless counterpart of its deviatoric/traceless tensor whose eigenvalues
![]() ${\it\xi}$
,
${\it\xi}$
,
![]() ${\it\varsigma}$
and
${\it\varsigma}$
and
![]() ${\it\zeta}$
satisfy
${\it\zeta}$
satisfy
![]() ${\it\xi}+{\it\varsigma}+{\it\zeta}=0$
. From (3.5) it follows that the eigenvalues of
${\it\xi}+{\it\varsigma}+{\it\zeta}=0$
. From (3.5) it follows that the eigenvalues of
![]() $\unicode[STIX]{x1D648}$
are
$\unicode[STIX]{x1D648}$
are
![]() $T(1+{\it\xi})$
,
$T(1+{\it\xi})$
,
![]() $T(1+{\it\varsigma})$
and
$T(1+{\it\varsigma})$
and
![]() $T(1+{\it\zeta})$
, and let us assume that the corresponding orthonormal set of eigendirections are
$T(1+{\it\zeta})$
, and let us assume that the corresponding orthonormal set of eigendirections are
![]() $|\unicode[STIX]{x1D614}_{1}\rangle$
,
$|\unicode[STIX]{x1D614}_{1}\rangle$
,
![]() $|\unicode[STIX]{x1D614}_{2}\rangle$
and
$|\unicode[STIX]{x1D614}_{2}\rangle$
and
![]() $|\unicode[STIX]{x1D614}_{3}\rangle$
(see figure 2), respectively. Therefore, we can express the second-moment tensor
$|\unicode[STIX]{x1D614}_{3}\rangle$
(see figure 2), respectively. Therefore, we can express the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
as
$\unicode[STIX]{x1D648}$
as
Referring to figure 2, we assume that the shear-plane eigenvectors
![]() $|\unicode[STIX]{x1D614}_{1}\rangle$
and
$|\unicode[STIX]{x1D614}_{1}\rangle$
and
![]() $|\unicode[STIX]{x1D614}_{2}\rangle$
can be obtained by rotating the system of axes at an angle
$|\unicode[STIX]{x1D614}_{2}\rangle$
can be obtained by rotating the system of axes at an angle
![]() $({\rm\pi}/4+{\it\phi})$
, with
$({\rm\pi}/4+{\it\phi})$
, with
![]() ${\it\phi}$
being unknown, in the anticlockwise sense about the
${\it\phi}$
being unknown, in the anticlockwise sense about the
![]() $z$
-axis which coincides with
$z$
-axis which coincides with
![]() $|\unicode[STIX]{x1D614}_{3}\rangle$
:
$|\unicode[STIX]{x1D614}_{3}\rangle$
:
 $$\begin{eqnarray}|\unicode[STIX]{x1D614}_{1}\rangle =\left[\begin{array}{@{}c@{}}\cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ 0\end{array}\right],\quad |\unicode[STIX]{x1D614}_{2}\rangle =\left[\begin{array}{@{}c@{}}-\text{sin}\left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ 0\end{array}\right]\quad \text{and}\quad |\unicode[STIX]{x1D614}_{3}\rangle =\left[\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D614}_{1}\rangle =\left[\begin{array}{@{}c@{}}\cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ 0\end{array}\right],\quad |\unicode[STIX]{x1D614}_{2}\rangle =\left[\begin{array}{@{}c@{}}-\text{sin}\left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ 0\end{array}\right]\quad \text{and}\quad |\unicode[STIX]{x1D614}_{3}\rangle =\left[\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right].\end{eqnarray}$$
We further assume that the contact vector
![]() $\boldsymbol{k}$
makes an angle
$\boldsymbol{k}$
makes an angle
![]() ${\it\varphi}$
with
${\it\varphi}$
with
![]() $|\unicode[STIX]{x1D614}_{3}\rangle \,$
, and
$|\unicode[STIX]{x1D614}_{3}\rangle \,$
, and
![]() ${\it\theta}$
is the angle between
${\it\theta}$
is the angle between
![]() $|\unicode[STIX]{x1D614}_{1}\rangle$
and
$|\unicode[STIX]{x1D614}_{1}\rangle$
and
![]() $\boldsymbol{k}-(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{z})\boldsymbol{z}$
, the projection of
$\boldsymbol{k}-(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{z})\boldsymbol{z}$
, the projection of
![]() $\boldsymbol{k}$
on the shear plane, as shown in figure 2. Inserting (3.7) into (3.6), we obtain the following expression for the second-moment tensor
$\boldsymbol{k}$
on the shear plane, as shown in figure 2. Inserting (3.7) into (3.6), we obtain the following expression for the second-moment tensor
and its deviatoric part is
 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D648}}=T\left[\begin{array}{@{}ccc@{}}{\it\lambda}^{2}+{\it\eta}\sin 2{\it\phi} & -{\it\eta}\cos 2{\it\phi} & 0\\ -{\it\eta}\cos 2{\it\phi} & {\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi} & 0\\ 0 & 0 & -2{\it\lambda}^{2}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D648}}=T\left[\begin{array}{@{}ccc@{}}{\it\lambda}^{2}+{\it\eta}\sin 2{\it\phi} & -{\it\eta}\cos 2{\it\phi} & 0\\ -{\it\eta}\cos 2{\it\phi} & {\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi} & 0\\ 0 & 0 & -2{\it\lambda}^{2}\end{array}\right],\end{eqnarray}$$
where we have introduced the following notation
Note that while
![]() ${\it\eta}\sim (T_{x}-T_{y})$
is a measure of the anisotropy of the second-moment tensor in the shear plane,
${\it\eta}\sim (T_{x}-T_{y})$
is a measure of the anisotropy of the second-moment tensor in the shear plane,
![]() ${\it\lambda}^{2}$
is a measure of the excess temperature (
${\it\lambda}^{2}$
is a measure of the excess temperature (
![]() ${\sim}(T-T_{z})$
, where
${\sim}(T-T_{z})$
, where
![]() $T_{i}$
is the temperature along the
$T_{i}$
is the temperature along the
![]() $i$
th direction, see § 6.1) along the mean vorticity direction. It is straightforward to verify that the eigenvalues in the shear plane can be expressed in terms of
$i$
th direction, see § 6.1) along the mean vorticity direction. It is straightforward to verify that the eigenvalues in the shear plane can be expressed in terms of
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\lambda}$
via
${\it\lambda}$
via
with the eigenvalue,
![]() ${\it\zeta}$
, along the vorticity direction (
${\it\zeta}$
, along the vorticity direction (
![]() $z$
), being given by (3.10).
$z$
), being given by (3.10).
Let us define the dimensionless shear rate (Savage & Jeffrey Reference Savage and Jeffrey1981)
which can be interpreted as the inverse of the square root of dimensionless temperature. Equation (3.12) is called the Savage–Jeffrey parameter (Savage & Jeffrey Reference Savage and Jeffrey1981) which is a measure of the mean shear velocity (
![]() $v_{sh}={\it\sigma}\dot{{\it\gamma}}/2$
over a particle diameter) relative to the thermal velocity (
$v_{sh}={\it\sigma}\dot{{\it\gamma}}/2$
over a particle diameter) relative to the thermal velocity (
![]() $v_{th}\propto \sqrt{T}$
) associated with the random motion of particles. The second-moment tensor (3.8) in USF, constructed from its eigenbasis, is therefore completely determined when
$v_{th}\propto \sqrt{T}$
) associated with the random motion of particles. The second-moment tensor (3.8) in USF, constructed from its eigenbasis, is therefore completely determined when
![]() $R$
,
$R$
,
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\lambda}^{2}$
are specified.
${\it\lambda}^{2}$
are specified.
3.2 The balance of second moment in USF
In steady uniform shear flow, the number density
![]() $n$
, the velocity gradient
$n$
, the velocity gradient
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
and the components of the second-moment tensor
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
and the components of the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
are constants and the contracted third moment vanishes. Therefore, the mass and momentum balance equations, (2.5) and (2.6), are identically satisfied. The remaining balance equation (2.7),
$\unicode[STIX]{x1D648}$
are constants and the contracted third moment vanishes. Therefore, the mass and momentum balance equations, (2.5) and (2.6), are identically satisfied. The remaining balance equation (2.7),
![]() $\unicode[STIX]{x1D617}_{{\it\delta}{\it\beta}}u_{{\it\alpha},{\it\delta}}+\unicode[STIX]{x1D617}_{{\it\delta}{\it\alpha}}u_{{\it\beta},{\it\delta}}=\aleph _{{\it\alpha}{\it\beta}}$
, for the second-moment tensor simplifies to
$\unicode[STIX]{x1D617}_{{\it\delta}{\it\beta}}u_{{\it\alpha},{\it\delta}}+\unicode[STIX]{x1D617}_{{\it\delta}{\it\alpha}}u_{{\it\beta},{\it\delta}}=\aleph _{{\it\alpha}{\it\beta}}$
, for the second-moment tensor simplifies to
where we made use of
![]() $u_{{\it\alpha},{\it\delta}}=(\unicode[STIX]{x1D60B}_{{\it\alpha}{\it\delta}}+\unicode[STIX]{x1D61E}_{{\it\alpha}{\it\delta}})$
,
$u_{{\it\alpha},{\it\delta}}=(\unicode[STIX]{x1D60B}_{{\it\alpha}{\it\delta}}+\unicode[STIX]{x1D61E}_{{\it\alpha}{\it\delta}})$
,
![]() $\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}={\it\rho}\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}+{\it\Theta}_{{\it\alpha}{\it\beta}}$
and the following decomposition for the collisional source of second moment (Jenkins & Richman Reference Jenkins and Richman1988; Chou & Richman Reference Chou and Richman1998; Saha & Alam Reference Saha and Alam2014):
$\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}={\it\rho}\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}+{\it\Theta}_{{\it\alpha}{\it\beta}}$
and the following decomposition for the collisional source of second moment (Jenkins & Richman Reference Jenkins and Richman1988; Chou & Richman Reference Chou and Richman1998; Saha & Alam Reference Saha and Alam2014):
The integral expression for the collisional stress tensor is
the tensor
![]() $\unicode[STIX]{x1D608}_{{\it\alpha}{\it\beta}}$
is
$\unicode[STIX]{x1D608}_{{\it\alpha}{\it\beta}}$
is
and the traceless tensors (denoted by a hat),
![]() $\widehat{\unicode[STIX]{x1D60C}}_{{\it\alpha}{\it\beta}}$
and
$\widehat{\unicode[STIX]{x1D60C}}_{{\it\alpha}{\it\beta}}$
and
![]() $\widehat{\unicode[STIX]{x1D60E}}_{{\it\alpha}{\it\beta}}$
, are
$\widehat{\unicode[STIX]{x1D60E}}_{{\it\alpha}{\it\beta}}$
, are
The integrals (3.15)–(3.18) are to be evaluated over
![]() $\text{d}\boldsymbol{k}$
such that
$\text{d}\boldsymbol{k}$
such that
![]() $\text{d}\boldsymbol{k}=\sin {\it\varphi}\,\text{d}{\it\varphi}\,\text{d}{\it\theta}$
, with the limits of the integrations being
$\text{d}\boldsymbol{k}=\sin {\it\varphi}\,\text{d}{\it\varphi}\,\text{d}{\it\theta}$
, with the limits of the integrations being
![]() ${\it\theta}\in (0,2{\rm\pi})$
and
${\it\theta}\in (0,2{\rm\pi})$
and
![]() ${\it\varphi}\in (0,{\rm\pi})$
.
${\it\varphi}\in (0,{\rm\pi})$
.
In (3.17)–(3.18),
![]() $\boldsymbol{j}$
represents an unit vector perpendicular to the contact vector
$\boldsymbol{j}$
represents an unit vector perpendicular to the contact vector
![]() $\boldsymbol{k}$
that lies in the plane formed by
$\boldsymbol{k}$
that lies in the plane formed by
![]() $\boldsymbol{g}$
and
$\boldsymbol{g}$
and
![]() $\boldsymbol{k}$
such that
$\boldsymbol{k}$
such that
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{k}=\left[\begin{array}{@{}c@{}}\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\sin {\it\varphi}\\ \sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\sin {\it\varphi}\\ \cos {\it\varphi}\end{array}\!\!\!\right] & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{k}=\left[\begin{array}{@{}c@{}}\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\sin {\it\varphi}\\ \sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\sin {\it\varphi}\\ \cos {\it\varphi}\end{array}\!\!\!\right] & \displaystyle\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{j}=\frac{1}{\sqrt{2}}\left[\begin{array}{@{}c@{}}\cos {\it\varphi}\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)-\sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \cos {\it\varphi}\sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)+\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ -\text{sin}\,{\it\varphi}\end{array}\!\!\!\right]. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{j}=\frac{1}{\sqrt{2}}\left[\begin{array}{@{}c@{}}\cos {\it\varphi}\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)-\sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ \cos {\it\varphi}\sin \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)+\cos \left({\it\theta}+{\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right)\\ -\text{sin}\,{\it\varphi}\end{array}\!\!\!\right]. & \displaystyle\end{eqnarray}$$
The following two analytic functions (Araki & Tremaine Reference Araki and Tremaine1986) appear in the integrand of (3.15)–(3.18):
where
The origin of
![]() ${\it\chi}$
can be traced to the excluded volume effects of macroscopic particles (Jenkins & Richman Reference Jenkins and Richman1988; Saha & Alam Reference Saha and Alam2014), and hence
${\it\chi}$
can be traced to the excluded volume effects of macroscopic particles (Jenkins & Richman Reference Jenkins and Richman1988; Saha & Alam Reference Saha and Alam2014), and hence
![]() ${\it\chi}=0$
in the dilute limit and, consequently,
${\it\chi}=0$
in the dilute limit and, consequently,
3.3 Second-moment balance in rotated coordinate frame
Let us now rewrite (3.13) in a new coordinate system
![]() $x^{\prime }y^{\prime }z^{\prime }$
, formed by the orthonormal triad of eigenvectors of
$x^{\prime }y^{\prime }z^{\prime }$
, formed by the orthonormal triad of eigenvectors of
![]() $\unicode[STIX]{x1D648}$
, i.e., with respect to the coordinate system whose axes coincide with
$\unicode[STIX]{x1D648}$
, i.e., with respect to the coordinate system whose axes coincide with
![]() $|\unicode[STIX]{x1D614}_{1}\rangle \,$
,
$|\unicode[STIX]{x1D614}_{1}\rangle \,$
,
![]() $|\unicode[STIX]{x1D614}_{2}\rangle$
and
$|\unicode[STIX]{x1D614}_{2}\rangle$
and
![]() $|\unicode[STIX]{x1D614}_{3}\rangle \,$
, respectively. This amounts to a transformation, see figure 2, via the following rotation matrix,
$|\unicode[STIX]{x1D614}_{3}\rangle \,$
, respectively. This amounts to a transformation, see figure 2, via the following rotation matrix,
 $$\begin{eqnarray}\mathscr{R}=\left[\begin{array}{@{}ccc@{}}\cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & -\!\sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & 0\\ \sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & \cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & 0\\ 0 & 0 & 1\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}=\left[\begin{array}{@{}ccc@{}}\cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & -\!\sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & 0\\ \sin \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & \cos \left({\it\phi}+{\displaystyle \frac{{\rm\pi}}{4}}\right) & 0\\ 0 & 0 & 1\end{array}\right],\end{eqnarray}$$
that transforms the second-moment tensor,
 $$\begin{eqnarray}\unicode[STIX]{x1D648}^{\prime }=T\left[\begin{array}{@{}ccc@{}}1+{\it\lambda}^{2}-{\it\eta} & 0 & 0\\ 0 & 1+{\it\lambda}^{2}+{\it\eta} & 0\\ 0 & 0 & 1-2{\it\lambda}^{2}\end{array}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D648}^{\prime }=T\left[\begin{array}{@{}ccc@{}}1+{\it\lambda}^{2}-{\it\eta} & 0 & 0\\ 0 & 1+{\it\lambda}^{2}+{\it\eta} & 0\\ 0 & 0 & 1-2{\it\lambda}^{2}\end{array}\right],\end{eqnarray}$$
into a diagonal matrix. With a prime over a quantity denoting its value in the new coordinate frame, the following relations hold:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\prime }=\dot{{\it\gamma}}\left[\begin{array}{@{}ccc@{}}\cos 2{\it\phi} & -\text{sin}\,2{\it\phi} & 0\\ -\text{sin}\,2{\it\phi} & -\text{cos}\,2{\it\phi} & 0\\ 0 & 0 & 0\end{array}\right]\quad \text{and}\quad \unicode[STIX]{x1D652}^{\prime }=\unicode[STIX]{x1D652}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D63F}^{\prime }=\dot{{\it\gamma}}\left[\begin{array}{@{}ccc@{}}\cos 2{\it\phi} & -\text{sin}\,2{\it\phi} & 0\\ -\text{sin}\,2{\it\phi} & -\text{cos}\,2{\it\phi} & 0\\ 0 & 0 & 0\end{array}\right]\quad \text{and}\quad \unicode[STIX]{x1D652}^{\prime }=\unicode[STIX]{x1D652}. & \displaystyle\end{eqnarray}$$
The last equation confirms that the spin tensor
![]() $\unicode[STIX]{x1D652}$
is invariant under the planar rotation (3.24).
$\unicode[STIX]{x1D652}$
is invariant under the planar rotation (3.24).
With the aid of (3.25)–(3.29), the second-moment balance equation (3.13) transforms into four independent equations in the rotated coordinate frame: (i) the trace of (3.13),
(ii) the
![]() $z^{\prime }$
–
$z^{\prime }$
–
![]() $z^{\prime }$
component of its deviatoric part
$z^{\prime }$
component of its deviatoric part
(iii) the difference between the
![]() $x^{\prime }$
–
$x^{\prime }$
–
![]() $x^{\prime }$
and
$x^{\prime }$
and
![]() $y^{\prime }$
–
$y^{\prime }$
–
![]() $y^{\prime }$
components
$y^{\prime }$
components
and, finally, (iv) the off-diagonal
![]() $x^{\prime }$
–
$x^{\prime }$
–
![]() $y^{\prime }$
component
$y^{\prime }$
component
where
see (3.14)–(3.18). Various collision integrals (
![]() ${\it\Theta}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
,
${\it\Theta}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
,
![]() $\unicode[STIX]{x1D608}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
and
$\unicode[STIX]{x1D608}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
and
![]() ${\it\Gamma}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
) appearing in (3.30)–(3.33) can be expressed in terms of the following three integrals (see appendix A in supplementary materials available at http://dx.doi.org/10.1017/jfm.2016.237):
${\it\Gamma}_{{\it\alpha}^{\prime }{\it\beta}^{\prime }}$
) appearing in (3.30)–(3.33) can be expressed in terms of the following three integrals (see appendix A in supplementary materials available at http://dx.doi.org/10.1017/jfm.2016.237):
 $$\begin{eqnarray}\displaystyle \mathscr{H}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle \times \,(1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2))^{{\it\gamma}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{F}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{H}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle \times \,(1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2))^{{\it\gamma}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{F}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle \times \,(1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2))^{{\it\gamma}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{G}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi}\nonumber\\ \displaystyle & & \displaystyle \times \,(1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2))^{{\it\gamma}/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{G}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{K}_{{\it\alpha}{\it\beta}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi} [\,\!(1-2{\it\lambda}^{2})(\sin (2{\it\phi}+2{\it\theta})\nonumber\\ \displaystyle & & \displaystyle -\cos {\it\varphi}\times \cos (2{\it\phi}+2{\it\theta}))+\sin ^{2}{\it\varphi}(3{\it\lambda}^{2}\sin (2{\it\phi}+2{\it\theta})-{\it\eta}\sin 2{\it\phi})]\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{G}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{K}_{{\it\alpha}{\it\beta}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}) & \equiv & \displaystyle \int _{{\it\theta}=0}^{2{\rm\pi}}\int _{{\it\varphi}=0}^{{\rm\pi}}\sin ^{{\it\alpha}}2{\it\theta}\cos ^{{\it\beta}}2{\it\theta}\sin ^{{\it\delta}}{\it\varphi}\cos ^{p}{\it\varphi} [\,\!(1-2{\it\lambda}^{2})(\sin (2{\it\phi}+2{\it\theta})\nonumber\\ \displaystyle & & \displaystyle -\cos {\it\varphi}\times \cos (2{\it\phi}+2{\it\theta}))+\sin ^{2}{\it\varphi}(3{\it\lambda}^{2}\sin (2{\it\phi}+2{\it\theta})-{\it\eta}\sin 2{\it\phi})]\nonumber\\ \displaystyle & & \displaystyle \times \,\mathfrak{G}({\it\chi}[{\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}])\,\text{d}{\it\varphi}\,\text{d}{\it\theta},\end{eqnarray}$$
with
![]() $\mathfrak{F}({\it\chi})$
and
$\mathfrak{F}({\it\chi})$
and
![]() $\mathfrak{G}({\it\chi})$
being given by (3.20) and (3.21) respectively. Of course, the integrals (3.35)–(3.37) can be evaluated numerically via any quadrature method.
$\mathfrak{G}({\it\chi})$
being given by (3.20) and (3.21) respectively. Of course, the integrals (3.35)–(3.37) can be evaluated numerically via any quadrature method.
In § 4, we outline an approximate method to evaluate the integrals (3.35)–(3.37) analytically via a power series expansion which helps to reduce the integro-algebraic equations (3.30)–(3.33) into a set of algebraic equations for four unknowns
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() $R$
,
$R$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\lambda}$
. More importantly, we derive ‘closed-form’ analytical solutions of the second-moment balance at the Burnett order (see § 4.1) and beyond (§ 4.2).
${\it\lambda}$
. More importantly, we derive ‘closed-form’ analytical solutions of the second-moment balance at the Burnett order (see § 4.1) and beyond (§ 4.2).
4 Closed-form solutions of ‘truncated’ second-moment equations
We substitute the power series representations for the complementary error function and the exponential into (3.20) and (3.21). After some straightforward algebra, the expressions for
![]() $\mathfrak{F}({\it\chi})$
and
$\mathfrak{F}({\it\chi})$
and
![]() $\mathfrak{G}({\it\chi})$
can be written as (Saha & Alam Reference Saha and Alam2014)
$\mathfrak{G}({\it\chi})$
can be written as (Saha & Alam Reference Saha and Alam2014)
 $$\begin{eqnarray}\displaystyle \mathfrak{F}({\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}) & = & \displaystyle -\sqrt{{\rm\pi}}\left[\vphantom{\left\{\displaystyle \frac{\sin ^{2}}{\{\sin ^{2}\}}\right\}^{3}}\frac{3R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\!\left\{\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right\}^{3}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=0}^{\infty }\frac{(-1)^{n}}{n!}\frac{3}{(2n-1)(2n-3)}\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right]^{2n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{F}({\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}) & = & \displaystyle -\sqrt{{\rm\pi}}\left[\vphantom{\left\{\displaystyle \frac{\sin ^{2}}{\{\sin ^{2}\}}\right\}^{3}}\frac{3R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\!\left\{\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right\}^{3}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=0}^{\infty }\frac{(-1)^{n}}{n!}\frac{3}{(2n-1)(2n-3)}\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right]^{2n},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathfrak{G}({\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}) & = & \displaystyle \sqrt{{\rm\pi}}\left[\frac{1}{2}+\frac{4R^{2}\sin ^{4}{\it\varphi}\cos ^{2}(2{\it\phi}+2{\it\theta})}{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=0}^{\infty }\frac{(-1)^{n}}{n!}\frac{2}{(2n-1)(2n+1)}\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right]^{2n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{G}({\it\eta},R,{\it\phi},{\it\lambda};{\it\theta},{\it\varphi}) & = & \displaystyle \sqrt{{\rm\pi}}\left[\frac{1}{2}+\frac{4R^{2}\sin ^{4}{\it\varphi}\cos ^{2}(2{\it\phi}+2{\it\theta})}{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=0}^{\infty }\frac{(-1)^{n}}{n!}\frac{2}{(2n-1)(2n+1)}\nonumber\\ \displaystyle & & \displaystyle \times \left[\frac{2R\sin ^{2}{\it\varphi}\cos (2{\it\phi}+2{\it\theta})}{\{1-{\it\eta}\sin ^{2}{\it\varphi}\cos 2{\it\theta}+{\it\lambda}^{2}(3\sin ^{2}{\it\varphi}-2)\}^{1/2}}\right]^{2n+1}.\end{eqnarray}$$
Substituting (4.1)–(4.2) into (3.35)–(3.37) and carrying out term-by-term integrations over
![]() ${\it\theta}\in (0,2{\rm\pi})$
and
${\it\theta}\in (0,2{\rm\pi})$
and
![]() ${\it\varphi}\in (0,{\rm\pi})$
results in an infinite series in
${\it\varphi}\in (0,{\rm\pi})$
results in an infinite series in
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() $R$
and
$R$
and
![]() ${\it\lambda}$
for each integral in (3.35)–(3.37), see (A 3)–(A 17) in appendix A (supplementary materials).
${\it\lambda}$
for each integral in (3.35)–(3.37), see (A 3)–(A 17) in appendix A (supplementary materials).
4.1 Exact solution at Burnett order
Retaining terms up to second order
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 2)$
in the resulting infinite series for each integral (3.35)–(3.37) and substituting them into (3.30)–(3.33), we obtain the following set of coupled nonlinear algebraic equations
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 2)$
in the resulting infinite series for each integral (3.35)–(3.37) and substituting them into (3.30)–(3.33), we obtain the following set of coupled nonlinear algebraic equations
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}20\sqrt{{\rm\pi}}\{1+{\textstyle \frac{4}{5}}(1+e){\it\nu}g_{0}\}{\it\eta}R\cos 2{\it\phi}+128(1+e){\it\nu}g_{0}R^{2}\\ \quad -\,3(1-e^{2}){\it\nu}g_{0}(10+{\it\eta}^{2}+32R^{2}+8\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi})=0\end{array}\\ \begin{array}{@{}l@{}}35\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}+(1+e){\it\nu}g_{0}\{32(1+3e)R^{2}-3(3-e)({\it\eta}^{2}+21{\it\lambda}^{2})\\ \quad -\,8\sqrt{{\rm\pi}}(4-3e){\it\eta}R\cos 2{\it\phi}\}=0\end{array}\\ 5\sqrt{{\rm\pi}}R\cos 2{\it\phi}-(1+e){\it\nu}g_{0}\{3(3-e){\it\eta}+2(1-3e)\sqrt{{\rm\pi}}R\cos 2{\it\phi}\}=0\\ 5({\it\eta}-\sin 2{\it\phi})+2(1+e)(1-3e){\it\nu}g_{0}\sin (2{\it\phi})=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}20\sqrt{{\rm\pi}}\{1+{\textstyle \frac{4}{5}}(1+e){\it\nu}g_{0}\}{\it\eta}R\cos 2{\it\phi}+128(1+e){\it\nu}g_{0}R^{2}\\ \quad -\,3(1-e^{2}){\it\nu}g_{0}(10+{\it\eta}^{2}+32R^{2}+8\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi})=0\end{array}\\ \begin{array}{@{}l@{}}35\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}+(1+e){\it\nu}g_{0}\{32(1+3e)R^{2}-3(3-e)({\it\eta}^{2}+21{\it\lambda}^{2})\\ \quad -\,8\sqrt{{\rm\pi}}(4-3e){\it\eta}R\cos 2{\it\phi}\}=0\end{array}\\ 5\sqrt{{\rm\pi}}R\cos 2{\it\phi}-(1+e){\it\nu}g_{0}\{3(3-e){\it\eta}+2(1-3e)\sqrt{{\rm\pi}}R\cos 2{\it\phi}\}=0\\ 5({\it\eta}-\sin 2{\it\phi})+2(1+e)(1-3e){\it\nu}g_{0}\sin (2{\it\phi})=0.\end{array}\right\}\end{eqnarray}$$
These equations represent the second-moment balance equations at ‘Burnett order’ (Burnett Reference Burnett1935) since all terms up to the second order in the shear rate have been retained.
Equations (4.3) admit an exact solution
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\eta}={\displaystyle \frac{\{5-2(1+e)(1-3e){\it\nu}g_{0}\}}{5}}\sin 2{\it\phi}\\ \begin{array}{@{}rcl@{}}{\it\lambda}^{2}\, & =\, & {\displaystyle \frac{10(1-e)}{21(3-e)}}+{\displaystyle \frac{[(7-3e)\{5-2(1+e)(1-3e){\it\nu}g_{0}\}-18(1+e)^{2}(3-e){\it\nu}g_{0}]}{525(3-e)}}\\ \, & \, & \times \,\{5-2(1+e)(1-3e){\it\nu}g_{0}\}\sin ^{2}2{\it\phi}\end{array}\\ R={\displaystyle \frac{3(1+e)(3-e)}{5\sqrt{{\rm\pi}}}}{\it\nu}g_{0}\tan 2{\it\phi}\\ {\displaystyle \frac{{\it\eta}}{R}}\cos (2{\it\phi})={\displaystyle \frac{\sqrt{{\rm\pi}}}{3(1+e)(3-e)}}\cos ^{2}(2{\it\phi})\left({\displaystyle \frac{5}{{\it\nu}g_{0}}}+2(1+e)(3e-1)\right),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\eta}={\displaystyle \frac{\{5-2(1+e)(1-3e){\it\nu}g_{0}\}}{5}}\sin 2{\it\phi}\\ \begin{array}{@{}rcl@{}}{\it\lambda}^{2}\, & =\, & {\displaystyle \frac{10(1-e)}{21(3-e)}}+{\displaystyle \frac{[(7-3e)\{5-2(1+e)(1-3e){\it\nu}g_{0}\}-18(1+e)^{2}(3-e){\it\nu}g_{0}]}{525(3-e)}}\\ \, & \, & \times \,\{5-2(1+e)(1-3e){\it\nu}g_{0}\}\sin ^{2}2{\it\phi}\end{array}\\ R={\displaystyle \frac{3(1+e)(3-e)}{5\sqrt{{\rm\pi}}}}{\it\nu}g_{0}\tan 2{\it\phi}\\ {\displaystyle \frac{{\it\eta}}{R}}\cos (2{\it\phi})={\displaystyle \frac{\sqrt{{\rm\pi}}}{3(1+e)(3-e)}}\cos ^{2}(2{\it\phi})\left({\displaystyle \frac{5}{{\it\nu}g_{0}}}+2(1+e)(3e-1)\right),\end{array}\right\}\end{eqnarray}$$
where
![]() $\sin ^{2}(2{\it\phi})=\mathscr{Y}$
is the real positive root of the quadratic equation
$\sin ^{2}(2{\it\phi})=\mathscr{Y}$
is the real positive root of the quadratic equation
For specified values of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
, the non-coaxiality angle
$e$
, the non-coaxiality angle
![]() ${\it\phi}$
is determined from (4.5) and the remaining quantities are from (4.4): this is dubbed the ‘Burnett-order’ solution for
${\it\phi}$
is determined from (4.5) and the remaining quantities are from (4.4): this is dubbed the ‘Burnett-order’ solution for
![]() ${\it\phi}$
,
${\it\phi}$
,
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\lambda}^{2}$
and
${\it\lambda}^{2}$
and
![]() $R$
as functions of
$R$
as functions of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
.
$e$
.
4.2 Beyond Burnett order: perturbation solution
To obtain solutions beyond the Burnett order, i.e. at
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q>2)$
, we must solve related nonlinear algebraic equations as given by (B 1) in appendix B. We could not find an ‘exact’ solution of (B 1) either at super-Burnett or super–super Burnett order (except in the dilute limit, see appendix B.2). Therefore we look for perturbation solution of (B 1) by taking our Burnett-order solution (4.4)–(4.5) as the leading solution:
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q>2)$
, we must solve related nonlinear algebraic equations as given by (B 1) in appendix B. We could not find an ‘exact’ solution of (B 1) either at super-Burnett or super–super Burnett order (except in the dilute limit, see appendix B.2). Therefore we look for perturbation solution of (B 1) by taking our Burnett-order solution (4.4)–(4.5) as the leading solution:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\eta}={\it\eta}^{(2)}+{\it\varepsilon}{\it\eta}^{(3)}+{\it\varepsilon}^{2}{\it\eta}^{(4)}+\cdots \\ {\it\lambda}={\it\lambda}^{(2)}+{\it\varepsilon}{\it\lambda}^{(3)}+{\it\varepsilon}^{2}{\it\lambda}^{(4)}+\cdots \\ R=R^{(2)}+{\it\varepsilon}R^{(3)}+{\it\varepsilon}^{2}R^{(4)}+\cdots \\ \sin 2{\it\phi}=\sin 2{\it\phi}^{(2)}+{\it\varepsilon}\sin 2{\it\phi}^{(3)}+{\it\varepsilon}^{2}\sin 2{\it\phi}^{(4)}+\cdots \,.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\eta}={\it\eta}^{(2)}+{\it\varepsilon}{\it\eta}^{(3)}+{\it\varepsilon}^{2}{\it\eta}^{(4)}+\cdots \\ {\it\lambda}={\it\lambda}^{(2)}+{\it\varepsilon}{\it\lambda}^{(3)}+{\it\varepsilon}^{2}{\it\lambda}^{(4)}+\cdots \\ R=R^{(2)}+{\it\varepsilon}R^{(3)}+{\it\varepsilon}^{2}R^{(4)}+\cdots \\ \sin 2{\it\phi}=\sin 2{\it\phi}^{(2)}+{\it\varepsilon}\sin 2{\it\phi}^{(3)}+{\it\varepsilon}^{2}\sin 2{\it\phi}^{(4)}+\cdots \,.\end{array}\right\}\end{eqnarray}$$
In the above expressions
![]() ${\it\varepsilon}\sim \dot{{\it\gamma}}$
and the superscript ‘2’ corresponds to the ‘Burnett-order’ solution and the superscripts ‘3’ and ‘4’ correspond to the corrections at the third and fourth order, respectively, in the shear rate. Plugging (4.6) into the corresponding third- and fourth-order equations and after performing some cumbersome algebra, we obtain the following solution for the correction terms at third order:
${\it\varepsilon}\sim \dot{{\it\gamma}}$
and the superscript ‘2’ corresponds to the ‘Burnett-order’ solution and the superscripts ‘3’ and ‘4’ correspond to the corrections at the third and fourth order, respectively, in the shear rate. Plugging (4.6) into the corresponding third- and fourth-order equations and after performing some cumbersome algebra, we obtain the following solution for the correction terms at third order:
The fourth-order correction terms are found to be non-zero and are given in appendix B.1 (supplementary materials).

Figure 3. Variations of (a)
![]() ${\it\eta}$
, (b)
${\it\eta}$
, (b)
![]() ${\it\lambda}^{2}$
, (c)
${\it\lambda}^{2}$
, (c)
![]() $R$
and (d)
$R$
and (d)
![]() ${\it\phi}$
(degrees) with density (
${\it\phi}$
(degrees) with density (
![]() ${\it\nu}$
). While the solid black lines denote the exact numerical solution of second-moment equations, the blue dashed and the red dot-dashed lines denote the exact Burnett-order solution and the perturbation solution at fourth order, respectively.
${\it\nu}$
). While the solid black lines denote the exact numerical solution of second-moment equations, the blue dashed and the red dot-dashed lines denote the exact Burnett-order solution and the perturbation solution at fourth order, respectively.
4.3 Comparison between analytical and numerical solutions for
 ${\it\eta}$
,
${\it\eta}$
,
 ${\it\phi}$
,
${\it\phi}$
,
 ${\it\lambda}$
and
${\it\lambda}$
and
 $R$
$R$
Figure 3(a–d) shows a comparison of the ‘exact’ numerical solution of second-moment equations with its (i) exact Burnett-order solution and (ii) perturbation solution at the fourth order for the variations of the shear-plane anisotropy
![]() ${\it\eta}$
, the excess temperature
${\it\eta}$
, the excess temperature
![]() ${\it\lambda}^{2}$
, the dimensionless shear rate
${\it\lambda}^{2}$
, the dimensionless shear rate
![]() $R$
and the non-coaxiality angle
$R$
and the non-coaxiality angle
![]() ${\it\phi}$
(degrees) with density (
${\it\phi}$
(degrees) with density (
![]() ${\it\nu}$
) for three values of the restitution coefficient
${\it\nu}$
) for three values of the restitution coefficient
![]() $e=0.9$
, 0.7 and 0.5. In each panel, while the solid black lines denote the exact numerical solution, the blue dashed lines and red dot-dashed lines denote the analytical solutions at the second and fourth order, respectively. It is seen that while the Burnett-order solution provides a good agreement for
$e=0.9$
, 0.7 and 0.5. In each panel, while the solid black lines denote the exact numerical solution, the blue dashed lines and red dot-dashed lines denote the analytical solutions at the second and fourth order, respectively. It is seen that while the Burnett-order solution provides a good agreement for
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\lambda}^{2}$
,
${\it\lambda}^{2}$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $R$
up to a restitution coefficient of
$R$
up to a restitution coefficient of
![]() $e\geqslant 0.9$
, the fourth-order solution is required for more dissipative particles (
$e\geqslant 0.9$
, the fourth-order solution is required for more dissipative particles (
![]() $e=0.5$
) for a reasonable agreement over the whole range of density (for
$e=0.5$
) for a reasonable agreement over the whole range of density (for
![]() ${\it\lambda}^{2}$
,
${\it\lambda}^{2}$
,
![]() $R$
and
$R$
and
![]() ${\it\phi}$
, see panels
${\it\phi}$
, see panels
![]() $b$
,
$b$
,
![]() $c$
and
$c$
and
![]() $d$
respectively). On the other hand, panel
$d$
respectively). On the other hand, panel
![]() $a$
indicates that even the fourth-order perturbation solution is not enough to quantitatively predict the shear-plane anisotropy
$a$
indicates that even the fourth-order perturbation solution is not enough to quantitatively predict the shear-plane anisotropy
![]() ${\it\eta}$
at
${\it\eta}$
at
![]() $e=0.5$
in the dense limit (for
$e=0.5$
in the dense limit (for
![]() ${\it\nu}>0.3$
).
${\it\nu}>0.3$
).
All transport coefficients in USF can be expressed as functions of
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\lambda}^{2}$
,
${\it\lambda}^{2}$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $R$
as discussed in §§ 5.1–5.4. We will further check the ability of the Burnett- and fourth-order solutions of the second-moment equation to predict
$R$
as discussed in §§ 5.1–5.4. We will further check the ability of the Burnett- and fourth-order solutions of the second-moment equation to predict
![]() $p$
,
$p$
,
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
in § 5.5 as functions of
$\unicode[STIX]{x1D615}_{2}$
in § 5.5 as functions of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
.
$e$
.
5 Constitutive relations for non-Newtonian stress and collisional dissipation
The dimensionless stress tensor in USF can be written as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64B}^{\ast } & = & \displaystyle \frac{\unicode[STIX]{x1D64B}}{{\it\rho}_{p}U_{R}^{2}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D617}_{xx}^{\ast } & \unicode[STIX]{x1D617}_{xy}^{\ast } & 0\\ \unicode[STIX]{x1D617}_{yx}^{\ast } & \unicode[STIX]{x1D617}_{yy}^{\ast } & 0\\ 0 & 0 & \unicode[STIX]{x1D617}_{zz}^{\ast }\end{array}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \left(\begin{array}{@{}ccc@{}}p^{\ast } & 0 & 0\\ 0 & p^{\ast } & 0\\ 0 & 0 & p^{\ast }\end{array}\right)+\left(\begin{array}{@{}ccc@{}}{\textstyle \frac{2}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }+{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{2}^{\ast } & -{\it\mu}^{\ast } & 0\\ -{\it\mu}^{\ast } & -{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }+{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{2}^{\ast } & 0\\ 0 & 0 & -{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }-{\textstyle \frac{2}{3}}\unicode[STIX]{x1D615}_{2}^{\ast }\end{array}\right),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64B}^{\ast } & = & \displaystyle \frac{\unicode[STIX]{x1D64B}}{{\it\rho}_{p}U_{R}^{2}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D617}_{xx}^{\ast } & \unicode[STIX]{x1D617}_{xy}^{\ast } & 0\\ \unicode[STIX]{x1D617}_{yx}^{\ast } & \unicode[STIX]{x1D617}_{yy}^{\ast } & 0\\ 0 & 0 & \unicode[STIX]{x1D617}_{zz}^{\ast }\end{array}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle \left(\begin{array}{@{}ccc@{}}p^{\ast } & 0 & 0\\ 0 & p^{\ast } & 0\\ 0 & 0 & p^{\ast }\end{array}\right)+\left(\begin{array}{@{}ccc@{}}{\textstyle \frac{2}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }+{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{2}^{\ast } & -{\it\mu}^{\ast } & 0\\ -{\it\mu}^{\ast } & -{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }+{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{2}^{\ast } & 0\\ 0 & 0 & -{\textstyle \frac{1}{3}}\unicode[STIX]{x1D615}_{1}^{\ast }-{\textstyle \frac{2}{3}}\unicode[STIX]{x1D615}_{2}^{\ast }\end{array}\right),\qquad\end{eqnarray}$$
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}p^{\ast }={\textstyle \frac{1}{3}}(\unicode[STIX]{x1D617}_{xx}^{\ast }+\unicode[STIX]{x1D617}_{yy}^{\ast }+\unicode[STIX]{x1D617}_{zz}^{\ast })\\ {\it\mu}^{\ast }=-\unicode[STIX]{x1D617}_{xy}^{\ast },\\ \unicode[STIX]{x1D615}_{1}^{\ast }=(\unicode[STIX]{x1D617}_{xx}^{\ast }-\unicode[STIX]{x1D617}_{yy}^{\ast }),\\ \unicode[STIX]{x1D615}_{2}^{\ast }=(\unicode[STIX]{x1D617}_{yy}^{\ast }-\unicode[STIX]{x1D617}_{zz}^{\ast })\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}p^{\ast }={\textstyle \frac{1}{3}}(\unicode[STIX]{x1D617}_{xx}^{\ast }+\unicode[STIX]{x1D617}_{yy}^{\ast }+\unicode[STIX]{x1D617}_{zz}^{\ast })\\ {\it\mu}^{\ast }=-\unicode[STIX]{x1D617}_{xy}^{\ast },\\ \unicode[STIX]{x1D615}_{1}^{\ast }=(\unicode[STIX]{x1D617}_{xx}^{\ast }-\unicode[STIX]{x1D617}_{yy}^{\ast }),\\ \unicode[STIX]{x1D615}_{2}^{\ast }=(\unicode[STIX]{x1D617}_{yy}^{\ast }-\unicode[STIX]{x1D617}_{zz}^{\ast })\end{array}\right\}\end{eqnarray}$$
is the pressure, the shear viscosity and the first and second normal stress differences, respectively; here
![]() ${\it\rho}_{p}$
is the material/intrinsic density of particles and
${\it\rho}_{p}$
is the material/intrinsic density of particles and
![]() $U_{R}=2\dot{{\it\gamma}}{\it\sigma}$
is the reference velocity scale.
$U_{R}=2\dot{{\it\gamma}}{\it\sigma}$
is the reference velocity scale.
The power series (4.2) for
![]() $\mathfrak{G}({\it\eta},R,{\it\phi},{\it\lambda})$
is inserted into (3.15) to evaluate the collisional stress, and the total stress tensor is subsequently obtained from (2.8) by summing the kinetic stress and the collisional stress. We will express constitutive relations in terms of the dimensionless temperature, which is defined as
$\mathfrak{G}({\it\eta},R,{\it\phi},{\it\lambda})$
is inserted into (3.15) to evaluate the collisional stress, and the total stress tensor is subsequently obtained from (2.8) by summing the kinetic stress and the collisional stress. We will express constitutive relations in terms of the dimensionless temperature, which is defined as
The final analytical expressions for the components of the stress tensor are provided in the following subsections, and the related algebraic details can be found in appendix C.
5.1 Shear stress and viscosity
Retaining all terms up to the fourth order
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, the dimensionless shear stress can be written as (see appendix C)
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, the dimensionless shear stress can be written as (see appendix C)
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{xy}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle -{\it\eta}\cos 2{\it\phi}-\frac{4(1+e){\it\nu}g_{0}}{105\sqrt{{\rm\pi}}}\left[21R\left\{8+\sqrt{{\rm\pi}}\frac{{\it\eta}\cos 2{\it\phi}}{R}\right\}+48{\it\lambda}^{2}R\right.\nonumber\\ \displaystyle & & \displaystyle +\left.4R^{3}\left\{32-\frac{{\it\eta}^{2}}{R^{2}}(2+(1+2\cos ^{2}2{\it\phi}))\right\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{xy}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle -{\it\eta}\cos 2{\it\phi}-\frac{4(1+e){\it\nu}g_{0}}{105\sqrt{{\rm\pi}}}\left[21R\left\{8+\sqrt{{\rm\pi}}\frac{{\it\eta}\cos 2{\it\phi}}{R}\right\}+48{\it\lambda}^{2}R\right.\nonumber\\ \displaystyle & & \displaystyle +\left.4R^{3}\left\{32-\frac{{\it\eta}^{2}}{R^{2}}(2+(1+2\cos ^{2}2{\it\phi}))\right\}\right],\end{eqnarray}$$
with the dimensionless temperature
![]() $T^{\ast }$
being given by (5.3). The expression for the dimensionless shear viscosity,
$T^{\ast }$
being given by (5.3). The expression for the dimensionless shear viscosity,
![]() ${\it\mu}^{\ast }=-\unicode[STIX]{x1D617}_{xy}/{\it\rho}_{p}U_{R}^{2}=-\unicode[STIX]{x1D617}_{xy}^{\ast }$
, follows from (5.4):
${\it\mu}^{\ast }=-\unicode[STIX]{x1D617}_{xy}/{\it\rho}_{p}U_{R}^{2}=-\unicode[STIX]{x1D617}_{xy}^{\ast }$
, follows from (5.4):
 $$\begin{eqnarray}\displaystyle {\it\mu}^{\ast } & = & \displaystyle \frac{{\it\nu}\sqrt{T^{\ast }}}{8}\left[\frac{{\it\eta}\cos 2{\it\phi}}{R}+\frac{4(1+e){\it\nu}g_{0}}{105\sqrt{{\rm\pi}}}\left(21\left\{8+\sqrt{{\rm\pi}}\frac{{\it\eta}\cos 2{\it\phi}}{R}\right\}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left.\underbrace{48{\it\lambda}^{2}+128R^{2}-4{\it\eta}^{2}\{2+(1+2\cos ^{2}2{\it\phi})\}}_{}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\mu}^{\ast } & = & \displaystyle \frac{{\it\nu}\sqrt{T^{\ast }}}{8}\left[\frac{{\it\eta}\cos 2{\it\phi}}{R}+\frac{4(1+e){\it\nu}g_{0}}{105\sqrt{{\rm\pi}}}\left(21\left\{8+\sqrt{{\rm\pi}}\frac{{\it\eta}\cos 2{\it\phi}}{R}\right\}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left.\underbrace{48{\it\lambda}^{2}+128R^{2}-4{\it\eta}^{2}\{2+(1+2\cos ^{2}2{\it\phi})\}}_{}\right)\right],\end{eqnarray}$$
where the under-braced terms represent nonlinear contributions beyond the NS order.
Neglecting quadratic- and higher-order terms in (5.5), we obtain the NS-order expression for the shear viscosity:
The elastic limit of the Burnett-order solution (4.4) for
![]() ${\it\eta}\cos 2{\it\phi}/R$
, with
${\it\eta}\cos 2{\it\phi}/R$
, with
![]() ${\it\phi}\rightarrow 0$
(which holds at NS order),
${\it\phi}\rightarrow 0$
(which holds at NS order),
can be substituted into (5.6) to arrive at
This expression (5.8) matches exactly with the shear viscosity for an elastic hard-sphere system (Chapman & Cowling Reference Chapman and Cowling1970).
5.2 Normal stress components and the pressure
The diagonal components of the stress tensor, correct up to
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, have the following expressions:
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, have the following expressions:
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{xx}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1+{\it\lambda}^{2}+{\it\eta}\sin 2{\it\phi})+\frac{2(1+e){\it\nu}g_{0}}{1155}\left[\vphantom{\displaystyle \frac{8}{\sqrt{{\rm\pi}}}}33(35+96R^{2}+14{\it\eta}\sin 2{\it\phi}+14{\it\lambda}^{2})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{3(66+5{\it\eta}^{2}-22{\it\lambda}^{2})-160R^{2}-22{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{xx}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1+{\it\lambda}^{2}+{\it\eta}\sin 2{\it\phi})+\frac{2(1+e){\it\nu}g_{0}}{1155}\left[\vphantom{\displaystyle \frac{8}{\sqrt{{\rm\pi}}}}33(35+96R^{2}+14{\it\eta}\sin 2{\it\phi}+14{\it\lambda}^{2})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{3(66+5{\it\eta}^{2}-22{\it\lambda}^{2})-160R^{2}-22{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{yy}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1+{\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi})+\frac{2(1+e){\it\nu}g_{0}}{1155}\left[\vphantom{\displaystyle \frac{8}{\sqrt{{\rm\pi}}}}33(35+96R^{2}-14{\it\eta}\sin 2{\it\phi}+14{\it\lambda}^{2})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{3(66+5{\it\eta}^{2}-22{\it\lambda}^{2})-160R^{2}+22{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{yy}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1+{\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi})+\frac{2(1+e){\it\nu}g_{0}}{1155}\left[\vphantom{\displaystyle \frac{8}{\sqrt{{\rm\pi}}}}33(35+96R^{2}-14{\it\eta}\sin 2{\it\phi}+14{\it\lambda}^{2})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{3(66+5{\it\eta}^{2}-22{\it\lambda}^{2})-160R^{2}+22{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{zz}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1-2{\it\lambda}^{2})+\frac{2(1+e){\it\nu}g_{0}}{1155}\nonumber\\ \displaystyle & & \displaystyle \times \left[33(35+32R^{2}-28{\it\lambda}^{2})+\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{(66+3{\it\eta}^{2}-32R^{2})\}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D617}_{zz}^{\ast }}{{\it\nu}T^{\ast }} & = & \displaystyle (1-2{\it\lambda}^{2})+\frac{2(1+e){\it\nu}g_{0}}{1155}\nonumber\\ \displaystyle & & \displaystyle \times \left[33(35+32R^{2}-28{\it\lambda}^{2})+\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{(66+3{\it\eta}^{2}-32R^{2})\}\right].\end{eqnarray}$$
The dimensionless mean pressure, correct up to
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, is given by
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, is given by
 $$\begin{eqnarray}p^{\ast }={\it\nu}T^{\ast }\left[1+\frac{2(1+e){\it\nu}g_{0}}{315}\left\{315+\underbrace{672R^{2}+\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}(42+3{\it\eta}^{2}-32R^{2}-12{\it\lambda}^{2})}_{}\right\}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}p^{\ast }={\it\nu}T^{\ast }\left[1+\frac{2(1+e){\it\nu}g_{0}}{315}\left\{315+\underbrace{672R^{2}+\frac{8}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}(42+3{\it\eta}^{2}-32R^{2}-12{\it\lambda}^{2})}_{}\right\}\right]\!.\end{eqnarray}$$
Neglecting the ‘under-braced’ nonlinear terms in (5.12), we obtain the well-known expression for pressure,
at the NS order.
5.3 First and second normal stress differences
Subtracting (5.10) from (5.9) the expression for the first normal stress difference (third equation in (5.2)) is found to be
Similarly, the expression for the second normal stress difference (last equation in (5.2)) is
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D615}_{2}^{\ast } & = & \displaystyle [3{\it\lambda}^{2}-{\it\eta}\sin (2{\it\phi})]{\it\nu}T^{\ast }+\frac{32(1+e){\it\nu}^{2}T^{\ast }g_{0}}{1155}\left[264\left(\frac{1}{2}+\frac{7}{{\it\nu}}\unicode[STIX]{x1D615}_{2}^{k\ast }\right)R^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{66+6{\it\eta}^{2}-64R^{2}-33{\it\lambda}^{2}+11{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D615}_{2}^{\ast } & = & \displaystyle [3{\it\lambda}^{2}-{\it\eta}\sin (2{\it\phi})]{\it\nu}T^{\ast }+\frac{32(1+e){\it\nu}^{2}T^{\ast }g_{0}}{1155}\left[264\left(\frac{1}{2}+\frac{7}{{\it\nu}}\unicode[STIX]{x1D615}_{2}^{k\ast }\right)R^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\{66+6{\it\eta}^{2}-64R^{2}-33{\it\lambda}^{2}+11{\it\eta}\sin 2{\it\phi}\}\right],\end{eqnarray}$$
where
![]() $T^{\ast }$
is the dimensionless temperature (5.3). Both (5.14) and (5.15) are correct at fourth order
$T^{\ast }$
is the dimensionless temperature (5.3). Both (5.14) and (5.15) are correct at fourth order
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
.
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
.
5.4 Source of the second moment and the collisional dissipation
In USF the collisional source of the second moment (3.14) takes the following form:
 $$\begin{eqnarray}\boldsymbol{\aleph }=\left(\begin{array}{@{}ccc@{}}\aleph _{xx} & \aleph _{xy} & 0\\ \aleph _{yx} & \aleph _{yy} & 0\\ 0 & 0 & \aleph _{zz}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\aleph }=\left(\begin{array}{@{}ccc@{}}\aleph _{xx} & \aleph _{xy} & 0\\ \aleph _{yx} & \aleph _{yy} & 0\\ 0 & 0 & \aleph _{zz}\end{array}\right),\end{eqnarray}$$
with its non-zero components being given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\aleph _{xx}=\unicode[STIX]{x1D608}_{xx}+\widehat{\unicode[STIX]{x1D60C}}_{xx}+\widehat{\unicode[STIX]{x1D60E}}_{xx}+2\dot{{\it\gamma}}{\it\Theta}_{xy}\\ \aleph _{yy}=\unicode[STIX]{x1D608}_{yy}+\widehat{\unicode[STIX]{x1D60C}}_{yy}+\widehat{\unicode[STIX]{x1D60E}}_{yy}-2\dot{{\it\gamma}}{\it\Theta}_{xy}\\ \aleph _{zz}=\unicode[STIX]{x1D608}_{zz}+\widehat{\unicode[STIX]{x1D60C}}_{zz}+\widehat{\unicode[STIX]{x1D60E}}_{zz}\\ \aleph _{xy}=\unicode[STIX]{x1D608}_{xy}+\widehat{\unicode[STIX]{x1D60C}}_{xy}+\widehat{\unicode[STIX]{x1D60E}}_{xy}+\dot{{\it\gamma}}({\it\Theta}_{yy}-{\it\Theta}_{xx}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\aleph _{xx}=\unicode[STIX]{x1D608}_{xx}+\widehat{\unicode[STIX]{x1D60C}}_{xx}+\widehat{\unicode[STIX]{x1D60E}}_{xx}+2\dot{{\it\gamma}}{\it\Theta}_{xy}\\ \aleph _{yy}=\unicode[STIX]{x1D608}_{yy}+\widehat{\unicode[STIX]{x1D60C}}_{yy}+\widehat{\unicode[STIX]{x1D60E}}_{yy}-2\dot{{\it\gamma}}{\it\Theta}_{xy}\\ \aleph _{zz}=\unicode[STIX]{x1D608}_{zz}+\widehat{\unicode[STIX]{x1D60C}}_{zz}+\widehat{\unicode[STIX]{x1D60E}}_{zz}\\ \aleph _{xy}=\unicode[STIX]{x1D608}_{xy}+\widehat{\unicode[STIX]{x1D60C}}_{xy}+\widehat{\unicode[STIX]{x1D60E}}_{xy}+\dot{{\it\gamma}}({\it\Theta}_{yy}-{\it\Theta}_{xx}).\end{array}\right\}\end{eqnarray}$$
The integral expressions for
![]() ${\it\Theta}_{{\it\alpha}{\it\beta}}$
(3.15),
${\it\Theta}_{{\it\alpha}{\it\beta}}$
(3.15),
![]() $\unicode[STIX]{x1D608}_{{\it\alpha}{\it\beta}}$
(3.16),
$\unicode[STIX]{x1D608}_{{\it\alpha}{\it\beta}}$
(3.16),
![]() $E_{{\it\alpha}{\it\beta}}$
(3.17) and
$E_{{\it\alpha}{\it\beta}}$
(3.17) and
![]() $G_{{\it\alpha}{\it\beta}}$
(3.18) have been evaluated (appendix A) in terms of
$G_{{\it\alpha}{\it\beta}}$
(3.18) have been evaluated (appendix A) in terms of
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() $R$
, correct up to
$R$
, correct up to
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, and the resulting truncated series for each term in (5.17) is written down in appendix D (supplementary materials).
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
, and the resulting truncated series for each term in (5.17) is written down in appendix D (supplementary materials).
5.4.1 Collisional dissipation
The constitutive expression for the collisional dissipation rate (2.16) follows directly from the trace of (5.16):
 $$\begin{eqnarray}\displaystyle \mathscr{D} & = & \displaystyle -\frac{1}{2}\aleph _{{\it\beta}{\it\beta}}=-\frac{1}{2}(\unicode[STIX]{x1D608}_{xx}+\unicode[STIX]{x1D608}_{yy}+\unicode[STIX]{x1D608}_{zz})=\frac{3(1-e^{2}){\it\rho}{\it\nu}g_{0}T^{3/2}}{{\it\sigma}{\rm\pi}^{3/2}}\mathscr{H}_{003}^{10}({\it\eta},{\it\lambda}^{2},R,{\it\phi})\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\rho}{\it\nu}g_{0}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}\left[840+32\left\{\left(84+21\sqrt{{\rm\pi}}\frac{{\it\eta}}{R}\cos 2{\it\phi}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\!\left.32R^{2}-2{\it\eta}^{2}(2+\cos 4{\it\phi})+24{\it\lambda}^{2}\vphantom{\left\{\!\left(\displaystyle \frac{{\it\eta}}{R}\right)\right\}}\right\}R^{2}+3(28{\it\eta}^{2}+{\it\eta}^{4}-8{\it\eta}^{2}{\it\lambda}^{2}+84{\it\lambda}^{4})\right],\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{D} & = & \displaystyle -\frac{1}{2}\aleph _{{\it\beta}{\it\beta}}=-\frac{1}{2}(\unicode[STIX]{x1D608}_{xx}+\unicode[STIX]{x1D608}_{yy}+\unicode[STIX]{x1D608}_{zz})=\frac{3(1-e^{2}){\it\rho}{\it\nu}g_{0}T^{3/2}}{{\it\sigma}{\rm\pi}^{3/2}}\mathscr{H}_{003}^{10}({\it\eta},{\it\lambda}^{2},R,{\it\phi})\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\rho}{\it\nu}g_{0}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}\left[840+32\left\{\left(84+21\sqrt{{\rm\pi}}\frac{{\it\eta}}{R}\cos 2{\it\phi}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\!\left.32R^{2}-2{\it\eta}^{2}(2+\cos 4{\it\phi})+24{\it\lambda}^{2}\vphantom{\left\{\!\left(\displaystyle \frac{{\it\eta}}{R}\right)\right\}}\right\}R^{2}+3(28{\it\eta}^{2}+{\it\eta}^{4}-8{\it\eta}^{2}{\it\lambda}^{2}+84{\it\lambda}^{4})\right],\qquad\end{eqnarray}$$
where we have retained terms up to
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
. In the isotropic limit (
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
. In the isotropic limit (
![]() ${\it\eta}\rightarrow 0$
and
${\it\eta}\rightarrow 0$
and
![]() ${\it\lambda}^{2}\rightarrow 0$
), we obtain
${\it\lambda}^{2}\rightarrow 0$
), we obtain
where
is the corresponding bare part valid at NS order (Jenkins & Richman Reference Jenkins and Richman1985). The quadratic-order shear-rate dependence in (5.18) agrees qualitatively with that calculated by Sela & Goldhirsch (Reference Sela and Goldhirsch1998) via a Burnett-order Chapman–Enskog expansion of the inelastic Boltzmann equation. The dependence of (5.18) on
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\lambda}$
indicates that the Grad-level collisional dissipation depends on both normal stress differences,
${\it\lambda}$
indicates that the Grad-level collisional dissipation depends on both normal stress differences,
since
![]() $({\it\eta},{\it\lambda})\sim (\unicode[STIX]{x1D615}_{1},\unicode[STIX]{x1D615}_{2})$
as we demonstrate below.
$({\it\eta},{\it\lambda})\sim (\unicode[STIX]{x1D615}_{1},\unicode[STIX]{x1D615}_{2})$
as we demonstrate below.
5.4.2 Dilute limit: dependence on NSDs
To clarify the functional dependence of (5.18) on normal stress differences, we focus on the dilute limit. In appendix B.2 (supplementary materials) we showed that the second-moment equations admit an exact solution in the dilute limit (
![]() ${\it\nu}\rightarrow 0$
):
${\it\nu}\rightarrow 0$
):
where
![]() $\unicode[STIX]{x1D615}_{1}^{k}=(\unicode[STIX]{x1D617}_{xx}^{k}-\unicode[STIX]{x1D617}_{yy}^{k})/p$
and
$\unicode[STIX]{x1D615}_{1}^{k}=(\unicode[STIX]{x1D617}_{xx}^{k}-\unicode[STIX]{x1D617}_{yy}^{k})/p$
and
![]() $\unicode[STIX]{x1D615}_{2}^{k}=(\unicode[STIX]{x1D617}_{yy}^{k}-\unicode[STIX]{x1D617}_{zz}^{k})/p$
are the kinetic parts of the ‘scaled’ first and second normal stress differences, respectively. Substituting (5.22) into (5.18) and retaining terms up to quadratic order in
$\unicode[STIX]{x1D615}_{2}^{k}=(\unicode[STIX]{x1D617}_{yy}^{k}-\unicode[STIX]{x1D617}_{zz}^{k})/p$
are the kinetic parts of the ‘scaled’ first and second normal stress differences, respectively. Substituting (5.22) into (5.18) and retaining terms up to quadratic order in
![]() $\unicode[STIX]{x1D615}_{1}^{k}$
and
$\unicode[STIX]{x1D615}_{1}^{k}$
and
![]() $\unicode[STIX]{x1D615}_{2}^{k}$
, we obtain the following expression for the collisional dissipation rate,
$\unicode[STIX]{x1D615}_{2}^{k}$
, we obtain the following expression for the collisional dissipation rate,
 $$\begin{eqnarray}\displaystyle \mathscr{D} & = & \displaystyle \frac{3{\it\rho}_{p}{\it\nu}^{2}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}[280+{\it\eta}^{2}(28+{\it\eta}^{2}-8{\it\lambda}^{2})+84{\it\lambda}^{4}]+\text{h.o.t.},\nonumber\\ \displaystyle & = & \displaystyle \frac{3{\it\rho}_{p}{\it\nu}^{2}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}\left[280+\frac{\unicode[STIX]{x1D615}_{1}^{k}}{2}\left(28+\frac{1}{2}\unicode[STIX]{x1D615}_{1}^{k}+\frac{10}{3}(\unicode[STIX]{x1D615}_{1}^{k}+2\unicode[STIX]{x1D615}_{2}^{k})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{7}{3}(\unicode[STIX]{x1D615}_{1}^{k}+2\unicode[STIX]{x1D615}_{2}^{k})^{2}\vphantom{\displaystyle \frac{\unicode[STIX]{x1D615}_{1}^{k}}{2}}\right]+O((N_{i}^{k})^{3}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{D} & = & \displaystyle \frac{3{\it\rho}_{p}{\it\nu}^{2}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}[280+{\it\eta}^{2}(28+{\it\eta}^{2}-8{\it\lambda}^{2})+84{\it\lambda}^{4}]+\text{h.o.t.},\nonumber\\ \displaystyle & = & \displaystyle \frac{3{\it\rho}_{p}{\it\nu}^{2}(1-e^{2})T^{3/2}}{70{\it\sigma}\sqrt{{\rm\pi}}}\left[280+\frac{\unicode[STIX]{x1D615}_{1}^{k}}{2}\left(28+\frac{1}{2}\unicode[STIX]{x1D615}_{1}^{k}+\frac{10}{3}(\unicode[STIX]{x1D615}_{1}^{k}+2\unicode[STIX]{x1D615}_{2}^{k})\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{7}{3}(\unicode[STIX]{x1D615}_{1}^{k}+2\unicode[STIX]{x1D615}_{2}^{k})^{2}\vphantom{\displaystyle \frac{\unicode[STIX]{x1D615}_{1}^{k}}{2}}\right]+O((N_{i}^{k})^{3}),\end{eqnarray}$$
which holds in the dilute limit. That the Grad-level dissipation rate depends on the normal stress difference was pointed out previously (Saha & Alam Reference Saha and Alam2014) for the case of granular shear flow in two dimensions.
5.5 Validation of non-Newtonian constitutive relations
For the ‘exact’ numerical solution of (3.30)–(3.33), first we evaluate the integrals
![]() $\mathscr{H}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
(3.35),
$\mathscr{H}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
(3.35),
![]() $\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
(3.36), and
$\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
(3.36), and
![]() $\mathscr{K}_{{\it\alpha}{\it\beta}}^{{\it\delta}p}$
(3.37), that appear in (A 1)–(A 2), numerically using the standard quadrature rule, for specified values of
$\mathscr{K}_{{\it\alpha}{\it\beta}}^{{\it\delta}p}$
(3.37), that appear in (A 1)–(A 2), numerically using the standard quadrature rule, for specified values of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
. Substituting the numerically evaluated integrals into (3.30)–(3.33) results in a system of nonlinear algebraic equations which again is solved by the same Newton’s method. The values of
$e$
. Substituting the numerically evaluated integrals into (3.30)–(3.33) results in a system of nonlinear algebraic equations which again is solved by the same Newton’s method. The values of
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() $R$
,
$R$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\lambda}$
thus obtained are inserted into the expressions for pressure (
${\it\lambda}$
thus obtained are inserted into the expressions for pressure (
![]() $p$
, (C 6)), viscosity (
$p$
, (C 6)), viscosity (
![]() ${\it\mu}$
, (C 8)) and the normal stress differences (
${\it\mu}$
, (C 8)) and the normal stress differences (
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
, (C 9)) as given in appendix C. Such numerically obtained transport coefficients are dubbed ‘exact’ numerical solutions since a very high accurate solution can be obtained, limited only by the truncation error of the quadrature rule and the machine precision. In the following, such exact numerical solutions for
$\unicode[STIX]{x1D615}_{2}$
, (C 9)) as given in appendix C. Such numerically obtained transport coefficients are dubbed ‘exact’ numerical solutions since a very high accurate solution can be obtained, limited only by the truncation error of the quadrature rule and the machine precision. In the following, such exact numerical solutions for
![]() $p$
,
$p$
,
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() $T$
,
$T$
,
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
are compared with those obtained from (i) the (exact) Burnett-order solution (§ 4.1) and (ii) the perturbation solution at fourth order (§ 4.2) for
$\unicode[STIX]{x1D615}_{2}$
are compared with those obtained from (i) the (exact) Burnett-order solution (§ 4.1) and (ii) the perturbation solution at fourth order (§ 4.2) for
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() $R$
,
$R$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\lambda}$
.
${\it\lambda}$
.

Figure 4. Comparison between the ‘Burnett-order’ analytical solution (blue dashed lines), fourth-order perturbation solution (red dot-dashed lines) and the ‘exact’ numerical solution (black solid lines) for the variations of the (a) pressure, (b) shear viscosity and (c) granular temperature with volume fraction
![]() $({\it\nu})$
. The filled circles denote the simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for
$({\it\nu})$
. The filled circles denote the simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for
![]() $e=0.9$
.
$e=0.9$
.
Figure 4(a–c) displays the density variations of (a) the pressure
![]() $p$
, (b) the shear viscosity
$p$
, (b) the shear viscosity
![]() ${\it\mu}$
and (c) granular temperature
${\it\mu}$
and (c) granular temperature
![]() $T$
for three values of the restitution coefficient 0.9, 0.7 and 0.5. In each panel, the ‘exact’ numerical solution (denoted by the black solid line) is compared with (i) Burnett order (blue dashed line) and (ii) the perturbation solution at fourth order (red dot-dashed line). It is seen that the Burnett-order solutions for
$T$
for three values of the restitution coefficient 0.9, 0.7 and 0.5. In each panel, the ‘exact’ numerical solution (denoted by the black solid line) is compared with (i) Burnett order (blue dashed line) and (ii) the perturbation solution at fourth order (red dot-dashed line). It is seen that the Burnett-order solutions for
![]() $p$
,
$p$
,
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $T$
are almost indistinguishable from their exact numerical value at small dissipation (
$T$
are almost indistinguishable from their exact numerical value at small dissipation (
![]() $e=0.9$
); moreover, this agreement seems to hold uniformly for the whole range of density. On the other hand, retaining the fourth-order terms yields a better agreement for
$e=0.9$
); moreover, this agreement seems to hold uniformly for the whole range of density. On the other hand, retaining the fourth-order terms yields a better agreement for
![]() $p$
,
$p$
,
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $T$
at large dissipation (
$T$
at large dissipation (
![]() $e=0.5$
).
$e=0.5$
).
The ability of the fourth-order series solution to quantitatively predict
![]() $p$
and
$p$
and
![]() ${\it\mu}$
at any density also holds for both the first and second normal stress differences, see figure 5(a,b). Note that the plotted quantities in figure 5 are the ‘scaled’ first and second normal stress differences defined via
${\it\mu}$
at any density also holds for both the first and second normal stress differences, see figure 5(a,b). Note that the plotted quantities in figure 5 are the ‘scaled’ first and second normal stress differences defined via
respectively, with the expressions for
![]() $\unicode[STIX]{x1D617}_{xx}$
,
$\unicode[STIX]{x1D617}_{xx}$
,
![]() $\unicode[STIX]{x1D617}_{yy}$
,
$\unicode[STIX]{x1D617}_{yy}$
,
![]() $\unicode[STIX]{x1D617}_{zz}$
and
$\unicode[STIX]{x1D617}_{zz}$
and
![]() $p$
given in (5.9)–(5.12); equations (5.24) and (5.25) are measures of two normal stress differences with respect to the mean pressure. In figure 5(b) we find that
$p$
given in (5.9)–(5.12); equations (5.24) and (5.25) are measures of two normal stress differences with respect to the mean pressure. In figure 5(b) we find that
![]() $\unicode[STIX]{x1D615}_{2}$
undergoes a sign reversal at some finite density. The location (
$\unicode[STIX]{x1D615}_{2}$
undergoes a sign reversal at some finite density. The location (
![]() ${\it\nu}={\it\nu}_{cr}$
) of the sign reversal of
${\it\nu}={\it\nu}_{cr}$
) of the sign reversal of
![]() $\unicode[STIX]{x1D615}_{2}$
appears to be independent of the restitution coefficient, see figure 5(b).
$\unicode[STIX]{x1D615}_{2}$
appears to be independent of the restitution coefficient, see figure 5(b).
The event-driven simulation data for the uniform shear flow of inelastic hard spheres, previously carried out by Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for a restitution coefficient of
![]() $e=0.9$
, are superimposed in figures 4 and 1. Note that Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) used event-driven techniques to conduct these simulations of smooth inelastic hard spheres in a cubic box by implementing the Lees–Edwards boundary condition (Lees & Edwards Reference Lees and Edwards1972) along the gradient (
$e=0.9$
, are superimposed in figures 4 and 1. Note that Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) used event-driven techniques to conduct these simulations of smooth inelastic hard spheres in a cubic box by implementing the Lees–Edwards boundary condition (Lees & Edwards Reference Lees and Edwards1972) along the gradient (
![]() $y$
) direction with periodic boundary conditions along the streamwise (
$y$
) direction with periodic boundary conditions along the streamwise (
![]() $x$
) and spanwise (
$x$
) and spanwise (
![]() $z$
) directions: the other details of simulation can be obtained from the original paper. Figure 4(a–c) indicates that our theoretical predictions are in good agreement with the simulation data for
$z$
) directions: the other details of simulation can be obtained from the original paper. Figure 4(a–c) indicates that our theoretical predictions are in good agreement with the simulation data for
![]() $p$
,
$p$
,
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $T$
as well as for two normal stress differences
$T$
as well as for two normal stress differences
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
(figure 1) over a large range of density up to the freezing density (
$\unicode[STIX]{x1D615}_{2}$
(figure 1) over a large range of density up to the freezing density (
![]() ${\it\nu}\sim 0.5$
).
${\it\nu}\sim 0.5$
).
We may conclude from the comparative study in figures 3–5 that the terms retained up to the fourth order (
![]() $\text{super}^{2}$
-Burnett solutions) in the series expansion (4.1)–(4.2) (that appear in various collision integrals (3.35)–(3.37) in the second-moment balance equations (3.30)–(3.33)) provide an adequate accuracy to predict all transport coefficients (
$\text{super}^{2}$
-Burnett solutions) in the series expansion (4.1)–(4.2) (that appear in various collision integrals (3.35)–(3.37) in the second-moment balance equations (3.30)–(3.33)) provide an adequate accuracy to predict all transport coefficients (
![]() $p$
,
$p$
,
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
) in a sheared granular fluid over a large range of
$\unicode[STIX]{x1D615}_{2}$
) in a sheared granular fluid over a large range of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
.
$e$
.

Figure 5. Same as figure 4, but for the variations of (a) the scaled first
![]() $(\unicode[STIX]{x1D615}_{1})$
and (b) second
$(\unicode[STIX]{x1D615}_{1})$
and (b) second
![]() $(\unicode[STIX]{x1D615}_{2})$
normal stress differences with volume fraction
$(\unicode[STIX]{x1D615}_{2})$
normal stress differences with volume fraction
![]() $({\it\nu})$
.
$({\it\nu})$
.
6 Origin of normal stress differences
It is clear from (3.9) that the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
is anisotropic, and the measure of its anisotropy is given by
$\unicode[STIX]{x1D648}$
is anisotropic, and the measure of its anisotropy is given by
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\lambda}^{2}$
. Note that
${\it\lambda}^{2}$
. Note that
![]() ${\it\eta}$
[(3.10)] is the difference between the two shear-plane eigenvalues of
${\it\eta}$
[(3.10)] is the difference between the two shear-plane eigenvalues of
![]() $\unicode[STIX]{x1D648}$
which, in physical terms, is a measure of the anisotropy of the second-moment tensor
$\unicode[STIX]{x1D648}$
which, in physical terms, is a measure of the anisotropy of the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
on the shear plane. On the other hand,
$\unicode[STIX]{x1D648}$
on the shear plane. On the other hand,
![]() ${\it\lambda}^{2}$
[(3.10)] is a measure of the excess temperature,
${\it\lambda}^{2}$
[(3.10)] is a measure of the excess temperature,
along the vorticity direction (which is proportional to the out-of-plane eigenvalue
![]() ${\it\zeta}$
of
${\it\zeta}$
of
![]() $\unicode[STIX]{x1D648}$
). The latter implies that, when a granular material is sheared, the kinetic temperature along the vorticity direction is always smaller than the mean temperature (
$\unicode[STIX]{x1D648}$
). The latter implies that, when a granular material is sheared, the kinetic temperature along the vorticity direction is always smaller than the mean temperature (
![]() $T=(T_{x}+T_{y}+T_{z})/3$
). This theoretical result has been verified via a comparison of event-driven simulations for a sheared granular fluid, see figure 6. It is seen that the excess temperature
$T=(T_{x}+T_{y}+T_{z})/3$
). This theoretical result has been verified via a comparison of event-driven simulations for a sheared granular fluid, see figure 6. It is seen that the excess temperature
![]() $T_{z}^{ex}$
decreases with increasing density but remains positive for all
$T_{z}^{ex}$
decreases with increasing density but remains positive for all
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $e$
. Due to the linear relationship (6.1) between
$e$
. Due to the linear relationship (6.1) between
![]() ${\it\lambda}^{2}$
and
${\it\lambda}^{2}$
and
![]() $T_{z}^{ex}$
,
$T_{z}^{ex}$
,
![]() ${\it\lambda}^{2}$
will henceforth be termed as excess temperature too.
${\it\lambda}^{2}$
will henceforth be termed as excess temperature too.

Figure 6. Variation of excess temperature (6.1) with density for different restitution coefficient:
![]() $e=0.9$
(solid line) and
$e=0.9$
(solid line) and
![]() $e=0.1$
(dashed line). While the lines denote the present theory, the circles denote the simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for
$e=0.1$
(dashed line). While the lines denote the present theory, the circles denote the simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for
![]() $e=0.9$
.
$e=0.9$
.
6.1 The Boltzmann/dilute limit
To see whether the anisotropy of
![]() $\unicode[STIX]{x1D648}$
can be tied with the non-Newtonian nature of the stress tensor, we recall that the exact expression for the stress tensor (2.8) is
$\unicode[STIX]{x1D648}$
can be tied with the non-Newtonian nature of the stress tensor, we recall that the exact expression for the stress tensor (2.8) is
![]() $\unicode[STIX]{x1D64B}\equiv {\it\rho}\unicode[STIX]{x1D648}$
in the dilute limit. The first normal stress difference is given by
$\unicode[STIX]{x1D64B}\equiv {\it\rho}\unicode[STIX]{x1D648}$
in the dilute limit. The first normal stress difference is given by
while the second normal stress difference is
and both are non-zero, and hence the stress tensor is non-Newtonian if
![]() ${\it\phi}\neq 0$
and/or
${\it\phi}\neq 0$
and/or
![]() ${\it\eta}\neq 0$
and
${\it\eta}\neq 0$
and
![]() ${\it\lambda}\neq 0$
. Therefore, the anisotropy of
${\it\lambda}\neq 0$
. Therefore, the anisotropy of
![]() $\unicode[STIX]{x1D648}$
gives rise to finite normal stress differences, resulting in the stress tensor being non-Newtonian.
$\unicode[STIX]{x1D648}$
gives rise to finite normal stress differences, resulting in the stress tensor being non-Newtonian.
It is clear from (6.2)–(6.3) that the normal stress differences and the anisotropy of the second-moment tensor are intertwined with each other. If the eigendirections of
![]() $\unicode[STIX]{x1D648}$
are coaxial with those of the shear tensor
$\unicode[STIX]{x1D648}$
are coaxial with those of the shear tensor
![]() $\unicode[STIX]{x1D63F}$
, i.e.
$\unicode[STIX]{x1D63F}$
, i.e.
![]() ${\it\phi}=0$
, the first normal stress difference (6.2) vanishes; however, the second normal stress difference (6.3) can still be non-zero (
${\it\phi}=0$
, the first normal stress difference (6.2) vanishes; however, the second normal stress difference (6.3) can still be non-zero (
![]() $=3{\it\lambda}^{2}$
) even if
$=3{\it\lambda}^{2}$
) even if
![]() ${\it\phi}=0$
since the ‘excess’ temperature (6.1) along the vorticity direction could differ from zero in USF (see figure 6). Therefore, the origin of
${\it\phi}=0$
since the ‘excess’ temperature (6.1) along the vorticity direction could differ from zero in USF (see figure 6). Therefore, the origin of
![]() $\unicode[STIX]{x1D615}_{1}$
is tied to the ‘non-coaxiality’ between the eigendirections of
$\unicode[STIX]{x1D615}_{1}$
is tied to the ‘non-coaxiality’ between the eigendirections of
![]() $\unicode[STIX]{x1D648}$
and
$\unicode[STIX]{x1D648}$
and
![]() $\unicode[STIX]{x1D63F}$
, but that of
$\unicode[STIX]{x1D63F}$
, but that of
![]() $\unicode[STIX]{x1D615}_{2}$
is the non-zero ‘excess’ temperature along the vorticity direction.
$\unicode[STIX]{x1D615}_{2}$
is the non-zero ‘excess’ temperature along the vorticity direction.
6.2 Effect of density
In this section we discuss the effects of finite density on the origins of two NSDs.
6.2.1 First normal stress difference
The kinetic and collisional contributions (
![]() $\unicode[STIX]{x1D615}_{1}^{\ast }=\unicode[STIX]{x1D615}_{1}^{k\ast }+\unicode[STIX]{x1D615}_{1}^{c\ast }$
) to the first normal stress difference (5.14) are given by
$\unicode[STIX]{x1D615}_{1}^{\ast }=\unicode[STIX]{x1D615}_{1}^{k\ast }+\unicode[STIX]{x1D615}_{1}^{c\ast }$
) to the first normal stress difference (5.14) are given by
Note that both (6.4) and (6.5) vanish in the limits of
![]() ${\it\eta}\rightarrow 0$
and/or
${\it\eta}\rightarrow 0$
and/or
![]() ${\it\phi}\rightarrow 0$
: while the former represents the limit of vanishing temperature anisotropy in the shear plane (3.10), the latter corresponds to the eigendirections of the second-moment tensor
${\it\phi}\rightarrow 0$
: while the former represents the limit of vanishing temperature anisotropy in the shear plane (3.10), the latter corresponds to the eigendirections of the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
and the shear tensor
$\unicode[STIX]{x1D648}$
and the shear tensor
![]() $\unicode[STIX]{x1D63F}$
being coaxial (viz. figure 2). Therefore we conclude that the origin of first normal stress difference is tied to (i) the ‘finite’ temperature anisotropy and/or (ii) the ‘non-coaxiality’ between the eigendirections of
$\unicode[STIX]{x1D63F}$
being coaxial (viz. figure 2). Therefore we conclude that the origin of first normal stress difference is tied to (i) the ‘finite’ temperature anisotropy and/or (ii) the ‘non-coaxiality’ between the eigendirections of
![]() $\unicode[STIX]{x1D648}$
and
$\unicode[STIX]{x1D648}$
and
![]() $\unicode[STIX]{x1D63F}$
at any density.
$\unicode[STIX]{x1D63F}$
at any density.
The leading terms in both (6.4) and (6.5) are
of Burnett order in the shear rate. The leading-order corrections in (6.5) are
It is noteworthy that the excess temperature (6.1),
![]() $T_{z}^{ex}\propto {\it\lambda}^{2}$
, does not affect the kinetic part of the first NSD, but it affects the collisional part of the first NSD at sixth order and beyond in the shear rate.
$T_{z}^{ex}\propto {\it\lambda}^{2}$
, does not affect the kinetic part of the first NSD, but it affects the collisional part of the first NSD at sixth order and beyond in the shear rate.
6.2.2 Second normal stress difference and its sign reversal
The kinetic and collisional components of the second normal stress difference (5.15) at
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
are given by
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
are given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D615}_{2}^{c\ast } & = & \displaystyle \frac{32(1+e){\it\nu}^{2}T^{\ast }g_{0}}{1155}\left[264\left(\frac{1}{2}+\frac{7}{{\it\nu}}\unicode[STIX]{x1D615}_{2}^{k\ast }\right)R^{2}+\frac{1}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.(66+6{\it\eta}^{2}-64R^{2}-33{\it\lambda}^{2}+11{\it\eta}\sin 2{\it\phi})\vphantom{\left(\displaystyle \frac{1}{\sqrt{{\rm\pi}}}\right)}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D615}_{2}^{c\ast } & = & \displaystyle \frac{32(1+e){\it\nu}^{2}T^{\ast }g_{0}}{1155}\left[264\left(\frac{1}{2}+\frac{7}{{\it\nu}}\unicode[STIX]{x1D615}_{2}^{k\ast }\right)R^{2}+\frac{1}{\sqrt{{\rm\pi}}}{\it\eta}R\cos 2{\it\phi}\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.(66+6{\it\eta}^{2}-64R^{2}-33{\it\lambda}^{2}+11{\it\eta}\sin 2{\it\phi})\vphantom{\left(\displaystyle \frac{1}{\sqrt{{\rm\pi}}}\right)}\right],\end{eqnarray}$$
where
![]() $T^{\ast }$
is the dimensionless temperature (5.3). In the limit of vanishing of the ‘shear-plane’ temperature anisotropy (
$T^{\ast }$
is the dimensionless temperature (5.3). In the limit of vanishing of the ‘shear-plane’ temperature anisotropy (
![]() ${\it\eta}\rightarrow 0$
) and/or the coaxiality (
${\it\eta}\rightarrow 0$
) and/or the coaxiality (
![]() ${\it\phi}\rightarrow 0$
) between the eigendirections of
${\it\phi}\rightarrow 0$
) between the eigendirections of
![]() $\unicode[STIX]{x1D648}$
and
$\unicode[STIX]{x1D648}$
and
![]() $\unicode[STIX]{x1D63F}$
, we can simplify (6.8) and (6.9) into
$\unicode[STIX]{x1D63F}$
, we can simplify (6.8) and (6.9) into
Both (6.10) and (6.11) hold strictly in the dense limit since
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\phi}$
approach zero as
${\it\phi}$
approach zero as
![]() ${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
. Note that even the kinetic part of the second normal stress difference (6.10) remains positive in the dense limit as long as
${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
. Note that even the kinetic part of the second normal stress difference (6.10) remains positive in the dense limit as long as
![]() ${\it\lambda}^{2}\propto T_{z}^{ex}>0$
(see figure 6).
${\it\lambda}^{2}\propto T_{z}^{ex}>0$
(see figure 6).
It is evident from (6.10) and (6.11) that the second normal stress difference in the dense limit (6.11) remains finite and positive, which is in contrast to the zero first normal stress difference in the same limit. Moreover, even if
![]() ${\it\lambda}^{2}=0$
and
${\it\lambda}^{2}=0$
and
![]() ${\it\eta}=0$
,
${\it\eta}=0$
,
![]() $\unicode[STIX]{x1D615}_{2}\equiv \unicode[STIX]{x1D615}_{2}^{c\ast }$
remains finite as
$\unicode[STIX]{x1D615}_{2}\equiv \unicode[STIX]{x1D615}_{2}^{c\ast }$
remains finite as
![]() ${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
as long as the shear rate is finite (
${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
as long as the shear rate is finite (
![]() $R^{2}>0$
) and hence this is ‘shear induced’. Therefore, the origin of non-zero second normal stress difference in the dense limit is tied to the imposed shear field.
$R^{2}>0$
) and hence this is ‘shear induced’. Therefore, the origin of non-zero second normal stress difference in the dense limit is tied to the imposed shear field.
Equation (6.8) indicates that the
![]() $\unicode[STIX]{x1D615}_{2}^{k\ast }$
can be positive or negative depending on the relative magnitudes of
$\unicode[STIX]{x1D615}_{2}^{k\ast }$
can be positive or negative depending on the relative magnitudes of
![]() $3{\it\lambda}^{2}$
and
$3{\it\lambda}^{2}$
and
![]() ${\it\eta}\sin (2{\it\phi})$
and can undergo a sign change at a finite density if
${\it\eta}\sin (2{\it\phi})$
and can undergo a sign change at a finite density if
(Recall from figure 5
b that
![]() $\unicode[STIX]{x1D615}_{2}$
undergoes a sign reversal at a finite density.) The density variation of (6.12), obtained by solving (3.30)–(3.33) numerically, as depicted in figure 7(a), clarifies the above point:
$\unicode[STIX]{x1D615}_{2}$
undergoes a sign reversal at a finite density.) The density variation of (6.12), obtained by solving (3.30)–(3.33) numerically, as depicted in figure 7(a), clarifies the above point:
![]() $3{\it\lambda}^{2}<{\it\eta}\sin (2{\it\phi})$
in the dilute limit and
$3{\it\lambda}^{2}<{\it\eta}\sin (2{\it\phi})$
in the dilute limit and
![]() $3{\it\lambda}^{2}>{\it\eta}\sin (2{\it\phi})$
in the dense limit for any value of the restitution coefficient. The variation of the critical density
$3{\it\lambda}^{2}>{\it\eta}\sin (2{\it\phi})$
in the dense limit for any value of the restitution coefficient. The variation of the critical density
![]() ${\it\nu}_{cr}^{k}$
, at which (6.12) holds, with the restitution coefficient is shown in figure 7(b) – clearly,
${\it\nu}_{cr}^{k}$
, at which (6.12) holds, with the restitution coefficient is shown in figure 7(b) – clearly,
![]() ${\it\nu}_{cr}^{k}(e)$
is a decreasing function of
${\it\nu}_{cr}^{k}(e)$
is a decreasing function of
![]() $e$
and can be fitted via the following linear function:
$e$
and can be fitted via the following linear function:
denoted by the solid line in figure 7(b). Since
![]() $\unicode[STIX]{x1D615}_{2}^{c}=0$
at
$\unicode[STIX]{x1D615}_{2}^{c}=0$
at
![]() ${\it\nu}=0$
and is a monotonically increasing function of
${\it\nu}=0$
and is a monotonically increasing function of
![]() ${\it\nu}$
, the critical density,
${\it\nu}$
, the critical density,
![]() ${\it\nu}_{cr}$
, at which total second normal stress difference (
${\it\nu}_{cr}$
, at which total second normal stress difference (
![]() $\unicode[STIX]{x1D615}_{2}=\unicode[STIX]{x1D615}_{2}^{k}+\unicode[STIX]{x1D615}_{2}^{c}=0$
) changes sign from negative to positive would be slightly lower than (6.13).
$\unicode[STIX]{x1D615}_{2}=\unicode[STIX]{x1D615}_{2}^{k}+\unicode[STIX]{x1D615}_{2}^{c}=0$
) changes sign from negative to positive would be slightly lower than (6.13).
In conclusion, the second normal stress difference is negative and positive in the dilute and dense limits, respectively, and the ‘sign reversal’ of
![]() $\unicode[STIX]{x1D615}_{2}$
at some finite density is directly tied to the sign reversal of its kinetic component
$\unicode[STIX]{x1D615}_{2}$
at some finite density is directly tied to the sign reversal of its kinetic component
![]() $\unicode[STIX]{x1D615}_{2}^{k}$
. The above analysis further confirms that the origin of
$\unicode[STIX]{x1D615}_{2}^{k}$
. The above analysis further confirms that the origin of
![]() $\unicode[STIX]{x1D615}_{2}$
is tied to the ‘excess’ temperature (
$\unicode[STIX]{x1D615}_{2}$
is tied to the ‘excess’ temperature (
![]() $T_{z}^{ex}\propto {\it\lambda}^{2}$
, viz. (6.1)) along the mean vorticity direction in the dilute limit, but its origin in the dense limit is tied to the imposed shear field.
$T_{z}^{ex}\propto {\it\lambda}^{2}$
, viz. (6.1)) along the mean vorticity direction in the dilute limit, but its origin in the dense limit is tied to the imposed shear field.

Figure 7. (a) Variation of
![]() $(3{\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi})$
with density
$(3{\it\lambda}^{2}-{\it\eta}\sin 2{\it\phi})$
with density
![]() ${\it\nu}$
for two values of restitution coefficient
${\it\nu}$
for two values of restitution coefficient
![]() $e=0.9$
(thick solid line) and
$e=0.9$
(thick solid line) and
![]() $e=0.1$
(dashed line); the arrows locate the respective critical density at which the above quantity is zero. (b) Variation of the critical density
$e=0.1$
(dashed line); the arrows locate the respective critical density at which the above quantity is zero. (b) Variation of the critical density
![]() ${\it\nu}_{cr}^{k}$
, at which
${\it\nu}_{cr}^{k}$
, at which
![]() ${\it\eta}\sin 2{\it\phi}=3{\it\lambda}^{2}$
, with
${\it\eta}\sin 2{\it\phi}=3{\it\lambda}^{2}$
, with
![]() $e$
; the circles denote numerical solution and the solid line is a linear fit (6.13).
$e$
; the circles denote numerical solution and the solid line is a linear fit (6.13).
7 Summary and outlook
The motivation to develop a higher-order (non-Newtonian) theory came from the fact that the normal stress differences remain order-one quantities (see figures 1 and 5) in a granular fluid and hence cannot be neglected. This ruled out Navier–Stokes-order models (for which
![]() $\unicode[STIX]{x1D615}_{1}=0=\unicode[STIX]{x1D615}_{2}$
) and the ‘minimal’ model that incorporates normal stress differences is the well-known ‘10-moment’ model of Grad (Reference Grad1949) in terms of an extended set of 10 hydrodynamic fields (density, velocity vector and the second-moment tensor) as detailed in § 2. The constitutive relations were then derived by choosing the anisotropic/triaxial Gaussian as the single-particle distribution function which is the zeroth-order distribution function (Goldreich & Tremaine Reference Goldreich and Tremaine1978; Araki & Tremaine Reference Araki and Tremaine1986; Jenkins & Richman Reference Jenkins and Richman1988; Richman Reference Richman1989; Lutsko Reference Lutsko2004; Saha & Alam Reference Saha and Alam2014) for a non-equilibrium system like the steady uniform shear flow of smooth inelastic spheres. The equation for the second-moment tensor has been solved (i) exactly at the Burnett order (§ 4.1) and (ii) via a regular perturbation expansion at super-Burnett orders (§ 4.2), yielding closed-form expression for the ‘non-Newtonian’ stress tensor at finite densities which is likely to be valid far away from the limit of nearly elastic collisions.
$\unicode[STIX]{x1D615}_{1}=0=\unicode[STIX]{x1D615}_{2}$
) and the ‘minimal’ model that incorporates normal stress differences is the well-known ‘10-moment’ model of Grad (Reference Grad1949) in terms of an extended set of 10 hydrodynamic fields (density, velocity vector and the second-moment tensor) as detailed in § 2. The constitutive relations were then derived by choosing the anisotropic/triaxial Gaussian as the single-particle distribution function which is the zeroth-order distribution function (Goldreich & Tremaine Reference Goldreich and Tremaine1978; Araki & Tremaine Reference Araki and Tremaine1986; Jenkins & Richman Reference Jenkins and Richman1988; Richman Reference Richman1989; Lutsko Reference Lutsko2004; Saha & Alam Reference Saha and Alam2014) for a non-equilibrium system like the steady uniform shear flow of smooth inelastic spheres. The equation for the second-moment tensor has been solved (i) exactly at the Burnett order (§ 4.1) and (ii) via a regular perturbation expansion at super-Burnett orders (§ 4.2), yielding closed-form expression for the ‘non-Newtonian’ stress tensor at finite densities which is likely to be valid far away from the limit of nearly elastic collisions.
We found that the normal stress differences and the anisotropy of the second-moment tensor
![]() $\unicode[STIX]{x1D648}=\langle \boldsymbol{C}\boldsymbol{C}\rangle$
(where
$\unicode[STIX]{x1D648}=\langle \boldsymbol{C}\boldsymbol{C}\rangle$
(where
![]() $\boldsymbol{C}=(\boldsymbol{c}-\boldsymbol{u})$
is the peculiar velocity of a particle,
$\boldsymbol{C}=(\boldsymbol{c}-\boldsymbol{u})$
is the peculiar velocity of a particle,
![]() $\boldsymbol{c}$
is its instantaneous velocity and
$\boldsymbol{c}$
is its instantaneous velocity and
![]() $\boldsymbol{u}$
is the coarse-grained/hydrodynamic velocity) are intertwined with each other in uniform shear flow. This can be easily appreciated by focusing on the dilute limit of shear flow for which the following relations hold (see (5.22) and appendix B.2):
$\boldsymbol{u}$
is the coarse-grained/hydrodynamic velocity) are intertwined with each other in uniform shear flow. This can be easily appreciated by focusing on the dilute limit of shear flow for which the following relations hold (see (5.22) and appendix B.2):
Therefore, the temperature anisotropy in the shear plane (
![]() ${\it\eta}$
), the non-coaxiality angle (
${\it\eta}$
), the non-coaxiality angle (
![]() ${\it\phi}$
) and the excess temperature (
${\it\phi}$
) and the excess temperature (
![]() $T_{z}^{ex}=(T-T_{z})\propto {\it\lambda}^{2}$
, where
$T_{z}^{ex}=(T-T_{z})\propto {\it\lambda}^{2}$
, where
![]() $T_{z}$
and
$T_{z}$
and
![]() $T$
are the
$T$
are the
![]() $z$
-component and the average of the granular temperature respectively) along the mean vorticity (
$z$
-component and the average of the granular temperature respectively) along the mean vorticity (
![]() $z$
) direction vanish if the two normal stress differences are zero. This results in an ‘isotropic’ second-moment tensor for which only the granular temperature is a field variable, in addition to density and velocity, leading to the standard NS-order hydrodynamic model.
$z$
) direction vanish if the two normal stress differences are zero. This results in an ‘isotropic’ second-moment tensor for which only the granular temperature is a field variable, in addition to density and velocity, leading to the standard NS-order hydrodynamic model.
A detailed comparison between the ‘exact’ numerical solution of the second-moment equation and two different analytical solutions has been made (see figures 3–5). We found that the super–super-Burnett terms (i.e. fourth order in the shear rate) must be retained in the constitutive relations to quantitatively predict the behaviour of the pressure (
![]() $p$
), the shear viscosity (
$p$
), the shear viscosity (
![]() ${\it\mu}$
) and two normal stress differences (
${\it\mu}$
) and two normal stress differences (
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
) for all values of density (
$\unicode[STIX]{x1D615}_{2}$
) for all values of density (
![]() ${\it\nu}$
) and restitution coefficient (
${\it\nu}$
) and restitution coefficient (
![]() $e$
). Furthermore, a similar comparison with the event-driven simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for the uniform shear flow of inelastic hard spheres confirmed the reliability of our theoretical expressions for transport coefficients over a large range of density (see figures 1 and 4). Therefore we conclude that the beyond-Navier–Stokes contributions up to the super–super-Burnett order must be retained in all transport coefficients so as to make them valid for a large range of density and restitution coefficient.
$e$
). Furthermore, a similar comparison with the event-driven simulation data of Alam & Luding (Reference Alam, Luding, Garcia-Rojo, Herrmann and McNamara2005) for the uniform shear flow of inelastic hard spheres confirmed the reliability of our theoretical expressions for transport coefficients over a large range of density (see figures 1 and 4). Therefore we conclude that the beyond-Navier–Stokes contributions up to the super–super-Burnett order must be retained in all transport coefficients so as to make them valid for a large range of density and restitution coefficient.
The ‘scaled’ first normal stress difference (
![]() $\unicode[STIX]{x1D615}_{1}=(\unicode[STIX]{x1D617}_{xx}-\unicode[STIX]{x1D617}_{yy})/p$
, scaled with respect to the mean pressure) is positive in the dilute limit and decreases monotonically to zero in the dense limit. In contrast, the scaled second normal stress difference (
$\unicode[STIX]{x1D615}_{1}=(\unicode[STIX]{x1D617}_{xx}-\unicode[STIX]{x1D617}_{yy})/p$
, scaled with respect to the mean pressure) is positive in the dilute limit and decreases monotonically to zero in the dense limit. In contrast, the scaled second normal stress difference (
![]() $\unicode[STIX]{x1D615}_{2}=(\unicode[STIX]{x1D617}_{yy}-\unicode[STIX]{x1D617}_{zz})/p$
) is negative and positive in the dilute and dense limits, respectively, and the sign change of
$\unicode[STIX]{x1D615}_{2}=(\unicode[STIX]{x1D617}_{yy}-\unicode[STIX]{x1D617}_{zz})/p$
) is negative and positive in the dilute and dense limits, respectively, and the sign change of
![]() $\unicode[STIX]{x1D615}_{2}$
at some finite density is directly tied to the sign change of its kinetic component
$\unicode[STIX]{x1D615}_{2}$
at some finite density is directly tied to the sign change of its kinetic component
![]() $\unicode[STIX]{x1D615}_{2}^{k}$
. In physical terms, the vanishing of the first normal stress difference is tied to the ‘coaxiality’ (i.e. the non-coaxiality angle is
$\unicode[STIX]{x1D615}_{2}^{k}$
. In physical terms, the vanishing of the first normal stress difference is tied to the ‘coaxiality’ (i.e. the non-coaxiality angle is
![]() ${\it\phi}=0$
) of the eigendirections of the shear tensor
${\it\phi}=0$
) of the eigendirections of the shear tensor
![]() $\unicode[STIX]{x1D63F}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}})/2$
and the second-moment tensor
$\unicode[STIX]{x1D63F}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}})/2$
and the second-moment tensor
![]() $\unicode[STIX]{x1D648}$
. On the other hand, the second normal stress difference can be non-zero even if the above coaxiality condition (
$\unicode[STIX]{x1D648}$
. On the other hand, the second normal stress difference can be non-zero even if the above coaxiality condition (
![]() ${\it\phi}=0$
) is satisfied since the ‘excess’ temperature (
${\it\phi}=0$
) is satisfied since the ‘excess’ temperature (
![]() $T_{z}^{ex}=(T-T_{z})\propto {\it\lambda}^{2}$
, where
$T_{z}^{ex}=(T-T_{z})\propto {\it\lambda}^{2}$
, where
![]() $T$
and
$T$
and
![]() $T_{z}$
are the average and
$T_{z}$
are the average and
![]() $z$
-component of the granular temperature) along the mean vorticity (
$z$
-component of the granular temperature) along the mean vorticity (
![]() $z$
) direction could differ from zero in uniform shear flow.
$z$
) direction could differ from zero in uniform shear flow.
Although the present theory can quantitatively predict the correct behaviour of both first and second normal stress differences (
![]() $\unicode[STIX]{x1D615}_{1}$
and
$\unicode[STIX]{x1D615}_{1}$
and
![]() $\unicode[STIX]{x1D615}_{2}$
) in addition to low-order transport coefficients (shear viscosity and pressure) from the dilute to dense regimes up to close to the freezing density (
$\unicode[STIX]{x1D615}_{2}$
) in addition to low-order transport coefficients (shear viscosity and pressure) from the dilute to dense regimes up to close to the freezing density (
![]() ${\it\nu}_{f}\sim 0.5$
), the scaling of the transport coefficients in the dense limit is found to be incorrect (see appendix E); for example, the shear viscosity diverges like
${\it\nu}_{f}\sim 0.5$
), the scaling of the transport coefficients in the dense limit is found to be incorrect (see appendix E); for example, the shear viscosity diverges like
![]() $({\it\nu}_{\mathit{max}}-{\it\nu})^{-{\it\delta}}$
with an exponent
$({\it\nu}_{\mathit{max}}-{\it\nu})^{-{\it\delta}}$
with an exponent
![]() ${\it\delta}=1$
which is much different from 2 (based on experimental and simulation data). The latter finding may not be surprising since certain assumptions of the Enskog–Boltzmann equation are not likely to hold in very dense flows with sustained contacts and correlated motions of particles (Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006; Kumar & Luding Reference Kumar and Luding2016). How the present theory can be augmented, by incorporating velocity correlations (Mitarai & Nakanishi Reference Mitarai and Nakanishi2007; Alam & Chikkadi Reference Alam and Chikkadi2010) and related many-body effects in the kinetic equation so as to push its upper limit of validity beyond the freezing density, remains to be seen in future work. Nevertheless we believe that the extended hydrodynamic theory (in terms of 10 hydrodynamic fields) can serve as a small stepping stone to formulate a theory of flowing granular matter over the whole range of density which is likely to hold at large dissipation levels. In future, this 10-moment theory must be completed by deriving constitutive relation for the heat flux (Saha & Alam Reference Saha and Alam2014) so as to apply it to non-uniform shear flows too.
${\it\delta}=1$
which is much different from 2 (based on experimental and simulation data). The latter finding may not be surprising since certain assumptions of the Enskog–Boltzmann equation are not likely to hold in very dense flows with sustained contacts and correlated motions of particles (Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006; Kumar & Luding Reference Kumar and Luding2016). How the present theory can be augmented, by incorporating velocity correlations (Mitarai & Nakanishi Reference Mitarai and Nakanishi2007; Alam & Chikkadi Reference Alam and Chikkadi2010) and related many-body effects in the kinetic equation so as to push its upper limit of validity beyond the freezing density, remains to be seen in future work. Nevertheless we believe that the extended hydrodynamic theory (in terms of 10 hydrodynamic fields) can serve as a small stepping stone to formulate a theory of flowing granular matter over the whole range of density which is likely to hold at large dissipation levels. In future, this 10-moment theory must be completed by deriving constitutive relation for the heat flux (Saha & Alam Reference Saha and Alam2014) so as to apply it to non-uniform shear flows too.
Acknowledgements
M.A. acknowledges support from JNCASR, and S.S. acknowledges the PhD-fellowship (2011–2016) from the ‘Council of Scientific and Industrial Research’ (CSIR), Government of India. We sincerely thank the referees for their constructive comments as well as the editor for suggestions to improve presentation of this paper.
Supplementary materials
Supplementary materials are available at http://dx.doi.org/10.1017/jfm.2016.237.
Appendix A. Collision integrals of (3.30)–(3.33) and their algebraic form
Appendix A, with (A 1)–(A 17), is available as supplementary materials.
Appendix B. The second-moment balance at third and fourth orders and its solution
Retaining terms up to
![]() $O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
in the infinite series for each integral (3.35)–(3.37) and substituting them into (3.30)–(3.33), we obtain the following set of coupled nonlinear algebraic equations:
$O({\it\eta}^{m}{\it\lambda}^{n}R^{p}\sin ^{q}(2{\it\phi}),m+n+p+q\leqslant 4)$
in the infinite series for each integral (3.35)–(3.37) and substituting them into (3.30)–(3.33), we obtain the following set of coupled nonlinear algebraic equations:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle 1680\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}-3(1-e^{2}){\it\nu}g_{0} (840+84{\it\eta}^{2}+2688R^{2}+672\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}\\ \quad +\,\underline{3{\it\eta}^{4}+1024R^{4}-128R^{2}{\it\eta}^{2}+768R^{2}{\it\lambda}^{2}-24{\it\eta}^{2}{\it\lambda}^{2}+252{\it\lambda}^{4}-64{\it\eta}^{2}R^{2}\cos 4{\it\phi}})\\ \quad +\,64(1+e){\it\nu}g_{0}R\{21\sqrt{{\rm\pi}}{\it\eta}\cos 2{\it\phi}+4R(42-\underline{2{\it\eta}^{2}+12{\it\lambda}^{2}+32R^{2}-{\it\eta}^{2}\cos 4{\it\phi}})\}=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 2310\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}+(1+e){\it\nu}g_{0} [32R^{2}\{66+\underline{8{\it\eta}^{2}-165{\it\lambda}^{2}}+3e(66-\underline{4{\it\eta}^{2}+33{\it\lambda}^{2}})\}\\ \quad -\,9(3-e)\{\underline{{\it\eta}^{4}}+11{\it\eta}^{2}(2-\underline{{\it\lambda}^{2}})+66{\it\lambda}^{2}(7-\underline{{\it\lambda}^{2}})\}+\underline{1024(5+3e)R^{4}}\\ \quad -\,16R{\it\eta}\{33\sqrt{{\rm\pi}}(4-3e)\cos 2{\it\phi}-\underline{4R{\it\eta}(2-3e)\cos 4{\it\phi}}\}]=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 210\sqrt{{\rm\pi}}(1+{\it\lambda}^{2})R\cos 2{\it\phi}-(1+e){\it\nu}g_{0} [12\sqrt{{\rm\pi}}\{7(1-3e)+4(4-3e){\it\lambda}^{2}\\ \quad -\,32(1+e)R^{2}\,\}R\cos 2{\it\phi}+{\it\eta}\{126(3-e)-3(3-e){\it\eta}^{2}+36(3-e){\it\lambda}^{2}\\ \quad +\,64(4-3e)R^{2}-32(5+3e)R^{2}\cos 4{\it\phi}\}]=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 105\sqrt{{\rm\pi}}\{{\it\eta}-(1+{\it\lambda}^{2})\sin 2{\it\phi}\}-2(1+e){\it\nu}g_{0}\sin 2{\it\phi}[16(5+3e){\it\eta}R\cos 2{\it\phi}\\ \quad -\,3\sqrt{{\rm\pi}}\{7(1-3e)+4(4-3e){\it\lambda}^{2}-32(1+e)R^{2}\}]=0\end{array}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}l@{}}\displaystyle 1680\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}-3(1-e^{2}){\it\nu}g_{0} (840+84{\it\eta}^{2}+2688R^{2}+672\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}\\ \quad +\,\underline{3{\it\eta}^{4}+1024R^{4}-128R^{2}{\it\eta}^{2}+768R^{2}{\it\lambda}^{2}-24{\it\eta}^{2}{\it\lambda}^{2}+252{\it\lambda}^{4}-64{\it\eta}^{2}R^{2}\cos 4{\it\phi}})\\ \quad +\,64(1+e){\it\nu}g_{0}R\{21\sqrt{{\rm\pi}}{\it\eta}\cos 2{\it\phi}+4R(42-\underline{2{\it\eta}^{2}+12{\it\lambda}^{2}+32R^{2}-{\it\eta}^{2}\cos 4{\it\phi}})\}=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 2310\sqrt{{\rm\pi}}{\it\eta}R\cos 2{\it\phi}+(1+e){\it\nu}g_{0} [32R^{2}\{66+\underline{8{\it\eta}^{2}-165{\it\lambda}^{2}}+3e(66-\underline{4{\it\eta}^{2}+33{\it\lambda}^{2}})\}\\ \quad -\,9(3-e)\{\underline{{\it\eta}^{4}}+11{\it\eta}^{2}(2-\underline{{\it\lambda}^{2}})+66{\it\lambda}^{2}(7-\underline{{\it\lambda}^{2}})\}+\underline{1024(5+3e)R^{4}}\\ \quad -\,16R{\it\eta}\{33\sqrt{{\rm\pi}}(4-3e)\cos 2{\it\phi}-\underline{4R{\it\eta}(2-3e)\cos 4{\it\phi}}\}]=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 210\sqrt{{\rm\pi}}(1+{\it\lambda}^{2})R\cos 2{\it\phi}-(1+e){\it\nu}g_{0} [12\sqrt{{\rm\pi}}\{7(1-3e)+4(4-3e){\it\lambda}^{2}\\ \quad -\,32(1+e)R^{2}\,\}R\cos 2{\it\phi}+{\it\eta}\{126(3-e)-3(3-e){\it\eta}^{2}+36(3-e){\it\lambda}^{2}\\ \quad +\,64(4-3e)R^{2}-32(5+3e)R^{2}\cos 4{\it\phi}\}]=0\end{array}\\ \begin{array}{@{}l@{}}\displaystyle 105\sqrt{{\rm\pi}}\{{\it\eta}-(1+{\it\lambda}^{2})\sin 2{\it\phi}\}-2(1+e){\it\nu}g_{0}\sin 2{\it\phi}[16(5+3e){\it\eta}R\cos 2{\it\phi}\\ \quad -\,3\sqrt{{\rm\pi}}\{7(1-3e)+4(4-3e){\it\lambda}^{2}-32(1+e)R^{2}\}]=0\end{array}\end{array}\right\}\end{eqnarray}$$
for four unknowns
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\lambda}^{2}$
,
${\it\lambda}^{2}$
,
![]() $R$
and
$R$
and
![]() ${\it\phi}$
, given that the restitution coefficient (
${\it\phi}$
, given that the restitution coefficient (
![]() $e$
) and the volume fraction (
$e$
) and the volume fraction (
![]() ${\it\nu}$
) are known. Equation (B 1) represent the second-moment balance at the super–super-Burnett order since they contain all terms up to the fourth order in the shear rate. Removing the underlined terms in the first two equations of (B 1), we obtain the second-moment balance at the super-Burnett (third order in the shear rate) order.
${\it\nu}$
) are known. Equation (B 1) represent the second-moment balance at the super–super-Burnett order since they contain all terms up to the fourth order in the shear rate. Removing the underlined terms in the first two equations of (B 1), we obtain the second-moment balance at the super-Burnett (third order in the shear rate) order.
B.1 Perturbation solutions at finite density: beyond Burnett order
Appendix B.1, with (B 2)–(B 7), is available as supplementary materials.
B.2 Exact solution in the dilute limit
Let us consider the dilute limit (
![]() ${\it\nu}\rightarrow 0$
) of the second-moment balance (3.30)–(3.33) which was analysed previously by Richman (Reference Richman1989). In this limit, the collisional contribution to flux terms vanishes (e.g.
${\it\nu}\rightarrow 0$
) of the second-moment balance (3.30)–(3.33) which was analysed previously by Richman (Reference Richman1989). In this limit, the collisional contribution to flux terms vanishes (e.g.
![]() ${\it\Theta}_{{\it\alpha}{\it\beta}}=0$
) and consequently the stress tensor is given by
${\it\Theta}_{{\it\alpha}{\it\beta}}=0$
) and consequently the stress tensor is given by
![]() $\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}={\it\rho}\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}$
. Moreover, as
$\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}={\it\rho}\unicode[STIX]{x1D614}_{{\it\alpha}{\it\beta}}$
. Moreover, as
![]() ${\it\nu}\rightarrow 0$
,
${\it\nu}\rightarrow 0$
,
![]() $\mathfrak{F}({\it\chi}\rightarrow 0)=1$
and
$\mathfrak{F}({\it\chi}\rightarrow 0)=1$
and
![]() $\mathfrak{G}({\it\chi}\rightarrow 0)=\sqrt{{\rm\pi}}/2$
(see (3.23)) it can be verified that the integrals
$\mathfrak{G}({\it\chi}\rightarrow 0)=\sqrt{{\rm\pi}}/2$
(see (3.23)) it can be verified that the integrals
![]() $\widehat{\unicode[STIX]{x1D60E}}_{{\it\alpha}{\it\beta}}({\it\nu}\rightarrow 0)=0$
and
$\widehat{\unicode[STIX]{x1D60E}}_{{\it\alpha}{\it\beta}}({\it\nu}\rightarrow 0)=0$
and
![]() ${\it\Gamma}_{x^{\prime }y^{\prime }}({\it\nu}\rightarrow 0)=0$
vanish too. Therefore, the balance equations (3.30)–(3.33) for the second moment simplify to
${\it\Gamma}_{x^{\prime }y^{\prime }}({\it\nu}\rightarrow 0)=0$
vanish too. Therefore, the balance equations (3.30)–(3.33) for the second moment simplify to
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}-4{\it\eta}{\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=\unicode[STIX]{x1D608}_{x^{\prime }x^{\prime }}+\unicode[STIX]{x1D608}_{y^{\prime }y^{\prime }}+\unicode[STIX]{x1D608}_{z^{\prime }z^{\prime }},\\ -4{\it\eta}{\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=-3\widehat{{\it\Gamma}}_{z^{\prime }z^{\prime }},\\ 4(1+{\it\lambda}^{2}){\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=({\it\Gamma}_{x^{\prime }x^{\prime }}-{\it\Gamma}_{y^{\prime }y^{\prime }}),\\ 2{\it\rho}T\dot{{\it\gamma}}[{\it\eta}-(1+{\it\lambda}^{2})\sin 2{\it\phi}]={\it\Gamma}_{x^{\prime }y^{\prime }}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}-4{\it\eta}{\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=\unicode[STIX]{x1D608}_{x^{\prime }x^{\prime }}+\unicode[STIX]{x1D608}_{y^{\prime }y^{\prime }}+\unicode[STIX]{x1D608}_{z^{\prime }z^{\prime }},\\ -4{\it\eta}{\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=-3\widehat{{\it\Gamma}}_{z^{\prime }z^{\prime }},\\ 4(1+{\it\lambda}^{2}){\it\rho}T\dot{{\it\gamma}}\cos 2{\it\phi}=({\it\Gamma}_{x^{\prime }x^{\prime }}-{\it\Gamma}_{y^{\prime }y^{\prime }}),\\ 2{\it\rho}T\dot{{\it\gamma}}[{\it\eta}-(1+{\it\lambda}^{2})\sin 2{\it\phi}]={\it\Gamma}_{x^{\prime }y^{\prime }}=0.\end{array}\right\}\end{eqnarray}$$
The last equation of (B 8) yields an expression for the non-coaxiality angle
![]() ${\it\phi}$
in terms of
${\it\phi}$
in terms of
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() ${\it\lambda}$
:
${\it\lambda}$
:
By evaluating the integrals on the right-hand side of (B 8) to within an error of
![]() $O({\it\eta}^{m}{\it\lambda}^{2n},m+n>2)$
, the remaining three equations simplify to
$O({\it\eta}^{m}{\it\lambda}^{2n},m+n>2)$
, the remaining three equations simplify to
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}8{\rm\pi}^{3/2}R{\it\eta}\cos 2{\it\phi}-{\textstyle \frac{6}{5}}(1-e^{2}){\rm\pi}{\it\nu}(10+{\it\eta}^{2}+3{\it\lambda}^{4})=0,\\ 8{\rm\pi}^{3/2}R{\it\eta}\cos 2{\it\phi}-{\textstyle \frac{24}{35}}(3-e)(1+e){\rm\pi}{\it\nu}\{{\it\eta}^{2}+3{\it\lambda}^{2}(7-{\it\lambda}^{2})\}=0,\\ 35\sqrt{{\rm\pi}}R(1+{\it\lambda}^{2})\cos 2{\it\phi}-3(3+2e-e^{2}){\it\nu}{\it\eta}(7+2{\it\lambda}^{2})=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}8{\rm\pi}^{3/2}R{\it\eta}\cos 2{\it\phi}-{\textstyle \frac{6}{5}}(1-e^{2}){\rm\pi}{\it\nu}(10+{\it\eta}^{2}+3{\it\lambda}^{4})=0,\\ 8{\rm\pi}^{3/2}R{\it\eta}\cos 2{\it\phi}-{\textstyle \frac{24}{35}}(3-e)(1+e){\rm\pi}{\it\nu}\{{\it\eta}^{2}+3{\it\lambda}^{2}(7-{\it\lambda}^{2})\}=0,\\ 35\sqrt{{\rm\pi}}R(1+{\it\lambda}^{2})\cos 2{\it\phi}-3(3+2e-e^{2}){\it\nu}{\it\eta}(7+2{\it\lambda}^{2})=0.\end{array}\right\}\end{eqnarray}$$
The solutions for
![]() $R$
and
$R$
and
![]() ${\it\eta}$
are given by
${\it\eta}$
are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle R=\frac{3(1-e^{2}){\it\nu}}{140\sqrt{{\rm\pi}}{\it\eta}\cos 2{\it\phi}}(70+7{\it\eta}^{2}+21{\it\lambda}^{4}),\\ \displaystyle {\it\eta}^{2}=\frac{3{\it\lambda}^{2}(7+6{\it\lambda}^{2}-{\it\lambda}^{4})}{6+{\it\lambda}^{2}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle R=\frac{3(1-e^{2}){\it\nu}}{140\sqrt{{\rm\pi}}{\it\eta}\cos 2{\it\phi}}(70+7{\it\eta}^{2}+21{\it\lambda}^{4}),\\ \displaystyle {\it\eta}^{2}=\frac{3{\it\lambda}^{2}(7+6{\it\lambda}^{2}-{\it\lambda}^{4})}{6+{\it\lambda}^{2}},\end{array}\right\}\end{eqnarray}$$
where
![]() ${\it\lambda}^{2}$
satisfies a cubic equation, which after truncating at the second order, takes the form
${\it\lambda}^{2}$
satisfies a cubic equation, which after truncating at the second order, takes the form
yielding an approximate solution for
![]() ${\it\lambda}^{2}$
.
${\it\lambda}^{2}$
.
A comparison of the analytical solutions (B 9), (B 11), (B 12) for
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\phi}$
,
${\it\phi}$
,
![]() $R$
and
$R$
and
![]() ${\it\lambda}^{2}$
with those of Richman (Reference Richman1989) have been made (not shown). We found that the present solutions are better than those of Richman (Reference Richman1989) at lower values of the restitution coefficient (
${\it\lambda}^{2}$
with those of Richman (Reference Richman1989) have been made (not shown). We found that the present solutions are better than those of Richman (Reference Richman1989) at lower values of the restitution coefficient (
![]() $e<0.5$
), but are almost indistinguishable for
$e<0.5$
), but are almost indistinguishable for
![]() $e>0.5$
.
$e>0.5$
.
Appendix C. Stress tensor and transport coefficients in terms of collision integrals
The non-zero components of the dimensionless stress tensor in USF,
 $$\begin{eqnarray}\unicode[STIX]{x1D64B}^{\ast }=\frac{\unicode[STIX]{x1D64B}}{{\it\rho}_{p}U_{R}^{2}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D617}_{xx}^{\ast } & \unicode[STIX]{x1D617}_{xy}^{\ast } & 0\\ \unicode[STIX]{x1D617}_{yx}^{\ast } & \unicode[STIX]{x1D617}_{yy}^{\ast } & 0\\ 0 & 0 & \unicode[STIX]{x1D617}_{zz}^{\ast }\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64B}^{\ast }=\frac{\unicode[STIX]{x1D64B}}{{\it\rho}_{p}U_{R}^{2}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D617}_{xx}^{\ast } & \unicode[STIX]{x1D617}_{xy}^{\ast } & 0\\ \unicode[STIX]{x1D617}_{yx}^{\ast } & \unicode[STIX]{x1D617}_{yy}^{\ast } & 0\\ 0 & 0 & \unicode[STIX]{x1D617}_{zz}^{\ast }\end{array}\right),\end{eqnarray}$$
can be expressed in terms of the collision integral
![]() $\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}^{2})$
as defined in (3.36),
$\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}({\it\eta},R,{\it\phi},{\it\lambda}^{2})$
as defined in (3.36),
In (C 1),
![]() $U_{R}=2\dot{{\it\gamma}}{\it\sigma}$
is the reference velocity scale and
$U_{R}=2\dot{{\it\gamma}}{\it\sigma}$
is the reference velocity scale and
![]() ${\it\rho}_{p}={\it\rho}/{\it\nu}$
is the material/intrinsic density of particles. The series expansion for
${\it\rho}_{p}={\it\rho}/{\it\nu}$
is the material/intrinsic density of particles. The series expansion for
![]() $\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
given in (A 10)–(A 14) can be substituted in (C 1)–(C 5) to obtain final expressions for
$\mathscr{J}_{{\it\alpha}{\it\beta}{\it\gamma}}^{{\it\delta}p}$
given in (A 10)–(A 14) can be substituted in (C 1)–(C 5) to obtain final expressions for
![]() $\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}$
as in (5.4), (5.9)–(5.11).
$\unicode[STIX]{x1D617}_{{\it\alpha}{\it\beta}}$
as in (5.4), (5.9)–(5.11).
The dimensionless pressure is given by
where
![]() $T^{\ast }$
is the granular temperature
$T^{\ast }$
is the granular temperature
The expression for the dimensionless shear viscosity is given by
The ‘scaled’ first and second normal stress differences are defined with respect to mean pressure via
Appendix D. Source of the second-moment tensor
Appendix D, with (D 1)–(D 4), is available as supplementary materials.
Appendix E. Scaling of transport coefficients in the dense limit
There exist hundreds of recent papers on non-Brownian suspensions and dense granular media (Brady & Morris Reference Brady and Morris1997; Singh & Nott Reference Singh and Nott2003; Boyer et al. Reference Boyer, Pouliquen and Guazzelli2011; Couturier et al. Reference Couturier, Boyer, Pouliquen and Guazzelli2011; Trulsson et al. Reference Trulsson, Andreotti and Claudin2012; Dbouk et al. Reference Dbouk, Lobry and Lemaire2013; Denn & Morris Reference Denn and Morris2014; Suzuki & Hayakawa Reference Suzuki and Hayakawa2015) dealing solely with ‘how the shear viscosity diverges near the jamming/maximum-packing density’. Based on numerous simulation and experimental data, there is now a consensus that the shear viscosity follows a power-law scaling,
with the exponent having a value close to
![]() ${\it\delta}=2$
(for non-Brownian systems); here
${\it\delta}=2$
(for non-Brownian systems); here
![]() ${\it\nu}_{\mathit{max}}$
is identified with the jamming density having a value close to the random packing density 0.64. In the following we decipher the scaling of the transport coefficients near the maximum packing limit based on our theory.
${\it\nu}_{\mathit{max}}$
is identified with the jamming density having a value close to the random packing density 0.64. In the following we decipher the scaling of the transport coefficients near the maximum packing limit based on our theory.
It is straightforward to verify that both pressure and viscosity scale with
![]() $g_{0}$
(the pair-correlation function at contact) in the dense limit. Using Torquato’s form (Torquato Reference Torquato1995) for an ‘equilibrium’ hard-sphere system, we have
$g_{0}$
(the pair-correlation function at contact) in the dense limit. Using Torquato’s form (Torquato Reference Torquato1995) for an ‘equilibrium’ hard-sphere system, we have
This exponent is much different from 2 (Boyer et al.
Reference Boyer, Pouliquen and Guazzelli2011) which follows from many experiments and simulations on non-Brownian suspensions. Among two normal stress differences, the first normal stress difference decays to zero as
![]() ${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
but the second normal stress difference diverges like
${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
but the second normal stress difference diverges like
since
![]() $\unicode[STIX]{x1D615}_{2}$
remains finite at
$\unicode[STIX]{x1D615}_{2}$
remains finite at
![]() ${\it\nu}={\it\nu}_{\mathit{max}}$
(see figure 5
b).
${\it\nu}={\it\nu}_{\mathit{max}}$
(see figure 5
b).
Here we put forward some tentative arguments, based on ad hoc assumptions, to reason out why the scaling exponent for viscosity should be greater than unity. It is known from experiments and simulations that the onset of jamming is associated with a diverging length scale,
![]() $L_{J}\sim ({\it\nu}_{\mathit{max}}-{\it\nu})^{-{\it\alpha}}$
, with
$L_{J}\sim ({\it\nu}_{\mathit{max}}-{\it\nu})^{-{\it\alpha}}$
, with
![]() ${\it\alpha}\sim 0.73$
(Hatano Reference Hatano2009). This is clearly tied with a lesser amount of dissipation of kinetic energy (
${\it\alpha}\sim 0.73$
(Hatano Reference Hatano2009). This is clearly tied with a lesser amount of dissipation of kinetic energy (
![]() $\mathscr{D}\sim L_{J}^{-1}$
) as
$\mathscr{D}\sim L_{J}^{-1}$
) as
![]() ${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
and hence the temperature is likely to diverge as
${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
and hence the temperature is likely to diverge as
![]() $T\sim ({\it\nu}_{\mathit{max}}-{\it\nu})^{-2{\it\alpha}}$
which follows from the energy balance equation. (The present theory predicts a finite, shear-rate dependent, temperature at
$T\sim ({\it\nu}_{\mathit{max}}-{\it\nu})^{-2{\it\alpha}}$
which follows from the energy balance equation. (The present theory predicts a finite, shear-rate dependent, temperature at
![]() ${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
.) Incorporating the above information into the expression of shear viscosity (
${\it\nu}\rightarrow {\it\nu}_{\mathit{max}}$
.) Incorporating the above information into the expression of shear viscosity (
![]() ${\it\mu}\sim g_{0}L_{J}\sqrt{T}$
) yields an exponent for the divergence of viscosity as
${\it\mu}\sim g_{0}L_{J}\sqrt{T}$
) yields an exponent for the divergence of viscosity as
![]() $\tilde{{\it\delta}}=(1+2{\it\alpha})\approx 2.4$
.
$\tilde{{\it\delta}}=(1+2{\it\alpha})\approx 2.4$
.
It is known that the Enskog–Boltzmann equation incorporates only density correlations via the pair-correlation function but the velocity correlations and multi-particle collisions (as well as the ‘evolving’ anisotropic fabric networks (Kumar & Luding Reference Kumar and Luding2016)) which are equally important in the dense limit, are completely left out. Incorporating the correct dense-phase phenomenology into the present theory surely requires additional assumptions starting from the BBGKY (Bogoliubov–Born–Green–Kirkwood–Yvon) hierarchy or the Liouville equation. These theoretical issues are left for the future.