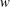1 Introduction and basic equations

We study two-dimensional (2D) potential motion of an ideal incompressible fluid of infinite depth with a free surface. The fluid occupies the infinite region $-\infty <x<\infty$ in the horizontal direction $x$ and extends down to $y\rightarrow -\infty$ in the vertical direction $y$ , as schematically shown in figure 1(a). The time-dependent fluid free surface is represented in parametric form as

(1.1a,b ) $$\begin{eqnarray}\displaystyle x=x(u,t),\quad y=y(u,t), & & \displaystyle\end{eqnarray}$$

with the parameter $u$ spanning the range $-\infty <u<\infty$ such that

(1.2a,b ) $$\begin{eqnarray}\displaystyle x(u,t)\rightarrow \pm \infty \quad \text{and}\quad y(u,t)\rightarrow 0\quad \text{as }u\rightarrow \pm \infty . & & \displaystyle\end{eqnarray}$$

We assume that the free surface does not have self-intersection, i.e. $\boldsymbol{r}(u_{1},t)\neq \boldsymbol{r}(u_{2},t)$ for any $u_{1}\neq u_{2}$ . In other words, the free surface is a simple plane curve. Here $\boldsymbol{r}(u,t)\equiv (x(u,t),y(u,t))$ .

Figure 1. The dark area represents the domain occupied by the fluid in the physical plane $z=x+\text{i}y$ (a) and the same domain in the $w=u+\text{i}v$ plane (b). The thick solid black line corresponds to the fluid’s free surface in both planes.

In the particular case when the free surface can be represented by a single-valued function of $x$ ,

(1.3) $$\begin{eqnarray}\displaystyle y=\unicode[STIX]{x1D702}(x,t), & & \displaystyle\end{eqnarray}$$

one can also represent the domain occupied by the fluid as $-\infty <y\leqslant \unicode[STIX]{x1D702}$ and $-\infty <x<\infty$ . Such a single-valued case has been widely considered (see e.g. Stoker Reference Stoker1957). However, we do not restrict ourselves to that particular case, which is recovered by choosing $u=x$ .

Potential motion implies that the velocity $\boldsymbol{v}$ of the fluid is determined by the velocity potential $\unicode[STIX]{x1D6F7}(\boldsymbol{r},t)$ as $\boldsymbol{v}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}$ with $\unicode[STIX]{x1D735}\equiv (\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$ . The incompressibility condition $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0$ results in the Laplace equation

(1.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D6F7}=0 & & \displaystyle\end{eqnarray}$$

inside the fluid. Equation (1.4) is supplemented with a decaying boundary condition (BC) at infinity in the horizontal direction,

(1.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\rightarrow 0\quad \text{for }|x|\rightarrow \infty , & & \displaystyle\end{eqnarray}$$

and a vanishing normal velocity at the fluid’s bottom,

(1.6) $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}n}\right|_{y\rightarrow -\infty }=0. & & \displaystyle\end{eqnarray}$$

Without loss of generality BCs (1.5) and (1.6) can be replaced by the Dirichlet BC

(1.7) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}\rightarrow 0\quad \text{at }|\boldsymbol{r}|\rightarrow \infty . & & \displaystyle\end{eqnarray}$$

The BCs at the free surface are time-dependent and consist of kinematic and dynamic BCs. The kinematic BC ensures that free surface moves with the normal velocity component $v_{n}$ of the fluid particles at the free surface. The motion of the free surface is determined by time derivatives of the parametrization (1.1), and the kinematic BC is given by a projection into normal directions as

(1.8) $$\begin{eqnarray}\displaystyle \boldsymbol{n}\boldsymbol{\cdot }(x_{t},y_{t})=v_{n}\equiv \boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}|_{x=x(u,t),\,y=y(u,t)}, & & \displaystyle\end{eqnarray}$$

where

(1.9) $$\begin{eqnarray}\displaystyle \boldsymbol{n}=\frac{(-y_{u},x_{u})}{(x_{u}^{2}+y_{u}^{2})^{1/2}} & & \displaystyle\end{eqnarray}$$

is the outward unit normal vector to the free surface, and the subscripts here and below mean partial derivatives, $x_{t}\equiv \unicode[STIX]{x2202}x(u,t)/\unicode[STIX]{x2202}t$ , etc.

Equations (1.8) and (1.9) result in a compact expression

(1.10) $$\begin{eqnarray}\displaystyle y_{t}x_{u}-x_{t}y_{u}=[x_{u}\unicode[STIX]{x1D6F7}_{y}-y_{u}\unicode[STIX]{x1D6F7}_{x}]|_{x=x(u,t),\,y=y(u,t)} & & \displaystyle\end{eqnarray}$$

for the kinematic BC.

The tangential component of the vector $\boldsymbol{r}_{t}=(x_{t},y_{t})$ is not fixed by the kinematic BC (1.10) but can be chosen at our convenience. For example, one can define $u$ to be the Lagrangian coordinate of fluid particles at the free surface (fluid particles once on the free surface never leave it). Then the tangential component of $\boldsymbol{r}_{t}$ would coincide with the tangential component of $\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}|_{x=x(u,t),\,y=y(u,t)}$ . Another possible choice is to choose $u$ to be the arclength along the free surface. However, we use neither Lagrangian nor arclength formulation below. Instead, throughout the paper we use the conformal variables for the free surface parametrization as described below in § 2. Another particular form of (1.1) is given by (1.3), which corresponds to choosing $u=x$ (as mentioned above, this is possible only if $\unicode[STIX]{x1D702}(x,t)$ is a single-valued function of $x$ ). In that case (1.9) is reduced to $\boldsymbol{n}=(-\unicode[STIX]{x1D702}_{x},1)(1+\unicode[STIX]{x1D702}_{x}^{2})^{-1/2}$ and the kinematic BC equation (1.10) is given by

(1.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{t}=(1+\unicode[STIX]{x1D702}_{x}^{2})^{1/2}v_{n}=(-\unicode[STIX]{x1D702}_{x}\unicode[STIX]{x1D6F7}_{x}+\unicode[STIX]{x1D6F7}_{y})|_{y=\unicode[STIX]{x1D702}(x,t)}. & & \displaystyle\end{eqnarray}$$

This form of the kinematic BC has been widely used (see e.g. Stoker Reference Stoker1957).

A dynamic BC, which is the time-dependent Bernoulli equation (see e.g. Landau & Lifshitz Reference Landau and Lifshitz1989) at the free surface, is given by

(1.12) $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}_{t}+{\textstyle \frac{1}{2}}(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7})^{2}+gy)|_{x=x(u,t),\,y=y(u,t)}=-P_{\unicode[STIX]{x1D6FC}}, & & \displaystyle\end{eqnarray}$$

where $g$ is the acceleration due to gravity and

(1.13) $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D6FC}}=-\frac{\unicode[STIX]{x1D6FC}(x_{u}y_{uu}-x_{uu}y_{u})}{(x_{u}^{2}+y_{u})^{3/2}} & & \displaystyle\end{eqnarray}$$

is the pressure jump at the free surface due to the surface tension coefficient $\unicode[STIX]{x1D6FC}$ . Here, without loss of generality, we have assumed that the pressure is zero above the free surface (i.e. in vacuum). All the results below apply both to the surface gravity wave case ( $g>0$ ) and to the Rayleigh–Taylor problem ( $g<0$ ). Below we also consider a particular case $g=0$ when inertia forces greatly exceed the gravity force. For the case of single-valued parametrization (1.3), equation (1.13) is reduced to the well-known expression (see e.g. Zakharov Reference Zakharov1968)

(1.14) $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D6FC}}=-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}[\unicode[STIX]{x1D702}_{x}(1+\unicode[STIX]{x1D702}_{x}^{2})^{-1/2}]=-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D702}_{xx}(1+\unicode[STIX]{x1D702}_{x}^{2})^{-1/2}. & & \displaystyle\end{eqnarray}$$

Equations (1.12) and (1.13), together with decaying BCs (1.2) and (1.5), imply that the Bernoulli constant (generally located on the right-hand side (RHS) of equation (1.12)) is zero.

Equations (1.1), (1.2), (1.4)–(1.9), (1.12) and (1.13) form a closed set of equations which is equivalent to the Euler equations for the dynamics of an ideal fluid with a free surface for any chosen free surface parametrization (1.1). Here, at each moment of time $t$ , the Laplace equation (1.4) has to be solved with the Dirichlet BC

(1.15) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(x,t)\equiv \unicode[STIX]{x1D6F7}(\boldsymbol{r},t)|_{x=x(u,t),\,y=y(u,t)} & & \displaystyle\end{eqnarray}$$

and BCs (1.5) and (1.6). That boundary-value problem has a unique solution. Knowledge of $\unicode[STIX]{x1D6F7}(\boldsymbol{r},t)$ allows one to find the normal velocity $v_{n}$ at the free surface as in (1.10). This can be interpreted as finding the Dirichlet–Neumann operator for the Laplace equation (1.4) (Craig & Sulem Reference Craig and Sulem1993). Then one can advance in time to find a new value of $\unicode[STIX]{x1D713}(x,t)$ from (1.10) and (1.12) using

(1.16) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}=[\unicode[STIX]{x1D6F7}_{t}+x_{t}\unicode[STIX]{x1D6F7}_{x}+y_{t}\unicode[STIX]{x1D6F7}_{y}]|_{x=x(u,t),\,y=y(u,t)} & & \displaystyle\end{eqnarray}$$

as well as evolving a parametrization (1.1) and so on. Here (1.16) results from the definition (1.15).

The set (1.1), (1.2), (1.4), (1.7), (1.9) and (1.12) preserves the total energy

(1.17) $$\begin{eqnarray}\displaystyle H=K+P, & & \displaystyle\end{eqnarray}$$

where

(1.18) $$\begin{eqnarray}\displaystyle K=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7})^{2}\,\text{d}x\,\text{d}y & & \displaystyle\end{eqnarray}$$

is the kinetic energy and

(1.19) $$\begin{eqnarray}\displaystyle P=g\int _{\unicode[STIX]{x1D6FA}}y\,\text{d}x\,\text{d}y-g\int _{y\leqslant 0}y\,\text{d}x\,\text{d}y+\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{x_{u}^{2}+y_{u}^{2}}-x_{u}\right)\text{d}u & & \displaystyle\end{eqnarray}$$

is the potential energy. Here $\text{d}x\,\text{d}y$ is the element of fluid volume (more precisely it is the fluid’s area because we have restricted ourselves to 2D fluid motion, with the third spatial dimension being trivial), and $\unicode[STIX]{x1D6FA}$ is the area occupied by the fluid which extends down to $y\rightarrow -\infty$ in the vertical direction. The term $g\int _{y\leqslant 0}y\,\text{d}x\,\text{d}y$ corresponds to the gravitational energy of the unperturbed fluid (flat free surface) and it is subtracted from the integral over $\unicode[STIX]{x1D6FA}$ to ensure that the total contribution of the gravitational energy, $g\int _{\unicode[STIX]{x1D6FA}}y\,\text{d}x\,\text{d}y-g\int _{y\leqslant 0}y\,\text{d}x\,\text{d}y$ , is finite. In other words, one can understand these two terms as the limit $h\rightarrow \infty$ and $L\rightarrow \infty ,$ where $h$ is the fluid depth with the bottom at $y=-h$ , and $L$ is the horizontal extent of the fluid. Then $g\int _{y\leqslant 0}y\,\text{d}x\,\text{d}y=-(gh^{2}L/2)$ , where using this expression below we assume that we take the limits $h\rightarrow \infty$ and $L\rightarrow \infty .$ The surface tension energy $\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }(\sqrt{x_{u}^{2}+y_{u}^{2}}-x_{u})\,\text{d}u$ in (1.19) is determined by the arclength of free surface, with the $-x_{u}$ term added to ensure that the surface energy is zero for an unperturbed fluid with $y\equiv 0$ .

If we introduce the vector field $\boldsymbol{F}={\hat{y}}y^{2}/2$ , with ${\hat{y}}$ being the unit vector in the positive $y$ direction, then the gravitational energy in (1.19) takes the following form: $g\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y-(gh^{2}L/2)|_{h,L\rightarrow \infty }$ . By the divergence theorem of vector analysis (in our 2D case it can also be reduced to Green’s theorem), this gravitational energy is converted into the surface integral $g\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{F}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}s+(gh^{2}L/2)|_{h,L\rightarrow \infty }$ (line integral in 2D over arclength $\text{d}s=\sqrt{x_{u}^{2}+y_{u}^{2}}\,\text{d}u$ with $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$ being the boundary of $\unicode[STIX]{x1D6FA}$ ), which together with (1.9) results in

(1.20) $$\begin{eqnarray}\displaystyle P=\frac{g}{2}\int _{-\infty }^{\infty }y^{2}x_{u}\,\text{d}u+\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{x_{u}^{2}+y_{u}^{2}}-x_{u}\right)\,\text{d}u. & & \displaystyle\end{eqnarray}$$

In the simplest case of the single-valued surface parametrization equation (1.3), equations (1.18) and (1.20) take the simpler forms

(1.21) $$\begin{eqnarray}\displaystyle K=\frac{1}{2}\int _{-\infty }^{\infty }\text{d}x\int _{-\infty }^{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7})^{2}\,\text{d}y & & \displaystyle\end{eqnarray}$$

and

(1.22) $$\begin{eqnarray}\displaystyle P=\frac{g}{2}\int _{-\infty }^{\infty }\unicode[STIX]{x1D702}^{2}\,\text{d}x+\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{1+\unicode[STIX]{x1D702}_{x}^{2}}-1\right)\text{d}x, & & \displaystyle\end{eqnarray}$$

respectively.

It was proved in Zakharov (Reference Zakharov1968) that $\unicode[STIX]{x1D713}$ and $\unicode[STIX]{x1D702}$ for the single-valued surface parametrization (1.3) satisfy the canonical Hamiltonian system:

(1.23a,b ) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}},\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}t}=-\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}}, & & \displaystyle\end{eqnarray}$$

with $H$ given by (1.17), (1.21) and (1.22). The Hamiltonian formalism of Zakharov (Reference Zakharov1968) has been widely used for water waves (for reviews, see e.g. Zakharov, Lvov & Falkovich Reference Zakharov, Lvov and Falkovich1992, Kharif & Pelinovsky Reference Kharif and Pelinovsky2003) as well as being generalized to the dynamics of the interface between two fluids (Kuznetsov & Lushnikov Reference Kuznetsov and Lushnikov1995). In this paper we show that for the general ‘multi-valued’ case of the parametrization (1.1), the system of dynamical equations (1.10) and (1.12) for $x(u,t)$ , $y(u,t)$ and $\unicode[STIX]{x1D713}(u,t)$ also has a Hamiltonian structure if we additionally assume that $x(u,t)$ and $y(u,t)$ are defined from the conformal map of § 2. However, that structure is non-canonical with the non-canonical Poisson bracket and depends on the choice of the parametrization of the surface.

Apparently, the system (1.10) has an infinite number of degrees of freedom. The most important feature of integrable systems is the existence of ‘additional’ constants of motion which are different from ‘natural’ motion constants (integrals) (see Gardner et al. Reference Gardner, Greene, Kruskal and Miura1967; Zakharov & Faddeev Reference Zakharov and Faddeev1971; Zakharov & Shabat Reference Zakharov and Shabat1972; Novikov et al. Reference Novikov, Manakov, Pitaevskii and Zakharov1984; Arnold Reference Arnold1989)). For system (1.23) the natural integrals are the energy $H$ (1.17), the total mass of fluid,

(1.24) $$\begin{eqnarray}\displaystyle M=\int _{-\infty }^{\infty }\unicode[STIX]{x1D702}(x,t)\,\text{d}x, & & \displaystyle\end{eqnarray}$$

and the horizontal component of the momentum,

(1.25) $$\begin{eqnarray}\displaystyle P_{x}=\int _{-\infty }^{\infty }\text{d}x\int _{-\infty }^{\unicode[STIX]{x1D702}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}x}\,\text{d}y. & & \displaystyle\end{eqnarray}$$

Here $\unicode[STIX]{x1D6F7}$ is a harmonic function inside the fluid because it satisfies the Laplace equation (1.4). The harmonic conjugate of $\unicode[STIX]{x1D6F7}$ is a streamfunction $\unicode[STIX]{x1D6E9}$ defined by

(1.26a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{x}=-\unicode[STIX]{x1D6F7}_{y}\quad \text{and}\quad \unicode[STIX]{x1D6E9}_{y}=\unicode[STIX]{x1D6F7}_{x}. & & \displaystyle\end{eqnarray}$$

Similar to (1.7), without loss of generality we set the zero Dirichlet BC for $\unicode[STIX]{x1D6E9}$ as

(1.27) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}\rightarrow 0\quad \text{at }|\boldsymbol{r}|\rightarrow \infty . & & \displaystyle\end{eqnarray}$$

We define a complex velocity potential $\unicode[STIX]{x1D6F1}(z,t)$  as

(1.28) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F7}+\text{i}\unicode[STIX]{x1D6E9}, & & \displaystyle\end{eqnarray}$$

where

(1.29) $$\begin{eqnarray}\displaystyle z=x+\text{i}y & & \displaystyle\end{eqnarray}$$

is the complex coordinate. Then equations (1.26) turn into Cauchy–Riemann equations ensuring the analyticity of $\unicode[STIX]{x1D6F1}(z,t)$ in the domain of $z$ plane occupied by the fluid (with the free fluid’s boundary defined by (1.1) and (1.2)). A physical velocity with the components $v_{x}$ and $v_{y}$ (in $x$ and $y$ directions, respectively) is recovered from $\unicode[STIX]{x1D6F1}$ as $\text{d}\unicode[STIX]{x1D6F1}/\text{d}z=v_{x}-\text{i}v_{y}$ .

Using $\unicode[STIX]{x1D6E9}_{y}=\unicode[STIX]{x1D6F7}_{x}$ from (1.26), we immediately convert the horizontal momentum (1.25) into $P_{x}=\int _{-\infty }^{\infty }\unicode[STIX]{x1D6E9}\,\text{d}x$ through integration by parts and equation (1.27), which results in

(1.30) $$\begin{eqnarray}\displaystyle P_{x}=\int _{-\infty }^{\infty }\unicode[STIX]{x1D6E9}(x(u,t),y(u,t),t)x_{u}(u,t)\,\text{d}u. & & \displaystyle\end{eqnarray}$$

Equation (1.30) is also valid for the general multi-valued case (contrary to (1.25), which requires the particular parametrization (1.3)). To check that, we replace (1.25) by $P_{x}=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6E9}_{y}\,\text{d}x\,\text{d}y=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y$ with $\boldsymbol{F}={\hat{y}}\unicode[STIX]{x1D6E9}$ and, similar to the derivation of (1.20), we then obtain (1.30) from the divergence theorem and (1.9).

One can use equation (1.26) to obtain the equivalent form of $P_{x}$ as $P_{x}=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6F7}_{x}\,\text{d}x\,\text{d}y=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y$ with $\boldsymbol{F}=\hat{x}\unicode[STIX]{x1D6F7}.$ Then the divergence theorem together with (1.9) results in

(1.31) $$\begin{eqnarray}\displaystyle P_{x}=-\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}(x(u,t),t)y_{u}(u,t)\,\text{d}u. & & \displaystyle\end{eqnarray}$$

In a similar way, a vertical component of momentum is given by

(1.32) $$\begin{eqnarray}\displaystyle P_{y}=\int _{-\infty }^{\infty }\text{d}x\int _{-\infty }^{\unicode[STIX]{x1D702}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}y}\,\text{d}y=\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}\,\text{d}x, & & \displaystyle\end{eqnarray}$$

where we have used integration by parts and equations (1.7) and (1.15). Here $P_{y}$ is the integral of motion only for the zero-gravity case, $g=0$ . A change of integration variable in (1.32) results in

(1.33) $$\begin{eqnarray}\displaystyle P_{y}=\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}x_{u}\,\text{d}u. & & \displaystyle\end{eqnarray}$$

Equation (1.33) is also valid for the general multi-valued case. To check that, in the general case we define $P_{y}=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6F7}_{y}\,\text{d}x\,\text{d}y=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y$ with $\boldsymbol{F}={\hat{y}}\unicode[STIX]{x1D6F7}$ and, similar to the derivation of (1.20), we obtain (1.33) from the divergence theorem and (1.9).

One can use (1.26) to obtain the equivalent form of $P_{y}$ as $P_{y}=-\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6E9}_{x}\,\text{d}x\,\text{d}y=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y$ with $\boldsymbol{F}=-\hat{x}\unicode[STIX]{x1D6E9}.$ Then the divergence theorem together with (1.9) results in

(1.34) $$\begin{eqnarray}\displaystyle P_{x}=\int _{-\infty }^{\infty }\unicode[STIX]{x1D6E9}(x(u,t),y(u,t),t)y_{u}(u,t)\,\text{d}u. & & \displaystyle\end{eqnarray}$$

For the parametrization (1.1), equation (1.24) is replaced by $M=\int _{\unicode[STIX]{x1D6FA}}\,\text{d}x\,\text{d}y-\int _{y\leqslant 0}\,\text{d}x\,\text{d}y=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}\,\text{d}x\,\text{d}y-hL|_{h,L\rightarrow \infty }$ with $\boldsymbol{F}={\hat{y}}y$ . Similar to the derivation of (1.20) we then use the divergence theorem and (1.9) to obtain that

(1.35) $$\begin{eqnarray}\displaystyle M=\int _{-\infty }^{\infty }y(u,t)x_{u}(u,t)\,\text{d}u. & & \displaystyle\end{eqnarray}$$

In this paper we develop a Hamiltonian formalism for the general multi-valued case for comparison with the single-valued case established in Zakharov (Reference Zakharov1968). The plan of the paper is the following. In § 2 we introduce the conformal variables as the particular case of the general parametrization (1.1). In § 3 we introduce the Hamiltonian formalism for system (1.1), (1.2), (1.4)–(1.9) and (1.12) with the non-local non-canonical symplectic form and the corresponding Poisson bracket. Section 4 provides the explicit expression for the Hamiltonian equations resolved with respect to time derivatives. Section 5 rewrites these dynamic equations in complex form and introduces other complex unknowns $R$ and $V$ . Section 6 introduces a generalization of the Hamiltonian of the Euler equations with a free surface to include additional physical effects such as the interaction of dielectric fluids with an electric field and two-fluid hydrodynamics of superfluid helium with a free surface. It is shown that these equations allow very powerful reductions, which suggests a complete integrability. Section 7 provides a summary of obtained results and discussion on future directions.

2 Conformal mapping

To choose a convenient version of the general parametrization (1.1), we consider the time-dependent conformal mapping

(2.1) $$\begin{eqnarray}\displaystyle z(w,t)=x(u,v,t)+\text{i}y(u,v,t) & & \displaystyle\end{eqnarray}$$

of the lower complex half-plane $\mathbb{C}^{-}$ of the auxiliary complex variable

(2.2) $$\begin{eqnarray}\displaystyle w\equiv u+\text{i}v,\quad -\infty <u<\infty , & & \displaystyle\end{eqnarray}$$

into the area in the $(x,y)$ plane occupied by the fluid. Here the real line $v=0$ is mapped into the fluid free surface (see figure 1) and $\mathbb{C}^{-}$ is defined by the condition $-\infty <v<0$ . The function $z(w,t)$ is an analytic function of $w\in \mathbb{C}^{-}$ . The conformal mapping (2.1) at $v=0$ provides a particular form of the free surface parametrization (1.1) for the parameter  $u$ .

The conformal mapping (2.1) ensures that the function $\unicode[STIX]{x1D6F1}(z,t)$ in (1.28) transforms into $\unicode[STIX]{x1D6F1}(w,t)$ , which is an analytic function of $w$ for $w\in \mathbb{C}^{-}$ (in the bulk of the fluid). Here and below we abuse notation and use the same symbols for functions of either $w$ or $z$ (in other words, we assume that, for example, $\tilde{\unicode[STIX]{x1D6F1}}(w,t)=\unicode[STIX]{x1D6F1}(z(w,t),t)$ and remove the $\tilde{\,}$ sign). The conformal transformation (2.1) also ensures Cauchy–Riemann equations $\unicode[STIX]{x1D6E9}_{u}=-\unicode[STIX]{x1D6F7}_{v}$ and $\unicode[STIX]{x1D6E9}_{v}=\unicode[STIX]{x1D6F7}_{u}$ in the $w$ plane.

The idea of using a time-dependent conformal transformation like (2.1) to address systems equivalent/similar to equations (1.1), (1.2), (1.4)–(1.9) and (1.12) has been exploited by several authors, including Ovsyannikov (Reference Ovsyannikov1973), Meison, Orzag & Izraely (Reference Meison, Orzag and Izraely1981), Tanveer (Reference Tanveer1991, Reference Tanveer1993), Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996), Chalikov & Sheinin (Reference Chalikov and Sheinin1998, Reference Chalikov and Sheinin2005), Zakharov, Dyachenko & Vasiliev (Reference Zakharov, Dyachenko and Vasiliev2002) and Chalikov (Reference Chalikov2016). We follow Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996) to recast the system (1.1), (1.2), (1.4)–(1.9) and (1.12) into the equivalent form for $x(u,t),y(u,t)$ and $\unicode[STIX]{x1D713}(u,t)$ at the real line $w=u$ of the complex plane $w$ using the conformal transformation (2.1). We show that the kinematical BC takes the form

(2.3) $$\begin{eqnarray}\displaystyle y_{t}x_{u}-x_{t}y_{u}=-\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}, & & \displaystyle\end{eqnarray}$$

where

(2.4) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{H}}}\,f(u)=\frac{1}{\unicode[STIX]{x03C0}}\,\text{p.v.}\int _{-\infty }^{+\infty }\frac{f(u^{\prime })}{u^{\prime }-u}\,\text{d}u^{\prime } & & \displaystyle\end{eqnarray}$$

is the Hilbert transform (Hilbert Reference Hilbert and Krazer1905) with $\text{p.v.}$ denoting a Cauchy principal value of the integral. The dynamic BC takes the form

(2.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}y_{u}-\unicode[STIX]{x1D713}_{u}y_{t}+gyy_{u}=-\hat{{\mathcal{H}}}(\unicode[STIX]{x1D713}_{t}x_{u}-\unicode[STIX]{x1D713}_{u}x_{t}+gyx_{u})-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}+\unicode[STIX]{x1D6FC}\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}, & & \displaystyle\end{eqnarray}$$

where $x(u,t)$ is expressed through $y(u,t)$ as follows:

(2.6) $$\begin{eqnarray}\displaystyle \tilde{x}\equiv x-u=-\hat{{\mathcal{H}}}y & & \displaystyle\end{eqnarray}$$

(see (A 8) of appendix A for the justification of (2.6) as well as the complementary expression $\hat{{\mathcal{H}}}\tilde{x}=y$ ).

Equation (2.6) exemplifies the general relation between the harmonically conjugated functions in $\mathbb{C}^{-}$ as was first obtained by David Hilbert (Reference Hilbert and Krazer1905). The particular case of equation (2.6) results from the analyticity of $z(w,t)$ for $w\in \mathbb{C}^{-}$ , which implies that $\tilde{x}$ and $y$ are harmonically conjugated functions for $w\in \mathbb{C}^{-}.$ Similarly, $\unicode[STIX]{x1D6F1}(w,t)$ in (1.28) is also an analytic function for $w\in \mathbb{C}^{-}$ , which results in

(2.7a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}|_{w=u}=\hat{{\mathcal{H}}}\unicode[STIX]{x1D713},\quad \unicode[STIX]{x1D713}=-\hat{{\mathcal{H}}}\unicode[STIX]{x1D6E9}|_{w=u}\quad \text{for }w=u. & & \displaystyle\end{eqnarray}$$

We notice that the left-hand side (LHS) of equation (2.3) is the same as the LHS of equation (1.10) multiplied by $(x_{u}^{2}+y_{u}^{2})^{1/2}=|z_{u}|$ . The RHS of equation (1.10) multiplied by $(x_{u}^{2}+y_{u}^{2})^{1/2}$ is given by $\unicode[STIX]{x1D6F7}_{v}|_{v=0}=-\unicode[STIX]{x1D6E9}_{u}|_{v=0}$ (which is the normal velocity $v_{n}$ to the surface in the $w$ plane multiplied by the Jacobian $x_{u}^{2}+y_{u}^{2}$ of the conformal transformation (2.1) (see e.g. Dyachenko et al. Reference Dyachenko, Kuznetsov, Spector and Zakharov1996; Dyachenko, Lushnikov & Korotkevich Reference Dyachenko, Lushnikov and Korotkevich2016)). Then using (1.15) and (2.7), we obtain (2.3).

Equation (2.5) can also be obtained from (1.4)–(1.9), (1.12), (1.13) and (1.15) by the change of variables (2.1). We do not provide it here to avoid somewhat bulky calculations. Instead, we derive both equations (2.3) and (2.5) from the Hamiltonian formalism in § 3. See also appendix A.2 of Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for a detailed derivation of similar equations for the case of periodic BCs along $x$ instead of decaying BCs (1.2) and (1.5).

We now transform the kinetic energy (1.18) into the integral over the real line $w=u$ . The Laplace equation (1.4) implies that we can apply Green’s formula to equation (1.18) as $K=(1/2)\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D6F7}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7})\,\text{d}x\,\text{d}y=(1/2)\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D713}v_{n}\,\text{d}s=(1/2)\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D713}v_{n}\sqrt{x_{u}^{2}+y_{u}^{2}}\,\text{d}u$ . Using (1.9), (1.15) and (2.7) and rewriting $v_{n}$ in conformal variable $w$ (see e.g. appendix A.1 of Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for explicit expressions of the respective derivatives), one obtains that (Dyachenko et al. Reference Dyachenko, Kuznetsov, Spector and Zakharov1996)

(2.8) $$\begin{eqnarray}\displaystyle K=-\frac{1}{2}\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\,\text{d}u. & & \displaystyle\end{eqnarray}$$

3 Hamiltonian formalism

Conformal mapping makes possible an extension of the Hamiltonian formalism of (1.23) for a single-valued function $\unicode[STIX]{x1D702}$ of $x$ into a general multi-valued case, i.e. to the parametrization (1.1). For that we note that the Hamiltonian equations (1.23) can be obtained from the minimization of the action functional

(3.1) $$\begin{eqnarray}\displaystyle S=\int L\,\text{d}t, & & \displaystyle\end{eqnarray}$$

with the Lagrangian

(3.2) $$\begin{eqnarray}\displaystyle L=\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}\unicode[STIX]{x1D702}_{t}\,\text{d}x-H. & & \displaystyle\end{eqnarray}$$

We now generalize the Lagrangian (3.2) into multi-valued $\unicode[STIX]{x1D702}$ through the parametrization (1.1) as

(3.3) $$\begin{eqnarray}\displaystyle L=\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}(y_{t}x_{u}-x_{t}y_{u})\,\text{d}u-H, & & \displaystyle\end{eqnarray}$$

with the Hamiltonian

(3.4) $$\begin{eqnarray}\displaystyle H=-\frac{1}{2}\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\,\text{d}u+\frac{g}{2}\int _{-\infty }^{\infty }y^{2}x_{u}\,\text{d}u+\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{x_{u}^{2}+y_{u}^{2}}-x_{u}\right)\text{d}u, & & \displaystyle\end{eqnarray}$$

as follows from (1.17), (1.20) and (2.8). Here we have used the change of variables in $\unicode[STIX]{x1D702}_{t}\,\text{d}x$ of equation (3.2) from $(x,t)$ into $(u,t)$ , which results in $\unicode[STIX]{x1D702}_{t}\,\text{d}x=(y_{t}x_{u}-x_{t}y_{u})\,\text{d}u$ (see also appendix A.2 of Dyachenko et al. (Reference Dyachenko, Lushnikov and Korotkevich2016) for more details).

Using (2.6) to explicitly express $x(u,t)$ as a functional of $y(u,t)$ , one can rewrite the Hamiltonian $H$ (3.4) as follows:

(3.5) $$\begin{eqnarray}\displaystyle H & = & \displaystyle -\frac{1}{2}\int _{-\infty }^{\infty }\unicode[STIX]{x1D713}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\,\text{d}u+\frac{g}{2}\int _{-\infty }^{\infty }y^{2}(1-\hat{{\mathcal{H}}}y_{u})\,\text{d}u\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}\int _{-\infty }^{\infty }\left(\sqrt{(1-\hat{{\mathcal{H}}}y_{u})^{2}+y_{u}^{2}}-1+\hat{{\mathcal{H}}}y_{u}\right)\text{d}u.\end{eqnarray}$$

We can use either (3.4) or (3.5) at our convenience for finding the dynamic equations.

Vanishing of a variation $\unicode[STIX]{x1D6FF}S=0$ of (3.1) over $\unicode[STIX]{x1D713}$ together with (3.3) results in

(3.6) $$\begin{eqnarray}\displaystyle y_{t}x_{u}-x_{t}y_{u}=-\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$

which gives kinematic BC (2.3).

Variations over $x$ and $y$ must satisfy the condition (2.6). To ensure that condition, we introduce the modification $\tilde{L}$ of the Lagrangian (3.3) and the modified action $\tilde{S}$ by adding the term with the Lagrange multiplier $f(u,t)$ as

(3.7a,b ) $$\begin{eqnarray}\displaystyle \tilde{L}=L+\int _{-\infty }^{\infty }f[y-\hat{{\mathcal{H}}}(x-u)]\,\text{d}u,\quad \tilde{S}=\int \tilde{L}\,\text{d}t, & & \displaystyle\end{eqnarray}$$

which does not change (3.6).

To ensure the most compact derivation of the dynamical equations from the variation of $\tilde{S}$ , we use the Hamiltonian (3.5) (which does not contain $x$ ) while we keep $x$ (not expressing it as a functional of $y$ ) in the remaining terms of the modified action $\tilde{S}$ beyond $H$ . Then a vanishing of a variation $\unicode[STIX]{x1D6FF}\tilde{S}=0$ over $x$ and $y,$ together with (3.3), (3.4) and (3.7), result in the equations

(3.8) $$\begin{eqnarray}\displaystyle y_{u}\unicode[STIX]{x1D713}_{t}-y_{t}\unicode[STIX]{x1D713}_{u}+\hat{{\mathcal{H}}}\,f=0 & & \displaystyle\end{eqnarray}$$

and

(3.9) $$\begin{eqnarray}\displaystyle -x_{u}\unicode[STIX]{x1D713}_{t}+x_{t}\unicode[STIX]{x1D713}_{u}+f=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}=gyx_{u}-g\hat{{\mathcal{H}}}(yy_{u})-\unicode[STIX]{x1D6FC}\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}, & & \displaystyle\end{eqnarray}$$

respectively. Here we have used that

(3.10) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}F(x-u)}{\unicode[STIX]{x1D6FF}y}=\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x1D6FF}F(x-u)}{\unicode[STIX]{x1D6FF}x} & & \displaystyle\end{eqnarray}$$

for any functional $F$ of $x(u)-u=-\hat{{\mathcal{H}}}y$ .

Excluding the Lagrange multiplier $f$ from (3.8) and (3.9) by applying $\hat{{\mathcal{H}}}$ to (3.9) and subtracting the result from (3.8), we recover (2.5).

We note that there are two alternatives to using (3.8) and (3.9). The first one is to keep $x$ in the Hamiltonian $H$ (1.17), (1.20) and (2.8) (instead of replacing it by $u-\hat{{\mathcal{H}}}(x-u)$ as was done in (3.5)). Then vanishing variations of $\tilde{S}$ (3.7) over $x$ or $y$ result in modification of (3.8) and (3.9). Excluding $f$ from these modified equations still results in (2.5) as was obtained in Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996). The second alternative is to replace $x$ by $u-\hat{{\mathcal{H}}}(x-u)$ in (3.1) and (3.3) and use the Hamiltonian (3.5). Then a vanishing variation of $S$ (3.1) over $y$ results in

(3.11) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{H}}}(\unicode[STIX]{x1D713}_{t}y_{u}-\unicode[STIX]{x1D713}_{u}y_{t})-\unicode[STIX]{x1D713}_{t}x_{u}+\unicode[STIX]{x1D713}_{u}x_{t}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}=gyx_{u}-g\hat{{\mathcal{H}}}(yy_{u})-\unicode[STIX]{x1D6FC}\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}.\qquad & & \displaystyle\end{eqnarray}$$

Applying $-\hat{{\mathcal{H}}}$ to (3.11) we again recover (2.5). A variational derivative of the Hamiltonian over $\unicode[STIX]{x1D713}$ in all cases is given by (3.6).

The second alternative above allows one to obtain (2.5) without the use of the Lagrange multiplier $f$ . Below we use (3.8) and (3.9) because they allow significant simplification of the subsequent transformations.

Applying $-\hat{{\mathcal{H}}}$ to (3.8) and adding it to (3.9) recovers (3.11). We use (3.6) and (3.11) to rewrite (2.3) and (2.5) in the ‘symplectic’ Hamiltonian form (Zakharov & Dyachenko Reference Zakharov and Dyachenko2012)

(3.12a,b ) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}\boldsymbol{Q}_{t}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\boldsymbol{Q}},\quad \boldsymbol{Q}\equiv \left(\begin{array}{@{}c@{}}y\\ \unicode[STIX]{x1D713}\end{array}\right), & & \displaystyle\end{eqnarray}$$

where the symplectic operator $\hat{\unicode[STIX]{x1D6FA}}$ is given by

(3.13) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}=\left(\begin{array}{@{}cc@{}}\hat{\unicode[STIX]{x1D6FA}}_{11} & \hat{\unicode[STIX]{x1D6FA}}_{12}\\ \hat{\unicode[STIX]{x1D6FA}}_{21} & 0\end{array}\right), & & \displaystyle\end{eqnarray}$$

which is $2\times 2$ skew-symmetric matrix operator with

(3.14) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}_{21}^{\dagger }=-\hat{\unicode[STIX]{x1D6FA}}_{12}. & & \displaystyle\end{eqnarray}$$

Here $\hat{\unicode[STIX]{x1D6FA}}_{21}^{\dagger }$ is the adjoint operator, $\langle f,\hat{\unicode[STIX]{x1D6FA}}_{ij}g\rangle \equiv \langle \hat{\unicode[STIX]{x1D6FA}}_{ij}^{\dagger }\,f,g\rangle$ , $i,j=1,2$ , with respect to the scalar product $\langle f,g\rangle =\int _{-\infty }^{\infty }f(u)g(u)\,\text{d}u$ . Also $\hat{\unicode[STIX]{x1D6FA}}_{11}$ is the skew-symmetric operator

(3.15) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}_{11}^{\dagger }=-\hat{\unicode[STIX]{x1D6FA}}_{11}. & & \displaystyle\end{eqnarray}$$

Equations (3.12) and (3.13) expressed in components are given by

(3.16) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{\unicode[STIX]{x1D6FA}}_{11}y_{t}+\hat{\unicode[STIX]{x1D6FA}}_{12}\unicode[STIX]{x1D713}_{t}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y},\\ \displaystyle -\hat{\unicode[STIX]{x1D6FA}}_{12}^{\dagger }y_{t}=\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Using (3.6) and (3.11) we obtain that

(3.17) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}_{21}q=x_{u}q+y_{u}\hat{{\mathcal{H}}}q=(1-\hat{{\mathcal{H}}}y_{u})q+y_{u}\hat{{\mathcal{H}}}q & & \displaystyle\end{eqnarray}$$

for any function $q=q(u).$ Using (2.6) and (3.11) we obtain that

(3.18a,b ) $$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D6FA}}_{11}q=-\hat{{\mathcal{H}}}(\unicode[STIX]{x1D713}_{u}q)-\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}q,\quad \unicode[STIX]{x1D6FA}_{12}q=-x_{u}q+\hat{{\mathcal{H}}}(y_{u}q)=-(1-\hat{{\mathcal{H}}}y_{u})q+\hat{{\mathcal{H}}}(y_{u}q). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Using integration by parts and definition (2.4) in (3.17) and (3.18) ensures the validity of (3.14) and (3.15). We note that (3.12)–(3.18) are valid for any Hamiltonian, not only for the Hamiltonian (3.5), provided we derive them from the variation of the action (3.7). Because (3.6) and (3.11) are obtained directly from the variation principle, the symplectic form, corresponding to the symplectic operator $\hat{\unicode[STIX]{x1D6FA}}$ (3.13), is closed and non-degenerate (see Arnold Reference Arnold1989).

Equations (3.6) and (3.11) are not resolved with respect to the time derivatives $y_{t}$ and $\unicode[STIX]{x1D713}_{t}$ . It is remarkable that the symplectic operator $\hat{\unicode[STIX]{x1D6FA}}$ (3.13) can be explicitly inverted. We first find the explicit expression for $y_{t}$ using (3.6) rewritten in the complex form

(3.19) $$\begin{eqnarray}\displaystyle z_{t}\bar{z}_{u}-\bar{z}_{t}z_{u}=-2\text{i}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}=2\text{i}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$

where $\bar{f}(w)$ means the complex conjugate of the function $f(w)$ . Note that the complex conjugation $\bar{f}(w)$ of $f(w)$ in this paper is understood as applied with the assumption that $f(w)$ is the complex-valued function of the real argument $w$ even if $w$ takes complex values so that

(3.20) $$\begin{eqnarray}\displaystyle \bar{f}(w)\equiv \overline{f(\bar{w})}. & & \displaystyle\end{eqnarray}$$

That definition ensures the analytical continuation of $f(w)$ from the real axis $w=u$ into the complex plane of $w\in \mathbb{C.}$

We use the Jacobian

(3.21) $$\begin{eqnarray}\displaystyle J=x_{u}^{2}+y_{u}^{2}=z_{u}\bar{z}_{u}=|z_{u}|^{2}, & & \displaystyle\end{eqnarray}$$

which is non-zero for $w\in \mathbb{C}^{-}$ because $z=z(w,t)$ is the conformal mapping there. Dividing (3.19) by $J$ we obtain that

(3.22) $$\begin{eqnarray}\displaystyle \frac{z_{t}}{z_{u}}-\frac{\bar{z}_{t}}{\bar{z}_{u}}=-\frac{2\text{i}}{J}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}=\frac{2\text{i}}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}. & & \displaystyle\end{eqnarray}$$

Here $z_{t}/z_{u}$ is analytic in $\mathbb{C}^{-}$ and $\bar{z}_{t}/\bar{z}_{u}$ is analytic in $\mathbb{C}^{+}$ .

It is convenient to introduce the operators

(3.23a,b ) $$\begin{eqnarray}\displaystyle \hat{P}^{-}={\textstyle \frac{1}{2}}(1+\text{i}\hat{{\mathcal{H}}})\quad \text{and}\quad \hat{P}^{+}={\textstyle \frac{1}{2}}(1-\text{i}\hat{{\mathcal{H}}}), & & \displaystyle\end{eqnarray}$$

which are the projection operators of a function $q(u)$ defined on the real line $w=u$ into functions $q^{+}(u)$ and $q^{-}(u)$ analytic in $w\in \mathbb{C}^{-}$ and $w\in \mathbb{C}^{+}$ , respectively, such that

(3.24) $$\begin{eqnarray}\displaystyle q=q^{+}+q^{-}. & & \displaystyle\end{eqnarray}$$

Here we assume that $q(u)\rightarrow 0$ for $u\rightarrow \pm \infty$ . Equations (3.23) imply that

(3.25a,b ) $$\begin{eqnarray}\displaystyle \hat{P}^{+}(q^{+}+q^{-})=q^{+}\quad \text{and}\quad \hat{P}^{-}(q^{+}+q^{-})=q^{-} & & \displaystyle\end{eqnarray}$$

(see more discussion of the operators (3.23) in appendix A). Also note that equations (3.23) result in the identities

(3.26) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{H}}}q=\text{i}[q^{+}-q^{-}] & & \displaystyle\end{eqnarray}$$

and

(3.27a-d ) $$\begin{eqnarray}\displaystyle \hat{P}^{+}+\hat{P}^{-}=1,\quad (\hat{P}^{+})^{2}=\hat{P}^{+},\quad (\hat{P}^{-})^{2}=\hat{P}^{-},\quad \hat{P}^{+}\hat{P}^{-}=\hat{P}^{-}\hat{P}^{+}=0.\qquad & & \displaystyle\end{eqnarray}$$

After applying $\hat{P}^{-}$ to (3.22) and multiplying by $z_{u}$ , we find that

(3.28) $$\begin{eqnarray}\displaystyle z_{t}=-z_{u}\hat{P}^{-}\left[\frac{2\text{i}}{J}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]=z_{u}\hat{P}^{-}\left[\frac{2\text{i}}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right], & & \displaystyle\end{eqnarray}$$

which is an explicit solution for the time derivative in complex form. Taking the real and imaginary parts we obtain that

(3.29) $$\begin{eqnarray}\displaystyle y_{t}=(y_{u}\hat{{\mathcal{H}}}-x_{u})\left[\frac{1}{J}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]=-(y_{u}\hat{{\mathcal{H}}}-x_{u})\left[\frac{2}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right] & & \displaystyle\end{eqnarray}$$

and

(3.30) $$\begin{eqnarray}\displaystyle x_{t}=(x_{u}\hat{{\mathcal{H}}}+y_{u})\left[\frac{1}{J}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]=-(x_{u}\hat{{\mathcal{H}}}+y_{u})\left[\frac{2}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right]. & & \displaystyle\end{eqnarray}$$

We now multiply (3.8) by $x_{u}$ and add to (3.9) multiplied by $y_{u}$ to exclude $\unicode[STIX]{x1D713}_{t}$ , which results in

(3.31) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{u}(y_{t}x_{u}-y_{u}x_{t})+y_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}=x_{u}\hat{{\mathcal{H}}}\,f+y_{u}\,f=-\text{i}z_{u}\hat{P}^{-}f+\text{i}\bar{z}_{u}\hat{P}^{+}f. & & \displaystyle\end{eqnarray}$$

We use (3.6) in the LHS of (3.31) to exclude the time derivative and apply $P^{-}$ to it to obtain

(3.32) $$\begin{eqnarray}\displaystyle \hat{P}^{-}f=\frac{\text{i}}{z_{u}}\hat{P}^{-}\left[y_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}-\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]=\frac{\text{i}}{z_{u}}\hat{P}^{-}\left[y_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}+\unicode[STIX]{x1D713}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right], & & \displaystyle\end{eqnarray}$$

which does not contain any time derivative. Taking the sum of equation (3.8) multiplied by $\text{i}$ and (3.9) results in

(3.33) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}\bar{z}_{u}-\bar{z}_{t}\unicode[STIX]{x1D713}_{u}-2\hat{P}^{-}f=-\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}. & & \displaystyle\end{eqnarray}$$

Excluding $\hat{P}^{-}f$ and $\bar{z}_{t}$ in equation (3.33) through equations (3.32) and (3.28) we obtain

(3.34) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}=-\unicode[STIX]{x1D713}_{u}\hat{P}^{+}\left[\frac{2\text{i}}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right]+\frac{2\text{i}}{J}\hat{P}^{-}\left[y_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}+\unicode[STIX]{x1D713}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right]-\frac{1}{\bar{z}_{u}}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}. & & \displaystyle\end{eqnarray}$$

Using (3.25) we transform (3.34) into

(3.35) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}=-\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\left[\frac{1}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right]-\frac{1}{J}\hat{{\mathcal{H}}}\left[\unicode[STIX]{x1D713}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right]-\frac{x_{u}}{J}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}-\frac{1}{J}\hat{{\mathcal{H}}}\left[y_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right]. & & \displaystyle\end{eqnarray}$$

Equations (3.29) and (3.35) can be written in the general Hamiltonian form

(3.36a,b ) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}_{t}=\hat{{\mathcal{R}}}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\boldsymbol{Q}},\quad \boldsymbol{Q}\equiv \left(\begin{array}{@{}c@{}}y\\ \unicode[STIX]{x1D713}\end{array}\right), & & \displaystyle\end{eqnarray}$$

where

(3.37) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{R}}}=\hat{\unicode[STIX]{x1D6FA}}^{-1}=\left(\begin{array}{@{}cc@{}}0 & \hat{{\mathcal{R}}}_{12}\\ \hat{{\mathcal{R}}}_{21} & \hat{{\mathcal{R}}}_{22}\end{array}\right) & & \displaystyle\end{eqnarray}$$

is $2\times 2$ skew-symmetric matrix operator with the components

(3.38) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{{\mathcal{R}}}_{11}q=0,\\ \displaystyle \hat{{\mathcal{R}}}_{12}q=\frac{x_{u}}{J}q-y_{u}\hat{{\mathcal{H}}}\left(\frac{q}{J}\right),\\ \displaystyle \hat{{\mathcal{R}}}_{21}q=-\frac{x_{u}}{J}q-\frac{1}{J}\hat{{\mathcal{H}}}(y_{u}q),\quad \hat{{\mathcal{R}}}_{21}^{\dagger }=-\hat{{\mathcal{R}}}_{12},\\ \displaystyle \hat{{\mathcal{R}}}_{22}q=-\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\left(\frac{q}{J}\right)-\frac{1}{J}\hat{{\mathcal{H}}}(\unicode[STIX]{x1D713}_{u}q),\quad \hat{{\mathcal{R}}}_{11}^{\dagger }=-\hat{{\mathcal{R}}}_{11}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

We call $\hat{{\mathcal{R}}}=\hat{\unicode[STIX]{x1D6FA}}^{-1}$ the ‘implectic’ operator (sometimes such a type of inverse of the symplectic operator is also called the co-symplectic operator; see e.g. Weinstein (Reference Weinstein1983) and Morrison (Reference Morrison1998)).

Writing (3.36) in components we also obtain that

(3.39) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle y_{t}=\hat{{\mathcal{R}}}_{12}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}},\\ \displaystyle \unicode[STIX]{x1D713}_{t}=\hat{{\mathcal{R}}}_{21}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}+\hat{{\mathcal{R}}}_{22}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

Comparing (3.12) and (3.36) we conclude that $\hat{{\mathcal{R}}}=\hat{\unicode[STIX]{x1D6FA}}^{-1}$ , which can be confirmed by the direct calculation that

(3.40) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{R}}}\hat{\unicode[STIX]{x1D6FA}}=\hat{\unicode[STIX]{x1D6FA}}\hat{{\mathcal{R}}}=I, & & \displaystyle\end{eqnarray}$$

where $I$ is the identity operator.

We use (3.36) and (3.37) to define the Poisson bracket

(3.41) $$\begin{eqnarray}\displaystyle \{F,G\} & = & \displaystyle \mathop{\sum }_{i,j=1}^{2}\int _{-\infty }^{\infty }\text{d}u\left(\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}Q_{i}}\hat{{\mathcal{R}}}_{ij}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}Q_{j}}\right)\nonumber\\ \displaystyle & = & \displaystyle \int _{-\infty }^{\infty }\text{d}u\left(\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}y}\hat{{\mathcal{R}}}_{12}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}+\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\hat{{\mathcal{R}}}_{21}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}y}+\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\hat{{\mathcal{R}}}_{22}\frac{\unicode[STIX]{x1D6FF}G}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}\right)\end{eqnarray}$$

between arbitrary functionals $F$ and $G$ of $\boldsymbol{Q}$ . It is clear from that definition that any functionals $\unicode[STIX]{x1D709}$ and $\unicode[STIX]{x1D702}$ of $y$ only commute with each other, i.e. $\{\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}\}=0$ .

Equation (3.41) allows one to rewrite (3.36) and (3.37) in the non-canonical Hamiltonian form corresponding to Poisson mechanics as follows:

(3.42) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}_{t}=\{\boldsymbol{Q},H\}. & & \displaystyle\end{eqnarray}$$

The Poisson bracket requires the Jacobi identity

(3.43) $$\begin{eqnarray}\displaystyle \{F,\{G,L\}\}+\{G,\{L,F\}\}+\{L,\{F,G\}\}=0 & & \displaystyle\end{eqnarray}$$

to be satisfied for arbitrary functionals $F$ , $G$ and $L$ of $\boldsymbol{Q}$ . The Jacobi identity is ensured by our use of the variational principle for the action (3.7).

A functional $F$ is the constant of motion of (3.42) provided $\{F,H\}=0.$ It follows from (3.41) that any functionals $F$ and $G,$ which depend only on $y$ , commute with each other, i.e. $\{F,G\}=0$ . We note that the derivation of (3.36)–(3.42) is valid for any Hamiltonian, not only for the Hamiltonian (3.5), because we derive these equations starting from the variation of action (3.7). This implies that (3.41) has no Casimir invariant (a constant of motion that does not depend on the particular choice of the Hamiltonian $H$ ; see e.g. Weinstein (Reference Weinstein1983) and Zakharov & Kuznetsov (Reference Zakharov and Kuznetsov1997)). Beyond our standard Hamiltonian (3.5), one can also apply (3.41) and (3.42) to more general cases, as discussed in § 6.

4 Dynamic equations for the Hamiltonian (3.5)

Equation (3.29) provides the kinematic BC solved for $y_{t}$ . Equation (3.35) with the Hamiltonian (3.5) can be simplified as follows. We first note that using equation (3.18), the gravity part of the variational derivative (3.11) can be represented as follows:

(4.1) $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right|_{\unicode[STIX]{x1D6FC}=0}=gyx_{u}-g\hat{{\mathcal{H}}}(yy_{u})=-g\hat{\unicode[STIX]{x1D6FA}}_{12}y. & & \displaystyle\end{eqnarray}$$

Then the contribution of that gravity part to the RHS of (3.18) is given by

(4.2) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{R}}}_{21}\left.\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right|_{\unicode[STIX]{x1D6FC}=0}=-g\hat{{\mathcal{R}}}_{21}\hat{\unicode[STIX]{x1D6FA}}_{12}y=-gy, & & \displaystyle\end{eqnarray}$$

where we use the definition (3.38) and (3.40).

The second step is to simplify the surface tension part

(4.3) $$\begin{eqnarray}\displaystyle \left.\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right|_{g=0}=-\unicode[STIX]{x1D6FC}\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|} & & \displaystyle\end{eqnarray}$$

of the variational derivative (3.11). We also note the identity

(4.4) $$\begin{eqnarray}\displaystyle x_{u}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}+y_{u}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}=\frac{1}{2|z_{u}|}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(x_{u}^{2}+y_{u}^{2})+(x_{u}^{2}+y_{u}^{2})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{1}{|z_{u}|}=0, & & \displaystyle\end{eqnarray}$$

which is a particular case of the identity

(4.5) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}x}x_{u}+\frac{\unicode[STIX]{x1D6FF}F}{\unicode[STIX]{x1D6FF}y}y_{u}\equiv 0 & & \displaystyle\end{eqnarray}$$

for general parametrization-invariant functionals $F(x(u),y(u))$ ; see e.g. Morrison (Reference Morrison2005) and Flierl, Morrison & Swaminathan (Reference Flierl, Morrison and Swaminathan2018). Equation (4.4) corresponds to $F=\int _{-\infty }^{\infty }(|z_{u}|-x_{u})\,\text{d}u$ , which is a parametrization-invariant functional because it represents the arclength of the surface (minus the arclength of the unperturbed surface) and thus is independent of the particular surface parametrization $(x(u),y(u))$ ; see also (1.19) and the discussion after it.

The contribution of the surface tension part to the RHS of equation (3.18) is given by

(4.6) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{R}}}_{21}\left.\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right|_{g=0}=\hat{{\mathcal{R}}}_{21}\left[-\unicode[STIX]{x1D6FC}\hat{{\mathcal{H}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{x_{u}}{|z_{u}|}-\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}\right]=\frac{\unicode[STIX]{x1D6FC}}{x_{u}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}\frac{y_{u}}{|z_{u}|}, & & \displaystyle\end{eqnarray}$$

where we used (3.38) and (3.40) and expressed $(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}u)(x_{u}/|z_{u}|)$ through the identity (4.4). Equation (4.6) has a removable singularity at $x_{u}=0$ . To explicitly remove that singularity, we perform the explicit differentiation on the RHS of this equation to obtain

(4.7) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{R}}}_{21}\left.\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}y}\right|_{g=0}=\frac{\unicode[STIX]{x1D6FC}(x_{u}y_{uu}-x_{uu}y_{u})}{|z_{u}|^{3}}, & & \displaystyle\end{eqnarray}$$

which provides the expression for the pressure jump (1.13). Using (3.6), (4.2) and (4.7), we obtain a particular form of (3.35) for the Hamiltonian (3.5) as follows:

(4.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}=\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\left[\frac{1}{|z_{u}|^{2}}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]+\frac{1}{|z_{u}|^{2}}\hat{{\mathcal{H}}}[\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}]-gy+\frac{\unicode[STIX]{x1D6FC}(x_{u}y_{uu}-x_{uu}y_{u})}{|z_{u}|^{3}}. & & \displaystyle\end{eqnarray}$$

Equations (2.6), (3.29) and (4.8) form a closed set of equations defined on the real line $w=u$ . That system was first obtained in Dyachenko et al. (Reference Dyachenko, Kuznetsov, Spector and Zakharov1996) with the surface tension term in the form (4.6). We note that the same system can be obtained directly from (1.1), (1.2), (1.4)–(1.9), (1.12), (1.13) and the definition of the conformal mapping (2.1) without any use of the variational principle of § 3. However, such an alternative derivation is significantly more cumbersome.

5 Dynamic equations in the complex form

Dynamical equations (3.35) are defined on the real line $w=u$ with the analyticity of $z(w,t)$ and $\unicode[STIX]{x1D6F1}(w,t)$ in $w\in \mathbb{C}^{-}$ taken into account through the Hilbert operator $\hat{{\mathcal{H}}}.$ For the analysis of surface hydrodynamics, it is efficient to consider the analytical continuation of $z(w,t)$ and $\unicode[STIX]{x1D6F1}(w,t)$ into $w\in \mathbb{C}^{+}$ with the time-dependent complex singularities of these functions fully determining their properties. The projection operators (3.23) are convenient tools for such analytical continuation with

(5.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D713}+\text{i}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}=2\hat{P}^{-}\unicode[STIX]{x1D713} & & \displaystyle\end{eqnarray}$$

and

(5.2) $$\begin{eqnarray}\displaystyle z-u=-\hat{{\mathcal{H}}}y+\text{i}y=2\text{i}\hat{P}^{-}y & & \displaystyle\end{eqnarray}$$

(see appendix A for more details). Analytical continuation of (5.1) and (5.2) into the complex plane $w\in \mathbb{C}$ amounts to a straightforward replacement of $u$ by $w$ in (A 4) (as well as in (A 11) and (A 12), see also appendix A), which is always allowed provided that $w\in \mathbb{C}^{+}$ and $w\in \mathbb{C}^{-}$ for $\hat{P}^{+}q(w)$ and $\hat{P}^{-}q(w)$ , respectively. This is possible because the pole singularity at $u^{\prime }=u\pm \text{i}0$ in the integrand of (A 4) does not cross the integration contour $-\infty <u^{\prime }<\infty$ as $w$ continuously changes from $w=u$ into the complex values. Analytical continuation in the opposite direction (i.e. into $w\in \mathbb{C}^{+}$ for $\hat{P}^{-}q(w)$ and $w\in \mathbb{C}^{-}$ for $\hat{P}^{+}q(w)$ ), however, requires moving/deforming the integration contour $-\infty <u^{\prime }<\infty$ , which is possible only so long as complex singularities are not reached. We also recall our definition (3.20) of complex conjugation, which ensures how to define $\bar{f}(w)$ for $w\in \mathbb{C}$ . Another convenient way of analytical continuation from the real line $w=u$ into $\mathbb{C}$ is to use (A 10)–(A 12). However, such continuation into $w\in \mathbb{C}^{+}$ for $\hat{P}^{-}q(w)$ and $w\in \mathbb{C}^{-}$ for $\hat{P}^{+}q(w)$ is limited by the convergence of the integrals in (A 11) and (A 12), which implies that $|\text{Im}(w)|$ cannot exceed the distance of the singularity closest to the real axis. We also note that if the function $q(w)$ is analytic in $\mathbb{C}^{-}$ then $\bar{q}(w)$ is analytic in $\mathbb{C}^{+}$ and vice versa.

We replace variations over $y$ and $\unicode[STIX]{x1D713}$ of § 3 by variation over $z$ , $\bar{z}$ , $\unicode[STIX]{x1D6F1}$ and $\bar{\unicode[STIX]{x1D6F1}}$ according to

(5.3a,b ) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}y}=2\text{i}\hat{P}^{+}\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}z}-2\text{i}\hat{P}^{-}\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}\bar{z}}\quad \text{and}\quad \frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}}=2\hat{P}^{+}\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F1}}+2\hat{P}^{-}\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}\bar{\unicode[STIX]{x1D6F1}}}, & & \displaystyle\end{eqnarray}$$

as follows from (5.1) and (5.2); see also (3.10). Here we used that

(5.4a-c ) $$\begin{eqnarray}\displaystyle x=\frac{z+\bar{z}}{2},\quad y=\frac{z-\bar{z}}{2\text{i}}\quad \text{and}\quad \unicode[STIX]{x1D713}=\frac{\unicode[STIX]{x1D6F1}+\bar{\unicode[STIX]{x1D6F1}}}{2}, & & \displaystyle\end{eqnarray}$$

as follows from (2.1) and (1.28). In variational derivatives (5.3) we assume that $z$ , $\bar{z}$ , $\unicode[STIX]{x1D6F1}$ and $\bar{\unicode[STIX]{x1D6F1}}$ are independent variables.

Applying $\hat{P}^{-}$ to (3.28) and (3.34) together with (5.3) and (5.4), we obtain the following dynamic equations:

(5.5) $$\begin{eqnarray}\displaystyle & z_{t}=\text{i}Uz_{u}, & \displaystyle\end{eqnarray}$$

(5.6) $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6F1}_{t}=\text{i}U\unicode[STIX]{x1D6F1}_{u}-B-{\mathcal{P}} & \displaystyle\end{eqnarray}$$

where

(5.7) $$\begin{eqnarray}\displaystyle U=4\hat{P}^{-}\left\{\frac{1}{J}\left[\hat{P}^{-}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\bar{\unicode[STIX]{x1D6F1}}}+\hat{P}^{+}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F1}}\right]\right\}, & & \displaystyle\end{eqnarray}$$

is the complex transport velocity,

(5.8) $$\begin{eqnarray}\displaystyle {\mathcal{P}}=-4\text{i}\hat{P}^{-}\left\{\frac{1}{J}\left[\hat{P}^{-}\left(\bar{z}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\bar{z}}\right)-\hat{P}^{+}\left(z_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}z}\right)\right]\right\} & & \displaystyle\end{eqnarray}$$

and

(5.9) $$\begin{eqnarray}\displaystyle B=-4\text{i}\hat{P}^{-}\left\{\frac{1}{J}\left[\hat{P}^{-}\left(\bar{\unicode[STIX]{x1D6F1}}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\bar{\unicode[STIX]{x1D6F1}}}\right)-\hat{P}^{+}\left(\unicode[STIX]{x1D6F1}_{u}\frac{\unicode[STIX]{x1D6FF}H}{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6F1}}\right)\right]\right\}. & & \displaystyle\end{eqnarray}$$

Here we have used that $z$ and $\unicode[STIX]{x1D6F1}$ and analytic in $\mathbb{C}^{-}$ while $\bar{z}$ and $\bar{\unicode[STIX]{x1D6F1}}$ are analytic in $\mathbb{C}^{+}$ . Taking the imaginary part of equation (5.5) and the real part of equation (5.6), one can recover (3.29) and (3.35).

Equations (5.5)–(5.9) are convenient for analytical study. A version of dynamic equations is obtained by the change of variables (as suggested in Dyachenko (Reference Dyachenko2001))

(5.10) $$\begin{eqnarray}\displaystyle & \displaystyle R=\frac{1}{z_{u}}, & \displaystyle\end{eqnarray}$$

(5.11) $$\begin{eqnarray}\displaystyle & \displaystyle V=\text{i}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F1}}{\unicode[STIX]{x2202}z}=\text{i}R\unicode[STIX]{x1D6F1}_{u}. & \displaystyle\end{eqnarray}$$

Equations (5.5) and (5.6) in terms of variables (5.10) and (5.11) take the following form:

(5.12) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}=\text{i}(UR_{u}-RU_{u}), & \displaystyle\end{eqnarray}$$

(5.13) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}[UV_{u}-R(B_{u}+{\mathcal{P}}_{u})]. & \displaystyle\end{eqnarray}$$

These dynamic equations are valid for any Hamiltonian. They are also convenient for numerical simulations to avoid numerical instability at small spatial scales; see e.g. Zakharov, Dyachenko & Prokofiev (Reference Zakharov, Dyachenko and Prokofiev2006) and related analysis of the weakly nonlinear case in Lushnikov & Zakharov (Reference Lushnikov and Zakharov2005). Note that $R$ and $V$ include only a derivative of the conformal mapping (2.1) and the complex potential $\unicode[STIX]{x1D6F1}$ over $w$ while $z(w,t)$ and $\unicode[STIX]{x1D6F1}(w,t)$ are recovered from solution of these equations as $z=\int (1/R)\,\text{d}w$ and $\unicode[STIX]{x1D6F1}=-\text{i}\int (V/R)\,\text{d}w$ . Respectively, these relation can be used to recover the integrals of motion (1.30), (1.33) and (1.35) from $R$ and  $V$ .

We now rewrite our standard Hamiltonian (3.5) in terms of variables $z$ , $\bar{z}$ , $\unicode[STIX]{x1D6F1}$ and $\bar{\unicode[STIX]{x1D6F1}}$ , which gives that

(5.14) $$\begin{eqnarray}\displaystyle H=\int _{-\infty }^{\infty }\text{d}u\left[\frac{\text{i}}{8}(\unicode[STIX]{x1D6F1}_{u}\bar{\unicode[STIX]{x1D6F1}}-\unicode[STIX]{x1D6F1}\bar{\unicode[STIX]{x1D6F1}}_{u})-\frac{g}{16}(z-\bar{z})^{2}(z_{u}+\bar{z}_{u})+\unicode[STIX]{x1D6FC}\left(\sqrt{z_{u}\bar{z}_{u}}-\frac{z_{u}+\bar{z}_{u}}{2}\right)\right].\qquad & & \displaystyle\end{eqnarray}$$

Equations (5.7)–(5.9) and (5.14) result in

(5.15) $$\begin{eqnarray}\displaystyle & \displaystyle U=\text{i}\hat{P}^{-}\left\{\frac{1}{J}[\unicode[STIX]{x1D6F1}_{u}-\bar{\unicode[STIX]{x1D6F1}}_{u}]\right\}=\hat{P}^{-}(R\bar{V}+\bar{R}V), & \displaystyle\end{eqnarray}$$

(5.16) $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{P}}=-\text{i}g(z-w)-2\text{i}\unicode[STIX]{x1D6FC}\hat{P}^{-}(Q_{u}\bar{Q}-Q\bar{Q}_{u}) & \displaystyle\end{eqnarray}$$

and

(5.17) $$\begin{eqnarray}\displaystyle B=\hat{P}^{-}\left\{\frac{|\unicode[STIX]{x1D6F1}_{u}|^{2}}{|z_{u}|^{2}}\right\}=\hat{P}^{-}(|V|^{2}), & & \displaystyle\end{eqnarray}$$

where

(5.18) $$\begin{eqnarray}\displaystyle Q\equiv \frac{1}{\sqrt{z_{u}}}=\sqrt{R}. & & \displaystyle\end{eqnarray}$$

Plugging (5.15)–(5.17) into (5.12) and (5.13) we obtain

(5.19) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}=\text{i}(UR_{u}-RU_{u}), & \displaystyle\end{eqnarray}$$

(5.20) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}[UV_{u}-RB_{u}]+g(R-1)-2\unicode[STIX]{x1D6FC}R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(Q_{u}\bar{Q}-Q\bar{Q}_{u}). & \displaystyle\end{eqnarray}$$

Other authors have referred to these equations as the ‘Dyachenko’ equations (Dyachenko Reference Dyachenko2001), which serve as a basis for numerical study of free surface hydrodynamics. They can also be immediately rewritten fully in terms of $Q$ and $V$ as follows:

(5.21) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}Q}{\unicode[STIX]{x2202}t}=\text{i}(UQ_{u}-\frac{1}{2}QU_{u}), & \displaystyle\end{eqnarray}$$

(5.22) $$\begin{eqnarray}\displaystyle & \displaystyle U=\hat{P}(Q^{2}\bar{V}+\bar{Q}^{2}V), & \displaystyle\end{eqnarray}$$

(5.23) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}\left[UV_{u}-Q^{2}\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(|V|^{2})\right]+g(Q^{2}-1)-2\unicode[STIX]{x1D6FC}Q^{2}\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(Q_{u}\bar{Q}-Q\bar{Q}_{u}). & \displaystyle\end{eqnarray}$$

5.1 Dynamic equations in complex form without non-local operators

Equations (5.19), (5.20) and (5.21)–(5.23) involve $\hat{P}^{-}$ , which is a non-local operator. Sometimes for analytical study and in looking for explicit solutions, one may need to avoid such non-local operators. To do that, we use (3.19) with the RHS rewritten through equation (5.1), which gives

(5.24) $$\begin{eqnarray}\displaystyle z_{t}\bar{z}_{u}-\bar{z}_{t}z_{u}=\bar{\unicode[STIX]{x1D6F1}}_{u}-\unicode[STIX]{x1D6F1}_{u} & & \displaystyle\end{eqnarray}$$

for the kinematic BC in complex form.

To satisfy the dynamic BC, we use (4.8), where the term $\hat{{\mathcal{H}}}[(1/|z_{u}|^{2})\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}]$ is expressed through the complex conjugate of (3.28) and equations (3.23), which results in

(5.25) $$\begin{eqnarray}\displaystyle \hat{{\mathcal{H}}}\left[\frac{1}{|z_{u}|^{2}}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}\right]=\frac{\bar{z}_{t}}{\bar{z}_{u}}-\text{i}\frac{1}{|z_{u}|^{2}}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}. & & \displaystyle\end{eqnarray}$$

Plugging (5.25) into (4.8) and using (3.23) we obtain that

(5.26) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}=\unicode[STIX]{x1D713}_{u}\frac{\bar{z}_{t}}{\bar{z}_{u}}-\frac{1}{|z_{u}|^{2}}2\text{i}\hat{P}^{-}[\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}]-gy+\frac{\unicode[STIX]{x1D6FC}(x_{u}y_{uu}-x_{uu}y_{u})}{|z_{u}|^{3}}. & & \displaystyle\end{eqnarray}$$

We now note that using (3.26) and (5.4) allows us to write that $\hat{P}^{-}[\unicode[STIX]{x1D713}_{u}\hat{{\mathcal{H}}}\unicode[STIX]{x1D713}_{u}]=(\text{i}/4)\hat{P}^{-}[\bar{\unicode[STIX]{x1D6F1}}_{u}^{2}-\unicode[STIX]{x1D6F1}_{u}^{2}]=-(\text{i}/4)\unicode[STIX]{x1D6F1}_{u}^{2}$ , thus reducing (5.26) to

(5.27) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{t}\bar{z}_{u}-\unicode[STIX]{x1D713}_{u}\bar{z}_{t}+\frac{\unicode[STIX]{x1D6F1}_{u}^{2}}{2z_{u}}+\frac{g}{2\text{i}}\bar{z}_{u}(z-\bar{z})+\frac{\text{i}\unicode[STIX]{x1D6FC}\bar{z}_{u}}{2|z_{u}|}\left(\frac{z_{uu}}{z_{u}}-\frac{\bar{z}_{uu}}{\bar{z}_{u}}\right)=0, & & \displaystyle\end{eqnarray}$$

where we also expressed gravity and surface tension terms through $z$ and $\bar{z}$ using (5.4). Equation (5.28) for the particular case $g=\unicode[STIX]{x1D6FC}=0$ was first derived in Zakharov & Dyachenko (Reference Zakharov and Dyachenko2012) (except there are trivial misprints in equation (3.54) of that reference). Equation (5.28) is the complex version of the Bernoulli equation. Using (5.4) one can also express $\unicode[STIX]{x1D713}$ in (5.28) through $\unicode[STIX]{x1D6F1}$ and $\bar{\unicode[STIX]{x1D6F1}}$ , which gives a fully complex form of Bernoulli equation as follows:

(5.28) $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F1}_{t}+\bar{\unicode[STIX]{x1D6F1}}_{t})\bar{z}_{u}-(\unicode[STIX]{x1D6F1}_{u}+\bar{\unicode[STIX]{x1D6F1}}_{u})\bar{z}_{t}+\frac{\unicode[STIX]{x1D6F1}_{u}^{2}}{z_{u}}-\text{i}g\bar{z}_{u}(z-\bar{z})+\frac{\text{i}\unicode[STIX]{x1D6FC}\bar{z}_{u}}{|z_{u}|}\left(\frac{z_{uu}}{z_{u}}-\frac{\bar{z}_{uu}}{\bar{z}_{u}}\right)=0. & & \displaystyle\end{eqnarray}$$

Equations (5.24) and (5.28) are the dynamic equations in complex form. They are not resolved with respect to the time derivative but they do not contain any non-local operator.

6 Generalized hydrodynamics and integrability

We note that all the expressions derived in § 3 starting from (3.12) and in § 5 before (5.14) are valid for arbitrary Hamiltonian $H$ . In this section we go beyond the standard Hamiltonian (5.14) to apply our Hamiltonian formalism for other physical systems beyond the Euler equations with free surface, gravity and surface tension. We call the corresponding dynamical equations ‘generalized hydrodynamics’.

The new Hamiltonian is written as

(6.1) $$\begin{eqnarray}\displaystyle H=H_{Eul}+\tilde{H}, & & \displaystyle\end{eqnarray}$$

where $H_{Eul}$ is the standard Hamiltonian (5.14) and

(6.2) $$\begin{eqnarray}\displaystyle \tilde{H}=\frac{\text{i}\unicode[STIX]{x1D6FD}}{8}\int (z_{u}+\bar{z}_{u}-2)(z-\bar{z})\,\text{d}u=\frac{\unicode[STIX]{x1D6FD}}{2}\int y\hat{{\mathcal{H}}}y_{u}\,\text{d}u & & \displaystyle\end{eqnarray}$$

is the ‘generalized’ part, which adds up to the potential energy. Here $\unicode[STIX]{x1D6FD}$ is a real constant. Using Fourier transform (FT) (A 9), one can also rewrite (6.2) through Parseval’s identity as

(6.3) $$\begin{eqnarray}\displaystyle \tilde{H}=-\frac{\unicode[STIX]{x1D6FD}}{2}\int |k||y_{k}|^{2}\,\text{d}k, & & \displaystyle\end{eqnarray}$$

which shows that $\tilde{H}$ is a sign-definite quantity. Here we also used that the Hilbert operator $\hat{{\mathcal{H}}}$ turns into a multiplication operator under FT as $(\hat{{\mathcal{H}}}_{u}\,f)_{k}=\text{i}\,\text{sign}(k)f_{k}$ , which follows from (3.23) and appendix A. Thus the additional potential energy $\tilde{H}$ is positive for $\unicode[STIX]{x1D6FD}<0$ and negative for $\unicode[STIX]{x1D6FD}>0.$

There are several physical interpretations of $\tilde{H}$ . The first case $\unicode[STIX]{x1D6FD}>0$ corresponds, for example, to a dielectric fluid with a charged and ideally conducting free surface in a vertical electric field (Zubarev Reference Zubarev2000, Reference Zubarev2002, Reference Zubarev2008). Such a situation is realized on the charged free surface of superfluid helium (Cole & Cohen Reference Cole and Cohen1969; Shikin Reference Shikin1970). Then (6.2) is valid provided surface charges fully screen the electric field above the fluid free surface. This limit was first realized experimentally in Edelman (Reference Edelman1980). A negative sign of $\tilde{H}$ implies instability due to the presence of the electric field. Another application occurs for the quantum Kelvin–Helmholtz instability of counterflow of two components of superfluid helium (Lushnikov & Zubarev Reference Lushnikov and Zubarev2018). The second case $\unicode[STIX]{x1D6FD}<0$ corresponds, for example, to a dielectric fluid with a free surface in a horizontal electric field (see Zubarev & Zubareva Reference Zubarev and Zubareva2006, Reference Zubarev and Zubareva2008; Zubarev & Kochurin Reference Zubarev and Kochurin2014, and references therein). A positive sign of $\tilde{H}$ implies a stabilizing effect of the horizontal electric field. Similar effects can occur in magnetic fluids. See Zubarev (Reference Zubarev2008), Zubarev & Kochurin (Reference Zubarev and Kochurin2014) and Lushnikov & Zubarev (Reference Lushnikov and Zubarev2018) for more references on physical realizations of the generalized hydrodynamics.

We now consider the dynamics (5.12) and (5.13) for the Hamiltonian (6.1) and (6.2). Then $U$ is still given by (5.15) according to equation (5.7) because $\tilde{H}$ does not depend on $\unicode[STIX]{x1D6F1}$ . Equation (5.8) results in

(6.4) $$\begin{eqnarray}\displaystyle {\mathcal{P}}=-\text{i}g(z-w)-2\text{i}\unicode[STIX]{x1D6FC}\hat{P}^{-}(Q_{u}\bar{Q}-Q\bar{Q}_{u})+\unicode[STIX]{x1D6FD}\hat{P}^{-}(R\bar{R}-1), & & \displaystyle\end{eqnarray}$$

while $B$ remain the same as in (5.15) and (5.17) because the definitions (5.7) and (5.9) involve only variations over $\unicode[STIX]{x1D6F1}$ and $\bar{\unicode[STIX]{x1D6F1}}$ .

Equations (5.12), (5.13), (5.15), (5.17), (5.18) and (6.4) result in the generalization of the Dyachenko equations (5.19) and (5.20) as follows:

(6.5) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}R}{\unicode[STIX]{x2202}t}=\text{i}(UR_{u}-RU_{u}), & \displaystyle\end{eqnarray}$$

(6.6) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}t}=\text{i}\left[UV_{u}-RB_{u}-\unicode[STIX]{x1D6FD}R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(R\bar{R})\right]+g(R-1)-2\unicode[STIX]{x1D6FC}R\hat{P}^{-}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}u}(Q_{u}\bar{Q}-Q\bar{Q}_{u}).\qquad & \displaystyle\end{eqnarray}$$

As a particular example, until the end of this section we consider (6.5) and (6.6) for $g=\unicode[STIX]{x1D6FC}=0.$ We define $r$ as

(6.7) $$\begin{eqnarray}\displaystyle r=R-1 & & \displaystyle\end{eqnarray}$$

and linearize (5.15), (5.17), (6.5) and (6.6) over small-amplitude solutions in $r$ and $V$ , which gives

(6.8) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}r_{t}=-\text{i}V_{u},\\ V_{t}=-\text{i}\unicode[STIX]{x1D6FD}r_{u},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where we used that $r$ does not have zeroth Fourier harmonics, implying $\hat{P}^{-}r=r$ and $\hat{P}^{-}\bar{r}=0.$ Excluding $V$ from (6.8) results in

(6.9) $$\begin{eqnarray}\displaystyle r_{tt}=-\unicode[STIX]{x1D6FD}r_{uu}. & & \displaystyle\end{eqnarray}$$

If $\unicode[STIX]{x1D6FD}=-s^{2}<0,$ $s>0$ , then (6.9) turns into a wave equation,

(6.10) $$\begin{eqnarray}\displaystyle r_{tt}=s^{2}r_{uu}, & & \displaystyle\end{eqnarray}$$

while for $\unicode[STIX]{x1D6FD}=s^{2}>0$ we obtain an elliptic equation.

We now go beyond linearization and consider fully nonlinear equations (5.15), (5.17), (6.5) and (6.6) for $\unicode[STIX]{x1D6FD}=-s^{2}.$ We assume a reduction

(6.11) $$\begin{eqnarray}\displaystyle V=\text{i}sr. & & \displaystyle\end{eqnarray}$$

Then equations (5.15) and (5.17) result in $B=s^{2}\hat{P}^{-}(|r|^{2})$ and $U=\text{i}sr$ . Plugging these expressions into (6.5) and (6.6) results in a single equation

(6.12) $$\begin{eqnarray}\displaystyle r_{t}=sr_{u}, & & \displaystyle\end{eqnarray}$$

with a general solution

(6.13) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}r=f(u+st),\\ v=\text{i}sf(u+st)\end{array}\right\} & & \displaystyle\end{eqnarray}$$

for the arbitrary function $f(u)$ . This is a remarkable result because it is valid for an arbitrary level of nonlinearity. In a similar way, a reduction

(6.14) $$\begin{eqnarray}\displaystyle V=-\text{i}sr & & \displaystyle\end{eqnarray}$$

in equations (5.15), (5.17), (6.5) and (6.6) results in a single equation

(6.15) $$\begin{eqnarray}\displaystyle r_{t}=-sr_{u}, & & \displaystyle\end{eqnarray}$$

with a general solution

(6.16) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}r=g(u-st),\\ v=-\text{i}sg(u-st)\end{array}\right\} & & \displaystyle\end{eqnarray}$$

for the arbitrary function $g(u)$ .

The existence of the general solutions (6.13) and (6.16) for the reductions (6.11) and (6.14), however, does not imply that one can obtain the explicit solution of the general equations (6.5) and (6.6) because a linear superposition of solutions (6.13) and (6.16) is not generally a solution of (6.5) and (6.6).

We now consider the second case $\unicode[STIX]{x1D6FD}=s^{2}>0$ and look at a reduction

(6.17) $$\begin{eqnarray}\displaystyle V=sr. & & \displaystyle\end{eqnarray}$$

Then (5.15) and (5.17) result in $B=s^{2}\hat{P}^{-}(|r|^{2})$ and $U=s[r+2\hat{P}^{-}(|r|^{2})]$ . Plugging these expressions into (6.5) and (6.6) results in a single equation (the two equations for $r_{t}$ and $V_{t}$ coincide)

(6.18) $$\begin{eqnarray}\displaystyle r_{t}=\text{i}s(r_{u}[-1+2\hat{P}^{-}(|r|^{2})]-(1+r)2\hat{P}^{-}(|r|^{2})_{u}). & & \displaystyle\end{eqnarray}$$

In a similar way, a reduction

(6.19) $$\begin{eqnarray}\displaystyle V=-sr & & \displaystyle\end{eqnarray}$$

in (5.15), (5.17), (6.5) and (6.6) results in a single equation

(6.20) $$\begin{eqnarray}\displaystyle r_{t}=-\text{i}s(r_{u}[-1+2\hat{P}^{-}(|r|^{2})]-(1+r)2\hat{P}^{-}(|r|^{2})_{u}). & & \displaystyle\end{eqnarray}$$

Equations (6.18) and (6.20) interchange under a change of sign of the time, so it is sufficient to study one of them.

An infinite number of explicit solutions of (6.18) and (6.20) can be constructed. However, we do that indirectly by first considering the reduction (6.17) for variables $z$ and $\unicode[STIX]{x1D6F1}$ instead of $R$ and $V$ . We use (5.5) and its complex conjugate $\bar{z}_{t}=-\text{i}\bar{U}\bar{z}_{u}$ together with (5.15) and (5.10) to obtain that

(6.21) $$\begin{eqnarray}\displaystyle \text{i}\left(\frac{\bar{z}_{t}}{\bar{z}_{u}}-\frac{z_{t}}{z_{u}}\right)=R\bar{V}+\bar{R}V=\frac{\bar{V}}{z_{u}}+\frac{V}{\bar{z}_{u}}. & & \displaystyle\end{eqnarray}$$

Equation (6.17) and its complex conjugate imply that

(6.22) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle V=s(R-1)=s\frac{1-z_{u}}{z_{u}},\\ \displaystyle \bar{V}=s(\bar{R}-1)=s\frac{1-\bar{z}_{u}}{\bar{z}_{u}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

which allows us to exclude $V$ and $\bar{V}$ from (6.21), resulting in the closed equation for $z$ as

(6.23) $$\begin{eqnarray}\displaystyle \text{i}(\bar{z}_{t}z_{u}-z_{t}\bar{z}_{u})=s(2-z_{u}-\bar{z}_{u}). & & \displaystyle\end{eqnarray}$$

A change of variables $z=G-\text{i}st$ in (6.23) results in the Laplace growth equation (LGE) given by (Zubarev Reference Zubarev2000, Reference Zubarev2002, Reference Zubarev2008)

(6.24) $$\begin{eqnarray}\displaystyle \text{Im}(\bar{G}_{t}G_{u})=-s. & & \displaystyle\end{eqnarray}$$

The LGE is integrable in the sense of the existence of an infinite number of integrals of motion and its relation to the dispersionless limit of the integrable Toda hierarchy (Mineev-Weinstein, Wiegmann & Zabrodin Reference Mineev-Weinstein, Wiegmann and Zabrodin2000).

One can also mention that the LGE was derived as the approximation of Hele-Shaw flow (an ideal fluid pushed through a viscous fluid in a narrow gap between two parallel plates) (see Galin Reference Galin1945; Polubarinova-Kochina Reference Polubarinova-Kochina1945; Shraiman & Bensimon Reference Shraiman and Bensimon1984; Bensimon et al. Reference Bensimon, Kadanoff, Liang, Shraiman and Tang1986; Howison Reference Howison1986; Mineev-Weinstein & Dawson Reference Mineev-Weinstein and Dawson1994). Also Crowdy (Reference Crowdy2000b ) found that exact solutions for free surface Euler flows with surface tension (such as Crapper’s classic capillary water wave solutions (Crapper Reference Crapper1957) and the solutions of Tanveer (Reference Tanveer1996) and Crowdy (Reference Crowdy1999, Reference Crowdy2000a )) are related to steady solutions of Hele-Shaw flows (with non-zero surface tension).

The reduction (6.19) also results in the LGE by the trivial change of sign in (6.24). Similar to the case $\unicode[STIX]{x1D6FD}=-s^{2}<0$ above, the existence of an infinite number of solutions for the reductions (6.17) and (6.19) in the case $\unicode[STIX]{x1D6FD}=s^{2}>0$ does not imply that one can obtain the explicit solution of the general (6.5) and (6.6) because a linear superposition of solutions of the corresponding LGEs is not generally a solution of (6.5) and (6.6). Nevertheless, we make a conjecture that the full system (5.15), (5.17), (6.5) and (6.6) is integrable for both $\unicode[STIX]{x1D6FD}<0$ and $\unicode[STIX]{x1D6FD}>0$ .

7 Conclusion and discussion

We derived the non-canonical Hamiltonian system (3.36) which is equivalent to the Euler equation with a free surface for general multi-valued parametrization of the surface by the conformal transformation (2.1). This generalizes the canonical Hamiltonian system (1.23) of Zakharov (Reference Zakharov1968), which is valid only for single-valued surface parametrization. The Hamiltonian coincides with the total energy (kinetic plus potential energy) of an ideal fluid in a gravitational field with surface tension. A non-canonical Hamiltonian system (3.36) can be written in terms of Poisson mechanics (3.42) with the non-degenerate Poisson bracket (3.41), i.e. it does not have any Casimir invariant. That bracket is identically zero between any two functionals of the canonical transformation (2.1). In future work we plan to focus on finding integrals of motion that are are functional of that conformal map only so they will commute with each other, which might be a sign of the complete integrability of the Hamiltonian system (3.36). It was conjectured in Dyachenko & Zakharov (Reference Dyachenko and Zakharov1994) that the system (1.23) is completely integrable at least for the case of zero surface tension. Since then arguments pro and contra have been presented – see e.g. Dyachenko, Kachulin & Zakharov (Reference Dyachenko, Kachulin and Zakharov2013). Thus this question of possible integrability is still open and very important.

We also reformulated the Hamiltonian system (3.36) in complex form, which is convenient to analyse the dynamics in terms of analytical continuation of solutions into the upper complex half-plane. Full knowledge of such singularities would provide a complete description of the free surface hydrodynamics and corresponding Riemann surfaces, as was demonstrated, for example, on the particular example of Stokes wave in Lushnikov (Reference Lushnikov2016).

Additionally, we analysed the generalized hydrodynamics with multiple applications ranging from a dielectric fluid with a free surface in an electric field to the two-fluid hydrodynamics of superfluid helium. In that case we identified powerful reductions which allowed us to find general classes of particular solutions. We conjecture that the generalized hydrodynamics might be completely integrable.

Extension of the 2D results of this paper to three dimensions is beyond the scope of this work. We only note that the Hamiltonian equations (1.23) for single-valued parametrization are valid in three dimensions also (Zakharov Reference Zakharov1968). Also multi-valued parametrization can be extended to three dimensions provided the variation of waves is slow in the third dimension as shown in Ruban (Reference Ruban2005).