2.1 Equations of motion

The continuity, momentum and energy equations for inviscid, non-heat-conducting flow of a perfect gas, pressure $p$ , density ${\it\rho}$ , velocity $\boldsymbol{u}$ , specific reservoir enthalpy $h$ and specific heat ratio ${\it\gamma}$ acted on by a body force per unit mass $\boldsymbol{f}$ in an inertial frame and time $t$ are:

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}{\it\rho}}{\text{D}t}+{\it\rho}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\,\frac{\text{D}\boldsymbol{u}}{\text{D}t}=-\boldsymbol{{\rm\nabla}}p+{\it\rho}\,\boldsymbol{f}, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\,\frac{\text{D}h}{\text{D}t}=\frac{\partial p}{\partial t}+{\it\rho}\,\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{f}, & \displaystyle\end{eqnarray}$$

with

(2.4) $$\begin{eqnarray}h=\frac{{\it\gamma}}{{\it\gamma}-1}\,\frac{p}{{\it\rho}}+\frac{|\boldsymbol{u}|^{2}}{2}.\end{eqnarray}$$

The specific reservoir enthalpy, denoted here by $h$ , is sometimes called the specific total enthalpy and given the subscript $t$ or $0$ . However, since specific enthalpy only occurs as its reservoir value throughout this study, the subscript is omitted.

In accordance with the assumption of axial symmetry, introduce cylindrical polar coordinates $(x,y)$ , velocity components $(u,v)$ , and choose the axial coordinate $x$ to lie on the axis of the jet issuing radially from the spherical moon’s surface.

The equations become:

(2.5) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\rho}}{\partial t}+\frac{\partial {\it\rho}u}{\partial x}+\frac{\partial {\it\rho}v}{\partial y}+\frac{{\it\rho}v}{y}=0, & \displaystyle\end{eqnarray}$$

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial t}+u\,\frac{\partial u}{\partial x}+v\,\frac{\partial u}{\partial y}=-\frac{1}{{\it\rho}}\,\frac{\partial p}{\partial x}+f_{x}, & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v}{\partial t}+u\,\frac{\partial v}{\partial x}+v\,\frac{\partial v}{\partial y}=-\frac{1}{{\it\rho}}\,\frac{\partial p}{\partial y}+f_{y}, & \displaystyle\end{eqnarray}$$

(2.8) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial h}{\partial t}+u\,\frac{\partial h}{\partial x}+v\,\frac{\partial h}{\partial y}=\frac{1}{{\it\rho}}\,\frac{\partial p}{\partial t}+u\,f_{x}+v\,f_{y}. & \displaystyle\end{eqnarray}$$

With an inverse-square gravity field, and acceleration due to gravity $g$ at the moon’s surface ( $r=r_{0}$ ),

(2.9a,b ) $$\begin{eqnarray}f_{x}=-g\,\frac{r_{0}^{2}}{r^{2}}\,\frac{x}{r},\quad f_{y}=-g\,\frac{r_{0}^{2}}{r^{2}}\,\frac{y}{r},\quad r^{2}=x^{2}+y^{2}.\end{eqnarray}$$

Although the computational part deals with unsteady flow, it is instructive to consider steady flow first. A possible scenario is that an erupting jet flow eventually reaches a steady state. The appropriate equations are (2.5)–(2.8) with the five time derivatives set to zero. Along the $x$ -axis $v=0$ , $y=0$ and $x=r$ , so that, along the jet axis, which by assumption is also a streamline, the steady-flow energy equation becomes ( $u\neq 0$ ):

(2.10) $$\begin{eqnarray}\frac{\text{d}h}{\text{d}r}=-g\,\frac{r_{0}^{2}}{r^{2}},\end{eqnarray}$$

stating that the only agency that reduces $h$ along $x=r$ is the work done against gravity. This may be integrated to give

(2.11) $$\begin{eqnarray}h(r)=h(r_{0})-g\,r_{0}\left(1-\frac{r_{0}}{r}\right).\end{eqnarray}$$

2.2 Escape velocity

Assume that there is a constriction at the surface of the moon, so that the flow from a reservoir inside the moon to the outside passes through a minimum cross-sectional flow area. Assume also that the pressure ratio between the reservoir and the moon’s surface ( $p_{r}/p_{0}$ ) is sufficiently large to make the constriction a sonic throat, so that ( $a=$ speed of sound)

(2.12) $$\begin{eqnarray}u_{0}^{2}=a_{\ast }^{2}=\frac{{\it\gamma}p_{\ast }}{{\it\rho}_{\ast }}.\end{eqnarray}$$

Here the asterisk denotes the state at the sonic throat. Equation (2.12) identifies the jet speed at the surface ( $u_{0}$ ) with the sonic speed within the jet at the throat ( $a_{\ast }$ ). Note that the state at the throat ( $p_{\ast },{\it\rho}_{\ast }$ ) is determined by the isentropic expansion from the reservoir state ( $p_{r},{\it\rho}_{r}$ ) and is independent of the surface state ( $p_{0},{\it\rho}_{0}$ ).

Substituting in (2.11) for $h(r_{0})=h_{\ast }$ from (2.4) and setting $h(r)=0$ at $r=\infty$ then gives

(2.13) $$\begin{eqnarray}0=\frac{{\it\gamma}}{{\it\gamma}-1}\,\frac{p_{\ast }}{{\it\rho}_{\ast }}+\frac{u_{0}^{2}}{2}-g\,r_{0}=\frac{a_{\ast }^{2}}{{\it\gamma}-1}+\frac{u_{0}^{2}}{2}-g\,r_{0}=\frac{{\it\gamma}+1}{{\it\gamma}-1}\,\frac{u_{0}^{2}}{2}-g\,r_{0}.\end{eqnarray}$$

This represents the escape condition at which the jet speed at the surface is just large enough to overcome gravity. Solving for this special speed,

(2.14) $$\begin{eqnarray}u_{0}^{2}=u_{eg}^{2}=2\,g\,r_{0}\,\frac{{\it\gamma}-1}{{\it\gamma}+1}.\end{eqnarray}$$

The ‘ $g$ ’ in the subscript ‘ $eg$ ’ distinguishes $u_{eg}$ as the escape velocity of a gas, because it is significantly smaller than ( ${\it\gamma}>1$ ) the escape velocity $u_{es}=\sqrt{2gr_{0}}$ of a solid body. The reason is that the thermal energy of the gas at $r=r_{0}$ is converted to ordered kinetic energy in the isentropic expansion of the gas as it flows to increasing $r$ ; isentropic, because dissipative processes have been excluded by assumption.

This result is not to be confused with the so-called Jeans escape. The latter describes the escape of molecules from the collision-rare condition at high altitude by virtue of their thermal speed. The result in (2.14) represents a (collision-rich) continuum phenomenon. Some particular values of the escape velocities $u_{eg}$ and $u_{es}$ on moons in our solar system are given in the Appendix.

2.3 Maximum penetration radius

Still within the confines of steady flow, consider the case when the jet velocity at the surface is smaller than the escape velocity, $u_{0}<u_{eg}$ . In that case, $h\rightarrow 0$ at a finite value of $r$ , $r_{p}$ say. Substituting $h(r)=0$ and $r=r_{p}$ in (2.11) and using (2.12) and (2.14), the maximum steady-state penetration radius is obtained:

(2.15) $$\begin{eqnarray}\frac{r_{p}}{r_{0}}=\left(1-\frac{u_{0}^{2}}{u_{eg}^{2}}\right)^{-1}.\end{eqnarray}$$

The surface to escape velocity ratio may be related to the reservoir conditions by using the relations for isentropic flow from the reservoir (at zero velocity) to the throat (sonic condition):

(2.16) $$\begin{eqnarray}\frac{u_{0}^{2}}{u_{eg}^{2}}=\frac{{\it\gamma}}{{\it\gamma}-1}\,\frac{p_{r}}{{\it\rho}_{r}}\,\frac{1}{gr_{0}}.\end{eqnarray}$$

2.4 Atmosphere

The earlier mention of the pressure ratio $p_{r}/p_{0}$ implies that the moon has an atmosphere. Two idealised cases of the structure of the atmosphere are considered: isothermal and adiabatic. In an isothermal atmosphere, $p/{\it\rho}=p_{0}/{\it\rho}_{0}$ . Using this in the static equilibrium of the atmosphere gives

(2.17) $$\begin{eqnarray}\frac{\text{d}p}{\text{d}r}=-{\it\rho}g\,\frac{r_{0}^{2}}{r^{2}}=-\frac{{\it\rho}_{0}gr_{0}^{2}}{p_{0}}\,\frac{p}{r^{2}},\end{eqnarray}$$

and integrating,

(2.18) $$\begin{eqnarray}\frac{p}{p_{0}}=\frac{{\it\rho}}{{\it\rho}_{0}}=\exp \left[-\frac{{\it\rho}_{0}gr_{0}}{p_{0}}\left(1-\frac{r_{0}}{r}\right)\right].\end{eqnarray}$$

The corresponding result for an adiabatic atmosphere, for which $p/{\it\rho}^{{\it\gamma}}=p_{0}/{\it\rho}_{0}^{{\it\gamma}}$ , is

(2.19) $$\begin{eqnarray}\frac{p}{p_{0}}=\left(\frac{{\it\rho}}{{\it\rho}_{0}}\right)^{{\it\gamma}}=\left[1-\frac{{\it\gamma}-1}{{\it\gamma}}\,\,\frac{{\it\rho}_{0}gr_{0}}{p_{0}}\left(1-\frac{r_{0}}{r}\right)\right]^{{\it\gamma}/({\it\gamma}-1)}.\end{eqnarray}$$

Equation (2.18) is, of course, the limiting case of (2.19) as ${\it\gamma}\rightarrow 1$ . In both cases, the scale height $\ell _{s}$ , defined as the height above the surface where the pressure would go to zero if it were to decrease from $p_{0}$ with its surface gradient, is

(2.20) $$\begin{eqnarray}\ell _{s}=\frac{p_{0}}{{\it\rho}_{0}g}.\end{eqnarray}$$

Figure 1 shows examples of the atmospheric structure.

Figure 1. Examples of the structure of isothermal (full line) and adiabatic (chain-dotted line, ${\it\gamma}=1.4$ ) atmospheres with $\ell _{s}/r_{0}=0.1$ .

2.5 Parameters of the problem

Within the scheme of the assumptions made, the problem reduces to one in which any dimensionless quantity $Q$ depends on five independent parameters:

(2.21) $$\begin{eqnarray}Q=Q\left(\frac{p_{r}}{p_{0}},\,\frac{{\it\rho}_{r}}{{\it\rho}_{0}},\,\frac{p_{0}}{{\it\rho}_{0}\,g\,r_{0}},\,{\it\gamma},\,\frac{r_{\ast }}{r_{0}}\right),\end{eqnarray}$$

where $r_{\ast }$ is the radius of the opening in the moon’s surface. The third of these is $\ell _{s}/r_{0}$ , which is held constant at 0.1 throughout this study. The remaining four independent parameters represent the space that is explored by the computational study. It turns out that the variable that influences the results most strongly is the velocity ratio $u_{0}/u_{eg}$ which depends on all of the first four parameters in (2.21), see (2.16). When describing the results this variable is therefore chosen in place of ${\it\rho}_{r}/{\it\rho}_{0}$ . It is also convenient for comparison with the analytical result of (2.15). Most of the results presented in the following have been obtained with $r_{\ast }/r_{0}=0.1$ . However, some results showing the effect of the opening radius are presented in § 4.6.

The space and time scaling may be expressed by

(2.22) $$\begin{eqnarray}\left(\frac{r}{r_{0}},\sqrt{\frac{{\it\rho}_{r}}{p_{r}}}gt\right).\end{eqnarray}$$

3.1 Equations

For numerical solutions of the Euler equations (2.5)–(2.8) they are usually written in the equivalent form

(3.1) $$\begin{eqnarray}\frac{\partial \boldsymbol{W}}{\partial t}+\frac{\partial \boldsymbol{F}}{\partial x}+\frac{\partial \boldsymbol{G}}{\partial y}={\it\rho}\boldsymbol{B}-\frac{{\it\rho}v}{y}\boldsymbol{S},\end{eqnarray}$$

in which the vector of dependent variables, $\boldsymbol{W}$ , the flux vectors $\boldsymbol{F}$ and $\boldsymbol{G}$ , specific body-force vector $\boldsymbol{B}$ and axial symmetry vector $({\it\rho}v/y)\boldsymbol{S}$ are determined by

(3.2a-e ) $$\begin{eqnarray}\boldsymbol{W}=\left[\begin{array}{@{}c@{}}{\it\rho}\\ {\it\rho}u\\ {\it\rho}v\\ {\it\rho}h-p\end{array}\right],\quad \boldsymbol{F}=\left[\begin{array}{@{}c@{}}{\it\rho}u\\ {\it\rho}u^{2}+p\\ {\it\rho}uv\\ {\it\rho}uh\end{array}\right],\quad \boldsymbol{G}=\left[\begin{array}{@{}c@{}}{\it\rho}v\\ {\it\rho}vu\\ {\it\rho}v^{2}+p\\ {\it\rho}vh\end{array}\right],\quad \boldsymbol{B}=\left[\,\begin{array}{@{}c@{}}0\\ f_{x}\\ f_{y}\\ f_{x}u+f_{y}v\end{array}\right],\quad \boldsymbol{S}=\left[\begin{array}{@{}c@{}}1\\ u\\ v\\ h\end{array}\right],\end{eqnarray}$$

with $f_{x}$ and $f_{y}$ as given by (2.9).

3.2 Software

The software system Amrita, constructed by James Quirk, see Quirk (Reference Quirk1998), was used. Amrita is a system that automates and packages computational tasks in such a way that the packages can be combined (dynamically linked) according to instructions written in a high-level scripting language. The present application uses features of Amrita that include the automatic construction of the Euler solver, documentation of the code, adaptive mesh refinement according to simply chosen criteria, and scripting-language-driven computation, archiving and post-processing of the results. The automation of the assembly and sequencing of the tasks makes for dramatically reduced possibility of hidden errors. It also makes computational investigations transparent and testable by others. The ability to change one package at a time, without changing the rest of the scheme, facilitates detection of sources of error. The Euler solver generated for the present computations was an operator-split scheme with HLLE flux and kappa-MUSCL reconstruction. The bare bones Amrita system did not include a body force, so that the necessary code to include $\boldsymbol{B}$ was constructed and extensively debugged.

3.3 Initial and boundary conditions, discretisation

Figure 2 shows a pseudo-schlieren image of an example of the initial condition of a computation. The ( $x,y$ ) plane is discretised by a Cartesian grid of $600\times 600$ coarse-grid cells that are adaptively refined by a factor of 3 to make an effective grid of $1800\times 1800$ cells. The criterion for adaptation is a chosen threshold of the magnitude of the fractional density gradient (density gradient divided by local density). The grey-shading of the visualisation is a monotonic function of the magnitude of the fractional density gradient; fractional in order to maintain sensitivity at small densities. In the initial state shown in figure 2 the spatial variation of density is solely due to the atmospheric structure, in this instance isothermal. The graph above shows the distribution of pressure ratio $p/p_{0}$ (solid line) and density ratio ${\it\rho}/{\it\rho}_{0}$ (dashed line) along the symmetry axis, which is the bottom edge of the figure. The strength of the gravity field is chosen to give $\ell _{s}=0.1r_{0}$ , as in figure 1.

Figure 2. Meridional section through one quadrant of the flow field around a hollow spherical moon with an opening at a pole, showing the initial conditions for the computation (see text). $p_{r}/p_{0}=15$ , ${\it\gamma}=1.4$ , ${\it\rho}_{r}/{\it\rho}_{0}=7.500$ , $u_{0}/u_{e}=0.8367$ .

One quadrant of the moon is shown with a radius of 100 coarse grid cells. It is hollow with the reservoir inside, in which the pressure and density are initially uniform (see the graph). The solid moon shell is modelled by a level set that specifies the smallest distance of a field point from any solid boundary. It makes the solid surface a no-through-flow boundary. The opening on the axis is initially closed. The conditions on most of the domain boundary are open. The exceptions are the symmetry axis and the portion of the left boundary that lies inside the reservoir. The latter is reflecting, i.e. like a solid boundary.

4.1 Some features of the flow

To set the scene, it is useful to describe some of the features of the jet. Figure 3 shows an image of a late phase of a jet with $p_{r}/p_{0}=60$ , $u_{0}/u_{eg}=0.8367$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . The expansion of the gas from the hot, high-pressure reservoir through the sonic constriction to a supersonic flow encounters an opposing pressure from the atmosphere that causes the flow to be deflected back closer to the $x$ -direction by the ‘barrel’ shock, and parallel to a shear layer that issues from the lip of the constriction. The resistance provided by gravity causes a nearly normal shock to appear in the flow close to the axis. This is sometimes referred to as the Mach disk in jet parlance.

Figure 3. Example of result of a computation showing features of a jet that has reached near-steady state. $p_{r}/p_{0}=60$ , $u_{0}/u_{eg}=0.8367$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ .

The normal shock and the barrel shock intersect at a triple shock point, as a third shock results from the clash of the flows that have passed through the normal and barrel shocks. These two flows are separated by a shear layer that issues from the triple point on the downstream side of the third shock. The jet reaches a maximum penetration radius on its axis, and the material that has passed through the normal shock – as well as the material that has come through the barrel and third shocks – spills to lower latitudes (pole on $x$ -axis) and falls down onto the moon surface at an impingement area. The outside field shows some weak shock waves that have been emitted into the tenuous atmosphere by the unsteadiness of the jet.

The triple ‘point’ is, of course a triple ‘line’. In this axisymmetric flow the shock waves are axisymmetric surfaces and the intersection of these three shock surfaces is the triple line, a perfect circle around the symmetry axis. Its trace in the meridional plane is the triple point.

4.2 Development of the jet with time

Figure 4 shows a time sequence of the development of the flow with the same parameters as in the case of figure 3. After the constriction is opened to start the jet erupting, figure 4(a) shows a nearly spherical shock wave that is generated by the initial eruption and that has propagated into the atmosphere to $x\simeq 3r_{0}$ on the axis. This is followed by the mushrooming jet that already contains some of the features illustrated in figure 3. In figure 4(a–c) this develops further and the rim of the mushroom begins to fall. In the second row, the jet height on the axis decreases somewhat as impingement wanders toward the equator, and the barrel shock exhibits some unsteadiness. In the bottom row, the supersonic part of the jet becomes virtually steady, but the rest of the jet remains unsteady, so that the ‘maximum steady-state penetration radius’ necessarily has to be quoted with an error bar that characterises the fluctuation around a mean value. Note that, during the unsteady phase of the flow, the mushroom overshoots the eventual steady-state penetration radius.

Figure 4. Time sequence of pseudo-schlieren images. $p_{r}/p_{0}=60$ , $u_{0}/u_{eg}=0.8367$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . The time intervals between images are equal. See supplementary movie 1 available at http://dx.doi.org/10.1017/jfm.2016.184.

It should be pointed out that during the whole of the development of the jet the pressure and density changes in the reservoir are extremely small in all cases, indicating that the drainage of the reservoir is insignificant. The reservoir pressure and density also remain uniform except in the immediate vicinity of the throat where they fall in accordance with steady isentropic expansion.

Figure 5 shows another, similar, time sequence, with $p_{r}/p_{0}=250$ . Particularly evident at this high pressure ratio, the initial eruption sends a narrow axial jet far ahead of the main mushroom. As time evolves, this axial jet falls back into the mushrooming main jet. Also, the transverse expansion of the jet is greater than at lower pressure ratio, so that the shear layer leaves the throat lip at a larger angle from the axis and the barrel shock is conical rather than barrel-shaped. Furthermore, the impingement area moves beyond the equator at later times. Because this is outside the computational domain and flow across the boundary can occur in both directions, it has to be considered with some care. The upstream influence from the left domain boundary is less important if the impingement area is inside the domain.

Figure 5. Time sequence of pseudo-schlieren images. $p_{r}/p_{0}=250$ , $u_{0}/u_{eg}=0.8367$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . The time intervals between images are the same as in figure 4.

4.3 Effect of the velocity ratio

Figure 6 shows the effect of changing the velocity ratio $u_{0}/u_{eg}$ in late-phase images at a pressure ratio of 250. As the velocity ratio is increased, the maximum steady-state penetration radius of the jet increases dramatically. The conical shape of the barrel shock that is characteristic for this high pressure ratio is evident in all frames and its angle is approximately constant. The impingement area moves to lower latitudes with increasing $u_{0}/u_{eg}$ at low values, but disappears entirely as $u_{0}/u_{eg}\rightarrow 1$ . In the last image, at $u_{0}/u_{eg}=0.9354$ , the jet continues to expand and the normal shock is outside the region shown. In fact, at this condition it even leaves the computational domain completely.

Figure 6. Effect of the velocity ratio. $p_{r}/p_{0}=250$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . $u_{0}/u_{eg}=0.5401$ (a), 0.6236 (b), 0.7071 (c), 0.7638 (d), 0.8367 (e), 0.9354 (f).

Figure 7 is the same as figure 6, but for a pressure ratio of 60. The features are qualitatively similar, except that the barrel shock exhibits a barrel shape and the angle at which it leaves the throat lip is smaller.

Figure 7. Effect of the velocity ratio. $p_{r}/p_{0}=60$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . $u_{0}/u_{eg}=0.5401$ (a), 0.6614 (b), 0.7071 (c), 0.7638 (d), 0.8367 (e), 0.9354 (f).

4.4 Effect of the pressure ratio

Next, figure 8 shows the effect of changing the pressure ratio in late-phase images at a constant velocity ratio of 0.7071. Figure 8(a) with $p_{r}/p_{0}=4$ exhibits a tiny barrel shock and normal shock. The shock pattern increases dramatically in size, the shear layer angle increases and the impingement area moves to lower latitudes with increasing pressure ratio. These features are qualitatively the same in figure 9, showing late-phase images at a larger velocity ratio.

Figure 8. Effect of the pressure ratio. $u_{0}/u_{eg}=0.7071$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . $p_{r}/p_{0}=4$ (a), 15 (b), 60 (c), 250 (d).

Figure 9. Effect of the pressure ratio. $u_{0}/u_{eg}=0.8367$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . $p_{r}/p_{0}=4$ (a), 15 (b), 60 (c), 250 (d).

Figure 10 shows two images of jets that escape gravity. A feature of such cases is that the jet spills little material back onto the moon’s surface. Thus, the decrease of the impingement latitude that accompanies increase of $u_{0}/u_{eg}$ at small values is followed by an impingement-latitude increase at higher velocity ratios.

Figure 10. Two cases where $u_{0}/u_{eg}>1$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ , $u_{0}/u_{e}=1.0801$ . (a) $p_{r}/p_{0}=15$ , ${\it\rho}_{r}/{\it\rho}_{0}=4.500$ ; (b) $p_{r}/p_{0}=60$ , ${\it\rho}_{r}/{\it\rho}_{0}=18$ . Note how, when the jet escapes gravity, very little of it spills back onto the moon. The ripples in the jet, as in other cases at later times, are caused by the reverberation of waves in the reservoir.

4.5 Maximum steady-state penetration radius

While figures 6 and 7 show a substantial increase in $r_{p}$ as the velocity ratio is increased, it is interesting to compare this growth quantitatively with (2.15). This is done in figure 11 for pressure ratios of 15 and 3. Each of the square points in the figure represents an average of measurements from several late-phase computed images with an error bar representative of the fluctuation amplitude. The dashed line  is arbitrarily drawn at 70 % of the altitude above the moon surface of the theoretical line because it passes approximately through the points of the case $p_{r}/p_{0}=15$ . This also serves as a reference in the case $p_{r}/p_{0}=3$ in figure 11(b) and in figure 12.

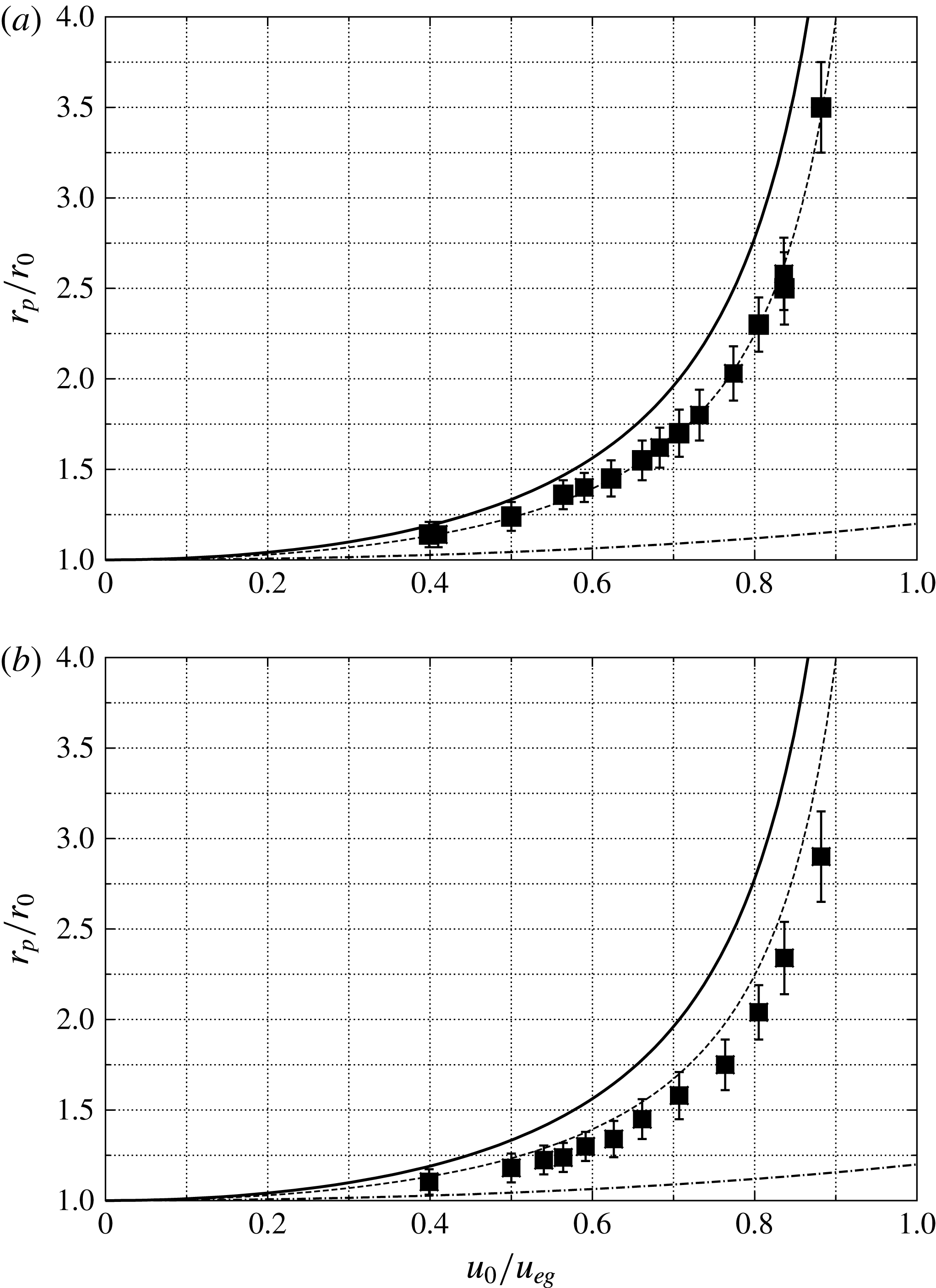
Figure 11. Plot of dimensionless steady-state jet penetration radius versus $u_{0}/u_{eg}$ for ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . (a) $p_{r}/p_{0}=15$ ; (b) $p_{r}/p_{0}=3$ . For notation, see text.

Figure 12. Plot of dimensionless steady-state jet penetration radius versus $u_{0}/u_{eg}$ for ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . (a) $p_{r}/p_{0}=50$ ; (b) $p_{r}/p_{0}=250$ . For notation, see text.

Also shown in these figures as a chain-dotted line is the dimensionless penetration radius that would be reached by a solid object leaving the moon’s surface at the same speed. This is very much smaller than that of the gas because the escape velocity of the solid is larger by a factor of $\sqrt{({\it\gamma}+1)/({\it\gamma}-1)}$ than that of the gas.

Figure 12 repeats figure 11 for the case of pressure ratios of 50 and 250. The curves are exactly the same as those in figure 11. Note that, as the pressure ratio is increased from 3 to 250, the points approach the theoretical isentropic curve more closely. As $p_{r}/p_{0}$ is increased, the impediment to the jet that is provided by the presence of the atmosphere is reduced. This is shown in another form in figure 13(a).

Figure 13. Plot of dimensionless steady-state jet penetration radius. (a) Effect of $p_{r}/p_{0}$ for $u_{0}/u_{eg}=0.71$ , ${\it\gamma}=1.4$ , $r_{\ast }/r_{0}=0.1$ . (b) Effect of ${\it\gamma}$ for $u_{0}/u_{eg}=0.71$ and $p_{r}/p_{0}=15$ , $r_{\ast }/r_{0}=0.1$ . The heavy black line represents the value given by (2.15) in both graphs.

It is interesting to observe how strongly ${\it\gamma}$ affects $r_{p}/r_{0}$ (see figure 13 b). One might speculate that the discrepancy between the computed penetration radius and the theoretical isentropic value could be related in part to the entropy increase across the normal shock which is given by

(4.1) $$\begin{eqnarray}\frac{{\rm\Delta}s}{R}=\frac{1}{{\it\gamma}-1}\,f(M,{\it\gamma}),\end{eqnarray}$$

where $s$ is specific entropy, $R$ is the specific gas constant, $M$ is the Mach number upstream of the shock and the function $f$ depends relatively weakly on ${\it\gamma}$ . The behaviour exhibited by figure 13(b), showing the dependence of $r_{p}/r_{0}$ on ${\it\gamma}$ with $p_{r}/p_{0}$ , $u_{0}/u_{eg}$ and $r_{\ast }/r_{0}$ held constant, seems to mirror the prefactor of $f$ . However, since $M$ is not quite the same in the five cases plotted, a quantitative comparison is not warranted.

4.6 Effect of throat radius

In all of the results presented so far, $r_{\ast }/r_{0}=0.1$ . To examine the effect of this parameter, several computations were performed with the reduced value of 0.03. At this value the radius of the opening amounts to only nine fine grid cells and is near the limit of reasonable resolution. The throat radius does not enter the derivation of (2.15), so that it is not expected to influence the steady-state penetration radius significantly.

Figure 14 shows four late-phase images from computations with $r_{\ast }/r_{0}=0.1$ in (a,c) and 0.03 in (b,d). Figure 14(a,b) is at $p_{r}/p_{0}=60$ , (c,d) at 250. The high velocity ratio has been chosen for this comparison because the effect of throat radius is largest there. However, note that, though the throat radius is changed by a factor of more than 3, the scale of the jet geometry is clearly not determined by $r_{\ast }$ . The throat radius does influence the maximum steady-state penetration radius to some extent, as can be seen in figure 15. Reduction of $r_{\ast }$ also reduces the transverse extent of the jet somewhat.

Figure 14. (a,c) From computations with a throat diameter $r_{\ast }/r_{0}=0.1$ and (b,d) with $r_{\ast }/r_{0}=0.03$ . (a,b) From computations with $p_{r}/p_{0}=60$ , ${\it\rho}_{r}/{\it\rho}_{0}=27$ ; (c,d) with $p_{r}/p_{0}=250$ , ${\it\rho}_{r}/{\it\rho}_{0}=112.500$ . Velocity ratio $u_{0}/u_{eg}=0.8819$ , ${\it\gamma}=1.4$ .

Figure 15. Maximum steady-state penetration radius obtained with the reduced throat diameter ( $r_{\ast }/r_{0}=0.03$ ). Because the curves in this figure are the same as those in figures 11 and 12, it can be seen that the smaller throat gives slightly reduced penetration relative to the case $r_{\ast }/r_{0}=0.1$ . Since error bars would be confusing here, they have been omitted.

4.7 Atmosphere structure

All the computational results shown are for an isothermal atmosphere. The same parameter space has been covered by computations with an adiabatic atmosphere. However, the results differ so little from the cases with isothermal atmosphere that no additional information would be conveyed by presenting them. The insensitivity of the results to atmospheric structure indicates that the effect of the atmosphere comes about through the atmospheric pressure and density in a region close to the moon’s surface, where the two structures are similar, see figure 1.