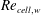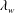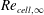1 Introduction
Accurate calculation of aerodynamic heating is crucial for the design of thermal protection systems of hypersonic vehicles. There are many uncertainties in numerical calculation when a vehicle flies at high altitude where the atmosphere is relatively rarefied and the flow often belongs to the slip flow regime and transition flow regime (Tsien Reference Tsien1946). Even though some fitting formulas for the heat flux of vehicle surfaces have been developed (Fay Reference Fay1958; Sutton & Graves Jr Reference Sutton and Graves1971; Singh & Schwartzentruber Reference Singh and Schwartzentruber2017), these methods are not applicable to all parts of a complex-shape vehicle. When the classical computational fluid dynamics (CFD) method and the direct simulation Monte Carlo (DSMC) method (Myong Reference Myong2011; Brandis & Johnston Reference Brandis and Johnston2014; Singh & Schwartzentruber Reference Singh and Schwartzentruber2016; Yang & Liu Reference Yang and Liu2017) are used to simulate the aerodynamic environment, the accuracy is affected by many factors, such as discrete methods, boundary conditions, numerical formats and grid size (Siddiqui et al.
Reference Siddiqui, Hoffmann, Chiang and Rutledge1992). The grid size near vehicle surfaces, especially the grid size of the first cell in the normal direction next to a vehicle’s surface, is considered to be one of the most important factors (Hoffmann, Siddiqui & Chiang Reference Hoffmann, Siddiqui and Chiang1991; Xiang, Wei & Haibo Reference Xiang, Wei and Haibo2017). For steady-state flow, the Navier–Stokes (NS) equations are reduced to diffusion–convection equations whose numerical accuracy is affected by the cell Reynolds number
$Re_{\mathit{cell}}$
(Ciment, Leventhal & Weinberg Reference Ciment, Leventhal and Weinberg1978; Berger et al.
Reference Berger, Solomon, Ciment, Leventhal and Weinberg1980; Kellogg, Shubin & Stephens Reference Kellogg, Shubin and Stephens1980). Therefore, the CFD method generally uses
$Re_{\mathit{cell}}$
as the basis for determining the cell height of the first layer. There are currently two methods used to define
$Re_{\mathit{cell}}$
: one is
$Re_{\mathit{cell},\infty }$
based on the free-stream parameters (Klopfer & Yee Reference Klopfer and Yee1988; Dilley Reference Dilley and McClinton2001), and the other is
$Re_{\mathit{cell},w}$
based on the flow parameters near a vehicle’s surfaces (Papadopoulos et al.
Reference Papadopoulos, Venkatapathy, Prabhu, Loomis and Olynick1999; Men’shov & Nakamura Reference Men’shov and Nakamura2000). Although
$Re_{\mathit{cell},\infty }$
can be directly calculated, its feasibility has not been studied exactly. While
$Re_{\mathit{cell},w}$
has a clear meaning, it needs to be calculated on a coarse grid to estimate the local flow parameters first. On the other hand, Bird’s research (Bird Reference Bird2013) shows that the aerodynamic heating solution in DSMC is also affected by the grid size near vehicle surfaces. Since the DSMC method is a direct simulation method based on molecular collisions, the grid size needs to be taken as a fraction of the local mean free path (MFP), which is generally taken as one-third to two-thirds of the MFP, and also relies on local flow parameters.
Although grid size for the CFD and DSMC methods is generally determined by the three criteria, the rationality of these three criteria, as well as the relationship between them, are not very clear. In addition, there are no descriptions of the relationship between the aerodynamic heating determined by the CFD and DSMC methods when the grid is not set properly. In this paper the grid effect of the CFD and DSMC methods in hypersonic aerothermodynamics simulation was studied. One of the main goals of this paper is to obtain the relationship between the grid sizes determined by the three criteria using one-dimensional assumption and theoretical derivation. The second goal is to analyse the relationship between the free-stream velocity and the grid size through flow field simulation. The third goal is to study the errors of aerodynamic heating obtained using the two simulation methods (CFD and DSMC) under different grid sizes.
This paper is organized as follows. Section 2 discusses the three grid criteria and their relationship in theory; § 3 describes the physical model and the solvers used in this work; § 4 is devoted to the numerical results and discussion; and § 5 contains the conclusions.
2 Theory of boundary grid size criteria
The conservation laws NS equations can be written in the form (Klopfer & Yee Reference Klopfer and Yee1988)
$$\begin{eqnarray}{\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{U}}}{\unicode[STIX]{x2202}t}}+{\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{F}}_{i,inv}}{\unicode[STIX]{x2202}x_{i}}}-{\displaystyle \frac{1}{Re}}{\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{F}}_{i,vis}}{\unicode[STIX]{x2202}x_{i}}}=0,\end{eqnarray}$$
where
${\mathcal{U}}$
is the vector of conserved quantities, and
${\mathcal{F}}_{i,inv}$
and
${\mathcal{F}}_{i,vis}$
are the flux vectors from inviscid and viscous contributions.
For steady-state flow problems, the time terms are negligible, and the NS equations are reduced to diffusion–convection equations, which have both hyperbolic and parabolic properties. It has been shown that the convergence, stability and numerical precision of diffusion–convection flow problems rely on
$Re_{\mathit{cell}}$
, particularly in fluid boundary layer problems (Ciment et al.
Reference Ciment, Leventhal and Weinberg1978; Berger et al.
Reference Berger, Solomon, Ciment, Leventhal and Weinberg1980; Kellogg et al.
Reference Kellogg, Shubin and Stephens1980).
The parameter
$Re_{\mathit{cell}}=1$
is often used to determine the normal grid size next to vehicle surfaces when using the classical CFD method to solve the hypersonic flow around a vehicle. There are two kinds of definition for
$Re_{\mathit{cell}}$
. The first is based on free-stream parameters, written as
$Re_{\mathit{cell},\infty }$
, and the other is based on local parameters next to surfaces, written as
$Re_{\mathit{cell},w}$
. Those are defined as (Papadopoulos et al.
Reference Papadopoulos, Venkatapathy, Prabhu, Loomis and Olynick1999; Dilley Reference Dilley and McClinton2001)
$$\begin{eqnarray}\displaystyle & Re_{\mathit{cell},\infty }={\displaystyle \frac{\unicode[STIX]{x1D70C}_{\infty }V_{\infty }l}{\unicode[STIX]{x1D707}_{\infty }}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & Re_{\mathit{cell},w}={\displaystyle \frac{\unicode[STIX]{x1D70C}_{w}c_{w}l}{\unicode[STIX]{x1D707}_{w}}}, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}$
,
$V$
,
$c$
and
$\unicode[STIX]{x1D707}$
are, respectively, the density, velocity, speed of sound and viscosity of gas, and
$l$
is the normal size of the first cell next to surfaces. The subscript
$\infty$
denotes the free-stream parameters and the subscript
$w$
denotes the parameters near surfaces. When
$Re_{\mathit{cell},\infty }=1$
, the two kinds of grid size are, respectively,
$$\begin{eqnarray}\displaystyle & l_{\mathit{cell},\infty }={\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D70C}_{\infty }V_{\infty }}}={\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D70C}_{\infty }Ma_{\infty }\sqrt{\unicode[STIX]{x1D6FE}RT_{\infty }}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & l_{\mathit{cell},w}={\displaystyle \frac{\unicode[STIX]{x1D707}_{w}}{\unicode[STIX]{x1D70C}_{w}c_{w}}}={\displaystyle \frac{\unicode[STIX]{x1D707}_{w}}{\unicode[STIX]{x1D70C}_{w}\sqrt{\unicode[STIX]{x1D6FE}RT_{w}}}}. & \displaystyle\end{eqnarray}$$
For DSMC, the local MFP is used to determine the grid size, and the minimum appears at the stagnation point of surfaces, which is defined as (Cercignani Reference Cercignani1988)
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{w}=A{\displaystyle \frac{\unicode[STIX]{x1D707}_{w}}{\unicode[STIX]{x1D70C}_{w}}}\sqrt{{\displaystyle \frac{1}{2\unicode[STIX]{x03C0}RT_{w}}}},\end{eqnarray}$$
where
$A$
is a constant determined by the selected collision model in the DSMC method. The value of
$A$
is
${\textstyle \frac{16}{5}}$
when the hard-sphere (HS) model is used;
$A={\textstyle \frac{2}{15}}(7-2\unicode[STIX]{x1D714})(5-2\unicode[STIX]{x1D714})$
for the variable hard-sphere (VHS) model; and
$A=4\unicode[STIX]{x1D6FC}(7-2\unicode[STIX]{x1D714})(5-2\unicode[STIX]{x1D714})/5(\unicode[STIX]{x1D6FC}+1)(\unicode[STIX]{x1D6FC}+2)$
for the variable soft-sphere model. Unless otherwise specified, the following theoretical derivation and simulation used the MFP under the definition of the HS model.
The density at the stagnation point is necessary to determine the grid size using (2.5) and (2.6). According to the thin boundary layer theory (Zel’Dovich & Raizer Reference Zel’Dovich and Raizer2012), there is a temperature boundary layer near the surface in hypersonic flow. Therefore, the density at the stagnation point cannot be directly determined, and its solution depends strongly on the grid size. However, the pressure at the stagnation point, or
$p_{w}$
, is relatively stable, and it can be calculated from the gas dynamics, even if the wall temperature is set differently. Therefore (2.5) and (2.6) can be transformed to a form with
$p_{w}$
using the ideal gas state equation, as well as (2.4). The variation of flow along the stagnation point line can be decomposed into two processes. First, the free-stream hypersonic flow decelerates to a subsonic flow through the bow shock in front of the vehicle. The physical parameters before and after the shock meet the Rankine–Hugoniot relations (Anderson Jr Reference Anderson2010). Then, the subsonic flow gradually decelerates and stagnates at surfaces. Therefore,
$p_{w}$
can be expressed as
$$\begin{eqnarray}{\displaystyle \frac{p_{w}}{p_{\infty }}}={\displaystyle \frac{\left[{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2}}Ma_{\infty }^{2}\right]^{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}-1}}{\left[{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}}Ma_{\infty }^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}+1}}\right]^{1/\unicode[STIX]{x1D6FE}-1}}}.\end{eqnarray}$$
Simultaneously establishing (2.4)–(2.7) and the ideal gas state equation,
$\unicode[STIX]{x1D706}_{w}$
is written as
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{w}=A{\displaystyle \frac{\unicode[STIX]{x1D707}_{w}}{p_{\infty }}}\sqrt{{\displaystyle \frac{RT_{w}}{2\unicode[STIX]{x03C0}}}}{\displaystyle \frac{\left[{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}}Ma_{\infty }^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}+1}}\right]^{1/\unicode[STIX]{x1D6FE}-1}}{\left[{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2}}Ma_{\infty }^{2}\right]^{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}-1}}},\end{eqnarray}$$
and the ratios of
$l_{\mathit{cell},\infty }$
and
$l_{\mathit{cell},w}$
to
$\unicode[STIX]{x1D706}_{w}$
are respectively written as
$$\begin{eqnarray}\displaystyle & {\displaystyle \frac{l_{\mathit{cell},\infty }}{\unicode[STIX]{x1D706}_{w}}}={\displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{\unicode[STIX]{x1D6FE}}}}{\displaystyle \frac{\left[{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2}}Ma_{\infty }^{2}\right]^{\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1)}}{\left[{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}}Ma_{\infty }^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}+1}}\right]^{1/\unicode[STIX]{x1D6FE}-1}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\displaystyle \frac{l_{\mathit{cell},w}}{\unicode[STIX]{x1D706}_{w}}}=f_{1}(\unicode[STIX]{x1D6FE})={\displaystyle \frac{1}{A}}\sqrt{{\displaystyle \frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FE}}}}. & \displaystyle\end{eqnarray}$$
The ratio
$l_{\mathit{cell},w}/\unicode[STIX]{x1D706}_{w}$
is only related to the specific heat ratio
$\unicode[STIX]{x1D6FE}$
of the gas, which is a constant that depends on the gas composition. For monatomic molecules
$\unicode[STIX]{x1D6FE}={\textstyle \frac{5}{3}}$
,
$f_{1}(\unicode[STIX]{x1D6FE})=0.607$
, while for diatomic molecules
$\unicode[STIX]{x1D6FE}={\textstyle \frac{7}{5}}$
,
$f_{1}(\unicode[STIX]{x1D6FE})=0.662$
; for other molecules or mixtures,
$f_{2}(\unicode[STIX]{x1D6FE})=0.6$
–
$0.8$
. Therefore, the grid size calculated by
$Re_{\mathit{cell},w}=1$
is equal to a fraction of the local MFP. In other words, the
$Re_{\mathit{cell},w}$
criterion in CFD is consistent with the MFP criterion in DSMC.
In hypersonic flow (
$Ma_{\infty }>5$
), the last item in (2.9),
$-[(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)]$
, can be ignored (the simplification is shown appendix A). Thus the ratio
$l_{\mathit{cell},\infty }/\unicode[STIX]{x1D706}_{w}$
is simplified to
$$\begin{eqnarray}\displaystyle & {\displaystyle \frac{l_{\mathit{cell},\infty }}{\unicode[STIX]{x1D706}_{w}}}=f_{2}(\unicode[STIX]{x1D6FE}){\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}Ma_{\infty }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{2}(\unicode[STIX]{x1D6FE})={\displaystyle \frac{\sqrt{2\unicode[STIX]{x03C0}}}{A}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2\sqrt{\unicode[STIX]{x1D6FE}}}}\right)^{\unicode[STIX]{x1D6FE}+1/\unicode[STIX]{x1D6FE}-1}. & \displaystyle\end{eqnarray}$$
The ratio
$l_{\mathit{cell},\infty }/\unicode[STIX]{x1D706}_{w}$
is determined by the specific heat ratio
$\unicode[STIX]{x1D6FE}$
, the viscosity coefficient ratio
$\unicode[STIX]{x1D707}_{\infty }/\unicode[STIX]{x1D707}_{w}$
, the temperature ratio
$T_{\infty }/T_{w}$
and
$Ma_{\infty }$
. For monatomic molecules
$\unicode[STIX]{x1D6FE}={\textstyle \frac{5}{3}}$
,
$f_{2}(\unicode[STIX]{x1D6FE})=0.891$
and for diatomic molecules
$\unicode[STIX]{x1D6FE}={\textstyle \frac{7}{5}}$
,
$f_{2}(\unicode[STIX]{x1D6FE})=0.852$
. The viscosity coefficient
$\unicode[STIX]{x1D707}$
is an intrinsic property of a gas which depends on temperature. In the classical CFD, there are many models to calculate viscosity coefficient, such as the constant model (const.), the Sutherland model (
$\unicode[STIX]{x1D707}=A_{s}\sqrt{T}/(1+T_{s}/T)$
), the polynomial model (
$\unicode[STIX]{x1D707}=\sum _{i=0}^{N-1}a_{i}T^{i}$
), the logPolynomial model (
$\ln \unicode[STIX]{x1D707}=\sum _{i=0}^{N-1}a_{i}[\ln (T)]^{i}$
), etc. (Anderson Jr Reference Anderson2010). The viscous coefficient and temperature present a function in DSMC according to binary elastic collisions (Bird Reference Bird1994), such as the inverse power-law model, the HS model, the VHS model, the Maxwell model, the generalized hard sphere model, etc. There is a general formula,
$\unicode[STIX]{x1D707}=B\cdot T^{\unicode[STIX]{x1D714}}$
, where the constant
$B$
and the temperature index
$\unicode[STIX]{x1D714}$
depend on the collision model and gas species, which is equivalent to the first-order logPolynomial model in the classical CFD. Therefore, the ratio
$\unicode[STIX]{x1D707}_{\infty }/\unicode[STIX]{x1D707}_{w}$
depends on the relation between free-stream temperature and surface temperature.
For a special case, when the surface is set as adiabatic, the temperature at the stagnation point of surfaces is satisfied with
$$\begin{eqnarray}{\displaystyle \frac{T_{w}}{T_{\infty }}}=1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{2}}Ma_{\infty }^{2}.\end{eqnarray}$$
According to (2.13) and (2.11), the ratio
$l_{\mathit{cell},\infty }/\unicode[STIX]{x1D706}_{w}$
is
$$\begin{eqnarray}\displaystyle & {\displaystyle \frac{l_{\mathit{cell},\infty }}{\unicode[STIX]{x1D706}_{w}}}={\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}f_{3}(\unicode[STIX]{x1D6FE}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{3}(\unicode[STIX]{x1D6FE})=\sqrt{{\displaystyle \frac{2}{\unicode[STIX]{x1D6FE}-1}}}f_{2}(\unicode[STIX]{x1D6FE}). & \displaystyle\end{eqnarray}$$
In addition, according to (2.9) and (2.10), under the adiabatic condition of surfaces, the ratio of the grid size defined by two types of
$Re_{\mathit{cell}}$
in CFD is
$$\begin{eqnarray}{\displaystyle \frac{l_{\mathit{cell},\infty }}{l_{\mathit{cell},w}}}={\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}{\displaystyle \frac{f_{3}(\unicode[STIX]{x1D6FE})}{f_{1}(\unicode[STIX]{x1D6FE})}}.\end{eqnarray}$$
The ratio
$l_{\mathit{cell},\infty }/l_{\mathit{cell},w}$
is only related to the ratio of the viscosity
$\unicode[STIX]{x1D707}_{\infty }/\unicode[STIX]{x1D707}_{w}$
and the specific heat ratio
$\unicode[STIX]{x1D6FE}$
. If the viscous coefficient of gas is assumed to be a constant, the ratio is
$2.544$
for monatomic molecules, while it is
$2.879$
for diatomic molecules. It should be noted that the values specified here for
$\unicode[STIX]{x1D6FE}$
are only meaningful at low temperatures. In hypersonic flow, processes such as internal energy excitation and relaxation, dissociation, ionization, etc., occur, and these processes are not considered in this paper.
3 Physical model and numerical method
3.1 Physical model
A hypersonic flow over a two-dimensional cylinder (Lofthouse, Scalabrin & Boyd Reference Lofthouse, Scalabrin and Boyd2008) is considered to study the grid effect in the aerothermodynamics simulation in this article. The diameter of the cylinder is 12 inches (0.3048 m). The temperature of the cylinder wall is 500 K. Two different free-stream gases are used, Ar and
$\text{N}_{2}$
, representing monatomic molecules and diatomic molecules. The free-stream density is
$\unicode[STIX]{x1D70C}_{\infty }=2.818\times 10^{-5}~\text{kg}~\text{m}^{-3}$
, corresponding to
$Kn=0.01$
, which is located at the demarcation point between the continuum and the rarefied regime, as shown in table 1.
Figure 1. Computation field and grid settings.
Table 1. Free-stream flow settings.
a Taken from Lofthouse et al. (Reference Lofthouse, Scalabrin and Boyd2008). Based on the VHS model, it is actually 0.0092.
The flow at the back of the cylinder is subsonic, which leads to a slow convergence rate in simulation calculation, and we mainly focus on the pressure and heat transfer at the stagnation point, where the flow field at the rear of the cylinder has little effect, computing the field only takes the first half of the cylinder, and the body-fitted quadrilateral grid is used, as shown in figure 1. The free-stream boundary profile is an arc with a certain eccentricity from the cylinder, and its radius varies with the shock position under different free-stream Mach numbers. In the subsequent simulation verification and § 4.2, the outer radius of the simulation domain is
$2.4d$
, and its eccentricity is
$1.2d$
. In § 4.1, under lower free-stream Mach number, the outer radius of the simulation domain is set greater than
$2.4d$
. The circumferential grid number
$num_{c}$
is 700 and the circumferential grid size near the wall is
$2.09\times 10^{-3}~\text{m}$
, which is applicable to all conditions in this article. The radial grid size distribution is based on an exponential function, that is, the
$n$
th layer grid size is
$$\begin{eqnarray}l_{n}=l_{w}\exp [a(n-1)],\end{eqnarray}$$
where
$n$
is the layer number,
$l_{w}$
the initial height, or the normal grid size next to the cylinder, and
$a$
the exponent constant. In the subsequent verification and § 4.1, to ensure grid independence,
$l_{w}$
is set according to
$Re_{\mathit{cell},\infty }=1$
, and in § 4.2,
$l_{w}$
is considered separately to explore the mesh effect of surface parameters.
3.2 Numerical approach
The DSMC and CFD codes used in this paper are, respectively, dsmcFoam (Scanlon et al.
Reference Scanlon, Roohi, White, Darbandi and Reese2010) and sonicFoam solvers in Open Source Field Operation and Manipulation (OpenFOAM) (Jasak Reference Jasak1996), which is a C
$++$
toolbox for the development of customized numerical solvers, and pre-/post-processing utilities for the solution of engineering problems. The code is released as free and open-source software under the GNU General Public Licence. This code is a three-dimensional solver using an unstructured or structured grid; therefore, the two-dimensional domain should be converted to a three-dimensional one, while the front and back planes are set as symmetry planes.
The solver dsmcFoam is based on Bird’s original formulation (Bird Reference Bird1994), which has been validated in rarefied hypersonic flow (Scanlon et al. Reference Scanlon, Roohi, White, Darbandi and Reese2010). The solver sonicFoam belongs to the classical CFD, by solving the NS equations. It is a transient solver for transonic/supersonic, laminar or turbulent flows of a compressible flow.
In the solver dsmcFoam, the VHS model is used, which assumes that the collision cross-section
$\unicode[STIX]{x1D70E}_{T}$
is a function of the relative collision velocity
$c_{r}$
. The Larsen–Borgnakke model is used for reassigning the total energy between translational and internal modes, while the rotational relaxation number
$Z_{rot}=5$
is used. Actually there is no internal energy for a monatomic gas such as Ar. The surface of the cylinder is set to the Maxwell boundary model, while the momentum accommodation coefficient and thermal accommodation coefficient are both set to 1. The no time counter method is used for the collision method.
In the solver sonicFoam, due to
$Re_{\infty }=200{-}4000$
, laminar flow condition is selected. The pimple algorithm is used to solve the NS equations. The numerical schemes for terms in the NS equations are set as follows. The first-order Euler discretization scheme is used for the time derivative
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$
terms. The leastSquares scheme is used for the gradient
$\unicode[STIX]{x1D735}$
terms. The first-order Gauss-upwind scheme is used for the divergence
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }$
term. The second-order Gauss-limitedLinear scheme is used for other divergence
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{U})$
terms. The Gauss linear corrected scheme is used for the Laplacian
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D735}\boldsymbol{U})$
terms. The linear scheme is used for interpolations of values from cell centres to face centres. In addition, the calculation is second-order accurate for surface-normal gradient terms because the vector connecting the cell centres is orthogonal to the face. The surface of the cylinder is respectively set as slip boundary and non-slip boundary to analyse the influence of velocity slip and temperature jump on wall parameters.
In order to ensure the consistency of the transport properties between CFD and DSMC, the VHS model in DSMC is adopted uniformly. The viscosity coefficient
$\unicode[STIX]{x1D707}$
and the heat transfer coefficient
$\unicode[STIX]{x1D705}$
are redefined for CFD, which is introduced into the solver sonicFoam as a dynamic link library. According to Chapman–Enskog theory and molecular dynamics theory, these are defined as (Bird Reference Bird1994)
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D705}={\displaystyle \frac{9\unicode[STIX]{x1D6FE}-5}{4\unicode[STIX]{x1D6FE}-4}}{\displaystyle \frac{k}{m}}\unicode[STIX]{x1D707}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{ref}\left({\displaystyle \frac{T}{T_{ref}}}\right)^{\unicode[STIX]{x1D714}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D707}_{ref}={\displaystyle \frac{15\sqrt{\unicode[STIX]{x03C0}mkT_{ref}}}{2\unicode[STIX]{x03C0}d_{ref}^{2}(5-2\unicode[STIX]{x1D714})(7-2\unicode[STIX]{x1D714})}}, & \displaystyle\end{eqnarray}$$
where
$T$
is the translational temperature,
$\unicode[STIX]{x1D714}$
is the temperature exponent in the VHS model,
$m$
is the molecule mass,
$k$
is the Boltzmann constant and
$d$
the molecular diameter. The VHS properties for Ar and
$\text{N}_{2}$
are from the literature, Lofthouse et al. (Reference Lofthouse, Scalabrin and Boyd2008) and Bird (Reference Bird1994), respectively, shown in table 2.
Table 2. The VHS molecular model parameters.
Since the free stream is relatively thin, considering the slip effect near the wall, the Maxwell–Smoluchowski slip boundary model (Maxwell Reference Maxwell1878; Smoluchowski von Smolan Reference Smoluchowski von Smolan1898) is added to the solver sonicFoam, as (3.5) and (3.6):
$$\begin{eqnarray}\displaystyle & u_{s}=A\left({\displaystyle \frac{2-\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70E}}}\right)\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x2202}u_{x}}{\unicode[STIX]{x2202}n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & T_{s}-T_{w}={\displaystyle \frac{2-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}}}{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{(\unicode[STIX]{x1D6FE}+1)Pr}}\unicode[STIX]{x1D706}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}n}}, & \displaystyle\end{eqnarray}$$
where
$Pr$
is Prandtl number,
$\unicode[STIX]{x1D70E}$
is tangential momentum accommodation coefficient,
$\unicode[STIX]{x1D6FC}$
is energy accommodation coefficient and
$n$
is in the direction normal to the surface. Here
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}=1$
is used, indicating that all solutions are computed assuming a fully diffuse wall.
In this study, for the purpose of verifying the simulation accuracy, the solvers sonicFoam and dsmcFoam were used to simulate the condition for Ar in table 1 and compared with the DSMC simulation results in the literature (Lofthouse et al. Reference Lofthouse, Scalabrin and Boyd2008). The surface distribution of heat transfer and pressure is shown in figure 2. The surface properties are plotted as a function of the angle around the cylinder, with the stagnation point being located at an angle of zero. The surface properties are presented in terms of non-dimensional coefficients with the following definitions:
$$\begin{eqnarray}\displaystyle & C_{p}={\displaystyle \frac{p_{w}-p_{\infty }}{{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}_{\infty }U_{\infty }^{2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & C_{H}={\displaystyle \frac{q_{w}}{{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}_{\infty }U_{\infty }^{3}}}, & \displaystyle\end{eqnarray}$$
where
$p_{w}$
is the surface pressure,
$q_{w}$
is the heat flux and
$p_{\infty }$
,
$\unicode[STIX]{x1D70C}_{\infty }$
and
$U_{\infty }$
are the pressure, density and velocity of the free stream.
It can be seen that the surface pressure obtained by the two solvers is in good agreement with the one in the literature, while the surface heat flux error between the DSMC and CFD simulation results is about 6.7 % of the maximum of surface heat flux, which is tolerable in hypersonic simulation. Moreover, the CFD results between non-slip boundary and Maxwell–Smoluchowski slip boundary show that the slip effect at the wall is not obvious.
In the calculation for CFD and DSMC, the iteration time step is equivalent to the minimum value of molecular mean collision time. All the cases were solved using a HPC Linux Cluster platform.
Figure 2. Correctness of the two solvers. (a) Surface distribution of pressure. (b) Surface distribution of heat flux.
4 Results and discussion
This section is divided into two parts. First, through the CFD simulation, the relationship between the three kinds of grid size determined by the three criteria corresponding to the CFD and DSMC methods is obtained, and it is compared with the theoretical values of the previous section. Then, the relationship between surface properties obtained by the two simulation methods and the grid size is studied.
4.1 The relation between size criteria under different
$Ma_{\infty }$
For the two types of case in table 1, the free-stream velocity is set as
$Ma_{\infty }=2$
, 3, 5, 10, 15 and 20 shown in table 3, where
$Ma_{\infty }=10$
is from the literature (Lofthouse et al.
Reference Lofthouse, Scalabrin and Boyd2008), and the other data are 0.2, 0.3, 0.5, 1.5 and 2 times 10. The surface of the cylinder is set as adiabatic wall conditions and constant temperature wall conditions (
$T_{w}=500~\text{K}$
). The solver sonicFoam is used to calculate these cases.
The relationship between the grid size determined by the grid criteria and
$Ma_{\infty }$
is shown in figure 3(a,b) when the gas transport parameters are calculated according to the VHS model (3.2)–(3.4). Figure 3(c,d) shows the results when the gas transport parameter is assumed to be a constant, i.e. the temperature index
$\unicode[STIX]{x1D714}$
in table 2 is taken as 0.
Table 3. The free-stream velocity.
Figure 3. For different gases,
$l_{\mathit{cell},\infty }$
and
$\unicode[STIX]{x1D706}_{w}$
change with
$Ma_{\infty }$
: (a,c) Ar and (b,d)
$\text{N}_{2}$
. In (a,b), transport parameters are relayed on the VHS model, and in (c,d), these are constant.
In figure 3, the
$x$
-axis is
$Ma_{\infty }$
, and the
$y$
-axis is two kinds of grid size,
$l_{\mathit{cell},\infty }$
and
$\unicode[STIX]{x1D706}_{w}$
, required in CFD and DSMC, respectively, under the constant temperature wall condition and adiabatic wall condition. In order to observe the magnitude variation of the dimension, the
$y$
-axis is displayed in logarithmic form and normalized with the free-stream MFP, which is indicated in table 1. The solid line represents
$l_{\mathit{cell},\infty }$
obtained directly from (2.4). The dashed lines represent
$\unicode[STIX]{x1D706}_{w}$
obtained from the hypothesis theory which is expressed as (2.8) and the points represent
$\unicode[STIX]{x1D706}_{w}$
calculated by the results of solver sonicFoam using (2.6).
First, figure 3 shows that values of
$\unicode[STIX]{x1D706}_{w}$
obtained by the theoretical derivation and numerical simulation agree with each other, and the relative error (
$(\unicode[STIX]{x1D706}_{thoer}-\unicode[STIX]{x1D706}_{num})/\unicode[STIX]{x1D706}_{num}$
) is mostly less than 2 %, whether a constant temperature wall condition or an adiabatic wall condition. This indicates that the corresponding hypothesis and theoretical deduction in § 2 are applicable. The theoretical method could be used to predict the flow field parameters at the stagnation point and provide a reference for determining the grid size.
Second, it can be seen from figure 3(a,b) that
$\unicode[STIX]{x1D706}_{w}$
is very different for the two kinds of wall condition when the VHS model is used to determine the viscous coefficient. As
$Ma_{\infty }$
gradually increases from 1 to 25,
$\unicode[STIX]{x1D706}_{w}$
decreases from
$1.8\unicode[STIX]{x1D706}_{\infty }$
to
$0.006\unicode[STIX]{x1D706}_{\infty }$
under the condition of the constant temperature boundary. While under the adiabatic boundary,
$\unicode[STIX]{x1D706}_{w}$
first decreases and then increases, and its range is
$0.4\unicode[STIX]{x1D706}_{\infty }$
–
$0.8\unicode[STIX]{x1D706}_{\infty }$
. The two curves intersect at
$Ma_{\infty }=2.7$
for Ar (
$Ma_{\infty }=2.9$
for
$\text{N}_{2}$
), which corresponds with the free-stream stagnation temperature
$T_{\infty }^{\ast }$
being exactly 500 K. After the intersect point,
$T_{w}$
under the adiabatic wall boundary condition will be greater than the constant temperature 500 K if
$Ma_{\infty }$
increases. Because the viscous coefficient is proportional to
$T^{\unicode[STIX]{x1D714}}$
, the grid size becomes larger with
$Ma_{\infty }$
increasing. The required grid sizes,
$l_{\mathit{cell},\infty }$
and
$\unicode[STIX]{x1D706}_{w}$
, become smaller as
$Ma_{\infty }$
increases under the condition of the constant temperature boundary, which means more memory is needed to store grids and smaller time steps should be selected for numerical simulation in both the CFD and DSMC methods.
Third, figure 3(c,d) shows that both
$\unicode[STIX]{x1D706}_{w}$
and
$l_{\mathit{cell},\infty }$
decrease with an increase of
$Ma_{\infty }$
under the two kinds of wall condition when the viscosity coefficient is assumed as a constant. Parameter
$\unicode[STIX]{x1D706}_{w}$
under the constant temperature wall condition drops more severely than under the adiabatic wall condition, and the two lines intersect with each other at
$Ma_{\infty }=2.1$
for Ar (
$Ma_{\infty }=2.8$
for
$\text{N}_{2}$
). In addition,
$l_{\mathit{cell},\infty }$
changes in the same proportion as
$\unicode[STIX]{x1D706}_{w}$
under the adiabatic wall condition. And the ratio is the function of specific heat ratio
$f_{3}(\unicode[STIX]{x1D6FE})$
, derived from the previous section.
Finally, the curve representing
$l_{\mathit{cell},w}$
is not shown in figure 3, because in the previous section it was deduced that the ratio of
$l_{\mathit{cell},w}$
to
$\unicode[STIX]{x1D706}_{w}$
is a constant between 0.6 and 0.8, as in (2.10). That means, if
$l_{\mathit{cell},w}$
is plotted, it is always below the
$\unicode[STIX]{x1D706}_{w}$
curve.
4.2 The effect of grid size
As is well known, for high
$Ma$
number, the numerical simulation error is highly dependent on the grid size. On the other hand, high
$Ma$
number will cause gas vibration excitation, dissociation and corresponding non-equilibrium effects, and this phenomenon is not the focus of the present study, so we only consider Ar in this section. In order to verify the effect of the normal grid size near surfaces on hypersonic aerothermodynamics, 10 structural meshes are set with different grid number
$num_{n}$
in the normal direction, the first normal grid size
$l_{w}$
and the maximum radial grid size
$l_{max}$
, which are shown in table 4.
The solvers dsmcFoam and sonicFoam are used for the case of Ar in table 1. The free-stream velocity is set as
$Ma=5$
, 10 and 20. The surface is set to a constant temperature (
$T_{w}=500~\text{K}$
) boundary. The parameters of gas properties are uniformly defined according to the VHS model.
Table 4. Wall-normal grid settings.
According to (2.4)–(2.6), three kinds of grid size
$l_{\mathit{cell},\infty }$
,
$l_{\mathit{cell},w}$
and
$\unicode[STIX]{x1D706}_{w}$
under different free-stream velocities are shown in table 5, where the ratio
$l_{\mathit{cell},w}/\unicode[STIX]{x1D706}_{w}$
is a constant, namely 0.607 derived from (2.10), and the ratio
$l_{\mathit{cell},\infty }/\unicode[STIX]{x1D706}_{w}$
is satisfied by (2.14), which is already reflected in figure 3(a).
Figure 4. Comparison of flow fields between DSMC and CFD: (a) pressure; (b) temperature; (c)
$Ma$
number; (d) density.
Table 5. The normal grid size based on three criteria (units:
$10^{-4}~\text{m}$
).
For Grid 1 in table 4, when the free-stream velocity is
$U_{\infty }=2624~\text{m}~\text{s}^{-1}$
, the flow fields obtained by solvers sonicFoam and dsmcFoam are shown as figure 4, including pressure, temperature,
$Ma$
number and density, which are normalized with free-stream parameters. In front of the cylinder, a bow shock wave is formed, and the pressure, temperature and density behind the wave increase significantly, while the gas velocity drops to the subsonic (
$Ma<1$
) condition. At the same time, the flow fields obtained by the two solvers are completely symmetric about the central axis. This shows that when
$Kn=0.01$
, both methods are suitable for solving the flow field.
Figure 5 shows the pressure and heat flux distributions of the cylinder surface calculated by the two solvers under different grid sizes, where the meaning of the coordinates is the same as in figure 2. It can be seen from figure 5(a) that the surface pressure is insensitive to the grid size compared to the heat flux. Even when using the largest size, Grid 10, the pressure coefficient error is still less than 0.1. The maximum relative error at the stagnation point is not exceeding 6 %. The heat flux, especially at the stagnation point, shown in figure 5(b), has a significant dependence on the grid size. Among them, the heat flux obtained by the DSMC method increases with increasing normal grid size, while the heat flux calculated by the CFD method decreases. Compared with Grid 1, the heat flux at the stagnation point calculated by DSMC increases by 53 % when using Grid 10, while it decreases by 47 % calculated by CFD. The mechanism behind this phenomenon will be explained below.
Figure 5. (a) Surface pressure and (b) surface heat flux computed by the two solvers under different grid sizes.
Figure 6 shows the variation of the surface properties at the stagnation point with the grid size, taking into account the effects of different free-stream velocity conditions, where the
$x$
-axis repre-sents the normal grid size next to the surface and is normalized with the
$\unicode[STIX]{x1D706}_{w}$
calculated from (2.6), shown as table 5.
Figure 6. According to the two solvers under different grid sizes, (a) the pressure and (b) the heat flux at the stagnation point.
Figure 6(a) shows that the pressure decreases slightly with the continuous refinement of the wall-normal mesh for either the CFD method or the DSMC method. Note that the ordinate is sufficiently refined in the figure. Especially when
$l_{n}/\unicode[STIX]{x1D706}_{w}<10$
, the relative error between the pressure obtained by the two algorithms under the three kinds of free-stream velocity conditions is below 0.6 %, which indicates that the dependency between pressure and grid size is relatively weak. Second, the pressures calculated by (2.7) for the three kinds of free-stream velocity are 1.784, 1.768 and 1.764, which are similar to the simulation results here. Third, the free-stream velocity increased by a factor of four (
$Ma_{\infty }=5{-}20$
), while the pressure changed slightly and was located between 1.79 and 1.81, which verifies the independence of pressure
$P_{w}$
and the free-stream velocity
$Ma_{\infty }$
under hypersonic conditions.
Figure 6(b) shows that the heat flux calculated by the CFD and DSMC methods is consistent when the mesh size is small enough. Using the Fay–Riddell formula (Fay Reference Fay1958) to estimate the heat flux, it is 0.160, 0.192 and 0.204, which is approximately 1.1–1.5 times the simulated value. Second, with a gradual decrease of grid size, the heat flux calculated by CFD and DSMC converges to the same value, indicating that the accuracy of these two methods is consistent with the grid size requirements. This verifies the conclusion drawn above that the
$Re_{w}$
criterion for CFD is consistent with the
$\unicode[STIX]{x1D706}_{w}$
criterion for DSMC. However, the heat flux obtained by the CFD method decreases as the grid size increases, while the heat flux obtained by the DSMC method increases. For example, for the condition of
$Ma_{\infty }=10$
, when
$l_{n}/\unicode[STIX]{x1D706}_{w}=100$
, the heat flux obtained by the CFD method drops from 0.15 to 0.1, while the heat flux obtained by the DSMC method rises from 0.15 to nearly 0.2. The difference in heat flux between them is exactly a factor of two. And when the mesh size is larger, the difference in heat flux obtained by these two algorithms will be greater.
When the grid size does not meet requirements, the changing trend of the heat flux obtained by CFD and DSMC is opposite. The reason is that the DSMC method performs a direct physical simulation of the gas at the molecular level and realizes the transfer of momentum and energy by simulating the collision between particles, but the collision between particles and particle motions are decoupled, and the selection of collision pairs and the speed of particles after collision within each grid are generated by random numbers in each collision process in the loop. Theoretically, the MFP means the average distance between two collisions of a gas molecule while its states change. That also means, at the macroscale level, the flow parameters at two locations apart by one MFP are different, especially near the surface. The selection of collision pairs is random within each grid. When the grid size near the wall is larger than the local MFP, it may cause direct collision between the near-wall particles and the far-wall particles. That is, the probability of collision between high-energy far-wall particles and the wall increases.
In addition to the main reasons above, a coarse mesh would cause the macroscopic transport properties of DSMC to be distorted. This is due to the basic assumption of the DSMC method: decoupling of collisionless motion and collisions. The mesh size and time step must be small enough to ensure that the phenomenological collision model of DSMC is realistic. It can be seen from figure 7(a) that the coarse mesh causes the viscosity coefficient of the DSMC to increase, resulting in a thickening of the boundary layer and the forward movement of the shock wave.
Figure 7. Axis temperature distribution obtained by the two solvers under different grid sizes: (a) DSMC; (b) CFD.
The CFD method in this paper uses the finite volume method to solve the NS equations. The surface heat flux mainly depends on the temperature gradient at vertical direction of surfaces. Figure 7(b) shows the temperature distribution at the axis near the surface. When the grid is gradually coarsened,
$\unicode[STIX]{x2202}T_{w}/\unicode[STIX]{x2202}l_{n}$
is smaller, so that the heat flux is smaller. The dependence of such grid size on heat flow is also affected by factors such as numerical flux format, solution algorithm and interpolation format. Some modifications can be made by appropriate methods, but this dependency cannot be eliminated.
In fact, the thickness of the shock wave is equivalent to the local MFP. The results in figure 7 show that the large-size mesh increases the shock thickness, but the shock position does not change significantly, and the flow field parameters after the shock wave are basically the same. On the other hand, the fineness of the shock wave has little effect on the wall parameters during hypersonic flow over a cylinder.
5 Conclusions
This article focused on the
$Re_{\mathit{cell},\infty }$
criterion and the
$Re_{\mathit{cell},w}$
criterion used in CFD methods and the
$\unicode[STIX]{x1D706}_{w}$
criterion for DSMC, and discussed the relation between the three kinds of grid size through a simple one-dimensional theoretical flow around a cylinder. The results show that
$l_{\mathit{cell},w}$
and
$\unicode[STIX]{x1D706}_{w}$
are equivalent and their ratio is a constant, while the ratio of
$l_{\mathit{cell},\infty }$
to the other is constant only under the assumption of the constant viscosity coefficient and the constant temperature wall condition.
Then, the dependence of aerodynamic heating on grid size was studied in hypersonic simulations using CFD and DSMC methods. On multiple sets of grids, the solvers sonicFoam and dsmcFoam in OpenFOAM were used to numerically simulate the flow around the cylinder. And the flow field, wall parameters and especially the heat flux at the stagnation point were analysed.
The results show that when the real gas effect is neglected, the flows over a simple blunt body obtained by the two numerical methods are almost the same near
$Kn_{\infty }=0.01$
. The calculation accuracy of the heat flux obtained by the two methods is consistent with the requirements of the grid scale. And as the grid size increases, the heat flux calculated by the DSMC increases while the heat flux determined by the CFD decreases. For this phenomenon, the algorithm mechanism itself is properly interpreted.
The grid estimation method proposed in this paper provides guidance for setting the normal grid size near vehicle surfaces in numerical simulation of hypersonic condition. At the same time, it provides support for the hybrid of CFD and DSMC methods on the basis of a unified grid.
In actual hypersonic conditions, the shock-layer temperature increases from 5000 to 20 000 K. This leads to thermal excitation, dissociation, ionization and even radiation, which strongly affect the aerothermodynamic environment of hypersonic vehicles. For flow simulations with real gas effects, whether the grid criteria considered above are still applicable requires further study. The method discussed in this article is only applicable to simple bluff-body flow, and the applicability to complex flow and complex shape issues needs to be considered.
Appendix A
There are some simplifications from (2.9) to (2.11). The details are as follows:
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{l_{\mathit{cell},\infty }}{\unicode[STIX]{x1D706}_{w}}} & = & \displaystyle {\displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{\unicode[STIX]{x1D6FE}}}}{\displaystyle \frac{\left[{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2}}Ma_{\infty }^{2}\right]^{\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1)}}{\left[{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}}Ma_{\infty }^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{\unicode[STIX]{x1D6FE}+1}}\right]^{1/\unicode[STIX]{x1D6FE}-1}}}\nonumber\\ \displaystyle & {\approx} & \displaystyle {\displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}\sqrt{{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{\unicode[STIX]{x1D6FE}}}}{\displaystyle \frac{\left[{\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2}}Ma_{\infty }^{2}\right]^{\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1)}}{\left[{\displaystyle \frac{2\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D6FE}+1}}Ma_{\infty }^{2}\right]^{1/\unicode[STIX]{x1D6FE}-1}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}(\unicode[STIX]{x1D6FE}+1)^{(1/2)+(\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1))+(1/\unicode[STIX]{x1D6FE}-1)}\left({\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}}}\right)^{(1/2)+(1/\unicode[STIX]{x1D6FE}-1)}\nonumber\\ \displaystyle & & \displaystyle \times \,\left({\displaystyle \frac{1}{2}}\right)^{(\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1))+(1/\unicode[STIX]{x1D6FE}-1)}Ma_{\infty }^{2}\left({\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2(\unicode[STIX]{x1D6FE}-1)}}-{\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}-1}}\right)\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}(\unicode[STIX]{x1D6FE}+1)^{\unicode[STIX]{x1D6FE}+1/\unicode[STIX]{x1D6FE}-1}\left({\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}}}\right)^{\unicode[STIX]{x1D6FE}+1/2(\unicode[STIX]{x1D6FE}-1)}\left({\displaystyle \frac{1}{2}}\right)^{(\unicode[STIX]{x1D6FE}+1/\unicode[STIX]{x1D6FE}-1)-(1/2)}Ma_{\infty }\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\sqrt{2\unicode[STIX]{x03C0}}}{A}}{\displaystyle \frac{\unicode[STIX]{x1D707}_{\infty }}{\unicode[STIX]{x1D707}_{w}}}\sqrt{{\displaystyle \frac{T_{\infty }}{T_{w}}}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FE}+1}{2\sqrt{\unicode[STIX]{x1D6FE}}}}\right)^{\unicode[STIX]{x1D6FE}+1/\unicode[STIX]{x1D6FE}-1}Ma_{\infty },\end{eqnarray}$$
where the second term
$(\unicode[STIX]{x1D6FE}-1)/(\unicode[STIX]{x1D6FE}+1)$
in (2.9) is omitted, because it is much smaller than the first term
$(2\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D6FE}+1))Ma_{\infty }^{2}$
.
