Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-15T13:22:14.141Z Has data issue: false hasContentIssue false
  • English
  • Français

The granular Blasius problem

Published online by Cambridge University Press:  14 June 2019

Jonathan Michael Foonlan Tsang Open the ORCID record for Jonathan Michael Foonlan Tsang [Opens in a new window] ,
Stuart B. Dalziel Open the ORCID record for Stuart B. Dalziel [Opens in a new window]  and
N. M. Vriend Open the ORCID record for N. M. Vriend [Opens in a new window]
Jonathan Michael Foonlan Tsang*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Stuart B. Dalziel
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
N. M. Vriend
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: jmft2@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the steady flow of a granular current over a uniformly sloped surface that is smooth upstream (allowing slip for 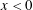$x<0$) but rough downstream (imposing a no-slip condition on 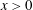$x>0$), with a sharp transition at 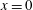$x=0$. This problem is similar to the classical Blasius problem, which considers the growth of a boundary layer over a flat plate in a Newtonian fluid that is subject to a similar step change in boundary conditions. Our discrete particle model simulations show that a comparable boundary-layer phenomenon occurs for the granular problem: the effects of basal roughness are initially localised at the base but gradually spread throughout the depth of the current. A rheological model can be used to investigate the changing internal velocity profile. The boundary layer is a region of high shear rate and therefore high inertial number 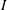$I$; its dynamics is governed by the asymptotic behaviour of the granular rheology for high values of the inertial number. The 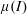$\unicode[STIX]{x1D707}(I)$ rheology (Jop et al., Nature, vol. 441 (7094), 2006, pp. 727–730) asserts that 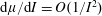$\text{d}\unicode[STIX]{x1D707}/\text{d}I=O(1/I^{2})$ as 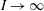$I\rightarrow \infty$, but current experimental evidence is insufficient to confirm this. We show that this rheology does not admit a self-similar boundary layer, but that there exist generalisations of the 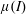$\unicode[STIX]{x1D707}(I)$ rheology, with different dependencies of 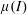$\unicode[STIX]{x1D707}(I)$ on 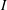$I$, for which such self-similar solutions do exist. These solutions show good quantitative agreement with the results of our discrete particle model simulations.

JFM classification

Granular media: Granular media Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 784 - 817
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acheson, D. J. 1990 Elementary Fluid Dynamics. Oxford University Press.Google Scholar
Andreotti, B., Forterre, Y. & Pouliquen, O. 2015 Granular Media. Cambridge University Press.Google Scholar
Artoni, R., Santomaso, A. & Canu, P. 2009 Effective boundary conditions for dense granular flows. Phys. Rev. E 79, 031304.Google Scholar
Baker, J. L., Johnson, C. G. & Gray, J. M. N. T. 2016 Segregation-induced finger formation in granular free-surface flows. J. Fluid Mech. 809, 168–212.Google Scholar
Barker, T., Schaeffer, D. G., Shearer, M. & Gray, J. M. N. T. 2017 Well-posed continuum equations for granular flow with compressibility and 𝜇(I)-rheology. Proc. R. Soc. A 473 (2201), 20160846.Google Scholar
Bharathraj, S. & Kumaran, V. 2017 Effect of base topography on dynamics and transition in a dense granular flow. J. Fluid Mech. 832, 600–640.Google Scholar
Billingham, J. & King, A. C. 2001 Wave Motion. Cambridge University Press.Google Scholar
Bouzid, M., Trulsson, M., Claudin, P., Clément, E. & Andreotti, B. 2013 Nonlocal rheology of granular flows across yield conditions. Phys. Rev. Lett. 111 (23), 238301.Google Scholar
Chow, V. T. 1959 Open-Channel Hydraulics. Blackburn Press.Google Scholar
da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72 (2), 021309.Google Scholar
Denissen, I. F. C., Weinhart, T., Voortwis, A. T., Luding, S., Gray, J. M. N. T. & Thornton, A. R. 2019 Bulbous head formation in bidispersed shallow granular flow over an inclined plane. J. Fluid Mech. 866, 263–297.Google Scholar
Evans, L. 2010 Partial Differential Equations. American Mathematical Society.Google Scholar
Fichman, M. & Hetsroni, G. 2005 Viscosity and slip velocity in gas flow in microchannels. Phys. Fluids 17 (12), 123102.Google Scholar
GDR MiDi 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged 𝜇(I)-rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503–534.Google Scholar
Gray, J. M. N. T., Wieland, M. & Hutter, K. 1999 Gravity-driven free surface flow of granular avalanches over complex basal topography. Proc. R. Soc. Lond. A 455 (1985), 1841–1874.Google Scholar
Hákonardóttir, K. M.2004 The interaction between snow avalanches and dams. PhD thesis, University of Bristol.Google Scholar
Henann, D. L. & Kamrin, K. 2013 A predictive, size-dependent continuum model for dense granular flows. Proc. Natl Acad. Sci. USA 110 (17), 6730–6735.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Hinze, J. O. 1975 Turbulence (McGraw-Hill Series in Mechanical Engineering). McGraw-Hill College.Google Scholar
Hogg, A. J. & Jóhannesson, T. 2016 Avalanche defence schemes. In UK Success Stories in Industrial Mathematics, pp. 53–58. Springer International Publishing.Google Scholar
Holyoake, A. J.2011 Rapid granular flows in an inclined chute. PhD thesis, University of Cambridge.Google Scholar
Holyoake, A. J. & McElwaine, J. N. 2012 High-speed granular chute flows. J. Fluid Mech. 710, 35–71.Google Scholar
Hui, K., Haff, P. K., Ungar, J. E. & Jackson, R. 1984 Boundary conditions for high-shear grain flows. J. Fluid Mech. 145, 223–233.Google Scholar
Jing, L., Kwok, C. Y., Leung, Y. F. & Sobral, Y. D. 2016 Characterization of base roughness for granular chute flows. Phys. Rev. E 94 (5), 052901.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Kamrin, K. & Henann, D. L. 2015 Nonlocal modeling of granular flows down inclines. Soft Matt. 11 (1), 179–185.Google Scholar
Longo, S. & Valiani, A. 2014 Analysis of a boundary layer of a granular mixture flowing past a plate at zero incidence. Eur. J. Mech. (B/Fluids) 46, 59–73.Google Scholar
Lueptow, R. M., Akonur, A. & Shinbrot, T. 2000 PIV for granular flows. Exp. Fluids 28 (2), 183–186.Google Scholar
Maxwell, J. C. 1879 On stresses in rarified gases arising from inequalities of temperature. Phil. Trans. R. Soc. Lond. A 170, 231–256.Google Scholar
Morris, D. L., Hannon, L. & Garcia, A. L. 1992 Slip length in a dilute gas. Phys. Rev. A 46, 5279–5281.Google Scholar
O’Sullivan, C. 2014 Particulate Discrete Element Modelling: A Geomechanics Perspective. CRC Press.Google Scholar
Peregrine, D. H. 1967 Long waves on a beach. J. Fluid Mech. 27, 815–827.Google Scholar
Petley, D. 2012 Global patterns of loss of life from landslides. Geology 40 (10), 927–930.Google Scholar
Pouliquen, O., Delour, J. & Savage, S. B. 1997 Fingering in granular flows. Nature 386 (6627), 816–817.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.Google Scholar
Prandtl, L. 1905 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Proceedings of the Third International Mathematic Congress, Heidelberg, 1904 (ed. Krazer, A.), pp. 484–491.Google Scholar
Rajchenbach, J. 2005 Rheology of dense granular materials: steady, uniform flow and the avalanche regime. J. Phys.: Condens. Matter 17 (24), S2731–S2742.Google Scholar
Ruschak, K. J. & Weinstein, S. J. 2003 Laminar, gravitationally driven flow of a thin film on a curved wall. Trans. ASME J. Fluids Engng 125 (1), 10–17.Google Scholar
Saingier, G., Deboeuf, S. & Lagrée, P.-Y. 2016 On the front shape of an inertial granular flow down a rough incline. Phys. Fluids 28 (5), 053302.Google Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.Google Scholar
Savage, S. B. & Hutter, K. 1991 The dynamics of avalanches of granular materials from initiation to runout. Part I. Analysis. Acta Mechanica 86 (1–4), 201–223.Google Scholar
Schlichting, H. & Gersten, K. 2017 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Thornton, A. R., Krijgsman, D., te Voortwis, A., Ogarko, V., Luding, S., Fransen, R., Gonzalez, S., Bokhove, O., Imole, O. & Weinhart, T. 2013 A review of recent work on the discrete particle method at the University of Twente: an introduction to the open-source package MercuryDPM. In DEM6 – International Conference on DEMs. Colorado School of Mines.Google Scholar
Thornton, A. R., Weinhart, T., Luding, S. & Bokhove, O. 2012 Modeling of particle size segregation: calibration using the discrete particle method. Intl J. Mod. Phys. C 23 (08), 1240014.Google Scholar
Tsang, J. M. F., Dalziel, S. B. & Vriend, N. M. 2018 Interaction between the Blasius boundary layer and a free surface. J. Fluid Mech. 839, R1.Google Scholar
Weinhart, T., Hartkamp, R., Thornton, A. R. & Luding, S. 2013 Coarse-grained local and objective continuum description of three-dimensional granular flows down an inclined surface. Phys. Fluids 25 (7), 070605.Google Scholar
Weinhart, T., Thornton, A. R., Luding, S. & Bokhove, O. 2012 From discrete particles to continuum fields near a boundary. Granul. Matt. 14 (2), 289–294.Google Scholar
Weinhart, T., Tunuguntla, D. R., Lantman, M. P., van Schrojenstein, D., Windows-Yule, I. F. C., Polman, C. R., Tsang, H., Jin, J. M. F., Orefice, B., van der Vaart, L. et al. 2017 MercuryDPM: fast, flexible particle simulations in complex geometries. Part B. Applications. In V International Conference on Particle-based Methods – Fundamentals and Applications, Particles 2017. International Center for Numerical Methods in Engineering.Google Scholar
Woodhouse, M. J., Phillips, J. C. & Hogg, A. J. 2016 Unsteady turbulent buoyant plumes. J. Fluid Mech. 794, 595–638.Google Scholar