Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-17T20:12:51.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion in hydrogel-supported phospholipid bilayer membranes

Published online by Cambridge University Press:  16 April 2013

Chih-Ying Wang  and
Reghan J. Hill
Chih-Ying Wang
Affiliation:
Department of Chemical Engineering, McGill University, Montreal, Quebec H3A 0C5, Canada
Reghan J. Hill*
Affiliation:
Department of Chemical Engineering, McGill University, Montreal, Quebec H3A 0C5, Canada
*
†Email address for correspondence: reghan.hill@mcgill.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We model a cylindrical inclusion (lipid or membrane protein) translating with velocity 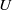$U$ in a thin planar membrane (phospholipid bilayer) that is supported above and below by Brinkman media (hydrogels). The total force 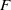$F$, membrane velocity, and solvent velocity are calculated as functions of three independent dimensionless parameters: 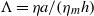$\Lambda = \eta a/ ({\eta }_{m} h)$, 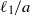${\ell }_{1} / a$ and 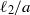${\ell }_{2} / a$. Here, 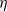$\eta $ and 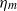${\eta }_{m} $ are the solvent and membrane shear viscosities, $a$ is the particle radius, 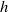$h$ is the membrane thickness, and 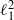${ \ell }_{1}^{2} $ and 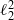${ \ell }_{2}^{2} $ are the upper and lower hydrogel permeabilities. As expected, the dimensionless mobility 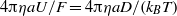$4\mathrm{\pi} \eta aU/ F= 4\mathrm{\pi} \eta aD/ ({k}_{B} T)$ (proportional to the self-diffusion coefficient, 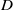$D$) decreases with decreasing gel permeabilities (increasing gel concentrations), furnishing a quantitative interpretation of how porous, gel-like supports hinder membrane dynamics. The model also provides a means of inferring hydrogel permeability and, perhaps, surface morphology from tracer diffusion measurements.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Membranes Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 352 - 373
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahearme, M., Yang, Y., Haj, A. J. E., Then, K. Y. & Liu, K.-K. 2005 Characterizing the viscoelastic properties of thin hydrogel-based constructs for tissue engineering applications. J. R. Soc. Interface 2 (5), 455–463.CrossRefGoogle Scholar
Al-Abdul-Wahid, M. S., Demill, C. M., Serwin, M. B., Prosser, R. S. & Stewart, B. A. 2012 Effect of juxtamembrane tryptophans on the immersion depth of synaptobrevin, an integral vesicle membrane protein. Biochim. Biophys. Acta 1818, 2994–2999.CrossRefGoogle ScholarPubMed
Alessandrini, A. & Facci, P. 2012 Nanoscale mechanical properties of lipid bilayers and their relevance in biomembrane organization and function. Micron 43, 1212–1223.CrossRefGoogle ScholarPubMed
An, Y. & Hubbell, J. A. 2000 Intraarterial protein delivery via intimally-adherent bilayer hydrogels. J. Control. Release 64, 205–215.CrossRefGoogle ScholarPubMed
Batchelor, R., Windle, C. J., Buchoux, S. & Lorch, M. 2010 Cholesterol and lipid phases influence the interactions between serotonin receptor agonists and lipid bilayers. J. Biol. Chem. 285, 41402–41411.Google Scholar
Bayley, H. & Cremer, P. S. 2001 Stochastic sensors inspired by biology. Nature 413, 226–230.Google Scholar
Brameshuber, M., Weghuber, J., Ruprecht, V., Gombos, I., Horvath, I., Vigh, L., Eckerstorfer, P., Kiss, E., Stockinger, H. & Schutz, G. J. 2010 Imaging of mobile long-lived nanoplatforms in the live cell plasma membrane. J. Biol. Chem. 285, 41765–41771.CrossRefGoogle ScholarPubMed
Brinkman, H. C. 1947 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1, 27–34.CrossRefGoogle Scholar
Bussell, S. J., Koch, D. L. & Hammer, D. A. 1994 The effect of hydrodynamic interactions on the tracer and gradient diffusion of integral membrane proteins in lipid bilayers. J. Fluid Mech. 258, 167–190.Google Scholar
Calvert, D., Wong, J. Y. & Giasson, S. 2004 Rheological monitoring of polyacrylamide gelation: importance of cross-link density and temperature. Macromolecules 37, 7762–7771.CrossRefGoogle Scholar
Castellana, E. T. & Cremer, P. S. 2006 Solid supported lipid bilayers: from biophysical studies to sensor design. Surf. Sci. Rep. 61, 429–444.Google Scholar
Evans, E. & Sackmann, E. 1988 Translational and rotational drag coefficients for a disk moving in a liquid membrane associated with a rigid substrate. J. Fluid Mech. 194, 553–561.CrossRefGoogle Scholar
Farias, G. G., Cuitino, L., Guo, X., Ren, X., Jarnik, M., Mattera, R. & Bonifacino, J. S. 2012 Signal-mediated, ap-1/clathrin-dependent sorting of transmembrane receptors to the somatodendritic domain of hippocampal neurons. Neuron 75, 810–823.Google Scholar
Fuchs, P., Parola, A., Robbins, P. W. & Blout, E. R. 1975 Fluorescence polarization and viscosity of membrane lipids 3t3 cells. Proc. Natl Acad. Sci. USA 72, 3351–3354.CrossRefGoogle Scholar
Grandshteyn, I. S. & Ryzhik, I. M. 1965 Tables of Integrals, Series and Products. Academic.Google Scholar
Grattoni, C. A., Al-Sharji, H. H., Yang, C., Muggeridge, A. H. & Zimmerman, R. W. 2001 Rheology and permeability of corsslinked polyacrylamide gel. J. Colloid Interface Sci. 240, 601–607.Google Scholar
Haque, M. A., Kamita, G., Kurokawa, T., Tsujii, K. & Gong, J. P. 2010 Unidirectional alignment of lamellar bilayer in hydrogel: one-dimensional swelling, anisotropic modulus, and stress/strain tunable structural color. Adv. Mater. 22, 5110–5114.Google Scholar
von Heijne, G. 2007 Membrane-protein topology. Nature Rev. Mol. Cell Biol. 7, 910–918.Google Scholar
Hildebrand, F. B. 1956 Advanced Calculus for Engineers. Prentice Hall.Google Scholar
Hoare, T. R. & Kohane, D. S. 2008 Hydrogels in drug delivery: progress and challenges. Polymer 49, 1993–2007.CrossRefGoogle Scholar
Hughes, B. D., Pailthorpe, B. A. & White, L. R. 1981 The translational and rotational drag on a cylinder moving in a membrane. J. Fluid Mech. 110, 349–372.CrossRefGoogle Scholar
Johnson, E. M. & Deen, W. M. 1996 Hydraulic permeability of agarose gels. AIChE J. 42, 1220–1224.CrossRefGoogle Scholar
Jülichera, R., Krusea, K., Prost, J. & Joanny, J.-F. 2007 Active behavior of the cytoskeleton. Phys. Rep. 449, 3–28.Google Scholar
Kiser, P. F., Wilson, G & Needham, D. 1998 A synthetic mimic of the secretory granule for drug delivery. Nature 394, 459–462.CrossRefGoogle ScholarPubMed
Lomize, M. A., Lomize, A. L., Pogozheva, I. D. & Mosberg, H. I. 2006 OPM: orientations of proteins in membranes database. Bioinformatics 22 (5), 623–625.Google Scholar
Lucas, S. K. 1995 Evaluating infinite integrals involving products of Bessel functions of arbitrary order. J. Comput. Appl. Maths 64, 269–282.Google Scholar
Magnus, W., Oberhettinger, F. & Soni, R. P. 1966 Formulas and Theorems for the Special Functions of Mathematical Physics. Springer.Google Scholar
Meyer, H. W., Westermann, M., Stumpf, M., Richter, W., Ulrich, A. S. & Hoischen, C. 1998 Minimal radius of curvature of lipid bilayers in the gel phase state corresponds to the dimension of biomembrane structures‘caveolae’. J. Struct. Biol. 124, 77–87.Google Scholar
Nicodemus, G. D. & Bryant, S. J. 2008 Cell encapsulation in biodegradable hydrogels for tissue engineering applications. Tissue Engng B - Rev. 14, 149–165.Google Scholar
Noble, G. T., Flitsch, S. L., Liem, K. P. & Webb, S. J. 2009 Assessing the cluster glycoside effect during the binding of concanavalin a to mannosylated artificial lipid rafts. Org. Biomol. Chem. 7, 5245–5254.CrossRefGoogle ScholarPubMed
Okano, T. 1993 Molecular design of temperature-responsive polymers as intelligent materials. Adv. Polym. Sci. 110, 179–197.CrossRefGoogle Scholar
Orsini, F., Cremona, A., Arosio, P., Corsetto, P. A., Montorfano, G., Lascialfari, A. & Rizzo, A. M. 2012 Atomic force microscopy imaging of lipid rafts of human breast cancer cells. Biochim. Biophys. Acta 1818, 2943–2949.Google Scholar
Pike, L. J. 2008 The challenge of lipid rafts. J. Lipid Res. 50, 323–328.CrossRefGoogle ScholarPubMed
Ruel-Gariépy, E., Leclair, G., Hildgen, P., Gupta, A. & Leroux, J.-C. 2002 T hermosensitive chitosan-based hydrogel containing liposomes for the delivery of hydrophilic molecules. J. Control. Release 82, 373–383.Google Scholar
Sackmann, E. 1996 Supported membranes: scientific and practical applications. Science 271, 43–48.Google Scholar
Sackmann, E. & Tanaka, M. 2000 Supported membranes on soft polymer cushions: fabrication, characterization and applications. Trends Biotechnol. 18, 58–64.CrossRefGoogle ScholarPubMed
Saffman, P. G. 1976 Brownian motion in thin sheets of viscous fluid. J. Fluid Mech. 73, 593–602.Google Scholar
Saffman, P. G. & Delbruck, M. 1975 Brownian motion in biological membranes. Proc. Natl Acad. Sci. USA 72, 3111–3113.CrossRefGoogle ScholarPubMed
Sneddon, I. N. 1966 Mixed Boundary Value Problems in Potential Theory. John Wiley & Sons.Google Scholar
Steinhoff, G., Purrucker, O., Tanaka, M., Stutzmann, M. & Eickhoff, M. 2003 ${\mathrm{Al} }_{x} {\mathrm{Ga} }_{1- x} \mathrm{N} $ -A new material system for biosensors. Adv. Funct. Mater. 13 (11), 841–846.Google Scholar
Stone, H. A. & Ajdari, A. 1998 Hydrodynamics of particles embedded in a flat surfactant layer overlying a subphase of finite depth. J. Fluid Mech. 369, 151–173.Google Scholar
Sunamoto, J., Sato, T., Hirota, M., Fukushima, K., Hiratani, K. & Hara, K. 1987 A newly developed immunoliposome – an egg phosphatidylcholine liposome coated with pullulan bearing both a cholesterol moiety and an IgMs fragment. Biochim. Biophys. Acta 898, 323–330.Google Scholar
Tanzosh, J. P. & Stone, H. A. 1995 Transverse motion of a disk through a rotating viscous fluid. J. Fluid Mech. 301, 295–324.CrossRefGoogle Scholar
Tokita, M. & Tanaka, T. 1991 Friction coefficient of polymer networks of gels. J. Chem. Phys. 95 (6), 4613–4619.Google Scholar
Tranter, C. J. 1966 Integral Transforms in Mathematical Physics. John Wiley & Sons.Google Scholar
Yeung, T., Georges, P. C., Flanagan, L. A., Marg, B., Ortiz, M., Funaki, M., Nastaran, Z., Ming, W., Weaver, V. & Janmey, P. A. 2005 Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskel. 60, 24–34.CrossRefGoogle ScholarPubMed
Zaitsev, S. Y., Solovyeva, D. O. & Nabiev, I. 2012 Thin films and assemblies of photosensitive membrane proteins and colloidal nanocrystals for engineering of hybrid materials with advanced properties. Adv. Colloid Interface Sci. 183–184, 14–29.Google Scholar
Zhao, J. & Granick, S. 2007 How polymer surface diffusion depends on surface coverage. Macromolecules 40, 1243–1247.CrossRefGoogle Scholar