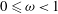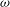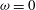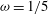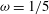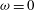1 Introduction
Questions concerning the development of flows above isolated sources of buoyancy may be approached either with the aim of computing full velocity and density fields, thereby requiring solution of the Navier–Stokes equations, or with the aim of computing a limited number of parameters only and as functions of height. The latter approach is exemplified in the seminal work of Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956) (hereafter MTT). They concentrate on time-averaged fluxes through horizontal planes. They work in the Boussinesq case (small density variations), and use buoyancy flux
![]() $B(z)$
, volume flux
$B(z)$
, volume flux
![]() $Q(z)$
and momentum flux
$Q(z)$
and momentum flux
![]() $M(z)$
, where
$M(z)$
, where
![]() $z$
denotes the height above the physical source at
$z$
denotes the height above the physical source at
![]() $z=0$
. In order to generalise to large density variations, Carlotti & Hunt (Reference Carlotti and Hunt2005) showed that it is more straightforward to use mass flux
$z=0$
. In order to generalise to large density variations, Carlotti & Hunt (Reference Carlotti and Hunt2005) showed that it is more straightforward to use mass flux
![]() $G(z)$
than volume flux, leading to the following definition of the fluxes (with
$G(z)$
than volume flux, leading to the following definition of the fluxes (with
![]() $\unicode[STIX]{x1D70C}_{a}$
denoting the ambient density, which is assumed to be uniform in the present paper):
$\unicode[STIX]{x1D70C}_{a}$
denoting the ambient density, which is assumed to be uniform in the present paper):
where
![]() $W$
denotes the vertical velocity of the plume,
$W$
denotes the vertical velocity of the plume,
![]() $\unicode[STIX]{x1D70C}$
the local density,
$\unicode[STIX]{x1D70C}$
the local density,
![]() $\unicode[STIX]{x1D70C}_{a}$
the ambient density,
$\unicode[STIX]{x1D70C}_{a}$
the ambient density,
![]() $g$
the acceleration due to gravity, and integration is over horizontal planes
$g$
the acceleration due to gravity, and integration is over horizontal planes
![]() $S$
.
$S$
.
Regarding notation, we adopt the following throughout: subscript
![]() $a$
refers to the ambient, subscript 0 to the reference cases of uniform entrainment or of a pure plume (which reduces to uniform entrainment with our model), subscript
$a$
refers to the ambient, subscript 0 to the reference cases of uniform entrainment or of a pure plume (which reduces to uniform entrainment with our model), subscript
![]() $T$
denotes ‘top-hat’ profile, subscript
$T$
denotes ‘top-hat’ profile, subscript
![]() $s$
denotes the quantities at the source in the theory, i.e. the lowest possible height of existence of the plume considered, and subscript
$s$
denotes the quantities at the source in the theory, i.e. the lowest possible height of existence of the plume considered, and subscript
![]() $n$
refers to quantities at the exit plane of the plume nozzle in experiments.
$n$
refers to quantities at the exit plane of the plume nozzle in experiments.
From these fluxes, MTT define the so-called top-hat radius
![]() $b_{T}$
, vertical velocity
$b_{T}$
, vertical velocity
![]() $W_{T}$
and density
$W_{T}$
and density
![]() $\unicode[STIX]{x1D70C}_{T}$
from
$\unicode[STIX]{x1D70C}_{T}$
from
Mass, momentum and enthalpy conservation then leads to the following ordinary differential equations for an unstratified ambient fluid (MTT actually used a slightly different formulation, but with the same assumptions):
The first equation carries the main insight of the MTT paper: the plume is conjectured to entrain ambient fluid with an entrainment speed
![]() $u_{e}(z)$
at the plume perimeter. MTT further assume that the entrainment velocity is proportional to the vertical velocity,
$u_{e}(z)$
at the plume perimeter. MTT further assume that the entrainment velocity is proportional to the vertical velocity,
![]() $u_{e}(z)=\unicode[STIX]{x1D6FC}W_{T}(z)$
, with
$u_{e}(z)=\unicode[STIX]{x1D6FC}W_{T}(z)$
, with
![]() $\unicode[STIX]{x1D6FC}$
the entrainment coefficient (these ideas were already germinating in Taylor’s work during World War II, see Taylor (Reference Taylor1958), and independently, pre-war, by Zeldovich (Reference Zeldovich1937)). The latter assumption leads to a full set of closed equations for which self-similar solutions may be found (for the so-called pure plume), together with more complicated solutions for forced plumes (Morton Reference Morton1959) or lazy plumes (Hunt & Kaye Reference Hunt and Kaye2001) depending on the value of the plume Richardson number
$\unicode[STIX]{x1D6FC}$
the entrainment coefficient (these ideas were already germinating in Taylor’s work during World War II, see Taylor (Reference Taylor1958), and independently, pre-war, by Zeldovich (Reference Zeldovich1937)). The latter assumption leads to a full set of closed equations for which self-similar solutions may be found (for the so-called pure plume), together with more complicated solutions for forced plumes (Morton Reference Morton1959) or lazy plumes (Hunt & Kaye Reference Hunt and Kaye2001) depending on the value of the plume Richardson number
![]() $\unicode[STIX]{x1D6E4}$
:
$\unicode[STIX]{x1D6E4}$
:
The MTT theory is applicable to Boussinesq plumes in which the density contrast is small (i.e.
![]() $|\unicode[STIX]{x1D70C}_{a}-\unicode[STIX]{x1D70C}_{T}|\ll \unicode[STIX]{x1D70C}_{a}$
). This theory was generalised to non-Boussinesq plumes by Rooney & Linden (Reference Rooney and Linden1996) by introducing a factor
$|\unicode[STIX]{x1D70C}_{a}-\unicode[STIX]{x1D70C}_{T}|\ll \unicode[STIX]{x1D70C}_{a}$
). This theory was generalised to non-Boussinesq plumes by Rooney & Linden (Reference Rooney and Linden1996) by introducing a factor
![]() $\sqrt{\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}}$
, assuming a closure of the form
$\sqrt{\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}}$
, assuming a closure of the form
The subscript
![]() $0$
on
$0$
on
![]() $\unicode[STIX]{x1D6FC}$
is introduced here to indicate that its value is assumed to be independent of other plume quantities, being kept equal to its pure-plume value.
$\unicode[STIX]{x1D6FC}$
is introduced here to indicate that its value is assumed to be independent of other plume quantities, being kept equal to its pure-plume value.
With the present notation, the pure-plume self-similar solution of Rooney & Linden (Reference Rooney and Linden1996) leads to a constant value of the Richardson number
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
, with
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
, with
Carlotti & Hunt (Reference Carlotti and Hunt2005) derived a general (lazy and forced) solution based on the assumptions of Rooney & Linden (Reference Rooney and Linden1996). This general solution was further explored and discussed by Hunt & van den Bremer (Reference Hunt and van den Bremer2010) and Candelier & Vauquelin (Reference Candelier and Vauquelin2012), who expressed it in a simpler way. However, these solutions still contain two weaknesses with regards to their applicability in the prediction of very hot gas plumes rising in a cooler environment: they assume constant specific heat of the gas and a constant entrainment coefficient. Our primary focus herein is to address the latter weakness.
The paper is organised as follows. Section 2 discusses formulations of entrainment dependent on the local plume Richardson number and proposes a power-law formulation. This is applied to lazy plumes in § 3, and § 4 considers the specific case of a lazy plume issuing from a nozzle, allowing comparison of the theory presented in §§ 2 and 3 with the experimental results of Kaye & Hunt (Reference Kaye and Hunt2009). In § 5, we present our conclusions. To address the second weakness, appendix A focuses on an alternative definition of buoyancy flux for hot gaseous plumes with variable specific heat which allows one to apply the theory presented in the present paper to this context, namely where the traditional buoyancy flux is not constant.
2 Variable-entrainment plume models
2.1 Basic set of equations and variable entrainment
In the following, we work only with the flux variables
![]() $(B,M,G)$
and use algebra to recast the plume conservation equations in this context, leading to
$(B,M,G)$
and use algebra to recast the plume conservation equations in this context, leading to
We assume that entrainment depends on local plume quantities
![]() $(B,M,G,\unicode[STIX]{x1D70C}_{T},\unicode[STIX]{x1D70C}_{a})$
only. From dimensional analysis we find that
$(B,M,G,\unicode[STIX]{x1D70C}_{T},\unicode[STIX]{x1D70C}_{a})$
only. From dimensional analysis we find that
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a})$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a})$
.
Use of (2.3) allows us to compute
![]() $\unicode[STIX]{x1D6FC}$
solely from the knowledge of fluxes:
$\unicode[STIX]{x1D6FC}$
solely from the knowledge of fluxes:
Using this equation, Pham, Plourde & Kim (Reference Pham, Plourde and Kim2005) measured entrainment as a function of height in a nearly Boussinesq plume (their figure 16) and showed that, close to the source, where their plume is very lazy, entrainment is much increased. This measurement is also confirmed by the relatively low-resolution large-eddy simulation (LES) of Lamalle et al. (Reference Lamalle, Carlotti, Salizzoni, Perkins and Iordanoff2013). For lazy-plume sources, where the near-field behaviour is of primary interest, the classic MTT approach to plume modelling has been applied previously with some success (e.g. Hunt & Kaye Reference Hunt and Kaye2001, Fannelop & Webber Reference Fannelop and Webber2003, Candelier & Vauquelin Reference Candelier and Vauquelin2012) despite the underlying modelling assumptions, e.g. the morphology being long and thin in the near field and the pressure being hydrostatic, not strictly applying. Wang & Law (Reference Wang and Law2002) review the literature covering models for turbulent entrainment (mainly Priestley & Ball Reference Priestley and Ball1955 and List Reference List and Rodi1982), and suggest the following two formulations primarily designed for forced and pure plumes:
Here,
![]() $\unicode[STIX]{x1D6FC}_{0}$
is the entrainment constant in a pure plume and
$\unicode[STIX]{x1D6FC}_{0}$
is the entrainment constant in a pure plume and
![]() $\unicode[STIX]{x1D6FC}_{jet}$
is the entrainment constant in a jet. Besides reducing to the entrainment coefficients for a pure jet and a pure plume in the limits as
$\unicode[STIX]{x1D6FC}_{jet}$
is the entrainment constant in a jet. Besides reducing to the entrainment coefficients for a pure jet and a pure plume in the limits as
![]() $\unicode[STIX]{x1D6E4}\rightarrow 0$
and as
$\unicode[STIX]{x1D6E4}\rightarrow 0$
and as
![]() $\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{0}$
, the physical justification for the variation with local Richardson number for forced plumes was somewhat limited for both models when first posed. That said, experimental measurements on thermal plumes (e.g. by Ezzamel, Salizzoni & Hunt Reference Ezzamel, Salizzoni and Hunt2015) and predictions of direct numerical simulations (e.g. by van Reeuwijk et al.
Reference van Reeuwijk, Salizzoni, Hunt and Craske2016) support the use of these models within classic plume theory. Note that these formulations lead to unrealistic values of the entrainment coefficient for very lazy plumes
$\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{0}$
, the physical justification for the variation with local Richardson number for forced plumes was somewhat limited for both models when first posed. That said, experimental measurements on thermal plumes (e.g. by Ezzamel, Salizzoni & Hunt Reference Ezzamel, Salizzoni and Hunt2015) and predictions of direct numerical simulations (e.g. by van Reeuwijk et al.
Reference van Reeuwijk, Salizzoni, Hunt and Craske2016) support the use of these models within classic plume theory. Note that these formulations lead to unrealistic values of the entrainment coefficient for very lazy plumes
![]() $\unicode[STIX]{x1D6E4}\gg 1$
; see Kaye & Hunt (Reference Kaye and Hunt2009) who use values of
$\unicode[STIX]{x1D6E4}\gg 1$
; see Kaye & Hunt (Reference Kaye and Hunt2009) who use values of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
of order up to
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
of order up to
![]() $10^{7}$
.
$10^{7}$
.
Wang & Law (Reference Wang and Law2002) use Gaussian profiles and follow List (Reference List and Rodi1982) for the values of
![]() $\unicode[STIX]{x1D6FC}_{jet}$
and
$\unicode[STIX]{x1D6FC}_{jet}$
and
![]() $\unicode[STIX]{x1D6FC}_{0}$
, taking
$\unicode[STIX]{x1D6FC}_{0}$
, taking
![]() $\unicode[STIX]{x1D6FC}_{jet}=0.0535$
and
$\unicode[STIX]{x1D6FC}_{jet}=0.0535$
and
![]() $\unicode[STIX]{x1D6FC}_{0}=0.0833$
. With top-hat profiles, as in the present paper, the corresponding values are
$\unicode[STIX]{x1D6FC}_{0}=0.0833$
. With top-hat profiles, as in the present paper, the corresponding values are
![]() $\unicode[STIX]{x1D6FC}_{jet}=0.0757$
and
$\unicode[STIX]{x1D6FC}_{jet}=0.0757$
and
![]() $\unicode[STIX]{x1D6FC}_{0}=0.118$
.
$\unicode[STIX]{x1D6FC}_{0}=0.118$
.
In the present work, we focus on pure and lazy plumes and consider the power-law formulation (with
![]() $0\leqslant \unicode[STIX]{x1D714}<1$
, as we will see later),
$0\leqslant \unicode[STIX]{x1D714}<1$
, as we will see later),
The reasons for this proposed form of entrainment function are essentially threefold. First, consistent at least qualitatively with measurement (e.g. Pham et al.
Reference Pham, Plourde and Kim2005, Ezzamel et al.
Reference Ezzamel, Salizzoni and Hunt2015), this form results in enhanced entrainment in lazy plumes compared with pure plumes, while being robust for very large values of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
. Second, the natural scalings that arise from the application of plume theory with an entrainment model as per (2.7) enable the near-field measurements of mass flow rate made in lazy plumes to be collapsed when scaled (see § 4), and the predictions show good agreement with the available data. A survey of the open literature reveals that there are limited experimental data available on the near-field behaviour of highly lazy plumes, with measurements pertaining to entrainment restricted to those on saline Boussinesq plumes in freshwater environments made by Kaye & Hunt (Reference Kaye and Hunt2009). Surprisingly, there appears to be a complete absence of experimental data on the near-field entrainment behaviour of highly lazy non-Boussinesq plumes with the exception of Pham et al., for which the values of buoyancy and flow rates are not documented. We should also stress that this formulation is consistent with energy constraints and entrainment formulations proposed by van Reeuwijk & Craske (Reference van Reeuwijk and Craske2015). Finally, with a suitable choice of
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
. Second, the natural scalings that arise from the application of plume theory with an entrainment model as per (2.7) enable the near-field measurements of mass flow rate made in lazy plumes to be collapsed when scaled (see § 4), and the predictions show good agreement with the available data. A survey of the open literature reveals that there are limited experimental data available on the near-field behaviour of highly lazy plumes, with measurements pertaining to entrainment restricted to those on saline Boussinesq plumes in freshwater environments made by Kaye & Hunt (Reference Kaye and Hunt2009). Surprisingly, there appears to be a complete absence of experimental data on the near-field entrainment behaviour of highly lazy non-Boussinesq plumes with the exception of Pham et al., for which the values of buoyancy and flow rates are not documented. We should also stress that this formulation is consistent with energy constraints and entrainment formulations proposed by van Reeuwijk & Craske (Reference van Reeuwijk and Craske2015). Finally, with a suitable choice of
![]() $\unicode[STIX]{x1D714}$
, our formulation for the entrainment coefficient and that of Priestley & Ball (Reference Priestley and Ball1955) (2.5) are very close for
$\unicode[STIX]{x1D714}$
, our formulation for the entrainment coefficient and that of Priestley & Ball (Reference Priestley and Ball1955) (2.5) are very close for
![]() $\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. In other words, (2.7) not only reduces to the widely accepted pure-plume behaviour as
$\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. In other words, (2.7) not only reduces to the widely accepted pure-plume behaviour as
![]() $\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{0}$
, but also is very close for weakly lazy plumes,
$\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{0}$
, but also is very close for weakly lazy plumes,
![]() $\unicode[STIX]{x1D6E4}\gtrsim \unicode[STIX]{x1D6E4}_{0}$
, as now shown. The three expressions for variable entrainment, (2.5)–(2.7), have the following gradients at
$\unicode[STIX]{x1D6E4}\gtrsim \unicode[STIX]{x1D6E4}_{0}$
, as now shown. The three expressions for variable entrainment, (2.5)–(2.7), have the following gradients at
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
:
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
:
Therefore, if we let
![]() $\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D6FC}_{0}-\unicode[STIX]{x1D6FC}_{jet})/\unicode[STIX]{x1D6FC}_{0}$
, the Priestley & Ball (Reference Priestley and Ball1955) formulation (2.5) and our proposed power-law formulation (2.7) are very close for
$\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D6FC}_{0}-\unicode[STIX]{x1D6FC}_{jet})/\unicode[STIX]{x1D6FC}_{0}$
, the Priestley & Ball (Reference Priestley and Ball1955) formulation (2.5) and our proposed power-law formulation (2.7) are very close for
![]() $\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. Further, if we have
$\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. Further, if we have
![]() $(\unicode[STIX]{x1D6FC}_{0}-\unicode[STIX]{x1D6FC}_{jet})/\unicode[STIX]{x1D6FC}_{0}\ll 1$
, all three formulations are very close for
$(\unicode[STIX]{x1D6FC}_{0}-\unicode[STIX]{x1D6FC}_{jet})/\unicode[STIX]{x1D6FC}_{0}\ll 1$
, all three formulations are very close for
![]() $\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. It should be noted that if we take, following Wang & Law (Reference Wang and Law2002),
$\unicode[STIX]{x1D6E4}\approx \unicode[STIX]{x1D6E4}_{0}$
. It should be noted that if we take, following Wang & Law (Reference Wang and Law2002),
![]() $\unicode[STIX]{x1D6FC}_{jet}=0.0757$
and
$\unicode[STIX]{x1D6FC}_{jet}=0.0757$
and
![]() $\unicode[STIX]{x1D6FC}_{0}=0.118$
, this leads us to assume
$\unicode[STIX]{x1D6FC}_{0}=0.118$
, this leads us to assume
![]() $\unicode[STIX]{x1D714}\approx 0.36$
.
$\unicode[STIX]{x1D714}\approx 0.36$
.
For lazy plumes,
![]() $\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6E4}_{0}$
, our formulation for
$\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6E4}_{0}$
, our formulation for
![]() $\unicode[STIX]{x1D6FC}$
, (2.7), consistent with measurements, yields entrainment coefficients that exceed the pure-plume value
$\unicode[STIX]{x1D6FC}$
, (2.7), consistent with measurements, yields entrainment coefficients that exceed the pure-plume value
![]() $\unicode[STIX]{x1D6FC}_{0}$
. For pure plumes,
$\unicode[STIX]{x1D6FC}_{0}$
. For pure plumes,
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
, (2.7) reduces to
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
, (2.7) reduces to
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{0}$
, as do the Priestley & Ball (Reference Priestley and Ball1955) and List (Reference List and Rodi1982) formulations. However, for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{0}$
, as do the Priestley & Ball (Reference Priestley and Ball1955) and List (Reference List and Rodi1982) formulations. However, for
![]() $\unicode[STIX]{x1D6E4}\ll \unicode[STIX]{x1D6E4}_{0}$
, (2.7) does not recover
$\unicode[STIX]{x1D6E4}\ll \unicode[STIX]{x1D6E4}_{0}$
, (2.7) does not recover
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{jet}$
and, as such, we will not consider our model further for these highly forced plumes.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{jet}$
and, as such, we will not consider our model further for these highly forced plumes.
2.2 Plume invariant
Combining (2.3) and (2.2), with entrainment given by (2.7), one finds
Some algebra leads to
The above equation may be integrated, and we find that, for
![]() $0\leqslant \unicode[STIX]{x1D714}<1$
, the quantity
$0\leqslant \unicode[STIX]{x1D714}<1$
, the quantity
is independent of height
![]() $z$
in the plume and, thereby, provides us with a plume invariant (the factor of
$z$
in the plume and, thereby, provides us with a plume invariant (the factor of
![]() $1/2$
is included for simplicity in the next section). The constant
$1/2$
is included for simplicity in the next section). The constant
![]() $J$
may be computed from its value at the source (recalling that the subscript
$J$
may be computed from its value at the source (recalling that the subscript
![]() $(\cdot )_{s}$
refers to the source and
$(\cdot )_{s}$
refers to the source and
![]() $(\cdot )_{0}$
to the pure-plume reference case),
$(\cdot )_{0}$
to the pure-plume reference case),
This is a generalisation of the concept first presented in Carlotti & Hunt (Reference Carlotti and Hunt2005) (therein constant entrainment was assumed, i.e.
![]() $\unicode[STIX]{x1D714}=0$
), where, for the present notation, the invariant
$\unicode[STIX]{x1D714}=0$
), where, for the present notation, the invariant
![]() $J_{\unicode[STIX]{x1D714}=0}=[G^{2}-(\unicode[STIX]{x1D6E4}_{0}/(\sqrt{\unicode[STIX]{x1D70C}_{a}}B))M^{5/2}]/2$
was used as an intermediate step to solve the general (pure, lazy and forced) constant-entrainment plume equations.
$J_{\unicode[STIX]{x1D714}=0}=[G^{2}-(\unicode[STIX]{x1D6E4}_{0}/(\sqrt{\unicode[STIX]{x1D70C}_{a}}B))M^{5/2}]/2$
was used as an intermediate step to solve the general (pure, lazy and forced) constant-entrainment plume equations.
2.3 Case
 $\unicode[STIX]{x1D714}=1$
$\unicode[STIX]{x1D714}=1$
The above formulation of entrainment does not hold when
![]() $\unicode[STIX]{x1D714}=1$
since (2.10) becomes
$\unicode[STIX]{x1D714}=1$
since (2.10) becomes
which may not be integrated with power laws but instead with logarithms, leading to
As a consequence, in such a plume, we would have
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{s}$
independent of height; this is contradictory to all experimental evidence which shows that
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{s}$
independent of height; this is contradictory to all experimental evidence which shows that
![]() $\unicode[STIX]{x1D6E4}(z)$
converges towards the pure-plume value with height (e.g. Ezzamel et al.
Reference Ezzamel, Salizzoni and Hunt2015), regardless of the source value
$\unicode[STIX]{x1D6E4}(z)$
converges towards the pure-plume value with height (e.g. Ezzamel et al.
Reference Ezzamel, Salizzoni and Hunt2015), regardless of the source value
![]() $\unicode[STIX]{x1D6E4}_{s}$
. For this reason, we will not consider any further the case
$\unicode[STIX]{x1D6E4}_{s}$
. For this reason, we will not consider any further the case
![]() $\unicode[STIX]{x1D714}=1$
.
$\unicode[STIX]{x1D714}=1$
.
2.4 Pure plume
 $J=0$
$J=0$
When
![]() $J=0$
, (2.11) leads directly to
$J=0$
, (2.11) leads directly to
![]() $G^{2}=[\unicode[STIX]{x1D6E4}_{0}/(\sqrt{\unicode[STIX]{x1D70C}_{a}}B)]M^{5/2}$
for any value of
$G^{2}=[\unicode[STIX]{x1D6E4}_{0}/(\sqrt{\unicode[STIX]{x1D70C}_{a}}B)]M^{5/2}$
for any value of
![]() $\unicode[STIX]{x1D714}\in [0,1)$
. Therefore,
$\unicode[STIX]{x1D714}\in [0,1)$
. Therefore,
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
at all heights, showing that this case corresponds to a pure plume. Adopting the expression for
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}$
at all heights, showing that this case corresponds to a pure plume. Adopting the expression for
![]() $G^{2}$
in (2.2), we get
$G^{2}$
in (2.2), we get
leading to the classic non-Boussinesq point-source solution (Rooney & Linden Reference Rooney and Linden1996; Carlotti & Hunt Reference Carlotti and Hunt2005) on taking
![]() $M_{s}=0$
and
$M_{s}=0$
and
![]() $G_{s}=0$
at the source,
$G_{s}=0$
at the source,
3 Lazy plumes,
 $J>0$
$J>0$
3.1 General plume equations
Together with
![]() $J$
, we introduce
$J$
, we introduce
As a consequence of this definition,
Differentiating (3.2) and using (2.3), some algebra shows that
Equation (3.4), together with the fact that
![]() $J$
is independent of height, gives the complete set of equations for the plume in the
$J$
is independent of height, gives the complete set of equations for the plume in the
![]() $J>0$
case. Evidently, the solution for the plume will depend on the value of
$J>0$
case. Evidently, the solution for the plume will depend on the value of
![]() $J$
. Note that this set of equations is also valid when
$J$
. Note that this set of equations is also valid when
![]() $J=0$
, even though we did not need to use it because there was a simpler method.
$J=0$
, even though we did not need to use it because there was a simpler method.
3.2 Non-dimensional form of the
 $I$
-equation and acceleration length
$I$
-equation and acceleration length
Since
![]() $J\neq 0$
for a lazy plume, we may define
$J\neq 0$
for a lazy plume, we may define
![]() ${\mathcal{I}}=I/J$
. Note that
${\mathcal{I}}=I/J$
. Note that
![]() ${\mathcal{I}}\geqslant 1$
for any value of height. The case
${\mathcal{I}}\geqslant 1$
for any value of height. The case
![]() ${\mathcal{I}}=1$
corresponds to
${\mathcal{I}}=1$
corresponds to
![]() $I=J$
; this is
$I=J$
; this is
![]() $M=0$
. Since
$M=0$
. Since
![]() $M$
increases with height, this corresponds to the lowest possible height of existence of the lazy plume. In the present section, we will therefore consider this height as the origin of heights and as the source of the plume. Since
$M$
increases with height, this corresponds to the lowest possible height of existence of the lazy plume. In the present section, we will therefore consider this height as the origin of heights and as the source of the plume. Since
![]() $M_{s}=0$
at this height, we also have, with
$M_{s}=0$
at this height, we also have, with
![]() $G_{s}$
the value of
$G_{s}$
the value of
![]() $G$
at the source,
$G$
at the source,
Non-dimensionalising, (3.4) reduces to
with
![]() ${\mathcal{Z}}=z/L$
, and
${\mathcal{Z}}=z/L$
, and
The quantity
![]() $L$
is a modified formulation of the plume acceleration length scale (e.g. Fischer et al.
Reference Fischer, List, Koy, Imberger and Brooks1979; Caulfield Reference Caulfield1991; Kaye Reference Kaye2008), and represents the characteristic vertical scale over which the very lazy plume accelerates to approach its large-height asymptotic pure-plume state.
$L$
is a modified formulation of the plume acceleration length scale (e.g. Fischer et al.
Reference Fischer, List, Koy, Imberger and Brooks1979; Caulfield Reference Caulfield1991; Kaye Reference Kaye2008), and represents the characteristic vertical scale over which the very lazy plume accelerates to approach its large-height asymptotic pure-plume state.
Writing
![]() $L_{0}$
as the acceleration length scale for a constant-entrainment plume,
$L_{0}$
as the acceleration length scale for a constant-entrainment plume,
![]() $\unicode[STIX]{x1D714}=0$
, we have
$\unicode[STIX]{x1D714}=0$
, we have
This ratio increases from
![]() $L/L_{0}=1$
to 2.2 as
$L/L_{0}=1$
to 2.2 as
![]() $\unicode[STIX]{x1D714}$
increases from
$\unicode[STIX]{x1D714}$
increases from
![]() $\unicode[STIX]{x1D714}=0$
to 0.8, and then decreases rapidly to reach the value
$\unicode[STIX]{x1D714}=0$
to 0.8, and then decreases rapidly to reach the value
![]() $L/L_{0}=0$
as
$L/L_{0}=0$
as
![]() $\unicode[STIX]{x1D714}\rightarrow 1$
. This change of behaviour is to be analysed bearing in mind that
$\unicode[STIX]{x1D714}\rightarrow 1$
. This change of behaviour is to be analysed bearing in mind that
![]() $\unicode[STIX]{x1D714}=1$
is physical, as explained before, and values near
$\unicode[STIX]{x1D714}=1$
is physical, as explained before, and values near
![]() $\unicode[STIX]{x1D714}=1$
are unlikely to be realistic.
$\unicode[STIX]{x1D714}=1$
are unlikely to be realistic.
3.3 Integration of the
 $I$
-equation
$I$
-equation
For general
![]() $\unicode[STIX]{x1D714}$
, the ordinary differential equation (3.6), although first order, does not permit a solution in terms of usual functions, and we define
$\unicode[STIX]{x1D714}$
, the ordinary differential equation (3.6), although first order, does not permit a solution in terms of usual functions, and we define
With the choice of origin of height previously discussed, (3.6) leads to
![]() $\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}({\mathcal{I}})-\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}(1)={\mathcal{Z}}$
. Since
$\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}({\mathcal{I}})-\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}(1)={\mathcal{Z}}$
. Since
![]() $\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}(1)=0$
, we get
$\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}(1)=0$
, we get
This is also, with
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}$
being defined as the inverse function of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}$
being defined as the inverse function of
![]() $\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}$
,
$\hat{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D714}}$
,
From (3.2) and (3.3), we may now write
This is the solution of the plume equations in the lazy case for the variable entrainment considered herein. Defining the top-hat density ratio at the source as
we may use (1.4) to express
![]() $G_{s}$
as
$G_{s}$
as
3.4 Pure-plume asymptotics for large height
For large
![]() ${\mathcal{Z}}$
, using classic theorems for the asymptotics of integrals depending on their bounds,
${\mathcal{Z}}$
, using classic theorems for the asymptotics of integrals depending on their bounds,
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}({\mathcal{Z}})\sim \{3{\mathcal{Z}}/[10(1-\unicode[STIX]{x1D714})]\}^{10(1-\unicode[STIX]{x1D714})/3}$
, and therefore
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}({\mathcal{Z}})\sim \{3{\mathcal{Z}}/[10(1-\unicode[STIX]{x1D714})]\}^{10(1-\unicode[STIX]{x1D714})/3}$
, and therefore
After some algebra, this reduces to
Thus, whatever the value of
![]() $\unicode[STIX]{x1D714}$
, asymptotically for large
$\unicode[STIX]{x1D714}$
, asymptotically for large
![]() $z$
, pure-plume behaviour (see (2.16) and (2.17)) is recovered.
$z$
, pure-plume behaviour (see (2.16) and (2.17)) is recovered.
3.5 Lazy plumes with
 $\unicode[STIX]{x1D714}=1/5$
$\unicode[STIX]{x1D714}=1/5$
The case
![]() $\unicode[STIX]{x1D714}=1/5$
is interesting because it is simple to solve for as (3.9) may be integrated directly and the inverse
$\unicode[STIX]{x1D714}=1/5$
is interesting because it is simple to solve for as (3.9) may be integrated directly and the inverse
![]() $\unicode[STIX]{x1D6F7}_{1/5}$
expressed in terms of usual functions; thus,
$\unicode[STIX]{x1D6F7}_{1/5}$
expressed in terms of usual functions; thus,
![]() $\unicode[STIX]{x1D6F7}_{1/5}({\mathcal{Z}})=(3{\mathcal{Z}}/8+2^{3/8})^{8/3}-1$
. Equations (3.12) and (3.13) for
$\unicode[STIX]{x1D6F7}_{1/5}({\mathcal{Z}})=(3{\mathcal{Z}}/8+2^{3/8})^{8/3}-1$
. Equations (3.12) and (3.13) for
![]() $G$
and
$G$
and
![]() $M$
become
$M$
become
From (1.4), one may compute the corresponding top-hat quantities of velocity, density and radius,
 $$\begin{eqnarray}W_{T}=\frac{M}{G},\quad \frac{\unicode[STIX]{x1D70C}_{T}}{\unicode[STIX]{x1D70C}_{a}}=\frac{1}{1+{\displaystyle \frac{\unicode[STIX]{x1D70C}_{a}B}{gG}}},\quad b_{T}=\sqrt{\frac{1}{\unicode[STIX]{x03C0}}\frac{G^{2}}{\unicode[STIX]{x1D70C}_{T}M}},\end{eqnarray}$$
$$\begin{eqnarray}W_{T}=\frac{M}{G},\quad \frac{\unicode[STIX]{x1D70C}_{T}}{\unicode[STIX]{x1D70C}_{a}}=\frac{1}{1+{\displaystyle \frac{\unicode[STIX]{x1D70C}_{a}B}{gG}}},\quad b_{T}=\sqrt{\frac{1}{\unicode[STIX]{x03C0}}\frac{G^{2}}{\unicode[STIX]{x1D70C}_{T}M}},\end{eqnarray}$$
leading to
 $$\begin{eqnarray}\displaystyle & \displaystyle W_{T}=\left(\frac{\unicode[STIX]{x1D70C}_{a}B^{2}}{\unicode[STIX]{x1D6E4}_{0}^{2}G_{s}}\right)^{1/5}\frac{\left[\left({\textstyle \frac{3}{8}}{\mathcal{Z}}+2^{3/8}\right)^{8/3}-2\right]^{1/2}}{\left({\textstyle \frac{3}{8}}{\mathcal{Z}}+2^{3/8}\right)^{5/3}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle W_{T}=\left(\frac{\unicode[STIX]{x1D70C}_{a}B^{2}}{\unicode[STIX]{x1D6E4}_{0}^{2}G_{s}}\right)^{1/5}\frac{\left[\left({\textstyle \frac{3}{8}}{\mathcal{Z}}+2^{3/8}\right)^{8/3}-2\right]^{1/2}}{\left({\textstyle \frac{3}{8}}{\mathcal{Z}}+2^{3/8}\right)^{5/3}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D70C}_{T}}{\unicode[STIX]{x1D70C}_{a}}=\frac{1}{1+{\displaystyle \frac{1-\unicode[STIX]{x1D702}_{s}}{\unicode[STIX]{x1D702}_{s}}}\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{-5/3}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D70C}_{T}}{\unicode[STIX]{x1D70C}_{a}}=\frac{1}{1+{\displaystyle \frac{1-\unicode[STIX]{x1D702}_{s}}{\unicode[STIX]{x1D702}_{s}}}\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{-5/3}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle b_{T}=\frac{1}{\sqrt{\unicode[STIX]{x03C0}}}\left(\frac{3}{8}\right)^{2/3}\unicode[STIX]{x1D6E4}_{0}L_{0}\frac{\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{5/3}\left[1+{\displaystyle \frac{1-\unicode[STIX]{x1D702}_{s}}{\unicode[STIX]{x1D702}_{s}}}\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{-5/3}\right]^{1/2}}{\left[\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{8/3}-1\right]^{1/4}}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{T}=\frac{1}{\sqrt{\unicode[STIX]{x03C0}}}\left(\frac{3}{8}\right)^{2/3}\unicode[STIX]{x1D6E4}_{0}L_{0}\frac{\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{5/3}\left[1+{\displaystyle \frac{1-\unicode[STIX]{x1D702}_{s}}{\unicode[STIX]{x1D702}_{s}}}\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{-5/3}\right]^{1/2}}{\left[\left({\displaystyle \frac{3}{8\times 2^{3/8}}}{\mathcal{Z}}+1\right)^{8/3}-1\right]^{1/4}}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
For the computation of density, we used (3.15) to express
![]() $G_{s}$
as a function of the density ratio at the source
$G_{s}$
as a function of the density ratio at the source
![]() $\unicode[STIX]{x1D702}_{s}$
. Figures 1–3 give the evolution of these three quantities with
$\unicode[STIX]{x1D702}_{s}$
. Figures 1–3 give the evolution of these three quantities with
![]() ${\mathcal{Z}}$
. Note that the evolutions of
${\mathcal{Z}}$
. Note that the evolutions of
![]() $\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}$
and
$\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}$
and
![]() $b_{T}$
with non-dimensional height
$b_{T}$
with non-dimensional height
![]() ${\mathcal{Z}}=z/L$
depend on the density ratio at the source
${\mathcal{Z}}=z/L$
depend on the density ratio at the source
![]() $\unicode[STIX]{x1D702}_{s}$
, whereas
$\unicode[STIX]{x1D702}_{s}$
, whereas
![]() $W_{T}$
is independent of this quantity, giving a clear confirmation that
$W_{T}$
is independent of this quantity, giving a clear confirmation that
![]() $L$
is a relevant characteristic length for height.
$L$
is a relevant characteristic length for height.

Figure 1. Normalised plume vertical velocity
![]() $W_{T}/W_{ref}$
as a function of normalised distance from the source
$W_{T}/W_{ref}$
as a function of normalised distance from the source
![]() ${\mathcal{Z}}=z/L$
for
${\mathcal{Z}}=z/L$
for
![]() $\unicode[STIX]{x1D714}=1/5$
, with
$\unicode[STIX]{x1D714}=1/5$
, with
![]() $W_{ref}=[(\unicode[STIX]{x1D70C}_{a}B^{2})/(\unicode[STIX]{x1D6E4}_{0}^{2}G_{s})]^{1/5}$
. The dashed line shows the large-
$W_{ref}=[(\unicode[STIX]{x1D70C}_{a}B^{2})/(\unicode[STIX]{x1D6E4}_{0}^{2}G_{s})]^{1/5}$
. The dashed line shows the large-
![]() ${\mathcal{Z}}$
pure-plume asymptotics
${\mathcal{Z}}$
pure-plume asymptotics
![]() $(8/3)^{1/3}{\mathcal{Z}}^{1/3}$
.
$(8/3)^{1/3}{\mathcal{Z}}^{1/3}$
.

Figure 2. Normalised plume density
![]() $\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}$
as a function of distance from source
$\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}$
as a function of distance from source
![]() ${\mathcal{Z}}=z/L$
for
${\mathcal{Z}}=z/L$
for
![]() $\unicode[STIX]{x1D714}=1/5$
and source density ratios of
$\unicode[STIX]{x1D714}=1/5$
and source density ratios of
![]() $\unicode[STIX]{x1D702}_{s}=\{0.1,0.3,0.5,0.7~\text{and}~0.9\}$
.
$\unicode[STIX]{x1D702}_{s}=\{0.1,0.3,0.5,0.7~\text{and}~0.9\}$
.

Figure 3. Normalised plume width
![]() $b_{T}/(\unicode[STIX]{x1D6FC}_{0}L)$
as a function of distance from source
$b_{T}/(\unicode[STIX]{x1D6FC}_{0}L)$
as a function of distance from source
![]() ${\mathcal{Z}}=z/L$
for
${\mathcal{Z}}=z/L$
for
![]() $\unicode[STIX]{x1D714}=1/5$
and source density ratios of
$\unicode[STIX]{x1D714}=1/5$
and source density ratios of
![]() $\unicode[STIX]{x1D702}_{s}=\{0.1,0.3,0.5,0.7~\text{and}~0.9\}$
.
$\unicode[STIX]{x1D702}_{s}=\{0.1,0.3,0.5,0.7~\text{and}~0.9\}$
.

Figure 4. Variation of the entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}$
divided by its pure-plume value
$\unicode[STIX]{x1D6FC}$
divided by its pure-plume value
![]() $\unicode[STIX]{x1D6FC}_{0}$
as a function of the normalised distance from the source
$\unicode[STIX]{x1D6FC}_{0}$
as a function of the normalised distance from the source
![]() ${\mathcal{Z}}=z/L$
for
${\mathcal{Z}}=z/L$
for
![]() $\unicode[STIX]{x1D714}=1/5$
.
$\unicode[STIX]{x1D714}=1/5$
.
Combining (3.12) and (3.13) with the definition of the Richardson number (1.8) and the expression for
![]() $\unicode[STIX]{x1D6FC}$
(2.7), we get
$\unicode[STIX]{x1D6FC}$
(2.7), we get
Figure 4 shows the evolution of
![]() $\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FC}_{0}$
with height, which is qualitatively similar to the experimental curve of Pham et al. (Reference Pham, Plourde and Kim2005) (their figure 16). Unfortunately, a quantitative comparison is not possible because the value of
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FC}_{0}$
with height, which is qualitatively similar to the experimental curve of Pham et al. (Reference Pham, Plourde and Kim2005) (their figure 16). Unfortunately, a quantitative comparison is not possible because the value of
![]() $B$
is unknown in Pham et al. (Reference Pham, Plourde and Kim2005).
$B$
is unknown in Pham et al. (Reference Pham, Plourde and Kim2005).
Figure 1 shows that for small
![]() ${\mathcal{Z}}=z/L$
the plume acceleration is strong and
${\mathcal{Z}}=z/L$
the plume acceleration is strong and
![]() $W_{T}/W_{ref}$
reaches a local maximum, here within (approximately) 2.5 characteristic length scales of the source. Subsequently, the plume fluid decelerates gradually to follow the pure-plume asymptotic trend of
$W_{T}/W_{ref}$
reaches a local maximum, here within (approximately) 2.5 characteristic length scales of the source. Subsequently, the plume fluid decelerates gradually to follow the pure-plume asymptotic trend of
![]() $W_{T}/W_{ref}=(8/3)^{1/3}{\mathcal{Z}}^{1/3}$
(dashed line) at large
$W_{T}/W_{ref}=(8/3)^{1/3}{\mathcal{Z}}^{1/3}$
(dashed line) at large
![]() ${\mathcal{Z}}$
.
${\mathcal{Z}}$
.
Evidently, dilution of the plume within the near-field region of strong acceleration is also strong (e.g. figure 2 for
![]() ${\mathcal{Z}}=z/L\lesssim 2.5$
); moreover, the rate of dilution decreases with increasing density ratio
${\mathcal{Z}}=z/L\lesssim 2.5$
); moreover, the rate of dilution decreases with increasing density ratio
![]() $\unicode[STIX]{x1D702}_{s}$
. Further above the source, the rate of dilution slows and, at a given height, the weakest dilution is achieved with the largest density ratio.
$\unicode[STIX]{x1D702}_{s}$
. Further above the source, the rate of dilution slows and, at a given height, the weakest dilution is achieved with the largest density ratio.
Consistent with the acceleration and dilution of the plume (figures 1 and 2), figure 3 shows that the plume contracts for small
![]() ${\mathcal{Z}}$
, before expanding at greater heights. In all cases, a pronounced narrowing of the plume is predicted; the height above the source that corresponds to the plume neck (its narrowest width) is reduced as the density ratio increases and the plume neck is narrower. Notably, the vertical non-dimensional height corresponding to the narrowest width depends on the value of the density at the source
${\mathcal{Z}}$
, before expanding at greater heights. In all cases, a pronounced narrowing of the plume is predicted; the height above the source that corresponds to the plume neck (its narrowest width) is reduced as the density ratio increases and the plume neck is narrower. Notably, the vertical non-dimensional height corresponding to the narrowest width depends on the value of the density at the source
![]() $\unicode[STIX]{x1D702}_{s}$
, while the height at which the plume velocity reaches a local maximum (figure 1) does not depend on it. For highly non-Boussinesq plumes (typically
$\unicode[STIX]{x1D702}_{s}$
, while the height at which the plume velocity reaches a local maximum (figure 1) does not depend on it. For highly non-Boussinesq plumes (typically
![]() $\unicode[STIX]{x1D702}_{s}\lesssim 0.3$
), the neck is higher than the maximal velocity height, whereas it is below this height for
$\unicode[STIX]{x1D702}_{s}\lesssim 0.3$
), the neck is higher than the maximal velocity height, whereas it is below this height for
![]() $\unicode[STIX]{x1D702}_{s}\gtrsim 0.3$
. This prediction of the model is rather subtle but can be understood physically on account of the reduction in entrainment experienced by highly non-Boussinesq plumes (the
$\unicode[STIX]{x1D702}_{s}\gtrsim 0.3$
. This prediction of the model is rather subtle but can be understood physically on account of the reduction in entrainment experienced by highly non-Boussinesq plumes (the
![]() $\sqrt{\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}}$
term in (1.9)). With this in mind, if one considers two plumes, one of which is highly non-Boussinesq, with identical source fluxes of buoyancy and mass (and hence each with the same acceleration length
$\sqrt{\unicode[STIX]{x1D70C}_{T}/\unicode[STIX]{x1D70C}_{a}}$
term in (1.9)). With this in mind, if one considers two plumes, one of which is highly non-Boussinesq, with identical source fluxes of buoyancy and mass (and hence each with the same acceleration length
![]() $L$
), while they reach their maximum velocity at the same height as it is set by the value of
$L$
), while they reach their maximum velocity at the same height as it is set by the value of
![]() $L$
, the height required to attain the local state of balance corresponding to the neck is greater for the highly non-Boussinesq plume as a consequence of the aforementioned reduced entrainment. Specifically, reduced entrainment results in a slower dynamical variability in the plume with height, e.g. due to slower vertical variation in mass flux.
$L$
, the height required to attain the local state of balance corresponding to the neck is greater for the highly non-Boussinesq plume as a consequence of the aforementioned reduced entrainment. Specifically, reduced entrainment results in a slower dynamical variability in the plume with height, e.g. due to slower vertical variation in mass flux.
3.6 Effect of varying
 $\unicode[STIX]{x1D714}$
$\unicode[STIX]{x1D714}$
In the general case, the function
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}(\cdot )$
has to be computed numerically. It is fruitful to compare plume solutions with different
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}(\cdot )$
has to be computed numerically. It is fruitful to compare plume solutions with different
![]() $\unicode[STIX]{x1D714}$
for a given source condition. Following Hunt & van den Bremer (Reference Hunt and van den Bremer2010) and also Candelier & Vauquelin (Reference Candelier and Vauquelin2012), to perform this comparison we concentrate on diagrams of
$\unicode[STIX]{x1D714}$
for a given source condition. Following Hunt & van den Bremer (Reference Hunt and van den Bremer2010) and also Candelier & Vauquelin (Reference Candelier and Vauquelin2012), to perform this comparison we concentrate on diagrams of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
as a function of height, since
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
as a function of height, since
![]() $G(z)$
and
$G(z)$
and
![]() $M(z)$
may be reconstructed from knowledge of
$M(z)$
may be reconstructed from knowledge of
![]() $B$
,
$B$
,
![]() $G_{s}$
and
$G_{s}$
and
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
at any height, from (2.11), which becomes, after some algebra
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
at any height, from (2.11), which becomes, after some algebra
and
![]() $M$
as a function of
$M$
as a function of
![]() $\unicode[STIX]{x1D6E4}$
follows from (1.8) and the above expression for
$\unicode[STIX]{x1D6E4}$
follows from (1.8) and the above expression for
![]() $G$
.
$G$
.
However, the scaling used so far for height depends on
![]() $\unicode[STIX]{x1D714}$
. Therefore, to perform a comparison that is straightforward to interpret, we rescale the height so as to be independent of
$\unicode[STIX]{x1D714}$
. Therefore, to perform a comparison that is straightforward to interpret, we rescale the height so as to be independent of
![]() $\unicode[STIX]{x1D714}$
. To this end, we take the acceleration length for the reference entrainment coefficient
$\unicode[STIX]{x1D714}$
. To this end, we take the acceleration length for the reference entrainment coefficient
![]() $\unicode[STIX]{x1D6FC}_{0}$
as
$\unicode[STIX]{x1D6FC}_{0}$
as
and define
We have
and, from (3.12) and (3.13), after some algebra,
Figure 5 shows the influence of the value of the exponent
![]() $\unicode[STIX]{x1D714}$
on the variation of
$\unicode[STIX]{x1D714}$
on the variation of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
with height
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
with height
![]() $\unicode[STIX]{x1D701}$
. It is seen that for small
$\unicode[STIX]{x1D701}$
. It is seen that for small
![]() $\unicode[STIX]{x1D714}$
, the curves are very close to each other; the difference between the cases
$\unicode[STIX]{x1D714}$
, the curves are very close to each other; the difference between the cases
![]() $\unicode[STIX]{x1D714}=0$
and
$\unicode[STIX]{x1D714}=0$
and
![]() $\unicode[STIX]{x1D714}=1/5$
is barely visible. This close similarity indicates that the bulk local plume dynamics, as captured by
$\unicode[STIX]{x1D714}=1/5$
is barely visible. This close similarity indicates that the bulk local plume dynamics, as captured by
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701})$
, is relatively insensitive to changes in entrainment caused by these variations in
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701})$
, is relatively insensitive to changes in entrainment caused by these variations in
![]() $\unicode[STIX]{x1D714}$
. The fact that the model with
$\unicode[STIX]{x1D714}$
. The fact that the model with
![]() $\unicode[STIX]{x1D714}=1/5$
is purely algebraic, while yielding results very close to the constant-entrainment model (the latter, by contrast, requiring tedious calculations, cf. Carlotti & Hunt Reference Carlotti and Hunt2005), may be regarded as good news for enabling the simple and rapid application of plume models. On the other hand, for larger
$\unicode[STIX]{x1D714}=1/5$
is purely algebraic, while yielding results very close to the constant-entrainment model (the latter, by contrast, requiring tedious calculations, cf. Carlotti & Hunt Reference Carlotti and Hunt2005), may be regarded as good news for enabling the simple and rapid application of plume models. On the other hand, for larger
![]() $\unicode[STIX]{x1D714}$
, the curves tend to separate more and more for a given incremental change in
$\unicode[STIX]{x1D714}$
, the curves tend to separate more and more for a given incremental change in
![]() $\unicode[STIX]{x1D714}$
, and thus the plume behaviour is sensitive to
$\unicode[STIX]{x1D714}$
, and thus the plume behaviour is sensitive to
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.

Figure 5. Plume Richardson number normalised by its pure-plume value
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
as a function of non-dimensional distance to the source
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{0}$
as a function of non-dimensional distance to the source
![]() $\unicode[STIX]{x1D701}=z/L_{0}$
.
$\unicode[STIX]{x1D701}=z/L_{0}$
.
4 Comparisons with the available lazy-plume data
4.1 Lazy turbulent plumes issuing from injection nozzles
So far, the model for a plume with variable entrainment was used over its complete range of validity, from the origin (where
![]() $M=M_{s}=0$
and
$M=M_{s}=0$
and
![]() $G=G_{s}$
) to infinite height. Moreover, at the source, as may be seen from our previous considerations, the density ratio is given by (3.15), the top-hat velocity is zero (figure 1) and the top-hat radius is infinite (figure 3). This is not an effect of the choice of normalisation, but comes from the definition of the top-hat radius in (1.4) and the asymptotic behaviour of the fluxes. However, in practical cases, these theoretical source conditions are never met. Depending on the context or application, plumes may rise from a heated plate, a combustion source or a nozzle discharging fluid at a given rate and temperature. To obtain a description of the source conditions at a heated plate or at a combustion source we would need to apply specific models (heat transfer at the plate or combustion), and we therefore decide to concentrate on plumes produced by fluid issuing turbulently from a nozzle. We consider a circular nozzle of radius
$G=G_{s}$
) to infinite height. Moreover, at the source, as may be seen from our previous considerations, the density ratio is given by (3.15), the top-hat velocity is zero (figure 1) and the top-hat radius is infinite (figure 3). This is not an effect of the choice of normalisation, but comes from the definition of the top-hat radius in (1.4) and the asymptotic behaviour of the fluxes. However, in practical cases, these theoretical source conditions are never met. Depending on the context or application, plumes may rise from a heated plate, a combustion source or a nozzle discharging fluid at a given rate and temperature. To obtain a description of the source conditions at a heated plate or at a combustion source we would need to apply specific models (heat transfer at the plate or combustion), and we therefore decide to concentrate on plumes produced by fluid issuing turbulently from a nozzle. We consider a circular nozzle of radius
![]() $b_{n}$
, located at a height
$b_{n}$
, located at a height
![]() $z=0$
. It is assumed that the design of the nozzle is such that the flow is uniform across the nozzle exit, with density
$z=0$
. It is assumed that the design of the nozzle is such that the flow is uniform across the nozzle exit, with density
![]() $\unicode[STIX]{x1D70C}_{n}$
(we define
$\unicode[STIX]{x1D70C}_{n}$
(we define
![]() $\unicode[STIX]{x1D702}_{n}=\unicode[STIX]{x1D70C}_{n}/\unicode[STIX]{x1D70C}_{a}$
) and vertical discharge velocity
$\unicode[STIX]{x1D702}_{n}=\unicode[STIX]{x1D70C}_{n}/\unicode[STIX]{x1D70C}_{a}$
) and vertical discharge velocity
![]() $W_{n}$
. The fluxes at the nozzle are
$W_{n}$
. The fluxes at the nozzle are
and therefore all parameters at the nozzle may be written as functions of
![]() $W_{n}$
,
$W_{n}$
,
![]() $b_{n}$
and
$b_{n}$
and
![]() $\unicode[STIX]{x1D702}_{n}$
,
$\unicode[STIX]{x1D702}_{n}$
,
From (3.5), we have
We define the virtual origin as the location of a source
![]() $(M_{s}=0,G_{s})$
needed to create the desired conditions at the nozzle. If the height of the virtual origin is written
$(M_{s}=0,G_{s})$
needed to create the desired conditions at the nozzle. If the height of the virtual origin is written
![]() $z_{v}$
, and defining
$z_{v}$
, and defining
![]() ${\mathcal{Z}}_{v}=z_{v}/L$
, from (3.12), we have
${\mathcal{Z}}_{v}=z_{v}/L$
, from (3.12), we have
leading to
Now, using (3.12) and (3.13), the evolutions of
![]() $G$
and
$G$
and
![]() $M$
are given by
$M$
are given by
4.2 Evolution of mass flow with height
We introduce the so-called source flow rate length (Kaye & Hunt Reference Kaye and Hunt2009)
Using (3.7) and (4.7), after some algebra, we may express
![]() $L/L_{q}$
as a function of the density ratio
$L/L_{q}$
as a function of the density ratio
![]() $\unicode[STIX]{x1D70C}_{n}/\unicode[STIX]{x1D70C}_{a}$
and
$\unicode[STIX]{x1D70C}_{n}/\unicode[STIX]{x1D70C}_{a}$
and
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
,
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
,
We define
Therefore, with the single source parameter
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
, one may compute
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
, one may compute
![]() ${\mathcal{Z}}_{v}$
from (4.8) and
${\mathcal{Z}}_{v}$
from (4.8) and
![]() $G/G_{n}$
as a function of
$G/G_{n}$
as a function of
![]() $\hat{z}$
,
$\hat{z}$
,
 $$\begin{eqnarray}\frac{G}{G_{n}}=\left(\frac{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}\left({\displaystyle \frac{L_{q}}{L}}\hat{z}+{\mathcal{Z}}_{v}\right)+1}{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}({\mathcal{Z}}_{v})+1}\right)^{1/(2(1-\unicode[STIX]{x1D714}))}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{G}{G_{n}}=\left(\frac{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}\left({\displaystyle \frac{L_{q}}{L}}\hat{z}+{\mathcal{Z}}_{v}\right)+1}{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D714}}({\mathcal{Z}}_{v})+1}\right)^{1/(2(1-\unicode[STIX]{x1D714}))}.\end{eqnarray}$$
For very lazy plumes,
![]() $(\unicode[STIX]{x1D6E4}_{0}/\unicode[STIX]{x1D6E4}_{n})^{1-\unicode[STIX]{x1D714}}\ll 1$
. As a consequence, from (4.12),
$(\unicode[STIX]{x1D6E4}_{0}/\unicode[STIX]{x1D6E4}_{n})^{1-\unicode[STIX]{x1D714}}\ll 1$
. As a consequence, from (4.12),
![]() $L/L_{q}\propto (\unicode[STIX]{x1D6E4}_{0}/\unicode[STIX]{x1D6E4}_{n})^{1/5}$
, and thus
$L/L_{q}\propto (\unicode[STIX]{x1D6E4}_{0}/\unicode[STIX]{x1D6E4}_{n})^{1/5}$
, and thus
![]() $(L_{q}/L)\hat{z}\propto (\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}\hat{z}$
. Therefore, according to this model, the curves of
$(L_{q}/L)\hat{z}\propto (\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}\hat{z}$
. Therefore, according to this model, the curves of
![]() $G/G_{n}$
plotted as a function of
$G/G_{n}$
plotted as a function of
![]() $(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}\hat{z}$
will coincide.
$(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}\hat{z}$
will coincide.
4.3 Comparison of our model with experiments
An experimental study of very lazy Boussinesq plumes, based on saline releases (NaCl) in fresh water, was performed by Kaye & Hunt (Reference Kaye and Hunt2009). Based on their measurements, they plotted
![]() $\unicode[STIX]{x1D70C}_{n}G/\unicode[STIX]{x1D70C}_{T}G_{n}$
as a function of
$\unicode[STIX]{x1D70C}_{n}G/\unicode[STIX]{x1D70C}_{T}G_{n}$
as a function of
![]() $\hat{z}$
for four plumes,
$\hat{z}$
for four plumes,
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=\{9.1\times 10^{4},1.6\times 10^{5},5.4\times 10^{5},5.7\times 10^{6}~\text{and}~5.4\times 10^{7}\}$
. Note that since, in their case, the flow fulfils the Boussinesq approximation,
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=\{9.1\times 10^{4},1.6\times 10^{5},5.4\times 10^{5},5.7\times 10^{6}~\text{and}~5.4\times 10^{7}\}$
. Note that since, in their case, the flow fulfils the Boussinesq approximation,
![]() $\unicode[STIX]{x1D70C}_{T}=\unicode[STIX]{x1D70C}_{n}=\unicode[STIX]{x1D70C}_{a}$
to a good precision, and, therefore,
$\unicode[STIX]{x1D70C}_{T}=\unicode[STIX]{x1D70C}_{n}=\unicode[STIX]{x1D70C}_{a}$
to a good precision, and, therefore,
![]() $\unicode[STIX]{x1D70C}_{n}G/\unicode[STIX]{x1D70C}_{T}G_{n}=G/G_{n}$
.
$\unicode[STIX]{x1D70C}_{n}G/\unicode[STIX]{x1D70C}_{T}G_{n}=G/G_{n}$
.

Figure 6. Evolution of
![]() $G/G_{n}$
as a function of
$G/G_{n}$
as a function of
![]() $\hat{z}=z/L_{q}$
predicted by the present model with
$\hat{z}=z/L_{q}$
predicted by the present model with
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=5.4\times 10^{5}$
for
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=5.4\times 10^{5}$
for
![]() $\unicode[STIX]{x1D714}=\{0.60,0.62~\text{and}~0.64\}$
compared with the experimental results of Kaye & Hunt (Reference Kaye and Hunt2009).
$\unicode[STIX]{x1D714}=\{0.60,0.62~\text{and}~0.64\}$
compared with the experimental results of Kaye & Hunt (Reference Kaye and Hunt2009).
The first step towards a comparison of our model with experiment is to choose appropriate values for the two parameters of the model, namely
![]() $\unicode[STIX]{x1D6FC}_{0}$
and
$\unicode[STIX]{x1D6FC}_{0}$
and
![]() $\unicode[STIX]{x1D714}$
. Here, we choose to fix, rather arbitrarily, the pure-plume constant-entrainment coefficient as
$\unicode[STIX]{x1D714}$
. Here, we choose to fix, rather arbitrarily, the pure-plume constant-entrainment coefficient as
![]() $\unicode[STIX]{x1D6FC}_{0}=0.1$
and to determine a value of
$\unicode[STIX]{x1D6FC}_{0}=0.1$
and to determine a value of
![]() $\unicode[STIX]{x1D714}$
that gives a good comparison with the measurements of Kaye & Hunt (Reference Kaye and Hunt2009). For
$\unicode[STIX]{x1D714}$
that gives a good comparison with the measurements of Kaye & Hunt (Reference Kaye and Hunt2009). For
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=5.4\times 10^{5}$
we find
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}=5.4\times 10^{5}$
we find
![]() $\unicode[STIX]{x1D714}=0.62$
(see figure 6). As an aside, we find that the value of
$\unicode[STIX]{x1D714}=0.62$
(see figure 6). As an aside, we find that the value of
![]() $\unicode[STIX]{x1D714}$
is relatively insensitive to the choice of
$\unicode[STIX]{x1D714}$
is relatively insensitive to the choice of
![]() $\unicode[STIX]{x1D6FC}_{0}$
, with
$\unicode[STIX]{x1D6FC}_{0}$
, with
![]() $\unicode[STIX]{x1D714}$
decreasing marginally to
$\unicode[STIX]{x1D714}$
decreasing marginally to
![]() $\unicode[STIX]{x1D714}=0.61$
with
$\unicode[STIX]{x1D714}=0.61$
with
![]() $\unicode[STIX]{x1D6FC}_{0}=0.118$
.
$\unicode[STIX]{x1D6FC}_{0}=0.118$
.
Having chosen these values for
![]() $\unicode[STIX]{x1D6FC}_{0}$
and
$\unicode[STIX]{x1D6FC}_{0}$
and
![]() $\unicode[STIX]{x1D714}$
, we compare the predictions of the model with the Kaye & Hunt (Reference Kaye and Hunt2009) data for other values of
$\unicode[STIX]{x1D714}$
, we compare the predictions of the model with the Kaye & Hunt (Reference Kaye and Hunt2009) data for other values of
![]() $\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
. These comparisons are shown in figure 7. In spite of the simplistic character of the assumptions made regarding the entrainment with (2.7), surprisingly good agreement is shown between the model predictions and the available experimental data. It should be noted that a constant-entrainment solution would not lead to the same result at all, even in terms of order of magnitude – indeed, the result would not be visible on the figure.
$\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0}$
. These comparisons are shown in figure 7. In spite of the simplistic character of the assumptions made regarding the entrainment with (2.7), surprisingly good agreement is shown between the model predictions and the available experimental data. It should be noted that a constant-entrainment solution would not lead to the same result at all, even in terms of order of magnitude – indeed, the result would not be visible on the figure.
Finally, to highlight the implications of the scalings arrived at in (4.12)–(4.14), in figure 8 we replot the scaled mass flux data
![]() $G/G_{n}$
, now as a function of
$G/G_{n}$
, now as a function of
![]() $\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
. Evidently, this scaling collapses the data well, particularly for small
$\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
. Evidently, this scaling collapses the data well, particularly for small
![]() $\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
. Kaye & Hunt (Reference Kaye and Hunt2009) scaled their data on the
$\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
. Kaye & Hunt (Reference Kaye and Hunt2009) scaled their data on the
![]() $1/3$
rd power, and although this resulted in a reasonable collapse of their data, they were not able to offer an argument for this choice of exponent.
$1/3$
rd power, and although this resulted in a reasonable collapse of their data, they were not able to offer an argument for this choice of exponent.

Figure 7. Evolution of
![]() $G/G_{n}$
as a function of
$G/G_{n}$
as a function of
![]() $\hat{z}$
: experimental results of Kaye & Hunt (Reference Kaye and Hunt2009) and prediction from the present model with
$\hat{z}$
: experimental results of Kaye & Hunt (Reference Kaye and Hunt2009) and prediction from the present model with
![]() $\unicode[STIX]{x1D6FC}_{0}=0.1$
and
$\unicode[STIX]{x1D6FC}_{0}=0.1$
and
![]() $\unicode[STIX]{x1D714}=0.62$
.
$\unicode[STIX]{x1D714}=0.62$
.

Figure 8. Evolution of
![]() $G/G_{n}$
as a function of
$G/G_{n}$
as a function of
![]() $\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
predicted by the present model for
$\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
predicted by the present model for
![]() $\unicode[STIX]{x1D714}=0.62$
compared with the experimental results of Kaye & Hunt (Reference Kaye and Hunt2009); with this scaling an approximate collapse of the data is evident, notably for small
$\unicode[STIX]{x1D714}=0.62$
compared with the experimental results of Kaye & Hunt (Reference Kaye and Hunt2009); with this scaling an approximate collapse of the data is evident, notably for small
![]() $\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
.
$\hat{z}(\unicode[STIX]{x1D6E4}_{n}/\unicode[STIX]{x1D6E4}_{0})^{1/5}$
.
5 Conclusion
The present paper focuses on variable-entrainment lazy plumes. Section 2 discusses the possibility of entrainment varying with local Richardson number in the plume. After a brief review of existing formulations, a power-law variation was used, with an empirical coefficient
![]() $\unicode[STIX]{x1D714}$
, which may have a value between 0 and 1 (1 being excluded). Taking
$\unicode[STIX]{x1D714}$
, which may have a value between 0 and 1 (1 being excluded). Taking
![]() $\unicode[STIX]{x1D714}=0$
corresponds to the usual model, wherein the entrainment does not depend on the Richardson number, while
$\unicode[STIX]{x1D714}=0$
corresponds to the usual model, wherein the entrainment does not depend on the Richardson number, while
![]() $\unicode[STIX]{x1D714}=0.36$
corresponds to the variation of entrainment suggested by several references in the literature based on weakly lazy plumes. For a pure plume, the model is independent of the value of
$\unicode[STIX]{x1D714}=0.36$
corresponds to the variation of entrainment suggested by several references in the literature based on weakly lazy plumes. For a pure plume, the model is independent of the value of
![]() $\unicode[STIX]{x1D714}$
, being always identical to the MTT model.
$\unicode[STIX]{x1D714}$
, being always identical to the MTT model.
The plume equations were subsequently solved for any
![]() $\unicode[STIX]{x1D714}$
, for pure and lazy plumes, and the solutions were then analysed in more detail (§ 3). It was shown, in particular, that the cases
$\unicode[STIX]{x1D714}$
, for pure and lazy plumes, and the solutions were then analysed in more detail (§ 3). It was shown, in particular, that the cases
![]() $\unicode[STIX]{x1D714}=0$
and
$\unicode[STIX]{x1D714}=0$
and
![]() $\unicode[STIX]{x1D714}=1/5$
lead to very similar quantitative results, while the case
$\unicode[STIX]{x1D714}=1/5$
lead to very similar quantitative results, while the case
![]() $\unicode[STIX]{x1D714}=1/5$
may be computed easily with usual functions (especially polynomials) only. This advocates the idea of selecting systematically
$\unicode[STIX]{x1D714}=1/5$
may be computed easily with usual functions (especially polynomials) only. This advocates the idea of selecting systematically
![]() $\unicode[STIX]{x1D714}=1/5$
for cases where the effect of variation of entrainment is weak, instead of
$\unicode[STIX]{x1D714}=1/5$
for cases where the effect of variation of entrainment is weak, instead of
![]() $\unicode[STIX]{x1D714}=0$
which leads to tedious calculations.
$\unicode[STIX]{x1D714}=0$
which leads to tedious calculations.
For very lazy plumes, for which it is known that a constant-entrainment model is not at all appropriate, we concentrated (§ 4) on plumes that develop when fluid is released from turbulent injection nozzles. We compared the outcome of the present model with experimental data from Kaye & Hunt (Reference Kaye and Hunt2009). Good agreement was shown with
![]() $\unicode[STIX]{x1D714}=0.62$
, and, to the best of our knowledge, this is the first model to give such good agreement with experiments for very lazy plumes. It shows that the concept of a simple entrainment model is good, even in cases far from the initial assumptions underlying MTT. A next step in this study will be to compare the results of the model with other very lazy plumes in order to determine whether the value of
$\unicode[STIX]{x1D714}=0.62$
, and, to the best of our knowledge, this is the first model to give such good agreement with experiments for very lazy plumes. It shows that the concept of a simple entrainment model is good, even in cases far from the initial assumptions underlying MTT. A next step in this study will be to compare the results of the model with other very lazy plumes in order to determine whether the value of
![]() $\unicode[STIX]{x1D714}$
is comparable across all plume experiments, which would mean that its dependence on the precise conditions of release of the fluid is weak. Evidently, this step will first require additional measurements to be made on lazy plumes.
$\unicode[STIX]{x1D714}$
is comparable across all plume experiments, which would mean that its dependence on the precise conditions of release of the fluid is weak. Evidently, this step will first require additional measurements to be made on lazy plumes.
Acknowledgements
The authors would like to thank R. J. Perkins, P. Salizzoni and D. Lamalle for fruitful discussions, and anonymous referees of a previous version of this paper.
Appendix A. Taking into account variable specific heat in hot gaseous plumes
For a hot gaseous plume, the buoyancy equation is obtained using enthalpy and mass conservation (see, for example, Carlotti & Hunt Reference Carlotti and Hunt2005). When it is assumed that the specific heat is constant,
![]() $C_{P}(T)=C_{P}^{0}$
, so that the enthalpy is
$C_{P}(T)=C_{P}^{0}$
, so that the enthalpy is
![]() $H(T)=H(T_{ref})+C_{P}^{0}(T-T_{ref})$
(
$H(T)=H(T_{ref})+C_{P}^{0}(T-T_{ref})$
(
![]() $T_{ref}$
being a reference temperature), then the buoyancy flux
$T_{ref}$
being a reference temperature), then the buoyancy flux
![]() $B$
as defined by (1.1) is independent of height in an unstratified environment.
$B$
as defined by (1.1) is independent of height in an unstratified environment.
However, in the general case,
![]() $C_{P}$
is not constant,
$C_{P}$
is not constant,
![]() $C_{P}=(\unicode[STIX]{x2202}H/\unicode[STIX]{x2202}T)|P$
, which, in a context of low-Mach flow with constant thermodynamic pressure (see, for example, Carlotti Reference Carlotti2013), leads to
$C_{P}=(\unicode[STIX]{x2202}H/\unicode[STIX]{x2202}T)|P$
, which, in a context of low-Mach flow with constant thermodynamic pressure (see, for example, Carlotti Reference Carlotti2013), leads to
![]() $H(T)=H(T_{ref})+\int _{T_{ref}}^{\text{T}}C_{P}(T^{\prime })\,\text{d}T^{\prime }$
. Defining
$H(T)=H(T_{ref})+\int _{T_{ref}}^{\text{T}}C_{P}(T^{\prime })\,\text{d}T^{\prime }$
. Defining
we have for variable specific heat
![]() $H(T)=H(T_{ref})+C_{P}^{\prime }(T)\times (T-T_{ref})$
. In the low-Mach-number formulation, one may combine the general tridimensional enthalpy and mass conservation equations to obtain an equation where the time derivative terms cancel (Carlotti Reference Carlotti2013),
$H(T)=H(T_{ref})+C_{P}^{\prime }(T)\times (T-T_{ref})$
. In the low-Mach-number formulation, one may combine the general tridimensional enthalpy and mass conservation equations to obtain an equation where the time derivative terms cancel (Carlotti Reference Carlotti2013),
where
![]() $\boldsymbol{u}$
is the velocity field,
$\boldsymbol{u}$
is the velocity field,
![]() $\unicode[STIX]{x1D705}$
is the diffusivity and
$\unicode[STIX]{x1D705}$
is the diffusivity and
![]() ${\mathcal{S}}$
represents sources and sinks of heat. Note that this combination of mass and enthalpy conservation may be interpreted as a justification of the so-called volume conservation in the present context.
${\mathcal{S}}$
represents sources and sinks of heat. Note that this combination of mass and enthalpy conservation may be interpreted as a justification of the so-called volume conservation in the present context.
Defining
(with
![]() $C_{P}^{0}=C_{P}(T_{ref})$
), the previous equation may be written, using the ideal gas law and after some algebra,
$C_{P}^{0}=C_{P}(T_{ref})$
), the previous equation may be written, using the ideal gas law and after some algebra,
Then, integrating on a cylinder of diameter
![]() $R$
(with
$R$
(with
![]() $R$
larger than the plume radius) centred on the vertical axis starting at the source, between heights
$R$
larger than the plume radius) centred on the vertical axis starting at the source, between heights
![]() $z$
and
$z$
and
![]() $z+\text{d}z$
, and using the divergence theorem,
$z+\text{d}z$
, and using the divergence theorem,
![]() $\iiint _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}\,\text{d}V=\iint _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}$
, where
$\iiint _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}\,\text{d}V=\iint _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\boldsymbol{v}\boldsymbol{\cdot }\text{d}\boldsymbol{S}$
, where
![]() $\unicode[STIX]{x1D6FA}$
is a closed control volume and
$\unicode[STIX]{x1D6FA}$
is a closed control volume and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
is the boundary of this volume, one obtains in the limit
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
is the boundary of this volume, one obtains in the limit
![]() $\text{d}z\rightarrow 0$
$\text{d}z\rightarrow 0$
As in the constant-
![]() $C_{P}$
model, the diffusive terms on the right-hand side may be neglected (see MTT), and, taking the limit
$C_{P}$
model, the diffusive terms on the right-hand side may be neglected (see MTT), and, taking the limit
![]() $R\rightarrow \infty$
, one recovers, in the absence of sources,
$R\rightarrow \infty$
, one recovers, in the absence of sources,
As a consequence, provided that this modified definition of buoyancy flux is taken, the conservation of buoyancy flux with height is still valid in gaseous plumes with specific heat varying with temperature. The effect of this correction for a
![]() $400\,^{\circ }\text{C}$
air plume issuing from a nozzle into an ambient at room temperature was estimated through LES by Lamalle (2013, private communication) to be of order 10 %. Using the definition of classic buoyancy flux, some algebra leads to
$400\,^{\circ }\text{C}$
air plume issuing from a nozzle into an ambient at room temperature was estimated through LES by Lamalle (2013, private communication) to be of order 10 %. Using the definition of classic buoyancy flux, some algebra leads to
Calculation of
![]() $C_{P}^{\prime }$
confirms a 10 % order of magnitude for air and typical temperature between 20 and
$C_{P}^{\prime }$
confirms a 10 % order of magnitude for air and typical temperature between 20 and
![]() $500\,^{\circ }\text{C}$
(e.g. Carlotti Reference Carlotti2013).
$500\,^{\circ }\text{C}$
(e.g. Carlotti Reference Carlotti2013).