Hostname: page-component-6dbcb7884d-hdw28 Total loading time: 0 Render date: 2025-02-14T01:43:22.559Z Has data issue: false hasContentIssue false
  • English
  • Français

Advective balance in pipe-formed vortex rings

Published online by Cambridge University Press:  12 December 2017

Karim Shariff Open the ORCID record for Karim Shariff [Opens in a new window]  and
Paul S. Krueger Open the ORCID record for Paul S. Krueger [Opens in a new window]
Karim Shariff*
Affiliation:
NASA Ames Research Center, Moffett Field, CA 94035, USA
Paul S. Krueger*
Affiliation:
Department of Mechanical Engineering, Southern Methodist University, P.O. Box 750337, Dallas, TX 75275-0337, USA
*
†Email addresses for correspondence: karim.shariff@nasa.gov, pkrueger@lyle.smu.edu
†Email addresses for correspondence: karim.shariff@nasa.gov, pkrueger@lyle.smu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Vorticity distributions in axisymmetric vortex rings produced by a piston–pipe apparatus are numerically studied over a range of Reynolds numbers, 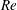$Re$, and stroke-to-diameter ratios, 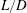$L/D$. It is found that a state of advective balance, such that 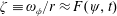$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r\approx F(\unicode[STIX]{x1D713},t)$, is achieved within the region (called the vortex ring bubble) enclosed by the dividing streamline. Here 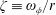$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r$ is the ratio of azimuthal vorticity to cylindrical radius, and 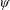$\unicode[STIX]{x1D713}$ is the Stokes streamfunction in the frame of the ring. Some, but not all, of the 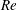$Re$ dependence in the time evolution of 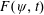$F(\unicode[STIX]{x1D713},t)$ can be captured by introducing a scaled time 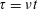$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D708}t$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity. When $\unicode[STIX]{x1D708}t/D^{2}\gtrsim 0.02$, the shape of 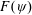$F(\unicode[STIX]{x1D713})$ is dominated by the linear-in-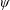$\unicode[STIX]{x1D713}$ component, the coefficient of the quadratic term being an order of magnitude smaller. An important feature is that, as the dividing streamline (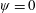$\unicode[STIX]{x1D713}=0$) is approached, 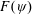$F(\unicode[STIX]{x1D713})$ tends to a non-zero intercept which exhibits an extra 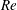$Re$ dependence. This and other features are explained by a simple toy model consisting of the one-dimensional cylindrical diffusion equation. The key ingredient in the model responsible for the extra 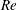$Re$ dependence is a Robin-type boundary condition, similar to Newton’s law of cooling, that accounts for the edge layer at the dividing streamline.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 773 - 796
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover.Google Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Berezovski, A. A. & Kaplanski, F. B. 1987 Diffusion of a ring vortex. Fluid Dyn. 22 (6), 832–837; Transl. of Izv. Akad. Nauk, Mekh. Zhidk. Gaza.Google Scholar
Cater, J. E., Soria, J. & Lim, T. T. 2004 The interaction of the piston vortex with a piston-generated vortex ring. J. Fluid Mech. 499, 327–343.Google Scholar
Couder, Y. & Basdevant, C. 1986 Experimental and numerical study of vortex couples in two-dimensional flows. J. Fluid Mech. 173, 225–251.Google Scholar
Eydeland, A. & Turkington, B. 1988 A computational method of solving free-boundary problems in vortex dynamics. J. Comput. Phys. 78, 194–214.Google Scholar
Ferziger, J. H. & Perić, M. 2002 Computational Methods for Fluid Dynamics. Springer.Google Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Harper, J. F. & Moore, D. W. 1968 The motion of a spherical liquid drop at high Reynolds number. J. Fluid Mech. 32 (2), 367–391.Google Scholar
Kambe, T. & Oshima, Y. 1975 Generation and decay of viscous vortex rings. J. Phys. Soc. Japan 38 (1), 271–280.Google Scholar
Kaplanski, F., Fukumoto, Y. & Rudi, Y. 2012 Reynolds-number effect on vortex ring evolution in a viscous fluid. Phys. Fluids 24 (3), 033101.Google Scholar
Kaplanski, F. B. & Rudi, Y. A. 2001 Evolution of a viscous vortex ring. Fluid Dyn. 36 (1), 16–25; Transl. of Izv. Akad. Nauk, Mekh. Zhidk. Gaza.Google Scholar
Kaplanski, F. B. & Rudi, Y. A. 2005 A model for the formation of ‘optimal’ rings taking into account viscosity. Phys. Fluids 17, 087101.Google Scholar
Kirde, K. 1962 Untersuchungen über die zeitliche Weiterentwicklung eines Wirbels mit Vorgegebener Anfangsverteilung. Ing.-Arch. 31 (6), 385–404.Google Scholar
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19, 59–98.Google Scholar
Linden, P. F. & Turner, J. S. 2001 The formation of ‘optimal’ vortex rings and the efficiency of propulsive devices. J. Fluid Mech. 427, 61–72.Google Scholar
Mohseni, K. & Gharib, M. 1998 A model for universal time scale of vortex ring formation. Phys. Fluids 10, 2436–2438.Google Scholar
Moore, D. W. 1980 The velocity of a vortex ring with a thin core of elliptical cross section. Proc. R. Soc. Lond. A 370 (1742), 407–415.Google Scholar
Nitsche, M. & Krasny, R. 1994 A numerical study of vortex ring formation at the edge of a circular tube. J. Fluid Mech. 276, 139–161.Google Scholar
Norbury, J. 1973 A family of steady vortex rings. J. Fluid Mech. 57, 417–431.CrossRefGoogle Scholar
Phillips, O. M. 1956 The final period of decay of non-homogeneous turbulence. Math. Proc. Cambridge Phil. Soc. 52 (1), 135–151.CrossRefGoogle Scholar
Pullin, D. 1979 Vortex ring formation at tube and orifice openings. Phys. Fluids 22 (3), 401–403.Google Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.Google Scholar
Rott, N. & Cantwell, B. 1993a Vortex drift. I: dynamic interpretation. Phys. Fluids A 5 (6), 1443–1450.Google Scholar
Rott, N. & Cantwell, B. 1993b Vortex drift. II: the flow potential surrounding a drifting vortical region. Phys. Fluids A 5 (6), 1451–1455.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49 (4), 371–380.Google Scholar
Saffman, P. G. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84 (4), 625–639.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12 (3), 618–621.Google Scholar
Stanaway, S., Cantwell, B. J. & Spalart, P. R.1988 A numerical study of viscous vortex rings using a spectral method. Technical Memorandum 101041. NASA.Google Scholar