1 INTRODUCTION
A classical literature on the measurement of inequality claims that SD provides a robust criterion to rank income distributions. This literature originated in papers by Kolm (Reference Kolm, Margolis and Guitton1969) and Atkinson (Reference Atkinson1970), and was extended by Dasgupta, Sen, and Starrett (Reference Dasgupta, Sen and Starrett1973), Rothschild and Stiglitz (Reference Rothschild and Stiglitz1973), Saposnik (Reference Saposnik1981), Shorrocks (Reference Shorrocks1983) and Foster and Shorrocks (Reference Foster and Shorrocks1988a, Reference Foster and Shorrocks1988b) among many.Footnote 1 As summarized by Foster and Shorrocks (Reference Foster and Shorrocks1988a), first order stochastic dominance (FSD) “can be regarded as the welfare ordering that corresponds to unanimous agreement among all monotonic utilitarian functions.” As such, FSD seemingly provides a robust criterion for policy evaluation because it only requires minimal knowledge of the social welfare function. A natural prescription of this literature would be to look for policies that improve the distribution of income in the FSD sense.
An important application of SD is the one by Chu and Koo (Reference Chu and Koo1990) (CK henceforth). They use FSD to evaluate the consequences of changing the reproduction rate of a particular income group. Using a Markovian branching framework with differential fertility among income groups, they show that an exogenous reduction in the fertility of the poor results in a sequence of income distributions that conditionally first-degree stochastically dominate (CFSD) the original distribution. CFSD implies FSD. CK argues that SD “provides us with very strong theoretical support in favor of family-planning programs that encourage the poor in developing countries to reduce their reproductive rate (pp. 1136).” Numerical simulations of CK’s model further confirm that more general fertility reduction programs that disproportionately targets lower income groups, such as the One Child Policy, or policies that promote fertility of high income groups, should increase social welfare.Footnote 2 These policies generally result in a sequence of income distributions that dominates the distribution without the program in the first order stochastic sense.
CK’s results are nevertheless puzzling. Basic economic principles suggest that, absent externalities or market failures, individuals’ decisions should be efficient. In fact, various authors have shown that fertility choices made by altruistic parents, i.e. parents who care about the number and welfare of their children, are socially optimal under certain conditions. Early papers in this category include Pazner and Razin (Reference Pazner and Razin1980), Willis (Reference Willis, Johnson and Lee1987), and Eckstein and Wolpin (Reference Eckstein and Wolpin1985). Golosov, Jones and Tertilt (Reference Golosov, Jones and Tertilt2007) further show that market allocations are Pareto optimal in a variety of models of endogenous fertility. These findings suggest that family planning programs aiming at reducing the fertility of the poor do not necessarily have the strong theoretical support claimed by CK. Lam (Reference Lam, Rosenzweig and Stark1997) expresses similar skepticism.
Unfortunately CK does not fully spell out the decision problem of individuals, a common feature of the literature cited in the first paragraph, in particular the microfoundations of the fertility choice. However, their two main assumptions, grounded on empirical evidence, are in fact hard to rationalize by frictionless models of fertility. First, they assume intergenerational mobility across income and consumption groups but complete market models, such as the Barro–Becker model, predict no mobility.Footnote 3 Second, they assume that fertility decreases with individual income, a feature that is also difficult to rationalize by efficient models of fertility (see Cordoba and Ripoll (forthcoming)). It is possible that implicit in these two assumptions there are market frictions that would explain why fertility is suboptimal in CK’s model and intervention is welfare enhancing.
This paper revisits the question of optimality of family planning programs, as envisioned by CK, but takes into consideration the household decision problem explicitly. For this purpose, we use a version of the Barro–Becker fertility model enriched to include issues of income distribution. Individuals in our model differ in their innate abilities, are altruistic toward their descendants, and choose their own fertility optimally. Abilities are random, determined at birth and correlated with parental abilities. Insurance markets are available but parents cannot leave negative bequests to their children. Due to the assumed market incompleteness, mobility arises in equilibrium and fertility differs across ability groups.
The equilibrium of the model satisfies the two assumptions postulated by CK. First, fertility decreases with ability in the presence of uncertainty about children’s abilities. To the extent of our knowledge, this result is novel and of independent interest by itself. Although there is a literature documenting and studying a negative relationship between fertility and ability, obtaining such negative relationship within a fully dynamic altruistic model with uncertainty is novel.Footnote 4 The negative relationship arises from the interplay of two opposite forces. On the one hand, higher ability individuals face a larger opportunity cost of having children due to the time cost of raising children. On the other hand, higher ability individuals enjoy a larger benefit of having children when abilities are intergenerationally persistent. We find that the effect of ability on the MC dominates its effect on the MB if the intergenerational persistence of abilities is not perfect. This explains why fertility decreases with ability. Second, the equilibrium of the model exhibits mobility. In particular, the equilibrium is characterized by a Markov branching process satisfying the CSMproperty. This requirement means that if a kid from a poor family and a kid from a rich family both fall into one of the poorest classes, it is more likely that the poor kid will be poorer than the rich kid.
Given that the equilibrium of our model satisfies the assumptions postulated by CK, direct application of their Theorem 2 implies that a reduction in the fertility of the poor generates a sequence of income distributions that dominates the original distribution in all periods in the first order stochastic sense. In particular, average income and consumption increase for all periods. This result comes from two forces. First, average ability of (born) individuals increases because the poor have proportionally more low ability children as a result of the assumed CSM property. Second, consumption and income of the poor strictly increase because they spend less time and resources raising children. However, contrary to CK’s claim, we find that individual and social welfare fall. Our main results, Propositions 7 and 8 show that fertility restrictions of any type, not only for the poor, unequivocally reduce individual and social welfare in our model, in spite of the strong degree of market incompleteness. Hence, we conclude that SD alone is not a sound criterion to rank social welfare as claimed by Chu and Koo in particular, and by a larger literature in general.
The primary reason why SD fails to rank welfare properly is because it does not take into account the fact that indirect utility functions are not invariant to the policies in place. As we show, a policy that restricts fertility in our model reduces the set of feasible choices and invariably reduces welfare of all individuals in all generations, even those whose fertility is not directly affected by the policy. This is because altruistic parents care not only about their own consumption and fertility but also care about the consumption and fertility of all their descendants. Furthermore, the welfare of those individuals who are not born under the new policy also falls, or at least does not increase. Social welfare falls because the welfare of all individuals, born and unborn, either falls or remain the same. This is the case, for example, if social welfare is defined as classical (Bentham) utilitarianism, a weighted sum of the welfare of all present and future individuals. The result also holds for versions of classical utilitarianism that are consistent with the Barro–Becker concept of diminishing altruism. An interpretation of our results is that the positive effect on welfare of fertility restrictions, namely higher average consumption, is dominated by the negative effect of a smaller dynasty size.
CK define social welfare as average (Mills) utilitarianism rather than classical utilitarianism. Under this definition, social welfare can increase even if the welfare of all individuals falls if population falls even more. The net effect of fertility restrictions on social welfare depends in this case on the relative strength of two opposite forces. On the one hand, distributions of abilities and incomes improve for all periods, as stressed by CK. On the other hand, the welfare of all individuals falls. Propositions 9 and 10 provide two examples in which the later force dominates and social welfare, defined as average welfare, falls not only in present value but also for all periods. These are counterexamples to the claim that SD is a sufficient condition to rank social welfare, even when welfare is defined as average utilitarianism. We further provide a variety of numerical simulations to illustrate that our results are more general, not just extreme examples.
Our findings challenge CK’s main normative conclusion and at the same time provides counterexamples to the broader literature, mentioned in the first paragraph, claiming that SD alone provides robust normative implications. We show that carefully modeling the microfoundations of the problem makes a difference and can reverse the conclusions obtained by simple SD criteria. Our findings are an application of the Lucas’ critique. CK’s results are based on the assumption that reduced form parameters and indirect utility functions are invariant to policy changes. Specifically, fertility rates as well as indirect utility functions of individuals are assumed to be invariant to the policies in place. However, these are not structural parameters but function of deeper parameters, those governing preferences, technologies and policies in place. Policy evaluations based on the assumed constancy of the parameters may be misleading. In his classic critique, Lucas (Reference Lucas1976) argued that the observed negative relationship between unemployment and inflation cannot be exploited by policymakers to systematically reduce unemployment. The analogous argument in our context is that the observed negative relationship between fertility and income cannot be exploited by policymakers to improve social welfare.
In addition to the papers already mentioned, our paper is related to Alvarez (Reference Alvarez1999). He studies an economy with idiosyncratic shocks, incomplete markets and endogenous fertility choices by altruistic parents. Our endowment economy is a version of his model, one with non-negative bequest constraints. In equilibrium no individual leaves positive bequests. This is a stronger degree of market incompleteness than that in Alvarez and it explains why mobility arises in the equilibrium of our model but not in his. As a result, our model maps exactly into CK’s Markovian model.
Golosov, Jones and Tertilt (Reference Golosov, Jones and Tertilt2007) proves that equilibrium outcomes are efficient in Barro–Becker models of fertility. However, their welfare theorem does not apply to our model due to the presence of bequest constraints. Schoonbroodt and Tertilt (Reference Schoonbroodt and Tertilt2014) have shown that, under certain assumptions, incomplete markets models result in inefficiently low fertility. In those cases, it is natural to expect that policies seeking to reduce fertility even more, such as One Child Policy, would reduce social welfare. We show in a companion paper, Cordoba and Liu (Reference Cordoba and Liu2014), that under different assumptions incomplete markets models can result in too much fertility relative to the complete markets case. In those cases, it is not obvious that policies limiting fertility are welfare reducing. We show that restricting fertility in incomplete markets models, even if fertility is inefficiently high, can be welfare detrimental.
There is a related literature that studies fertility policies in general equilibrium. A recent example is Liao (Reference Liao2013) who studies the One Child Policy using a calibrated deterministic dynastic altruism model with two types of individuals, skilled and unskilled, in the spirit of Doepke (Reference Doepke2004). Although Liao’s model can generate fertility differentials, Doepke (Reference Doepke2004) documents that this channel alone is relatively weak. Part of the issue is that the model only generates upward mobility in equilibrium. Our model, in contrast, generates significant upward and downward mobility that can lead to significant fertility differentials. The mechanisms are different and therefore complementary. In addition, we are able to derive sharper analytical results. For example, we prove that fertility policies, like the one child policy, decrease every individual’s welfare for sure while Liao’s calibrated result suggests it is true for almost all generations but not all.
The rest of the paper is organized as follows: Section 2 revisits the basic connection between fertility, distribution of income, and social welfare in models with exogenous fertility. The section reviews the result of CK and provides further analysis. Section 3 endogenizes fertility and shows that fertility generally decreases with ability and income. Section 4 studies social policies. It shows the basic limitation of CK’s assumptions and argues that fertility policies typically reduce social welfare. Numerical simulations and robustness checks are performed in this section. Section 5 concludes. Proofs are in the Appendix.
2 DISTRIBUTION AND SOCIAL WELFARE WITH EXOGENOUS FERTILITY
Consider an economy populated by a large number of individuals who live for one period. Individuals differ in their labor endowments, or lifetime earning abilities (ability for short). Let Ω ≡ {ω1, ω2, . . ., ωn} be the set of possible abilities, where 0 < ω1 < ⋅⋅⋅ < ωn. The technology of production is linear in ability: an individual with ability ω can produce ω units of perishable output using one unit of labor. In this section, individuals inelastically supply one unit of labor and the income of an individual is equal to his/her ability. Let f(ω) be the fertility rate of an individual with ability ω. It satisfies the following assumption:
Assumption 1. f(ω) is nonincreasing in ability ω.
2.1 Abilities
Ability is determined at birth and correlated with the ability of the parent. Ability is drawn from the Markov chain M where 
$M_{ij}=\Pr (\omega _{\text{child}}=\omega _{i}|\omega _{\text{parent}}=\omega _{j})$ for ωi and ωj ∈ Ω. As in CK, we assume that M satisfies the following condition:
Assumption 2 Conditional Stochastic Monotonicity (CSM):
$$\begin{equation*}
\frac{\sum _{i=1}^{I}M_{i1}}{\sum _{j=1}^{J}M_{j1}}\ge \frac{\sum _{i=1} ^{I}M_{i2}}{\sum _{j=1}^{J}M_{j2}}\ge \cdots \ge \frac{\sum _{i=1}^{I}M_{in}}{\sum _{j=1}^{J}M_{jn}},\text{ }1\le I\le J\le n
\end{equation*}$$
Assumption 2 means that if a kid from a poor family and a kid from a rich family both fall into one of the poorest classes, it is more likely that the poor kid will be poorer than the rich kid. Assumption 2 assures intergenerational persistence of abilities: higher ability parents are more likely to have higher ability children. CSM implies FSD. To see this notice that when J = n the condition becomes
$$\begin{equation*}
\sum _{i=1}^{I}M_{i1}\ge \sum _{i=1}^{I}M_{i2}\ge \cdots \ge \sum _{i=1}^{I} M_{in}\text{, }1\le I\le n.
\end{equation*}$$
Two examples of Markov chains satisfying Assumption 2 are an i.i.d. process and quasi-diagonal matrices of the form
$$\begin{equation*}
M^{\prime }=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} a+b & c & 0 & 0 & .. & 0 & 0\\
a & b & c & 0 & .. & 0 & 0\\
0 & a & b & c & .. & 0 & 0\\
.. & .. & .. & .. & .. & 0 & 0\\
0 & 0 & 0 & 0 & a & b & c\\
0 & 0 & 0 & 0 & 0 & a & b+c \end{array} \right] ,
\end{equation*}$$
where (a, b, c) ≫ 0, a + b + c = 1 and b > 0.5.
We further assume that M has a unique invariant distribution, μ, where μ satisfies
$$\begin{equation*}
\mu \left( \omega _{j}\right) = {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} \mu \left( \omega _{i}\right) M(\omega _{j},\omega _{i})\text{ for all } \omega _{j}\in \Omega .
\end{equation*}$$
2.2 Fertility and the Distribution of Abilities
Let Pt(ω) be the size of population with ability ω at time t = 0, 1, 2, . . ., and 
$P_{t}\equiv {\displaystyle \sum \nolimits _{\omega \in \Omega }} P_{t}\left( \omega \right)$ be total population at time t. The initial distribution of population, {P 0(ωi)}ni = 1, is given. Assuming that a law of large number holds, the size of population in a particular income group evolves according to:
$$\begin{equation}
P_{t+1}( \omega _{j}) = {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f( \omega _{i}) P_{t}( \omega _{i}) M(\omega _{j},\omega _{i})\text{ for all }\omega _{j}\in \Omega .
\end{equation}$$
Let πt(ω) ≡ Pt(ω)/Pt be the fraction of population with ability ω ∈ Ω at time t. In this section income is equal to ability so that π also characterizes the income distribution of the economy. The law of motion of π is given by:
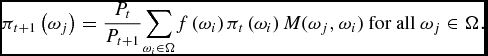$$\begin{equation}
\pi _{t+1}\left( \omega _{j}\right) =\frac{P_{t}}{P_{t+1}} {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) \pi _{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})\text{ for all }\omega _{j}\in \Omega .
\end{equation}$$
Let 
$\pi ^{\ast }\left( \omega \right) \equiv \lim \nolimits _{t\rightarrow \infty }\pi _{t}(\omega).$ As shown by CK, the limit is well defined.
A central topic of the paper is to characterize πt and π* as well as their relationship to fertility. The following proposition provides a simple but important benchmark. The first part states that when fertility is identical across types the limit distribution of incomes is equal to μ, the invariant distribution associated to M. This result provides a baseline distribution in absence of fertility differences. In that case, the distribution of income just reflects the genetic distribution of abilities, what can be termed nature rather than nurture. The second part of the Proposition shows that fertility differences alone do not necessarily affect the long-run distribution of income, π. In particular, fertility differences are irrelevant for income distribution when abilities are i.i.d.
Proposition 1. Whenπ*equalsμ. Suppose one of the following two assumptions hold: (i) f(ω) = f for all ω ∈ Ω; or (ii) M(ω′, ω) is independent of parental ability, ω, for all children’s ability, ω′ ∈ Ω. Then, π*(ω) = μ(ω) for all ω ∈ Ω.
Fertility differences affect the distribution of incomes when abilities are persistent. The following Proposition is an application of CK’s Theorem 2. It states that if the fertility of the poor is higher than the fertility of the rest of the population then π* is different from μ, and moreover, μ dominates π* in the first order stochastic sense.
Proposition 2. Suppose M satisfies Assumption 2 and f(ω1) > f(ωi) = f for all i > 1. Then ∑Ii = 1π*(ωi) > ∑Ii = 1μ(ωi) for all 1 ⩽ I ⩽ n.
Proof. See Chu and Koo (Reference Chu and Koo1990, pp.1136). 
$\Box$
Comparing Propositions 1 and 2, it follows that a reduction in the fertility of the poor results in a limit distribution that dominates the original distribution. More generally, CK shows that if fertility decreases with income and the initial distribution of incomes is at its steady state level, π*0(ωi), then a reduction in the fertility of the poor results in a sequence of income distributions that first order stochastically dominate π*0(ωi), that is, ∑Ii = 1πt(ωi) < ∑Ii = 1π*0(ωi) for all 1 ⩽ I ⩽ n and t > 0.
2.3 Social Welfare
CK considers average utilitarian welfare functions of the form
$$\begin{equation}
\overline{W}=\sum _{t=0}^{\infty }\sum _{\omega \in \Omega }\beta _{p}(t)U(\omega )\pi _{t}\left( \omega \right),
\end{equation}$$
where U(ω) is the utility of an individual with ability ω and βp(t) is the weight of generation t in social welfare. A particular case emphasized by CK is one where the planner cares only about steady state welfare: βp(t) = 0 for all t and 
$\lim \nolimits _{t\rightarrow \infty}\beta _{p}(t)=1$. In that case,
$$\begin{equation}
\overline{W}^{\ast }=\sum _{\omega \in \Omega }U(\omega )\pi ^{\ast }\left( \omega \right).
\end{equation}$$
The following corollary of Proposition 2 provides the theoretical support to family planning programs for the poor, as claimed by CK.
Corollary 3. Suppose social welfare is defined by (3) where U(ω) is a non-decreasing function of ability. Furthermore, suppose M satisfies Assumption 2 and f(ω1) > f(ωi) = f for all i > 1. Then (i) reducing the fertility of the poor increases social welfare; (ii) fertility policies that do not change the observed distribution of abilities, πt, does not change social welfare.
Corollary 3 holds because reducing fertility of the poor improves the observed distribution of abilities but does not alter U( · ). In the next two sections, we show counterexamples to Corollary 3 when fertility is endogenous. This is a crucial consideration because if fertility of the poor is to be restricted, one needs to rationalize why the poor choose to have more children in the first place. As a preview of the results, we show a case in which fertility is restricted by fertility policies, the observed distribution of income, πt, does not change in any period but social welfare as well as individual welfare decreases for all individuals in all periods compared to the unrestricted case. The reason why the previous Corollary fails to account for this possibility is that it presumes that U(ω) is invariant to policies. It lacks microfoundations. However, U(ω) is in fact an indirect utility function and therefore it is not invariant to policies.
3 AN ECONOMIC MODEL OF FERTILITY
We now consider the endogenous determination of fertility. Assumptions regarding earning abilities are the same as in the previous section. In particular, the initial distribution of population across abilities, {P 0(ωi)}ωi ∈ Ω, is given and abilities are random, determined at birth and described by a Markov chain M satisfying Assumption 2, and having a unique invariant distribution, μ. The technology of production is linear in labor: one unit of labor produces one unit of perishable output. Let ωt = [ω0, ω1, . . ., ωt] ∈ Ωt + 1 denotes a particular realization of ability history up to time t, for a particular family line. There is neither capital nor aggregate risk.
3.1 Individual and Aggregate Constraints
Markets open every period. The resources of an individual of ability ωt at time t are labor income and transfers from his parents. Labor income equals ωt · (1 − λft) where ft is the number of children and λ is the time cost of a child. Let ct(ωt) denotes the consumption of an individual with dynasty’s history ωt, bt(ωt) denotes transfers or bequests received from parents, and b t + 1(ωt + 1) ≡ b t + 1([ωt, ωt + 1]) denotes the transfer given to a child of ability ωt + 1. We use b t + 1(ωt, ωt + 1) as a shorthand for b t + 1([ωt, ωt + 1]). The transfer b t + 1(ωt, ωt + 1) has a price of qt(ωt, ωt + 1)Footnote 5. Resources are used to consume and to leave bequests to children. Insurance market exists as parents can leave bequest contingent on the ability of their children. The budget constraint of an individual at time t with history ωt is
$$\begin{equation}
c_{t}\left( \omega ^{t}\right) +f_{t}\left( \omega ^{t}\right) \sum _{i=1}^{n}q_{t}(\omega ^{t},\omega _{i})b_{t+1}\left( \omega ^{t},\omega _{i}\right) \le \omega _{t}\left( 1-\lambda f_{t}\left( \omega ^{t}\right) \right) +b_{t}( \omega ^{t}),
\end{equation}$$
for all ωt ∈ Ωt + 1. We assume that parents cannot leave negative bequests to their children
$$\begin{equation*}
b_{t+1}\left( \omega ^{t},\omega _{i}\right) \ge 0\text{ for all }\omega ^{t}\in \Omega ^{t+1},\omega _{i}\in \Omega \text{ and all }t>0.
\end{equation*}$$
Furthermore, suppose b 0(ωi) = 0 for all ωi ∈ Ω.
Since output is perishable, aggregate consumption must be equal to aggregate production. Alternatively, aggregate savings must be zero. Savings are equal to the total amount of bequests left by parents. Since bequests are non-negative then aggregate savings are zero if and only if all bequests are zero. Therefore, in any equilibrium the budget constraints (5) simplifies to
$$\begin{equation}
c_{t}\left( \omega ^{t}\right) \le \omega _{t}\left( 1-\lambda f_{t}\left( \omega ^{t}\right) \right) \text{ for all }\omega ^{t}\in \Omega ^{t+1}\text{ and all }t\ge 0\text{.}
\end{equation}$$
This is balanced budget constraint for every period and state. The lack of intergenerational transfers significantly simplifies the problem and explains why social mobility arises in the equilibrium. Otherwise, as shown by Alvarez (Reference Alvarez1999), parents would use family size to buffer against shocks and use transfers to smooth consumption across time and states regardless of ability which prevents any social mobility. Absent transfers, ability becomes the key determinant of consumption and fertility, as we see below.
In addition to budget constraints, individuals must satisfy time constraints. In particular, the time spent in raising children cannot exceed the time available to an individual, which is normalized to 1. Thus,
$$\begin{equation}
0\le f_{t}\left( \omega ^{t}\right) \le \frac{1}{\lambda }.
\end{equation}$$
3.2 Individual’s Problem
The lifetime utility of an individual born at time t is of the Barro–Becker type (Barro and Becker Reference Barro and Becker1989 and Becker and Barro Reference Becker and Barro1988):
$$\begin{equation}
U_{t}=u\left( c_{t}\right) +\beta f_{t}^{1-\epsilon }E_{t}U_{t+1}\text{, }t=0,1,2,\ldots .
\end{equation}$$
where 
$u\left( c\right) =\frac{c^{1-\sigma }}{1-\sigma }$ is the utility of consumption, σ ∈ (0, 1), ε ∈ [0, 1), U t + 1 is the utility of a child born in the time t + 1, and Et is the mathematical expectation operator conditional on the information up to time t. The term βf 1 − εt is the weight that parents place on their ft children.
The following parameter restrictions are needed in order to have a well-behaved bounded problem:
Assumption 3. σ > ε and λ1 − ε > β.
The first part of the assumption is identical to the one discussed by Becker and Barro (Reference Becker and Barro1988) to assure strict concavity of the problem. The second part guarantees bounded utility as the effective discount factor in that case satisfies βf 1 − εt ⩽ βλε − 1 < 1.Footnote 6
The individual’s problem is to choose a sequence {ft(ωt)}∞t = 0 to maximize U 0 subject to (6) and (7). The problem can be written in sequence form, by recursively using (8), to obtain
$$\begin{eqnarray}
U_{0}^{\ast }\left( \omega _{0}\right)& =&\sup _{\left\lbrace P_{t+1}\left( \omega ^{t-1},\omega _{t}\right) \right\rbrace _{t=0}^{\infty }}E_{0}\sum \limits _{t=0}^{\infty }\beta ^{t}P_{t}\left( \omega ^{t-1}\right) ^{1-\varepsilon }\nonumber\\
&&\times u\left( \omega _{t}\left( 1-\lambda \frac{P_{t+1}\left( \omega ^{t-1},\omega _{t}\right) }{P_{t}\left( \omega ^{t-1}\right) }\right) \right),
\end{eqnarray}$$
subject to
$$\begin{equation*}
0\le P_{t+1}( \omega ^{t-1},\omega _{t}) \le P_{t}( \omega ^{t-1}) /\lambda \text{ for all }\omega ^{t-1}\in \Omega ^{t}\text{, }\omega _{t}\in \Omega \text{ and }t\ge 0.
\end{equation*}$$
In this formulation, P t + 1(ωt)refers to family size in node ωt. In particular, P 0(ω−1) = 1 and 
$P_{t+1}( \omega ^{t}) \equiv P_{t+1}( [ \omega ^{t-1},\omega _{t}] ) =\prod \nolimits _{j=0}^{t}f_{j}( \omega ^{j})$. Fertility rates can be recovered as 
$f_{t}( \omega ^{t}) =\frac{P_{t+1}( \omega ^{t-1},\omega _{t}) }{P_{t}( \omega ^{t-1}) }.$
An alternative way to describe the household problem is by the functional equation:
$$\begin{equation}
U( \omega) = {\max\limits_{f\in [0,\frac{1}{\lambda }]}} u( \omega ( 1-\lambda f)) +\beta f^{1-\epsilon }E[ U( \omega ^{\prime }) |\omega],
\end{equation}$$
where the state variable ω is parental ability and ω′ is children’s ability.
The next proposition states that the principle of optimality holds for this problem. This result is novel because the functional equation is not standard due to the endogeneity of fertility. In particular, the discount factor is endogenous. Alvarez (Reference Alvarez1999) shows that the principle of optimality holds for a dynastic version of this problem while we show that it holds for the household version of the problem.Footnote 7 Our household problem is simpler because of the lack of intergenerational transfers in equilibrium.
Proposition 4. The functional equation (10) has a unique solution, U(ω). Moreover U(ω) = U*0(ω) for all ω ∈ Ω.
3.3 Optimal Fertility
The optimality condition for an interior fertility choice is
$$\begin{equation}
\lambda \omega u^{\prime }( \omega ( 1-\lambda f^{\ast }) ) =\beta ( 1-\epsilon ) f^{\ast -\epsilon }E[ U( \omega ^{\prime }) |\omega ] .
\end{equation}$$
Let f* = f(ω) be the optimal fertility rule and c* = c(ω) ≡ (1 − λf(ω))ω be the optimal consumption rule. The left hand side of this expression is the MC of a child while the right hand side is the MB. The MC is the product of the time cost per child, λω, and the marginal utility of consumption. The MB to the parent is the expected utility of a child, E[U(ω′)|ω], times the parental weight associated to the f child, β(1 − ε)f(ω)−ε.
Corner solutions are not optimal in the incomplete market case under the assumed functional forms because the MB of a child is infinite while the MC is finite. In particular, E[U(ω′)|ω] > 0 for all ω while limf → 0f −ε = ∞. Having the maximum number of children is also sub-optimal because the MC is infinite when parental consumption is zero, while the MB is finite.
Consider now the relationship between fertility, f*, and parental earning ability, ω. According to (11), both marginal benefits (MB) and marginal costs (MC) are affected by abilities. MB = β(1 − ε)f*−εE[U(ω′)|ω] is increasing in ω because of the postulated intergenerational persistence of abilities: high ability parents are more likely to have high ability children. Regarding MC, MC = λωc*−σ, there are two effects. On one hand, MC tends to rise with ω because high ability parents have high opportunity cost of raising children as their earnings per unit of labor is high. On the other hand, MC tends to fall because higher ability implies more consumption, c* = ω(1 − λf*), and lower marginal utility of consumption. When σ ∈ (0, 1), the first effect dominates the second one so that MC increases with ω.
The need for a small curvature, σ ∈ (0, 1), suggests a tension between the theory and the empirics. Existing estimates of 
$\frac{1}{\sigma }$ as the elasticity of intertemporal substitution (EIS) are typically lower than 1 (e.g. Guvenen Reference Guvenen2006). However, 
$\frac{1}{\sigma }$ is not the EIS in our model because parents only live for one period. The relevant concept is intergenerational elasticity of substitution (EGS) which determines the willingness to substitute consumption between parents and children. Cordoba and Ripoll (Reference Cordoba and Ripoll2014) uses a multiperiod model to disentangle the EIS from the EGS and find that individuals are more willing to substitute consumption intergenerationally than intertemporally (see also Cordoba, Liu, and Ripoll (in press)). In our model, only intergenerational substitution is possible and therefore 
$\frac{1}{\sigma }$ corresponds to the EGS not to the EIS.
Since both MB and MC increase with ω when σ is smaller than 1, it is not clear in principle whether fertility increases or decreases with ability. The following proposition considers three cases: i.i.d abilities across generations, perfect intergenerational persistence of abilities with no uncertainty and random walk (log) abilitiesFootnote 8
Proposition 5 (Persistence and the fertility-ability relationship). (i) Fertility decreases with ability if abilities are i.i.d across generations. In this case, f(ω) satisfies the equation 
$\frac{f\left( \omega \right) ^{\epsilon }}{\left( 1-\lambda f\left( \omega \right) \right) ^{\sigma }}=A\omega ^{\sigma -1}$ where A is a constant. Furthermore, fertility is independent of ability in one of the following two cases: (ii) M is the identity matrix (abilities are perfectly persistent and deterministic); or (iii) ln ωt = ln ωt − 1 + εt where εt ~ N(0, σ2ε).
According to Proposition 5, fertility decreases with ability when abilities are i.i.d.. The intuition is that without intergenerational persistence, parental ability affects the MC of a child but not the MB since E[U(ω′)|ω] = E[U(ω′)] for all ω ∈ Ω. On the other extreme, fertility is independent of parental ability when abilities are perfectly persistent across generations (cases ii and iii). This is because in those cases both the MC and the MB are proportional to ω1 − σ.
To better understand the second extreme, it is instructive to write the first order condition in an alternative way. First, use equation (11) to express (10) as
$$\begin{equation}
U_{t}=u\left( c\left( \omega \right) \right) +\frac{1}{1-\epsilon }f\left( \omega \right) \lambda \omega u^{\prime }\left( c\left( \omega \right) \right) .
\end{equation}$$
Next use (12) to rewrite (11) as
$$\begin{eqnarray}
u^{\prime }\left( c\left( \omega \right) \right) \left( f\left( \omega \right) \right) ^{\epsilon }=\beta E\left[ \left. u^{\prime }\left( c\left( \omega ^{\prime }\right) \right) \frac{\omega ^{\prime }}{\omega }\left( \frac{1}{\lambda }+\frac{\sigma -\epsilon }{1-\sigma }\left( \frac{1}{\lambda }-f\left( \omega ^{\prime }\right) \right) \right) \right|\omega \right] . \nonumber\\
\end{eqnarray}$$
This equation is useful because it only requires marginal utilities, rather than total utility as in equation (11), and corresponds to the Euler Equation of the problem describing the optimal consumption rule. Although savings are zero in equilibrium, fertility allows individuals to smooth consumption across generations.Footnote 9 If ω′ = ω, (13) becomes one equation with one unknown and f(ω) = f.
Given that fertility becomes only independent of ability in the extreme case of perfect persistent, it is natural to conjecture that fertility decreases with ability when persistence is less than perfect. We are able to confirm this conjecture numerically but analytical solutions are not obtained.
3.4 Dynamics of the Income Distribution
Given the optimal fertility rule f( · ), initial distribution π0( · ) of population across abilities, and initial population P 0, population and distribution of all income groups for all periods can be obtained using equations (1) and (2). Furthermore, average earning abilities and average income are given by:
$$\begin{equation*}
E_{t}=\sum _{\omega \in \Omega }\omega \pi _{t}\left( \omega \right) ;\text{ } I_{t}=\sum _{\omega \in \Omega }\omega \left( 1-\lambda f\left( \omega \right) \right) \pi _{t}\left( \omega \right).
\end{equation*}$$
In the next section, we use the microfounded model to perform welfare evaluations of family planning programs. The model also allows us to assess whether Assumption 1 and Assumption 2 are somewhat associated. We show they are. A mobility matrix with less than perfect persistence of intergenerational abilities can give rise to a negative relationship between fertility and ability. The following Proposition revisits Proposition 1 at the light of the microfounded model. It plays an important role in Section 4 when providing counter-examples to CK’s claims.
Proposition 6 (Persistence, fertility and ability distribution). (i) If M( ·, ω) is independent of ω then f(ω) decreases with ω and πt(ω) = μ(ω) for all ω ∈ Ω and t > 0; (ii) if M is the identity matrix then f(ω) = f and πt(ω) = π*(ω) = π0(ω) for all ω ∈ Ω and all t; (iii) if ln ω follows a Gaussian random walk then f(ω) = f, and given ω0 the variance of abilities diverges to ∞.
In words, if abilities are i.i.d. across generations, then fertility decreases with ability but the observed distribution of abilities is independent of fertility choices and equal to μ(ω). Furthermore, with certainty and perfect intergenerational persistence of abilities the observed distribution of abilities in any period is identical to the initial distribution of abilities. Finally, if (log) abilities follow a random walk then there is no limit distribution of abilities since its variance goes to infinity.
3.5 Fertility Policies and Individual Welfare
Consider now a family planning policy that sets lower and/or upper bounds on fertility choices. Let 
$\underline{f}$(ω) ⩾ 0 and 
$\overline{f} (\omega )\le 1/\lambda$ be the lower and upper bound respectively. Bounds potentially depend on individual abilities. The indirect utility Ur(ω) of the constrained problem is described by the following Bellman equation:
$$\begin{equation}
U^{r}\left( \omega \right) = \max\limits_{f\in [\underline{f}(\omega ),\overline{f}\left( \omega \right) ]}u\left( \left( 1-\lambda f\right) \omega \right) +\beta f^{1-\epsilon }E\left[ U^{r}\left( \omega ^{\prime }\right) |\omega \right] .
\end{equation}$$
Let fr(ω) denotes the optimal fertility rule. The following proposition is one of the main results of the paper. It states that binding fertility restrictions for at least one state reduces the indirect utility, or welfare, of all individuals even those whose fertility is not directly affected. The Proposition also states that fertility restrictions of any type (weakly) reduce the fertility of all individuals except perhaps those whose fertility rates are at or below the lower bound.
Proposition 7. Ur(ω) ⩽ U(ω) for all ω ∈ Ω with strict inequality for all ω if 
$f(\omega _{i})>\overline{f}(\omega _{i})$ or 
$f(\omega _{i})<\underline{f}(\omega _{i})$ for at least one ωi ∈ Ω. Furthermore, 
$f^{r}(\omega )=\underline{f}(\omega )$ if 
$f(\omega )\le \underline{f}(\omega )$ and fr(ω) ⩽ f(ω) otherwise.
According to this proposition fertility restrictions that only affect a particular group, say the lowest ability individuals, results in strictly lower welfare for all individuals in all income groups. The reason is that, regardless of current ability, there is a positive probability that a descendant of the dynasty will fall into the group directly affected in finite time. Since altruistic parents care about all of their descendants, the policy hurts everyone because it restricts the choice set without providing any compensation. This result holds exclusively in models with dynastic altruism. In contrast, CK assumes that the policy has no effect on parental welfare, less so for high income individuals.
4 FAMILY PLANNING AND SOCIAL WELFARE RECONSIDERED
Given that fertility policies reduce the welfare of all individuals, as stated in Proposition 7, it is natural to infer that social welfare should also fall. The answer, however, depends on how social welfare is defined and whether the policy reduces or increases population. In this section, we focus on fertility policies that impose upper limits on fertility rates such as those limiting the fertility of the poor or the One Child Policy.
4.1 Analytical Results
According to Proposition 7, upper limits on the fertility of any ability group reduce fertility of all ability groups. Therefore, upper limits on fertility unequivocally reduce population of all ability groups at all times after time 0. Given that both population and individual welfare fall for all ability types, we are able to show that fertility limits unequivocally decrease social welfare if social welfare is of the classical, or Bentham, utilitarian form. Classical utilitarianism defines social welfare as the total discounted welfare of all (born) individuals:Footnote 10
$$\begin{equation}
W=\sum _{t=0}^{\infty }\sum _{\omega \in \Omega }\beta _{p}(t)U(\omega )P_{t}\left( \omega \right) .
\end{equation}$$
In this formulation βp(t) ⩾ 0 is the weight the social planner assigns to generation t. Since individuals are altruistic toward their descendants, βp(t) > 0 means that the planner gives additional weight to generation t on top of what is implied by parental altruism. A particular case in which the planner weights only the original generation, and therefore adopts its altruistic weights, is the one with βp(0) = 1 and βp(t) = 0 for t > 0
$$\begin{equation}
W_{0}=\sum _{\omega \in \Omega }U(\omega )P_{0}\left( \omega \right).
\end{equation}$$
The following Proposition states the main conclusion of the paper: restricting fertility decreases classical utilitarian welfare.
Proposition 8. Imposing upper limits on fertility choices reduces social welfare as defined by (16).
An identical result is obtained if the planner exhibits positive but diminishing returns to population, say if Pt(ω) in expression (16) is replaced by Pt(ω)1 − εp where εp ∈ (0, 1). This formulation seems the natural extension of the Barro–Becker preferences for a planner.
An alternative definition of social welfare is average, or Mills, utilitarianism as defined by equation (3) for the general case, and with (4) as a special case. This definition of welfare, the one used by CK, is analogous to (16) but uses population shares, πt(ω), rather than population, Pt(ω). Under this definition, social welfare could increase even if the welfare of all individuals falls. The net effect depends on the relative strength of two potentially opposite forces: on the one hand individual welfare falls but on the other hand the distribution of abilities, π, may improve, as in CK. We next show analytical examples in which social welfare falls even under this definition. These are formal analytical counterexamples to CK’s claims that fertility limits on the poor are welfare enhancing.
The following Proposition states that fertility restrictions of any type reduce average utilitarian welfare if abilities are i.i.d.
Proposition 9. Suppose M( ·, ω) is independent of ω for all ω ∈ Ω. Then, upper limits on fertility choices reduce social welfare as defined by (3).
Proposition 9 relies on the earlier finding stated in Proposition 1 that, when abilities are i.i.d, the observed distribution of abilities, πt, is independent of fertility choices, even if the poor have more children, and the limit distribution of abilities is the invariant distribution of M. We show in the appendix that πt(ω) = μ(ω) for all t > 0 and for all ω ∈ Ω. Therefore, in the i.i.d case the effect of any fertility policy on social welfare, as defined by (3), is only determined by its effect on individual welfare, U.
A particular implication of Proposition 9 is that limiting the fertility of the poor reduces welfare which contradicts CK’s claim stated in Corollary 3. The i.i.d case in Proposition 9 satisfies CK’s Assumptions 1 and 2 since fertility rates are decreasing, as stated in Proposition 5, and i.i.d abilities satisfy CSM. Corollary 3 fails to properly describe the effect of the policy on social welfare because it implicitly assumes that U is unaffected by the policy change.
The following is a deterministic example showing that average utilitarian welfare unequivocally falls with “uniform” fertility restrictions such as the one child policy.
Proposition 10. Suppose M is the identity matrix and 
$\overline{f}\left( \omega \right) =\overline{f}$. Then, fertility restrictions reduces social welfare as defined by (3).
Proposition 10 provides another example in which fertility restriction do not affect π. Since in the deterministic case all ability groups have the same fertility choices, and the fertility restriction affects all ability groups equally, then it follows that πt = π0 for all t so that the effect of the policy on social welfare is only determined by the effect on individual welfare U.
4.2 Calibration and Simulations
We now turn to numerical simulations to investigate more generally the effects of policies restricting fertility choices on social welfare, particularly on average social welfare since the effects on total welfare are well characterized in Proposition 8. The numerical simulations show that, under plausible parameters, fertility restrictions reduce average welfare as well. It is also possible that under certain, less plausible parameter values, average social welfare could increase. Overall, the exercise shows that the “strong theoretical support” for curbing the fertility of the poor is unjustified.
4.2.1. Benchmark calibration
The following parameters are needed to simulate the model: the Markov process for abilities, M, preference parameter σ, altruistic parameters β and ε, cost of raising children λ, and social planner’s weight on generation t, βp(t).
A number of studies provide estimates of abilities and mobility matrices for relative high-income low fertility countries, such as OECD (HYPERLINK “https://en.wikipedia.org/wiki/Organisation_for_Economic_Co-operation_and_Development” Organization for Economic Cooperation and Development) countries, but studies are more scarce for low-income high-fertility countries which are more relevant for our purposes. This difficulty is exacerbated by the need to have additional information about fertility rates by income levels. Fortunately, Lam (Reference Lam1986) provides us with the information needed for a developing country: Brazil in 1976. It includes data on incomes and fertilities for different ability groups, as well as an estimated Markov chain for the income process. Brazil is one of the largest countries in the world and its development indicators, such as income, fertility, mortality, rural population, or schooling, are similar to many other developing countries. As such, our results are relevant for a typical developing country.
Lam (Reference Lam1986) data describes income classes of Brazilian male household heads aged from 40 to 45 in 1976. Average incomes for five income groups are
$$\begin{equation*}
\overrightarrow{I}\equiv \left[ I_{1},I_{1},\cdots ,I_{5}\right] =\left[ 553,968,1640,2945,10991\right] .
\end{equation*}$$
Average fertilities of each income group are given by
$$\begin{equation*}
\overrightarrow{f}\equiv \left[ f_{1},f_{1},\cdots ,f_{5}\right] =\left[ 6.189,5.647,5.065,4.441,3.449\right] /2.
\end{equation*}$$
We divide fertility by two to obtain fertility per-adult. Since in the model Ii = ωi(1 − λfi), we can solve earning abilities as 
$\omega _{i}=\frac{I_{i}}{1-\lambda f_{i}}$. For easy comparison, we re-scale abilities so that the lowest ability is normalized to 1. The Markov chain provided by Lam is
$$\begin{equation*}
M=\left[
\begin{array}{@{}lllll@{}}
0.50 & 0.25 & 0.15 & 0.10 & 0.05\\
0.25 & 0.40 & 0.20 & 0.20 & 0.10\\
0.15 & 0.20 & 0.35 & 0.20 & 0.20\\
0.05 & 0.10 & 0.20 & 0.35 & 0.25\\
0.05 & 0.05 & 0.10 & 0.15 & 0.40
\end{array} \right].
\end{equation*}$$
This matrix does not satisfy Assumption 2, the CSM property, and therefore CK’s results do not immediately apply. However, numerical simulations confirm that CK’s main argument would still apply in this case: fertility restrictions on the poor would lead to a better income distribution in the first order stochastic sense. The reason is that Assumption 2 is only a sufficient but not necessary condition for their results. In particular, the above matrix still exhibits significant degree of persistence as the diagonal elements dominate other elements. We also considered the Markov chain provided by CK, which satisfies CSM, and obtained similar results.
Our altruistic function, βf 1 − ε, is calibrated following Manuelli and Seshadri (Reference Manuelli and Seshadri2009) (MS henceforth).Footnote 11 For σ we initially use MS’s parameter of 0.62. However, the fertility rates implied by the calibrated model were too high and the range of fertilities too small compared to Brazilian fertility data. We set σ to be a lower value, 0.36, to better fit the fertility data. Another key parameter of the model is the time cost of raising a child, λ. We choose λ = 0.2 which implies a maximum number of 10 children per couple, or that each parent spends 10% of their time per child. For the social planner weights we assume βp(t) = δt with δ = 0.1. The set of parameters used for the benchmark exercises are summarized in Table 1. We perform robustness checks for these parameters in Section 4.2.3.
Table 1. Parameters setting
Finally, initial population is normalized to 1 and the initial distribution of abilities, π0, is approximated by the stationary distribution implied by M and 
$\overrightarrow{f}$.
4.2.2. Results
The simulated model reproduces a negative relationship between fertility and ability in line with Brazilian data.Footnote 12 Because abilities are persistent but not perfectly persistent across generations, the increase of the MC of children dominates that of the MB as ability increases when σ < 1. As shown in the first panel of Figure 1, fertility per household falls from 9 to 2 as earning ability increases from 1 to 12. This inverse relationship between fertility and ability is hard to obtain as argued by Jones, Schoonbroodt and Tertilt (Reference Jones, Schoonbroodt and Tertilt2008). Four aspects of our theory explain this result: imperfect persistence of abilities across generations, EGS larger than 1 (low curvature of the utility function), time cost of raising children and incomplete markets.
Figure 1. Effects of fertility restrictions.
The remaining panels in Figure 1 show the effect of fertility restrictions on average ability, average income, and various welfare measures. The horizontal axis shows the maximum fertility allowed, for everyone, a limit that goes from 0 to 10 children per household. The second panel plots average ability, 
$\overline{\omega },$ and average income, 
$\overline{y}$, as a function of this upper limit. As predicted by CK, tighter fertility limits, which affect lower income groups more severely, increase average income and ability of the economy. Panels third and fourth show that steady state average welfare, 
$\overline{W}^{\ast }$, average welfare of all generations, 
$\overline{W}$, total welfare of the initial generation, W 0, and total welfare of all generations, W, all increase as the upper limit is relaxed. These results confirm the main message of the paper: fertility restrictions, on the poor or other groups, do not have strong theoretical support for improving social welfare.
We also study the welfare consequences of enacting lower bounds on fertility rates.Footnote 13 Restrictions like these disproportionately affect the rich, or high ability individuals, because their unconstrained fertility is typically lower. Figure 2 shows that this policy increases average ability since children of high ability individuals are of higher ability on average. On the other hand, the policy reduces average income because individuals, especially high ability ones, spend more time raising children and this effect dominates the effect of an improved ability distribution. All four welfare measures unanimously decrease as the lower bound increases.
Figure 2. Effects of fertility restrictions.
In summary, results above show that fertility restrictions, on the poor and on the rich, do not result into higher social welfare although they may improve the distribution of abilities and income.
4.2.3. Robustness checks
We now report the results of various robustness checks. For this purpose, we change one parameter at a time while keeping all the other parameters at their benchmark values and study the effect on various welfare measures of imposing upper limits on fertility. We find that the qualitative results obtained above are mostly robust although there exists a set of parameters for which average steady state welfare, 
$\overline{W}^{\ast },$ improves with fertility restrictions. The set of parameters studied is further restricted by the need to have finite utility.
Results are robust to setting any value of σ and ε satisfying the concavity condition stated in Assumption 3. Results are also robust to setting β higher than 0.27 and below λ1 − ε, the condition to guarantee finite utility. If β is sufficiently low, a tighter fertility restriction may increase 
$\overline{W}^{\ast }$ as illustrated in the first panel of Figure 3 for the case β = 0.2. A low β implies that parents care little about future generations and have fewer kids. In this case, tighter fertility restrictions decrease individual welfare but the change of fertility restrictions on the distribution of earnings ability is the dominant effect determining average social welfare at steady state.
Figure 3. Robustness Checks.
Finally, if the cost of raising children, λ, is sufficiently large then a tighter fertility restriction may increase 
$\overline{W}^{\ast }$ as shown in the last panel of Figure 3 for the case λ = 0.4. As in the case of a low degree of parental altruism, high costs of raising children predicts counterfactually low fertility rates in the model. The high cost of raising children itself prevents households from having many children and the change in average social welfare is therefore primarily determined by the change in the distribution of abilities.
5 CONCLUSION
SD, or welfare dominance, seemingly provides a robust criterion for policy evaluation. It allows ranking policies by simply looking at the resulting income distribution without requiring much knowledge of individuals’ preferences and constraints, or knowledge of the social welfare function. Chu and Koo (Reference Chu and Koo1990) exploit such apparent generality to provide a striking policy recommendation. They assert that SD “provides us with very strong theoretical support in favor of family-planning programs that encourage the poor in developing countries to reduce their reproductive rate (CK, pp 1136).” Such fundamental claim has surprisingly remained unchallenged. In this paper, we show that SD alone does not provide the strong theoretical support claimed by CK. Our findings challenge CK’s main normative conclusion and provide a counterexample which casts doubts on the larger classical literature of welfare dominance which is the foundation of such conclusion.
Our model uses the same information basis as CK, in particular, observed income distributions and fertility choices, and consider the same welfare criteria average welfare. We also consider other welfare criteria such as total welfare. The substantive difference between our paper and CK’s is that we provide microfoundations for the fertility choice while CK does not. This is a major deficiency of their analysis because their paper is about the welfare implications of curbing fertility choices. CK makes judgements about the welfare impact of fertility policies only through its impact on the distribution of population across income groups. In addition to this channel, our paper also takes into account their effect on individual welfare. Our microfounded model leads to opposite conclusions.
The key features of our model are dynastic altruism, random abilities, labor costs of raising children, incomplete markets, and an endowment economy. The model is particularly useful because its equilibrium exactly maps into the Markov branching framework of CK and rationalizes their two key assumptions, which are grounded on empirical regularities: (i) why fertility decreases with ability; and (ii) why social mobility occurs in equilibrium. To the extent of our knowledge, these features have not previously been obtained by altruistic models of fertility.
Due to the presence of market frictions, family planning policies could in principle increase social welfare. Although fertility policies do not directly address the underlying frictions leading to inefficient fertility, these policies could improve welfare much in the same way as monetary policy could increase social welfare even if the policy by itself does not address price rigidities. The welfare effect of family planning policies can potentially depend on how social welfare is defined. When social welfare is defined as total welfare, as in classical utilitarianism, we find that policies directed toward reducing the fertility of the poor lowers social welfare in spite of the fact that those policies improve income distributions in the first order stochastic sense. Contrary to CK’s claim, SD fails to rank policies properly because it does not account for the fact that indirect utility functions are not invariant to the policies in place.
When social welfare is defined as average utilitarianism, policies restricting fertility choices could increase social welfare but only under certain conditions. For example, if parents discount the future heavily, the degree of altruism toward children is low, or children are very expensive. Average welfare, however, is not well micro-founded. For example, parents acting as social planners at the household level would maximize a weighted sum of the total utility of the family, not the average utility.
Our model abstracts from a number of aspects that are potentially important to fertility decisions such as intergenerational transfers and wealth inequality. We study various extensions in Cordoba and Liu (Reference Cordoba and Liu2014) and Cordoba, Liu, and Ripoll (in press). The models are significantly more complicated, and do not map into the simple Markov branching framework of CK, but our early results reinforce the finding that policies restricting fertility typically do not increase social welfare.
APPENDIX A
Proof of Proposition 1(i). If fertility is exogenously the same for every individual, divide both sides of (1) by P t + 1.
$$\begin{equation*}
\frac{P_{t+1}\left( \omega _{j}\right) }{P_{t+1}}=\frac{P_{t}}{P_{t+1}} {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) \frac{P_{t}\left( \omega _{i}\right) }{P_{t} }M(\omega _{j},\omega _{i})\text{ for all }\omega _{j}\in \Omega .
\end{equation*}$$
Using the definition of πt,
$$\begin{equation*}
\pi _{t+1}\left( \omega _{j}\right) =\frac{P_{t}}{P_{t+1}} {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) \pi _{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})= {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} \pi _{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i}).
\end{equation*}$$
The last equality holds because fertility is the same for all types.
$$\begin{equation*}
P_{t+1}=P_{t}\sum \limits _{\omega _{i}\in \Omega }f\pi _{t}\left( \omega _{i}\right) =P_{t}f.
\end{equation*}$$
Taking limit to both sides of the expression with π, we get
$$\begin{equation*}
\pi ^{\ast }\left( \omega _{j}\right) = \lim\limits_{t\rightarrow \infty } \pi _{t+1}\left( \omega _{j}\right) =\lim\limits_{t\rightarrow \infty} {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} \pi _{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})= {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} \pi ^{\ast }\left( \omega _{i}\right) M(\omega _{j},\omega _{i}).
\end{equation*}$$
Hence, π*( · ) = μ( · ) is the invariant distribution of M.
$\Box$
Proof of Proposition 1 (ii). In this case M(ωj, ωi) = μ(ωj) for all ωi, ωj ∈ Ω. By (1),
$$\begin{equation*}
\pi _{t+1}\left( \omega _{j}\right) =\frac{1}{P_{t+1}} {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) M(\omega _{j},\omega _{i})\pi _{t}\left( \omega _{i}\right) P_{t}=\mu (\omega _{j})\text{ for }t\ge 0.
\end{equation*}$$
$\Box$
Proof of Proposition 4. We first show that there exists a solution U( · ) that solves the functional equation (10). Define a set of functions.
$$\begin{equation*}
S=\left\lbrace \left. f:\Omega \rightarrow \mathbb {R} \right|\Vert f\Vert \le M\right\rbrace
\end{equation*}$$
where M =
$\frac{u\left( \omega _{n}\right) }{1-\beta \lambda ^{\epsilon -1}}$, and ‖ · ‖ is the sup norm. We can show that S is a complete metric space. Define operator T as
$$\begin{equation}
TU\left( \omega \right) \equiv \max\limits_{0\le \text{ }f\text{ }\le \frac{1}{\lambda }}u\left( \left( 1-\lambda f\right) \omega \right) +\beta f^{1-\varepsilon }E\left[ U\left( \omega ^{\prime }\right) |\omega \right]
\end{equation}$$
for all ω ∈ Ω and U ∈ S. Given U( · ) and ω, the right hand side of (A.1) has a solution that attains the maximum by the Weierstrass Theorem. We first show that T is a contraction. It suffices to show that T satisfies two properties, monotonicity and discounting. Standard arguments can show that given U and 
$\tilde{U}$ ∈ S satisfying U 
$\left( \omega \right) \le \tilde{U}\left( \omega \right)$ for all ω, TU 
$\left( \omega \right) \le T\tilde{U}\left( \omega \right)$ for all ω. The following arguments prove discounting property holds. For any given constant b,
$$\begin{eqnarray*}
T( U( \omega ) +b) & =& \max\limits_{0\le \text{ }f\text{ }\le \frac{1}{\lambda }}u( ( 1-\lambda f) \omega ) +\beta f^{1-\varepsilon }E[ U( \omega ^{\prime }) +b|\omega ] \\
&& \le \max\limits_{0\le \text{ }f\text{ }\le \frac{1}{\lambda }}u( ( 1-\lambda f) \omega ) +\beta f^{1-\varepsilon }E[ U( \omega ^{\prime }) |\omega ] +\beta b\left( \frac{1}{\lambda }\right) ^{1-\varepsilon }\\
&& =TU( \omega ) +\beta \lambda ^{\epsilon -1}b.
\end{eqnarray*}$$
By Contraction Mapping Theorem, there exists a unique fixed point 
$U:\Omega \rightarrow \mathbb {R}$ that solves the functional equation TU = U. The existence of a unique solution U( · ) has been proved. Next, we show U(ω0) = U*0(ω0) for all ω0 ∈ Ω, that is to show U(ω0) is the supremum in problem (9) for any ω0. Define 
$\prod \nolimits _{j=0}^{-1}f_{j}\left( \omega ^{j}\right) ^{1-\epsilon }=1.$ Then, for any feasible plan 
$\left\lbrace f_{t}\left( \omega ^{t}\right) \right\rbrace _{t=0}^{\infty },$
$$\begin{eqnarray*}
U( \omega _{0}) & =&\max\limits_{f\in [0,\frac{1}{\lambda }]}u( \omega _{0}( 1-\lambda f) ) +\beta f^{1-\epsilon }E_{0}[ U( \omega _{1}) |\omega _{0}] \\
&& \geqslant u( \omega _{0}( 1-\lambda f_{0}( \omega ^{0}) ) ) +\beta f_{0}( \omega ^{0}) ^{1-\epsilon }E_{0}[ U( \omega _{1}) |\omega _{0}] \\
&& \geqslant u( \omega _{0}( 1-\lambda f_{0}( \omega ^{0}) ) ) +\beta f_{0}( \omega ^{0}) ^{1-\epsilon }E_{0}\left(\begin{array}{c} u( \omega _{1}( 1-\lambda f_{1}( \omega ^{1}) ) ) \\
+\beta f_{1}( \omega ^{1}) ^{1-\epsilon }E_{1}[ U( \omega _{2}) |\omega _{1}] \end{array} \right) \\
&& \geqslant \cdots \\
&& \geqslant E_{0}\sum \limits _{t=0}^{T}\beta ^{t}\prod \limits _{j=0}^{t-1} f_{j}( \omega ^{j}) ^{1-\epsilon }u( \omega _{t}( 1-\lambda f_{t}( \omega ^{t}) ) )\\
&&\quad +\,\beta ^{T+1} E_{0}\prod \limits _{j=0}^{T}f_{j}( \omega ^{j}) ^{1-\epsilon } E_{T}[ U( \omega _{T+1}) |\omega _{T}] .
\end{eqnarray*}$$
For any ωT + 1 = [ωT, ωT + 1],
$$\begin{equation*}
\beta ^{T+1}\prod \limits _{j=0}^{T}f_{j}\left( \omega ^{j}\right) ^{1-\epsilon }U\left( \omega _{T+1}\right) \le \left( \beta \lambda ^{\epsilon -1}\right) ^{T+1}\frac{u\left( \omega _{n}\right) }{1-\beta \lambda ^{\varepsilon -1}}.
\end{equation*}$$
The right hand side of this inequality converges to 0 as T goes to infinite. Hence, for all feasible plan {ft(ωt)}∞t = 0
$$\begin{equation}
U\left( \omega _{0}\right) \geqslant E_{0}\sum \limits _{t=0}^{\infty }\beta ^{t}\prod \limits _{j=0}^{t-1}f_{j}\left( \omega ^{j}\right) ^{1-\epsilon }u\left( \omega _{t}\left( 1-\lambda f_{t}\left( \omega ^{t}\right) \right) \right) .
\end{equation}$$
We now show that U(ω0) is the smallest upper bound. Given ε1 > 0, choose a sequence of positive real numbers {δt}∞t = 1 such that 
$\sum _{t=0}^{\infty }\left( \beta \lambda ^{\epsilon -1}\right) ^{t}\delta _{t}\le \frac{\varepsilon _{1}}{2}.$ Let f*(ωt) be the solution that attains U(ωt), then for all t
$$\begin{equation*}
U\left( \omega _{t}\right) <u\left( \omega _{t}\left( 1-\lambda f^{\ast }\left( \omega _{t}\right) \right) \right) +\beta f^{\ast }\left( \omega _{t}\right) ^{1-\epsilon }E_{0}\left[ U\left( \omega _{t+1}\right) |\omega _{t}\right] +\delta _{t}.
\end{equation*}$$
Starting from period 0, iteratively substituting the value function U(ωt + 1) into the above inequality shows that for all ω0
$$\begin{eqnarray*}
U( \omega _{0}) && <E_{0}\sum \limits _{t=0}^{T}\beta ^{t} \prod \limits _{j=0}^{t-1}f^{\ast }( \omega _{j}) ^{1-\epsilon }u( \omega _{t}( 1-\lambda f^{\ast }( \omega _{t}) ) ) +\beta ^{T+1}E_{0}\prod \limits _{j=0}^{T}f^{\ast }( \omega _{j}) ^{1-\epsilon }U( \omega _{T+1}) \\
&& +E_{0}\sum \limits _{t=0}^{T}\beta ^{t}\prod \limits _{j=0}^{t-1}f^{\ast }( \omega _{j}) ^{1-\epsilon }\delta _{t}.
\end{eqnarray*}$$
The choice of {δt} guarantees that the last term is no more than 
$\frac{\varepsilon _{1}}{2}$ as T → ∞. We have shown that
$$\begin{equation*}
\lim \limits _{T\rightarrow \infty }\beta ^{T+1}\prod \limits _{j=0}^{T}f^{\ast }\left( \omega _{j}\right) ^{1-\epsilon }U\left( \omega _{T+1}\right) =0.
\end{equation*}$$
So for any given ε1 > 0, there exists a feasible plan {fj(ωj)}∞t = 0 = {f*(ωt)}∞t = 0 such that
$$\begin{equation}
U\left( \omega _{0}\right) <E_{0}\sum \limits _{t=0}^{T}\beta ^{t} \prod \limits _{j=0}^{t-1}f^{\ast }\left( \omega _{j}\right) ^{1-\epsilon }u\left( \omega _{t}\left( 1-\lambda f^{\ast }\left( \omega _{t}\right) \right) \right) +\frac{\varepsilon _{1}}{2}.
\end{equation}$$
Hence,
$$\begin{equation*}
U\left( \omega _{0}\right) =\sup _{\left\lbrace f_{t}\left( \omega ^{t}\right) \right\rbrace _{t=0}^{\infty }\in \left[ 0,\frac{1}{\lambda }\right] }E_{0} \sum \limits _{t=0}^{\infty }\beta ^{t}\prod \limits _{j=0}^{t-1}f_{j}\left( \omega ^{j}\right) ^{1-\epsilon }u\left( \omega _{t}\left( 1-\lambda f_{t}\left( \omega ^{t}\right) \right) \right) .
\end{equation*}$$
Therefore,
$$\begin{equation*}
U\left( \omega _{0}\right) =U^{\ast }\left( \omega _{0}\right) .
\end{equation*}$$
$\Box$
Proof of Proposition 5 (i). In this case, equation (11) can be written as 
$\frac{f\left( \omega \right) ^{\epsilon }}{\left( 1-\lambda f\left( \omega \right) \right) ^{\sigma }}=A\omega ^{\sigma -1}$ where A is a constant. Using the implicit function theorem, it follows that 
$f^{\prime }\left( \omega \right) =-\frac{\left( 1-\sigma \right) /\omega }{\frac{\epsilon }{f\left( \omega \right) }+\frac{\lambda \sigma }{1-\lambda f\left( \omega \right) }}<0.$
$\Box$
Proof of Proposition 5 (ii). In deterministic case, ω′ = ω, c(ω′) = c(ω) for all ω ∈ Ω and equation (13) simplifies to
$$\begin{equation}
f^{\ast \epsilon }=\beta \left( \frac{1}{\lambda }+\frac{\sigma -\epsilon }{1-\sigma }\left( \frac{1}{\lambda }-f^{\ast }\right) \right) .
\end{equation}$$
The left hand side of equation (A.4) is strictly increasing in f* while the right hand side is strictly decreasing in f*. Obviously f* > 0. An interior solution with f* < 1/λ exists since λ1 − ε > β. 
$\Box$
Proof of Proposition 5 (iii). Let f*(ω) denotes the optimal fertility given ω. Plug functional form of u( · ) into equation (12),
$$\begin{equation}
U\left( \omega \right) =h\left( f^{\ast }\left( \omega \right) \right) \omega ^{1-\sigma }.
\end{equation}$$
where
$$\begin{equation}
h\left( f^{\ast }\left( \omega \right) \right) \equiv \frac{1}{1-\sigma }\left( 1-\lambda f^{\ast }\left( \omega \right) \right) ^{1-\sigma } +\frac{1}{1-\epsilon }\lambda f^{\ast }\left( \omega \right) \left( 1-\lambda f^{\ast }\left( \omega \right) \right) ^{-\sigma }.
\end{equation}$$
We make a guess on the value function and let it take the form: U(ω) = Aω1 − σ where A is a constant, independent of ω. Equating this guess with (A.5) results in:
$$\begin{equation}
A=h\left( f^{\ast }\left( \omega \right) \right) .
\end{equation}$$
Thus, in order for A to be independent of ω, we must verify that the results f*(ω) is independent of ω. Notice that,
$$\begin{equation*}
E\left[ U\left( \omega ^{\prime }\right) |\omega \right] =E\left[ A\omega ^{\prime 1-\sigma }|\omega \right] =A\omega ^{1-\sigma }e^{\frac{\left( 1-\sigma \right) ^{2}\sigma _{\epsilon }^{2}}{2}}.
\end{equation*}$$
The last equality holds because the assumption that ω′ is lognormal distributed with ln ω and σε as the mean and variance of ln ω′. Plug this equality into (11) to obtain
$$\begin{equation*}
\lambda \left( 1-\lambda f^{\ast }\left( \omega \right) \right) ^{-\sigma }\omega ^{1-\sigma }=A\beta \left( 1-\epsilon \right) f^{\ast }\left( \omega \right) ^{-\epsilon }e^{\frac{\left( 1-\sigma \right) ^{2} \sigma _{_{\epsilon }}^{2}}{2}}\omega ^{1-\sigma },
\end{equation*}$$
where ω cancels out of this equation and therefore f*(ω) is independent of ω confirming our guess. This expression together with (A.6) and (A.7) gives a rule to solve the optimal fertility f*, as given by
$$\begin{equation*}
\frac{\lambda \left( 1-\sigma \right) f^{\ast \epsilon }}{\beta \left( 1-\epsilon \right) }\left[ e^{-\frac{\left( 1-\sigma \right) ^{2} \sigma _{\epsilon }^{2}}{2}}-\beta f^{\ast 1-\epsilon }\right] =1-\lambda f^{\ast }.
\end{equation*}$$
$\Box$
Proof of Proposition 6. Part (i) follows from Proposition 1 and Proposition 5. As for part (ii), when M is the identity matrix, fertility is independent of ability and 
$\pi _{t+1}\left( \omega _{j}\right) = {\displaystyle \sum \nolimits _{\omega _{i}\in \Omega }} \pi _{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})=\pi _{t}\left( \omega _{j}\right) .$ The first equality uses the proof of Proposition 1. More generally, πt(ω) = π0(ω) for all ω and all t and π*(ω) = π0(ω). Part (iii) follows Proposition 5 (iii). The conditional variance of ln ωt diverges to infinite because 
$\ln \omega _{t}=\ln \omega _{0}+\sum \nolimits _{i=1}^{t} \epsilon _{i},$E(ln ωt|ω0) = ln ω0, Var(ln ωt|ω0) = t 2σ2ε and limt → ∞Var(ln ωt|ω0) = ∞.
$\Box$
Proof of Proposition 7. Notice that
$$\begin{eqnarray*}
U( \omega ) & =&\max\limits_{f_{t}\in [0,1/\lambda ]}u( ( 1-\lambda f) \omega ) +\beta f^{1-\epsilon }E[ U( \omega ^{\prime }) |\omega ] \\
&& \ge \max\limits_{[\underline{f}(\omega ),\overline{f}( \omega ) ]}u( ( 1-\lambda f) \omega ) +\beta f^{1-\epsilon }E[ U( \omega ^{\prime }) |\omega ] :=U^{1}( \omega ^{\prime }) \\
&& \ge \max\limits_{[\underline{f}(\omega ),\overline{f}( \omega ) ]}u( ( 1-\lambda f) \omega ) +\beta f^{1-\epsilon }E[ U^{1}( \omega ^{\prime }) |\omega ] :=U^{2}( \omega ^{\prime }) \\
&& ..\\
&& \ge \max\limits_{[\underline{f}(\omega ),\overline{f}( \omega ) ]}u( ( 1-\lambda f) \omega ) +\beta f^{1-\epsilon }E[ U^{r}( \omega ^{\prime }) |\omega ] =U^{r}( \omega ^{\prime }),
\end{eqnarray*}$$
where the first inequality is strict if a constraint is binding for any particular ω, the remaining inequalities follow from the contraction mapping recursion. Furthermore, a strict inequality for a particular ω translates into a strict inequality for all ω′s since M is a regular Markov chain meaning that, regardless of initial ability there is positive probability that someone in the dynasty will reach a binding state in finite time. The second part of the proposition follows because fertility restrictions do not change the MCs of having children but it decreases (or has no effect on) the MB by reducing U(ω) for all ω (see equation (11)). Hence, an upper bound of fertility makes people have fewer children than (or the same number of children with) the unrestricted case. 
$\Box$
Proof of Proposition 8. Let Prt(ω) be the size of population with ability ω at time t when there are restrictions on fertility. By Proposition 7
$$\begin{eqnarray*}
P_{1}\left( \omega _{j}\right) & =& {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) P_{0}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})\\
&& \ge {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f^{r}\left( \omega _{i}\right) P_{0}^{r}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})=P_{1}^{r}\left( \omega _{j}\right)
\end{eqnarray*}$$
where P 0(ωi) = Pr 0(ωi). The following inductive argument guarantees that if Prt(ωi) ⩽ Pt(ωi) then Pr t + 1(ωi) ⩽ P t + 1(ωi) for all ωj and all t ⩾ 0,
$$\begin{equation*}
P_{t+1}\left( \omega _{j}\right) = {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f\left( \omega _{i}\right) P_{t}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})\ge {\displaystyle \sum \limits _{\omega _{i}\in \Omega }} f^{r}\left( \omega _{i}\right) P_{t}^{r}\left( \omega _{i}\right) M(\omega _{j},\omega _{i})=P_{t+1}^{r}\left( \omega _{j}\right) .
\end{equation*}$$
Therefore,
$$\begin{eqnarray*}
W^{r} & =&\sum _{t=0}^{\infty }\sum _{\omega \in \Omega }\beta _{p}(t)U^{r} (\omega )P_{t}^{r}\left( \omega \right) \\
&& \le \sum _{t=0}^{\infty }\sum _{\omega \in \Omega }\beta _{p}(t)U(\omega )P_{t} ^{r}\left( \omega \right) \\
&& \le \sum _{t=0}^{\infty }\sum _{\omega \in \Omega }\beta _{p}(t)U(\omega )P_{t}\left( \omega \right) =W\left( \beta _{p}\right).
\end{eqnarray*}$$
$\Box$
Proof of Proposition 9. When M( ·, ω) is independent of ω, the proof of Proposition 1(ii) shows that πt + 1(ωj) = μ(ωj) for t ⩾ 0. Moreover, π0( · ) is invariant to policy changes. So restrictions on fertility only reduce individual utility, by Proposition 7, but does not affect the ability distribution of any generation. Therefore, it decreases social welfare as defined by (3). 
$\Box$
Proof of Proposition 10. This Proposition relies on Proposition 6 (ii)’s results, f(ω) = f and πt(ω) = π*(ω) = π0(ω) when M is the identity matrix. Similar to Proposition 9, fertility restrictions do not alter the distribution of abilities, which together with Proposition 7, finishes the proof. 
$\Box$
