1. INTRODUCTION
The early process of structural transformation involves a transition from agriculture to manufacturing, leading to the rise of both the employment and value added shares of the manufacturing sector.Footnote 1 This process is typically characterized by productivity growth in both the farming and manufacturing sectors and by large changes in the population size. However, the timing and speed of structural transformation, as well as the underlying changes in technology and population size, vary across countries. In order to understand fully the unique experiences of various countries, it is imperative to spell out the mechanisms underlying the effects of the sectoral technological progress and population growth in the process of structural change and to clearly articulate the interactions and trade-offs between them. This is the objective of this paper.
The first country to undergo structural transformation was England. The main period of its structural change spanned from 1700 to 1900, during which the fraction of labor employed in agriculture declined from approximately 60% to 10% [Clark (Reference Clark2001)]. Other major European countries, such as France and Germany, went through the process somewhat later and with different time profiles. Whereas the urbanization process in England was steady, this was not always the case elsewhere.
Unfortunately, relevant data necessary to provide a detailed characterization of the structural change are generally unavailable, particularly for the early European period. Nonetheless, Figure 1 illustrates two key aspects of structural transformation for a set of developed countries. Figure 1a illustrates the dramatic uniform reduction in the agricultural employment share characterizing that period. Figure 1b illustrates the accompanying steady growth in population. It is clear that the speed of the transition varied across these countries. For example, in 1880, France, Germany, and the U.S. each employed roughly 50% of their labor force in agriculture. By 1920, the French agricultural employment share dropped to 40%, while the U.S. and German shares declined all the way to 30%. The U.S. and Germany also experienced a much more dramatic population growth during this period.
Figure 1. Structural change and population in developed countries.
Many emerging economies began their structural transformation during the latter half of the 20th century and are still in the process of transitioning. Productivity data are more readily available for this more recent period, which is an important reason for discussing these countries. Based on the World Bank's WDI Dataset, Figures 2 and 3 illustrate the key aspects of structural transformation in eight arbitrarily chosen developing economies. These include the value added share of agriculture, the size of the working age population, and the evolution of labor productivity in both the agricultural and nonagricultural sectors. Since around 1960, all eight countries have experienced steady declines in the share of value added attributed to the agricultural sector. These range from around 40 percentage point reductions in Indonesia to around 15 percentage point reductions in the Philippines and Egypt.
Figure 2. Structural change, sectoral productivity, and population density in emerging economies.
Figure 3. Structural change, sectoral productivity, and population density in emerging economies.
As a rule, the process of structural transformation from agriculture to manufacturing is characterized by productivity gains in both sectors together with population growth. In the well-documented case of England, for example, total population increased more than seven-fold between 1700 and 1900, while factor-neutral productivity in both sectors approximately doubled [see Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016)]. However, as is evident from Figures 2 and 3, the pattern can vary dramatically between countries, to the extent that each country's experience is almost unique. For example, in Egypt, Pakistan, and the Philippines, industrialization has proceeded with almost no changes in the relative productivity of the two sectors. In all three of these countries, working age population has increased dramatically, suggesting that population pressures have been playing a role. In contrast, in China, the rise in the productivity in the nonagricultural sector appears to be the most important feature of the industrialization, particularly since 1980. On the other hand, in Honduras, the increase in agricultural productivity is the most pronounced change. In addition, Figures 2 and 3 suggest that, in the latter stages of industrialization, productivity in the agricultural sector appears to be catching up (in some cases only slowly) with that in the manufacturing sector.
It seems clear from this evidence that the structural transformation reflects the interaction between sectoral productivity gains in the two productive sectors together with the pressures of population growth. Furthermore, which element has played the dominant role likely varies both over time and across the various countries.Footnote 2 Despite this, the existing literature on structural transformation focuses almost exclusively on the sectoral productivity gains as the main engines of change, labeling these as the “push” and “pull” effects. The former channel refers to productivity gains in the farm sector pushing resources into manufacturing. The latter refers to productivity gains in the manufacturing sector pulling resources away from agriculture. Most importantly, the literature has largely ignored the role of population growth in the process of structural transformation, notwithstanding its quantitative significance.Footnote 3
In this paper, we examine the role of the population size effect in the structural transformation process, together with the push and pull effects of sectoral productivity gains, and the interaction between them. Although we do not explicitly model the demographic variables such as fertility, mortality, and the age-structure of the population, these variables are all implicit in the population size. Thus, by highlighting the importance of population size for the process of structural transformation, we bring the literature on structural transformation and rural–urban migration closer to the body of literature that emphasizes the role of population size on output growth [e.g. Murphy et al. (Reference Murphy, Shleifer and Vishny1989); Kremer (Reference Kremer1993); Galor and Weil (Reference Galor and Weil2000); Tamura (Reference Tamura2002); Galor (Reference Galor2011)], thereby suggesting a more prominent role for the demographics in the overall development process.
We construct a parsimonious two-sector general equilibrium growth model and employ it to investigate the process of structural transformation, assuming more general forms of production and utility functions than those that are typically adopted. Our theoretical analysis clarifies how the production and demand characteristics of the economy shape the role of population growth and sectoral productivity progress in this process.
Most of the structural transformation literature employs Cobb–Douglas sectoral production functions. This assumption is strongly rejected by the data in applications to advanced economies in their developing stages or to developing economies today. For example, the empirical estimates obtained by Allen (Reference Allen2009) suggest that the elasticity of factor substitution in aggregate production in England around 1810 was approximately 0.2. This view is supported by other economic historians, who have consistently drawn attention to the limited opportunities to substitute capital for labor during the Industrial Revolution period [e.g. Mokyr (Reference Mokyr1977, Reference Mokyr1985, Reference Mokyr1993); von Tunzelmann (Reference Von Tunzelmann and Mokyr1985)]. Estimates of the elasticity of substitution in agricultural production for developing countries based on more recent data are also low, most falling below 0.5 [e.g. Duffy and Papageorgiou (Reference Duffy and Papageorgiou2000); Salhofer (Reference Salhofer2000)].Footnote 4
An overriding characteristic of our framework giving rise to the effect of population growth on structural change is the assumption that land is a fixed factor of production in the agricultural sector. Not only is this eminently realistic, but by abstracting from it, one is ignoring an important element of the development process.Footnote 5 If one neglects land and assumes instead that technology in both sectors exhibits constant returns to scale in capital and labor, then any population increase can be absorbed proportionately across the two sectors in the long run, without imposing any structural change.
With respect to consumption preferences, there is a wide range of assumptions made in existing literature with respect to the degree of substitutability between the two consumption goods. Most of the literature assumes a logarithmic (or Cobb–Douglas) specification, often modified by the introduction of subsistence consumption, as a benchmark. Examples include Matsuyama (Reference Matsuyama1992), Kongsamut et al. (Reference Kongsamut, Rebelo and Xie2001), Caselli and Colemen (Reference Caselli and Coleman II2001), Alvarez-Cuadrado and Poschke (Reference Alvarez-Cuadrado and Poschke2011), and Gollin and Rogerson (Reference Gollin and Rogerson2014).Footnote 6 Some studies employ a CES utility function, in most cases constraining the elasticity of substitution between the two consumption goods to be substantially less than unity.Footnote 7 In contrast, Hansen and Prescott (Reference Hansen and Prescott2002) assume that the same good can be produced in the industrial as well as the agricultural sector, in effect assuming that the goods produced in the two sectors are perfect substitutes in consumption. We also represent preferences by a CES utility function, and to accommodate the prevailing variation in assumptions, we allow for both complementarity and substitutability, although we regard some degree of complementarity as being the more plausible case.
Introducing generalizations along these dimensions is important for several reasons. First, as discussed above, the assumption of a unit elasticity in agriculture is widely rejected in most relevant applications. Second, population effects appear naturally when one deviates from the assumption of a unit elasticity of substitution in agricultural production. Third, all three effects may now coexist, working in the same direction and interacting in an important fashion.Footnote 8 The generalizations thus allow us to examine these interactions and to elucidate the critical roles played by the magnitudes of elasticities of substitution in the utility and both production functions in determining the relative significance of the push, pull, and population effects. Fourth, the more general form of production technology allows us to investigate factor-biased technological change, in addition to standard considerations of factor-neutral progress. Finally, generalizing functional forms allows for more flexible features of structural change. For example, it breaks the close link between the employment and value added shares that necessarily arises under the assumption of Cobb–Douglas technologies, thereby allowing us to explain the differential empirical trends in employment and value added shares often identified as puzzling [e.g. Buera and Kaboski (Reference Buera and Kaboski2008)].
We derive conditions for the positive influence of agricultural and manufacturing productivity gains, and population size on the employment share (the push, pull, and population effects) and the value added share of the manufacturing sector. We also derive the closed-form effects on the relative price of the farm good and several other relevant quantities. Our theoretical analysis clarifies how the production and demand characteristics of the economy shape the role of population growth and sectoral productivity progress in this process. We derive that population growth will exert a stronger positive effect on the manufacturing share of employment if production flexibility in the agricultural sector is low (i.e. low substitutability between labor, capital, and land) and if the consumer demand is flexible (i.e. manufacturing good can be more easily substituted for the consumption of the agricultural good). Intuitively, with land being a fixed factor and limited opportunity to substitute labor for land and capital, the extra labor is disproportionately deployed to the more flexible manufacturing sector as long as consumer demand is sufficiently flexible to accommodate the shift in the composition of their consumption bundle. In contrast, the push effect weakens as the consumer demand becomes more flexible. The pull effect is more complex, varying positively with the elasticity of substitution in agricultural production but negatively with that in the manufacturing sector. All three effects may co-exist over a plausible range of parameter values. In a detailed quantitative application to the British experience [Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016)], we find that the rapid population growth characterizing the 18th and 19th centuries was indeed an important force behind labor reallocation across sectors (the “urbanization” process), especially during the period of 1750 to 1850.Footnote 9 In contrast, the push effect was mainly responsible for the rise in the share of output produced in the manufacturing sector (the “industrialization” process) during the early phase of the British structural transformation. A further finding that population growth was relatively more important for the employment share rather than the value added share of agriculture is consistent with the findings of Crafts (Reference Crafts1980) and Mokyr (Reference Mokyr1985).
Since Herrendorf et al. (Reference Herrendorf, Rogerson, Valentinyi, Aghion and Durlauf2014) provide an extensive review of the recent literature on structural transformation, we need only briefly highlight its existing strands. Prevailing explanations of structural change typically focus on a specific channel. One approach assumes a nonhomothetic utility function, with a lower income elasticity for the agricultural good. Combined with agricultural productivity growth, nonhomotheticity pushes labor out of the farm sector. Agricultural productivity growth is necessary for this demand-side explanation to work.Footnote 10 Such demand-side channels appear in Matsuyama (Reference Matsuyama1992), Echevarria (Reference Echevarria1997), Laitner (Reference Laitner2000), Caselli and Coleman (Reference Caselli and Coleman II2001), Kongsamut et al. (Reference Kongsamut, Rebelo and Xie2001), Gollin et al. (Reference Gollin, Parente and Rogerson2002), and Buera and Kaboski (Reference Buera and Kaboski2008), among others.
An alternative strand of literature advocates a supply-side explanation, which postulates that the structural transformation is a result of differential productivity growth across sectors [see Baumol (Reference Baumol1967)]. In the case of substitutability between the two consumption goods in utility, faster productivity growth sector pulls labor in [e.g. Lewis (Reference Lewis1954); Hansen and Prescott (Reference Hansen and Prescott2002); Doepke (Reference Doepke2004), Bar and Leukhina (Reference Bar and Leukhina2010)]. In contrast, Ngai and Pissarides (Reference Ngai and Pissarides2007) assume complementarity and obtain a push effect from the relatively fast growing sector. Acemoglu and Guerrieri (Reference Acemoglu and Guerrieri2008) discuss an additional supply-side effect arising from capital accumulation and sectoral differences in capital intensities.Footnote 11
Because the existing literature typically focuses on only one of the channels of structural change, the relative importance of various channels remains unclear, although Buera and Kaboski (Reference Buera and Kaboski2008), Dennis and Iscan (Reference Dennis and Iscan2009), Alvarez-Cuadrado and Poschke (Reference Alvarez-Cuadrado and Poschke2011), and Guillo, Papageorgiou, and Perez-Sebastian (Reference Guillo, Papageorgiou and Perez-Sebastian2011) all provide important steps in addressing this issue. But the main limitation of the existing structural transformation literature, from our perspective, is that the role of population growth has been inadequately studied alongside the push and pull effects, despite its controversy among economic historians and the empirical evidence illustrated in Figures 1–3. We aim to address this shortcoming.
The remainder of the paper proceeds as follows. Section 2 sets out the analytical framework and derives the macroeconomic equilibrium. Section 3 discusses general conditions for the pull, push, and population effects, while Section 4 decomposes the push and pull effects into the different components characterizing the underlying factor-biased technological change. Section 5 discusses the related phenomenon of industrialization, indicating its trade-offs with urbanization, while Section 6 elaborates further on the population effect. Section 7 considers the change in the relative importance of the pull, push, and population effects in the development process. We discuss some of the modifications introduced by international trade through colonization in Section 8. In Section 9, we employ our results to discuss several issues that have arisen in the empirical literature on structural transformation. Section 10 concludes.
2. ANALYTICAL FRAMEWORK
We consider a two-sector economy, consisting of a farming sector that produces an agricultural good and an industrial sector that produces a nonfarm (or manufacturing) good.Footnote 12 We choose the manufacturing good as numeraire and denote the relative price of the agricultural good by pt .
2.1. Preferences and Households
We assume that the economy comprises Lt
representative agents at time t, with the population growing exogenously over time.Footnote
13
Each agent is endowed with an initial capital stock, k
0, and a unit of time. For simplicity, we assume that capital does not depreciate and may be augmented via investment purchased from the manufacturing sector. The economy is endowed with a fixed stock of land N, with the share
${N/ {{L_t}}}$
owned by each agent.
Each period, the representative agent inelastically supplies labor at a wage rate wt and rents out its capital and land holdings at rates rt and κ t , respectively. Given {wt , rt , κ t , pt }∞ t = 0, the representative household makes consumption and capital accumulation choices {at , ct , k t + 1}∞ t = 0 to maximize individual utility:
$$\begin{equation}
{\rm{Maximize}}\;\sum\limits_{t = 0}^\infty {{\beta ^t}} U({a_t} - \bar{a},{c_t}),\;0 < \beta < 1,
\end{equation}$$
subject to the budget constraint
$$\begin{equation}
{p_t}{a_t} + {c_t} + {k_{t + 1}}\frac{{L_{t + 1}^{}}}{{{L_t}}} = (1 + {r_t}){k_t} + {w_t} + {\kappa _t}\frac{N}{{{L_t}}},
\end{equation}$$
and non-negativity constraints on at
, ct
, and k
t + 1, where at
denotes individual consumption of the agricultural good,
$\bar{a}$
denotes its subsistence level, ct
refers to individual consumption of the manufacturing good, and kt
denotes capital holdings.
Conventional optimality conditions are obtained:
$$\begin{equation}
\frac{{{U_a}({a_t} - \bar{a},{c_t})}}{{{U_c}({a_t} - \bar{a},{c_t})}} = {p_t},
\end{equation}$$\\
$$\begin{equation}
\frac{{{U_c}({a_t} - \bar{a},{c_t})}}{{{U_c}({a_{t + 1}} - \bar{a},{c_{t + 1}})}} = \beta (1 + {r_{t + 1}})\frac{{{L_t}}}{{{L_{t + 1}}}},
\end{equation}$$
The utility function in (1a) incorporates the widely adopted assumption in the structural transformation literature that utility is subject to a subsistence level with respect to food consumption. This renders the utility function nonhomothetic, with the income elasticity of the demand for food being less than unity. While many studies assume a logarithmic utility, we adopt the general CES form:Footnote 15
$$\begin{equation}
U \equiv \frac{1}{\gamma }{\left[ {\alpha {{\left( {{a_t} - \bar{a}} \right)}^\rho } + (1 - \alpha ){{\left( {{c_t}} \right)}^\rho }} \right]^{\frac{\gamma }{\rho }}},
\end{equation}$$
where
$\sigma = {1
/ {(1 - \rho )}}$
represents the intratemporal elasticity of substitution between the two consumption goods, while the intertemporal elasticity of substitution (IES) is given by
${1
/ {(1 - \gamma )}}$
. We view this generalization as important since the degree of substitutability between the two consumption goods plays a critical role in the process of structural development. As noted earlier, σ has proven to be an elusive parameter and values ranging from perfect complementarity, σ = 0, [e.g. Buera and Kaboski (Reference Buera and Kaboski2008); Herrendorf et al. (Reference Herrendorf, Rogerson and Valentinyi2013)] to perfect substitutability, σ → ∞, [e.g. Hansen and Prescott (Reference Hansen and Prescott2002); Doepke (Reference Doepke2004); Bar and Leukhina Reference Bar and Leukhina2010)] have been considered.Footnote
16
Adopting (3), and introducing
${\tilde{c}_t} \equiv {[ {\alpha ({a_t} - \bar{a}){}^\rho + (1 - \alpha ){{({c_t})}^\rho }} ]^{{1
/ \rho }}}$
as a shorthand, the optimality conditions (2a) and (2b) become
$$\begin{equation}
\left( {\frac{\alpha }{{1 - \alpha }}} \right){\left( {\frac{{{a_t} - \bar{a}}}{{{c_t}}}} \right)^{\rho - 1}} = {p_t},
\end{equation}$$\\
$$\begin{equation}
{\left( {\frac{{{{\tilde{c}}_t}}}{{{{\tilde{c}}_{t + 1}}}}} \right)^{\gamma - \rho }}{\left( {\frac{{{c_{t + 1}}}}{{{c_t}}}} \right)^{1 - \rho }} = \beta (1 + {r_{t + 1}})\frac{{{L_t}}}{{{L_{t + 1}}}}.
\end{equation}$$
2.2. Technology and Firms
There is a large number of identical firms in the manufacturing sector, each endowed with an identical technology F which is homogeneous of degree 1 in its inputs. Analogously, there is a large number of identical firms in the agricultural sector, each endowed with an identical technology G, also homogeneous of degree 1 in its inputs. The homogeneity assumption allows us to restrict attention to a single aggregate firm for each sector exhibiting competitive behavior. We assume capital and labor to be perfectly mobile across sectors, so the two firms face the same capital rental rates and wages.
Output of the manufacturing sector is described by the neoclassical production function:Footnote 17
$$\begin{equation}
{Y_{M,t}} = F({K_{M,t}},{L_{M,t}},{B_{M,t}}),
\end{equation}$$
where K M, t and L M, t denote aggregate capital and labor employed by the manufacturing sector, and B M, t summarizes the general level of technology. Changes in B M, t potentially encompass both factor-neutral and factor-biased technical progress. Taking factor rental rates as given, the aggregate manufacturing firm maximizes profits:
$$\begin{equation}
\mathop {{\rm{Maximize}}}\limits_{{K_{M,t}},{L_{M,t}}} :\,\,F({K_{M,t}},{L_{M,t}},{B_{M,t}}) - {w_t}{L_{M,t}} - {r_t}{K_{M,t}}.
\end{equation}$$
Output of the agricultural sector is described by the neoclassical production function:
$$\begin{equation}
{Y_{A,t}} = G({K_{A,t}},{L_{A,t}},{N_t},{B_{A,t}}),
\end{equation}$$
where K A, t , L A, t , and Nt denote aggregate capital, labor, and land employed in agriculture; and B A, t denotes the general level of technology. Taking factor rental rates as given, the aggregate firm in the agricultural sector solves:
$$\begin{equation}
\mathop {{\rm{Maximize}}}\limits_{{K_{A,t}},{L_{A,t}},{N_t}} :\,\,{p_t}G({K_{A,t}},{L_{A,t}},{N_t},{B_{A,t}}) - {w_t}{L_{A,t}} - {r_t}{K_{A,t}} - {\kappa _t}{N_t}.
\end{equation}$$
The optimal sectoral allocations are described by the standard static efficiency conditions:
$$\begin{equation}
{F_K}({K_{M,t}},{L_{M,t}},{B_{M,t}}) = {p_t}{G_K}({K_{A,t}},{L_{A,t}},{N_t},{B_{A,t}}) = {r_t},
\end{equation}$$\\
$$\begin{equation}
{F_L}({K_{M,t}},{L_{M,t}},{B_{M,t}}) = {p_t}{G_L}({K_{A,t}},{L_{A,t}},{N_t},{B_{A,t}}) = {w_t}.
\end{equation}$$
Linear homogeneity of the production functions implies F = FKKM + FLLM and G = GKKA + GLLA + GNN.
2.3. Market Clearing
We use upper case letters to denote aggregate quantities of the manufacturing good consumption, agricultural good consumption, and aggregate supply of capital: Ct = ctLt , At = atLt , and Kt = ktLt .
Labor, capital, and land markets are assumed to clear at all times t, implying
$$\begin{equation}
{L_{M,t}} + {L_{A,t}} = {L_t},
\end{equation}$$\\
$$\begin{equation}
{K_{M,t}} + {K_{A,t}} = {K_t},
\end{equation}$$\\
$$\begin{equation}
{N_t} = N.
\end{equation}$$
Assuming that capital is produced in the manufacturing sector, clearance of the manufacturing and agricultural markets is described by
$$\begin{equation}
{K_{t + 1}} - {K_t} + {C_t} = F({K_{M,t}},{L_{M,t}},{B_{M,t}}),
\end{equation}$$\\
$$\begin{equation}
{A_t} = G({K_{A,t}},{L_{A,t}},{N_t},{B_{A,t}}).
\end{equation}$$
2.4. Competitive Equilibrium
A competitive equilibrium, for given parameter values, initial capital (K 0) and exogenous sequences {BAt , BMt , Lt }∞ t = 0, consists of allocation sequences {At ,Ct ,K t + 1,K A, t ,K M, t ,L A, t ,L M, t , Nt }∞ t = 0 and prices {pt , wt , rt , κ t }∞ t = 0 such that the household's maximization problem in (1a)–(1b) and the firms’ maximization problems in (4b) and (5b) are solved, and all markets clear.
The equilibrium is characterized by the following first-order and market clearing conditions:
$$\begin{equation}
\left( {\frac{\alpha }{{1 - \alpha }}} \right){\left( {\frac{{{A_t} - \bar{a}{L_t}}}{{{C_t}}}} \right)^{\rho - 1}} = {p_t},
\end{equation}$$\\
$$\begin{equation}
{F_K}({K_{M,t}},{L_{M,t}},{B_{M,t}}) = {p_t}{G_K}({K_{A,t}},{L_{A,t}},N,{B_{A,t}}) = {r_t},
\end{equation}$$\\
$$\begin{equation}
{F_L}({K_{M,t}},{L_{M,t}},{B_{M,t}}) = {p_t}{G_L}({K_{A,t}},{L_{A,t}},N,{B_{A,t}}),
\end{equation}$$\\
$$\begin{equation}
{L_{M,t}} + {L_{A,t}} = {L_t},
\end{equation}$$\\
$$\begin{equation}
{K_{M,t}} + {K_{A,t}} = {K_t},
\end{equation}$$\\
$$\begin{equation}
{A_t} = G({K_{A,t}},{L_{A,t}},N,{B_{A,t}}),
\end{equation}$$
These equations determine short-run solutions for At , pt , L M, t , L A, t , K M, t , K A, t and rt in terms of Kt , Lt , Ct . The dynamic evolution of those variables is obtained by substituting these solutions into the Euler equation, (3b),
$$\begin{equation}
{\left( {\frac{{{{{{\tilde{C}}_t}}
/ {{L_t}}}}}{{{{{{\tilde{C}}_{t + 1}}}
/ {{L_{t + 1}}}}}}} \right)^{\gamma - \rho }}{\left( {\frac{{{{{C_{t + 1}}}
/ {{L_{t + 1}}}}}}{{{{{C_t}}
/ {{L_t}}}}}} \right)^{1 - \rho }} = \beta (1 + {r_{t + 1}})\frac{{{L_t}}}{{{L_{t + 1}}}},
\end{equation}$$
(where
${\tilde{C}_t} \equiv {\tilde{c}_t}{L_t}$
) together with the goods market equilibrium relationship (8a) and the specification of the exogenous evolution of labor. In addition to the initial condition on the aggregate capital stock, the transversality condition, imposing intertemporal solvency, is assumed to hold. Because the utility and production function satisfy the standard assumptions, there is a unique equilibrium. Conditions (9a)–(9g), (8a), and the transversality condition are sufficient for its characterization.Footnote
18
As indicated, much of the discussion of the structural development literature has focused on the respective roles played by technological advances in the industrial versus the agriculture sector. We shall address this by considering the extent to which technological improvements in the industrial sector, represented by changes in B
M, t
, attract labor to the manufacturing sector, and compare them to the effects of technological change in the agricultural sector, as represented by changes in B
A, t
, referring to these two forces as the “pull” and “push” effects, respectively. However, we are also concerned with understanding the role played by population growth experienced by many economies undergoing structural transformations, most notably England and the U.S., and more recently, Egypt, Malaysia, and the Philippines. Thus, as a third factor, we consider the extent to which the substantial growth in population contributed to the urbanization and industrialization processes, by leading to a more than proportionate increase in the fraction of the population employed in the nonagricultural sector. We measure this by
${{({{d{L_M}}/ {{L_M}}})}\mathord{/ {\vphantom {{({{d{L_M}} / {{L_M}}})} {({{dL} / L})}}} \kern-\nulldelimiterspace} {({{dL}/L})}} - 1$
, and term it the “population” effect.
In contrast to Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016), which was focused on calibrating a similar model to match the empirical moments of the English data and on understanding the English case, our emphasis here is on identifying the underlying mechanisms involved in various aspects of the transformation process and examining the trade-offs between them.
Most of the theoretical literature analyzing the pull and push effects employs Cobb–Douglas production functions. In addition, the production function for the agricultural sector typically abstracts from land, thereby fixing the precise substitution possibilities between labor and capital.
As will become evident, the significance of the pull and push effects depends crucially upon two key elements of the production process. The first is the degree of factor substitution in production, most notably in the agricultural sector; the second is the effect of changes in technology B i, t on factor efficiency, which reflects the type of technological change such as Hicks neutral or factor-augmenting. The generality imposed on sectoral production technologies enables us to investigate the impact of both Hicks neutral and factor-augmenting technological change, the effects of which can be quite dissimilar. In addition, the fact that land is a fixed factor plays a critical role in determining the significance of the population effect.
Finally, since structural transformation is intrinsically a long-term process, we shall focus our attention on the steady-state consequences of the three effects we are addressing. Under the assumption that the exogenous sequences {B A, t , B M, t , Lt }∞ t = 0 converge to constant values in the long run, the model equilibrium converges to a steady state. In the case where the technological change is of the Hicks-neutral form, the steady state (denoted by tildes) is described by
$$\begin{equation}
\frac{{{B_M}{F_K}({{\tilde{K}}_M},{{\tilde{L}}_M})}}{{{B_A}{G_K}({{\tilde{K}}_A},{{\tilde{L}}_A},N)}} = \frac{{{B_M}{F_L}({{\tilde{K}}_M},{{\tilde{L}}_M})}}{{{B_A}{G_L}({{\tilde{K}}_A},{{\tilde{L}}_A},N)}}\nonumber\\
\qquad = \left( {\frac{\alpha }{{1 - \alpha }}} \right){\left( {\frac{{\tilde{A} - \bar{a}\tilde{L}}}{{\tilde{C}}}} \right)^{\rho - 1}} = \tilde{p},
\end{equation}$$\\
$$\begin{equation}
{B_M}{F_K}({\tilde{K}_M},{\tilde{L}_M}) = \frac{{1 - \beta }}{\beta },
\end{equation}$$\\
$$\begin{equation}
\tilde{C} = {B_M}F({\tilde{K}_M},{\tilde{L}_M}),
\end{equation}$$\\
$$\begin{equation}
\tilde{A} = {B_A}G({\tilde{K}_A},{\tilde{L}_A},N),
\end{equation}$$\\
$$\begin{equation}
{\tilde{L}_M} + {\tilde{L}_A} = L,
\end{equation}$$\\
$$\begin{equation}
{\tilde{K}_M} + {\tilde{K}_A} = \tilde{K}.
\end{equation}$$
The above equilibrium conditions highlight the channels through which the effects we are considering impinge on the long-run equilibrium. First, both the pull and the push effects operate through their impacts on the ratio of the marginal products, and its consequences for factor allocations across sectors, (10a). Second, the pull effect has a direct impact on the equilibrium capital–labor ratio in the manufacturing sector, via the modified golden rule relationship, (10b), and its effect on manufacturing output in (10c), while the push effect has an analogous effect on the agricultural output as specified by (10d). The primary channel of the population effect is through the labor market clearing condition, (10e), and the fact that the production of food involves the fixed factor of production, land. To the extent, there is a required subsistence level of food consumption,
$\bar{a}$
, as in (10a), the marginal rate of substitution between the consumption of the two goods provides a secondary channel.
3. CONDITIONS FOR PULL, PUSH, AND POPULATION EFFECTS: GENERAL OBSERVATIONS
To establish the conditions for the pull, push, and population size effects to hold, we differentiate the steady-state conditions (10a)–(10f) with respect to BM , BA , and L. To facilitate the analysis, we shall henceforth assume that the production functions of both sectors are of the CES form:
$$\begin{equation}
{B_M}F({K_M},{L_M}) \equiv {B_M}{\left[ {{b_M}K_M^{{\varepsilon _M}} + {c_M}L_M^{{\varepsilon _M}}} \right]^{\frac{1}{{{\varepsilon _M}}}}},\quad {b_M} + c_M^{} = 1,
\end{equation}$$
$$\begin{eqnarray}
{B_A}G({K_A},{L_A},N) \equiv {B_A}{\left[ {{b_A}K_A^{{\varepsilon _A}} + {c_A}L_A^{{\varepsilon _A}} + {d_A}{N^{{\varepsilon _A}}}} \right]^{\frac{1}{{{\varepsilon _A}}}}},\quad {b_A} + c_A^{} + {d_A} = 1.\nonumber\\
\end{eqnarray}$$
Using this notation, the constant elasticity of substitution in the manufacturing sector is
$$\begin{equation*}
{r_M} = \frac{{{F_K}{F_L}}}{{{F_{KL}}F}} = \frac{1}{{1 - {\varepsilon _M}}},
\end{equation*}$$
while the common, pairwise, elasticities of substitution across the three factors in the farm sector areFootnote 19
$$\begin{equation*}
{r_A} = \frac{{{G_K}{G_L}}}{{{G_{KL}}G}} = \frac{{{G_K}{G_N}}}{{{G_{KN}}G}} = \frac{{{G_L}{G_N}}}{{{G_{LN}}G}} = \frac{1}{{1 - {\varepsilon _A}}}.
\end{equation*}$$
In addition, equilibrium factor shares of income in the manufacturing sector are
${s_K} \equiv {{{F_K}{K_M}}
/ F}$
,
${s_L} \equiv {{{F_L}{L_M}}
/ {F,}}$
where sK
+ sL
= 1, while the agricultural income shares are
${a_K} \equiv {{{G_K}{K_A}}
/ G}$
,
${a_L} \equiv {{{G_L}{L_A}}
/ G}$
, and
${a_N} \equiv {{{G_N}N}
/ G}$
, where aK
+ aL
+ aN
= 1.
The resulting long-run structural changes of the pull, push, and population effects are reported in Tables 1–3, where we summarize the steady-state responses of sectoral factor movements, relative prices, and their impact on the production structure. As a general observation, we see that these responses are highly dependent upon three sets of factors: (i) the flexibility of production, as reflected in the sectoral elasticities of substitution, rM
, rA
; (ii) the complementarity/substitutability of the two goods in consumption, as reflected in σ; and (iii) nonhomotheticity in demand, as reflected in the subsistence term
$\chi \equiv {{\bar{a}}
/ {\tilde{a}}} \equiv {{(\bar{a}L)}
/ {\tilde{A}}}$
.
Table 1. Pull effects: Effects of productivity increase in manufacturing sector
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with CES production functions in both sectors and a CES utility function with subsistence consumption requirement. In the above, the following shorthand is used:
$Q \equiv {L_M}[ {\frac{{1 - {a_N}}}{{\sigma (1 - \chi )}} + \frac{{{a_N}}}{{{r_A}}}} ] + \frac{{{L_A}}}{\sigma } > 0$
.
Table 2. Push effects: Effects of productivity increase in agricultural sector
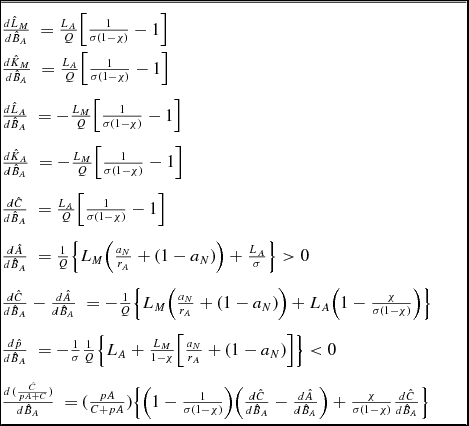
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with CES production functions in both sectors and a CES utility function with subsistence consumption requirement. In the above, the following shorthand is used:
$Q \equiv {L_M}[ {\frac{{1 - {a_N}}}{{\sigma (1 - \chi )}} + \frac{{{a_N}}}{{{r_A}}}} ] + \frac{{{L_A}}}{\sigma } > 0$
.
Table 3. Population effects: Effects of population increase
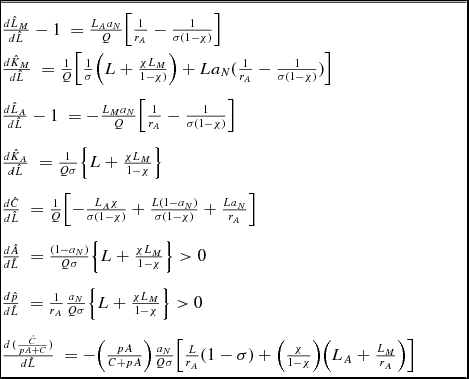
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with CES production functions in both sectors and a CES utility function with subsistence consumption requirement. In the above, the following shorthand is used:
$Q \equiv {L_M}[ {\frac{{1 - {a_N}}}{{\sigma (1 - \chi )}} + \frac{{{a_N}}}{{{r_A}}}} ] + \frac{{{L_A}}}{\sigma } > 0$
.
In addition, the population effect depends crucially upon aN
> 0, land appearing as a fixed factor in the agricultural sector. If aN
= 0, both production functions are homogeneous in capital and labor, and with the utility function being homogeneous in
$(A - \bar{a}L)$
and C, the steady-state conditions (9a)–(9e) imply that
$d{\hat{L}_M} = d{\hat{K}_M} = d{\hat{L}_A} = d{\hat{K}_A} = d\hat{C} = d\hat{A} = d\hat{L};\,\,d\hat{p} = 0$
. That is, in the long run, all quantities must change proportionately in response to an increase in population, with the relative price remaining unchanged. This is because in that case, the economy-wide production structure is sufficiently flexible so that the additional labor can be absorbed proportionately in both sectors without requiring any structural adjustments. This is analogous to the role played by population growth in the model developed by Goodfriend and McDermott (Reference Goodfriend and McDermott1995). In their analysis, the importance of population is due to the assumption that per capita output is an average of output produced under a diminishing returns technology and an increasing returns technology, so its allocation across the two sectors matters.
Since the main driving force in these adjustments is the movement of labor from rural to urban areas – the process of urbanization – we begin by determining the responses of sectoral employment to the three effects we have identified. From Tables 1–3, we see:Footnote 20
$$\begin{equation}
\frac{{d{{\hat{L}}_M}}}{{d{{\hat{B}}_M}}} = \frac{{{L_A}}}{{Q{s_L}}}\left\{ {\left[ {\frac{{{a_K}{r_A}}}{{\sigma (1 - \chi )}} + (1 - {a_K})} \right] - \frac{1}{\sigma }({s_L} + {s_K}{r_M})} \right\},
\end{equation}$$\\
$$\begin{equation}
\frac{{d{{\hat{L}}_M}}}{{d{{\hat{B}}_A}}} = \frac{{{L_A}}}{Q}\left[ {\frac{1}{{\sigma (1 - \chi )}} - 1} \right],
\end{equation}$$\\
$$\begin{equation}
\frac{{d{{\hat{L}}_M}}}{{d\hat{L}}} - 1 = \frac{{{L_A}{a_N}}}{Q}\left[ {\frac{1}{{{r_A}}} - \frac{1}{{\sigma (1 - \chi )}}} \right],
\end{equation}$$
$Q \equiv {L_M}[ {\frac{{1 - {a_N}}}{{\sigma (1 - \chi )}} + \frac{{{a_N}}}{{{r_A}}}} ] + \frac{{{L_A}}}{\sigma } > 0$
and
$\chi \equiv {{\bar{a}}
/ {\tilde{a}}} \equiv {{(\bar{a}L)}
/ {\tilde{A}}}$
.
These equations reveal a number of interesting implications and differences between the determinants of the three effects on sectoral allocation. First, beginning with the natural benchmark case where both production functions are Cobb–Douglas (rM = rA = 1) and the utility function is logarithmic (σ = 1), we see from (12a)–(12c) that the existence of both the pull effect and the push effect depends entirely on the presence of the subsistence effect, χ, confirming the result of Alvarez-Cuadrado and Poschke (Reference Alvarez-Cuadrado and Poschke2011).Footnote 21 In this case, the population effect is negative: For a given percentage of population increase, the urban population will increase less than proportionately. In this case, population growth increases the subsistence consumption requirement, driving up the demand for farm good consumption and thus shifting labor toward the farming sector.Footnote 22 If, further,χ = 0, neither changes in sectoral technology nor changes in population have any effect on relative sectoral employment. Because under these typical assumptions, population growth has either a negative or no impact on structural change, it is unsurprising that it has been largely dismissed as a potential driving force behind movements in sectoral employment shares.
The fact that under more general conditions regarding production and preferences, our analysis can generate all three effects (even simultaneously), independently of any arbitrary assumption regarding subsistence consumption, confirms the importance of generalizing the analysis in the directions we are proposing. This is particularly true in light of the empirical evidence questioning the appropriateness of the Cobb–Douglas production function, especially for countries in the early stages of development. The evidence, reviewed in the Introduction, overwhelmingly points to the elasticity of substitution well below 0.5.Footnote 23 In fact, economic historians focusing primarily on the early development of Britain, have even suggested that the Leontief fixed coefficient technology may be a reasonable approximation for the agricultural sector.
From (12a), we see that the pull effect generally depends upon the structural characteristics of the entire economy, including the production characteristics of both sectors, as summarized by their elasticities of substitution and factor shares, as well as the demand structure as reflected in σ and proximity to the subsistence level of food consumption, χ.
A higher elasticity of substitution in the production of agricultural goods, rA
, facilitates a positive pull effect on the level of urbanization. Intuitively, an increase in the productivity of the manufacturing sector, BM
, increases the return to capital, encouraging its accumulation, part of which is deployed to the agricultural sector. A high elasticity of substitution in that sector then enables farmers to substitute capital for labor, thereby freeing up labor to migrate to the urban sector. In contrast, a high elasticity of substitution in the manufacturing sector, rM
, weakens the pull effect: With high substitution possibilities in manufacturing, the increased return to capital induces firms to substitute away from labor and toward capital, thereby mitigating the labor pull effect. The fact that the pull effect has strong long-run influences working against it can be seen directly from the modified golden rule condition, (10b). With the marginal physical product of capital being fixed in the long run, the long-run effect of an increase in productivity in the manufacturing sector requires that the capital–labor ratio in that sector rises, which will be the case if and only if the proportionate increase in the capital stock exceeds
${{{r_M}}
/ {{s_L}}}$
.Footnote
24
In contrast, the existence of the push effect is determined entirely by demand conditions. The push effect is viable if and only if σ(1 − χ) < 1, that is, the two goods are complementary in consumption.Footnote 25 The intuition for this finding follows from (10a). An increase in BA raises the productivity of both factors in the agricultural sector, directly increasing its output and consumption. With the two goods being complements, the demand for the manufacturing good would increase to balance the increase in agricultural consumption. For the equilibrium to be maintained, factors must reallocate to the manufacturing sector.
Although we shall discuss the population effect in more detail in Section 6, we may note that its impact on the employment share of manufacturing involves a direct trade-off between rA and σ(1 − χ), as seen from the bracketed term in (12c). The population effect on the manufacturing employment share is strong if agricultural production is inflexible (low rA ) and demand conditions are flexible (high σ(1 − χ)). The intuition is as follows. If factors are not easily substitutable in agriculture, additional labor is not easily absorbed in farm production. It is pushed into the manufacturing sector, where production possibilities are more flexible. In the extreme case of a Leontief production function, all of the additional labor will be employed in manufacturing as long as χ < 1, which would ensure equilibrium existence. If the two goods are easily substitutable and nonhomotheticity is not too strong, i.e. the demand conditions are flexible, the labor pushed out of agriculture is easily absorbed in manufacturing, as the consumption of the manufacturing product is easily substituted for the consumption of the agricultural good.
Therefore, whether or not population growth will shift resources toward the nonfarm sector depends critically upon the relative magnitudes of the two elasticities, and most notably σ, which varies extensively in the structural change literature. The population effect will clearly apply if one assumes perfect substitutability between the two consumption goods (σ → ∞), as do Hansen and Prescott (Reference Hansen and Prescott2002), Doepke (Reference Doepke2004), and Bar and Leukhina (Reference Bar and Leukhina2010). But it will not apply if the utility function is of the Leontief form (σ = 0), which Buera and Kaboski (Reference Buera and Kaboski2008) and Herrendorf et al. (Reference Herrendorf, Rogerson and Valentinyi2013) (in the case of the value added definition of production sectors) suggest is a good approximation for the U.S. during the 20th century. The numerical simulations, reported in Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016), illustrate just how sensitive σ is to the underlying demand structure, and while σ ≈ 0 may be a good approximation in some circumstances, they show how in the case of England, it jeopardizes the industrialization aspect of structural change, by implying overly strong price responses.
The conditions for the existence of pull, push, and population effects on urbanization can be summarized by the following proposition:
Proposition 1:
-
(i) “Pull Effect”: A productivity increase in the industrial sector will attract labor to that sector if and only if
$\sigma > \frac{{(1 - \chi )({s_L} + {s_K}{r_M}) - {a_K}{r_A}}}{{(1 - \chi )(1 - {a_K})}}$
. -
(ii) “Push Effect”: A productivity increase in the agricultural sector will push the labor to the industrial sector if and only if σ(1 − χ) < 1, i.e. agricultural and manufacturing goods are gross complements.
-
(iii) “Population Effect”: An increase in the population will attract labor more than proportionately to the industrial sector if and only if σ(1 − χ) > rA .
The pull effect is more likely to hold if χ > 0, the elasticity of substitution in the industrial sector is relatively low, and the elasticity of substitution in the agricultural sector is relatively high.Footnote 26 The push effect is more likely to hold if χ > 0, but it is independent of production conditions in the two sectors. The population effect is less likely to hold if χ > 0 and if rA is relatively large, but it is independent of production conditions in the industrial sector. Importantly, the population effect exists, for a sufficiently low rA , regardless of the substitutability between the farm and the manufactured goods.
It is also evident from the adjustments in labor reported in (12) that it is possible for all three effects on urbanization to co-exist. Conditions that ensure that all three effects co-exist are summarized in the following proposition:
Proposition 2: The pull, push, and population effects will all contribute positively to the urbanization process if and only if the two consumption goods are gross complements satisfying
$$\begin{equation*}
1 > \sigma (1 - \chi ) > \max \left[ {\frac{{(1 - \chi )({s_L} + {s_K}{r_M}) - {a_K}{r_A}}}{{(1 - {a_K})}},{r_A}} \right].
\end{equation*}$$
This condition is more likely to hold if rM and rA are relatively small. It is also more likely to hold in the presence of a subsistence consumption level, although not if it is too large.Footnote 27 The condition cannot be satisfied if rM = rA = 1, χ = 0 or if χ = 1. In the former case, which was discussed earlier, the pull effect cannot co-exist with the push effect, and the degree of substitutability in consumption determines which effect prevails. In the latter case, the population effect is negative.
4. DECOMPOSITION OF PULL AND PUSH EFFECTS ON URBANIZATION
Further insight is obtained by considering the forces influencing the pull and push effects in terms of the sources of the underlying factor augmenting technological change. Focusing first on the pull effect, this can be examined by writing the production function in the urban sector as
$$\begin{equation}
{Y_M} = {B_M}F({K_M},{L_M}) = F({B_{MK}}{K_M},{B_{ML}}{L_M})\,\,,\,\,\,\,\,{B_{MK}} = {B_{ML}} = {B_M}.
\end{equation}$$
Written in this way, we can show that the total pull effect, represented by the Hicks neutral increase in technology, (12a), can be decomposed into one component due to enhanced productivity of capital,
$$\begin{equation}
\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_{MK}}}} = \frac{{{L_A}{s_K}}}{{Q{s_L}}}\left \{{\frac{{{a_K}{r_A}}}{{\sigma (1 - \chi )}} + (1 - {a_K}) - \frac{{{r_M}}}{\sigma }} \right\},
\end{equation}$$
and another component due to the enhanced productivity of labor,
$$\begin{equation}
\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_{ML}}}} = \frac{{{L_A}}}{Q}\left \{{\frac{{{a_K}{r_A}}}{{\sigma (1 - \chi )}} + (1 - {a_K}) - \frac{1}{\sigma }} \right\}.
\end{equation}$$
The two components can be seen to be generally similar, with the conditions for both to contribute positively to the pull effect being identical if the production function in the urban sector is Cobb–Douglas. In that case, the relative intensity of the two components is proportional to the relative shares of the two factors in the output of manufactures, i.e.
$$\begin{linenomath}{{({{\partial {{\hat{L}}_M}}
/ {\partial {{\hat{B}}_{MK}}}})}
\mathord{/ {\vphantom {{({{\partial {{\hat{L}}_M}}
/ {\partial {{\hat{B}}_{MK}}}})} {({{\partial {{\hat{L}}_M}}
/ {\partial {{\hat{B}}_{ML}}}})}}} \kern-\nulldelimiterspace} {({{\partial {{\hat{L}}_M}}
/ {\partial {{\hat{B}}_{ML}}}})}} = ({{{s_K}}
/ {{s_L}}}).\end{linenomath}$$
Writing the production function for agricultural output as
$$\begin{eqnarray}
{Y_A} = {B_A}G({K_A},{L_A},N) = G({B_{AK}}{K_M},{B_{AL}}{L_A},{B_{AN}}N)&\!,&\nonumber\\
{B_{AK}} = {B_{AL}} = {B_{AN}} = {B_A}&\!,&
\end{eqnarray}$$
the total push effect of a Hicks neutral technological increase in (12b) can be decomposed into three separate components due to the enhanced productivity of capital, labor, and land, respectively:
$$\begin{equation}
\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_{AK}}}} = \frac{{{L_A}{r_A}{a_K}}}{Q}\left[ {\frac{1}{{\sigma (1 - \chi )}} - \frac{1}{{{r_A}}}} \right],
\end{equation}$$\\
$$\begin{equation}
\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_{AL}}}} = - \frac{{{L_A}}}{Q}\left[ {\frac{{{r_A}}}{{\sigma (1 - \chi )}}\left[ {{a_K} - \frac{1}{{{r_A}}}(1 - {a_N})} \right] + \left[ {1 - {a_K} - \frac{1}{{{r_A}}}{a_N}} \right]} \right],\qquad
\end{equation}$$\\
$$\begin{equation}
\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_{AN}}}} = \frac{{{L_A}{a_N}}}{Q}\left[ {\frac{1}{{\sigma (1 - \chi )}} - \frac{1}{{{r_A}}}} \right].
\end{equation}$$
This decomposition reveals a sharp contrast between the effects due to the enhanced productivity of capital and land, which are very similar, and that due to labor. Indeed, the condition for an increase in productivity in capital or land to contribute to a positive push effect, given by the bracketed term in (16a) and (16c), is precisely opposite to that associated with the population effect, (12c), and will hold if and only if rA > σ(1 − χ). Assuming that the elasticity of substitution in the farm sector is low, this condition will not hold, and productivity increases associated with efficiency gains of capital or land will actually generate a negative push effect. Intuitively, an increase in the efficiency of capital or land results in the relative scarcity of labor in farming. If capital cannot be easily substituted for labor in agricultural production and if demand is sufficiently flexible to allow for a shift of consumption in favor of the agricultural good, then labor will flow to the farming sector.
From (16b), we see that the overall push effect associated with enhanced productivity in the agricultural sector is due to higher productivity of labor. As labor increases in efficiency, given a low elasticity of substitution, it is optimal for the farm sector to employ less labor, enabling the excess and more productive labor to migrate to the urban sector.
The Hicks neutral production function has the implication that the sectoral factor shares remain constant over time. In their empirical analysis of the British case, Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016) find this to be approximately true in the urban sector. However, for the agricultural sector, they find that the shares of income attributable to capital and labor increased beginning around 1800, while the land income share declined. This fact further motivates our generalization of the functional form representing production on the farm to allow for both neutral and biased technological change.
5. INDUSTRIALIZATION
A related phenomenon accompanying urbanization is industrialization of the economy – the relative increase in the value added of the manufacturing sector – a characteristic of most economies as they develop.Footnote 28 In our analysis, we measure the degree of industrialization by the ratio of the value of nonfarm output to total output. From Tables 1–3, this is seen to reflect a combination of quantity changes and price changes, leading to conflicting effects. The key insights may be summarized by the following proposition:
Proposition 3:
-
(i) A productivity increase in the industrial sector will raise the ratio of the manufacturing goods to farm goods. It will also raise the relative price of farm goods so that, in the absence of subsistence consumption (χ = 0), the degree of industrialization will rise if and only if σ > 1. If χ > 0, it may increase with σ < 1.
-
(ii) A productivity increase in the agricultural sector will reduce the relative price of farm goods. In the absence of subsistence consumption (χ = 0), the degree of industrialization will rise if and only if σ < 1. If χ > 0, it will increase if and only if σ(1 − χ) < 1, i.e. the farm and manufacturing goods are gross complements.
-
(iii) An increase in population will increase the relative price of farm goods. In the absence of subsistence consumption (χ = 0), it will induce industrialization if and only if σ > 1. The presence of subsistence consumption (χ > 0) works against it, and may reverse the positive effect on industrialization even in the case of σ > 1.
Several important observations can be made. First, these three sources of structural changes have highly conflicting consequences for the industrialization process. The model implies a very strong relative price effect, which may in fact dominate quantity adjustments.Footnote 29 One further issue is that because the relative price of agricultural goods rises with both the technological increase in the urban sector and with population growth, it is no longer clear that one can infer the nature of the underlying productivity change from the behavior of the relative price, as has been suggested; see e.g. Alvarez-Cuadrado and Poschke (Reference Alvarez-Cuadrado and Poschke2011). Finally, the fact that an increase in population induces industrialization only if σ > 1 suggests that one can accept population growth as a contributing factor to the industrialization process, only if one rejects the “push” hypothesis for urbanization.
6. POPULATION EFFECT: FURTHER INTUITION
Since the importance of the population effect for both the urbanization and industrialization processes has received less attention in the literature, in this section, we discuss it further, bringing out the intuition underlying the formal expressions in Table 3. We have already commented that its existence depends crucially upon the plausible assumption that land is a fixed factor in the agriculture sector, and pointed out that if the production function in that sector depends only on capital and labor, the overall production flexibility will permit any increase in labor to be absorbed proportionately in the two sectors, with no structural change. To the extent, the structural change literature typically makes this assumption, this would explain its apparent neglect in the literature.
Table 3 highlights how, given the importance of land, the impact of population growth on the structural development is dependent upon production flexibility, particularly in the agricultural sector, the relative demand for the rural and urban good, as well as the subsistence effect associated with food. Moreover, in some cases, these effects are mutually interactive in the sense that the strength of one depends upon the strength of another.
As derived in Section 5, population growth makes the farm good relatively more expensive. Log-linearizing the intratemporal relationship (9a) around the steady state gives
$$\begin{equation}
d\hat{p} = \frac{1}{\sigma }\left( {d\hat{C} - d\hat{A}} \right) - \frac{\chi }{{\sigma (1 - \chi )}}\left( {d\hat{A} - d\hat{L}} \right),
\end{equation}$$
which helps with the intuition. Due to the homogeneity of degree, one of the manufacturing production, an increase in the manufacturing employment leads to a proportional increase in KM , as seen from (10b), and therefore, to a proportional increase in the output and consumption of the manufacturing good, C. The same increase in agricultural employment leads to a less than proportional increase in the farm consumption, A, because land enters as a fixed factor effectively introducing decreasing returns to labor and capital. Thus, an increase in population, even without structural adjustments, introduces the relative scarcity of food output. This puts an upward pressure on the relative price of the farm good, as seen from the first term of (17). The relative price must rise to support the shift in consumption in favor of the manufacturing good. This effect is strengthened if, in addition, population growth induces astructural adjustment due to a sufficiently low rA , pushing additional labor away from agriculture and further exacerbating the relative scarcity of agricultural output.
The fact that additional population needs to consume food, at least at a subsistence level, ceteris paribus, applies additional upward pressure on the relative price of the agricultural good, as seen from the second term of (17). The farm good must get relatively more expensive to justify the shift in production in the face of increased needs to consume food for subsistence.
Note from (17) that the price response varies inversely with the elasticity of substitution in utility. This is because relative demand is much more responsive to price adjustments when elasticity of substitution is high. Suppose σ > 1 so that the two goods are gross substitutes. As population increases, implying the relative scarcity in agricultural production, the agricultural price need not rise much to induce a comparable shift in the relative demand for food. For small increases in its price, people easily substitute and switch their consumption in favor of the manufacturing good, thereby facilitating the urbanization process. Conversely, if σ < 1, increasing L has a significant effect on the price of the agricultural good. This reduces the demand for the farm good, but also for the industrial good, since they are complements, thereby impeding the urbanization process.
As seen from Table 3, the effect of population growth on industrialization reflects both price effects and quantity adjustments. The fact that population growth always raises the relative price of farm goods, thereby raising the value of farm production, is an adverse element insofar as industrialization is concerned. Thus, for the industrialization to result from population growth, the rise in urban production due to resource reallocation to the city must be sufficiently large, which may occur only if the two goods are substitutes.
An increase in the elasticity of substitution in agricultural production, rA , implies that the increase in population can be more easily absorbed in that sector. That decreases the pressure for people to migrate to the city and reduces the positive effect of population growth on the process of urbanization. In addition, with labor being more readily absorbed in agricultural production, there is less need for structural adjustments, which reduces the tendency for the price of agricultural goods to increase, thus moderating the demand for the manufacturing good. The moderating effects of rA on the implied rise in both C and p lead to offsetting impacts on the industrialization effect, with the net effect depending crucially upon the demand pressures as reflected in σ and χ.
7. CHANGING PULL, PUSH, AND POPULATION EFFECTS IN THE DEVELOPMENT PROCESS
Tables 4–6 summarize the potential for the relative importance of the pull, push, and population effects to change as the economy develops and both production and consumption conditions become more flexible. As discussed earlier, empirical evidence by Allen (Reference Allen2009) has suggested that the elasticity of substitution in the Britain in the 18th century was low, of the order of 0.2. Table 4 therefore reports the pull, push, and population effects on both urbanization and industrialization in the polar case where the elasticity of substitution in the agricultural sector is zero, so that its production function is described by a Leontief technology. With land being a fixed factor in the agricultural sector, and with no possibility of substitution in that sector, the economy is stuck with the existing configuration of factors in the agricultural sector.Footnote 30 Thus, neither the pull effect nor the push effect free any resources to move to the urban sector. In contrast, any increase in population must be fully absorbed by the manufacturing sector, which implies that the positive population effect is at its strongest.
Table 4. Leontief technology in agricultural sector (rA = 0)
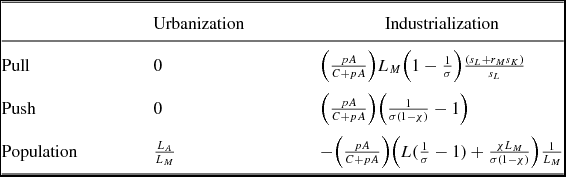
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with Leontief production function in the agricultural sector, a CES production function in the manufacturing sector and a CES utility function with subsistence consumption requirement.
Table 5. Subsistence economy (χ = 1)
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with Leontief production function in the agricultural sector, a CES production function in the manufacturing sector and a CES utility function with subsistence consumption requirement.
Table 6. Mature economy, flexible technology (rA = rM = 1, χ = 0)
Notes: The above results are based on log-linearized steady state relationships for the benchmark model with Leontief production function in the agricultural sector, a CES production function in the manufacturing sector and a CES utility function with subsistence consumption requirement. In the above, we use the following shorthand:
$Q' \equiv {L_M}[ {\frac{{1 - {a_N}}}{\sigma } + {a_N}} ] + \frac{{{L_A}}}{\sigma } > 0$
.
Because the pull effect induces no structural adjustment, it follows that the productivity increase in the manufacturing sector increases the supply of the manufactured output but leaves agricultural output unchanged. The relative price of the agricultural good increases in order to induce the appropriate shift in the relative demand. Manufactured output increases proportionately more than the relative price of the agricultural good if and only if σ > 1, in which case the net effect is for the relative value added of the manufacturing sector to increase. Approximately, the opposite applies in the case of the productivity increase in the agricultural sector, although the industrialization effect now reflects the subsistence component of the farm good. Finally, because the population effect raises the relative price of the agricultural good and shifts the demand in favor of the manufactured good, it operates very much like a pull effect insofar as industrialization is concerned.
We view subsistence food consumption constraint as potentially important for the economies in early stages of their development. Table 5 therefore reports the response to population and technological change in an economy that is constrained to consume its subsistence level of food. This inflexibility originating from the consumption side yields sharply contrasting effects from those implied by the inflexibility in production due to the Leontief technology in the farming sector. Specifically, the subsistence effect acts against both the urbanization and industrialization effects of population growth. As long as there is a subsistence level for food, the additional population needs to be fed and this increases the demand for the agricultural good, raises its relative price, and therefore its share of total output. Since food is produced in the agricultural sector, this limits the potential for people to migrate to the city. Indeed, it is even possible, in the case of
${a_N} > {{{L_M}}
/ L}$
, for an increase in population to attract people to the agricultural sector with such intensity that the urban population actually declines! This is because if land is a sufficiently important input and the economy is near its subsistence level of food production, as population grows and there are more people to feed, more labor must work in the agricultural sector in order to prevent food consumption from declining below its subsistence level. The economy is in effect in a Malthusian trap.
With the consumption and output of the agricultural good being held at the subsistence level, and constant population, the pull and the push effect now both operate in the same direction. In the case of the former, the increased productivity in the manufacturing sector attracts labor to that sector while it also stimulates more capital accumulation which is allocated to both sectors. In particular, the increased capital employed in the agricultural sector permits farmers to produce the subsistence level of food by substituting capital for labor, thus freeing the labor to move to the urban sector. With respect to the push effect, the increased productivity in the farm sector enables the subsistence level of output to be produced with less capital and labor, enabling these productive factors to migrate to the urban sector. For all three structural changes, the urbanization is almost certainly reflected in the industrialization.
Finally, Table 6 reports the effects in a mature economy, which enjoys a consumption of food far from the subsistence level and the technologies in both sectors have the flexibility associated with the Cobb–Douglas production function. In this case, all structural changes depend upon the relative elasticity (σ − 1). The pull and population effects operate both for urbanization and industrialization if and only if the two consumption goods are substitutes (σ > 1), while the push effect will prevail if and only if the two consumption goods are complements.
Overall, Tables 4–6 highlight how the qualitative effects and the relative importance of the pull, push, and population effects can vary dramatically, depending upon the level of development of the economy and sources and degree of any inflexibility.
8. ROLE OF INTERNATIONAL TRADE
So far our analysis has abstracted from the role of international trade and colonization, which was important particularly in the case of England in the latter part of the 19th century. It is straightforward to introduce a simple trade sector, as in Stokey (Reference Stokey2001), featuring exports of the manufacturing good in return for food. One can then show that all three effects are influenced by the degree of trade, as parameterized by the share of food that is imported, with the direction of impact depending upon the substitutability/complementarity relationship between the two consumption goods. To highlight the intuition, we shall assume that the two consumption goods are complements (σ < 1), and abstract from subsistence food consumption (χ = 0), which becomes less relevant as the economy develops and trade becomes more important.
In this case, as trade expands, it strengthens both the pull and population effects, but tends to reduce the push effect. To the extent that the pull effect attracts resources to the manufacturing sector, more trade will enable the economy to take greater advantage of productivity improvements in the urban area by making it possible to exchange its additional output for food. Trade reinforces the population effect in a similar way. Recall that additional labor reduces labor productivity on the farm, thereby inducing resource reallocation toward the city. The extent to which labor reallocation is possible no longer depends critically on the demand conditions, as trade allows the economy to transform the manufactured goods into food. In fact, the population effect is viable even in the extreme case of the Leontief utility function, provided that trade volume is sufficiently large. In contrast, an increase in agricultural productivity raises productivity of both factors in the agricultural sector, directly increasing its output. With complementarity of the two consumption goods, this raises the demand for the manufactured good, pushing resources to that sector. But trade allows the economy to meet this demand through imports, thereby reducing the pressure to reallocate resources across sectors.
Finally, all aspects of the population effect are impacted by trade, both directly, and indirectly through the urbanization effect as noted above. As trade volume increases, it reduces any influence of population – whether adverse or positive – on industrialization. In effect, trade serves as a substitute for population growth insofar as the composition of final output is concerned.
9. SIGNIFICANT EMPIRICAL IMPLICATIONS
Although the model is stylized, it offers insights into some of the empirical aspects associated with the structural transformation literature and provides guidance for empirical work aimed at identifying specific mechanisms at work. In this section, we shall focus on four issues.
There is a lot of variation in the urbanization experiences across countries. Developed economies urbanized predominantly through the expansion of the manufacturing sector. However, the relative size of the employment share and the value added share of the nonfarm sector varied across countries and across time during the transition. In England, for example, these two quantities evolved in a parallel fashion during the early transition [See Figure 1 in Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016)], whereas in the U.S., the employment share of agriculture declined at a much faster pace [see Figure 2 in Buera and Kaboski (Reference Buera and Kaboski2008)]. Gollin, Jedwab, and Vollrath (Reference Gollin, Jedwab and Vollrath2016) address the question of the extent to which the more recent episodes of urbanization are associated with the rise in the manufacturing share of output. They too emphasize the significant variation in urbanization experiences, providing empirical evidence to suggest that resource-rich developing economies such as Kuwait, Saudi Arabia, Angola, and Nigeria have urbanized through the expansion of the service sector, while other economies, such as Uruguay and Malaysia, more closely resembled the experience of developed countries, urbanizing through the expansion of manufacturing. Their explanation is that resource-rich economies export their resources in exchange for tradeable goods (such as food or manufactured products). If consumers value balanced consumption baskets, labor will have to reallocate toward services. In light of our discussion in the previous section, we would expect this mechanism as well as the introduction of the labor-intensive service sector to also reinforce the population size effect. Resource-rich economies would more easily absorb excess population into the urban sector because food can be imported in exchange for natural resources.Footnote 31
While our model cannot speak to the relative importance of the manufacturing and services, it helps us understand the distinct dynamics of the value added and employment share of agriculture. It is evident from Tables 1–3 that in general whether urbanization is associated with industrialization (i.e. one minus the value added share of agriculture) is highly sensitive both to the sources of the structural change (i.e. whether push, pull, or population effects dominate) as well as to the underlying structural parameters characterizing the economy. To illustrate the range of possibilities, we assume the absence of a subsistence effect, χ = 0. In this case, for σ, rA lying in the plausible range 1 > σ > rA , the population effect will lead to urbanization accompanied by a decline in industrialization. In contrast, for 1 > σ, the push effect will lead to an increase in both urbanization and industrialization. The difference is due to the fact that for these ranges of parameter values, the population increase is associated with a large increase in the relative price of the agricultural good, whereas the push effect leads to a corresponding decline.
The second issue pertains to the choice of mapping of sectoral output production and consumption expenditures to the data and its implication for the calibration of the elasticity of substitution in utility, σ. Herrendorf, Rogerson, and Valentinyi (Reference Herrendorf, Rogerson and Valentinyi2013) have explained that if sector-specific output is measured as value added, one must consistently measure sector-specific consumption as value added components of final consumption. Alternatively, one may choose the final expenditure approach to measuring both sectoral output and consumption. While this choice is arbitrary, it matters for the characterization of structural transformation. It also dictates the choice of quantities and price indices one would use to estimate σ. In the case of postwar U.S. data, for example, Herrendorf et al. (Reference Herrendorf, Rogerson and Valentinyi2013) obtain very different estimates under the two approaches (σ ≈ 0 using the value-added approach and σ ≈ 0.85 using the final expenditure approach). We showed that the magnitude of σ is a critical parameter in determining the prevalence of the push, pull, and population effects,Footnote 32 so we wish to emphasize that one must take great care in estimating σ consistently when conducting empirical analysis of structural change.
Third, Herrendorf, Herrington, and Valentinyi (Reference Herrendorf, Herrington and Valentinyi2015) conduct a parallel examination of the effect of the properties of technology on structural transformation. They conclude that Cobb–Douglas sectoral production functions are plausible and that U.S. postwar structural transformation can be accounted for mainly by differential technological progress across sectors. Table 6 summarizes the key transformational elements for a mature economy having Cobb–Douglas technologies. There it is seen that assuming σ < 1, sectoral technological progress, as specified by the push and the pull effects, drive both urbanization and industrialization. In contrast, population has an adverse effect on urbanization and industrialization, one that is proportional to, but much weaker than the push effect. While the pattern of responses in Table 6 support the Herrendorf et al. (Reference Herrendorf, Herrington and Valentinyi2015) conclusions for the postwar structural transformation in the U.S., they are inapplicable to the 19th century case of England, where the low elasticity of substitution in agricultural production played a crucial role; see Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016).
Finally, in principle, one can employ the decomposition of the structural transformation derived in this paper to help explain the diverse experiences of the various economies, such as those depicted in Figures 1–3. To illustrate how this can be done, consider the equilibrium labor allocation to the nonfarm sector, LM = LM (BM , BA , L). Taking the logarithmic derivative of this relationship yields
$$\begin{equation}
d{\hat{L}_M} - d\hat{L} = \left( {\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_M}}}} \right)d{\hat{B}_M} + \left( {\frac{{\partial {{\hat{L}}_M}}}{{\partial {{\hat{B}}_A}}}} \right)d{\hat{B}_A} + \left( {\frac{{\partial {{\hat{L}}_M}}}{{\partial \hat{L}}} - 1} \right)d\hat{L}.
\end{equation}$$
Thus, the long-run manufacturing employment share in a specific economy will reflect the relative sizes of the proportionate sectoral productivity changes (
$d{\hat{B}_M},d{\hat{B}_A}$
), together with the proportionate change in population (
$d\hat{L}$
), interacting with the corresponding pull, push, and population effects as reported by the partial derivatives appearing in (18) which, in turn, are obtained from the expressions repor_ted in Tables 1–3. Thus, different country urbanization experiences can be explained in terms of the different sizes of the three exogenous effects, as well as different structural characteristics as they impact the responses of sectoral labor movements. And a similar decomposition can be applied to industrialization.
10. CONCLUSIONS
The existing literature on structural transformation from agriculture to manufacturing has typically focused on one of two specific channels. One has been to assume gross substitutability between the farm and manufacturing goods, in which case faster growth in manufacturing productivity pulls labor into that sector. Alternatively, nonhomothetic preferences in conjunction with growth in farm productivity push resources out of agriculture. Most importantly, the effect of the population size has been neglected, despite its prodigious growth that has accompanied these developments. To comprehend fully the process of structural change, it is important to evaluate the relative significance of all three channels and to understand how they respond to different structural characteristics.
We have built a parsimonious general equilibrium two-sector growth model that incorporates all three channels. We have investigated analytically its properties under general forms of utility and production functions, with the purpose of understanding the mechanisms driving the three channels of structural development. We have examined the effects of (1) factor-neutral and factor-biased technological progress in agricultural and manufacturing sectors and (2) population growth on the employment share and output share attributed to manufacturing. Our analytical results clearly illustrate the production-side and preference-side conditions needed for the coexistence of the three effects. They also enable us to assess their comparative strengths and the trade-offs that exist between them.
One important characteristic of our analysis is that the population effect naturally emerges when production functions are generalized to CES with land appearing as a fixed factor. Thus, restricting technology to Cobb–Douglas, as has typically been the case, may not only be empirically inaccurate, but also necessarily conceals the role that population plays in the process of structural transformation. Therefore, our framework, with its less restrictive specification of production and preferences, should prove useful for future work interested in analyzing cross-country income differencesFootnote 33 or comparing histories of structural change across countries with different production and consumption characteristics. For example, the overall income level and therefore the proximity of a country to its subsistence level of food consumption at the start of a structural transformation determines the relative importance of the channels through which the transition transpires. Differential population growth and the type of technical progress will also matter for comparative patterns of development. Moreover, we discuss how these channels and the trade-offs between them change as the economy develops and engages increasingly in international trade.
Finally, since by its nature structural transformation is a slow evolutionary process we have focused our attention on the long-run responses to the structural changes experienced by the economy. At the same time, we should acknowledge that during the transition, an economy will likely pass through different phases during which the relative importance of the three effects we have identified may change. In this regard, we noted at the outset our earlier quantitative study, Leukhina and Turnovsky (Reference Leukhina and Turnovsky2016), of the British structural transformation over the period 1600–1900, and commented how the push effect was more important for industrialization in the early period, while the population effect was key for industrialization during the period 1750–1850. Since these transitions are slow, we feel that our focus on steady states nevertheless provides insights for these extended episodes. However, more explicit analysis of the transitions and how their internal dynamics may cause the relative importance of the different effects to change is an important direction in which the present framework could be extended.
