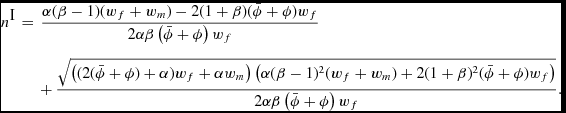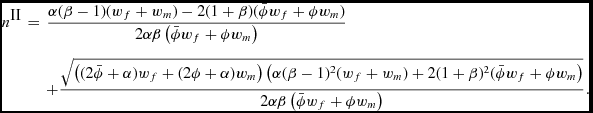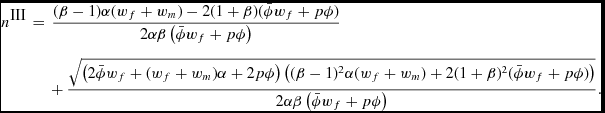2.1. The Model

The economy is populated by couples composed of a man and a woman, respectively, denoted by i = m, f. Each parent is endowed with one unit of time that is divided between childcare and work. A child needs $\phi >\bar{\phi }$ units of childcare, that can be supplied by either of the parents or outsourced, and a fixed time cost $\bar{\phi }\ge 0$ that can only be supplied by the mother.Footnote ³ Parents differ in their wages, w_i . Consumption goods and children are public goods in the household. Couples, therefore, cooperatively choose consumption, c, the amount of childcare time supplied by each individual, t_i , the amount of childcare time that is outsourced, t_n , and the number of children to have, n.

The expected cost of outsourcing childcare is denoted by p and writes as

where ε is the probability of having access to childcare services at a subsidized price p_s and (1 − ε) is the converse probability of not having access to those childcare services, which implies having to orient towards services a higher market price, p_m > p_s . At the aggregate level, the probability of having access to subsidized childcare corresponds to the coverage rate of subsidized formal childcare. This allows the model to account for an excess demand of childcare services due to the limited access to subsidized childcare – which is often the case for European countries, especially those with low-fertility rates [Thévenon (Reference Thévenon, Timmerman, Haers, Mels, Matthijs and Neels2015)]. The expected childcare cost will enter the budget constraint of the representative couple and we will perform comparative statics with respect to p. A increase in p should be understood as a decrease in childcare coverage. One may check that equation (1) implies that ∂p/∂ε < 0.

Denoting β ∈ (0, 1) as the parental preference for children relative to consumption, the maximization problem of a couple is the followingFootnote ⁴ :

subject to (1),

and t_f ⩾ 0, t_m ⩾ 0, t_n ⩾ 0.

The Lagrangian of this problem is as follows:

where (λ, μ, ν) are the Kuhn–Tucker multipliers associated to the nonnegativity constraints imposed on (t_f, t_m, t_n ), while (φ, γ) are those imposed on conditions (5) and (6). The first-order conditions with respect to (t_f, t_m, n) are as follows:

Moreover, the optimal solution satisfies

as well as equations (3) and (4).

Depending on the values of (w_m, w_f, p), the optimal solution can belong to one of the three main cases described below. Figure 2 illustrates when each of these cases arise, with respect to w_f, w_m , and p.

Figure 2. Possible cases with respect to w_f, p, and $w_{m}\in \left[ 0,p/\protect \beta \right]$ . Moreover, $\bar{\protect \phi }>\protect \phi \protect \beta /\left( 1+\protect \beta \right)$ .

Case I. The woman supplies all the childcare: t_f = ϕ and t_m = t_n = 0. In this case, condition (11) implies λ = γ = 0 and $n\le 1/\left( \phi +\bar{\phi }\right)$ . The latter inequality means that either the woman is not working and reaches the maximal fertility level given by her time constraint or she is working part-time and chooses a lower fertility level. Using conditions (8), (9), and (10), we obtain

Conversely, fertility can have an interior solution that is equal to

In Case I, the wage of the woman is lower than both the wage of the man and the expected cost of outsourcing childcare. The woman reaches the maximal fertility level when her wage is lower than βw_m , whereas she chooses a lower level of fertility when it is above. Both the constrained and unconstrained cases (denoted Case Ic and Case I, respectively) are represented in Figure 2.

When the optimal fertility is interior, we notice that an increase in the wage of the man positively affects the couple’s fertility (∂n/∂w_m > 0), while an increase in the woman’s wage affects it negatively (∂n/∂w_f < 0).

Case II. All the childcare is outsourced: t_n = ϕ and t_m = t_f = 0. In this case, condition (11) implies ν = γ = 0 and $n\le 1/\bar{\phi }$ . We notice that due to outsourcing possibilities, the maximal fertility level is higher than in Case I. Using conditions (8), (9), and (10), we obtain,

Conversely, fertility can have an interior solution that is equal to

A couple will outsource childcare when the expected cost of buying the service is not too high (below the wage of each spouse). If the cost is low, the maximal fertility level is then reached and when it increases, the fertility is more likely to be interior. In Figure 2, where it is assumed that w_m ⩽ p/β, only the unconstrained case is represented.

When the optimal fertility is interior, we notice that the wage of the man still has an income effect on fertility, ∂n/∂w_m > 0. However, an increase in the wage of the woman has both income and substitution effects, due to the childbearing time, $\bar{\phi }$ . We obtain

If $\bar{\phi }$ is relatively low compared to the time that is outsourced, then the income effect dominates the substitution effect and, then, ∂n/∂w_f > 0. Note that a marginal increase in the male’s wage increases fertility more than a marginal increase in the female’s wage, ∂n/∂w_m > ∂n/∂w_f . This is due to the fixed cost in terms of childcare $\bar{\phi }$ supported by the woman.

Case III. The man supplies all the childcare: t_m = ϕ and t_n = t_f = 0. In this case, conditions (11) and $\phi >\bar{\phi }$ imply μ = φ = 0 and n ⩽ 1/ϕ. Conditions (8), (9), and (10) can be used to obtain

and,

Case III is exactly symmetric to Case I for $\bar{\phi }=0$ . By adding the fixed cost specific to women, we see that the constrained case is less likely.

In Case III, an increase in the wages of both the woman and the man entails income and substitution effects. If the childbearing time is larger than the childrearing time, then an increase in the man’s wage has a positive effect on fertility, whereas an increase in the woman’s wage has a negative effect. The opposite case is seen when childbearing time is less than childrearing time.

The next subsection looks at the implications of the theory and compares them to cross-country evidence on how fertility relates to childcare coverage.

3.1. The Birth Order that Matters

We use the 2011 cross-sectional wave of the EU-SILC to understand whether fertility differences across 26 European countries are due to differences in starting a family or to enlarging the family size.Footnote ⁸

We base our calculations on the fertility rate for women aged 38 to 44 years old (i.e., the cohorts of 1967–1973). Women at younger ages are excluded in order to focus on completed fertility. Women at older ages are also excluded because the EU-SILC reports a decreasing number of children per woman for older ages, as these children move out of their parents’ homes and can no longer be observed. Due to this partial capture of children that live in the household only, as reported in the EU-SILC, these calculated “approximate” completed fertility rates (ACFR) are somewhat downward biased. Despite this bias, this approximate measure provides a country ranking that is similar to the unbiased completed fertility measured by the Human Fertility Data Base (wave 2012, cohort 1970).Footnote ⁹ The EU-SILC is thus used for our fertility analysis because it provides a large country coverage, an international comparability of socioeconomic measures, and a follow-up of individuals (used later in Section 3.3).Footnote ¹⁰

The data shows a weighted average ACFR of 1.61 children per woman across the 26 European countries covered by the 2011 cross-sectional wave of EU-SILC. The 12 countries with rates below this average are Germany, Spain, Italy, Switzerland, Bulgaria, Portugal, Luxembourg, Belgium, Latvia, Greece, Austria, and Estonia. The 14 countries above this average rate are the United Kingdom, the Netherlands, Lithuania, Denmark, France, Norway, the Czech Republic, Finland, Poland, Slovenia, Slovakia, Sweden, Hungary, and Iceland. The weighted average ACFR in high-fertility countries equals 1.73, whereas it is 1.46 in low-fertility countries; the absolute fertility difference between the two groups is thus 0.27 children.

Table B.1 in Appendix B shows that in both low- and high-fertility countries, having two children is the most frequent situation for women aged 38 to 44 years old (40% in low-fertility against 42% in high-fertility countries). Childlessness is higher in low-fertility countries, and the proportion of women having three and four children is higher in high-fertility countries. The absolute differences in the proportions give, however, no direct information about the birth order that is most responsible for fertility being low in the first group of countries. The proportion of women having three and four children might be higher in high-fertility countries, but at the same time, in both country groups, only a relatively small fraction of women is concerned. This lets us suggest that the weight of children of birth order three and four for explaining differences in fertility between the two groups is smaller than the absolute difference in the proportions lets expect. The same logic applies for childless women: The difference in the proportion of childless women between high- and low-fertility countries is considerable, but the proportions itself are relatively small in comparison to the proportion of women having one and two children. At the same time, the proportion of women having two children is important in the two country groups. Consequently, even if the difference between the two groups for this proportion is small, it can lead to high differences in fertility levels.

A decomposition of ACFR is thus needed to determine the contribution of each birth order to the difference in fertility levels between the two groups of countries. As detailed in Appendix 4, we first calculate for each group of countries the proportion of women having at least i children (fertility rate of birth order i). The sum of these cumulative frequencies actually yields the ACFR of each country group. Then, we calculate the differences in each fertility rate of birth order i between low- and high-fertility countries. These differences sum up to the absolute difference in ACFR between the two country groups.

According to these calculations, the absolute difference of 0.27 children per women between high- and low-fertility countries is composed as follows: 0.06 children are due to fewer children of birth order one in low-fertility countries, 0.10 children are due to fewer children of birth order two in low-fertility countries, 0.08 children are due to fewer children of birth order three in low-fertility countries, and 0.02 children are due to fewer children of birth order four in low-fertility countries. Therewith, the fertility gap is mainly explained by fewer children of birth order two. Figure 6 illustrates the relative contribution of each birth order to the fertility gap. Fewer children of birth order one account for 23% of the gap in ACFR between high- and low-fertility countries, fewer children of birth order two for 38%, fewer children of birth order three for 30%, and fewer children of birth order four for 9%.

Figure 6. Relative contribution of fewer children of birth order i to the fertility gap between high- and low-fertility countries in the EU(26).

Our calculations show that fertility differences between European countries mainly emerge due to fewer children of birth order two, suggesting that in low-fertility countries, most women have a first child, but fewer decide in favor of a second one. Following the same calculation method, Breton and Prioux (Reference Prioux2005) find a somewhat higher contribution of children of birth order three in comparison to children of birth order two to fertility differences between European countries. This is due to the fact that they do not include Eastern European countries in their sample and focus on a generation that is 10 years older. At the same time, their study and ours consistently find that fewer children of birth order one (i.e., higher childlessness) are not the main explanation for low-fertility levels.Footnote ¹¹

Additional evidence that fertility differences between European countries mainly result from differences in second child birth can be obtained when including younger cohorts in our analysis. We therefore look at the transition probabilities of women aged 15 to 44 years old. To observe the probabilities of child birth by birth order, we use the longitudinal database of the EU-SILC (waves 2003 to 2011). The rotational panel with a follow-up of individuals for a maximum period of four years allows identifying child births that occur during the observed period.

We observe that among women aged 15–44 years who are childless in the beginning of the observed period, 5% have a first child during the observed period. Among women having one child, 10% have a second child and among women having two children, 5% have a third child during the observed period.

Figure 7 plots each country’s average probability of observed birth of a child of birth order one, two, and three for women aged 15–44 years old against the country’s TFR. The probability to observe a child’s birth is higher in high-fertility countries for all birth orders. Figure 7 reveals a separation of European countries in two clearly distinguishable fertility regimes, low versus high ones, with low versus high probabilities of a child’s birth. The difference between the two regimes is most striking for a second child birth (middle panel of Figure 7), which is not only due to a level effect. In low-fertility countries, the probability of a second child birth is 66% lower than in high-fertility countries, against 40% for the probability of first and third child birth. Our finding that countries with low and high TFR differ most in the transition to a second child underlines the importance of children of birth order two that was revealed by the previous ACFR analysis focusing on older cohorts only which already have completed their family size.

Figure 7. Probability of child birth of birth order 1 (top), 2 (middle), and 3 (bottom) vs. TFR.

The following subsection depicts the mechanisms behind a couple’s decision of having a second child.

3.2. The Decision of Having a Second Child in Theory

To focus on the transition from the first to the second child, we modify the general model as structured above by considering that n is discrete rather than continuous. As the utility function is increasing and concave with respect to n, a couple will have two or more children if the indirect utility when n = 2 is higher than the indirect utility when n = 1.

Let us assume that the parameter restrictions are such that we are either in Case I, where the woman supplies all the childcare, or in Case II where all the childcare is outsourced (w_m > p and w_f > p), and that the fertility is interior (w_f > βw_m ). Let $\bar{u}_{n}^{\kappa }$ denote the indirect utility of having n children and being in Case $\kappa =\text{I}$ or $\kappa =\text{II}$ . For w_f = p, we can check that $\bar{u}_{n}^{\text{I}}=\bar{u}_{n}^{\text{II}}$ .

Moreover, let us define $W^{\text{I}}$ and $W^{\text{II}}$ the female wage thresholds such that $\bar{u}_{1}^{\text{I}}=\bar{u}_{2}^{\text{I}}$ and $\bar{u}_{1}^{\text{II}}=\bar{u}_{2}^{\text{II}}$ , respectively. We have

where λ ≔ (2^{β + 1} − 1)/(2^β − 1). We saw that in the case where the woman supplies all the childcare, fertility decreases with the woman’s wage. In this discrete variable setting, this relationship is given through the following inequality:

Moreover, provided that fixed costs are sufficiently large, and more precisely provided that

the threshold $W^{\text{I}}$ is larger than βw_m . This implies that $\bar{u}_{2}^{\text{I}}>\bar{u}_{1}^{\text{I}}$ , if the woman’s wage belongs to $\left( \beta w_{m},W^{\text{I}}\right)$ . Since $\partial \bar{u}_{1}^{\text{I}}/\partial w_{f}>\partial \bar{u}_{2}^{\text{I}}/\partial w_{f}$ for all w_f > 0, $\bar{u}_{2}^{\text{I}}$ and $\bar{u}_{1}^{\text{I}}$ will cross once for $w_{f}=W^{\text{I}}$ .

In the case where childcare is outsourced, fertility increases with the woman’s wage, which could be expressed here as

Provided that $\bar{\phi }\lambda <1$ , the condition for $W^{\text{II}}>W^{\text{I}}$ becomes

Then, the condition to obtain $\partial \bar{u}_{2}^{\text{II}}/\partial w_{f}>\partial \bar{u}_{1}^{\text{II}}/\partial w_{f}$ is $\phi p>w_{m}\bar{\phi }$ , which (as we have seen in the previous section) implies that fertility increases with the woman’s wage. This latter condition is compatible with the previous one provided that p is sufficiently large.

Figure 8 shows $\bar{u}_{1}^{\text{I}}$ , $\bar{u}_{2}^{\text{I}}$ , $\bar{u}_{1}^{\text{II}}$ , and $\bar{u}_{2}^{\text{II}}$ with respect to w_f and for a large p (left panel) and a small p (right panel). The left panel of Figure 8 illustrates a situation in which the utility of having two children is larger for women with low or high wages than the utility of having only one child. Conversely, women with middle wages have one child. For w_f < p, the couple is in Case I in which the woman supports all the childrearing. For $w_{f}<W^{\text{I}}$ , $\bar{u}_{2}^{\text{I}}>\bar{u}_{1}^{\text{I}}$ so that the couple will have (at least) two children. When $W^{\text{I}}\le w_{f}<p$ , $\bar{u}_{1}^{\text{I}}\ge \bar{u}_{2}^{\text{I}}$ and the couple will have one child. This is because for a woman with low wage, being out of the labor market entails a low cost. As her wage increases, however, this cost increases and as each child costs her $\phi +\bar{\phi }$ units of time, it is optimal for the couple to have less children.

Figure 8. Indirect utilities of having one or two children, Case I in red and Case II in black, with a Large p (left) and a Small p (right).

For w_f ⩾ p, the couple has enough income to be in Case II where it outsources childrearing. For $p\le w_{f}\le W^{\text{II}}$ , the couple has one child ( $\bar{u}_{1}^{\text{II}}\ge \bar{u}_{2}^{\text{II}}$ ) because the marginal expected cost of an extra child is larger than the utility gains. The cost of an extra child includes an increase in the opportunity cost of childbearing for the woman and a higher expected amount to pay for childrearing services. For $w_{f}>W^{\text{II}} $ , $\bar{u}_{2}^{\text{II}}>\bar{u}_{1}^{\text{II}}$ and the couple will have at least two children. This is due to the income effect of the increase that allows for the purchase of more childcare services in the market.

The right panel of Figure 8 shows the effect of decreasing the price of external childcare on the indirect utilities. In such configuration, $\bar{u}_{2}^{\text{II}}>\bar{u}_{1}^{\text{II}}$ for all w_f . A lower price for childcare implies that a lower female wage will allow the couple to reach Case II, where they can outsource childcare. Moreover, the figure also shows that couples will enter Case II before the substitution effect of the female wage becomes too large. This explains why the indirect utility of having two children always dominates the indirect utility of having one. As already present in Figure 4, Figure 8 also shows that women at the middle of the wage distribution are the most affected by changes in the expected price of childcare services.

The two panels of Figure 8 illustrate the differences in fertility patterns with respect to female wage for low- (left panel) and high- (right panel) fertility countries. The next section provides empirical evidence that the relation within European countries between the probability of having a second child and female potential wages is affected by the expected price of childcare, which will be proxied by access to/coverage of formal childcare.

3.3. Empirical Application

We estimate the probability of having a second child for partnered women as a function of individual, partner, and household characteristics as well as of aggregate childcare coverage. Our main determinant of interest is the woman’s education level, which serves as a proxy for her potential wage, and we analyze how the impact of education on the probability of second child birth differs with access to formal childcare. We thus do not study completed fertility, but we analyze the childbearing behaviour of women who are currently at childbearing age. This allows us applying panel data techniques that serve to reduce endogeneity between fertility and socioeconomic characteristics. We hereby focus on second child birth, as this birth order is crucial for explaining fertility differences between European countries.

Our analysis is based on 26 European countries, which, as illustrated in Figure 5, have either childcare coverage rates above or below the average of 0.31. To model the impact of education and other individual characteristics on women’s probability of second child birth, we mobilize the longitudinal data set of the EU Statistics on Income and Living Conditions, covering survey years 2003 to 2011. Figure 7 in Section 3.1 illustrates each country’s average of the probability of second child birth calculated with this data base. The longitudinal database is a rotational panel with individuals followed up for a maximum period of four years (individuals are observed from wave one to four). We select women aged 15 to 45, who already have a first child (at least one year old) in the beginning of the observed period, and their partners. The individual determinants of second child birth are observed during the year prior to the calendar year of potential second child birth. This helps reducing the risk of obtaining biased estimates due to reverse causality between the endogenous and the exogenous variables.

To allow for this time delay, individuals have to be observed for at least three consecutive waves: The third wave is needed to identify all births of birth order two that occur during the calendar year of the second wave. The first wave gives information about individual characteristics observed during the year prior to the calendar year of potential birth of a second child. Consequently, individuals who are observed for three waves have only one person-year in our compiled data base: This person-year contains information of the individual characteristics (education etc.) observed in the year prior to the calendar year of potential second child birth, as well as a dummy variable for second child birth.

For individuals who are observed for four waves, two calendar years of potential second child birth can be identified. Consequently, those who do not have a second child in the first period enter our sample with two person-years.

Individuals who are observed for only one or two waves are dropped. For these individuals, we cannot observe the individual characteristics in the year prior to the calendar year of potential second child birth. The panel contains individuals who are observed for less than four waves mainly due to the rotational design of the panel. Attrition in SILC is relatively small for individuals “at risk” of second child birth in comparison to first child birth, and attrition does not differ by socioeconomic characteristics, as shown by Greulich and Dasre (Reference Greulich and Dasre2017).

As the panel is short, our sample contains only either one or two person-years for each individual. This allows us applying a simple logit model, with a control for the number of person-years. We use a binary logit regression model while taking into account the characteristics of women, their partners, and the general household, as follows:

where y ∈ {0, 1} is a dummy variable for second child birth, X denotes the microlevel characteristics taken into account, and β the estimated coefficient of these variables.

Education of women and their partners are observed at the time of the survey of the year prior to the calendar year of potential second child birth. Only couples with completed education are considered (no pupils, students, trainees etc.). We construct three categories for the education level of women and their partners (by highest ISCED level attained), namely: low education for preprimary, primary, and lower secondary education, medium education for upper secondary and postsecondary nontertiary education, and high education for tertiary education. Grouping the initial six education categories into three categories allows us to obtain a sufficiently large number of observations for each category.

Besides women’s and their partners’ education level, we include a series of control variables in order to isolate the impact of women’s potential wage on the decision of having a second child from other determinants. We include information on women’s and the partners’ employment status. Information on employment status (self-declared) is available on a monthly basis in SILC, which allows us to observe the employment status during a certain period before the potential conception of a second child. In order to observe the same span of time for all individuals, we restrict this period to three months. For women, we distinguish between full-time employed (employed and self-employed), part-time employed (employed and self-employed), unemployed, and inactive. Those who experience a change in employment status during the observed period figure in an extra category, but this concerns only a minority of 2%. For partners, we distinguish only between full-time employed (employed and self-employed) and those who are not full-time employed, as those who are full-time employed represent the large majority of partners of women having one child (92%). Information on employment status is missing for only 1% of partners. The control for employment status allows us not only disentangling women’s wage options (as proxied by education) from their actual labour market participation, but also taking into account country heterogeneity in terms of the labour market structure (prevalence of part-time employment for women, of unemployment etc.).

In addition, we control for the woman’s age, the age and sex of the first child as well as for marital status. The model fits best when integrating age as a continuous variable – modeling a nonlinear impact for woman’s age and a linear impact for the age of the first child.

Information on individual-level access to formal childcare is not available in the longitudinal database of the SILC, which is why we have to limit our measure to cross-country variations. We use the aggregate measure of a country’s childcare coverage for children aged 0 to 2 (see Figure 5: OECD Family Database, 2012) as a proxy for parents’ access to childcare. Childcare coverage rates represent participation rates for 0-to-2-year-old in formal childcare and preschool services. Data generally include children using center-based services (e.g., nurseries or day care centers and pre-schools, both public and private), organized family day care, and care services provided by (paid) professional childminders, and exclude those using unpaid informal services provided by relatives, friends, or neighbors. We use this measure in both an implicit and an explicit way in the regression models.

The implicit way consists of estimating the impact of education on the probability of second child birth by distinguishing between two groups of countries among the 26 European countries: a first group of countries with childcare coverage for children aged 0 to 2 years old that is below the European average of 31%, and a second group with childcare coverage above this average (as identified in Figure 5).Footnote ¹²

The probability of having a second child varies considerably across countries, as already suggested in Figure 7. The weighted average for the probability of second child birth in our first group of countries is 0.075, while it amounts to 0.15 for the second group. For the first group of countries, we observe 18% of women with low education level, 60% with medium, and 22% with high education levels, whereas the distribution in the second group of countries is 20%, 42%, and 38%, respectively. As the distribution of women over education groups does not differ to a large extent in the two country groups, our estimation results are not too much sensitive to selection issues. Country-fixed effects capture, however, differences in the average returns to education between countries.

We group together all 26 countries while controlling for the country group and while interacting the country group dummy with woman’s education. This avoids us dividing the sample in two subgroups. With this large sample size, we are able to analyze the effect of education on the probability of second child birth within countries of each group. To focus on these within-country variations, we introduce country-fixed effects besides the country group dummy. As some specific years may influence the probability of deciding for or against a second child, we also introduce year-fixed effects in all our regressions. The regressions are run with robust standard errors.

The explicit way for modeling access to childcare as a determinant of second child birth consists of applying a mixed-effects logistic regression. Multilevel models are useful when individuals are supposed to be nested into higher level structures [Snijders and Bosker (Reference Snijders and Bosker1999)] that may play a role in explaining events that occur at the individual level. This is of particular interest in international comparative research: We can indeed consider that individuals are nested in countries, each country being characterized by specific national institutions, such as childcare coverage, that may play a role on individual choices. Country effects induce correlations across observations which need to be addressed; otherwise standard errors risk to be downward biased. Multilevel models adjust for these intracountry correlations. Moreover, multilevel models can deal with unbalanced data sets [Skrondal and Rabe-Hesketh (Reference Skrondal and Rabe-Hesketh2004)], which is important as our sample sizes vary across countries.

We integrate the country-specific contextual variable “childcare coverage” as a continuous variable in the model, and we interact childcare coverage with education. This serves to test if the effect of education differs across countries with different levels of childcare coverage, and if the effect of childcare coverage differs among education groups (cross-level effects). We apply a two-level random-intercept and random-coefficient model (by using the meqrlogit command in Stata), which fits mixed-effects models for binary responses. Country effects are specified in terms of a country error variance and fixed effects of our country-level predictor “childcare coverage.” The multilevel model is thus able to analyze the impact of contextual variables on individual behavior without the assumption of homogeneity-of-regression slopes. The slope is allowed to vary randomly; random parameters have a different value for each group/country. In addition, with the interaction terms (cross-level effects), we do not only allow the intercept of the model but also the slope for the individual-level variable “education” to be random and to possibly explain it with the macrolevel variable “childcare coverage.”Footnote ¹³

Table 1 presents the regression results of a partnered woman’s probability of having a second child as a function of her education. Model 1 implicitly controls for access to childcare by including a dummy variable for countries with childcare coverage above the European average, and model 2 shows regression results of the multilevel approach.

Model 1 shows that within countries with low childcare coverage, a woman’s probability of having a second child is lowest among medium-educated women. Women with high and low education levels have a significantly higher probability of having a second child in comparison to women with middle education. This result holds when controlling for partner education and woman’s as well as her partner’s employment status. The estimated coefficient for low education is 0.228 and for high education 0.239 in model 1 for the first group of countries with childcare coverage below the European average. Within countries with childcare coverage above the European average, a woman’s probability of having a second child is significantly increasing with education. This can be seen by combining the estimated coefficients of education with the interaction terms. The estimated coefficient for low education is − 0.108 (0.228–0.336) and 0.2638 (0.229+0.0348) for high education in model 1 for the second group of countries. In countries with high levels of childcare coverage, low-educated women have thus the lowest probability of second child birth. The difference between middle- and high-educated women is significant, as indicated by the p-value of joint significance at the bottom of the table. In addition to the importance of women’s education (figuring as potential wage) for family enlargement, we find that – in line with our argument that it is economic resources that are important for family enlargement – unemployed and inactive women have a lower probability of second child birth in comparison to employed women. Results are similar when running a probit instead of a logit model.Footnote ¹⁴

We now quantify the estimation results of model 1 by transforming the logit coefficients into estimated probabilities.Footnote ¹⁵ Comparing the two country groups, Figure 9 illustrates the estimated probabilities for the reference category of women who are married to a middle-educated partner, who are 28 years old and who have a first child who is male and aged four. Within countries of the the first country group, there is a U-shaped pattern between women’s education and the birth of the second child, while the relation is positive for the second group of countries. With 0.371 and 0.394, the estimated probabilities are quite similar for low-educated women in the two country groups. At the same time, middle-educated women have a lower probability of second child birth in country group 1 (0.320) in comparison to low educated women, but a higher probability in country group 2 (0.476). The probability is highest for high-educated women in country group 2 (0.485). In country group 1, high-educated women have, with 0.372, a higher probability of second child birth than middle-educated women, but this probability is low in comparison to high-educated women in countries of group two.

Figure 9. Estimated probabilities of second child birth according to woman’s education, countries with difficult vs. easy access to childcare.

Results of the multilevel analysis are shown in column 2. They show three main results. First, childcare coverage is significantly positively linked to women’s probability of having a second child, independent of their educational level. Second, the interaction terms confirm that the impact of education on the probability of second child birth is influenced by the level of childcare coverage: For countries without formal childcare, women with low and high education have a higher probability of second child birth than middle-educated women. Increasing childcare coverage reduces the positive impact of low education and reinforces the positive impact of high education. Third, the interaction terms also suggest that the positive impact of childcare coverage on the probability of second child birth is lower for low-educated women and higher for high-educated women in comparison to middle-educated women. Education (at the individual level) and childcare coverage (at the macrolevel) thus both have a positive impact on the probability of having a second child and the positive impact is reinforced when these two features are combined. Results are similar when running a multilevel-probit instead of a multilevel-logit model.Footnote ¹⁶

Figure 10 illustrates the estimated probabilities of the multilevel model for different levels of childcare coverage, varying between 3% (Slovakia) and 66% (Denmark), again for the reference category of women who are married to a middle-educated partner, who are 28 years old and who have a first child who is male and aged four. For low levels of childcare coverage below 31%, the relation between education and the probability of second child birth is U-shaped, while the relation gets positive for higher levels of childcare coverage. In addition, Figure 10 shows that in countries with high levels of childcare coverage, the probability of second child birth is generally higher for all levels of education in comparison to those countries with lower childcare coverage.

Figure 10. Estimated probabilities of second child birth according to woman’s education, by levels of childcare coverage (children aged 0–2).

Access to childcare facilitates thus the birth of a second child for all levels of female education. However, our results also suggest that in countries with high childcare coverage, the birth of a second child is facilitated in particular for middle- and high-educated women, while in countries with low childcare coverage, it is in particular the middle-educated women who face barriers to second child birth. Given the fact that the transition to a second child is an important determinant for a country’s aggregate fertility level, it seems that fertility levels are higher in countries with high childcare coverage in particular because more middle- and high-educated women pass from one to two children.

The model presented in Section 2.1 and the extended model in Section 3.2 allow us developing some intuitions for a better understanding of the patterns that are revealed by our empirical analysis. The empirical results correspond to the model’s prediction of a U-shaped relationship between a couple’s probability of having a second child and the woman’s potential wage in countries with difficult access to childcare. The model also predicts that an easier access to childcare leads to the the fact that the probability of having a second child is increasing with woman’s education. In countries with difficult access to childcare, middle-educated women face high opportunity costs and therefore tend to decide against second child birth, while high-educated women succeed in overcoming the substitution effect. An easier access to childcare reinforces the income effect, which explains that middle- and high-educated women have more facilities to enlarge the family than low-educated women.

Our results have to be interpreted with care, however, as the country-specific childcare levels can also capture other factors that might explain differences in the transition to second child birth between European countries. For example, countries might not only differ in access to childcare, but also in general wage levels for men and women. The higher the wages, the easier it may be for parents to decide in favor of an additional child. To test the robustness of our findings, we therefore run an additional specification where the country-specific wage level, gender wage inequality, and their interaction terms with education groups are also included.

To measure the wage level, we use median gross hourly wages for all employees (excluding apprentices), expressed in Euros, and in purchasing power standard (Eurostat Structure and Earnings Survey, 2010). The gender pay gap is calculated based on this measure and represents the difference between gross hourly earnings of male paid employees and of female paid employees as a percentage of gross hourly earnings of male paid employees.

The results of this robustness check (model 3) are presented in Table C.1 of Appendix C.

Even though childcare coverage itself is no longer significant, the results confirm that for low levels of childcare coverage, low-educated women have a significantly higher probability of having a second child than middle-educated women. The significantly negative interaction term “childcare coverage × low education” shows that the higher childcare coverage, the smaller gets the coefficient of low education. Combining information of the estimated coefficients of “low education” and the interaction term “childcare coverage × low education,” we find that from a childcare coverage level of 47% on, low-educated women have a lower probability of having a second child than middle-educated women.

The general wage level is found to be significantly positively related to second childbirth, whereas the impact does not significantly differ between education groups.

The results of model 3 confirm that childcare coverage shapes the educational gradient of second childbirth: In countries with high levels of childcare coverage, the educational gradient is positive, whereas in countries with low childcare coverage, the educational gradient is U-shaped. However, model 3 suggests also that general level-differences between European countries in terms of transition to second childbirth are not, or at least not only, linked to differences in childcare coverage. The general wage level seems to be an important driver for parents’ decisions in terms of family enlargement. This holds for all education groups. The higher a country’s wage level, the easier it seems for families to bear the financial burden of a second child.

The importance of childcare coverage, should, however, not be rejected, as results of model 3 risk being biased by multicollinearity between the wage level and childcare coverage. Richer countries tend to have both higher wage levels and higher public investments in formal childcare. One might also think of other country-specific unobserved factors that are correlated with both childcare coverage and income levels, such as gender and family norms, for example. Recent research has shown that the re-increases in TFR, that can be observed since the early 2000s, are strongest in those developed countries which have the most experienced changing gender relationships towards more gender equality, as measured, for example, by gender-equitable attitudes towards female employment, by an increasing number of out-of-wedlock births reflecting modern family norms or by increasing men’s involvement in the home [Balbo et al. (Reference Balbo, Billari and Mills2013); Neyer et al. (Reference Neyer, Lappegard and Vignoli2013); Arpino and Esping-Andersen (Reference Arpino and Esping-Andersen2015); Goldscheider et al. (Reference Goldscheider, Bernhardt and Lappegard2015)].