1. Introduction
The current magnitude and shape of populations in industrialized countries have been the outcome of a major process of mortality and fertility decline known as the demographic transition (DT). The DT emerged in Europe after 1750 [Chesnais (Reference Chesnais1987), Livi-Bacci (Reference Livi-Bacci2017)] after a phase of mortality decline that interrupted the long-term stagnation of Western populations around their Malthusian regime, with its high levels of mortality and fertility. Mortality decline, which was responsible for rapid population growth, was later followed (after 1850) by fertility decline, coming to rest (around 1930) on a modern stationary regime at lower levels of fertility and mortality [Chesnais (Reference Chesnais1987), Bulatao and Casterline (Reference Bulatao and Casterline2001), Livi-Bacci (Reference Livi-Bacci2017)]. The world's other regions followed their own paths later [Bulatao and Casterline (Reference Bulatao and Casterline2001), Bongaarts and Casterline (Reference Bongaarts and Casterline2012)]. Modern demo-economic theories of the DT emphasize its interplay with the industrial revolution and the related endogenous nature of mortality decline [Kalemli-Ozcan (Reference Kalemli-Ozcan2002), Cervellati and Sunde (Reference Cervellati and Sunde2005), Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008), Galor (Reference Galor2011)]. The latter triggered fertility decline by promoting investments in education, thus favoring the switch from the precautionary demand for children (quantity), which is typical of the Malthusian regime, to the demand for education (quality), which is typical of the modern regime [Galor (Reference Galor2011), and references therein], ultimately proving to be a major engine of sustained economic growth and development.
In Sub-Saharan Africa (SSA), which is the poorest setting worldwide also because of the highest mortality burden from infections [Bloom and Canning (Reference Bloom and Canning2004), Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008), IHME (2013), Weil (Reference Weil2017)], mortality decline was halted in the 1980s by the HIV/AIDS epidemic (Figure 1a) which, in high-prevalence settings, was able to reverse [UN (2015)] the long-term positive trend in life expectancy (Figure 1b). The memory of HIV and its effect on mortality is projected to persist for a long time (Figure 1b). For example, in Lesotho, life expectancy at age 15 (e 15), which was estimated to have fallen from 53 to 35 years during 1990–2010, is projected by the UN medium variant to return to its pre-HIV level only by 2060 (Figure 1b). In addition, the fertility transition in SSA was markedly delayed compared to other world regions which started from similar initial conditions, such as Asia and Latin America [Bongaarts and Casterline (Reference Bongaarts and Casterline2012)], resulting in several countries for the period 2010–2015 still recording total fertility rates (TFR) of about 6 [UN (2015)].
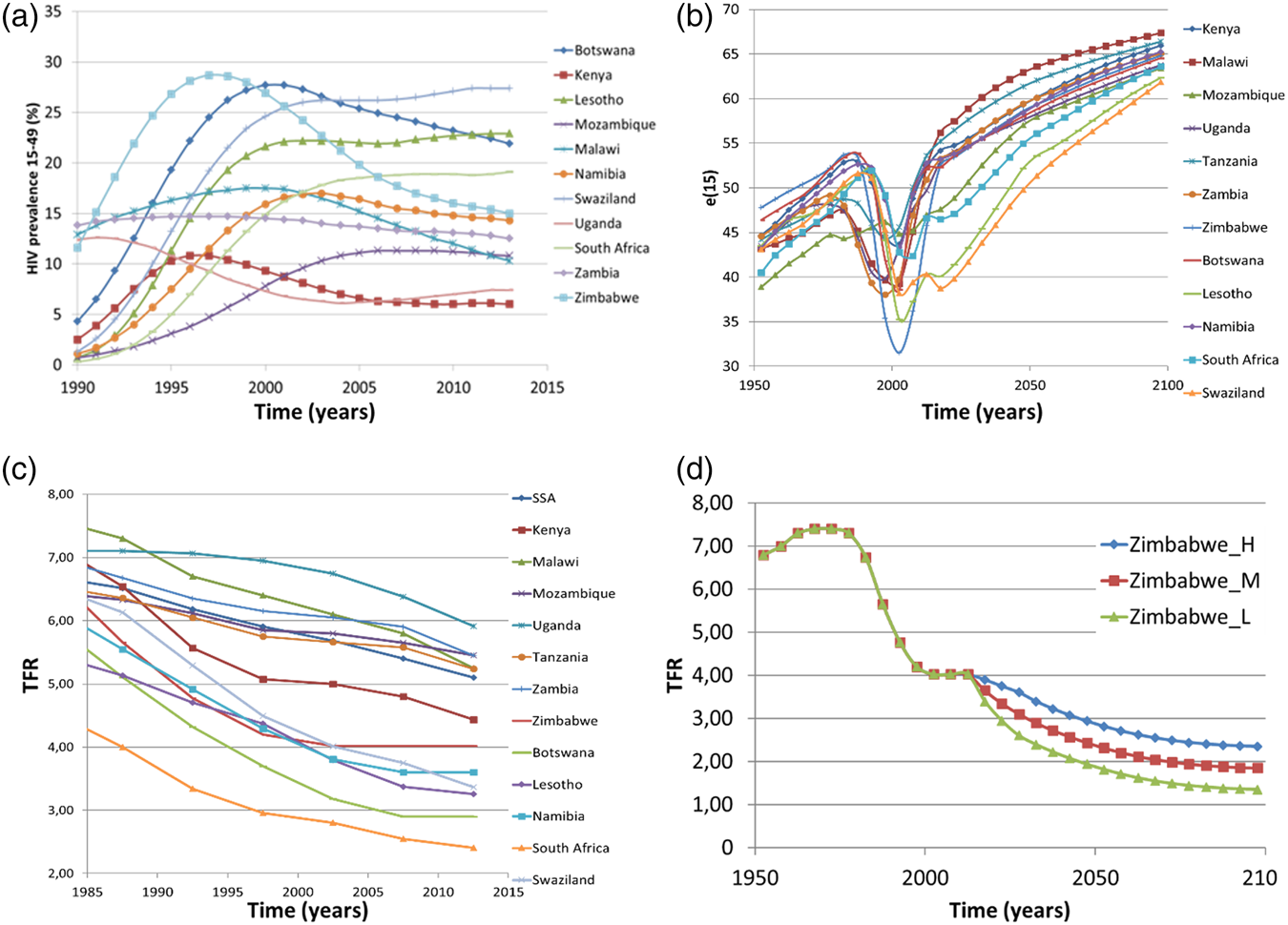
Figure 1. Demographic trends in SSA countries with higher HIV prevalence: (a) estimated trend of HIV prevalence in 15–49 year old individuals [source: UNAIDS (2017)]; (b) estimated and projected future evolution of mortality of young adults, as measured by e 15, life expectancy at 15 years [source: UN (2015)]; (c) estimated trend 1980–2015 in the TFR, [source: UN (2015)]; and (d) the case of Zimbabwe: projected future evolution of TFR according to UN projection variants (M = “medium”, L = “low”, and H = “high”) [source: UN (2015)].
However, according to UN data, fertility decline in SSA is stalling or even relapsing (Figure 1c) [Bongaarts and Casterline (Reference Bongaarts and Casterline2012), UN (2015)]. Worryingly, the four SSA countries showing the clearest evidence of this phenomenon, namely Botswana, Zimbabwe, Lesotho, and Namibia (Figure 1c), are among the countries currently showing the highest HIV prevalence. In addition, the TFR in South Africa, which was fast declining long before 1990, sharply slowed down thereafter when HIV prevalence became substantial. The only country with a high prevalence of HIV not showing evidence of stalling fertility is Swaziland. Notably, on the one hand all the above countries started at the onset of the epidemic (1980) from higher income and lower fertility conditions compared to other SSA countries. On the other hand, in countries suffering from intermediate HIV epidemics (e.g., Tanzania, Malawi, Zambia, Mozambique and Kenya, all experiencing very high fertility at the onset of HIV), fertility decline slowed during 1995–2005, but accelerated thereafter.
Though the reported association between HIV prevalence and stalling fertility does not imply a causal relationship, the possibility that massive AIDS-related adult mortality might compromise major social processes, such as fertility decline, is so alarming for Africa's development as to deserve careful consideration. This is pointed out in an article on exceptional SSA adult mortality [Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008)], showing that the latter is the main reason for the collapsed economic growth and development in the region via shortening time horizons, increasing risky behavior and eventually rising fertility: “In our regressions, adult mortality explains almost all of Africa's growth tragedy. This analysis underscores grim forecasts of the long-run economic costs of the ongoing AIDS epidemic” [Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008, p. 81)]. Nonetheless, this alert is acknowledged neither by observers who pinpointed the SSA anomalous pattern of fertility decline [Bongaarts and Casterline (Reference Bongaarts and Casterline2012)] nor by the last UN population projections [UN (2015)]. Indeed, while UN projections included AIDS mortality, possible feedback on fertility was deliberately ruled out: “The fertility projections for sub-Saharan Africa follow the general path from high to low fertility observed in other regions” [UN (2015, p. 19)]. However, the resulting fertility scenarios appear inconsistent with previously observed trends as well as on conceptual grounds, due to their lack of dynamic plausibility. This is well shown by the UN's projected fertility scenarios for Zimbabwe (Figure 1d), which seem to postulate a deus ex machina suddenly restoring the right fertility pathway in 2020 while the HIV epidemic is still very much under way.
The general equilibrium macroeconomic investigation of these complex phenomena and, in general, the theoretical investigation of the macro-economic effects of communicable diseases—be they epidemic or endemic—on economic development, is still in its infancy. Most available studies [Corrigan et al. (Reference Corrigan, Glomm and Mendez2005), Momota et al. (Reference Momota, Tabata and Futagami2005) Boucekkine and Laffargue (Reference Boucekkine and Laffargue2010), Ferreira et al. (Reference Ferreira, Pessôa and Dos Santos2011), Bell and Gersbach (Reference Bell and Gersbach2013), Aksan and Chakraborty (Reference Aksan and Chakraborty2014), Azomahou et al. (Reference Azomahou, Boucekkine and Diene2016)] have focused on epidemic diseases represented as short-term shocks on mortality. The only efforts explicitly modeling the transmission dynamics of infection in a macroeconomic set-up are those of Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), who derived a useful equation for infection spread and included it in an overlapping generations (OLG) framework. However, though these studies innovated on the side of the interplay between infectious diseases and economic variables, they disregarded the key fact that a long-term deadly infection, such as HIV/AIDS, will feedback endogenously into individual decisions about fertility (directly) and mortality (indirectly through education investments).
Our objective in this work is twofold. First, we aim to contribute to the macroeconomic literature on infectious diseases by developing a novel general equilibrium unified growth theory (UGT) model [Galor and Weil (Reference Galor and Weil2000), Kalemli-Ozcan (Reference Kalemli-Ozcan2002), Galor (Reference Galor2011)] with endogenous fertility, endogenous (child and adult) mortality and HIV spread [Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016)] to investigate the interplay between a deadly epidemic, such as HIV, and economic development in SSA. We develop a UGT-like model along the lines of Galor and Weil (Reference Galor and Weil2000) without endogenous technological progress [de la Croix and Doepke (Reference de la Croix and Doepke2003)], where the demographic and economic transitions in the absence of HIV are driven by the evolution of adult survival probability, which is endogenously determined by education and HIV prevalence. Adopting a UGT approach is crucial, first of all because it is the natural economic development set-up for analyzing the DT, and second because only a general equilibrium long-term analysis including demographic variables can ultimately explain the chain of events induced by the HIV epidemic and its ultimate feedback on fertility. Moreover, by departing from the strains of the recent empirical literature suggesting that HIV has the potential to halt or even reverse the fertility transition in SSA [Yamano and Jayne (Reference Yamano and Jayne2005), Ueyama and Yamauchi (Reference Ueyama and Yamauchi2009), Fortson (Reference Fortson2011), Kalemli-Ozcan and Turan (Reference Kalemli-Ozcan and Turan2011), Kalemli-Ozcan (Reference Kalemli-Ozcan2012), Akbulut-Yuksel and Turan (Reference Akbulut-Yuksel and Turan2013), Chin and Wilson (Reference Chin and Wilson2018)], we use our framework to show the possibility of an HIV-driven “reversal” of the fertility transition in SSA. The model is parameterized with SSA mortality data putting in appropriate balance the time scales of both the demographic transition and HIV spread. The main aim is to offer theoretical insights into the consequences of two main cases about the effects of HIV in SSA, namely those of (i) a fully uncontrolled epidemic (taken as a benchmark) and (ii) an epidemic brought under control by intervention programs. In recent years, the AIDS epidemic has finally started to decline in many SSA sites thanks to growing prevention campaigns and the increasing proportion of people accessing antiretroviral therapies [UNAIDS (2017)]. As most policy actions against HIV in SSA have relied so far on international financing [UNAIDS (2017)] either by private or public donors, such as, the Global Fund against AIDS, Tuberculosis and Malaria, we model interventions against HIV as fully exogenous.
Results show that the fertility reversal arising in high HIV-prevalence countries is due to the fall in the (demand for) quality of children (i.e., education) following the decrease in life expectancy of young adults, which ultimately positively feeds back on the quantity (precautionary demand) of children (i.e., fertility) at the general equilibrium level. This is at odds with the conclusions obtained in a partial equilibrium framework by Young (Reference Young2005) and Castro et al. (Reference Castro, Behrman and Kohler2015) as well as those of the general equilibrium setting of Boucekkine et al. (Reference Boucekkine, Desbordes and Latzer2009), who treated HIV/AIDS as an external shock under exogenous mortality. For example, Castro et al. (Reference Castro, Behrman and Kohler2015) provided evidence that HIV negatively affected both the quantity and quality of children in SSA. This is undoubtedly possible in the short term, but it is hardly realistic in a medium-long-term perspective, as it suggests that the quality of children can persistently fall without feeding back on the quantity.
Importantly, the reversal can be masked when the increase in fertility attributable to the epidemic is offset by a decrease in fertility following the decline in the general mortality from causes not attributable to HIV, along the overall ongoing process of mortality transition in SSA [Bongaarts and Casterline (Reference Bongaarts and Casterline2012)]. Moreover, should the reversal hypothesis prove correct, even under the highly effective intervention programs planned by the WHO for the next 15 years, fertility might remain high for several decades, compromising development prospects in the region at least in the medium term.
The rest of the paper proceeds as follows. Section 2 reviews the empirical literature focusing on the interplay between HIV/AIDS and fertility in SSA. Section 3 builds our UGT macro-dynamic model with AIDS, discussing the key ideas, the modeling assumptions, and the main characteristics of individual choices by relating them to the existing UGT literature. Section 4 reports some theoretical results and Section 5 presents the main simulation scenarios. Section 6 further discusses the implications of the main results and outlines possible streams of future research. Section 7 summarizes the main conclusions.
2. The empirical literature on the impact of HIV/AIDS on fertility and development in SSA
Given the critical role of fertility decline as an engine of sustained economic development, a major conundrum regards the ultimate impact of HIV on the pace and extent of the fertility transition. Two major opposing positions have emerged in the economic literature, stoking controversy especially as regard the different policy implications involved.
At the one extreme, focusing on South Africa, Young (Reference Young2005) concluded that AIDS, once brought under control, would allow future generations to enjoy higher welfare than current generations. This scenario, recalling the “world of opportunities after the Black Death” ensuring an epoch of sustained growth in 15th century Europe, would eventually prevail due to the increase in capital- and output-labor ratios triggered by the direct and indirect effects of AIDS-related mortality on the labor supply. This result is based on an econometric analysis supported by a partial equilibrium Beckerian sketch with a quantity–quality trade-off, embedded in a macroeconomic set up à la Solow (Reference Solow1956). According to Young, this should hold both in the medium term, due to the mortality of young individuals, and in the long term, due to the fertility decline allowed by the increased female labor market participation. These effects will dominate the main negative effect of HIV i.e., the disruption of human capital. As Young (Reference Young2005, p. 460) ultimately stated, “The AIDS epidemic is a humanitarian disaster of millennial proportions, one that cries for assistance. It is not, however, an economic disaster.” His conclusions, extended in Young (Reference Young2007) by using household data from Demographic Health Surveys (DHS) and World Fertility Surveys (WFS) for 29 SSA countries, were as follows: “The HIV epidemic is lowering fertility in sub-Saharan Africa… In sum, the behavioural response to the HIV epidemic creates the material resources to fight it” Young (Reference Young2007, p. 283).
At the other extreme, Kalemli-Ozcan (Reference Kalemli-Ozcan2002) noted that SSA countries with high HIV prevalence showed clear symptoms of stalling fertility and falling school enrolment rates, highlighting the potential of HIV to reverse the fertility transition in SSA. This was due to the upward pressure played by AIDS mortality on the precautionary demand for children and to its downward pressure on the demand for children's education. In subsequent studies based on World Bank and DHS data, Kalemli-Ozcan and Turan (Reference Kalemli-Ozcan and Turan2011) and Kalemli-Ozcan (Reference Kalemli-Ozcan2012) were the first to empirically document the hypothesis of the HIV-driven fertility reversal of Kalemli-Ozcan (Reference Kalemli-Ozcan2002), thereby questioning Young's main conclusions. First, Kalemli-Ozcan and Turan (Reference Kalemli-Ozcan and Turan2011) revisited Young's (Reference Young2005) regressions on South Africa's data, finding that “the effect of HIV prevalence on fertility turns out to be positive… Simulating Young's model utilizing these new estimates shows that the future generations of South Africa are worse off” [Kalemli-Ozcan and Turan (Reference Kalemli-Ozcan and Turan2011, p. 61)]. Second, by using the same data as Young (Reference Young2007), Kalemli-Ozcan (Reference Kalemli-Ozcan2012) found that “…the cross-country finding of the negative significant effect of HIV on fertility by Young (Reference Young2007) is not robust” [Kalemli-Ozcan (Reference Kalemli-Ozcan2012, p. 891)]. In that article, she showed the potential for HIV to reverse the fertility transition in SSA via both a positive direct effect on the quantity of children and a negative indirect effect on the quality of children because of the existence of a negative correlation between HIV prevalence and school enrolment.
Since these seminal contributions, empirical research on this issueFootnote 1 has grown rapidly, with many articles supporting one view or other. On the side supporting the reversal hypothesis and/or the detrimental effects of AIDS on Africa's development, Chin and Wilson (Reference Chin and Wilson2018) recently found for 14 SSA countries that: “…a doubling of HIV prevalence increased TFR by approximately 1.37 births” [Chin and Wilson (Reference Chin and Wilson2018, p. 431)]. Moreover, Juhn et al. (Reference Juhn, Kalemli-Ozcan and Turan2013), based on DHS data from all over SSA, concluded that: “Together with the results from other papers that document substantial declines in human capital accumulation, the results here suggest that HIV/AIDS is likely to decrease rather than increase future per capita incomes in Africa” [Juhn et al. (Reference Juhn, Kalemli-Ozcan and Turan2013, p. 851)]. In Bell and Gersbach (Reference Bell and Gersbach2013) and Fink and Linnemayr (Reference Fink and Linnemayr2013), the possibility of an economic collapse following the HIV-induced disruption of human capital was further emphasized. Based on a different argument, Ueyama and Yamauchi (Reference Ueyama and Yamauchi2009) found that Malawian women reacted to the HIV risk by lowering the age at marriage. Their main conclusion was that this has potential for reducing years of schooling and increasing fertility through the longer period of marriage, thereby negatively impacting on human capital formation. Several studies documented evidence of negative effects of HIV/AIDS on educational investments and school participation [Yamano and Jayne (Reference Yamano and Jayne2005), Fortson (Reference Fortson2011), Kalemli-Ozcan (Reference Kalemli-Ozcan2012), Akbulut-Yuksel and Turan (Reference Akbulut-Yuksel and Turan2013)]. Yamano and Jayne (Reference Yamano and Jayne2005) showed that AIDS-related adult mortality adversely affected primary school attendance among the poor in rural Kenya, with a dramatic gender gap: the probability of girls born into poor households staying at school dropped from 88% to 55%.
As for the articles supporting Young's view, we recall Castro et al.'s (Reference Castro, Behrman and Kohler2015) partial equilibrium model providing empirical evidence (based on microdata from rural Malawian families) that HIV risk sizably reduced both quality and quantity of children. Also, Boucekkine et al. (Reference Boucekkine, Desbordes and Latzer2009), departing from a general equilibrium OLG model with endogenous fertility and exogenous mortality, concluded that AIDS (adult) mortality had an unambiguous negative effect on net fertility in SSA. Finally, Noël-Miller (Reference Noël-Miller2003) found evidence (once again from rural Malawi) of reduced childbearing only in older women.
Finally, some studies found negligible or no effects of AIDS mortality on fertility in SSA. These include the studies from Malawi by Shapira (Reference Shapira2017) and Durevall and Lindskog (Reference Durevall and Lindskog2011, Reference Durevall and Lindskog2016), as well as those (from all over SSA) by Fink and Linnemayr (Reference Fink and Linnemayr2008) and Fortson (Reference Fortson2009). The studies of Fortson and Durevall and Lindskog ably represent the complexity of the problem also in this case. For example, Fortson documented the lack of significant effects of HIV on fertility, while Durevall and Lindskog identified a range of different interesting effects of HIV on fertility pattern by age (younger versus older women) and by women's sero-status, but showed that the above effects go in opposite directions, such that the overall balance on total fertility is negligible.Footnote 2
3. The macroeconomic dynamic framework
3.1 The UGT-like model with AIDS: basic assumptions
Besides endogenous fertility, the building block of the model is represented by the assumption of endogenous child and adult survival. Survival probabilities are taken as increasing functions of human capital to reproduce, in the absence of HIV, a regular DT pattern triggered by the interplay of increasing survival, education, and fertility, aiming to reflect the pre-AIDS setting in SSA countries where the DT was ongoing prior to HIV onset. In the presence of HIV, these survival probabilities are assumed to scale with infection prevalence to mirror the disruption of human capital caused by AIDS-related mortality on the assumption that all HIV-infected individuals die of AIDS. Unlike previous studies on development and the DT, which identified the ultimate trigger of the fertility transition in the decline in child mortality [Kalemli-Ozcan (Reference Kalemli-Ozcan2002), Doepke (Reference Doepke2005), Fioroni (Reference Fioroni2010)], our model also predicts a key role played by adult survival. Consequently, we eventually predict the possibility of an HIV-induced fertility reversal due to the upsurge in adult mortality caused by AIDS. AIDS mortality reduces people's need to make provision for the future, ultimately eroding resources for education and further human capital growth [Kalemli-Ozcan (Reference Kalemli-Ozcan2012)].
We consider an OLG-closed economy accounting for fertility, mortality, education, and human capital accumulation along the UGT narrative. The economy is populated by a continuum of rational and identical individuals (mothers) of size N t per generation. Time is discrete and indexed by t = 0, 1, 2, … and the length of each period is conventionally set at 20 years. The individual's lifetime is divided among three periods: childhood/adolescence, young adulthood (or adulthood, which represents the working period) and old age. Newborns of generation t may either die early (that is, before parents can spend time on their education), with probability 1 − Γt+1, or they may survive, with probability Γt+1 ∈ [0, 1], thus receiving education (e t+1) according to parents' decisions. As adolescents, they do not make economic decisions and do not work, but can become sexually active and be exposed to HIV infection. If they survive at the onset of adulthood (time t + 1), they become economically active. In particular, Γt+1 is assumed to depend positively on the level of human capital available at time t + 1 (h t+1) and negatively on the proportion i t+1 of HIV-infective parents (representing HIV prevalence among adults, which we simply term HIV prevalence), i.e., Γt+1 = Γ(h t+1, i t+1). As adults, they maximize their expected lifetime utility, they may acquire HIV infection, and have a probability Πt+1 = Π(h t+1, i t+1) of surviving up to the onset of old age. As for child survival, adult survival positively depends on the existing endowment of human capital and negatively on HIV prevalence. The assumption that child and adult mortality depend endogenously on human capital (through education) follows Blackburn and Cipriani's (Reference Blackburn and Cipriani2002) argument that a higher education increases individual awareness of healthier behaviors and lifestyles. The endowment of labor is supplied to firms in exchange for wage income w t+1 per unit of effective labor. The (expected) lifetime utility function captures the individual preferences toward material consumption (c t+1) and the number (quantity) of surviving children (n t+1) during young adulthood, as well as the total human capital of the surviving children during old age. The following relationship holds:

relating the number of born children of generation t ($n_t^g$ ) with the resulting number of surviving children, who become economically active at time t + 1 20 years later. The size of the young adult population living at time t + 1 is $N_{t + 1} = n_tN_t = n_{t-1}^g \Gamma _tN_t$
) with the resulting number of surviving children, who become economically active at time t + 1 20 years later. The size of the young adult population living at time t + 1 is $N_{t + 1} = n_tN_t = n_{t-1}^g \Gamma _tN_t$ .
.
3.2 Disease transmission
We represent HIV spread by following Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), who first proposed a Diamond-like OLG growth model incorporating the temporal diffusion of long-lasting fatal infectious diseases by explicitly representing the transmission process rather than considering a mere mortality shock. This allowed for both intra-generational transmission between young adults and inter-generational transmission between young adults and adolescents (Figure 2).
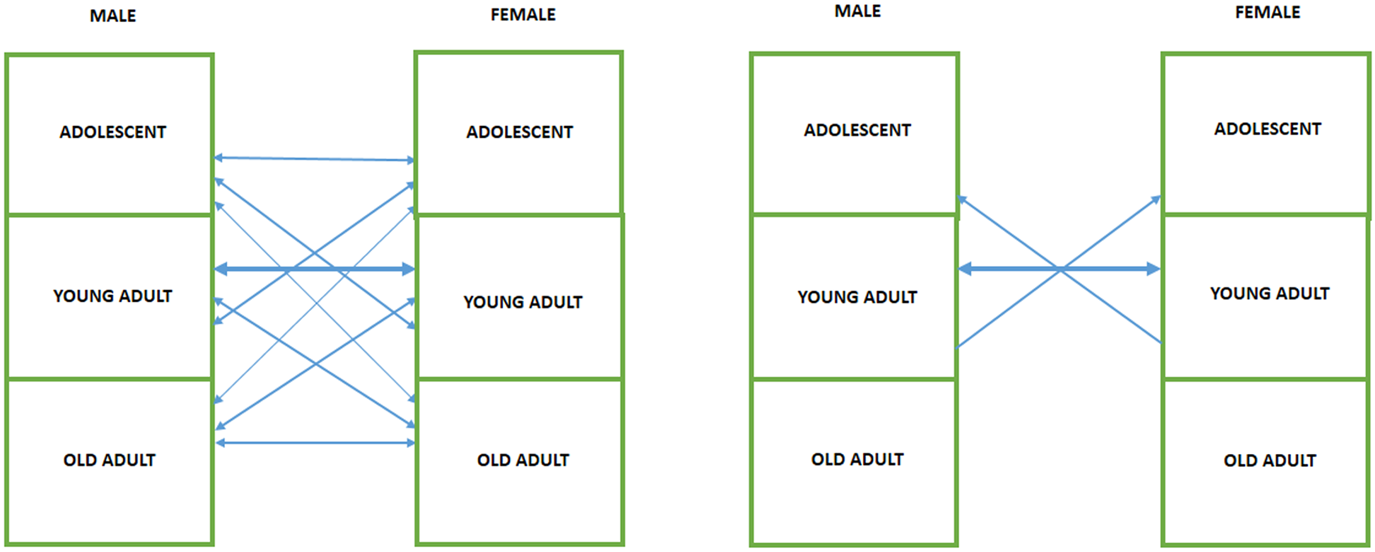
Figure 2. Mechanism of infection diffusion. Left panel: realistic patterns of HIV heterosexual transmission. Right panel: the stylized mechanism of HIV diffusion considered in Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016) and used in our model.
Let p t+1 be the probability that an HIV-susceptible young adult acquires HIV infection. Following Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), this can be represented as a function of HIV prevalence among individuals of generation t + 1, that is

where 0 < λ ≤ 1 is the constant probability of being infected per sexual partnership with an infected individual and μ > 0 represents the average number of sexual partnerships of a young adult individual during his/her entire adulthood. If the population is large, the prevalence rate at time t + 2 among young adults converges to the probability of an adult being HIV-infected, i.e., i t+2 = p t+1. Therefore, ultimately

Equation (3) describes the natural history of HIV in the absence of any control measures.
3.3 The model: individual choices
By normalizing the utility from death to zero, preferences of the representative mother born at time t, becoming economically active at time t + 1, are captured by the following inter-temporal (expected) utility function:

where ρ > 0 captures the relative taste for children and z > 0 is a scaling parameter tuning the relative degree of altruism. This allows the mother to receive utility (with certainty) from material consumption and the quantity of children during young adulthood, and from the total human capital embedded in all surviving children (n t+1h t+2) during old age. The quality of children is represented by their own level of human capital through education. As in Blackburn and Cipriani (Reference Blackburn and Cipriani2002) and Chakraborty (Reference Chakraborty2004), weighting the flow of utility when old with the adult survival probability Πt+1 captures the decision maker's responses to changing mortality and fertility conditions, thereby triggering—in the absence of HIV/AIDS—the child quantity/quality switch and ultimately the DT through the changes in child and adult mortality.Footnote 3 As we will show below, HIV/AIDS—whose dramatic mortality mainly frightens young adults (rather than children)—has the potential to break the quantity/quality switch in SSA, by preventing parents from enjoying any utility flow from educated children and altering the fertility transition.
A t-generation individual choice is made at time t + 1 subject to the budget constraint:

where m is the time endowment. Equation (5) implies that material consumption is constrained by the amount of resources available after accounting for the portions of time for giving birth to $n_{t + 1}^g$ children (ψ), and raising (ϕ t+1) and educating (e t+1) those who survive (n t+1).
children (ψ), and raising (ϕ t+1) and educating (e t+1) those who survive (n t+1).
The human capital of each child (h t+2) depends on the human capital already available (h t+1) and their time expenditure in education according to:

where q > 0 and 0 < α ≤ 1. As x + e t+1 > 0, it follows that h t+1 ∈ (0, + ∞) for any t ≥ 0 as h 1 >0 must hold. The term x > 0 guarantees that children's human capital is positive even if parents do not invest in education.
3.4 The model: main characteristics of individual choices and related literature
For clarity, before moving onto the analysis and results, we discuss the previous modeling choices and hypotheses in relation to the existing literature.
3.4.1 Relationships with the debate on economic development and the demographic transition
The core of our model is represented by the utility function (4), which draws inspiration from two main streams of research. The first is the UGT approach proposed by Galor and Weil (Reference Galor and Weil2000) and further developed among others by Kalemli-Ozcan (Reference Kalemli-Ozcan2002) and de la Croix and Doepke (Reference de la Croix and Doepke2003). The second was initiated by Blackburn and Cipriani (Reference Blackburn and Cipriani2002) and Chakraborty (Reference Chakraborty2004), stressing the importance of adult mortality on economic development. In the former, the representative individual enjoys (lifetime) utility, besides material consumption, from total human capital embedded in all surviving children. In this case, child survival emerges as the trigger of the quantity/quality switch. In the latter, the main ingredient is the survival of the decision maker (parent), which in least developed and developing economies becomes the principal individual discount factor related to future decisions. To sum up, our model builds on a UGT set-up generating the DT in the absence of HIV/AIDS and includes Blackburn and Cipriani (Reference Blackburn and Cipriani2002) and Chakraborty (Reference Chakraborty2004) endogenous survival of adults to capture the key demographic effects of HIV on economic development in SSA.
3.4.2 The HIV equation
From equation (3) we assumed a fully exogenous dynamics of HIV in the absence of control. This contrasts with Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), who related infection spread to agents' rational behavior. Expressed otherwise, our agents do not choose their risky sexual behavior by relating it to AIDS prevalence. This can be coarsely justified based on epidemiological arguments and the socio-economic context prevailing in SSA during most of the HIV epidemic, i.e., at least up to the AIDS-mortality peak around 2005. As for the first point, we recall that the entire HIV incubation period is asymptomatic, i.e., individuals remain in good health during the entire period in which they can acquire or retransmit the infection to others. Pairwise, population level information on HIV prevalence is typically unavailable in SSA. As for the second, we felt it was unreasonable to assume that agents from SSA countries, which is the poorest region worldwide [World Bank (2016)], could rationally choose their own private health investments for HIV prevention, given their utility function and budget constraint. In other words, we assumed that essentially all resources available to the family are expected to be used for upbringing and education purposes, leaving little room for private health prevention investments. Clearly, these arguments are far from satisfactory. For example, as regard the first argument, even if seropositive individuals are healthy and unaware of their sero-status, nonetheless they will observe, in their community, friends or neighbors falling sick and dying at increasing rates. So they must necessarily form some belief about the underlying causes of death. There is nonetheless evidence suggesting that, for a long time, SSA agents did not behave rationally toward sexual behavior and the AIDS risk. This has been pointed out to the demographic community since the discussion of the “context of sexual behaviour in SSA” by Caldwell et al. (Reference Caldwell, Caldwell and Quiggin1989). Further evidence has accumulated since then. For example, based on Malawi data, Peters et al. (Reference Peters, Walker and Kambewa2008) stress that people's understanding of mortality and AIDS is entrapped in beliefs that blind them to the consequences of rational behavior: “To expect [radical transformation in sexual and related practices] would be to misrepresent the capacity of people living in severely stressed situations to ‘choose’ to completely change well-established practices” [Peters et al. (Reference Peters, Walker and Kambewa2008, p. 663)]. A second line of thinking [Epstein (Reference Epstein2007)] stresses that the effectiveness of individual behavior is considerably weakened by social norms and the practice of multiple sexual partners in various areas of SSA.Footnote 4 Undoubtedly, risky sexual behavior changed slowly in several SSA areas despite the AIDS threat: for example, the first robust evidence of substantial sexual behavior change in Zimbabwe dates back not prior to 2010 [Halperin et al. (Reference Halperin, Mugurungi, Hallett, Muchini, Campbell, Magure, Benedikt and Gregson2013)]. Be things as they may, the adopted hypothesis might magnify the effect of an uncontrolled HIV epidemic on child quantity and quality, and therefore on fertility reversal. Nonetheless, given the stated complexities, we felt that following Occam's razor parsimony principle, there remained a useful departure point to be removed in future studies. Consistently, we preferred (section 5) to also model interventions against HIV/AIDS in the form of exogenous policies aimed at raising HIV awareness, in the form of a time-dependent transmission probability.
3.4.3 About AIDS mortality
A key hypothesis is that seropositive parents survive their entire young adulthood and suddenly die of AIDS at the onset of old age, being therefore in the position to bring up, look after and educate their surviving children, thus enjoying utility from them. We believe that this assumption is reasonable in view, first of all, of the long incubation period of HIV/AIDS, which means that a parent who acquires the infection at age say 25, might still be seropositive and therefore in good health at age 35 (as discussed in section 3.2). However, the representative mother living in a high HIV-prevalence community has seen her survival probability, which had been steadily increasing for many decades, dramatically fall in a span of 15 years. Therefore, the mother knows that she has quite a high probability of dying of AIDS (embedded in her utility function as a discount factor) at the onset of old age, thereby missing the utility she would enjoy from the human capital of children in the last part of her life.
3.4.4 The resulting notion of altruism
The argument in section 3.4.3 can also be discussed in relation to altruism. In this regard, there is a strand of literature acknowledging an entire spectrum of possible specifications of this hypothesis. This spectrum ranges from pure egoism [Galor and Weil (Reference Galor and Weil1996)], meaning that parents are selfish and draw (lifetime) utility from the number of children (child “quantity,” which generates the precautionary demand for children in the standard Diamond-like OLG model), to pure altruism [Barro (Reference Barro1974), Barro and Becker (Reference Barro and Becker1989), Becker et al. (Reference Becker, Murphy and Tamura1990)], implying that parents' lifetime utility depends, among other things, on the number and utility of children. The utility function adopted in this paper can belong to the notion of “impure altruism” [Andreoni (Reference Andreoni1989)], symmetrically valuing both quantity and quality of children, as embedded in equation (4), or alternatively “warm-glow altruism” simultaneously accounting for altruistic and egoistic (or selfish) motivations for giving to others.Footnote 5
4. Theoretical results
4.1 Solution of the individual problem
Maximization of the utility function (4) with respect to consumption, the number of children and the time spent in education, subject to the budget constraint (5), rule (6) for human capital accumulation, and the condition c t+1 > 0, gives the solution to the individual optimization program. This solution can be either interior (e t+1 > 0) or on the corner (e t+1 = 0). The interior solution is:



provided that (1) $\Pi _{t + 1} \gt \overline \Pi _{t + 1}$ , where
, where

is the threshold value of the adult survival probability [from equation (7)] ensuring that education is strictly positive at the interior equilibrium, and (2) Γt+1(ϕ t+1 − x) + ψ > 0 must hold to guarantee that the precautionary demand for children is strictly positive at the interior equilibrium. If $\Pi _{t + 1} \le \overline \Pi _{t + 1}$ , the solution of the individual optimization program is on the corner and it is given by:
, the solution of the individual optimization program is on the corner and it is given by:



The interior solution (7)–(9) and the corner solution (10)–(12) are in line with those obtained by Galor and Weil (Reference Galor and Weil2000), de la Croix and Doepke (Reference de la Croix and Doepke2003, Reference de la Croix and Doepke2004), Zhang and Zhang (Reference Zhang and Zhang2005), Fioroni (Reference Fioroni2010), Yakita (Reference Yakita2010) and Constant (Reference Constant2019).Footnote 6 The individual optimal behaviour can be interpreted (see Yakita, Reference Yakita2010) by comparing marginal benefits and marginal costs of education (ceteris paribus) versus those of giving birth to an extra child. The marginal benefit of additional education is represented by the marginal utility of child quality, that is  $\displaystyle{{\partial U_{t + 1}} \over {\partial h_{t + 2}}}\displaystyle{{\partial h_{t + 2}} \over {\partial e_{t + 1}}} = \displaystyle{{z\Pi _{t + 1}} \over {x + e_{t + 1}}}$, and the corresponding marginal opportunity cost is
$\displaystyle{{\partial U_{t + 1}} \over {\partial h_{t + 2}}}\displaystyle{{\partial h_{t + 2}} \over {\partial e_{t + 1}}} = \displaystyle{{z\Pi _{t + 1}} \over {x + e_{t + 1}}}$, and the corresponding marginal opportunity cost is  $\displaystyle{{\partial (w_{t + 1}e_{t + 1}n_{t + 1})} \over {\partial e_{t + 1}}} = w_{t + 1}n_{t + 1}$. The marginal benefit of giving birth to an extra child is represented by the marginal utility of child quantity (fertility), that is
$\displaystyle{{\partial (w_{t + 1}e_{t + 1}n_{t + 1})} \over {\partial e_{t + 1}}} = w_{t + 1}n_{t + 1}$. The marginal benefit of giving birth to an extra child is represented by the marginal utility of child quantity (fertility), that is  $\displaystyle{{\partial U_{t + 1}} \over {\partial n_{t + 1}}} = \displaystyle{{\rho + z\Pi _{t + 1}} \over {n_{t + 1}}}$, and the corresponding marginal opportunity cost is given by the partial derivative of the lifetime budget constraint (5) with respect to n t+1, which is given by
$\displaystyle{{\partial U_{t + 1}} \over {\partial n_{t + 1}}} = \displaystyle{{\rho + z\Pi _{t + 1}} \over {n_{t + 1}}}$, and the corresponding marginal opportunity cost is given by the partial derivative of the lifetime budget constraint (5) with respect to n t+1, which is given by  $w_{t + 1}\left( {\displaystyle{\psi \over {\Gamma_{t + 1}}} + \phi_{t + 1} + e_{t + 1}} \right)$. Therefore, comparison of marginal benefits and costs of child quality and child quantity at the optimum means that parents will be indifferent if
$w_{t + 1}\left( {\displaystyle{\psi \over {\Gamma_{t + 1}}} + \phi_{t + 1} + e_{t + 1}} \right)$. Therefore, comparison of marginal benefits and costs of child quality and child quantity at the optimum means that parents will be indifferent if  $\displaystyle{{z\Pi _{t + 1}} \over {x + e_{t + 1}}} = w_{t + 1}n_{t + 1}$ and
$\displaystyle{{z\Pi _{t + 1}} \over {x + e_{t + 1}}} = w_{t + 1}n_{t + 1}$ and  $\displaystyle{{\rho + z\Pi _{t + 1}} \over {n_{t + 1}}} = w_{t + 1}\left( {\displaystyle{\psi \over {\Gamma_{t + 1}}} + \phi_{t + 1} + e_{t + 1}} \right)$ hold, respectively. Now, indifference between educating or not educating a child involves comparison between the previous two equalities at e t+1 = 0. The indifference condition holds when $\Pi _{t + 1}-\overline \Pi _{t + 1} = 0$
$\displaystyle{{\rho + z\Pi _{t + 1}} \over {n_{t + 1}}} = w_{t + 1}\left( {\displaystyle{\psi \over {\Gamma_{t + 1}}} + \phi_{t + 1} + e_{t + 1}} \right)$ hold, respectively. Now, indifference between educating or not educating a child involves comparison between the previous two equalities at e t+1 = 0. The indifference condition holds when $\Pi _{t + 1}-\overline \Pi _{t + 1} = 0$ . If $\Pi _{t + 1}-\overline \Pi _{t + 1} \gt 0$
. If $\Pi _{t + 1}-\overline \Pi _{t + 1} \gt 0$ , the parent's net returns in terms of enjoying a higher future utility from well-educated children during her old age is positive and she prefers to invest in child quality rather than having more children. If $\Pi _{t + 1}-\overline \Pi _{t + 1} \lt 0$
, the parent's net returns in terms of enjoying a higher future utility from well-educated children during her old age is positive and she prefers to invest in child quality rather than having more children. If $\Pi _{t + 1}-\overline \Pi _{t + 1} \lt 0$ , the parent's net returns in terms of enjoying a higher future utility from well-educated children during her old age is negative and she prefers to invest in child quantity by changing the precautionary demand for children at e t+1 = 0.
, the parent's net returns in terms of enjoying a higher future utility from well-educated children during her old age is negative and she prefers to invest in child quantity by changing the precautionary demand for children at e t+1 = 0.
Regardless of HIV, this result highlights the existence of an endogenous mechanism allowing the switch from a low development regime, where both fertility and mortality (of children and adults) are “high” and the rate of human capital accumulation is low, to a high development regime, where education is positive, the rate of human capital accumulation is higher and hence both fertility and mortality (of children and adults) are set on a steadily declining path of DT.
To sum up, our analysis shows the existence of a critical threshold value of adult survival probability ($\overline \Pi _{t + 1}$ ) below which individual behaviors entrap the economy in its corner solution, where a positive relationship exists between fertility and adult survival. In this regime, individuals have no incentive to start investing in child quality and any external shocks in the standard of living temporarily increasing adult survival will simply be reflected in higher fertility, therefore implying a Malthusian relationship [this result resembles Tabata (Reference Tabata2003) and Fioroni (Reference Fioroni2010), who found a positive relationship between fertility and human capital in the low development regime]. This is because in the case of no education an increase in human capital raises adult survival prospects, allowing parents to live longer and expand the amount of resources for childrearing. Indeed, the related opportunity cost is lower than the opportunity cost of additional education, such that providing education to their children is still expensive relative to parents' income. On the other hand, above $\overline \Pi _{t + 1}$
) below which individual behaviors entrap the economy in its corner solution, where a positive relationship exists between fertility and adult survival. In this regime, individuals have no incentive to start investing in child quality and any external shocks in the standard of living temporarily increasing adult survival will simply be reflected in higher fertility, therefore implying a Malthusian relationship [this result resembles Tabata (Reference Tabata2003) and Fioroni (Reference Fioroni2010), who found a positive relationship between fertility and human capital in the low development regime]. This is because in the case of no education an increase in human capital raises adult survival prospects, allowing parents to live longer and expand the amount of resources for childrearing. Indeed, the related opportunity cost is lower than the opportunity cost of additional education, such that providing education to their children is still expensive relative to parents' income. On the other hand, above $\overline \Pi _{t + 1}$ individual behaviors let the economy lie on its interior development trajectory where a negative (resp. positive) relationship appears between fertility (resp. education) and adult survival. In this regime, an individual has an incentive to invest in child quality and increasingly reduces the precautionary demand of children as she becomes richer. The reason for the switch from quantity to quality of children depends on the higher probability of receiving a utility inflow in old age due to increasing adult survival. The main effect for the next period output is a higher level of human capital due to a larger investment in education. Besides the standard dependence of quality and quantity of children on child survival, which is the cornerstone of the UGT narrative allowing the main stylized facts of the DT to be captured [Doepke (Reference Doepke2005), Fioroni (Reference Fioroni2010)], we stress here the existing unambiguous relationship between education and adult survival and between fertility and adult survival.
individual behaviors let the economy lie on its interior development trajectory where a negative (resp. positive) relationship appears between fertility (resp. education) and adult survival. In this regime, an individual has an incentive to invest in child quality and increasingly reduces the precautionary demand of children as she becomes richer. The reason for the switch from quantity to quality of children depends on the higher probability of receiving a utility inflow in old age due to increasing adult survival. The main effect for the next period output is a higher level of human capital due to a larger investment in education. Besides the standard dependence of quality and quantity of children on child survival, which is the cornerstone of the UGT narrative allowing the main stylized facts of the DT to be captured [Doepke (Reference Doepke2005), Fioroni (Reference Fioroni2010)], we stress here the existing unambiguous relationship between education and adult survival and between fertility and adult survival.
Once HIV is introduced into the model, adult survival obviously also reflects HIV prevalence. The resulting feedback of AIDS-related mortality of adults on both the quality and quantity of children on demo-economic transition in SSA is the main feature of our modified UGT model and will be discussed later. Following Cervellati and Sunde (Reference Cervellati and Sunde2005), the current work represents a theoretical attempt to emphasize the role of adult survival (of the decision maker or parent) as a key factor for fertility transition. Results are also in line with Soares (Reference Soares2005), who emphasized the role of (child and adult) mortality in affecting individual incentives to have children (fertility) and being one of the determinants of the process of long-term growth and development.
4.2 Production
The production of final output (Y t) occurs under perfect competition according to the technology  $Y_{t + 1} = H_{t + 1} + \theta L_{t + 1}{\kern 1pt} $ that can also be written as
$Y_{t + 1} = H_{t + 1} + \theta L_{t + 1}{\kern 1pt} $ that can also be written as  $Y_{t + 1} = (h_{t + 1} + \theta ){\kern 1pt} L_{t + 1}$, where H t+1 = h t+1L t+1 is the aggregate stock of human capital (or total human capital of adult individuals), where
$Y_{t + 1} = (h_{t + 1} + \theta ){\kern 1pt} L_{t + 1}$, where H t+1 = h t+1L t+1 is the aggregate stock of human capital (or total human capital of adult individuals), where  $L_{t + 1} = \left( {m-\displaystyle{{\psi \,n_{t + 1}} \over {\Gamma_{t + 1}}}-\phi_{t + 1}n_{t + 1}-e_{t + 1}n_{t + 1}} \right)N_{t + 1}$ is the labour input and θ ≥ 0 is a parameter capturing workers’ productivity. By normalising the price of output to one, profit maximisation means that labour is paid according to its marginal product, that is w t+1 = h t+1 + θ. Unlike Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), who considered a model with physical capital, we deliberately ruled out any negative feedback of HIV on labor productivity not only because HIV-infected individuals are asymptomatic and in good health until they develop full-blown AIDS (as stated above), but especially because (in our model) the wage only affects material consumption and it has no effects on education, fertility, or the dynamics of the system [as in de la Croix and Doepke (Reference de la Croix and Doepke2003)]. As regard the assumption of perfect substitutability of the inputs, we departed from the formulation of Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010) that adds to the Cobb–Douglas production function (including physical capital and labor) a component representing natural endowment (land and animals), mimicking low-resource settings such as SSA. The technology used here represents a parsimonious version that slightly modifies their function by replacing the Cobb–Douglas term by a component only dependent on human capital. This is because we wanted to stress the primary effect of HIV/AIDS, namely the disruption of human capital through additional mortality, and the possibility of (a reversal of) the quantity/quality switch induced by the epidemic. Including total human capital in the production function is in line with Cervellati and Sunde (Reference Cervellati and Sunde2005, p. 1655): “…human capital is a central factor of production, and at the same time helps to improve the longevity and productivity of future generations.” Clearly, we could use a more standard technology e.g., Cobb–Douglas [as in Galor and Weil (Reference Galor and Weil2000)], that is $Y_{t + 1} = AH_{t + 1}^\alpha X_{t + 1}^{1-\alpha}$
$L_{t + 1} = \left( {m-\displaystyle{{\psi \,n_{t + 1}} \over {\Gamma_{t + 1}}}-\phi_{t + 1}n_{t + 1}-e_{t + 1}n_{t + 1}} \right)N_{t + 1}$ is the labour input and θ ≥ 0 is a parameter capturing workers’ productivity. By normalising the price of output to one, profit maximisation means that labour is paid according to its marginal product, that is w t+1 = h t+1 + θ. Unlike Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016), who considered a model with physical capital, we deliberately ruled out any negative feedback of HIV on labor productivity not only because HIV-infected individuals are asymptomatic and in good health until they develop full-blown AIDS (as stated above), but especially because (in our model) the wage only affects material consumption and it has no effects on education, fertility, or the dynamics of the system [as in de la Croix and Doepke (Reference de la Croix and Doepke2003)]. As regard the assumption of perfect substitutability of the inputs, we departed from the formulation of Chakraborty et al. (Reference Chakraborty, Papageorgiou and Pérez Sebastián2010) that adds to the Cobb–Douglas production function (including physical capital and labor) a component representing natural endowment (land and animals), mimicking low-resource settings such as SSA. The technology used here represents a parsimonious version that slightly modifies their function by replacing the Cobb–Douglas term by a component only dependent on human capital. This is because we wanted to stress the primary effect of HIV/AIDS, namely the disruption of human capital through additional mortality, and the possibility of (a reversal of) the quantity/quality switch induced by the epidemic. Including total human capital in the production function is in line with Cervellati and Sunde (Reference Cervellati and Sunde2005, p. 1655): “…human capital is a central factor of production, and at the same time helps to improve the longevity and productivity of future generations.” Clearly, we could use a more standard technology e.g., Cobb–Douglas [as in Galor and Weil (Reference Galor and Weil2000)], that is $Y_{t + 1} = AH_{t + 1}^\alpha X_{t + 1}^{1-\alpha}$ , where X t+1 = θL t+1 (for sufficiently large θ, consumption will be above one, and the utility will never be negative), but this would not affect our main findings. This is because the dynamics of the economy result only from human capital accumulation and HIV spread, and neither of these variables depend on the wage rate, which only affects material consumption [see equations (7)–(9) and (10)–(12)]. Therefore, using a production function including either perfect or imperfect substitutability between factor inputs has no influence. We also recall that a purely human-capital-dependent technology is central in the Boserupian mechanism, where skills acquired from learning-by-doing increase human capital and represent the key factor for agricultural economies to escape from the Malthusian trap in the demographic tradition [Boserup (Reference Boserup1981)].Footnote 7
, where X t+1 = θL t+1 (for sufficiently large θ, consumption will be above one, and the utility will never be negative), but this would not affect our main findings. This is because the dynamics of the economy result only from human capital accumulation and HIV spread, and neither of these variables depend on the wage rate, which only affects material consumption [see equations (7)–(9) and (10)–(12)]. Therefore, using a production function including either perfect or imperfect substitutability between factor inputs has no influence. We also recall that a purely human-capital-dependent technology is central in the Boserupian mechanism, where skills acquired from learning-by-doing increase human capital and represent the key factor for agricultural economies to escape from the Malthusian trap in the demographic tradition [Boserup (Reference Boserup1981)].Footnote 7
4.3 General equilibrium
By using the solution of the individual problem [equations (7)–(9) or (10)–(12)] together with equation (6) describing human capital accumulation, we obtain the following two-dimensional map describing the evolution of human capital and HIV prevalence over two subsequent periods, which completely characterizes the dynamics of the economy:

Remark 1 In the absence of HIV (i t = 0), the model becomes:

where $\overline{\overline \Pi} _{t + 1} = \overline{\overline \Pi} (h_{t + 1},0)$ , predicting convergence toward either a low development regime or a high development regime depending on the relative size of adult survival, which in turn depends only on human capital (education) in that case.
, predicting convergence toward either a low development regime or a high development regime depending on the relative size of adult survival, which in turn depends only on human capital (education) in that case.
Importantly, the UGT literature, whose main goal is to explain the fertility transition, has pinpointed different channels based on different thresholds. Such thresholds have been identified in terms of technological progress [Galor and Weil (Reference Galor and Weil2000)], in terms of individual heterogeneity [de la Croix and Doepke (Reference de la Croix and Doepke2003)], in child survival [Kalemli-Ozcan (Reference Kalemli-Ozcan2002), Fioroni (Reference Fioroni2010)] or in the individual's ability to acquire human capital [Cervellati and Sunde (Reference Cervellati and Sunde2005)].
The natural history of HIV in the absence of any control measures [equation (3)] is summarized in the following proposition (of which we omit the easy proof).
Proposition 1 Equation (3) always has an infection-free steady-state equilibrium (i t = 0), which is globally asymptotically stable if $\mu \, \lambda \lt 1$ . For $\mu \, \lambda \gt 1$
. For $\mu \, \lambda \gt 1$ a unique and epidemiologically meaningful steady-state equilibrium with infection present (a so-called endemic equilibrium) appears (i* < 1), which is globally asymptotically stable.
a unique and epidemiologically meaningful steady-state equilibrium with infection present (a so-called endemic equilibrium) appears (i* < 1), which is globally asymptotically stable.
Remark 2 The threshold parameter $\mu \, \lambda$ in Proposition 1 has a convenient epidemiological interpretation: sinceμ represents the number of different sexual partners of the representative agent during his/her sexually active life and λ represents the transmission probability per single sexual partnership, the product $\mu \, \lambda$
in Proposition 1 has a convenient epidemiological interpretation: sinceμ represents the number of different sexual partners of the representative agent during his/her sexually active life and λ represents the transmission probability per single sexual partnership, the product $\mu \, \lambda$ represents the expected number of new infections caused by a single infective agent during her entire sexually active life provided all her partners are susceptible to infection. The ensuing interpretation is that the infection can become endemic only if it is “reproductive,” i.e., each infective agent causes more than one secondary lifetime infection. Consequently, according to epidemiological and demographic jargon, the product $\mu \, \lambda$
represents the expected number of new infections caused by a single infective agent during her entire sexually active life provided all her partners are susceptible to infection. The ensuing interpretation is that the infection can become endemic only if it is “reproductive,” i.e., each infective agent causes more than one secondary lifetime infection. Consequently, according to epidemiological and demographic jargon, the product $\mu \, \lambda$ represents the basic reproduction number of the pathogen.
represents the basic reproduction number of the pathogen.
Given that the HIV equation is independent of other variables, the dynamics of HIV follows Proposition 1. Therefore, in the below-threshold case $\mu \, \lambda \lt 1$ , as HIV eventually goes extinct (i t → 0), the medium-long-term dynamics of the economy is essentially the one described by (14), where i t = 0. Here, by medium-long-term we mean a period of time such that the infection has reached its steady-state equilibrium (be this the extinction or the endemic steady state), but all the remaining demographic and economic variables—which are affected by the dynamics of HIV—are still in their transient phase. By contrast, in the above-threshold case $\mu \, \lambda \gt 1$
, as HIV eventually goes extinct (i t → 0), the medium-long-term dynamics of the economy is essentially the one described by (14), where i t = 0. Here, by medium-long-term we mean a period of time such that the infection has reached its steady-state equilibrium (be this the extinction or the endemic steady state), but all the remaining demographic and economic variables—which are affected by the dynamics of HIV—are still in their transient phase. By contrast, in the above-threshold case $\mu \, \lambda \gt 1$ HIV will eventually approach its long-term steady-state equilibrium i*. This in turn means that all relevant demo-economic variables depending on HIV prevalence will obey a medium-long-term pathway depending only on i*. In particular, when HIV has achieved its endemic steady-state equilibrium i*, the medium-long-term dynamics of the survival functions Πt+1 = Π(h t+1, i t+1) and Γt+1 = Γ(h t+1, i t+1) in the absence of any control measures are: Πt+1 = Π(h t+1, i*) and Γt+1 = Γ(h t+1, i*). Consequently, the medium-long-term form of human capital accumulation as described in (13) is the following:
HIV will eventually approach its long-term steady-state equilibrium i*. This in turn means that all relevant demo-economic variables depending on HIV prevalence will obey a medium-long-term pathway depending only on i*. In particular, when HIV has achieved its endemic steady-state equilibrium i*, the medium-long-term dynamics of the survival functions Πt+1 = Π(h t+1, i t+1) and Γt+1 = Γ(h t+1, i t+1) in the absence of any control measures are: Πt+1 = Π(h t+1, i*) and Γt+1 = Γ(h t+1, i*). Consequently, the medium-long-term form of human capital accumulation as described in (13) is the following:

Remark 3 The previous discussion shows that with HIV at its endemic equilibrium (i t = i*), the medium-long-term behavior of the economy depends on the magnitude of i*. Ceteris paribus, regarding human capital accumulation, if the economy were already on its interior path, the development conditions could either worsen (at low levels of endemicity) or even be brought back to the poverty trap (at high levels of endemicity).
5. Simulation scenarios of the impact of AIDS on fertility
This section describes the parameterization, including the effects of interventions (subsection 5.1), adopted to generate the scenarios concerning the impact of an uncontrolled HIV epidemic (subsection 5.2) and the effects of an exogenous intervention program (subsection 5.3).
5.1 Model parameterization
5.1.1 Functional forms for child and adult survival
Consistent with the hypotheses of section 3.1, we modeled the child survival probability Γt+1 as follows:

where $\Gamma _{t + 1}^{NA}$ represents the child survival probability in the absence of HIV and 0 < δ ≤ 1 is the conditional probability that a child of HIV-infected parents is vertically transmitted at birth, such that $\delta \, i_{t + 1}$
represents the child survival probability in the absence of HIV and 0 < δ ≤ 1 is the conditional probability that a child of HIV-infected parents is vertically transmitted at birth, such that $\delta \, i_{t + 1}$ is the probability of a child being born infected (and dying soon after). The adopted functional form for $\Gamma _{t + 1}^{NA}$
is the probability of a child being born infected (and dying soon after). The adopted functional form for $\Gamma _{t + 1}^{NA}$ is as follows:
is as follows:

where Γpre, Γpost ∈ [0, 1] are, respectively, child survival at birth in the Malthusian regime prevailing before mortality decline and child survival at birth in the modern regime at the end of the mortality transition [Galor (Reference Galor, Aghion and Durlauf2005, Reference Galor2011)], and b > 0 is a parameter tuning the shape of the mortality transition along the growth of human capital. The functional form (17) depicts a pattern of increasing child survival during the mortality transition (in the absence of HIV), departing from its Malthusian level Γpre and eventually approaching its modern level Γpost by the end of the mortality transition.
Similarly, the probability Πt+1 is modeled as follows:

where $\Pi _{t + 1}^{NA}$ represents the adult survival probability in the absence of HIV, which is assumed to take the following form:
represents the adult survival probability in the absence of HIV, which is assumed to take the following form:

where Πpre, Πpost ∈ [0, 1] and B > 0 have the corresponding meaning of Γpre, Γpost, and b in equation (16).
Finally, the cost of raising children is represented by an increasing function of human capital accumulation as in (17) and (18), that is:

5.1.2 Intervention programs against HIV by external donors
Intervention programs against HIV are modeled by an exogenous reduction in the transmission probability per partnership λ (it would be equivalent to intervening on the number of sexual partners μ). As discussed in the Introduction, this is motivated by the fact that the vast majority [up to 90% of AIDS funding in low-income countries in 2013, UNAIDS (2017)] are paid for through external financial donations. The chosen approach can capture a range of different medical treatments, e.g., anti-retroviral, with the potential to reduce individual infectivity, as well as non-medical interventions, e.g., aiming to increase awareness of HIV risk and favor spontaneous behavior changes, such as reducing the number of sexual partners and increasing the use of condoms. We believe that this is a good compromise between realism and the simplicity of the theoretical framework adopted. Indeed, a more realistic description of the complex set of interventions against HIV (to prevent new infections) and against AIDS (to treat the sick) would require a much more detailed modeling set-up. The intervention is introduced at time t = T and the evolution of λ is modeled in the simplest possible way, that is:

where λ represents the HIV transmission probability in the absence of any interventions and λ c < λ represents the corresponding probability after a control program initiated at time t = T. In what follows, we will focus on a fully successful control $\mu \, \lambda _c \lt 1$ , which will bring the HIV epidemic on an extinction path according to the first part of Proposition 1.
, which will bring the HIV epidemic on an extinction path according to the first part of Proposition 1.
5.1.3 Parameter assignment
Parameterization was carried out to broadly match the main quantitative traits of the DT and HIV spread in SSA. To this end, we attempted to pursue the following three sub-goals: namely (A) coarsely reproducing the scale of fertility and mortality transition in SSA; (B) matching HIV prevalence data; and (C) keeping in a reasonably correct empirical balance the relative time scales of the epidemic and of the fertility transition.
Demographic parameters were assigned from UN data for SSA [UN (2019)] in order to (i) reproduce the range of TFR decline during the fertility transition in SSA, departing from a pre-transitional level of about 6 and ending at about 2 (i.e., the replacement level) in line with UN projections medium variant [UN (2015)], and (ii) the pre- and post-transitional levels of the survival probabilities Πpre, Πpost and Γpre, Γpost in (17) and (19).
Parameters (μ,λ) of the HIV equation (2) were assigned to bound at equilibrium (in the absence of any intervention) the range of prevalence levels observed in the adult population in medium-high prevalence SSA countries, according to UNAIDS last estimates [UNAIDS (2017)]. This was motivated by the fact that in most cases such estimates showed a constant trend for several years before 2015 (Figure 1a). We considered the following idealized scenarios in terms of the HIV equilibrium prevalence (i*): “low”: i* = 0.1, “medium”: i* = 0.15, “high”: i* = 0.2, “very high”: i* = 0.3.
Summary information about model parameters is reported in Table 1. Parameter values were either borrowed from the literature or assigned for simulation purposes.
Table 1. Summary information about assignment of model parameters

t denotes time in OLG units i.e., it represents the length of an OLG time (set to 20 years in the model). Values of Πpre, Πpost and Γpre, Γpost were assigned to match the corresponding observed probabilities to survive from age 20 to 40 (for a person alive at age 20), and from birth to age 20, respectively.
5.2 Simulation scenarios: the benchmark case of an uncontrolled HIV epidemic
In the absence of HIV, our model predicts the onset of fertility transition—with the escape from the poverty trap—and its gradual completion as an endogenous response of education investments to the increase in survival of both children and young adults. This is represented by the S-shaped TFR decline from about 6 to a replacement level slightly in excess of 2 (the black curve represented on the left axis in Figure 3, both panels). Though in section 3 we focused on female fertility, meant as the average number of daughters of a representative mother during her adult phase in the absence of mortality, here we prefer to refer to total fertility and focus more intuitively on the trend of the TFR.

Figure 3. The predicted trajectories of SSA fertility in the absence of HIV (left axis) and of HIV prevalence (right axis) under uncontrolled HIV epidemics of different intensity. Left panel: the onset of HIV occurs at an advanced stage of the fertility transition. Right panel: the onset of HIV occurs at an earlier stage of the fertility transition.
We initialize the HIV epidemic for $\mu \, \lambda \gt 1$ along section 5.1.3 by assuming that the economy already lies on its development trajectory with a strictly positive level of education.Footnote 8 The onset and growth of HIV reduces adult survival (by way of AIDS mortality) and therefore impacts negatively on education and human capital, and ultimately brings fertility up along the direct effect shown in equations (7) and (8), as well as along the general equilibrium feedback effects due to the overall dynamics of the economy. We also point out that, in principle, nothing prevents HIV bringing a growing economy back to its corner solution, that is on its pre-transitional underdevelopment path. However, as this seems to require higher levels of HIV prevalence than those observed so far in SSA, we will rule out this case from subsequent simulations.
along section 5.1.3 by assuming that the economy already lies on its development trajectory with a strictly positive level of education.Footnote 8 The onset and growth of HIV reduces adult survival (by way of AIDS mortality) and therefore impacts negatively on education and human capital, and ultimately brings fertility up along the direct effect shown in equations (7) and (8), as well as along the general equilibrium feedback effects due to the overall dynamics of the economy. We also point out that, in principle, nothing prevents HIV bringing a growing economy back to its corner solution, that is on its pre-transitional underdevelopment path. However, as this seems to require higher levels of HIV prevalence than those observed so far in SSA, we will rule out this case from subsequent simulations.
The HIV epidemic in the absence of control takes off and gradually approaches its equilibrium prevalence i*, where it persists thereafter (the four colored curves depicted on the right axes in Figure 3, both panels). The two panels of Figure 3 can be mutually contrasted to mirror the empirically documented variability in the stage of the fertility transition of SSA countries at the onset of large HIV epidemics. In this regard, the left panel depicts a situation where the epidemic began at an advanced stage of the fertility transition (TFR about 3.5), such as for South Africa, while the right panel depicts a situation where the epidemic began at an early stage of the transition (TFR still in the range 5–6), such as for Kenya.Footnote 9
The impact of a persistent uncontrolled HIV epidemic on the fertility transition in SSA would be dramatic (Figure 4), with fertility reaching levels well above the replacement threshold. For high endemic levels of HIV, the TFR eventually stalls on levels higher than three children per woman. Moreover, medium-high HIV epidemics have the potential to cause a sharp reversal in the fertility transition pathway. Two main qualitative scenarios emerge depending on whether the onset of HIV occurred either at an advanced or at an earlier stage of the fertility transition as in Figure 3. In the former case, at the onset of HIV the TFR has already experienced most of its decline. The reversal occurs through a marked increase in TFR which essentially remains constant thereafter. Instead, in the latter case the TFR shows a temporary relapse, after which it resets on a declining path. This is because the fertility decline triggered by mortality progress from causes of deaths other than HIV had already initiated, so that there remains considerable room for further reductions in fertility attributable to such causes.

Figure 4. Potential impact of uncontrolled HIV epidemics on the fertility transition in SSA for different levels of HIV endemic equilibrium prevalence (i*). Left panel: the HIV onset occurs at an advanced stage of the transition. Right panel: the HIV onset occurs at an earlier stage of the transition.
Importantly, the HIV-induced fertility relapse is not a full reversal in the clock of history with fertility returning to its pre-transitional level. The range of the fertility relapse is indeed strictly bounded by the relapse in the mortality of adults, which is only one of the two components of the fertility transition, the other being the decline in child mortality, which is only slightly affected (at the aggregate level) by HIV.
The causation chain (illustrated in Figure 5 for the scenario of HIV onset at an advanced stage of the fertility transition, as in Figures 3 and 4, left panel) goes as follows: (a) AIDS mortality breaks-down the long-term declining trend in adult mortality, which suddenly upturns (Figure 5, left panel); (b) the upturn in adult mortality reverses the positive trend on education investments (Figure 5, central panel); and (c) the collapse in education investment sets the growth rate of human capital at lower levels, which are insufficient to further fuel the quantity–quality switch, and therefore to further promote fertility decline (Figure 5, right panel). Note that at its long-term equilibrium in the absence of intervention the model, which had been calibrated on data from Lesotho, mirrors the observed drop in the survival probability Πt+1 from more than 90% in the pre-HIV period to less than 65% in proximity of the most dramatic phase of the epidemic in 2005 (Figure 6). Note also that the observed trajectory in Figure 6 shows a gradual relapse after 2010 due to the onset of interventions against HIV, while the predicted curve in the left panel of Figure 5 just stabilizes because no intervention is assumed.

Figure 5. Fertility reversal in SSA under an uncontrolled HIV epidemic for different levels of HIV endemic equilibrium prevalence. Temporal trends of: adult survival probability Πt+1 (left panel), education e t+1 (center panel), and growth rate of human capital h t+1 (right panel).

Figure 6. Observed trend of the survival probability Πt+1 that a (female) individual who just entered young adulthood survives until entering old age in Zimbabwe and Lesotho, 1950–2015. The function Πt+1 was estimated by the conditional survival probability p 40/p 20, where p x represents the survival function up to exact age x [source: UN (2019)].
5.3 Simulation scenarios: the effects of interventions
The analysis in the previous section described a useful theoretical benchmark against which to ground the predicted effects of the current realistic scenarios of HIV control [WHO (2016), UNAIDS (2017)] on fertility. We now report the implications of exogenous interventions noted in section 5.1. For the sake of simplicity, we only consider interventions able to eventually eliminate HIV, and compare the effects of different timings, contrasting an early intervention, initiating shortly before the epidemic has reached its equilibrium prevalence, with a few delayed interventions (Figure 7). We hypothesize that the time span needed to bring HIV to elimination from the intervention onset is roughly comparable with the time span that the epidemic took to reach its peak (Figure 7, left panel), which in SSA lasted approximately two-three decades [UNAIDS (2017)]. The fact that it is hopeless to eliminate HIV more rapidly is motivated, on the one hand, by the large proportions of current seropositive individuals still unaware of their own health status that might remain infective for decades in the absence of large-scale screening, and, on the other, by the fact that effective anti-retroviral therapies will extend the duration of the sero-positive period for treated individuals [WHO (2016)].

Figure 7. HIV onset at an advanced stage of the fertility transition. Temporal trend of HIV prevalence (left panel) and total fertility (right panel) under different effective intervention programs able to eventually achieve HIV elimination. The intervention programs differ in the timing of initiation (t = 80, 100, 120).
For brevity, we report predictions of controlled HIV scenarios (Figure 7) just focusing on the case of late HIV onset (Figures 3 and 4, left panel). Bringing HIV under full control (Figure 7, left panel) will gradually remove obstacles to investments in education, such that the TFR will eventually settle on its replacement level (Figure 7, right panel). Nonetheless, even under the early intervention scenario, the time span needed to bring HIV to elimination, has the potential to delay the completion of fertility transition. Obviously, this scenario could substantially worsen in the presence of delays in the effectiveness of interventions (right panel).
6. Implications of the results and further discussions
This paper tackled a major unresolved question about economic development, namely the impact of HIV/AIDS on the fertility transition in SSA. Indeed, in some SSA countries suffering from large HIV epidemics, where life expectancies fell dramatically in the early phase of the epidemic and are also projected to return to pre-HIV levels only by 2060 [UN (2015)], fertility decline is now stalling [UN (2015)], and there is also evidence of negative effects on investments in education (see the discussion in section 2). We built a parsimonious UGT-like set-up: (i) to reassess the ultimate impact of HIV on SSA fertility in its natural (general equilibrium) economic modeling context of the fertility transition [Galor and Weil (Reference Galor and Weil2000), Galor (Reference Galor, Aghion and Durlauf2005, Reference Galor2011)]; (ii) to serve as a theoretical benchmark for the empirical evidence on the HIV-induced fertility reversal in SSA [Kalemli-Ozcan and Turan (Reference Kalemli-Ozcan and Turan2011), Kalemli-Ozcan (Reference Kalemli-Ozcan2012)]; (iii) to prioritize future economic interventions in countries suffering from large HIV epidemics from a more general social perspective; and (iv) to shed light on the economic theory of fertility with unambiguous predictions on demo-economic outcomes that HIV or, generally speaking, long-term deadly epidemics may generate on the welfare of future generations.
The adopted parameterization represented the relative time scales of the HIV epidemic and the fertility transition in a correct empirical balance. In the absence of HIV, the model predicts (as in the standard UGT) the completion of the fertility transition as an endogenous response to the decline in both child and adult mortality, which in turn promotes investments in education and ultimately the reduction in fertility via the quantity–quality switch. This switch—triggered by adult survival—allows a shift from a low development regime (no education) to a high development one (positive education). In the former (low adult survival), increasing human capital increases adult survival but the parent chooses to spend more resources on raising children rather than educating them. This is because the parent is poorly educated and the opportunity cost of raising children is lower than the opportunity cost of education, such that providing intra-family education is expensive relative to the parent's income. In the latter (high adult survival), the parent chooses to invest in education as the marginal benefit of educating children (the rate of return of human capital) outweighs the marginal cost of raising them. Thus, better educated parents choose to reduce their precautionary demand for children by devoting resources to additional education.
In the presence of a large uncontrolled HIV epidemic (that is, yielding an endemic prevalence in the adult population above 15–20%), HIV has the potential to prevent the completion of the fertility transition. Reversals in the fertility trajectory are more likely to emerge in countries where the onset of HIV occurred at a later stage of the fertility transition. The critical triggering factor of the fertility reversal was the AIDS-related increase in adult mortality, which reduced the parents' investment in children's education and therefore prevented the quantity–quality switch. The underlying mechanism is at odds with that generally acknowledged as the driving factor of fertility transitions, i.e., the fall in child mortality, as pointed out by Kalemli-Ozcan (Reference Kalemli-Ozcan2002) and Doepke (Reference Doepke2005).
Our results also showed that the fertility reversal persists under rather realistic hypotheses [WHO (2016), UNAIDS (2017)] about AIDS control. Although the achievement of HIV full control would eventually remove the obstacles to the completion of the fertility transition, the timing with which control measures will be enacted becomes critical. Indeed, any delay in controlling HIV would not only allow the direct negative effects of the epidemic (namely, its large mortality burden) to persist, but it might also cause fertility to remain persistently high due to the drop in private investments in education. In addition, the persistence of high fertility would promote continued population growth, therefore losing protracted periods potentially favorable to economic development. In relation to this, the timing of effective interventions is hard to predict for SSA, especially in view of the large number of seropositive individuals unaware of their sero-status [WHO (2016), UNAIDS (2017)]. This is aggravated by the fact that effective anti-retroviral therapies have the well-known shortcoming of increasing the infective period.
We believe that the relationships between HIV, education and fertility theoretically inferred here should be carefully considered from the policy standpoint considering the evidence supporting the reversal hypothesis.
The present model should be considered as a starting point whose primary goal was to develop a framework for the impact of HIV on fertility in SSA using a UGT-like set-up. Consequently, we disregarded other possible channels of influence of HIV on fertility that have been considered in the various literatures (epidemiologic, demographic, economic, etc.) ranging from the lower fecundity observed in sero-positive women to the long-term positive general equilibrium effect of higher mortality on women's labor participation, etc. In future studies, it will also be important to consider more flexible representations of HIV intervention programs, taken here as fully exogenous to mimic external donations by international organizations, by also including endogenous policies.Footnote 10
Further extensions of the present model should include, for instance, saving and the accumulation of physical capital. This was deliberately avoided here to mirror SSA economies, which show the lowest aggregate saving [World Bank (2016)], the highest income inequality [IMF (2015)], and the least-developed political and financial systems worldwide [Easterly and Levine (Reference Easterly and Levine1997)]. Inclusion of physical capital would allow us to capture also the impact of the HIV/AIDS on labor productivity, as in Chakraborty et al.(Reference Chakraborty, Papageorgiou and Pérez Sebastián2010, Reference Chakraborty, Papageorgiou and Pérez Sebastián2016). This hypothesis might become relevant under successful HIV control allowing good health survival of full-blown AIDS individuals. Accounting for heterogeneous agents may allow also capturing the heterogeneity between HIV and AIDS individuals and the issue of HIV-related orphan-hood [Bell and Gersbach (Reference Bell and Gersbach2013)].
Our last remark deals with the general issue of the factors triggering the fertility transition within the UGT framework. In our formulation, regardless of the presence of HIV, the fertility transition (and its reversal) is triggered by the interplay of total human capital embedded in surviving children [Galor and Weil (Reference Galor and Weil2000)] and adult survival [Chakraborty (Reference Chakraborty2004)]. This is captured by the last addendum in the utility function in equation (4), that is zΠt+1ln(n t+1h t+2). In particular, the total human capital n t+1h t+2 attributes the same “weight” to large families with low educated children, as in pre-industrial societies (where children produced income in the “backyard”), and to small families with high educated children, as in industrialized societies (where large levels of urbanization prevent children from being income producers). Therefore, taking the total human capital of the surviving children and discounting it by the parent's adult survival, ρ + zΠt+1(1 − α) > 0, represents a highly parsimonious dynamic formulation of the conditions for a quantity/quality switch in a mortality-evolving setting. From this standpoint, we felt to be compelled to combine Galor and Weil with Chakraborty to have an “optimal” setting to study the fertility transition and its interplay with HIV/AIDS.
7. Conclusions
“Development occurs only if people make provision for the future. If they see no future, there is no growth” [Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008, pp. 81–82)]. All successful stories of economic development were triggered by mortality decline that in turn promoted fertility decline, thus making resources available for investments in education and fuelling a virtuous circle of sustained economic growth and development [Becker et al. (Reference Becker, Murphy and Tamura1990), Kalemli-Ozcan (Reference Kalemli-Ozcan2002, Reference Kalemli-Ozcan2003), Fogel (Reference Fogel2004), Doepke (Reference Doepke2005), Galor (Reference Galor, Aghion and Durlauf2005, Reference Galor2011), Soares (Reference Soares2005), Tamura (Reference Tamura2006) Cervellati and Sunde (Reference Cervellati and Sunde2011), Livi-Bacci (Reference Livi-Bacci2017), Fiaschi and Fioroni (Reference Fiaschi and Fioroni2019)].
Despite its very poor health conditions, with the highest death toll of communicable diseases worldwide, first from malaria and TB [Bloom and Canning (Reference Bloom and Canning2004), WHO (2016)], SSA experienced continued (though slow) mortality decline until the onset of HIV/AIDS in the late 1970s. In high-prevalence countries, HIV rapidly became and was, until very recently, the leading cause of mortality [IHME (2013), UNAIDS (2017)], and was able to overturn the increasing trend in life expectancy by dramatically changing the value of the discount factor of the quantity/quality trade-off.
Possibly due to its dramatic mortality burden [see Lorentzen et al. (Reference Lorentzen, McMillan and Wacziarg2008)], SSA is the only region worldwide where the fertility transition is still dramatically delayed [Bongaarts and Casterline (Reference Bongaarts and Casterline2012)]. Therefore, the possibility that HIV might paralyze, or even reverse, the fertility transition by severely delaying it for several further decades, is somewhat alarming. This is because persistent high fertility would promote continued population growth, therefore causing the loss of entire epochs potentially favorable to economic development.
The controversial empirical evidence, with several field studies supporting the reversal hypothesis [Kalemli-Ozcan (Reference Kalemli-Ozcan2012), while others suggest that HIV is favoring fertility decline [Young (Reference Young2005)], might be seriously detrimental because of the dramatically different policy implications that the two positions implicitly promote. In Young's scenario, where future SSA generations will be better off than current ones, the implicit policy recommendation is no intervention. On the contrary, in the reversal scenario, where the fertility transition might be delayed for several decades even in the presence of effective HIV control, there seems to be only one possible policy recommendation, namely that maximum control effort should be made right now, without delays, and prioritizing those high-prevalence countries experiencing long-lasting effects of AIDS-related mortality. A first candidate would then be, for instance, Lesotho, where life expectancy is predicted to return to the pre-HIV level by 2060 (Figures 1 and 6) and where UN fertility data [UN (2015)] show clear symptoms of fertility stalling (Figure 1). In this context, SSA generations will have faced for about one century a dramatically larger mortality burden than in the pre-AIDS era. The complexities of HIV interventions, as well documented by the controversial Uganda “success story” [Green et al. (Reference Green, Halperin, Nantulya and Hogle2006), Shafer et al. (Reference Shafer, Biraro, Nakiyingi-Miiro, Kamali, Ssematimba, Ouma and Ojwiya2008)], or the fact that the first well documented decline in HIV prevalence in Zimbabwe is very recent [Halperin et al. (Reference Halperin, Mugurungi, Hallett, Muchini, Campbell, Magure, Benedikt and Gregson2013)], should again call for caution in handling such an emergency.
We fear that denying the potential consequence of the fertility reversal would be as dangerous as the “denialism” of the etiological link between the HIV virus and the AIDS disease, originated by Duesberg's (1996) book “Inventing the AIDS Virus” that influenced South Africa's public health policy on AIDS, dramatically delaying epidemic control thereof. This also makes it important to stress the peril of both conservative and generalist approaches to the fertility transition. An instance of the former viewpoint is the last round of the UN projections [UN (2015)], which gave up including the possible feedbacks of HIV on fertility in SSA because of the lack of a conceptual model for embedding the resulting complicated relationships. Instead, an instance of the latter viewpoint is the large-scale approach—including all countries from the developing world—relating the adjusted “conception” rate with the GDP growth rate, as in Chatterjee and Vogl (Reference Chatterjee and Vogl2018), who concluded there was a large-scale escape from the Malthusian trap. In our opinion, their conclusion straightforwardly follows from the fact that fertility decline is essentially—over appropriate time scales—an almost universal phenomenon. This, however, currently has only one major, but dramatically important, exception: SSA countries with large HIV epidemics.
In tackling such complex scenarios, the precautionary principle should be the main driver of policy actions in SSA [May and Turbat (Reference May and Turbat2017)]. Unlike Young (Reference Young2005), we believe that the HIV/AIDS epidemic is a humanitarian and economic disaster that should receive the highest priority among policy makers.
Acknowledgements
The authors warmly thank two anonymous reviewers of the journal, whose useful points allowed us to greatly improve the content and exposition of the paper. The authors also acknowledge Oded Galor, seminar participants at La Sapienza University of Rome (May 2018), conference participants at the 16th Nordic Conference in Development Economics 2017 (June 12–13, University of Gothenburg), NED-CICSE 2017 (September 7–9, University of Pisa, SIE 2017 (October 19–21, University of Calabria), and LAGV 2018 (June 25–26, Aix-en-Provence) for useful comments and suggestions on an earlier draft. Piero Manfredi contributed to this research in his position as scientific advisor of the European Research Council Grant Agreement 283955, “The impact of DEmographic Changes on Infectious DisEases transmission and control in middle- and low-income countries (DECIDE),” FP7/2007-2013. Usual disclaimers apply.
Conflict of interest
The authors declare that they have no conflict of interest.










