The average herd size in pasture-based production systems, such as those in New Zealand and Ireland, has been increasing through time (DairyNZ & LIC, 2011; ICBF, 2011). This trend is likely to continue and in some countries, such as Ireland, the removal of milk production quotas imposed by the European Union (EU) is expected to lead to a further increase in dairy herd expansion (O'Donnell et al. Reference O'Donnell, Horan, Butler and Shalloo2011). Milking the herd is the most time-consuming task on pasture-based dairy farms using batch milking, and thus requires significant labour input (O'Donovan et al. Reference O'Donovan, O'Brien, Ruane, Kinsella and Gleeson2008; Taylor et al. Reference Taylor, van der Sande and Douglas2009). As herd sizes expand, efficient milking parlour performance is critical to permit increased farm labour efficiency. Yet, to date there has been limited field evaluation of parlour efficiency.
The most common type of milking parlour in pasture-based systems is the swingover herringbone, accounting for 75% of the milking parlours in New Zealand and 91% in Ireland (Cuthbert, Reference Cuthbert2008; Kelly, Reference Kelly2009). The swingover herringbone is popular owing to its lower investment costs relative to other parlour types (double-up herringbone, rotary) and potential for expansion of the parlour. The high cluster utilisation of this parlour type is supported by relatively uniform cow milking durations owing to cows within a herd normally being at a similar stage of lactation in pasture-based systems. However, all milking parlours represent a significant capital investment, and therefore, careful consideration is required when selecting the appropriate number of milking units.
Milking parlour performance can be assessed in a number of ways using data extracted from parlours with electronic milk meters installed (Edwards et al. Reference Edwards, Jago and Lopez-Villalobos2013a). Data such as first and last cluster-attachment time, the number of cows milked and milk yield can be used to calculate benchmarks such as cow throughput, harvesting efficiency and the operator efficiencies associated with these measures. These values are affected by the number of units in the parlour, the work routine time of the operator (including idle time), and individual cow milking duration. As herd sizes have grown the number of units in parlours has increased accordingly in an attempt to limit the number of rows and, therefore, time required to milk the herd. A potential consequence of increasing the number of units in parlours not equipped with automatic cluster removers (ACR) is overmilking, where the operator has insufficient time to remove the cluster at the desired point, which is exacerbated by a long work routine time and low milk yields (O'Brien et al. Reference O'Brien, Jago, Edwards, Lopez-Villalobos and McCoy2012). In pastoral dairying it is common for swingover parlours not to have ACR installed, in Ireland this figure has been estimated to be 95% (Kelly, Reference Kelly2009), with a similar estimate of 91% in New Zealand (Cuthbert, Reference Cuthbert2008). Thus, there is a need to benchmark the performance of swingover herringbone dairies on commercial farms to determine whether increased throughput is being realised in larger parlours, and if so, estimate whether this increase is potentially affecting herd health through overmilking in those parlours without ACR.
The performance of milking parlours can be influenced by the milking duration of individual cows (Jago et al. Reference Jago, McGowan and Williamson2010b; Edwards et al. Reference Edwards, Lopez-Villalobos and Jago2012), where shorter cow milking durations can allow greater throughput. In herringbone parlours some operators choose to wait for slow-milking cows to milk out, hence creating longer row times and reducing throughput. For example, in a survey of 280 operators of herringbone parlours in New Zealand 56% answered that they always or sometimes wait for cows to milk out (Cuthbert, Reference Cuthbert2008). Research has indicated that an effective strategy to reduce cow milking duration is to apply a maximum milking time, thereby truncating the milking of cows with milking durations longer than this selected time (Clarke et al. Reference Clarke, Cuthbertson, Greenall, Hannah, Jongman and Shoesmith2004; Jago et al. Reference Jago, McGowan and Williamson2010b). Furthermore, minimal effects on overall production or indicators of udder health were reported in studies where a maximum milking time was applied (Clarke et al. Reference Clarke, Cuthbertson, Greenall, Hannah and Shoesmith2008; Jago et al. Reference Jago, Burke and Williamson2010a). Applying a maximum milking time is straightforward to implement in herringbone parlours (DairyNZ MilkSmart, 2013a).
The objective of this study was, firstly, to investigate the current level of milking efficiency and the influence of parlour size and work routine time on milking efficiency for a sample of Irish dairy farms with swingover herringbone parlours fitted with ACR, ranging in size from 12 to 32 units. Secondly, a model was developed to illustrate the effect of parlour size and implementation of a maximum milking time strategy on cow throughput, operator work routine time and overmilking (if no ACR installed) in swingover herringbone parlours. This information can potentially be used to advance knowledge for the design and operation of herringbone parlours.
Materials and methods
Data collection
Participating farms were selected for their ability to record milking data and all were equipped with a minimum level of technology including electronic identification of cows, electronic milk metres, automatic cluster removers (ACR) and herd management software that recorded individual milking events. Herringbone parlour sizes ranged from 12 to 32 units (12 units, n=2; 16 units, n=1; 18 units, n=3; 20 units, n=6; 22 units, n=2; 24 units, n=3; 30 units, n=1; 32 units, n=1) and two different parlour manufacturers (DairyMaster, Causeway, Ireland; DeLaval, Tumba, Sweden) were represented. Thirty and 50-degree parlours were included. Data were collected from 22 milking sessions at each of two time points, autumn (October–December 2011; 16 farms) and spring (April–May 2012; 19 farms). Cows were milked twice per day with an average milking interval of 14/10 h. A telephone survey was conducted to collect basic farm details such as herd size, the number of operators in the parlour and the presence of a hospital herd.
The herd management software on each farm was programmed to record similar data fields for each of the two systems. The variables recorded at each milking, according to manufacturer definitions, included cow identification (ID) number, milking date, ID time, cluster-attachment time (vacuum on; timestamp hh:mm:ss), row number, unit number, milk yield (kg), milking duration (s; vacuum-on to cluster-off), average milk flow rate (kg/min), and maximum milk flow rate (kg/min).
Calculations
Data were cleaned to exclude values outside the following ranges in a milking session: milk yield between 0·5 and 30 kg, milking duration between 120 and 1200 s, maximum milk flow rate between 0·5 and 10 kg/min, and average milk flow rate between 0·2 and 5 kg/min (Edwards et al. Reference Edwards, Jago and Lopez-Villalobos2013a). In DairyMaster systems average milk flow rate was calculated by dividing milk yield by milking duration. Cluster-removal time was calculated by adding the cow milking duration to the cluster-attachment time. Conservative limits were also placed on cow ID times, whereby within a row any ID times outside a given range (the median ID time ±6 s×the number of units in the parlour) were removed. Cluster-attachment times occurring before the ID time for a given unit within a row were also removed. Furthermore, it was assumed that the last cluster-attachment time in a row must occur before the first ID time of the next row, except row one because rows one and two could be loaded simultaneously.
Cow throughput (cows milked/h) was calculated using the formula 
$(id_{r = n} - id_{r = 1} )/\sum _{r = n - 2}^{r = 1} x_r $, where id was the first ID time of a given row, r was the row number, n was the total number of rows in the milking session (excluding any sick cows treated differently at the end of milking), and x was the number of cows in the row. The first ID time of the nth row was assumed to be the end of row n–2, as the systems did not record exit times and so the end point of the nth row could not be determined. Operator efficiency was determined by dividing cow throughput by the number of operators in the parlour. Milk harvesting efficiency and operator harvesting efficiency were calculated by multiplying cow throughput and operator efficiency respectively with the average cow milk yield at that session. The average amount of operator time per cow (average work routine time; s/cow) was calculated by dividing 3600 (the number of seconds in 1 h) by cow throughput. Work-routine time per operator was calculated by multiplying this average work-routine time by the number of operators. For farms where cluster attachment times were recorded, work-routine time was broken into five components, loading time, waiting time, time required to attach clusters, exit and post-milking teat spray time, and finish time. Loading-time was calculated as the time between the first ID time and last ID time of a row. Waiting-time was defined as the time between the last ID time of a row, at which point the row was assumed to be loaded, and the first cluster-attachment time. Negative values were possible for waiting-time if the operator began attaching clusters before the row was fully loaded. The time required to attach clusters was calculated as the time between the first cluster-attachment and the last cluster-attachment. Exit and post-spray time was defined as the time between the last cluster-attachment time and the first ID time of the next row. Each of these components was summed for row one to row n–2 and divided by the number of cows milked in these rows to give a time per cow. Finally, finish-time was the loading-time, waiting-time, time required to attach clusters and exit and post-spray time for row n–1 divided by the number of cows milked in rows one to n–2. All five components sum to give average work-routine time. A subsequent measure, waiting-and-attachment time, was created by adding waiting-time and time required to attach clusters. Average row time (min) was calculated using the formula 60u/t, where u was the number of units in the parlour, and t was cow throughput.
Statistical analysis
The milking data were combined to produce average values for each farm for each time point (season; spring/autumn) and milking session (AM/PM). Initially, data were analysed using a linear mixed model that included the fixed effects of season-session (e.g. spring-AM), parlour size and their interaction, and the random effect of farm. Linear and quadratic contrasts of parlour size were also tested in the model to aid interpretation of parlour size differences. All analyses were undertaken using GenStat 14.1 (VSN International, Hemel Hampstead, UK).
Model development
A model was created to estimate the effect of applying a maximum milking time. Milking duration data from AM and PM sessions of the 19 herringbone benchmark farms were combined. Data were examined and found to be skewed so were normalised using a log10 transformation. The normalised mean milking duration and sd were inputted in the NORM.INV function of Microsoft Excel 2010 (Redmond WA, USA) to estimate the time, where if clusters were removed in order of unit, then 1, 10, 20 and 30% of cows would have their milking truncated (for parlour sizes of 12–44 units). This range of sizes was chosen to cover common parlour sizes in use in pasture-based systems. Row loading-time was assumed to take 4 s/cow and 23 s/cow to apply any milking routine, attach clusters and post-milking teat spray, based on the figures in Table 1. The operator routine used was that recommended by DairyNZ MilkSmart (2013b) as the most efficient routine, where the operator moves along the parlour detaching/attaching clusters in order, instead of changing them as individual cows finish milking. Additionally, exiting occurs simultaneously while post-spraying the cows in this routine so time to exit is minimal and was not included in the work-routine time. Initially, it was assumed that only one operator was present, so in larger parlours there was no reason to truncate milkings due to absence of idle time.
Table 1. Milking efficiency benchmark values, components of milking routine and milking characteristics of 19 farms with swingover herringbone parlours of different sizes
† Average standard error of the difference
‡ Testing for a linear trend
§ Testing for a non-linear trend
The row times for the four levels of truncation were divided by the number of units to determine an average work-routine time. Operator idle time was calculated as the average work-routine time minus the cow loading and the time required to attach clusters. Cow throughput was calculated by dividing 3600 s by the average work-routine time. For each of the truncation levels used, overmilking occurred when the row time was greater than the milking duration of a cow, assuming ACRs were not installed. However, if there was operator idle time this was used to detach a cluster to prevent overmilking. Walking between units and detaching a cluster was assumed to require 4 s/cow, and thus, the number of clusters that could be detached in a given parlour size and level of truncation was calculated. The milking duration of cows was simulated using the log10 transformed distribution, described above. Overmilking time was then determined by subtracting the row time of the given level of truncation from the simulated cow milking durations. Average overmilking time was then calculated by summing the duration of those cows that were over milked (positive values) and dividing this value by the number of cows in the row. Subsequently, if work routine time was insufficient to reach the desired row time, additional operators were added to the model, which allowed 30% of milkings to be truncated for all parlour sizes. Identical calculations were then performed to determine work-routine time, operator idle time, throughput and average overmilking time.
Results
Benchmarking
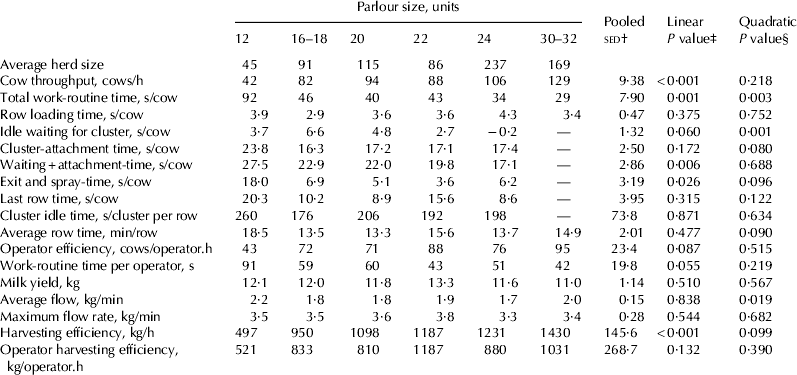
The milking efficiency characteristics of parlour sizes ranging from 12 to 32 units are presented in Table 1. No interactions were detected between season-session and parlour size. Cow throughput and milk harvesting efficiency (cows milked and kg of milk harvested/h) increased linearly with parlour size (Table 1; Fig. 1a). Conversely, work-routine time decreased linearly with parlour size but the non-linear effect was also significant. There were no differences in row loading time between parlour sizes. However, operator idle time waiting for a cluster decreased with increasing parlour size. No trend was detected between the time required to attach clusters and number of units. The combination of operator idle time waiting for a cluster and the time required to attach clusters decreased with increasing numbers of units. Likewise, exit and post-milking spray time decreased with increasing parlour size. No trend was detected between the last row time and number of units.
Fig. 1. Average throughput (a) and operator efficiency (b) from first cluster-on to last cluster-off, excluding hospital herds for each parlour size (12–32 units).
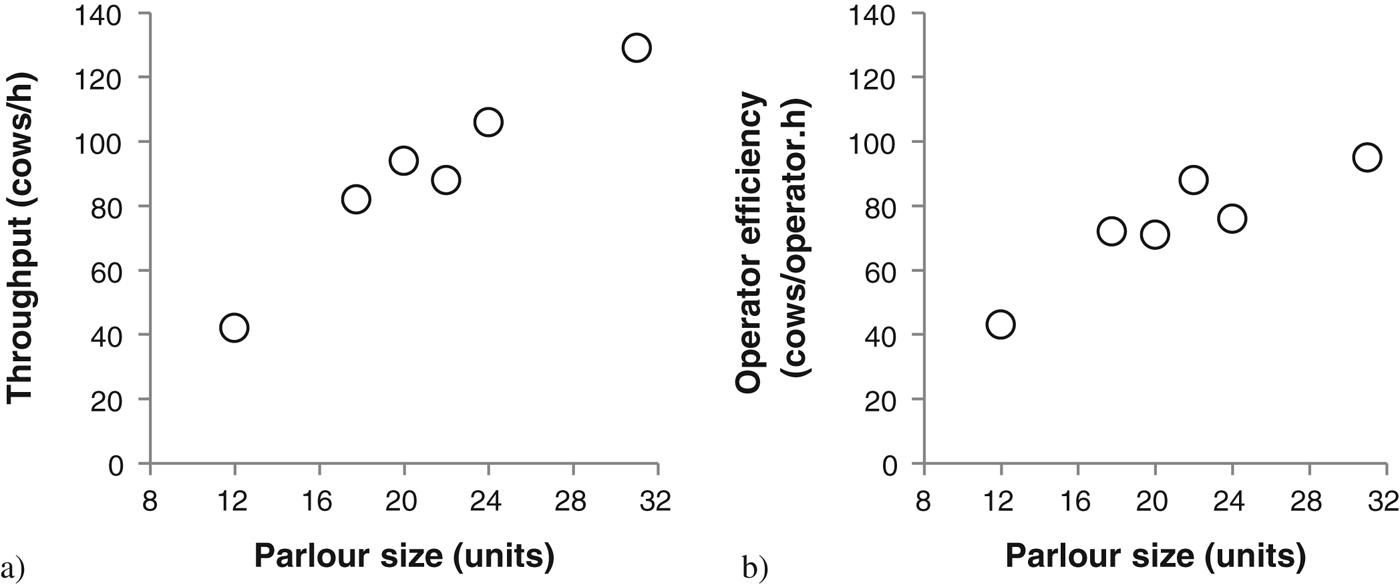
Cluster idle time was variable and no differences were detected between parlour sizes. Average row time, cows milked/operator per hour, and the work-routine times/operator were not different between the various parlours. Furthermore, milking characteristics, milk yield, average milk flow rate and maximum milk flow rate were not different between the parlour sizes. Harvesting efficiency increased with parlour size but operator harvesting efficiency was not different between parlour sizes (Table 1; Fig. 2).
Fig. 2. Average harvesting efficiency (a) and operator harvesting efficiency (b) from first cluster-on to last cluster-off, excluding hospital herds for each parlour size (12–32 units).
Modelling
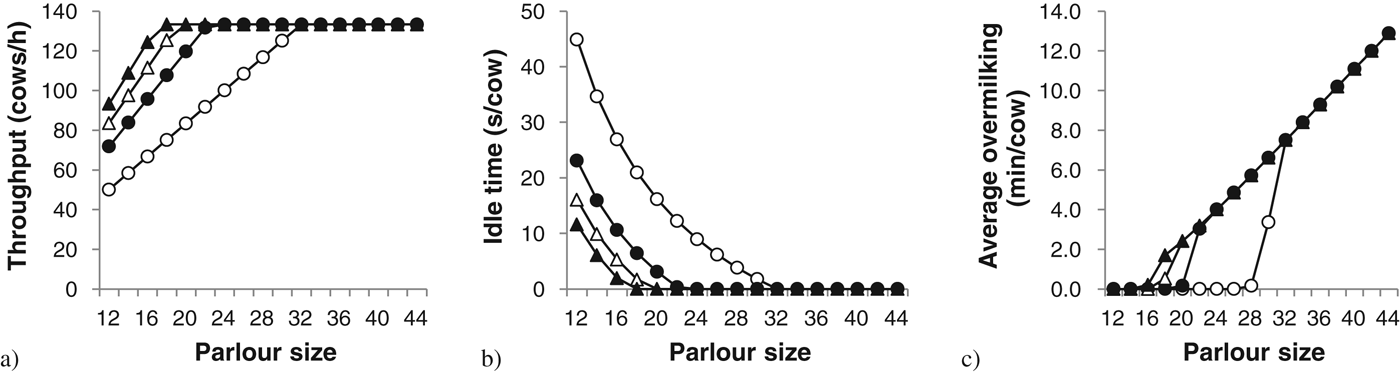
Transformed mean cluster-on time was 2·587 (386 s) with sd of 0·150 (1·4 s). Increasing parlour size and the percentage of cows with truncated milkings resulted in less operator idle time and improved cow throughput (Fig. 3a). However, higher levels of truncation were not achievable in parlours ⩾18 units owing to insufficient operator time for the routine applied, and thus maximum throughput (133 cows/h) was reached at this point. As the level of truncation decreased, larger parlours were required to reach this level of cow throughput. Subsequently, when an additional operator was added to ensure the desired level of truncation was achieved in all parlour sizes, throughput continued to increase up to the maximum parlour size examined (44 units). The highest throughput estimated was 342 cows/h by the 44-unit parlour with 30% of milking truncated (Fig. 4a), when 3 operators were required (Fig. 4c). However, operator efficiency in terms of cows milked/operator per hour peaked at different parlour sizes depending on the level of truncation (Fig. 4b). When it was assumed that operator idle time (Fig. 3b) in the core routine was allocated to the removal of clusters from cows that had finished milking (if no ACR installed), overmilking occurred in small parlours with greater levels of truncation but as the level of truncation decreased more units could be handled before cows were overmilked (Fig. 3c). With the addition of an operator(s) overmilking did not continue to increase as the greater operator idle time allowed time for cluster detachment (Fig. 4c, d).
Fig. 3. Predicted throughput (a), operator idle time (b) and average overmilking (c) over a range of parlours sizes (12–44 units) with a single operator while truncating the milking duration of a percentage of cows (1%, ○; 10%, ●; 20%, △; 30%, ▲).
Fig. 4. Predicted throughput (a), operator efficiency (b) operator idle time (c) and average overmilking (d) over a range of parlours sizes (12–44 units) with multiple operators (if required) while truncating the milking duration of a percentage of cows (1%, ○; 10%, ●; 20%, △; 30%, ▲).
Discussion
There was a linear association between parlour size and throughput whereby larger parlours achieved greater throughput. However, empirically, parlour throughput is determined only by the operator work-routine time, which may include time where the operator is idle. In theory, the time taken to complete the core components of the work routine should remain constant at a per cow level regardless of parlour size, which is supported by the results of the present study as no differences were detected for either cow loading time or cluster-attachment time in different parlour sizes (Table 1). Conversely, significant differences were detected in operator idle time, where the row was loaded and the operator was waiting for a cluster to become available to swing over from the previous row. However, there were low values recorded in 12-unit parlours. It is possible that the farmers with 12-unit parlours operated their routines differently and the milker only completed the filling of the row as the last cows of the previous row were finishing milking, meaning that idle time may have been occurring between attaching clusters. Therefore, the variable ‘waiting+attachment time’ (Table 1) was created, which had a linear trend. Consequently, if it is assumed that cluster-attachment time was constant between parlours then it could be ventured that the idle time component of the operator work routine decreased with increasing parlour size, allowing greater throughput. This hypothesis is supported by the results of O'Brien et al. (Reference O'Brien, Jago, Edwards, Lopez-Villalobos and McCoy2012), who reported less operator idle time in larger parlours. Additionally, the exit and post-milking spray time was significantly different between parlour sizes, with a linear association. Hypothetically, the time required to post-milking teat spray and exit should not be related to parlour size on a per cow basis. However, in practice, this difference was probably due to variances in when the operator opened the gate to release the row of cows, as in larger parlours the total time to exit is greater, therefore encouraging the operator to release the head gate earlier so cows are exiting while completing post-milking teat spraying of the last few cows. In comparison, operators in smaller parlours are more accustomed to idle time waiting for cows to finish milking, and are more likely to be milking a smaller herd, and therefore are less motivated to release the head gate before finishing the row. Thus, it appears that parlour size has an influence on two components of the operator work routine, reducing the time spent on both, consequently allowing greater throughput.
Larger parlours were not necessarily more operator efficient (cows milked and kg of milk harvester/operator per h) despite achieving greater throughput (Fig. 1b). A similar result was reported by Edwards et al. (Reference Edwards, Jago and Lopez-Villalobos2013a) in rotary dairies, where larger dairies achieved greater throughput but were not more operator efficient. However, unlike the results reported by Edwards et al. (Reference Edwards, Jago and Lopez-Villalobos2013a) there was no quadratic trend of parlour size with operator efficiency. Operator work-routine time, as discussed, decreased with increasing parlour size in a non-linear trend (an inverse relationship), probably through a reduction in operator idle time. In principle, what was operator idle time in smaller parlours was replaced by core components of the work routine, such as attaching clusters and post-milking teat spraying, as cluster number increased. This can continue until the routine contains no operator idle time, at which point if cluster number is increased there will be no throughput advantage and cluster idle time will begin to increase, as observed by O'Brien et al. (Reference O'Brien, Jago, Edwards, Lopez-Villalobos and McCoy2012). Thus, there is a trade-off between operator idle time and cluster idle time. At this point another operator can be added, effectively doubling the work-routine time available. Initially, the majority of this additional work-routine time will be operator idle time so there will only be a small improvement in throughput with a reduction in operator efficiency, but this will improve as clusters are added, consequently reducing operator idle time. Therefore, the relationship between operator efficiency and parlour size will have multiple repeating peaks and troughs, as illustrated in Fig. 3b. However, in practice there appeared to be variable operating practices between farms regarding the use of a second operator. These farm-specific differences are probably dependent on the work routine in use and cow milk yield. Milk yield and stage of lactation will influence the milking duration of the cows, and thus will determine the parlour size at which point operator idle time is exhausted and throughput is constrained if another operator is not added. Additionally, the number of fixed components of the work routine will influence operator efficiency, for example if performing foremilk inspection, as per EU regulation (EU, 2004), or pre-milking sanitisation. The inclusion of these components will increase the core work-routine time and change the parlour size at which operator idle time will be exhausted and throughput constrained if another operator is not added. Furthermore, the inclusion of additional components to the core work-routine time will reduce maximum potential throughput regardless of parlour size unless another operator is added. However, the operators work routine must be sustainable and accordingly can only be minimised so far. Thus, the individual farm situation will influence operator efficiency, and the parlour size when further operators are required, which is probably why no clear trend was recorded. Furthermore, when planning a new parlour, consideration should be given to the proposed milking routine and milk yield to ensure the parlour is correctly sized to achieve high levels of both throughput and operator efficiency, whilst minimising overmilking.
Larger parlours, without ACR, have a greater risk of overmilking because in some cases it results in more clusters being handled per operator (O'Brien et al. Reference O'Brien, Jago, Edwards, Lopez-Villalobos and McCoy2012). Overmilking has been reported to increase teat-end hyperkeratosis (Edwards et al. Reference Edwards, O'Brien, Lopez-Villalobos and Jago2013c), potentially increasing the risk of mastitis (Neijenhuis et al. Reference Neijenhuis, Barkema, Hogeveen and Noordhuizen2001). Overmilking was not directly measured in the present study because all parlours were equipped with ACR. However, the level of overmilking that may have occurred, assuming ACR had not been installed, could be estimated by examining cluster idle time. Cluster idle time was the time between the cluster being removed by the ACR and being swung over and re-attached to a cow in the following row. In a swingover parlour without ACR this would have effectively been overmilking unless operator idle time (if available) was available and being used to detach and hang up clusters between rows. Row times in the present study were not significantly different across all parlour sizes, as anticipated, and there were no differences in cluster idle time as would be expected based on similar row times. This result indicates that on these farms a second operator was being added as required to maximise cluster utilisation and throughput, not operator efficiency. Therefore, overmilking would not have increased in larger parlours if ACR had not been installed on these farms. However, cluster idle time was ∼200 s for all parlour sizes which, in the absence of ACR, would have been greater than the recommended overmilking limit of 120 s (Gleeson et al. Reference Gleeson, O'Callaghan and Rath2003).
The modelling results indicate that large increases in cow throughput could be achieved by applying a maximum milking time and, furthermore, illustrate the principles discussed. The throughput estimates of the 1% truncation level produced similar figures to that reported in the benchmarking part of the study (Fig. 3a). The results indicated that operator idle time existed in small parlours (⩽16 units) regardless of the level of truncation (Fig. 3b) and thus were less operator efficient. Moreover, it indicated with current milking practices, that, in a well-managed parlour, one operator can handle up to 30 clusters, which was recorded in this study, although ACR was required to limit overmilking (Fig. 3c). However, using a maximum milk out time aiming to truncate 20% of cows, a similar level of throughput was estimated in an 18-unit parlour (Fig. 3a), saving significantly on capital expenditure. Additionally, at this level of truncation maximum throughput in a single operator parlour was estimated with 20 clusters. Alternatively, within a given parlour size it highlights that large improvements in throughput were estimated by applying a maximum milking time. For example, expected throughput in an 18-unit parlour using current standard milking practices would be about 75 cows/h, but by truncating the milking duration of 20% of the herd throughput could be expected to increase to 125 cows/h (66% increase), while still only requiring one operator. In that scenario, if ACR were not installed overmilking would average 0·5 min/cow. Thus, the use of a maximum milking time can be used to improve the throughput in existing parlours allowing herd milking duration to be maintained as herd size increases, or when constructing a new parlour, enables the same level of throughput to be achieved in a smaller parlour, saving on capital expenditure.
Implementation of a maximum milking-time strategy may result in an increase in residual milk. The presence of residual milk is considered by many to be linked with increased mastitis. However, studies done in Australasia examining the use of a maximum milking time (Clarke et al. Reference Clarke, Cuthbertson, Greenall, Hannah, Jongman and Shoesmith2004; Jago et al. Reference Jago, Burke and Williamson2010a, Reference Jago, McGowan and Williamsonb) have reported no effect of setting a maximum milking-time on SCC, the incidence of clinical mastitis, number of infected quarters or milk production, even when truncating 30% of cows (Jago et al. Reference Jago, McGowan and Williamson2010b). Similar results have been reported by other studies examining the use of increased ACR thresholds to shorten cow milking duration (Edwards et al. Reference Edwards, Jago and Lopez-Villalobos2013b, Reference Edwards, Jago and Lopez-Villalobosd). This outcome is supported by historic advice by Thiel & Dodd (Reference Thiel and Dodd1979), who stated that contrary to popular belief there is little evidence to suggest incomplete milking results in lost production or increased infections. The modelling results demonstrate that large improvements can be made to milking efficiency through the application of a maximum milking-time and, therefore, validation of experiments in local environments are justified.
In conclusion, larger parlours were able to achieve greater throughput, most likely through a decrease in operator idle time due to sufficient numbers of clusters to keep the operator fully occupied and efficient gate release of the row resulting in the operator beginning to attach clusters before the row is fully loaded. Operator efficiency was variable between farms and probably dependent on milking routines in use and cow milk yields, and thus no clear trend with parlour size was detected. Estimated overmilking was not associated with parlour size, probably because additional operators were added as required, though it was greater than 120 s for all parlour sizes. Modelling indicated that through the use of a maximum milking time large improvements in throughput were possible, allowing herd milking duration to be maintained as herd sizes increase, or capital expenditure minimised.
This study was part of a programme of research funded by Teagasc (RMIS 5897). The authors would like to acknowledge DairyMaster (Causeway, Ireland) and DeLaval (Tumba, Sweden) for support with identification of potential parlours and data extraction, Barbara Dow (DairyNZ, Hamilton, New Zealand) for assistance with the data analysis, and the contribution of the farmers who provided benchmark data.
