Traditionally, most studies of maternal effects on nursing of offspring in ungulates have been based on social rank (Clutton-Brock et al. Reference Clutton-Brock, Iason, Albon and Guinness1982a, Reference Clutton-Brock, Albon and Guinness1984) or weight recorded at a few stages of reproduction (Bérubé et al. Reference Bérubé, Festa-Bianchet and Jorgenson1996; Festa-Bianchet et al. Reference Festa-Bianchet, Jorgenson and Réale2000). This is because in free-ranging animals it is easier to measure these parameters than to collect milk samples. Lactation is the most energetically demanding phase of reproduction for the mother (Oftedal, Reference Oftedal, Hudson and White1985) and, as calf birth weight is not always related to measures of milk provisioning (Landete-Castillejos et al. Reference Landete-Castillejos, García, López-Serrano and Gallego2005), studies on maternal care and lactation should include detailed measures of milk provisioning. In the ecological literature, suckling observations are frequently used as a measure of milk provisioning and are often related to maternal social rank. Nevertheless, this is of little use because suckling observations are unrelated to milk provisioning variables (Cameron, Reference Cameron1998). Conversely, the more detailed studies on milk provisioning from animal science have been based on body weight (BW) and direct measures of milk production (Kleiber, Reference Kleiber1961; Oldham & Friggens, Reference Oldham and Friggens1989) which are easy to measure in captive or domestic animals, but have paid little or no attention to social rank and social interactions (except Phillips & Rind, Reference Phillips and Rind2002). In general, there are few detailed studies in wild species. One reason for this is that detailed studies using repeated milking are impossible to conduct in free-ranging animals, and difficult to conduct using wild mammals in captivity (Landete-Castillejos et al. Reference Landete-Castillejos, García, Molina, Vergara, Garde and Gallego2000b, Reference Landete-Castillejos, García, López-Serrano and Gallego2005).
In addition to technical difficulties, discerning the relative importance of dominance rank, age, BW and body condition is difficult because they are usually correlated (Clutton-Brock et al. Reference Clutton-Brock, Albon and Guinness1986; Thouless & Guinness, Reference Thouless and Guinness1986; Landete-Castillejos et al. Reference Landete-Castillejos, García, López-Serrano and Gallego2005, Reference Landete-Castillejos, García, Carrión, Estevez, Ceacero, Gaspar-López and Gallego2009; Carrión et al. Reference Carrión, García, Gaspar-López, Landete-Castillejos and Gallego2008) which poses a problem in univariate or multivariate statistics (Mitchell-Olds & Shaw, Reference Mitchell-Olds and Shaw1987; James & McCulloch, Reference James and McCuloch1990). In contrast, path analysis – a special case of structural equation modelling – allows in such cases a distinction between direct effects and indirect effects i.e., those exerted through another variable or trait with which the variable in question is correlated (Shipley, Reference Shipley2000; Schumacker & Lomax, Reference Schumacker and Lomax2004; Iriondo et al. Reference Iriondo, Albert and Escudero2003; see an application in deer in Mysterud et al. Reference Mysterud, Yoccoz, Langvatn, Pettorelli and Stenseth2008) or sometimes even when data are incomplete (Ferrandis et al. Reference Ferrandis, Mateo, López-Serrano, Martínez-Haro and Martínez-Duro2008).
As mentioned above, there is usually a correlation among social rank, body condition, age, BW and milk production. However, although social rank is primarily related to age, at least in deer, BW explains a similar proportion of variability in rank compared with age (Clutton-Brock et al. Reference Clutton-Brock, Albon and Guinness1986; Thouless & Guinness, Reference Thouless and Guinness1986). In contrast to this, BW explains more variability than age does in regard to milk provisioning, owing to the physiological importance of maternal metabolic weight for lactation (Kleiber, Reference Kleiber1961; Oftedal, Reference Oftedal, Hudson and White1985). Thus, milk production and other lactation variables show a greater correlation with BW than with age (Landete-Castillejos et al. Reference Landete-Castillejos, García, López-Serrano and Gallego2005). There is a clear and direct effect of maternal weight on lactation performance exerted through mammary gland weight because milk production is constrained by mammary output capacity (Kimberly et al. Reference Kimberly, Lloyd and Diamond1996). Body condition also exerts a direct influence on milk production because body reserves, particularly fat, which is closely related to body condition, are mobilized to support lactation (White, Reference White and Brown1992). However, most mammals, including cervids, produce milk mainly from daily food intake (Oftedal, Reference Oftedal, Hudson and White1985) and food availability or quality is known to greatly influence milk production and composition (Oldham & Friggens, Reference Oldham and Friggens1989; Sutton, Reference Sutton1989; Chan-McLeod et al. Reference Chan-McLeod, White and Holleman1994; Landete-Castillejos et al. Reference Landete-Castillejos, García, Gómez and Gallego2003a). Food is a defendable resource, and a principal effect of social rank is to establish access order to food resources both in wild (Appleby, Reference Appleby1980; Thouless, Reference Thouless1990) or semi-domestic ungulates (Espmark, Reference Espmark1964). Aggressive encounters are inherently costly and thus hierarchies are often organized to minimize energy-demanding interactions (Clutton-Brock et al. Reference Clutton-Brock, Guinness and Albon1982b) as happens in several ungulates (Espmark, Reference Espmark1964; Côté, Reference Côte2000; Ceacero et al. Reference Ceacero, Landete-Castillejos, García, Estevez and Gallego2007). Thus, social rank appears to be a factor of indirect influence on milk production as it offers access to food, which increases both BW and body condition, in turn decreasing energetic costs. For similar reasons, hind age may also exert an indirect influence on milk production by way of greater social rank gained with experience, and growth effects on BW.
The aim of this study was to test a causal model of path analysis in order to discriminate direct versus indirect effects of hind age, BW, body condition and social rank on milk production. To our knowledge, no study has examined the relative importance of social rank versus body size or condition on milk provisioning. As mentioned above, our predictions were that once direct effects of hind BW and body condition had been fixed, some of the plausible models (Schumacker & Lomax, Reference Schumacker and Lomax2004) may incorporate indirect rather than direct effects of social rank and hind age.
Material and Methods
Sixty-two Iberian red deer hinds (Cervus elaphus hispanicus, Hilzheimer, 1909) and their calves were kept sequentially in two years in a 1-ha outdoor enclosure on an irrigated pasture including tall fescue (Festuca arundinacea, 50%), orchardgrass (Dactylis glomerata, 30%), lucerne (Medicago sativa, 15%) and white clover (Trifolium repens, 5%). In 2005 (group 1), 20 hinds which gave birth to 12 males and 8 females were studied. In contrast, in 2006 there were two groups: one consisting of 21 hinds with 10 males and 11 females (group 2), and another one consisting of 21 hinds with 12 male calves and 9 females (group 3). Hinds were weighed weekly as part of routine handling (±50 g). Body condition was also measured during handling routine by gluteus muscle palpation, scoring on a range from 1 (very poor condition) to 5 (very good condition), with the scale divided in quarters of a unit according to what is widely used by deer managers (Audigé et al. Reference Audigé, Wilson and Morris1998; Carrión et al. Reference Carrión, García, Gaspar-López, Landete-Castillejos and Gallego2008). We used the mean value from ten measurements recorded for every hind during the whole lactation period, i.e., every 2 weeks after calving. During gestation and throughout lactation, hinds were fed with diets based on suggestions by Brelurut et al. (Reference Brelurut, Pingard and Thériez1990) using barley straw and meal from barley, alfalfa, oat, and sugar beet (16% crude protein, 9% fibre, 2·2% fat). This supplemental high-protein meal was offered daily in only one feeder. Thus, dominant hinds had access to supplement ad libitum and could select the richest ration, while subordinate hinds could only feed on smaller amounts of supplement and with less protein (a hypothesis subjected to study and supported by unpublished data). Calves had access to feed placed for hinds, although they were not observed to feed on them during the experiment.
Milking was conducted in weeks 2, 4, 6, 10, 14 and 18 of lactation, as thereafter calves were weaned. Hinds were isolated from calves for 6 h without pre-isolation milking for ethical reasons, as explained in Landete-Castillejos et al. (Reference Landete-Castillejos, Garcia, Garde and Gallego2000a). Individuals were milked under anaesthesia (xylazine at 0·5 mg/kg BW; ketamine at 1 mg/kg; reversed with yohimbine 0·25 mg/kg BW) using machine milking set up to a 50/50 massage/milking ratio and 44 kPa of vacuum. Once anaesthesia was induced, 10 i.u. of oxytocin were injected into the right jugular vein 1 min before the start of milking to induce milk let-down. Total milk yields were assessed as explained in Landete-Castillejos et al. (Reference Landete-Castillejos, Garcia, Garde and Gallego2000a, Reference Landete-Castillejos, García, Molina, Vergara, Garde and Gallegob; Reference Landete-Castillejos, García and Gallego2001).
Social interactions to establish social rank hierarchy were monitored during lactation, from 15 June–15 August in 2005 and 2006. These observations were carried out for 2 h/d for 10 d. Observation covered the daily light period between 7.30 and 21.30 (i.e., 7 observation sessions), repeating three of the daily periods with most activity (i.e., fresh food delivery in the morning, and two evening sessions when temperatures were cooler and activity greater). Observations were made using the focal group sampling method (Altmann, Reference Altmann1974). The observer was placed outside the enclosure, hidden but with total vision of it. Aggression events registered were mainly bites and kicks, but also more subtle displacements when feeding on pasture (Clutton-Brock et al. Reference Clutton-Brock, Albon, Gibson and Guinness1979; Thouless & Guinness, Reference Thouless and Guinness1986). Social rank for each individual was calculated as a linear hierarchy entering the winner-loser outcome of interactions into Matman 1.1.4 matrix manipulation and analysis program (Noldus, Wageningen, The Netherlands) as explained by de Vries (Reference de Vries1998). Social ranks were transformed using the formula 1−(rank/N i) as described in Côté (Reference Côte2000). Therefore, social rank varied from 0 (subordinate) to 1 (dominant). Finally, social rank value was transformed into arcsin of the square root because it did not fit a normal distribution (Côté, Reference Côte2000; Ceacero et al. Reference Ceacero, Landete-Castillejos, García, Estevez and Gallego2007). Hinds showed a significant linear hierarchy in all groups (Ceacero et al. Reference Ceacero, Landete-Castillejos, García, Estevez and Gallego2007), although not all these hinds were used in the following analysis because some of them were not milked.
All handling procedures were designed to reduce stress and health risks for subjects, according to European and Spanish laws and current guidelines for ethical use of animals in research (ASAB, 2008).
Statistical analysis
Path analysis procedures were used to assess relationships between variables and how they influenced milk production. Path analysis is a special procedure of structural equation modelling (SEM) that allows building a model based on theoretical knowledge. This knowledge is used to fix or maintain certain effects on the dependent variable (milk production in this case) and compare different models and test alternative models including or excluding optional effects and covariances between independent variables or paths (Shipley, Reference Shipley2000; Schumacker & Lomax, Reference Schumacker and Lomax2004). In contrast to linear regression or generalized linear models (James & McCulloch, Reference James and McCuloch1990) based on least squares methods of fitting the model, SEM models use global-fit measures such as chi-square to test that the matrix of variances and covariances from the sample agrees with that of the model implied or proposed by the researcher (Schumacker & Lomax, Reference Schumacker and Lomax2004). A significant chi-square value indicates lack of fit. Because there is no single valid model, a second step involves examining the statistical significance of individual parameters for the effects or paths in the model, which often yield several plausible models differing in the goodness of fit (Schumacker & Lomax, Reference Schumacker and Lomax2004). Although univariate statistical methods have been argued to be best suited for the study of single processes or responses (Grace, Reference Grace2008), SEM models provide a set of univariate equations that are solved simultaneously and therefore are better suited to studying multiple processes that control the behaviour of complicated systems (Schumacker & Lomax, Reference Schumacker and Lomax2004; Grace, Reference Grace2008). They are more robust in cases of moderate multicollinearity (Schumacker & Lomax, Reference Schumacker and Lomax2004, but see Petraitis et al. Reference Petraitis, Dunham and Niewiarowski1996) and are particularly interesting because they can examine direct versus. indirect effects (Shipley, Reference Shipley2000; Iriondo et al. Reference Iriondo, Albert and Escudero2003; Schumacker & Lomax, Reference Schumacker and Lomax2004).
Goodness of fit indices
We used chi-square, root mean square error of approximation (RMSEA) and parsimony-adjusted comparative fit index (PCFI) to test for goodness of fit. As mentioned, a significant value of chi-square means that the model tested by the researcher is significantly different from that which best fits the data, and thus, the best model is that showing non-significant values of chi-square with an associated probability as high as possible. PCFI is the result of applying a parsimony adjustment to the CFI or comparative fit index, which falls between 0 and 1, and is better the higher the value (good fit is considered for values >0·9, Schumacker & Lomax, Reference Schumacker and Lomax2004). In contrast, RMSEA shows a better goodness of fit, the lower its values, and a value of 0·05 indicates a good fit of the model (Schumacker & Lomax, Reference Schumacker and Lomax2004). Usually, PCFI and RMSEA are preferred when sample size is small.
Selection of best and plausible models
Often, several models achieve the same or a similar level of fit. Programs often used for SEM modelling, such as the one used here (AMOS, see below), usually provide a range of information criteria that allow comparisons between models of a similar level of fit or plausible models to select the best among them, usually the one having the lowest number of parameters, also termed the most parsimonious one (Schumacker & Lomax, Reference Schumacker and Lomax2004). In our case most of those calculated by AMOS coincided; yet, after considering the deep differences among them revised according to Burnham & Anderson (Reference Burnham and Anderson2004) we chose AIC. This can be adjusted for small samples sizes to give an index termed AICc using the formula (Burnham & Anderson, Reference Burnham and Anderson2002, Reference Burnham and Anderson2004): AICc=AIC+[2K(K+1)/n−K−1], where K is the parameter estimated, and n is the sample size. AMOS allows the index to be standardized to the lowest value achieved setting it to 0. That is what we present here, so that instead of AICc, its relative index is shown, indicated as ΔAICc. Following Burnham & Anderson (Reference Burnham and Anderson2004) we include plausible models whose ΔAIC (i.e., not standardized for small samples) is <2, although the final model selected is the most parsimonious one (lowest number of parameters within plausible models).
The path analysis used in this study assessed effects on total milk yield of the observed variables, hind weight at calving, hind body condition, social rank and hind age. All variables were examined for fit to a normal distribution. To allow for year, sex and other unexamined effects, an error latent variable was added to total milk yield. Based on known evidence that milk production ability depends directly on mammary output capacity, digestive tract surface and other body size-dependent effects as mentioned above, the path from BW to milk production was set as fixed. Similarly, the known effect of mobilization of fat stores to support lactation (White, Reference White and Brown1992) supported fixing the path between hind body condition and milk production.
Whereas in classical models the null hypothesis is a non-significant effect or model (Burnham & Anderson, Reference Burnham and Anderson2004), in path analysis each model is, at least, compared with two opposite extremes: the independence model, or that where no relationship (path) has a significant effect, and the saturated model, or that with all possible paths (Schumacker & Lomax, Reference Schumacker and Lomax2004). Thus, goodness of fit, as indicated above, shows a significant difference from the saturated model, whereas information criteria show whether the model considered is markedly more parsimonious than the saturated one (i.e., ΔAIC). By fixing relationships between BW or body condition and milk production, the procedure also examined whether the remaining paths (age and dominance effects on milk production and the covariation between hind age, weight, body condition and social rank) could be removed, increasing parsimony (reducing ΔAIC) without creating significant differences from the saturated model.
To assess effects of milk production, maternal BW, condition, age and social rank on calf growth, we performed a Pearson correlation between these variables.
Statistical analyses were performed using version 17 of AMOS Structural Equation Modelling program (SPSS Inc., Chicago IL, USA).
Results
One way ANOVA showed no significant differences among three groups in hind BW, transformed social rank, age or milk production, except a somewhat smaller body condition in the group in 2005 (Body condition=3·68±0·96 v. 3·98±0·47 and 4·04±0·83, respectively, F 2,61=5·93, P=0·005). Adult female deer showed a linear hierarchy in both groups (2005: h'=0·12, P=0·083; 2006: h'=0·32, P<0·01). Table 1 shows the means of milk yield, hind BW, body condition, age and social rank.
Table 1. Estimated means of variables (Group number 1–Default model) included in the path analysis model examining hind body condition, body weight, age and social rank (transformed into arcsin of the square root to fit a normal distribution) on total milk yield during lactation in 62 Iberian red deer hinds (Cervus elaphus hispanicus)
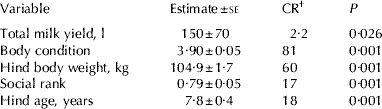
† CR stands for critical ratio of the mean, i.e., the ratio mean/se which gives a z score allowing assessment of the P value of the variable.
Figure 1 shows the most parsimonious model among the 69 possible. Chi-square was 0·476 (df=2), and the probability that the model fits perfectly the population was the highest (P=0·788). RMSEA and PCFI achieved values of RMSEA=0·000 (90% confidence interval: 0·000–0·163; showing a very good fit) and PCFI=0·20 (showing a rather poor fit). The relative Akaike information criterion corrected for small sample sizes (ΔAICc) achieved the lowest possible value (7·8, i.e. the correction term, as ΔAIC=0). The model showed that hind BW and body condition affected directly milk production, whereas social rank and age exerted indirect effects through their covariances with the latter variables. Squared multiple correlations show that despite being the best model, it explained 5·9% of the variability, suggesting large effects caused by some unassessed factor. Fig 2 shows the effects of two of these variables (hind weight after calving and social rank) plotted against milk production.

Fig. 1. Path analysis model of effects influencing total milk yield (litres) during lactation in 62 Iberian red deer hinds (Cervus elaphus hispanicus). Thick arrows connecting hind body weight and condition show the fixed influences derived from theoretical background. All other effects were optional including those connecting directly milk yield and hind social rank (transformed into arcsin of the square root to fit a normal distribution) or age. Numbers next to arrows shows the standardized regression weight or correlations among variables in the upper graph, and the unstandardized covariances in the bottom one (e.g. how many litres of milk are produced by each additional kg of body weight). Two additional models from 69 possible also achieved probability values of fitting perfectly the population above 15% (one where social rank influenced directly milk production and another one where hind age did it). The model shown is the more parsimonious one [best fitting and lower number of parameters: P=0·79, the only one where AIC (Akaike information criterion) achieved the lowest possible value, 0].

Fig. 2. Plot of total milk yield (l) during lactation v. social rank, hind weight, body condition and hind age in a group of 62 Iberian red deer hinds (Cervus elaphus hispanicus): 2a, social rank (transformed into arcsin of the square root to fit a normal distribution); 2b, hind weight after calving (kg); 2c, hind body condition score [ranging from 1 (very poor condition) to 5 (very good condition) ]; 2d, hind age.
Two additional models from the 69 possible also achieved ΔAIC of <2. In the most parsimonious of these, social rank but not age influenced directly milk production (correlation coefficient rank and milk production, R=0·07, unstandardized covariance 10·26; chi-square 0·208, df=1; P=0·65, and ΔAIC=1·73; PCFI=0·1, RMSEA=0·000, associated 90% confidence interval 0·000–0·262). In the other, hind age but not social rank influenced milk production (correlation coefficient age and milk production, R=−0·04, unstandardized covariance −0·68; chi-square 0·386, df=1; P=0·53 and ΔAIC=1·91; PCFI=0·1, RMSEA=0·000, associated 90% confidence interval 0·000–0·288).
Pearson correlations showed that milk production was correlated with calf growth (R=0·31, P=0·014). However, no correlation was significant with hind BW (R=0·15, P=0·25), body condition (R=−0·02, P=0·89), social rank (R=0·18, P=0·17) or age (R=0·22, P=0·09).
Discussion
Our results show for the first time that, in addition to a direct effect of BW and body condition, milk production is influenced by social rank and age through indirect effects on the former variables. Because milk production showed a significant correlation with calf growth, in contrast to maternal variables, the effects discussed below have direct implications for calf growth.
The best fitting and most parsimonious model shows where hind BW and body condition were the only variables exerting direct effects on milk production. In addition, the standardized coefficients show that the effect of BW is nearly twice as great as that of body condition. This result fits well with published evidence as the rest of the paragraph shows. The positive allometric relationships between maternal weight and lactation performance (e.g., milk production) has long been recognized in studies comparing different taxa (Kleiber, Reference Kleiber1961; Oftedal, Reference Oftedal, Hudson and White1985). This relationship has also been found within a population in Iberian red deer, between both body size and milk production, as well as maternal mass and percentage of protein (Landete-Castillejos et al. Reference Landete-Castillejos, García, Gómez and Gallego2003b). The reason for this allometric relationship seems to be a limit on mammary output capacity, which depends on body size, rather than a limit on food processing by the digestive tract (Kimberly et al. Reference Kimberly, Lloyd and Diamond1996; but see Guinard-Flament et al. Reference Guinard-Flament, Delamaire, Lamberton and Peyraud2007). The model also shows the interesting comparison between direct effects of body condition and BW. White (Reference White and Brown1992) discussed how fat reserves (directly related to body condition) could be rapidly mobilized in support of lactation. In fact, our own studies showed that deer can compensate for a reduction in milk production caused by reduced food availability by increasing fat percentage in milk (Landete-Castillejos et al. Reference Landete-Castillejos, García, Gómez and Gallego2003a), which causes a decrease in BW that reaches significance relative to the control group when hinds lose the ability to put extra fat into milk. This study did not show results on body condition, but it included full adult hinds over a short period of time, and because only 5% of protein reserves can be mobilized in support of lactation (Coppock et al. Reference Coppock, Tyrrell, Merrill and Reid1968), it is very likely that such weight decrease is produced by depletion of fat reserves and reduction in body condition (personal unmeasured observations). Our own studies have show indirect evidence of the smaller effect of body condition, as this effect is absorbed by factors modifying lactation when these are included in the GLM models (Carrión et al. Reference Carrión, García, Gaspar-López, Landete-Castillejos and Gallego2008).
The model also shows indirect effects of social rank and age on milk production. Milk in most mammals is produced mainly from daily food intake (Oftedal, Reference Oftedal, Hudson and White1985) and food availability and quality might, in itself, limit milk production ability and decrease milk nutritive quality in deer (Landete-Castillejos et al. Reference Landete-Castillejos, García, Gómez and Gallego2003b). Thus, it is not surprising that if social rank exerts a marked influence on access to food both in captive and free-foraging deer and other ungulates (Espmark, Reference Espmark1964; Thouless & Guinness, Reference Thouless and Guinness1986; Veiberg et al. Reference Veiberg, Loe, Mysterud, Langvatn and Stenseth2004), then it also influences milk production ability indirectly. This influence might not only refer to the amount of food, but also to the quality of food: lactating hinds search actively for pasture of high protein (Clutton-Brock et al. Reference Clutton-Brock, Guinness and Albon1982b), and it is widely known that isocaloric modifications of diet can increase milk production and change its composition (Sutton, Reference Sutton1989; Chan-McLeod et al. Reference Chan-McLeod, White and Holleman1994). However, the indirect effect of social rank probably reflects that, in order to take advantage of the possibilities for improved access to food and the resulting benefit to milk production, a larger body size and higher body condition is required in dominant mothers.
Age also exerted an indirect effect on milk production through its effects on BW and body condition. Recent research shows that lactating hinds that are still growing show a constraint in milk production so large that it is independent of the linear effect of age on growth (Landete-Castillejos et al. Reference Landete-Castillejos, García, Carrión, Estevez, Ceacero, Gaspar-López and Gallego2009). Carrión et al. (Reference Carrión, García, Gaspar-López, Landete-Castillejos and Gallego2008) also show a correlation of age and body condition which reflects partly the lower body condition of younger age classes. Our results here show a greater correlation of body condition with BW than with age, and the lowest of all with social rank. Similarly, age also showed a correlation with BW greater than with body condition, and the lowest with social rank. This may reflect more stable relationships between these variables than for social rank. Nevertheless, it should be noted that two additional models also fitted nearly as well as the most parsimonious one (both indicated in the legend of Fig. 1): one including only the additionally direct effect of social rank but not hind age; and other one (fitting somewhat worse), including only the additional effect of hind age but not social rank.
The results, thus, show that physiological variables seem to be more important than experience (age) or behavioural ones (dominance). Could this be the same situation in the wild? Our hinds had access to food ad libitum, although dominance gives priority access to the component of the diet of highest nutritive quality (unpublished results). This situation may resemble conditions in the wild of low population density or high availability of food, where dominance may allow access to the best quality patches of food, but nevertheless less dominant animals can obtain adequate food resources. It might be interesting to assess whether the indirect effects of social dominance or age may change into direct effects in situations of higher competition for food. Because lactation studies involving milking cannot be carried out in the wild, this would involve an experiment introducing food constraints, which involves a delicate balance of the level of the food constraint and ethical issues. In any case, we should expect either a direct effect of dominance when food is not available ad libitum, or a higher correlation with BW and body condition. We might even expect a change of effect of BW and condition from direct to indirect, as these would no longer be the limiting factor for milk production.
As mentioned above, milk production is usually closely linked with calf growth, usually shown by a high correlation coefficient. In fact, milk production is a close estimate of milk intake by calves (Landete-Castillejos et al. Reference Landete-Castillejos, Garcia, Garde and Gallego2000a) whilst behavioural estimates of milk transfer are often poor or even inadequate predictors of milk provisioning (Cameron, Reference Cameron1998). In the present study, the correlation between calf growth and BW, hind age and the other maternal variables did not achieve significance probably because of the smaller sample size and because we did not take into account confounding variables such as year effects. This is also likely to be the reason for the low R 2 of the model, as in most of our previous models based on GLM usual levels of variability explained in milk production are about 50% (Landete-Castillejos et al. Reference Landete-Castillejos, Garcia, Garde and Gallego2000a, Reference Landete-Castillejos, García, Molina, Vergara, Garde and Gallegob, Reference Landete-Castillejos, García, Gómez and Gallego2003b). Previous studies by our group have shown that calf growth shows the highest correlation with milk production, and lower correlations in decreasing order with hind BW and hind age (Landete-Castillejos et al. Reference Landete-Castillejos, García and Gallego2001, Reference Landete-Castillejos, García, Gómez and Gallego2003b, Reference Landete-Castillejos, García, López-Serrano and Gallego2005).
In conclusion, despite hind BW, body condition, age and social rank being correlated among themselves, path analysis showed that hind BW and body condition exerted a direct influence on milk production, whereas social rank and age exerted an indirect effect mediated by the former traits.
This research has been partly funded by MCEI-FEDER project CGL2008-00749/BOS. The authors thank Bernardo Albiñana, Fulgencio Cebrián, Enrique Gaspar-López and Debora Carrión for their help in data collection.





