Upon encountering new words, children generally assume that they differ in meaning from previously learned words. For example, when shown two objects – one novel, and the other familiar – and told to “Find the blicket”, children as young as 18 months preferentially select the novel referent (Halberda, Reference Halberda2003; Markman, Wasow, & Hansen, Reference Markman, Wasow and Hannsen2003; Spiegel & Halberda, Reference Spiegel and Halberda2011). Results like this have been reported for children's acquisition of nouns, verbs, adjectives, proper names, and even number words (e.g., Au & Markman, Reference Au and Markman1987; Carey & Bartlett, Reference Carey and Bartlett1978; Clark, Reference Clark and MacWhinney1987, Reference Clark1988, Reference Clark1990; Wynn, Reference Wynn1992), suggesting that children very generally assume that different words encode different meanings. According to many accounts, this reasoning reflects a more general pragmatic approach to language: children assume that speakers are cooperative Gricean interlocutors who seek to be truthful, informative, relevant, and clear (Grice, Reference Grice, Cole and Morgan1970). Thus, they reason that if the speaker had intended to refer to the object with the known label then they would have used that word, and thus must have intended to label the novel object. In this way, children can compute the exclusion inference that utterances like those in (1) differ in meaning, even without knowing the meanings for the words some and all or understanding how some and all are related to one another.
(1a) I ate some of the cookies.
(1b) I ate all of the cookies.
Taken alone, word learning assumptions like Clark's (Reference Clark and MacWhinney1987) Principle of Contrast and Au and Markman's (Reference Au and Markman1987) Mutual Exclusivity Assumption are useful, but incomplete, cues to word learning and interpretation. In the best case scenario, exclusion inferences support the supposition that two words differ somehow in meaning – even if only in connotation or conversational register. In the worst case, exclusion inferences can lead to false inferences – e.g., that a cat is not an animal. Very generally, in order to arrive at adult-like interpretations of words, exclusion inferences must be supplemented with additional information about the words under consideration (e.g., whether they are relevant alternatives to one another; whether one entails the other; other information about hierarchical, semantic, or scalar relationships). For example, to interpret the sentences in (1) in an adult-like way (e.g., that the speaker intends to convey that they ate some, but not all, of the cookies), children must know the literal meanings of some and all, including the fact that all is strictly stronger than some in this context, and that if (1b) were true, then it would have been a more informative/optimal thing to say. Only with this knowledge is it possible to infer that (1a) implies the negation of (1b). This particular inference – a ‘scalar implicature’ – is in some respects similar to exclusion inferences. Just as interpreting the novel word blicket may involve the negation of ‘cat’ as a possible meaning via contrast or mutual exclusivity, interpreting an utterance containing some to mean ‘not all’ involves negating a corresponding utterance that contains all. Indeed, several researchers have argued that exclusion inferences rely on similar computational architecture to scalar implicature (Barner & Bachrach, Reference Barner and Bachrach2010; Clark, Reference Clark1990; Gathercole, Reference Gathercole1989; Grice, Reference Grice, Cole and Morgan1970, Reference Grice1991; Katsos & Wilson, Reference Katsos, Wilson, Degen, Franke and Goodman2014; Wynn, Reference Wynn1992). Here, we ask whether claims of children's early abilities to compute scalar implicatures are supported by evidence of scalar implicature computation, or whether the evidence might instead be consistent with simpler exclusion inferences, like those required by contrast and mutual exclusivity. In doing so, we ask not only whether previous studies provide valid tests of implicature, but also whether the ability to compute implicatures might arise initially from the same machinery that supports word learning.
In order to understand how exclusion inferences like contrast and mutual exclusivity are related to scalar implicature, it is important to first characterize the computations that each involves. We first consider exclusion inferences – i.e., contrast and mutual exclusivity. Contrast inferences arise from the assumption that differences in linguistic form signal differences in meaning (for discussion see Clark, Reference Clark and MacWhinney1987, Reference Clark1988, Reference Clark1990). These inferences are relatively weak in the sense that they do not, in isolation, license strong assumptions about reference. For example, contrast allows expressions like couch and sofa to convey different connotations while still labeling the same referent. Much like contrast, mutual exclusivity inferences arise when listeners assume that each word has one meaning and each meaning is expressed by only one word, such that word A implies not-B, just as B negates A (Woodward & Markman, Reference Woodward and Markman1991). However, mutual exclusivity inferences also involve the assumption that differences in meaning predict differences in reference – e.g., that a particular object labeled as a blicket cannot also be called a toma. Thus, in this sense, they are stronger than contrast alone. For the purposes of the present study, we will refer to both forms of inference collectively as ‘exclusion inferences’, except in cases where the difference is important.
As described above, there is reason to believe that exclusion inferences and scalar implicature rely on similar computational architecture (Barner & Bachrach, Reference Barner and Bachrach2010; Clark, Reference Clark1990; Gathercole, Reference Gathercole1989; Grice, Reference Grice, Cole and Morgan1970, Reference Grice1991; Katsos & Wilson, Reference Katsos, Wilson, Degen, Franke and Goodman2014; Wynn, Reference Wynn1992; cf. de Marchena, Eigsti, Worek, Ono, & Snedeker, Reference de Marchena, Eigsti, Worek, Ono and Snedeker2011). According to Clark (Reference Clark1990), exclusion inferences can be characterized as Gricean in nature, and as such can be thought of as arising from similar mechanisms to scalar implicature. For example, in a context including a cat and a novel object, a speaker who intends to refer to the cat is expected to say “Look at the cat!” rather than “Look at the blicket”. In this case, on a standard Gricean analysis, the listener hears the word blicket and assumes that the speaker's intended referent is not a cat, since if they had intended to refer to the cat then they would have chosen the word cat instead. This reasoning is shared by Gricean models of scalar implicature: in (1a), if the speaker had actually eaten all of the cookies then they should have said so; thus, saying they ate some of the cookies licenses the implicature that the statement containing all is false.Footnote 1
However, despite their similarities, there are important differences between scalar implicature and exclusion inferences, both in their structure and their developmental trajectories. One structural difference between word learning constraints and scalar implicature is what linguists call ‘asymmetric entailment’. Whereas exclusion inferences involve a symmetrical exclusion relationship (hence ‘mutual exclusivity’), implicature generally does not. Specifically, scalar implicature involves not only the ability to contrast utterances, but also the ability to relate them to one another according to their relative informational strength in context. For example, whereas the truth of the utterance in (1b) entails that (1a) must also be true – i.e., if I ate all of the cookies I must have eaten some of them – the opposite is not true: eating some of the cookies does not entail that one has eaten all of them. Consequently, upon hearing, “I ate some of the cookies”, the listener infers that if the stronger alternative statement were true – i.e., “I ate all of the cookies” – then the speaker would have said so, and that consequently the speaker must not believe this stronger statement to be true (and instead believes that they ate some, but not all, of the cookies).
A second difference between exclusion inferences and scalar implicature is related to their reported developmental trajectories. While children readily compute exclusion inferences by the age of two or younger (Au & Markman, Reference Au and Markman1987; Carey & Bartlett, Reference Carey and Bartlett1978; Halberda, Reference Halberda2003; Heibeck & Markman, Reference Heibeck and Markman1987; Markman & Wachtel, Reference Markman and Wachtel1988; Wynn, Reference Wynn1992), the literature on scalar implicature is divided, with some studies reporting difficulties among children as old as ten years of age (Noveck, Reference Noveck2001; Papafragou & Musolino, Reference Papafragou and Musolino2003), and others finding evidence of scalar implicature in school-aged children (Chierchia, Crain, Guasti, Gualmini, & Meroni, Reference Chierchia, Crain, Guasti, Gualmini, Meroni, Do, Domínguez and Johansen2001; Guasti et al., Reference Guasti, Chierchia, Crain, Foppolo, Gualmini and Meroni2005; Katsos & Bishop, Reference Katsos and Bishop2011) and in preschoolers as young as three years of age (Miller, Schmitt, Chang, & Munn, Reference Miller, Schmitt, Chang and Munn2005; Papafragou & Tantalou, Reference Papafragou and Tantalou2004; Stiller, Goodman, & Frank, Reference Stiller, Goodman and Frank2015; Syrett & Arunachalam, Reference Syrett, Arunachalam, Scott and Waughtal2016; Yoon, Wu, & Frank, Reference Yoon, Wu and Frank2015).
Explanations for children's failures to compute scalar implicatures vary, but there is increasing evidence that at least part of their difficulty lies in summoning relevant scalar alternatives – e.g., that children fail to spontaneously conjure utterances containing all as relevant alternatives to utterances containing some, resulting in an inability to make a some-but-not-all inference (Barner, Brooks, & Bale, Reference Barner, Brooks and Bale2011; Hochstein, Bale, Fox, & Barner, Reference Hochstein, Bale, Fox and Barner2016; Skordos & Papafragou, Reference Skordos and Papafragou2016). In support of this view, children appear to perform better when scalar alternatives are either primed or visually or linguistically contrasted with one another, often in two-alternative forced choice paradigms (e.g., when one utterance is matched with one of two pictures, when one picture is matched with one of two utterances, or when two pictures differ in appearance in a way that encourages the spontaneous generation of linguistic descriptions of the pictures; Chierchia et al., 2011; Katsos & Bishop, Reference Katsos and Bishop2011; Miller et al., Reference Miller, Schmitt, Chang and Munn2005; Papafragou & Tantalou, Reference Papafragou and Tantalou2004; Stiller, Goodman, & Frank, Reference Stiller, Goodman and Frank2015). Critically, some of these studies use methods that closely resemble tasks used to assess contrast and Mutual Exclusivity, in that they either explicitly mention the relevant linguistic alternatives, or they provide a small set of referential choices, which children might use to generate contrasting linguistic labels (Mani & Plunkett, Reference Mani and Plunkett2010; Snedeker, Reference Snedeker2015). In fact, the high degree of similarity between tasks in these literatures raises the question of whether, instead of computing scalar implicatures, very young children who exhibit apparent successes might in fact rely on exclusion inferences, which are not sensitive to asymmetric entailment.
For example, in one report of early implicature use, Papafragou and Tantalou (Reference Papafragou and Tantalou2004) showed four- and five-year-old children a puppet who was asked to do a task – e.g., Elephant has to color four stars. The puppet then went into a house, and upon return, was asked: “Did you color the stars?” The puppet then reported what he had done – e.g., “I colored some”. In this case, children correctly judged that Elephant had not done the right thing (e.g., that some implied, in this case, ‘not all four’). While this study was interpreted as providing evidence of scalar implicature in the early preschool years, it is also possible that children's success was driven by exclusion inferences alone. Consider the dialogue in (2), adapted from Papafragou & Tantalou:
(2a) S1: [presents child with four toys] You have to clean them … Did you clean the toys?
(2b) S2: I cleaned some.
Here, if children compute a scalar implicature, they should infer that not all of the requested toys had been cleaned. This is because in cases where four toys are present, a statement containing either four, all, or them would have been stronger than the statement containing some (for discussion, see Caponigro, Pearl, Brooks, & Barner, Reference Caponigro, Pearl, Brooks and Barner2012).Footnote 2 However, they could also reach this conclusion that some implies not all four of the toys if they noted the utterance containing some contrasts with the utterance containing them or the utterance containing the toys. In such cases, it is impossible to differentiate whether the listener used exclusion inferences or scalar implicature (or some other process entirely). However, other cases do allow us to tease these two mechanisms apart. Consider the dialogue in (3), which contains an entailment relation:
(3a) S1: If you feed some of the frogs, you get a prize.
(3b) S2: I fed all of the frogs.
Here, children who compute exclusion inferences should judge that S2 did a bad job, because the reported fulfillment contrasts with the request. On the other hand, children who attend to entailment relations – or rely on other processesFootnote 3 in this task should judge that S2 did a good job, because by feeding all of the frogs, they necessarily fed some of them. In other words, if children attend only to surface level features of utterances and not their entailment relations, they should not perform like adults on this type of trial, despite appearing to make adult-like judgments on tests of implicature, like in (2).
In the present study, we test whether reports of early implicature computation in children necessarily show evidence of scalar implicatures, or instead might be explained by exclusion inferences alone. By testing this, we also asked whether scalar implicature might be rooted, in part, in the same inferential capacities that underlie exclusion inferences like contrast and mutual exclusivity. To test these questions, we built on Papafragou and Tantalou's (Reference Papafragou and Tantalou2004) study with two important modifications. First, in addition to trials like (2) that could be solved either by computing scalar implicatures or by using exclusion inferences, we also included trials that required sensitivity to asymmetric entailment, as in (3). This allowed us to ask whether children's inferences reflect the computation of exclusion inferences, or whether they also involve assumptions regarding asymmetric entailment, as required by scalar implicature. Second, in addition to trials that contained linguistically and logically non-equivalent utterances (e.g., three vs. some), we included trials in which logically equivalent statements contrasted in form (e.g., after a request to paint three out of 3 stars, hearing that Puppy painted all of the stars), and trials containing novel words (e.g., blick) about which the child should have no previous expectations about meaning. This allowed us to ask whether, outside of the special case of scalar implicature, children relied on exclusion inferences when making judgments about contrasting utterances. If children use exclusion inferences to guide their judgments, then they should perform as though any contrasting statements (regardless of their logical relations to one another) negate one another (e.g., behaving as though all implies ‘not some’). Alternatively, performance suggesting sensitivity to asymmetric entailment would provide strong evidence that children compute scalar implicatures.
Experiment 1
Materials and methods
Participants
Ninety-five monolingual English speaking participants aged 4;0 to 7;11 from the San Diego region participated (7 additional participants were tested outside of our age range). Children were recruited from a database maintained at UCSD, a local museum, and preschools and daycares in San Diego. Parental consent and child assent were obtained prior to testing. Fourteen children were excluded for: experimenter notes of inattention (n = 3), being bilingual (n = 2), experimenter error (n = 1), or providing only one type of response (e.g., always giving or withholding a prize; n = 8). Thus, a final N of 81 children (4 YOs n = 21; 5 YOs n = 27; 6+ YOs n = 33) were included in analyses; our data collection goal was to have a minimum of 20 participants in each age group. An additional 16 native English speaking undergraduates participated for course credit (no exclusions). We did not collect gender or other demographic information for either of our samples.
Materials and procedure
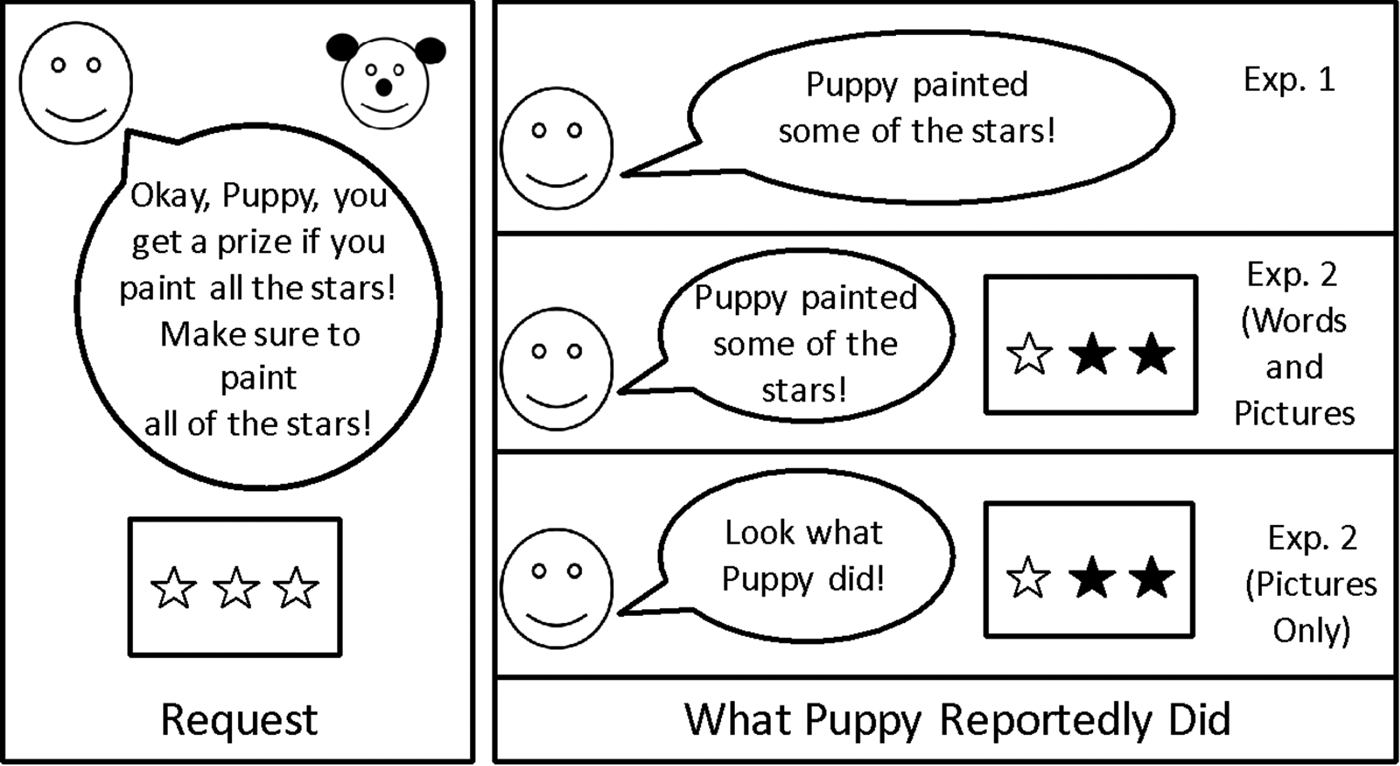
Our methods were modeled after Papafragou and Tantalou (Reference Papafragou and Tantalou2004). An experimenter served as narrator. A plastic container full of approximately 25 small plastic grapes served as prizes for a toy Puppy. For each trial, there was a Before picture of three items (e.g., a picture of 3 unpainted stars; see Figure 1 left panel). Pictures were presented on an 8.5´´ x 11´´ piece of paper, with three items laid out horizontally across the page.
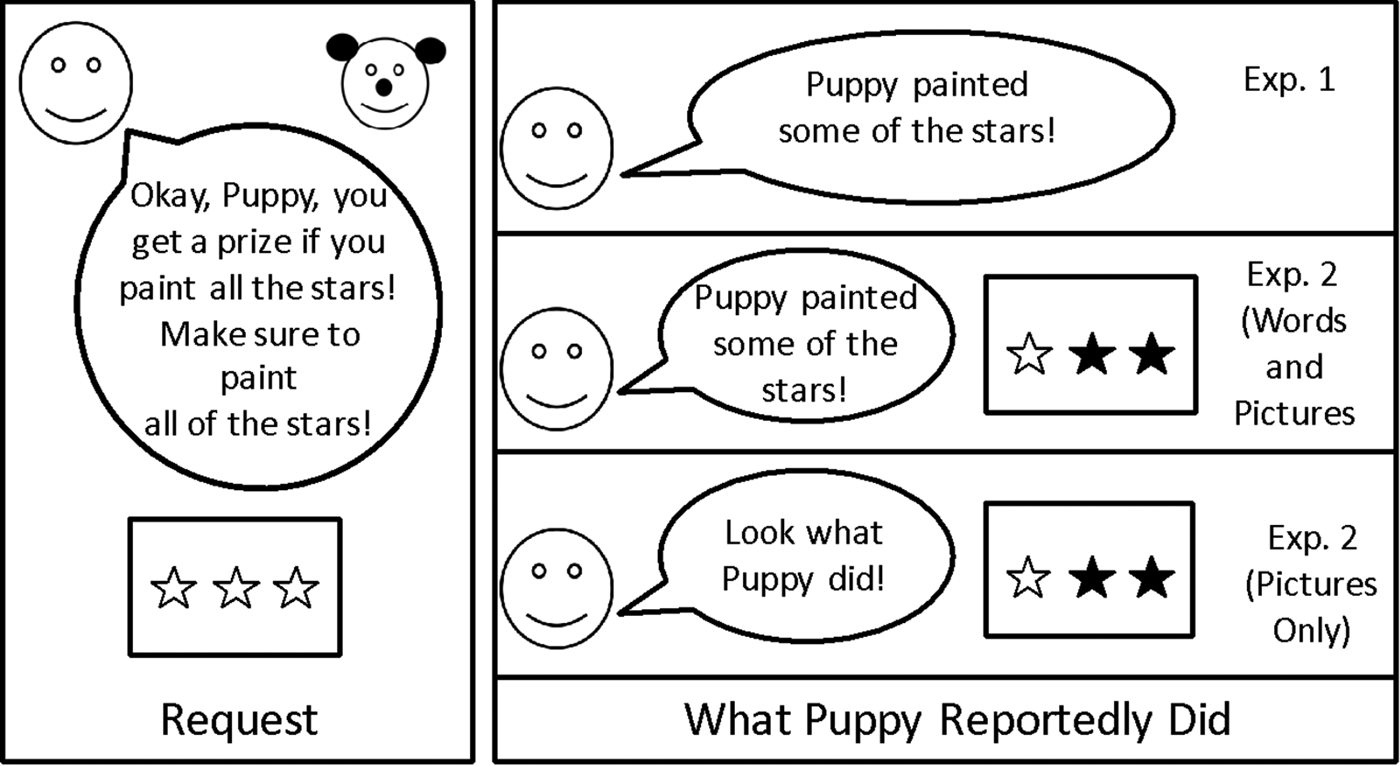
Figure 1. Schematic of methods for Experiment 1 and Experiment 2. Left panel indicates the experimenter's request (e.g., Puppy's task), while the right panel demonstrates how the participant learned about Puppy's actions.
For each trial, the experimenter requested that Puppy complete a task. For example, the experimenter requested that Puppy e.g., paint all/some/two/three/blick of the stars (list of all trials is in Table 1). Puppy's task was always described verbally and repeated twice, with the request first stated in a conditional ‘if…’ statement, where scalar implicatures are typically not calculated, minimizing the likelihood that participants would compute implicatures on the request itself. Participants were told that they could feed Puppy a prize (toy grapes) if he did his job well.
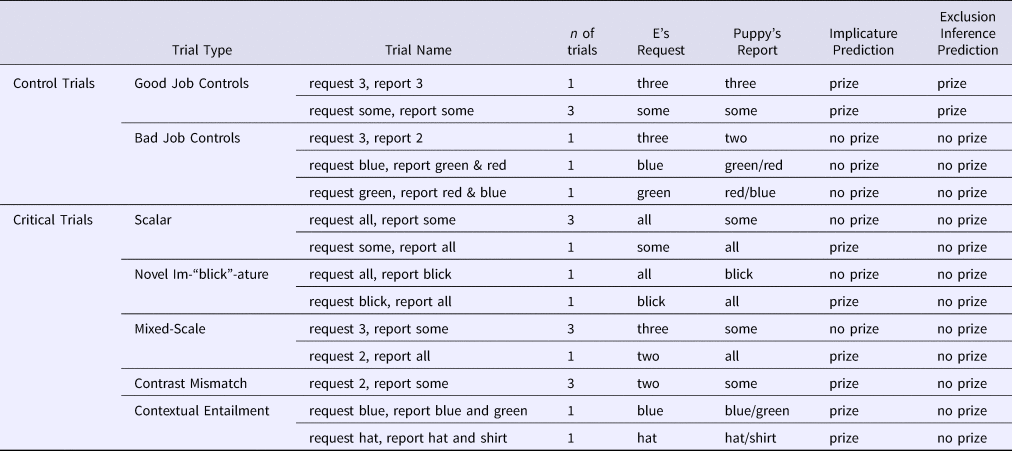
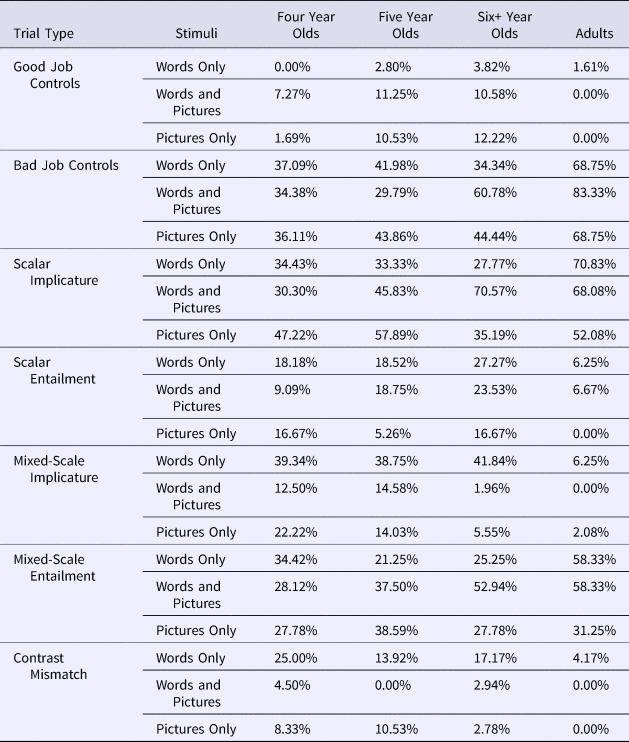
Table 1. Trial types, names, actions involved, and predictions for trials in Experiment 1
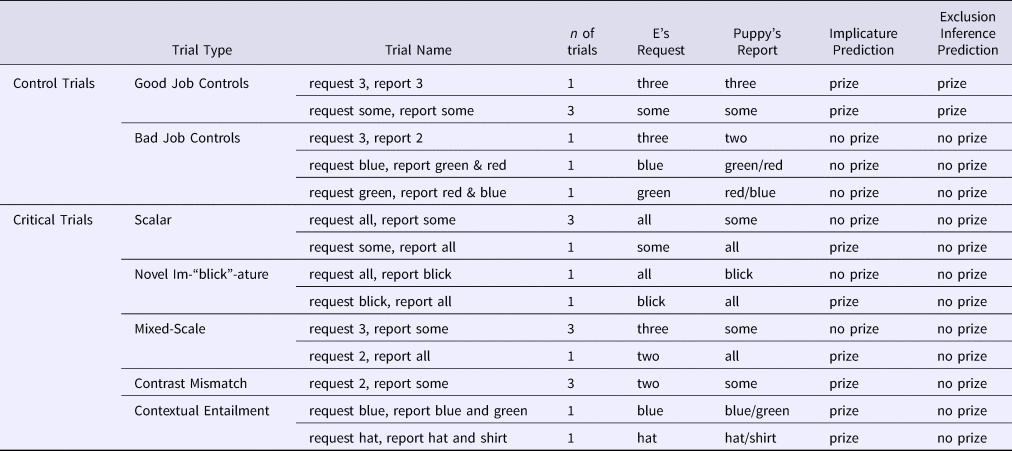
On each trial, the experimenter showed the Before picture (e.g., three unpainted stars) and then introduced Puppy's task: the experimenter said, “Wow, look! There are three [objects]. Okay Puppy, you get a prize if you [task]. Make sure to [task].” The participant then learned what Puppy did via a verbal description (e.g., “Alright, Puppy, did you [task]?” followed by a report of his actions: “Puppy painted some of the stars”), but saw no visual evidence of his actions (i.e., the picture did not change; Figure 1). After hearing about Puppy's actions, the participant was given an opportunity to offer a prize to Puppy (indicating that Puppy had successfully done what was asked of him), and to give justifications for their decisions. Participants completed 22 trials. Within each set of stimuli, there were two trial orders. We had seven trial types, described in detail below and in Table 1.
For each trial, we had two dependent measures. The first dependent measure was whether the participant awarded Puppy a prize (or not). This allowed us to assess whether the participant believed that Puppy's reported actions appropriately fulfilled the experimenter's initial request. Our second dependent measure was whether the participant included negation when justifying their prize-giving. Recall that exclusion inferences lead to symmetric negation (such that cat implies ‘not dog’ just as dog implies ‘not cat’), while scalar implicatures involve asymmetric negation (such that some implies ‘not all’ but all doesn't imply ‘not some’). Thus, by tracking participants’ spontaneous use of negation, we could assess whether their responses were most consistent with symmetric or asymmetric negation.
Trial types
There were two types of control trials: Good Job Controls and Bad Job Controls. For Good Job Control trials, the experimenter's request exactly matched what Puppy did, allowing us to measure whether participants would award Puppy a prize and avoid negation in their justifications when he reportedly did the right thing. For Bad Job Control trials, the experimenter's request clearly didn't match what the Puppy did, allowing us to measure whether participants would withhold a prize and include negation in their justification when he reportedly did the wrong thing.
There were five critical trial types: Scalar, Novel Im-‘blick’-ature, Mixed-Scale (in which quantifiers and numbers were both included), Contrast Mismatch, and Contextual Entailment (see Table 1). For each critical trial, Puppy's reported actions linguistically contrasted with the original request; as can be seen in Table 1, this leads to the prediction that – if participants rely on exclusion inferences – for all critical trials, participants should withhold a prize from Puppy and include negation in their justifications.Footnote 4 On the other hand, if participants truly compute implicature, then, for trials in which Puppy's reported actions are either (a) semantically equivalent to or (b) entail the original request, they should give Puppy a prize and avoid using negation in their justification.
On Scalar Implicature trials, we assessed whether participants computed implicatures (by inferring that some implies ‘not all’) by asking whether they would withhold a prize from Puppy when he reportedly did some after being asked to do all. We also asked whether participants’ justifications included negation (e.g., he said some therefore he didn't do ‘all’). The use of negation in these cases is consistent with either scalar implicature or exclusion inference (or something else altogether). On Scalar Entailment trials (and on all other entailment trials, described below), we measured whether participants made use of entailment relations (that all entails some) by asking whether they would reward Puppy when he reportedly did all after being asked to do some. For this and all critical trials, we also asked whether mentions of negation would be less frequent for entailment than for implicature trials, as would be predicted if participants were truly computing scalar inferences (any other process would predict symmetric negation use across the two trial types).
For the Novel Im-‘blick’-ature trials, we replaced the word some from the Scalar trials with the novel quantifier blick. In other words, the Im-‘blick’-ature trials were structurally identical to the Scalar Implicature trials, but involved a novel word instead of the word some, thus allowing us to assess the degree to which participants’ inferences were based on semantic or scale-specific knowledge, or instead on contrast alone. Previous studies have used ‘blick’ in similar contexts in order to establish children's performance in the absence of item-specific semantic knowledge (e.g., Caponigro et al., Reference Sullivan, Bale and Barner2012; Sullivan, Bale, & Barner, Reference Caponigro, Pearl, Brooks and Barner2018). For Mixed-Scale trials, participants heard a numerical request, but learned of Puppy's actions via utterances that contained quantifiers. Thus, while both the request and fulfillment were quantificational, the type of scale (numerical vs. quantifier) differed across request and fulfillment. For Contrast Mismatch trials, Puppy reportedly did what the experimenter requested, but Puppy's action was described using a different word from the request (see Table 1). Finally, on the Contextual Entailment trials, Puppy reported doing what was asked and more – however, unlike the similarly structured Scalar, Novel, and Mixed-Scale Entailment trials, these trials did not require scale-specific knowledge of numerals and quantifiers, but instead relied only on contextually defined alternatives. In this case, the set referred to in Puppy's response (e.g., “I ate the red, blue, and green lollipop”) entailed the set requested (e.g., “eat the blue and green lollipop!”).
Results
Data management
Exclusions
A total of nine trials were excluded prior to analyses due to experimenter error.
Coding
A researcher, blind to subject, Experiment, and trial-identifying information, coded children's justifications for each response. Justifications were arranged in alphabetical order. Responses were coded for whether they included negation (e.g., “he didn't paint the stars”). Also, while we did not intend to analyze these data in our main analyses, we classified each justification in a number of ways to facilitate post-hoc data exploration: we coded whether a justification referenced the original request, whether it referenced what Puppy did, whether it made a claim about the meaning of a word (e.g., “some means not all”), whether the participant simply labeled Puppy's actions as good/bad, whether the participant explicitly asked for the Puppy to do more/less in order to earn a prize, whether the justification included only or just, and whether the justification included an explicit contrast of request with action (full data are available here: https://osf.io/we98g/).
Analyses
Responses were binary (awarding a prize vs. no prize; mentioning negation or not mentioning negation in justifications) and were analyzed as binomial (though we also report the proportion of trials on which participants gave Puppy a prize). Whenever a participant provided responses to multiple trials of a given trial type, we included participant as a random factor in our models; analyses were conducted using the lme4 package in R (Bates, Machler, Bolker, & Walker, Reference Bates, Machler, Bolker and Walker2015). For all analyses, we first tested for age effects on children's performance; unless reported otherwise, we found no differences in performance between four-, five-, and six-year-olds. Thus, all subsequent analyses compared children's performance to adults’ performance, although we visually display performance for each age separately in our figures, in order to allow for comparisons with previous literature.Footnote 5
Control trials
Good Job Controls
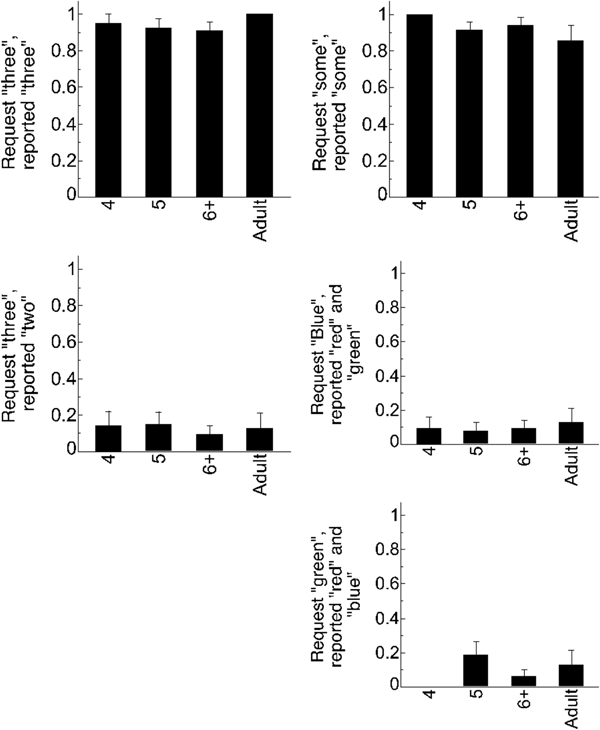
We first considered the trials on which there was an exact match between the experimenter's request and Puppy's actions – e.g., the experimenter asked Puppy to perform an action on three of the objects, and Puppy reportedly performed it on three of the objects. Across all ages, participants successfully gave Puppy a prize on these trials (see Figure 2), and did so the vast majority of the time (see Table 2). There was no difference in rate of prize-giving between children and adults (B = 0.44, SE = 1.84, p = .81). When providing justifications of their responses, neither children (2.5% of trials) nor adults (1.6% of trials; see Table 3) were likely to use negation, and there was no difference in negation production between these groups (B = 0.22, SE = 2.5, p = .93). This result is not surprising given the fact that Puppy reportedly did exactly what was asked: those rare individuals who did include negation were typically vague (e.g., “he didn't do it”), or provided justifications that indicated a misunderstanding of either the trial (“he ate 2 not all 3” after hearing a request for 2; “he didn't eat some” when, in fact, Puppy ate some).
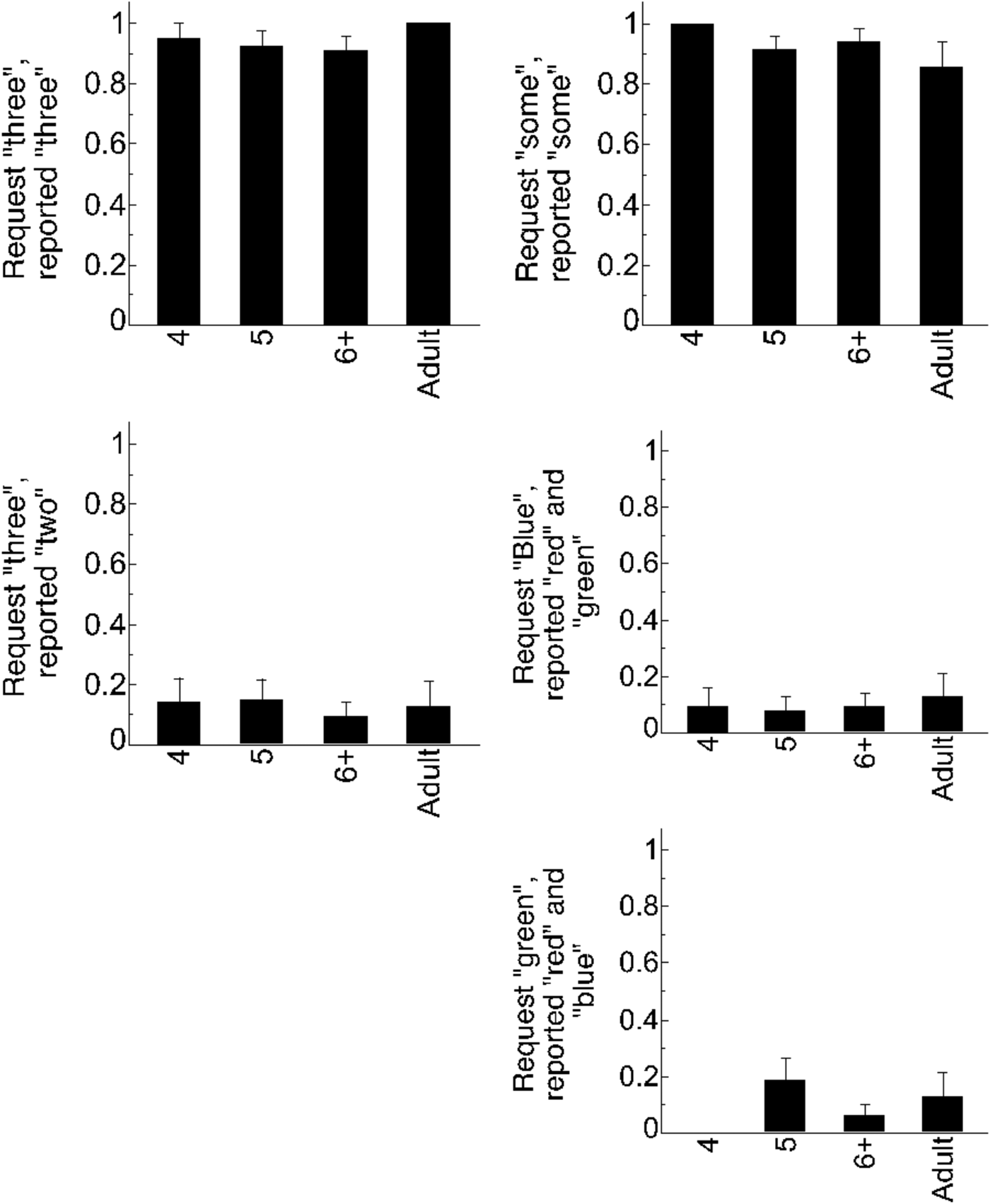
Figure 2. Mean rates of prize-giving for control trials; Good Job Control trials are on the top row and Bad Job Control trials are on the bottom two rows. Error bars are SEM.
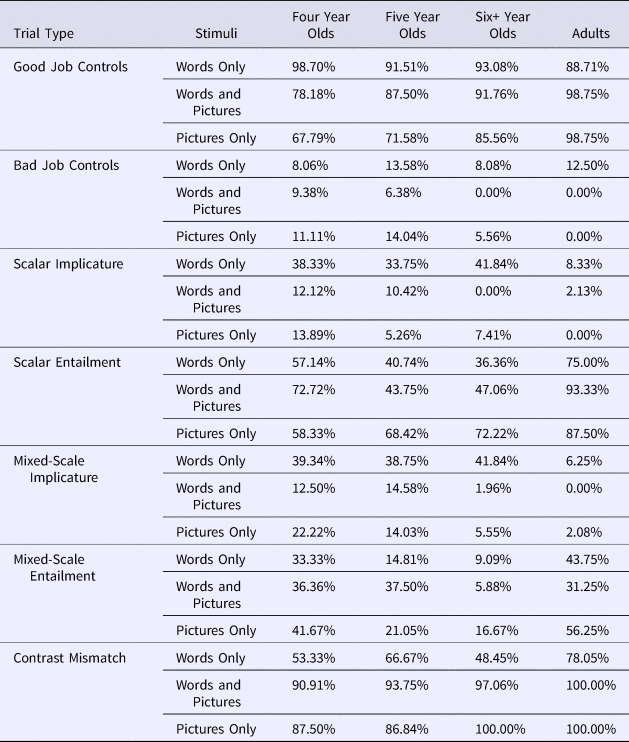
Table 2. Percent giving Puppy a prize in Experiment 1 (Words Only), and Experiment 2 (Words and Pictures; Pictures Only).
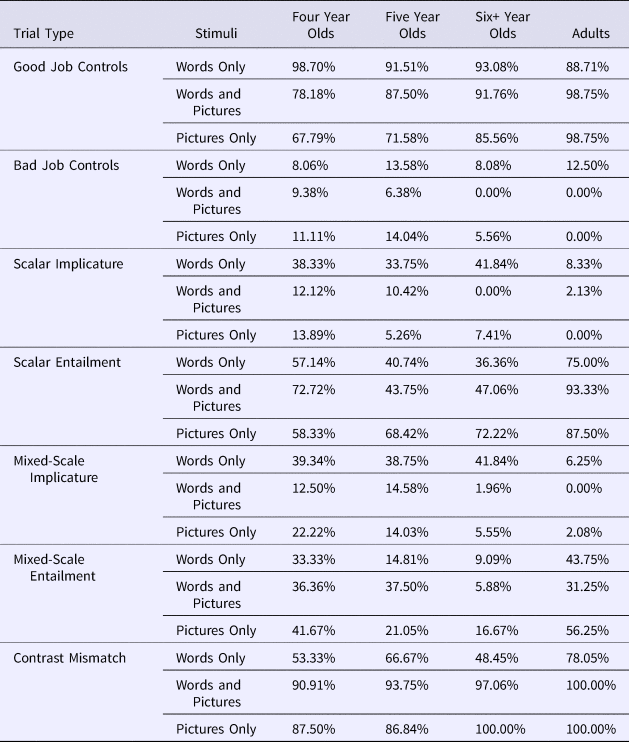
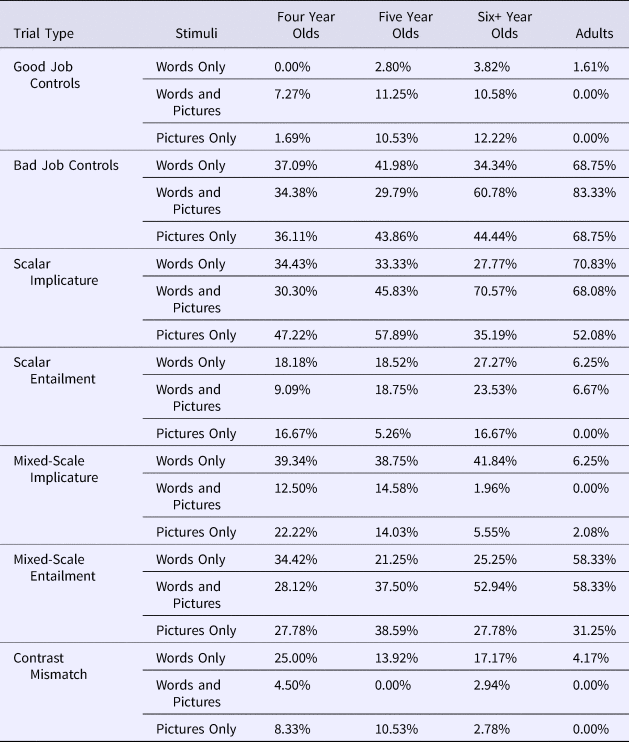
Table 3. Percent including negation in their responses in Experiment 1 (Words Only), and Experiment 2 (Words and Pictures; Pictures Only).
Bad Job Controls
We next considered the control trials on which Puppy's actions did not fulfill the experimenter's request. For example, the experimenter asked Puppy to perform an action on three of the objects, and instead Puppy reportedly performed an action on two of the objects. Across all ages, participants nearly always withheld a prize (see Figure 2; Table 2), suggesting that they did not believe that Puppy's actions fulfilled the experimenter's request. This suggests that participants attended to and understood the task, and were willing to withhold a prize from Puppy when they thought this was warranted. Again, there were no differences between children and adults (B = 0.14, SE = 1.8, p = .94). While adults were more likely than children to include negation in their justifications (B = –1.88, SE = 0.67, p = .005), both adults (68.75%) and children (37.6%) included negation on multiple trials. We use rates of negation on these Bad Job Control trials as a baseline against which to measure negation use on other trials (Table 3; see Supplementary materials for visualization of negation use, available at <https://doi.10.1017/S0305000919000096>).
Critical trials
Scalar implicatures generate asymmetric negation (such that some can imply ‘not all’, but all does not imply ‘not some’), while exclusion inferences generate symmetric negation (such that some implies ‘not all’ just as all implies ‘not some’). This observation leads to the prediction that individuals who compute implicatures should give prizes at different rates for implicature vs. entailment trials: they should withhold prizes on implicature trials, and give prizes on entailment trials. On the logic that scalar implicatures arise due to the negation of stronger alternatives, while entailment computations do not, we also predict that participants who compute implicatures should be more likely to use negation in their justifications on implicature trials than on entailment trials. In contrast, individuals who compute exclusion inferences should give prizes and include negation at similar rates for implicature and entailment trials, since this is the predicted result of computing symmetric negation (i.e., all implies ‘not some’ just as some implies ‘not all’).
Scalar Implicature and Scalar Entailment trials
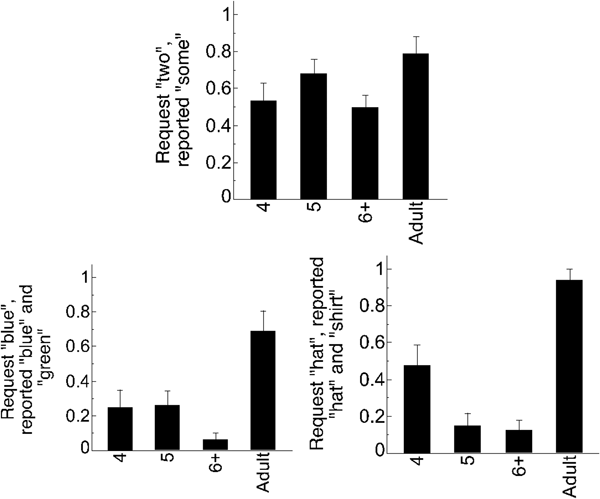
Scalar Implicature and Scalar Entailment trials contained only the scalar terms some and all. On these trials, participants who compute scalar implicatures should accept Puppy's actions in the ‘request some, reported all’ Scalar Entailment case (because all entails some), but should reject Puppy's actions on the ‘request all, reported some’ Scalar Implicature trials (because some implies that ‘not all’ were done). Therefore, performance on these two trial types should differ significantly. Consistent with this prediction, adults gave Puppy a prize 73.33% of the time on the Scalar Entailment trial, whereas they did so 8.33% of the time on the Scalar Implicature trials; performance on these two trial types differed significantly for adults (B = –3.41, SE = 0.78, p < .0001). Consistent with the use of implicature, there was a strong correspondence between performance on these two trial types for adults: nine out of the 11 adults who consistently withheld a prize on the Scalar Implicature trials rewarded Puppy with a prize on the Scalar Entailment trials.Footnote 6 When providing justifications of their responses, adults frequently used negation for scalar implicature trials (e.g., “He didn't do all”; 71% of trials), and rates of negation on Scalar Implicature trials did not differ from rates on ‘Bad Job Control’ trials (B = 0.24, SE = 0.48, p = .62). In contrast, adults rarely used negation for Scalar Entailment trials (6% of trials), and did so at rates not different from ‘Good Job Control’ trials (B = 1.40, SE = 1.44, p = .33). Adults were much more likely to include negation in their justifications on Scalar Implicature trials than on Scalar Entailment trials (B = 3.77, SE = 1.18, p = .001).
While computing scalar implicature predicts asymmetric judgments on Scalar Implicature and Scalar Entailment trials, the use of exclusion inference predicts that participants should reject Puppy's actions for both trial types because in both cases Puppy's actions are described using different words than in the original request. Children tended to withhold prizes for both trial types, giving Puppy a prize 43.21% of the time on the Scalar Entailment ‘request some did all’ trials, and 38.24% of the time on the Scalar Implicature ‘request all did some’ trials (B = –0.43, SE = 0.42, p = .31). As a point of comparison, this means that children performed in an implicature-consistent way approximately 62% of the time (a rate comparable to that reported in Papafragou & Tantalou, Reference Papafragou and Tantalou2004, who reported implicature-consistent performance 77.5% of the time). Importantly, the same children who rejected Puppy's actions for the ‘request all did some’ trials also rejected Puppy's actions for the ‘request some did all’ trials: only 4/40 (10%) of children who withheld prizes on the Scalar Implicature trials then gave Puppy a prize on the Scalar Entailment trial.
Children used negation slightly less frequently for Scalar Entailment (22%) than for Scalar Implicature trials (31%;Footnote 7 B = 0.81, SE = 0.40, p = .043), although, unlike adults, there were many instances of justifications that suggested symmetric negation. For example, on Scalar Entailment trials (requested some, reportedly did all), children provided justifications like “He didn't feed some”, or “He fed all of them, not some”. Also, while (like adults) children's rates of negation for Scalar Implicature trials did not differ from their rates of negation use for Bad Job Control trials (B = –0.43, SE = 0.24, p = .08), unlike adults, children used negation at significantly higher rates for Scalar Entailment trials than for Good Job Control trials (B = 0.26, SE = 51, p < .0001). In other words, while adults invoked negation very rarely and equally frequently on Scalar Entailment trials vs. Good Job Controls, children invoked negation significantly more often on Scalar Entailment trials than on trials where Puppy did exactly what was asked. This is consistent with the possibility that contrasting linguistic forms elicit symmetric negation in children.
Novel Im-‘blick’-ature and Novel Entailment trials
In order to understand the extent to which the above pattern of performance relied on scale-specific knowledge of the words some and all, we next considered trials that involved the novel word (blick) instead of the scalar word some. For trials on which all was requested and Puppy reportedly did blick, adults consistently rejected Puppy's actions (6.67% gave Puppy a prize), suggesting that they did not believe that blick was a fulfillment of a request for all. While the majority of children still withheld prizes, it is of note that, overall, children gave prizes at significantly higher rates (49.32% of the time) than did adults (B = 2.54, SE = 1.06, p = .02), and at significantly higher rates than on Scalar Implicature trials (B = –0.74, SE = 0.38, p = .050). While we cannot say with certainty why this might be (perhaps children use their knowledge of some, perhaps children believe that blick could mean all, perhaps children randomly guessed on blick trials), these data suggest that performance on Novel im-‘blick’-ature trials was not identical to performance on Scalar Implicature trials. When considering rates of negation in justifications, adults included negation on half of the trials (compared to on 29% of trials for Scalar Implicature; B = 0.97, SE = 0.63, p = .13), while children included negation on 16% of trials, significantly less frequently than for Scalar Implicature trials (31.25%; B = 1.31, SE = 0.42, p = .002).
On Novel Entailment trials, in which Puppy was asked to do blick and he reportedly did all, both adults and children rewarded Puppy around half of the time (Children: 44.87%; Adults: 53.33%; B = 0.34, SE = 0.57, p = .55). Consistent with the use of asymmetric negation, adults included negation for Novel Entailment trials very rarely (12.5% of trials) and significantly less often than on Novel Implicature trials (50% of trials; B = 15.05, SE = 6.01, p = .012). In contrast, consistent with the use of symmetric negation, children included negation in their responses at comparable rates for Novel Implicature (16%) and Novel Entailment trials (27%; B = 0.87, SE = 0.47, p = .064).
Mixed-Scale Implicature and Mixed-Scale Entailment trials
We next considered the Mixed-Scale Implicature trials. When the experimenter requested three, and Puppy reportedly did some, adults gave prizes 6.25% of the time, as would be expected if they inferred that some implies ‘not all 3’. In contrast, children gave a prize significantly more often than adults did (B = 4.43, SE = 1.38, p = .001; 40.17% of the time), suggesting that children were less likely than adults to judge that the reported actions mismatched the original request. This finding is consistent with the possibility that at least some children interpreted some as ‘some and possibly all’ (not computing a scalar implicature) or ‘a relatively small quantity’. Importantly, even though children awarded a prize more frequently than did adults, the majority still rejected Puppy's actions. Thus, modal performance for both children and adults was consistent with either computing an implicature or a contrast-based inference. To differentiate these possibilities, we turn to the Mixed-Scale Entailment trials, which were new to this study.
On trials on which Puppy was asked to do two actions (i.e., “feed 2 of the lions”), but ended up reporting doing all (i.e., “fed all of the lions”), Puppy's reported actions could be interpreted as entailing the original request (because the set of all in this context also contains 2). Participants adopting this interpretation would be predicted to give Puppy a prize, as adults did just under half of the time (Table 1). Alternatively, participants could compute an exclusion inference (that all implies ‘not 2’), or interpret the request as an exact request (e.g., “do two, but no more and no less”); both of these options predict withholding the prize. Consistent with these latter strategies, most children (and adults) preferred to withhold Puppy's prize (Table 2, Figure 3). From these data alone it is not possible to determine whether participants based their responses on an exact interpretation of the numeral (e.g., a request for two means ‘exactly 2’) or, instead, on an exclusion inference. However, participants’ verbal justifications help to differentiate these possibilities. If participants compute exclusion inferences, then they should include negation in their justifications as frequently on Mixed-Scale Entailment trials as they do on Mixed-Scale Implicature trails, consistent with judging that all is incompatible with two. Interestingly, adults rarely included negation in their justifications for Mixed-Scale Entailment trials (12.5%; see Supplementary materials for visualization of negation-use), and did so significantly less frequently than on Mixed-Scale Implicature trials (B = –2.6, SE = 0.89, p = .004). Only two adult responses were consistent with exclusion inference, and one of them reflected a misunderstanding of the trial (i.e., “he didn't do all”, “he did all instead of 2”). In contrast, children included negation in their justifications just as frequently for Mixed-Scale Entailment trials (25.9%) as for Mixed-Scale Implicature trials (26.3%; B = 0.02, SE = 0.38, p = .96). Thus, based on the justifications, it seems unlikely that adults were computing exclusion inferences, and likely that many children were.

Figure 3. Mean rates of prize-giving for Scalar, Im-‘blick’-ature, and Mixed-Scale trials; the left column shows implicatures, the right shows entailment; error bars are SEM.
Contrast mismatch
We next considered the case where reports of Puppy's actions were consistent with the experimenter's request, yet contrasted in linguistic format (i.e., when Puppy was asked to do two, and was reported to do some). Critically, on this trial type, Puppy's response was described using a different linguistic term than had been used in the initial request, leading to different predictions for scalar implicatures vs. exclusion inferences. Specifically, participants who computed a scalar implicature (that some implies ‘not all’) should give Puppy a prize, since some (and not all) is a good fulfillment of a request for two items in this context (as adults did 78% of the time; see Table 1). However, participants who (a) computed an exclusion inference (e.g., that two and some are different words and therefore correspond to different requests) or (b) failed to compute a scalar implicature (and believe that some was consistent with doing all 3) should reject Puppy's actions, as children did around half of the time of the time (Figure 3; Table 2). Children's rates of prize-giving on these trials was significantly lower than that of adults (B = –2.11, SE = 1.03, p = .04). When providing justifications, adults almost never included negation (4.2% of trials), and did so at rates comparable to the Good Job Control trials (B = –0.78, SE = 1.24, p = .43). In contrast, children included negation significantly more often than on Good Job Control trials (B = –2.47, SE = 0.44, p < .0001). These data suggest that children (but not adults) were likely computing exclusion inferences.
Contextual entailment
Finally, we considered trials on which Puppy did more than what was requested of him, and Puppy's actions were described using contextual (as opposed to scalar or numerical) alternatives. For example, these were trials where Puppy was asked to wash the hat, but he actually washed the hat and shirt, or he was asked to eat the blue lollipop but actually ate the blue and green lollipops (Figure 4). These trials allowed us to test whether children's reliance on exclusion inference was specific to quantifiers or reflected a more general indifference to entailment relations in this task. Consistent with making use of entailment relations, adults gave prizes on 81.25% of trials. In contrast, children gave Puppy a prize only 19.88% of the time (see Table 2); this performance is inconsistent with using entailment relations to guide performance.

Figure 4. Proportion giving prizes for Contrast Mismatch and Contextual Entailment trials; error bars are SEM.
Experiment 1 discussion
On control trials, participants of all ages demonstrated that they understood the task by giving (or withholding) prizes when appropriate. Also, on these control trials, participants included negation in their justifications when Puppy did something other than what was requested, and avoided negation when Puppy did exactly what was requested. This suggests that our two dependent measures were able to capture expected performance, across all ages, on our control trials.
Critical to our main question, we found that while both children and adults tended to (appropriately) withhold prizes from Puppy on Scalar Implicature trials (when Puppy was asked to do all and then was reported to do some), only adults reliably gave Puppy a prize on Scalar Entailment trials (when Puppy was asked to do some but reportedly did all). Recall that true scalar implicature involves strengthening expressions (like those that include some) by negating stronger alternative utterances. Consistent with this, participants tended to justify their responses to Scalar Implicature trials using negation (e.g., “he didn't do all of them”).
In contrast, reasoning about entailment relations in an adult-like way does not involve the negation of alternatives. Consistent with this, on Scalar Entailment trials, adults frequently gave prizes and rarely used negation when justifying their responses. Children, on the other hand, frequently withheld a prize from Puppy on Scalar Entailment trials, and included negation in their justifications for both Scalar Implicature and Scalar Entailment trials (e.g., “He fed all of them, not some”). These data suggest that children relied on exclusion inference and symmetrically negated alternatives – e.g., performing as though all implies ‘not some’ just as some implies ‘not all’. In support of this conclusion, the majority of children who initially appeared to succeed on Scalar Implicature trials (by withholding a prize from Puppy when he did some after being told to do all) failed to behave in an adult-like manner on Scalar Entailment trials.
Recall that scalar implicatures involve asymmetric negation (i.e., negation only of stronger alternatives), while exclusion inferences involve symmetric negation. While adults were much less likely to include negation in their justifications for Novel Entailment trials than for Novel Im-‘blick’-ature trials, children included negation in their justification at comparable rates for both Novel trial types. The simplest explanation of our data – across all trial types – is that children tend to compute exclusion inferences instead of relying on scale-specific entailment relations: whenever the form of the reported result differed from the form of the request, children typically withheld the prize for the Puppy, even if the result entailed the request.
While we found evidence that young children compute exclusion inferences – even when entailment-based inferences would be more appropriate – we want to be clear that these data do not show that young children can't reason about entailment at all. Our data are neutral with respect to this question. Instead, what they show is that, even if children can compute entailment relations, they fail to spontaneously deploy such knowledge in tasks like the ones used here, in which a simpler exclusion inference is also possible. From this, we conclude that, without explicit tests of whether children deploy their knowledge of entailment, it is impossible to know whether their behaviors reflect true scalar implicatures, or simpler strategies.
Although we explain children's behaviors in Experiment 1 by appeal to exclusion inferences, an alternative account may also be possible. Specifically, children's behaviors can also be explained if we assume that they computed full-fledged implicatures twice in the experiment – once at the moment of the original request, and once when the Puppy's behavior was reported. For example, when Puppy was asked to paint some of the stars, children may have computed an implicature at this time, interpreting the request as a demand to paint ‘some but not all of the stars’. This would predict that on Scalar Entailment trials (when Puppy reportedly painted all of the stars after being asked to paint some) children should act as though Puppy didn't do what was asked.
A problem with this interpretation is that it requires assuming that children are more likely than adults to compute scalar implicatures, a proposal at odds with any previous finding in the literature. Still, to differentiate this possibility from our explanation premised on exclusion inference, we conducted a second experiment. In Experiment 2, half of the participants did not have access to linguistic information regarding Puppy's behavior, thus removing linguistic contrast as a possible means by which children decided to reward Puppy. If children compute implicatures on the experimenter's original request then, even in the absence of contrasting linguistic evidence, they should reject Puppy's actions (as they did in Experiment 1) when he is reported to do ‘all’ after being asked to do some. If, in the absence of contrasting linguistic labels, children no longer reject Puppy's actions, this rules out the possibility that they computed an implicature at the moment of request.
Experiment 2
Materials and methods
Participants
Children (N = 119) between the ages of 4;0 and 7;11 were recruited from the same population and using the same methods as Experiment 1 (an additional 6 participants were tested outside our targeted age-range). Participants were excluded for failing to complete at least half of the task or inattention (n = 6), being bilingual (n = 2), experimenter error (n = 2), or having participated in a related study (n = 3), or for only providing one type of response (n = 13). Thus, a final N of 93 child participants (4 YOs n = 23; 5 YOs n = 35; 6+ YOs n = 35) were included in analyses; our data collection goal had been to include a minimum of 20 usable participants in each age group. An additional 32 native English speaking undergraduates participated for course credit (no exclusions).
Materials and procedure
The procedure in Experiment 2 was identical to that in Experiment 1, with the following exceptions. As in Experiment 1, participants saw the Before picture alongside the experimenter's request (e.g., a picture of 3 unpainted stars), but new to Experiment 2, they also saw an After picture, showing what Puppy had done (e.g., a picture of 2 painted and 1 unpainted stars; Figure 1, lower right panels). Thus, Experiment 2 provided participants with visual evidence of what Puppy did. Participants were randomly assigned to learn of Puppy's actions in one of two ways (see Figure 1). Participants in the Words and Pictures condition heard a verbal description of what Puppy did (e.g., “Puppy painted some of the stars”; as in Experiment 1) and also saw a picture of what that looked like (e.g., one unpainted star and two painted stars; new to Experiment 2). Participants in the Pictures Only condition (similar to a classic no-words condition in the word learning literature) saw a picture of what Puppy did (e.g., one unpainted star and two painted stars), but Puppy's actions weren't labeled except to draw attention to the picture (e.g., “Look what Puppy did!”). In this sense, the Words and Pictures condition gave children the opportunity to relate the visual evidence to a particular linguistic label, while in the Picture Only condition participants did not have access to labels. Thus, between-subjects, we manipulated access to linguistic information about Puppy's actions. Additional small changes to the Methods from Experiment 1 are reported in the Supplementary materials.
Results
Exclusions and coding
Again, nine individual trials were excluded due to experimenter error. All other analytic procedures and coding criteria are as reported in Experiment 1.
Supplemental results
For the sake of brevity, we present only the Scalar Implicature and Scalar Entailment analyses in the main paper, since these analyses were central to testing whether children were computing scalar implicatures at the moment of request. Analyses of other trial types are available in the Supplementary materials, and are consistent with the main conclusions of this paper. Mean rates of prize-giving and negation-inclusion for all trial types are included in Tables 2 and 3.
Scalar Implicature and Entailment trials
We first considered participants’ judgments for Scalar Implicature (‘request all, reportedly did some’) trials.Footnote 8 As in Experiment 1, adults in Experiment 2 believed that some (and/or a visual representation of ‘some’) was not a good fulfillment of a request for all, and withheld Puppy's prize (Table 2). Children also rejected Puppy's actions, as they did in Experiment 1, both when they heard that Puppy did some (only 6.8% accepted Puppy's actions) and when they didn't hear some but only saw that Puppy did 2 out of 3 (only 8.2% accepted Puppy's actions). Thus, like in Experiment 1, children and adults believed that if they had evidence that Puppy did ‘some’ after being asked to do all, he did a bad job.
For Scalar Entailment (‘request some, reportedly did all’) trials, adults gave Puppy a prize across all conditions and experiments (Table 2). As in Experiment 1, adults’ rates of prize-giving and of negation use were significantly different on the Scalar Entailment vs. Scalar Implicature trials (Prize Giving: B = –23.47, SE = 6.33, p = .0002; Negation: B = 4.05, SE = 1.09, p = .002). Importantly, children's prize-giving and rates of negation also differed on Scalar Entailment vs. Scalar Implicature trials (Prize-giving: B = –7.70, SE = 1.93, p < .0001; Negation: B = 2.61, SE = 0.43, p < .0001). Similar to Experiment 1, children in the Words and Pictures condition gave Puppy a prize around half of the time on Scalar Entailment trials (Experiment 1: 43.21%; Experiment 2 Words and Pictures: 52.27%). In contrast, children in the Pictures Only condition who heard that Puppy was asked to do some and then saw that he did 3/3 (without hearing the word all) readily accepted Puppy's actions (67.34% of the time), although performance on these trials did not differ (p = .14).Footnote 9
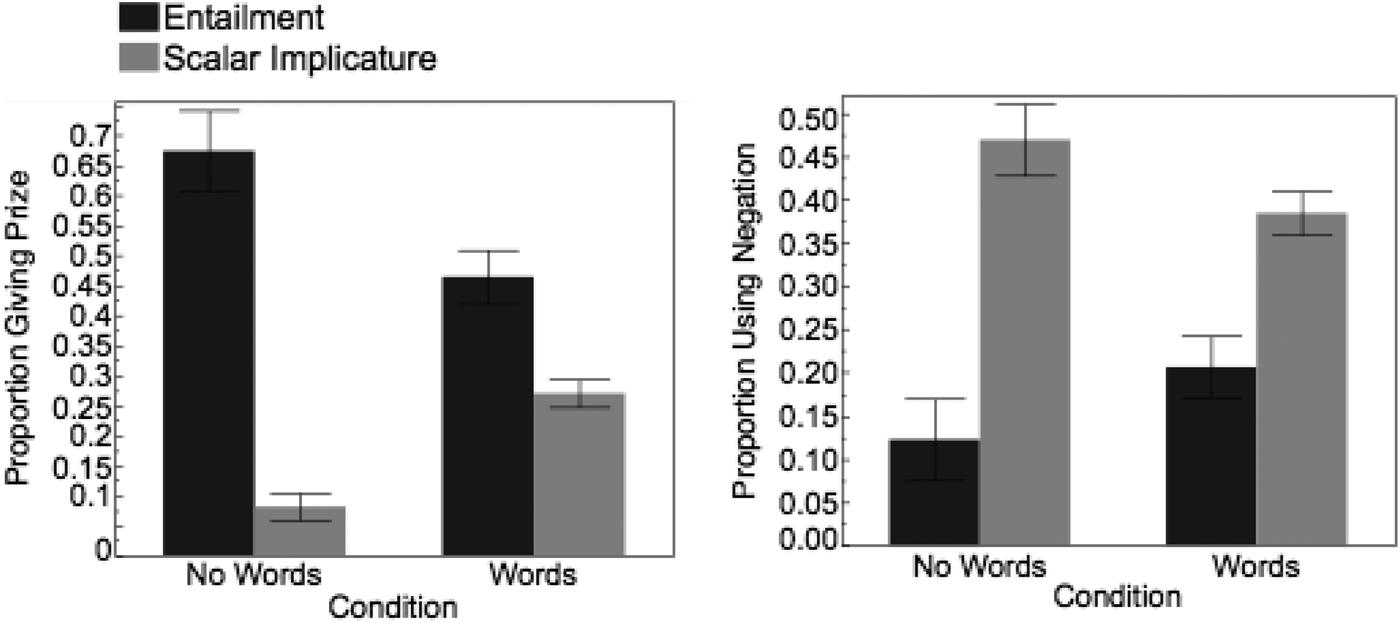
We next constructed a model predicting prize-giving and negation from condition (Pictures Only vs. Words and Pictures), computation type (Scalar Implicature vs. Scalar Entailment), and its interaction. There was an effect of computation type (Prize Giving: B = –9.3, SE = 2.29, p < .0001; Negation: B = 2.78, SE = 0.60, p < .0001), performance did not differ significantly based on condition (Prize-Giving: B = –2.87, SE = 1.88, p = .13; Negation: B = 0.64, SE = 0.81, p = .43), and there was no interaction. We next conducted post-hoc analyses on our entire dataset (Experiment 1 and Experiment 2), predicting prize-giving and negation from the presence of words (Words vs. No Words), computation type, and their interaction. For both Prize-Giving (B = 5.07, SE = 1.00, p < .0001) and Negation (B = –1.47, SE = 0.67, p = .03) we found a significant interaction of computation type and presence of words, such that performance was most similar between Scalar Entailment and Implicature trials when the words were present, and least similar when words were absent (Figure 5).

Figure 5. Proportion giving prize (left) and using negation (right) for Scalar Entailment (black) and Scalar Implicature (gray) trials. These data are for children only, and are combined across Experiments 1 and 2. Error bars are SEM.
Experiment 2 discussion
The goal of Experiment 2 was to test whether children's apparent failure to appropriately respond to cases of linguistic entailment might actually be due to computation of a scalar implicature at the moment of request (i.e., inferring that a request for some was a request to ‘not do all’). Had the child computed a scalar implicature at the moment of the request (and therefore inferred that the request was to do ‘some but not all’), then they should have rejected Puppy's actions whenever he was asked to do some but then reportedly did all. In Experiment 1 and the Pictures and Words condition of Experiment 2 – the conditions in which the children had access to contrasting linguistic labels (some and all) – children withheld a prize from Puppy when he was asked to do some but actually did all around half the time. In the Pictures Only condition, children didn't hear contrasting linguistic labels, and there was therefore no some/all linguistic contrast. Without access to contrasting linguistic labels, children gave Puppy a prize the majority of the time. This is inconsistent with the view that most children spontaneously computed a scalar implicature at the moment of request: if children did, then they should have interpreted the request for some as being for ‘some and not all’, and therefore should have found Puppy's reported actions incompatible with the initial request. In addition, when Experiments 1 and 2 are considered together, participants who had access to linguistic labels were less likely to perform differently on Scalar Implicature trials vs. Scalar Entailment trials, compared to participants who had access to linguistic labels. Importantly, adults’ performance was consistent across all trial types in Experiment 1 and Experiment 2. This suggests that, by adulthood, the presence (or absence) of linguistic contrast does not influence the mature linguistic processing of the types of dialogues presented in our experiments (Table 2).
General discussion
Many past studies have found that, while children readily apply exclusion inferences like contrast and mutual exclusivity during word learning, they take many years to exhibit adult-like behavior when computing scalar implicatures (e.g., that an utterance containing some implies ‘not all’). However, a number of recent studies have reported surprisingly early successes at scalar implicature, usually using forced choice paradigms or direct contrast of scalar alternatives (Miller et al., Reference Miller, Schmitt, Chang and Munn2005; Papafragou & Tantalou, Reference Papafragou and Tantalou2004; Skordos & Papafragou, Reference Skordos and Papafragou2016; Stiller et al., Reference Stiller, Goodman and Frank2015; Yoon et al., Reference Yoon, Wu and Frank2015). Based on these findings, we explored the possibility that some children's earliest successes on purported tests of scalar implicature could instead be explained by appeal to exclusion inference (e.g., inference driven by contrast or mutual exclusivity). When children successfully judge that some is not a good fulfillment of a request for all four (Papafragou & Tantalou, Reference Papafragou and Tantalou2004), they may do so either because they compute a scalar implicature or because they note that some is a different word than was used in the initial request, and therefore infer that the request and fulfillment must differ in some way in meaning (contrast) or even that they are incompatible (mutual exclusivity).
Our goal was to differentiate evidence for children's computation of scalar implicature from evidence consistent either with scalar implicature or with simpler, alternative exclusion inferences like contrast and mutual exclusivity. We began with the observation that, just like scalar implicature, exclusion inferences allow the symmetric negation of alternatives and can therefore give rise to the judgment that an utterance containing some implies ‘not all’. However, unlike in the case of scalar implicature, exclusion inferences can also give rise to the judgment that an utterance containing all implies ‘not some’. This is because, while exclusion inferences involve symmetric negation, scalar implicature generally involves asymmetric negation – e.g., such that “I ate some of the cookies” implies the negation of “I ate all of the cookies” but not vice versa. Based on this logic, in order to provide a strong test of scalar implicature computation, we asked whether children spontaneously invoked asymmetric entailment relations, as would be predicted if they applied all of the underlying components of the computation of a scalar implicature. Consistent with the computation of symmetrical exclusion inferences, we found that children rejected a character's actions whenever the descriptions of these actions linguistically contrasted with the experimenter's original request, independent of entailment relations. For example, if the experimenter requested some and then said that Puppy did all, in the Words Only condition children rejected Puppy's action to the same degree as when all was requested and Puppy reportedly did some. This pattern of performance is largely inconsistent with the possibility that children computed scalar implicatures on our task, because it suggests that when faced with our task, children were not basing their answers on asymmetric entailment relations. Instead these data are most consistent with the possibility that children allowed exclusion inferences to guide their performance.
As noted in Experiment 2, one alternative explanation of this pattern of results is that children may have computed a scalar implicature at the moment of the experimenter's request. For example, upon hearing the experimenter say “Puppy, paint some of the stars”, children may have computed a scalar implicature and inferred that the experimenter expected Puppy to paint some but not all of the stars. Like an account based on exclusion inferences, this also predicts that children should reject Puppy's actions when he reportedly does all after being told to do some. Against this interpretation, adults in Experiment 1 (who certainly can compute scalar implicatures) didn't reject Puppy's actions, suggesting that it is unlikely that, in this context, a mature language user would compute a scalar implicature at the moment of request. Similarly, in Experiment 2, children who didn't have access to contrasting linguistic labels accepted Puppy's actions the vast majority of the time; this pattern of performance is inconsistent with the possibility that children computed scalar implicatures at the moment of request. Had children computed a scalar implicature at the moment of request, they should have rejected Puppy's actions regardless of the modality in which they learned about his actions (linguistic vs. visual).Footnote 10 These data support the view that exclusion inferences – and not scalar implicature – were driving children's performance on our task.
We want to highlight that it is very unlikely that children in our task relied entirely on exclusion inferences. If children relied entirely on exclusion inferences, then we would expect that any time the request and fulfillment differed, participants would reject Puppy's actions and withhold a prize. This is not what we found – on some trials, children were essentially equally likely to give vs. withhold a prize.Footnote 11 Further, visual inspection of the data suggests that there may be differences in performance even across trials that provided linguistic contrast, and this would not be predicted if children relied solely on exclusion. For example, children may have treated requests containing numerals differently from requests containing quantifiers. Similarly, there is some suggestive evidence that other contextual factors shaped performance – for example, adults seemed more willing to accept Puppy's action when he washed too many shirts than when he ate too many lollipops, even though in both cases Puppy's actions entailed the initial request. Also, on some trials, performance appeared similar across ages four to six, while on other trials there appeared to be some developmental change. All of these observations, while tentative, suggest that, insofar as children relied on exclusion inferences, it is likely that they took other information into account too. We hope that future researchers will continue to study some of the tantalizing differences in performance across our trial types.
However, while it remains possible that some children used strategies not accounted for by exclusion inferences, we found no evidence that young children computed the sorts of asymmetric inferences that support scalar implicature. In other words, while our data are most consistent with the possibility of computing exclusion inferences, our data are incompatible with the view that young children computed adult-like scalar implicatures. While the results of this study do not show that young children, as a group, made use of asymmetric entailment relations to compute scalar implicatures, it is certainly possible that children may be able to compute entailment relations (and more specially, reason about entailment relations between all and some). There is some evidence that children can reason about asymmetric entailment (Chierchia et al., Reference Chierchia, Crain, Guasti, Gualmini, Meroni, Do, Domínguez and Johansen2001). More generally, our data do not suggest that young children can't compute scalar implicatures. Instead, our claim here is simply that it is critical to test whether children deploy their knowledge of asymmetric entailment in a task to be sure that they are indeed computing implicatures instead of exclusion inferences. The critical difference between implicature and exclusion inferences is not necessarily the form of the inference itself, but instead the nature of the alternatives and how they are represented by children in the service of this inference. In tasks like the those in Experiments 1 and 2, children do not appear to interpret alternative utterances according to their scalar relations, but instead assign all alternatives equal status, such that saying utterance A negates utterance B, regardless of whether one entails the other.
This last point is important to understanding the significance of our findings to the literature at large. A key difference between experiments which find early successes with implicature and those which find later successes is that the former studies tend to use forced choice paradigms that are similar to mutual exclusivity tasks, by presenting children with a set of salient alternative referents. According to some past reports, children's main difficulty with implicature computation is their ability to spontaneously access relevant alternatives – e.g., to access an utterance containing all when interpreting a sentence containing some (Barner et al., Reference Barner, Brooks and Bale2011; Chierchia et al., Reference Chierchia, Crain, Guasti, Gualmini, Meroni, Do, Domínguez and Johansen2001; Hochstein et al., Reference Hochstein, Bale, Fox and Barner2016; Skordos & Papafragou, Reference Skordos and Papafragou2016). Forced choice paradigms – and paradigms where the alternatives are visually salient – may help children appear to succeed on implicature tasks by providing them with a set of relevant alternative referents, which can be used by the child to generate linguistic alternatives. Consistent with this, adults are faster to compute implicatures in visual world paradigms when they can preview the visual referents before hearing the test sentence (Snedeker, Reference Snedeker2015). According to Snedeker, this suggests that such paradigms – and by extension forced choice paradigms like those used in recent tests of implicature in children – allow children to generate descriptions for different visual alternatives, and to then use these descriptions to compute inferences. In fact, infants as young as 18 months appear to also spontaneously conjure the referents of pictures upon viewing them, suggesting that even very young children can generate descriptions of visually presented alternatives (Mani & Plunkett, Reference Mani and Plunkett2010; for evidence in adults, see Meyer, Belke, Telling, & Humphreys, Reference Meyer, Belke, Telling and Humphreys2007; Meyer & Damian, Reference Meyer and Damian2007). How might this impact children's performance on scalar implicature tasks? Upon seeing a picture with “all of the socks” and another containing “some of the soccer balls” children may code the pictures with corresponding verbal descriptions, and use a relatively simple matching strategy to guide their looking at test – e.g., looking to the picture containing “some of the soccer balls” upon hearing some simply because it matches their prior expectation, without involving any appeal to the stronger alternative containing all. In this way, children may appear to succeed on scalar implicature tasks without needing to deploy any knowledge of asymmetric entailment. Once again, our data suggest that, by including trials that test scalar entailment, future researchers can rule out the possibility that performance on their task is driven by simple symmetric inferences (like exclusion inferences).
To summarize, we found that young children often compute symmetrical exclusion inferences rather than asymmetric scalar inferences when interpreting quantifiers. These data suggest that previous studies which report early success at computing scalar implicatures, which do not test children's knowledge of entailment relations, may overestimate young children's pragmatic knowledge.
Supplementary materials
For Supplementary materials for this paper, please visit <https://doi.10.1017/S0305000919000096>.
Acknowledgements
Thank you to Eleanor Chestnut, Jinsol Jung, and Ieva Razhas for help gathering and coding data, and to the staff and families at the Reuben H. Fleet Science Center for their collaboration. Thank you to the families who visited the lab to participate in this study, and to the numerous preschools who allowed us to participate. This work was supported by a Jacobs Graduate Fellowship and NSF Graduate Research Fellowship to JS, and by a James S. McDonnell Foundation grant to DB.