Introduction
In the early 1970s, China launched the so-called ‘later, longer, fewer’ population policy, because China's government viewed rapid population growth as an impediment to economic growth. In 1980, China issued An Open Letter to All Members of the Communist Party and Communist Youth League on the Issue of Controlling Population Growth, aimed at controlling the birth rate and population growth, boosting economic development, and improving living standards by adopting the one-child policy. China's one-child policy has been so successful in bringing down China's total fertility rate (TFR) that after a period of fluctuation around replacement level in the 1980s, the TFR dropped below replacement level in the 1990s. Analysis of the 2000 census reveals that by 2000 the total fertility rate of China had dropped to 1.4–1.6 (Gu et al., Reference Gu, Wang, Guo and Zhang2007; Morgan et al., Reference Morgan, Guo and Hayford2009; Cai, Reference Cai2010). The strict one-child policy of the past 30 years and the low fertility level exhibited in the past 20 years have had wide-ranging effects on China's economic and social development while simultaneously producing effects on population growth. These effects include a distorted sex ratio at birth within the context of strong preference for sons, resulting in a biased ratio between men and women and a biased ratio between adult children and dependent elderly parents (Hesketh et al., Reference Hesketh, Li and Zhu2005). In the mid-1980s, far-sighted demographers were already predicting that if the one-child policy were to achieve complete success, its subsequent side-effects would become much more serious (Bongaarts & Greenhalgh, Reference Bongaarts and Greenhalgh1985; Greenhalgh & Bongaarts, Reference Greenhalgh and Bongaarts1987).
One of the most important issues that some Chinese families face is that of the only child. In the years 1971 to 1975, it is estimated that 5.41% of female births and 6.45% of male births in urban areas, and 0.48% of female births and 1.06% of male births in rural areas, were of only children. In the years 1976 to 1980, these figures rose to 26.55%, 31.55%, 2.00% and 4.74% (Yang & Guo, Reference Yang and Guo2000). However, with the full implementation of China's birth control policy and the achievement of low fertility, the total number of only children has shown continuous and rapid growth. According to Wang (Reference Wang2011)'s estimate, there were 158.41 million only children aged 0 to 30 in 2005. Such a number implies that over 40% of Chinese households have only one child. Even if some families currently with a very young only child may have a second child in the future, it can be asserted that over a third of all Chinese households may well end up with only one child (Wang, Reference Wang2011).
The term ‘one-child family’ refers to a family that consists of the parents and an only child. Compared with a family that has two or more children, a family with one child faces a higher risk of becoming childless as a result of losing that child. Even though the child mortality rate is relatively low, considering the large number of one-child families, the families facing such risks of losing children cannot be ignored. In fact, the question of losing their child for one-child families aroused attention after the Wenchuan earthquake in 2008 in China (Gu & Cai, Reference Gu and Cai2009), in which a death toll of over 80,000 was estimated.
Accidents to children cause serious psychological trauma to relatives, and the influence of an accident to an only child is particularly significant for the whole family (Fenwick & Barresi, Reference Fenwick and Barresi1981). In general, government policies allow parents with an only child to give birth to another child if their child has a disease, disability or injury, or if he/she dies young. In fact, within China's localized one-child policy, provincial Birth Planning Regulations do take into account the possibility of losing a child. For example, in Jiangsu's Birth Planning Regulations, enacted in 1990, one exemption permitting a couple to have a second child is the death of the existing child (Cai, Reference Cai2010). However, if the only child has a disease, disability or injury, and dies as an adult, it is quite difficult to remedy the situation by giving birth again as parents are older and may no longer be fertile. Therefore, an adult only child's disability, injury or death is devastating for the parents (Pan & Jiang, Reference Pan and Jiang2007). On June 5th 2012, over 80 parents who had lost their only child gathered at the National Family and Birth Planning Commission of PRC expressing their vulnerability after losing their only child, and their hope for financial reimbursement from governments, and more importantly, the hope of establishing a corresponding department to which those who complied with the national family planning policy but now unfortunately had lost their only child could turn to when needed (http://news.ifeng.com/shendu/ndzk/detail_2012_07/17/16083719_0.shtml).
Studies concerning Chinese only children have mainly focused on their behaviour and psychology (Poston & Falbo, Reference Poston and Falbo1990; Falbo & Poston, Reference Falbo and Poston1993; Falbo et al., Reference Falbo, Soon and Poston2005). Generally speaking, only children are advantaged in academic skills, and disadvantaged in social skills (Falbo et al., Reference Falbo, Soon and Poston2005). But insufficient attention has been paid to the risk of child loss. Falbo & Poston (Reference Falbo and Poston1993) found that some only children do enjoy better nutrition and health advantages, but Mu (Reference Mu2009) found that the risk of losing only children and subsequently ending up with no children is much higher when compared with families with more than one child.
In this paper, using life-tables to analyse and estimate Chinese families' chances of losing their child and other relevant indicators, the aim is to provide a basis for the formulation of public policies concerning the death of the child in one-child families.
Methods
Generally fertility-related measures pertain to women, so it would be appropriate to consider losing a child from the point of view of a woman's life-cycle. In this article the mother's probability of losing a child is calculated; this can also be calculated by the father's probability of losing a child, which just requires changing the corresponding life-table in the formula.
Myers (Reference Myers1959) uses the life-table in his study to show the basic formula for calculating the probability of a male losing his spouse, but his calculation was based on the discrete age variable. Goldman & Lord (Reference Goldman and Lord1983) made some improvements on Myers' method, designing functions for measuring widowhood and related indicators with the continuous age variable and conditional probability. Keyfitz & Caswell (Reference Keyfitz and Caswell2005) introduced methods for analysing not only widowhood and related indicators, but also kinship relationships with life-tables. In this paper, drawing on the generality of Goldman & Lord (Reference Goldman and Lord1983) and Keyfitz & Caswell (Reference Keyfitz and Caswell2005)'s methods, formulae are designed to calculate the probability of the female losing a child. The following is a brief introduction to the formulae:
Let lm(t) and lf(t) represent the life-table probabilities of surviving from birth to exact age t, where superscripts m and f denote male and female, respectively. the terms μm(t) and μf(t) denote the corresponding risk of dying at age t, where μ(t)=−l′(t)/l(t). A female becomes a mother at the age x. It is assumed that a mother's survivorship is independent of that of the children; therefore the probability of losing a boy can be expressed as:
$$P^m_x = \vint ^w_0 {l^f (x+t) \over l^f (x)} {l^m (t) \over l^m (0) } \mu ^m (t)dt$$.
Here t is the length of time from birth to death; w is the upper age limit in the definite integral and it is assumed that the maximum age in the life-table is α, so w=α−x. The probability
$${l^f (x+t) \over l^f (X) } {l^m (t) \over l^m (0)} \mu ^m (t)$$is the probability of the boy's death after the mother and her son have both survived t years. It can be regarded as an age-specific probability of a mother losing her child.
When talking about a mother losing her child, this means an ‘average’ mother, without taking into consideration her age at childbirth. So the probabilities of a woman becoming a mother at age x are integrated, denoted by p(x), to get the ultimate probability of a mother losing her child:
$$P^m = \vint^w_0 \vint ^{n_x} _{m_x} {l^f (x+t) \over l^f (x) } {l^m (t) \over l^m (0) } \mu^m (t) p (x) dxdt$$, in which mx is the minimum age when a female becomes a mother and nx is the maximum age for becoming a mother. The term p(x) is the probability distribution of mothers with an only child and
$$\vint ^{n_x} _{m_x} p(x)dx = 1$$.
As far as the discrete age variable is concerned, p(x) is the proportion of women who are aged x at the birth of their only child. In formula (2), the term
$$\vint^{n_x}_{m_x} {l^{f} (x+t) \over l^{f}(x)} { l^m (t) \over l^m(0) } \mu^m (t) p (x)dx$$removes the effect on the probability of child loss as a result of mothers giving birth at different ages. The formula denotes the probability of a mother losing her child when the child is aged t after both the mother and her child have survived t years.
For a boy, the average age of his mother when the child is lost can be expressed as:
$$MA^m = { \displaystyle\vint^w_0 \vint ^{n_x}_{m_x} (x+t) \displaystyle{ l^{f} (x+t) \over l^{f} (x) } {l^{m} (t) \over l^{m} (0) } \mu^m (t) p(x)dxdt \over \displaystyle\vint^w_0 \vint ^{n_x} _{m_x} \displaystyle{l^{f} (x+t) \over l^{f} (x) } { l^{m} (t) \over l^{m} (0) } \mu^m (t) p (x)dxdt }$$.
The average number of years until a mother dies after losing her child, for a male, can be expressed as:
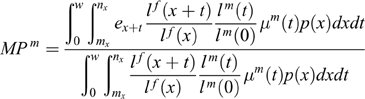$$MP^m = { \displaystyle\vint^w_0 \vint ^{n_x}_{m_x} e_{x+t} \displaystyle{ l^{f} (x+t) \over l^{f} (x) } {l^{m} (t) \over l^{m} (0) } \mu^m (t) p(x)dxdt \over \displaystyle\vint^w_0 \vint ^{n_x} _{m_x} \displaystyle{l^{f} (x+t) \over l^{f} (x) } { l^{m} (t) \over l^{m} (0) } \mu^m (t) p (x)dxdt }$$, where e x+t represents the remaining life expectancy at age x+t for females.
The formulae (2), (3) and (4) remove the age effect when a woman becomes a mother on the child loss indicator. If the corresponding indicators for a group when they become mothers at the age of x are examined, the formula (2) can be simplified into the formula (1) and the formulae (3) and (4) into the following formulae (5) and (6):
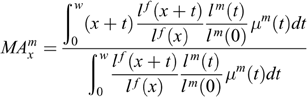$$MA^m_x = { \displaystyle\vint^w_0 (x+t) \displaystyle{ l^{f} (x+t) \over l^{f} (x) } {l^{m} (t) \over l^{m} (0) } \mu^m (t) dt \over \displaystyle\vint^w_0 \displaystyle{l^{f} (x+t) \over l^{f} (x) } { l^{m} (t) \over l^{m} (0) } \mu^m (t) dt }$$
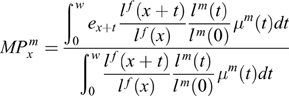$$MP^m_x = { \displaystyle\vint^w_0 e_{x+t} \displaystyle{ l^{f} (x+t) \over l^{f} (x) } {l^{m} (t) \over l^{m} (0) } \mu^m (t) dt \over \displaystyle\vint^w_0 \displaystyle{l^{f} (x+t) \over l^{f} (x) } { l^{m} (t) \over l^{m} (0) } \mu^m (t) dt }$$.
The above formulae apply only to the loss of a son. If it is a girl, only the child data need to be changed. For example, lm(t) and μm(t) can simply be replaced with lf(t) and μf(t).
Data
From the above it can be seen that the main data used in the article will be the life-tables and ages at childbirth, which come from China's 2000 population census. The life-tables are based on this census which was, generally speaking, judged successful but nevertheless suffered from a serious problem, namely that the rate of under-reporting is 1.81%. Although this rate is acceptable according to international standards, it is much higher than the 0.06% under-reporting rate in the 1990 population census (Lavely, Reference Lavely2001; Walfish, Reference Walfish2001). Population deaths in the census indicate the number of people who died between 1st November 1999 and 31st October 2000. The data on the death rate are also questionable because of under-reporting of death data (Li & Sun, Reference Li and Sun2003).
It is quite important to select life-tables in the study. Banister & Hill (Reference Banister and Hill2004) provided life-tables in their study, but these were only for the total population, not for urban and rural populations. Li et al. (Reference Li, Sun and Jiang2005) analysed the undercounting of deaths, adjusted the data in China's 2000 census and presented life-tables for total, city, town and rural population by sex, which are used here. Life expectancies for people by residence are shown in Table 1.
Table 1. Life expectancies at birth by residence, 2000 census, China
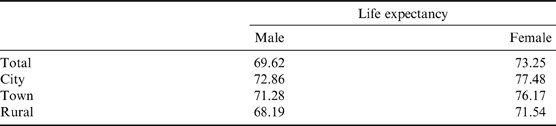
Data source: Li et al. (Reference Li, Sun and Jiang2005).
It should be pointed out that since only children are being studying, in actual fact first-order births, it would be better if life-tables were assumed for first-order-birth people. However, due to limited data, it was not possible to obtain such life-tables on first births.
China's legal minimum age for marriage is 22 years for males and 20 years for females. The 2000 census reveals that the average childbearing age is 24.83 if the childbearing age range falls between 15 and 49. The number of first births of mothers who are aged 20–29 years accounts for 91.2% of the total number of such births. The average childbearing age in this age group is 24.54. This article confines the national childbearing age to the 20–29 age group. The term p(x) is the percentage of first births for females at the age of x of the total number of children born to mothers aged 20–29 years. The average childbearing age in cities is 26.13, if the childbearing age is limited to between 15 and 49. The number of children born to females aged 21–30 years accounts for 90.3% of the total number of first births. The average childbearing age for this age group is 25.78. As far as the town group is concerned, the number of children born to females aged 20–29 accounts for 92.19% of all first-order births, and the average age at childbirth of this age group is 24.26 years, and the age for all mothers giving first birth is 24.61. The average childbearing age in the countryside is 24.24, if the traditional concept of the childbearing age falls between 15 and 49. The number of children born to the population aged 19–28 years accounts for 92.16% of the total number of first births. The average childbearing age is 23.84.
For the purpose of calculation convenience, this article limits the national childbearing age to the 20–29 age group. The term p(x) is the percentage of first child births for females at the age of x of the total number of children born to mothers aged between 20 and 29 years, and these percentages are normalized as:
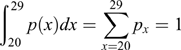$$\vint^{\hskip1 29}_{20} p(x)dx = \sum^{29} _{x=20} p_x = 1$$.
There is a large discrepancy between rural and urban areas in China when it comes to childbearing, particularly in terms of birth number and timing. Generally, urban females give birth later in life than their rural counterparts. In this paper, childbearing age is limited to the range of 21–30 for cities, 20–29 for towns and 19–28 for rural areas.
Results
Age-specific probability of losing a child
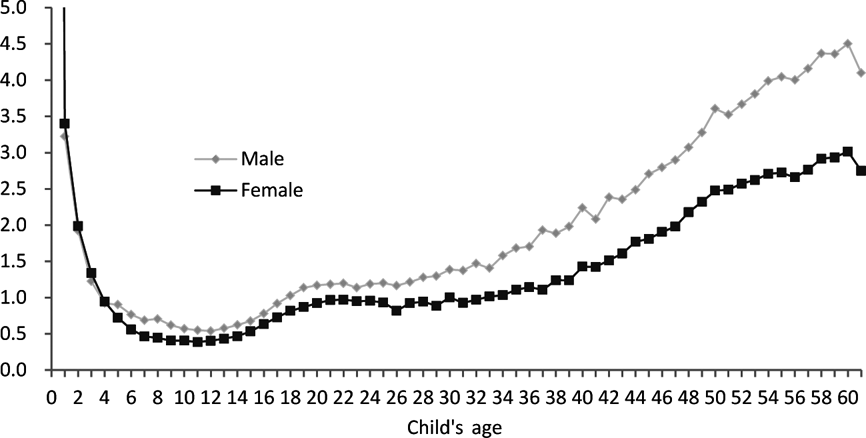
Figure 1 shows the age-specific probabilities of losing a child for a mother by age and sex of the child (as the probabilities of losing a child between birth and the age of one are too large to be reflected in Fig. 1, they are omitted from this figure, but Fig. 2 can be taken as a reference). In the curve of the child's age from 0 and 4, the age-specific probability of losing a girl is higher than that for a boy. In a normal population without sex discrimination, biomedical factors are the main elements determining sex differentials in mortality levels in infancy and early childhood (0–4 years old). There should be a normal level of ratio of the mortality rate for boys to that of girls (usually greater than 1), which reflects the biological sex differences in children's mortality rates. Hill & Upchurch's (Reference Hill and Upchurch1995) study, and Coale & Demeny's Western model life-tables (Coale & Demeny, Reference Coale and Demeny1966) all show that the mortality rate for boys is higher than that for girls. But in China, the gender pattern of infant mortality is significantly different. From Li et al.'s (Reference Li, Sun and Jiang2005) life-table, the male infant mortality rate is 28.14 per thousand and that of females is 35.51 per thousand. Banister & Hill (Reference Banister and Hill2004) found a similar pattern and estimated that in 2000, China's infant mortality rate for males was 22.66 per thousand and for females 33.51 per thousand. Several studies indicated that in China, the female mortality rate between 1 and 4 years of age is 10% higher than the male mortality rate for this age range, and the discrepancy is more obvious in the higher birth orders, reaching 15%. In particular, for higher-birth-order children who were born in rural areas and who have elder brothers and sisters, the discrepancy surprisingly reaches 25%. In other words, if parents in a rural area who already have both a son and a daughter give birth to a girl, the probability of the girl's death is 50% higher than that of a boy (Choe et al., Reference Choe, Hao and Wang1995). This excessive female child mortality is fundamentally caused by the strong preference for sons in traditional Chinese culture and exacerbated by the government-guided family planning programme and regulations (Li et al., Reference Li, Zhu and Feldman2004). Accordingly, these factors usually result in discrimination against girls in socioeconomic and health-related behavioural and environmental factors, such as nutrition, food and health care (Hill & Upchurch, Reference Hill and Upchurch1995; Li et al., Reference Li, Zhu and Feldman2004). Girls who have died from deliberate neglect (also referred to as active or passive infanticide) may be different from those who have died of causes beyond the control of their parents, but their deaths have still resulted in trauma to their parents and relatives.
Fig. 1. Probability of mothers losing a child by age and sex of the child (per thousand).
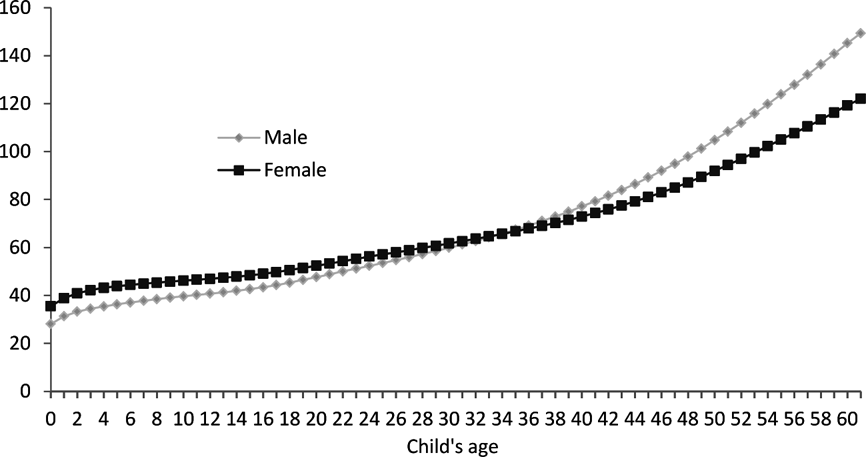
Fig. 2. Cumulative probability of mothers losing a child by age and sex of the child (per thousand).
Biologically, females have a survival advantage over males at the same age. In Fig. 1, this advantage begins to show after the child is 4 years old, as age-specific child-losing probability for a female child is lower than that for a male child. From Fig. 1, for the most of the curve, if the child is a boy, the mother faces a greater likelihood of the child's death. In usual situations, the age-specific death rate of males is higher than that of females, and this is reflected in most of the curve in Fig. 1.
It can be seen that the age-specific probability of a mother losing her child decreases for boys aged 0–12 years as well as for girls aged 0–11 years before it gradually increases. When a child reaches the age of 20, the age-specific probability of a mother losing a child is 1.17 per thousand for boys and 0.92 per thousand for girls. When a child reaches the age of 40, the age-specific probability of a mother losing a child is 2.24 per thousand for boys and 1.43 per thousand for girls.
Cumulative probability of losing a child
Figure 2 shows the cumulative probability of losing a child for a mother by age and sex of the child. Eventually the risk of losing a male child for a mother is 14.94%, while that for a female child is 12.21%. Before the child's age of 36, the cumulative probability of losing a girl is higher than that of losing a boy, which results from the huge discrepancy when the child is 0–4 years old. After the child's age of 36, the cumulative probability of losing a boy is higher than that of losing a girl. At the child's age of 30, the cumulative probabilities are 59.92 per thousand and 61.73 per thousand for a male and female child respectively. At the age of 40, the probabilities rise to 77.17 per thousand and 72.94 per thousand. At the age of 50, the probabilities increase to 104.83 per thousand and 91.93 per thousand.
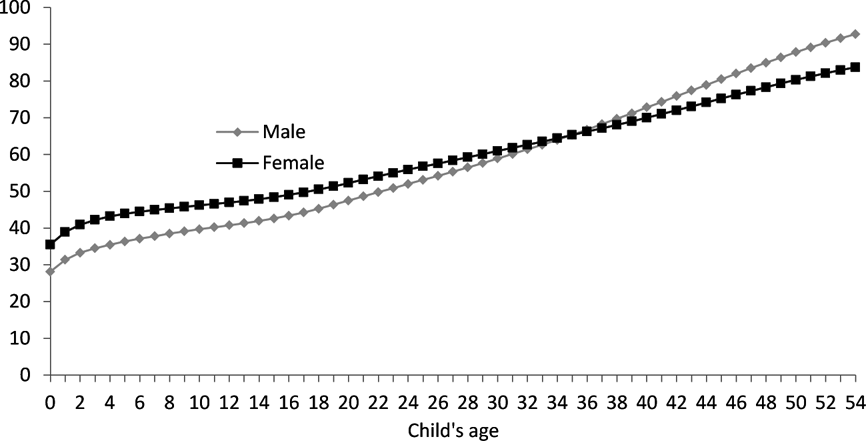
If a mother loses a child at younger age, say when the child is below 20 and she herself is in her 40s, she may have a chance of having another biological child. But if she loses the child when the child is over 20, she may lose such replacement chance. Figure 3 shows the cumulative probabilities for mothers who begin their motherhood at 36. It can be seen that these cumulative probabilities are lower than are those in Fig. 2.
Fig. 3. Cumulative probability of losing a child for mothers aged 36 years by age and sex of the child (per thousand).
Sensitivity analysis of effect of the age at which motherhood begins on indices
As Table 2 shows, the age at which a female becomes a mother has an influence on the indices of losing a child. During the increase of this age from 20 to 36, the probability of losing a boy falls from 16.61% to 9.27%, and the probability of losing a girl falls from 13.34% to 8.37%. However, the change in the age at which a female becomes a mother has little effect on the average age of losing a child and the average years spent until a mother dies after losing her child.
Table 2. Effect of mother's age at childbirth on indices of child loss, 2000 census, China
The total is derived using formulae (2), (3) and (4); the others are derived using formulae (1), (5) and (6).
Formula (1) reveals that when a mother's age increases from a relatively young age (e.g. 20 years old), w, the upper age limit in the definite integral, which is defined as w=α−x, decreases such that the cumulative probability of losing a child usually decreases. This finding still implies that as the age at childbearing increases, the risk of the mother dying before the child increases (as the probability of a mother predeceasing her child is the complementary probability of Pmx defined in formula (1)).
As for the difference in the mean age of the mother at the times of loss of a boy and a girl, it can be seen from formula (5) that the age at child loss is actually a weighted average of x+t, and the weights are:
$${l^{f} (x+t) \over l^{f} (x) } { l^{m} (t) \over l^{m} (0) } \mu^m (t) \hbox {\curr \ for a boy, and}$$
$${l^{f} (x+t) \over l^{f} (x) } { l^{f} (t) \over l^{f} (0) } \mu^f (t) \hbox {\curr \ for a girl}$$.
From the discussion above, it is known that female children have excessive mortality rates compared with those of their male counterparts; therefore, the higher proportion of girls who die at very young ages when their mothers are still very young depresses the mean age of mothers at the loss a female child.
Formula (5) still reveals that the child loss age can be attributed to a combination of several factors: the age-specific probability of losing a child, a mother's age x and the cumulative probability of losing a child. For a male child, the age for a mother at child loss does not change significantly with an increase in age at motherhood.
Rural–urban difference in child loss indices
With the implementation of China's family planning policy, there are more and more only children in urban and rural areas. There is a big difference between urban and rural areas in terms of social and economic development, as well as in the allocation of health resources (Zhang & Kanbur, Reference Zhang and Kanbur2005). In 2010, the gap in per capita disposable income between urban and rural areas was 3.23 to 1, making it one of the largest urban–rural gaps worldwide (Wang & Zhu, Reference Wang and Zhu2011). The large gap between urban and rural areas leads to different health results and mortality rates, with the rural population being at a great disadvantage. Table 3 shows the difference in indices of the loss of children between cities, towns and rural areas. Mothers in rural areas have a much higher risk of losing a child than their counterparts in towns and cities, and their average age when losing a child is lower than that for urban mothers. But due to their shorter life expectancy at birth, observed in Table 3, the remaining life expectancy for mothers from rural areas after the death of their only child is almost the same as that of their urban counterparts.
Table 3. Urban–rural difference in indices of child loss, China
Data are derived using formulae (2), (3) and (4).
Discussion
Because of the increase in the proportion and total number of one-child families, Chinese society as a whole has become concerned about the growth and development of only children, as well as related phenomena and problems concerning them, and only-child and related issues are receiving more and more attention from researchers. Once there is an accident to the only child, it affects the economic interests of family members, threatens the safety of family property and also affects the family culture, genetic heritage and also, to some degree, harms the emotions dependent on blood and marriage (Pan & Jiang, Reference Pan and Jiang2007). If the child dies at an early age when the parents are still young, they can have another child in compensation. However, if the parents are older when the child dies, it is more difficult to have another child. One-child families are more afraid of losing a child later in their life-cycle. The survival risks that appear in the early life-cycle can be dispelled by compensatory fertility, but survival risks that appear in the later stages of the life-cycle mean the possibility of compensatory fertility is lost because the parents are older. The loss of a child in middle-age would fully affect the material and emotional life of one-child families.
Through the above analysis, the main findings are as follows. Firstly, because of the preference for sons in China, there is a higher probability of girls' mortality than that of boys during infancy. Therefore, the mother's age-specific probability of losing a girl is higher than that of losing a boy when the children are 0–4 years old. But after the age of 5, the age-specific probability of losing a son is higher than that of losing a daughter. Secondly, the cumulative probability of losing a child increases as the age of the child increases. At the child's age of 30, the cumulative probabilities are 59.92 per thousand and 61.73 per thousand for a male and female child respectively. At the age of 40, the probabilities rise to 77.17 per thousand and 72.94 per thousand. The probability of losing a child (a son or a daughter), namely the cumulative probability of children dying before their parents, is 14.94% for a son and 12.21% for a daughter. Thirdly, it can be seen that with the increase in the age at childbirth, the cumulative probability of losing a child declines, and the average age at losing a child first increases and then declines, but generally the average age at losing a child does not change much, nor do the years survived after losing a child. Finally, there is also a difference between the probability of losing a child in urban and rural areas. The risk of losing a child in rural areas is higher than in urban areas, and the average age at which mothers lose their child is lower. Still, as the age range at childbirth is the same for the population in towns as it is for the total population, and the population in towns enjoys a lower mortality level and higher life expectancy, it can be seen that as the mortality level decreases, the probability of losing a child also decreases, and the age at child loss increases.
One may be concerned with the years survived for a woman after she loses her only child. For only-child families, a woman's family members include her husband and her son. The average age at losing an only son for a woman is 56.56 years, and that for losing an only daughter is 51.30 years. Let us examine the probability of losing her husband. According to Jiang et al. (Reference Jiang, Li and Sánchez-Barricarte2012)'s study, a woman at age 60 faces the cumulative probability of 0.2 of losing her husband, and at 70 she faces a probability of 0.4. So after losing her child, she has a probability of 0.8 of living with her husband (without taking into account divorce or separation), and at age 70 there is a 60% possibly of living with her husband.
One may argue that even if a woman has more than one child, she still faces the probability of losing children. But she will undeniably face a much lower probability of having no children. From Fig. 2 it can be seen that when the child is 30, the cumulative probability of losing a child is 6%. But if a woman has two children, then at the children's age 30, the probability of having no children for a woman is less than 3.6 per thousand. It is roughly estimated that the probability of having one child is 0.94, and that of having two children is two independent events, thus the probability of having no children is 1−(0.94+0.94−0.94×0.94).
The paper does have some drawbacks that may affect the study's results. One is the assumption of the independence of mother's and child's mortality. It is in fact known that hereditary and socioeconomic factors make children's life expectancy correlated with that of their mothers, and that the loss of a relative induces stress in individuals, thereby harming their health. However, due to the lack of life-tables for people who have lost their child, life-tables had to be used without distinguishing whether the population used to calculate them had lost their child or not. Also, childbearing age was limited to a small range around peak childbearing age; this lowers the age at childbearing, and will lower the cumulative probability of losing a child.
As the proportion and number of one-child families is increasing, some scholars have analysed the feelings of parents of only children towards the child's safety. If a car accident happens on a bustling city street, and the injured person is a child, when the parents of an only child hear such news, they normally show anxiety and agitation, and cannot control their emotions. Even if their child is not hurt, they will have feelings of insecurity with some kinds of external stimuli (Lin & Zhang, Reference Lin and Zhang2001). This sense of insecurity in the context of Chinese culture will become especially strong because the death of offspring is the most unacceptable thing in the tradition of ‘family first’. The fear of remaining childless makes ‘incomplete’ family-planning families caused by the death of the only child hold a grudge against society, as they attribute their childlessness to the one-child policy (Mu, Reference Mu2009). As many elderly people depend on their adult children for old-age support, being without a surviving child will certainly leave those child-losing parents in a dilemma in their old age. In fact, the Chinese government has paid attention to the issue of old-age support and the other needs of such parents. In China's 11th Five-Year Guidelines for National Economy and Social Development released in 2006, it is stated that a support system should be established for those only-child families whose only child dies or is disabled. And in the Law of the People's Republic of China on Population and Family Planning, it is stipulated that local governments should assist those parents whose only child is dead or disabled, on the condition that those parents are to give up a second birth and do not adopt a child (Huang, Reference Huang2009). But the assistance obtained from local governments is far from enough. There have been some family-planning families who have demanded compensation from the government, due to their loss of an only child. If the resentment cannot be resolved, and the compensation requests cannot be met and satisfied quickly, this will pose a threat to social harmony and stability (Mu, Reference Mu2009).
The one-child policy, which has been widely criticized around the world and has damaged China's international image (Zeng, Reference Zeng2007), is perhaps the most ambitious family planning policy in the world. The current fertility policy requires about 63% of families having only one child (Gu et al., Reference Gu, Wang, Guo and Zhang2007). In the 2009 World Population Data Sheet offered by the USA Population Reference Bureau, China's total fertility rate was 1.6, while some scholars estimate that it is currently between 1.4 and 1.6, and it may drop to 1.4 in 2020 (Morgan et al., Reference Morgan, Guo and Hayford2009). The preliminary results of China's latest census in 2010 indicate an approximate but low fertility rate, below 1.5 (Hvistendahl, Reference Hvistendahl2011). Although China is not yet ready to give up its current birth control policy, there are more and more appeals for its relaxation or even termination. The primary functions and powers of China's National People's Congress (NPC), the highest organ of state power of the People's Republic of China, include formulation of laws, delegating authority, policy formulation and supervision of other governing organs. During meetings between the NPC and CPPCC (Chinese People's Political Consultative Conference, a political advisory body in the People's Republic of China) in March 2011, scholars and many deputies of the two organizations debated the one-child policy and consequently aroused considerable controversy in Chinese society. Administrative control of personal decisions about fertility has generated, and will continue to generate, an increasing array of problems, and now the policy faces severe challenges (Peng, Reference Peng2011). Less-restrictive policies are realistic alternatives whose consequences are likely to be socially and economically positive for the nation. In the 1980 Open Letter, it was stated that the one-child policy was for one generation. Now, after 30 years of strict implementation, it is time to consider adjusting the policy.
Acknowledgments
This work was supported by the 985-3 Project of Xi'an Jiaotong University, and the Fundamental Research Funds for the Central Universities. It was also supported by the Spanish Ministry of Economy and Competitiveness (CSO2012-31206).
