Introduction
In recent decades and in many populations, motherhood has been increasingly postponed much later into the life course. Postponement raises the issue of fertility postponed versus fertility foregone. As women's ability to bear children declines with age, a question for many childless women is ‘How late can you wait?’ (Menken, Reference Menken1985). At what age does the decline in fecundability substantially increase the probability of remaining childless? Therefore, the age pattern of fecundability and primary sterility is of substantial recent interest, especially after age 30.
As fecundability and sterility are, in general, not directly observable, estimates are typically based on statistical models relating fecundability to the waiting time to conception. For each menstrual cycle, the observed outcome (1=conception, 0=non-conception) can be modelled as a Bernoulli random variable with the probability of success (conception) parameter, i.e. the fecundability, a function of cycle-specific characteristics, subject-specific characteristics and the number and timing of acts of intercourse relative to day of ovulation.
Most studies of the age patterns of fecundability and sterility have suffered from one or more of the following limitations: (1) use of aggregate versus individual-level data; (2) use of months or continuous time rather than menstrual cycles as the unit of analysis; (3) use of retrospectively collected birth or pregnancy histories; (4) use of live births rather than recognizable conceptions; and (5) lack of information on the number and timing of acts of intercourse within the menstrual cycle relative to day of ovulation. The Menstrual Cycle Fecundability Study (MCFS) data analysed in this study does not have these limitations (Colombo & Masarotto, Reference Colombo and Masarotto2000). Healthy subjects in the MCFS prospectively recorded daily menstrual bleeding, basal body temperature and cervical mucus quality, so that for each menstrual cycle the day of ovulation could be estimated using either of these surrogate markers of ovulation and the occurrence of a clinical pregnancy determined. Women also recorded daily every episode of sexual intercourse.
The MCFS data have been used to study various aspects of fecundability, infertility and sterility (Dunson et al., Reference Dunson, Colombo and Baird2002, Reference Dunson, Baird and Colombo2004). In this study, only MCFS data from nulliparous women are used in order to estimate the age patterns of conditional fecundability and primary sterility for childless women, while controlling for the pattern of intercourse in each menstrual cycle relative to the estimated day of ovulation based on cervical mucus quality. The analysis is based on a two-population (fecund, sterile) mixture model that simultaneously combines a discrete-time hazard model of waiting time to first conception for those fecund with a logistic regression model for primary sterility (McDonald & Rosina, Reference McDonald and Rosina2001).
Methods
The Menstrual Cycle Fecundability Study
The Menstrual Cycle Fecundability Study (MCFS) was a multinational longitudinal study conducted to determine the daily probability of conception relative to ovulation (Colombo & Masarotto, Reference Colombo and Masarotto2000). From 1992 to 1996, healthy women were recruited from seven European centres (Milan, Verona, Lugano, Paris, Dusseldorf, London and Brussels) providing services on fertility awareness and natural family planning to participate in the study. The entry criteria for women were: experienced in the use of a natural family planning method of contraception; married or in a stable relationship; between 18 and 40 years old at entry into the study; had at least one menses since last breast-feeding or delivery; and did not currently use hormonal treatment, or another treatment with effects on fecundability. Neither partner could be permanently infertile and both had to be free from any illness that might cause sub-fertility. The protocol also required that couples did not mix incidences of unprotected and protected intercourse, e.g. use of barrier methods or withdrawal, in a given cycle.
While the MCFS is rich in information about the timing and frequency of intercourse and cycle characteristics, there is only limited information about the characteristics of couples enrolled in the study. At entry, information was collected on: the month and year of birth of the woman and her partner; the number of previous pregnancies, if any; the date of her last delivery (or miscarriage) and of the end of breast-feeding, if relevant; and the date of last oral contraceptive pill taken, if any. After entry, date of marriage was collected from married couples.
During the study, for each menstrual cycle, various characteristics of the cycle (basal body temperature, cervical mucus quality) were recorded daily, together with information on menstrual bleeding for each day. Women were asked to record every episode of sexual intercourse, specifying if it was unprotected intercourse or protected. Cycles in which even a single act of protected intercourse or simple genital contact occurred were excluded from the MCFS dataset used for the analysis. The reliability of the information recorded on acts of intercourse was checked by the natural family planning teacher, in discussion with the subjects at the end of each menstrual cycle. The importance of continuing to keep the record chart when subjects were trying to conceive was emphasized. Further details on the research protocol, study methods and participants can be found in Colombo & Masarotto (Reference Colombo and Masarotto2000), along with an example of a completed menstrual cycle record chart.
Information on both reproductive physiology and sexual behaviour was collected for 881 women, 7017 menstrual cycles and 575 pregnancies. The number of subjects and contributed cycles varied markedly between study centres. Most women (93.7%) contributed fewer than twelve cycles of exposure. Although the Lugano centre enrolled mostly couples planning a pregnancy, most couples were trying to avoid pregnancy initially (although intentions can and did change during follow-up). The average age of women in the study population was close to 29 years and was relatively similar at each study centre. The median number of recorded acts of intercourse was six in the conception cycles and four in the non-conception cycles. Other descriptive statistics, such as the intercourse pattern by age, can be found in Colombo & Masarotto (Reference Colombo and Masarotto2000), but note that these statistics are for all couples, not just nulliparous women.
In this study, only menstrual cycles with peak mucus day identified are considered. This conventional marker of ovulation was identified locally in each study centre from daily records of cervical mucus symptoms in each cycle and the timing of intercourse is relative to this surrogate marker of ovulation, which is referred to as day 0 (mucus reference day).
The first five cycles just after stopping the contraceptive pill were excluded due to concerns that recent previous pill use may result in a short-term reduction in fecundability (the number of such cycles excluded was small as only 6.7% of the participants were pill users before entry into the study). The data used were limited to European centres participating in the MCFS, excluding data from New Zealand (two women with two pregnancies). In order to try to answer the question ‘Can women wait until their early thirties to try for a first birth?’, only waiting times to conception for nulliparous women between 20 and 36 years of age, whose husband/partner is aged less than 40 was studied, because there were too few first pregnancies after age 36. Only menstrual cycles with at least one intercourse in the 12-day interval (−8, 3) were used in the analysis. This interval of potential fertility was chosen so as to include the fertile window, i.e. those days during which intercourse has a non-zero probability of resulting in conception. Note that no pregnancies occurred when intercourse only occurred outside of this 12-day interval. Further details on how this 12-day interval of potential fertility was chosen are given in Colombo & Masarotto (Reference Colombo and Masarotto2000, Section 2.5, second paragraph).
Table 1 presents the number of couples, menstrual cycles and pregnancies after applying the successive selection criteria used. The last row is the analytic sample. It consists of 342 nulliparous women, 1595 menstrual cycles and 210 women (61.4%) who obtained a first pregnancy during the study (uncensored observations on time to first pregnancy and non-sterile couples) and 132 women who did not conceive (censored observations on time to first pregnancy and some of these couples may be sterile). Note that for many couples the number of cycles was often too small to provide much information about the probability that the couple was sterile. This is not a problem for the modelling approach chosen, but would be a problem for analysts trying to exclude sterile couples from the dataset analysed.
Table 1. Number of couples, menstrual cycles and pregnancies after applying successive selection criteria

The last row is the analytic sample.
a Woman's age at first entry and first observed cycle.
b Partner's age at woman's first entry and first observed cycle.
c Only cycles with at least one intercourse in the 12-day interval (−8, 3).
Table 2 presents the estimated probability of conception for women aged <24, 24–27, 28–31 and 32+, where each woman contributes at least one cycle in the age group and age is age at the beginning of the cycle. A traditional estimate of fecundability is based on observation done on a population during a fixed period of time. The MCFS is a mixture of observations done on subjects remaining under observation for variable periods of time. And there are further complications, since there are re-entries and, besides that, each entry is sometimes made of pieces of information given by the same unit (as happens when the sequence of cycles is interrupted because of exclusion of cycles, or simply when charts are missing informing on cycles, as it happens when one of the partners is away from home). For these reasons, a simple table of fecundability by age estimated in traditional fashion is not provided. Instead, this estimated probability of conception as a crude measure of fecundability is provided.
Table 2. Probability of conception by age of woman
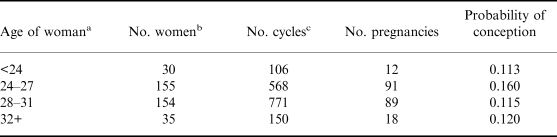
a Age at the first day of the menstrual cycle.
b Thirty-two women are counted more than once because of their having cycles in more than one age group; as a consequence, the total of column 2 differs from the figure of 342 couples given in the last row of Table 1.
c At least one menstrual cycle in the age group.
Mixture model for waiting time to conception with long-term survivors
The analysis is based on a two-population (fecund, sterile) mixture model that combines a discrete-time survival model incorporating unobserved heterogeneity in the risk of first conception for those fecund with a logistic regression model for the probability of being in the sterile subpopulation. The use of a survival model with long-term survivors (sterile subpopulation) explicitly allows for the possibility that some women have zero risk of conception.
The analysis is based on a ‘sterility/conditional fecundability’ mixture model that simultaneously combines a discrete-time hazard model for the cycle-specific probability of first conception with a logistic regression model for primary sterility (McDonald & Rosina, Reference McDonald and Rosina2001). The discrete-time survival model is used to model the sequence of menstrual cycles for each woman, where there is a positive probability of conception (non-sterile couple exposed to the risk of pregnancy in that cycle, i.e. at least one intercourse in the interval (−8, 3) relative to mucus reference day 0). Each cycle with positive exposure to the risk of conception is considered a discrete-time point. This may be conceptualized as the waiting time to conception for cycles with a positive probability of conception. The event of interest for each cycle is first conception, i.e. first clinical pregnancy.
In this study, the effect of age of woman on conditional fecundability is investigated, while simultaneously controlling for the effect of primary sterility, coital pattern and age of the male partner. Primary interest is in estimating the effect of age of woman, net of the coital pattern, rather than modelling the day-specific pregnancy probabilities and how these depend on the coital pattern. Therefore, the model used specified the effects of the coital pattern on the probability of conception differently from Dunson et al. (Reference Dunson, Colombo and Baird2002, Reference Dunson, Baird and Colombo2004) by defining three windows relative to day 0 and the presence or absence of intercourse on a day in each window.
The effect of age of woman is modelled using a cubic spline, in order to model the age pattern of fecundability in a smooth flexible non-parametric manner. Cubic splines do have a drawback in that they can behave poorly in the tails, i.e. before the first knot and after the last knot, especially when there are few observations in the tails. To avoid artificial end effects, constraints on the behaviour of the spline in thetails are added, e.g. one common constraint is that all the fitted values before the first knot and after the last knot are linear. With these constraints, one has restricted cubic splines (also termed natural splines), which constrain the function to be linear in the tails (for further details, see Harrell, Reference Harrell2001, pp. 20–24). As the ages of the couple are strongly correlated, to minimize potential multicollinearity problems, the effect of age of the man is simply specified with a dummy variable: <35 and 35+. Parameters for study centre are included in the model (the reference category is Verona). The ‘coital pattern and frequency’ is modelled by defining high (A), medium (B) and low (C) risk windows in the 12-day period of potential fertility and five categories, where ‘yes’ and ‘no’ refer to the presence or absence of intercourse on a day in the window: (1) 2+ acts of intercourse in A (reference category); (2) only one act of intercourse in A; (3) A no, B yes, C yes; (4) A no, B yes, C no; and (5) A no, B no, C yes. The classification of the 12-day interval of potential fertility into three windows relative to the conventional marker of ovulation (day 0): A (−2, −1, 0), B (−4, −3, 1) and C (−8, −7, −6, −5, 2, 3) was done using the daily fecundability estimates (with mucus reference day) presented in Colombo & Masarotto (Reference Colombo and Masarotto2000, Table 10). The 12 days were grouped into contiguous days on either side of window A on the basis of the estimated level of fecundability for each day based on the Schwartz et al. (Reference Schwartz, MacDonald and Heuchel1980) model.
Many couples were avoiding pregnancy, i.e. avoiders, in most cycles as in almost 50% of the cycles there were no acts of intercourse in the 12-day window of potential fertility. Fertility intentions of couples could and do change during the study (most couples don't want to remain childless their whole lives). In the dataset analysed, only cycles with at least one act of intercourse in the fertile window (−8, 3) were used. Many of the cycles in this study correspond to cycles where the couple are presumably trying to achieve pregnancy, i.e. achievers (plus some risky avoiders), given the concentration of intercourse near ovulation. Table 3 presents the percentage distribution of coital patterns for women of all ages, as well as those aged <24, 24–27, 28–31 and 32+. Table 3 shows that in almost 50% of the cycles there was at least one act of intercourse in window A, the 3-day period with the highest risk of conception, and the proportion of couples concentrating their intercourse near ovulation increases with age. Presumably older women concentrate more acts of intercourse in window A than younger women due to a desire to have a child.
Table 3. Percentage distribution of coital patterns by age of womana

a Age at the first day of the menstrual cycle.
b Window A includes days (−2, −1, 0), window B includes days (−4, −3, 1) and window C includes days (−8, −7, −6, −5, 2, 3) relative to day 0 (mucus reference day).
Model for the waiting time to conception
Let T denote the waiting time to first conception for fecund couples, i.e. the number of menstrual cycles until first conception (for cycles with intercourse in the fertile window). The geometric distribution results when the discrete-time hazard, pr(T=t|T≥t), is constant over time. Fitting a constant hazard model, with possibly censored data, by maximum likelihood estimation is straightforward using software for fitting logistic regression models to binomial distributed data. Letting the constant hazard vary from individual to individual on the basis of observed heterogeneity (covariate information) is also straightforward (McDonald & Rosina, Reference McDonald and Rosina2001). One approach to incorporating unobserved heterogeneity in this time-constant discrete-time hazard model is by using a logistic-normal-geometric model for survival times. The logistic-normal-geometric model is a ‘mixed-geometric’ random effects model which allows for unobserved heterogeneity in the hazard across the population. It uses a logit link relating the hazard to explanatory variables and includes a normally distributed random effect term, which incorporates unobserved heterogeneity into the survival model. For details, see McDonald & Rosina (Reference McDonald and Rosina2001).
The survival component of the mixture model uses a logistic-normal-geometric model for the waiting time to first conception. Time starts at entry into the MCFS study. The survival model includes a restricted cubic spline of age, s(age), and other covariates, X, and regression effects, γ, and a random effect, Zσ, representing unobserved heterogeneity in the risk of conception, i.e.:
where Z ∼ N(0, 1). The effect of age of woman is modelled by using a restricted cubic spline with knots at ages 24, 28 and 32 years. For standard hypothesis testing, the number and location of the knots must be specified in advance. Stone (Reference Stone1986) found that in a restricted cubic spline model: (1) the location of the knots is not very crucial in most situations and (2) more than five knots are seldom required. So the decision in practice is between using three, four or five knots. For most purposes, Durrleman & Simon (Reference Durrleman and Simon1989) recommended using three knots. The spline used included three equally spaced knots for simplicity and the belief that such a restricted cubic spline could model any curvilinear effects of age of woman on fecundability with sufficient flexibility over an age range of less than 20 years. This spline is a linear polynomial before age 24, a cubic polynomial between ages 24 and 28, a cubic polynomial between ages 28 and 32 and a linear polynomial after age 32, where all polynomials are joined smoothly. A restricted cubic spline with knots at ages 24, 28 and 32 years can be written as:
where δ( ) is an indicator function, equal to 1 if the argument is positive and 0 otherwise, and k 1, k 2, k 3 are the spline knot parameters at ages 24, 28 and 32 respectively. A restricted cubic spline can be represented in many forms and this truncated power basis form of the restricted cubic spline hides the fact that linear, quadratic and cubic functions of age are used between adjacent knots. This restricted cubic spline allows us to model non-linear relationships between age of woman and the logit of the hazard between ages 24 and 32 without specifying a given functional form.
Model for primary sterility
The analysis is based on a two-population (fecund, sterile) mixture model. Let Y=1 indicate a couple who would eventually conceive (those fecund) and Y=0 indicate a long-term survivor (those sterile). Note that Y is partly observable; the value of Y is known to equal 1 if a conception occurred, but the value of Y is unknown (missing) if a conception has not yet occurred, i.e. for right-censored observations.
For a couple with column vector F of explanatory variables, the distribution of Y can be modelled by a logistic regression model:
where α is a column vector of regression parameters to be estimated. Hence, the sterility component of the mixture model is a logistic model for primary sterility with covariates, F, and regression effects, α.
Model fitting using Gibbs sampling
Bayesian estimation of the regression parameters and unobserved heterogeneity parameter was carried out using the free software package BUGS, an acronym for ‘Bayesian inference Using Gibbs Sampling’, which is described by Thomas et al. (Reference Thomas, Spiegelhalter, Gilks, Bernardo, Berger, Dawid and Smith1992), because of its flexibility in fitting complex models. The BUGS code used to specify the model is available from the authors. The Gibbs sampler is a general purpose Monte Carlo method for generating random variables from a target distribution of interest indirectly, in this case, a multivariate posterior distribution. A burn-in of 5000 iterations was used and inference based on a sample of 50,000 observations from the posterior distribution. Inferences are based on numerical summaries of the univariate marginals of the posterior distribution; here the posterior mean and median are used as measures of location and 95% credible intervals defined by the 2.5% and 97.5% points of the univariate marginal posterior distribution are used as the measure of precision.
The non-informative priors used for the regression parameters were independent N(0, 0.0001) distributions, where the second parameter of the normal distribution is the precision, i.e. the reciprocal of the variance. A N(0, 1) prior for the unobserved Z and a mildly informative uniform prior of σ ∼ U[0, 5] was used. An informative beta prior was used for the proportion fecund, i.e. f ∼ beta(367.68, 15.32), which corresponds to a mean of 0.96 and 95% credible interval between 0.94 and 0.98. Note that for many couples the number of ‘unsuccessful’ cycles was often too small to provide much information about the probability that the couple was sterile. The beta prior was chosen as the proportion of couples with primary sterility has been estimated to be around 3% to 4%. Therefore, a 95% credible interval between 2% and 6% for the percentage sterile was used.
Results
Waiting time to conception
The first panel of Table 4 presents the mean as well as the 2.5% and 97.5% percentage points of the posterior distribution of the parameter estimates for the model for the waiting time to first conception when the effects of age of woman were modelled using a restricted cubic spline. The omitted category is the reference category. Age of man was not significantly related to the waiting time to first conception, but was in the expected direction, where men aged 35+ had a lower risk of conception. The only significant difference between the various centres and Verona (the reference category) was Lugano, which mostly enrolled couples planning a pregnancy. In the ‘subsample’ of nulliparous women, Lugano had only eight couples but seven pregnancies, so this result is explainable by the small number of couples and high proportion of first conceptions amongst couples trying to get pregnant. The results for coital frequency and pattern of intercourse are significant relative to the reference category of 2+ acts of intercourse in window A (−2, −1, 0). The pattern is as expected, with reduced risk of conception for fewer acts of coitus in window A, and with acts of coitus more distant from day 0.
Table 4. Parameter estimates from random effects discrete-time event history models for the waiting time to first conception

a Estimates are posterior means. The 95% credible intervals are defined by the 2.5% and 97.5% points of the univariate marginal posterior distribution.
b The spline is parameterized α+βage+k 1(age-24)3δ(age-24)+k 2(age-28)3δ(age-28) +k 3(age-32)3δ(age-32), where δ( ) is an indicator function, equal to 1 if the argument is positive and 0 otherwise, and k 1, k 2, k 3 are the spline knot parameters at ages 24, 28 and 32 respectively.
For the cubic spline model, age of woman was not significantly related to the waiting time to conception as the 95% credible interval for the age parameter included zero. The posterior means of the knot parameters at ages 24, 28 and 32 were very small, and all the 95% credible intervals for the knot parameters included zero. This suggests a simplified linear model with just a linear term in age of woman. The results of this model are presented in the second panel of Table 4. The results for the two models are very similar. The only substantial difference is that for the linear model the parameter for age of woman is now significant at the 5% level of significance. For both models, the parameter estimate for age of woman is negative, which implies a declining probability of first conception with age of woman.
As the differences between the cubic spline and linear model are small, the results from the cubic spline model are presented as it is more robust to model misspecification of age effects. However, as both sets of results are presented, the reader can if they wish focus on which model they prefer: one that makes the strong assumption of linearity, which may be unjustified, or the spline model, which is useful for detecting curvilinearity in effects and for checking that the linearity assumption is adequate. The important point is that both models give the same substantive conclusions.
The pattern of risk of conception by age of woman can be examined by plotting the median hazard by age along with 95% credible intervals for the reference group. For a fecund couple, the hazard is the per cycle probability of a clinically recognized conception for a woman of a given age with a young partner, who attends the Verona centre, and has 2+ acts of intercourse close to the mucus reference day 0. Figure 1 plots the median hazard for the reference group for the cubic spline model (dashed line) and linear model (solid line) along with the 95% credible interval for the median hazard for the cubic spline model. The differences between these two curves are small, especially considering the size of the 95% credible interval. The greatest difference is for the earliest ages. The decline in the median hazard for the reference group is almost linear with age of woman for both models. This is not surprising as the logit scale is approximately linear in the middle range and the estimated knot parameters were very small. The 95% credible intervals are widest at the earliest and oldest ages, where the number of menstrual cycles observed at a given age are fewer (see Table 2).

Fig. 1. Median hazard by age of woman for the reference group for the cubic spline model (dashed line) and linear model (solid line), along with the 95% credible interval between the dotted lines for the cubic spline model. All menstrual cycles must have at least one act of intercourse in the 12-day interval beginning 8 days prior to and ending 3 days after the estimated day of ovulation (day 0). The reference group is partner's age <35, 2+ acts of intercourse in window A (−2, −1, 0) and Verona centre.
As the differences between the cubic spline and linear model are small, the results from the cubic spline model are presented as it is more robust to model misspecification of age effects. Consider Fig. 1 and the dashed line. The median value at age 21 is 0.54 and at age 35 it is approximately 0.24. Consider postponing trying to conceive from age 23 to 33: the median hazard for the reference group declines from 0.48 to 0.27. Consider what might happen by postponing from the end of the twenties to the early thirties, say from age 28 to 33. From 28 to 33, the median hazard for the reference group declines from 0.34 to 0.27. This is a modest decline. Note that the size of the decline depends on the choice of reference group, namely those with 2+ acts of intercourse in window A (−2, −1, 0). An alternative reference group of no intercourse in window A, but yes in B and yes in C yields a median hazard plot with a weaker age effect. Figure 2 compares these plots with a dashed line for the 2+ acts of intercourse in A reference group and a solid line for the group of no intercourse in A, but yes in B and yes in C. The credible interval for the top line in Fig. 2 is given in Fig. 1, and the credible interval for the bottom line in Fig. 2 has similar width.

Fig. 2. Comparison of median hazards by age of woman for two groups with partner's age <35 and Verona centre. The dashed line corresponds to 2+ acts of intercourse in window A (−2, −1, 0) and the solid line corresponds to no intercourse in window A, but intercourse in window B (−4, −3, 1) and intercourse in window C (−8, −7, −6, −5, 2, 3). All menstrual cycles must have at least one act of intercourse in the 12-day interval beginning 8 days prior to and ending 3 days after the estimated day of ovulation (day 0).
For a geometric distribution with constant hazard, the reciprocal of the hazard is the mean waiting time in number of cycles to first conception. The distribution of the reciprocal of the hazard is easily estimated using the Gibbs sampler. The median of this posterior distribution is used as a robust estimator of the location of the distribution and used as an estimator of the mean waiting time to conception.
Figure 3 plots the median of the reciprocal of the hazard and the 2.5% and 97.5% percentage points of the posterior distribution of the reciprocal of the hazard by age of woman. For each case, the hazard is calculated by setting the covariate values in the linear predictor equal to the given age of woman plotted, partner's age <35, 2+ acts of intercourse in window A (−2, −1, 0), Verona centre and adding the estimated value of Zσ. Hence, the 95% credible intervals plotted take into account the variability in conditional fecundability. The reciprocal of the hazard is the mean waiting time in number of cycles to first conception for such a ‘synthetic woman’ with these time-constant characteristics for each menstrual cycle. The increase in the estimated mean waiting time is almost linear with age of woman until age 34, when there is an upturn. The value at age 21 is 1.85 cycles and at age 34 it is 3.90 cycles. Consider postponing trying to conceive from age 23 to 33: the estimated mean waiting time for the reference group increases from 2.01 to 3.77 cycles. From 28 to 33, the estimated mean waiting time for the reference group increases from 2.94 to 3.77 cycles. This is a very modest increase of little practical importance. Note that the 95% credible interval for the estimated mean waiting time increases around age 32 and is much wider at ages 34–36. This is expected as there are fewer women and fewer cycles observed at these ages, but it could also suggest that the oldest women might be experiencing longer waiting times to conception.

Fig. 3. Estimated mean waiting time to first conception in menstrual cycles by age of woman (solid line) for the reference group, along with 95% credible interval between the dashed lines. All menstrual cycles must have at least one act of intercourse in the 12-day interval beginning 8 days prior to and ending 3 days after the estimated day of ovulation (day 0). The reference group is partner's age <35, 2+ acts of intercourse in window A (−2, −1, 0) and Verona centre.
Unobserved heterogeneity
One advantage of the model used is that it explicitly incorporates a random effect that would be expected to capture time-constant unobserved heterogeneity at the couple level, whether behavioural or environmental, so that any conclusions are expected to be more robust than those based on an event history model that did not include a random effect.
The mean and median of the posterior distribution of unobserved heterogeneity, σ, for the cubic spline model were 0.631 and 0.647. The standard deviation of the posterior distribution was 0.234 and the 95% credible interval was [0.104, 1.052]. Therefore, there is substantial unobserved heterogeneity that is not accounted for by age of woman, coital pattern or the other covariates included in the model.
Logistic model for primary sterility
The only covariate considered in the logistic model for primary sterility was age of woman. This linear effect was in the expected positive direction, but was not significantly related to primary sterility. The mean and median of the posterior distribution of the slope parameter for age were 0.728 and 0.685 respectively. The standard deviation of the posterior distribution was 0.473 and the 95% credible interval was [−0.077, 1.775].
Note that only 23 (6.3%) couples contributed twelve or more cycles with at least one act of intercourse in the 12-day interval, so there is very limited information at the woman level on the probability of her fecundity status as the exposure period is too limited for most women. Hence, in this situation, no attempt was made to include other covariates in the model. The linear effect of age was retained in the final model, even though it was not significant, so as to control for age of woman.
One advantage of the Bayesian approach is that posterior probabilities of being sterile can be estimated for individual women who did not conceive. The posterior probability that an individual with vector of explanatory variables x comes from population Y=1 (fecund), given that no event has occurred by time t, is:
For each woman who did not conceive, the posterior probability that this particular woman is fecund was estimated using the Gibbs sampler. The posterior medians were one for all non-conceiving women, except for three women in their twenties with long periods of exposure. For these women the posterior medians were zero and their posterior means were 0.842 (26 cycles observed), 0.778 (20 cycles observed) and 0.004 (20 cycles observed). This last woman was aged 22 with a young partner and the couple was almost certainly sterile as no conception occurred after 20 menstrual cycles with four cycles with intercourse pattern A no, B yes, C yes, nine cycles with only one intercourse in A and seven cycles with 2+ intercourse in A.
Discussion
Data limitations and sample selection
The study of age patterns of fecundability and sterility is difficult for many reasons. The data requirements are high and the statistical models needed are complex. The MCFS data used in this study are unique and of high quality. It is unusual to have prospectively collected menstrual cycle data that permits the estimation of day of ovulation, as well as daily recorded data on the number and timing of acts of intercourse. While the MCFS study is rich in cycle-specific data, it is lacking in information collected about the study participants and their behaviour/attitudes. For example, for each cycle was the couple trying to avoid a pregnancy or achieve a pregnancy? While most couples were trying to avoid pregnancy initially, with the exception of the Lugano centre, many avoiders must have changed to achievers as 61.4% obtained a first pregnancy during the course of the study and the concentration of intercourse near ovulation is not the normal behaviour of avoiders. Therefore, the study population consisted of both avoiders and achievers. In general, excluding the Lugano centre, the majority of couples started as avoiders and most changed to achievers or risky avoiders. How cycle-specific fertility intentions relate to fecundability once the coital pattern is included in the model remains an open question as we do not have data for cycle-specific fertility intentions.
The MCFS participants were women experienced in the use of natural family planning and, therefore, unusual and ‘not representative’ of all women delaying childbearing. Few women are probably willing to participate in a prospective study over a substantial period of time that requires either providing frequent urine samples or recording basal body temperature or cervical mucus quality on a daily basis in order that day of ovulation can be estimated, as well as recording daily when intercourse occurs. As women using natural family planning are already recording basal body temperature and/or cervical mucus quality on a daily basis, they were an ideal group to approach as potential participants for a prospective study on daily fecundability. However, given the burden of recording such data daily, it is perhaps not surprising that less than 10% of childless couples contributed twelve or more cycles to the MCFS.
The participants in the MCFS came from a number of countries so there is some degree of generalizability of these results, at least to European couples. Most were initially trying to avoid a pregnancy or space a pregnancy by using natural family planning methods. Of course, these methods can also be used to increase the probability of conception by timing acts of intercourse around the expected time of ovulation, as presumably most of the Lugano centre participants did and many of the other centre participants did as their fertility intentions changed from avoiders to achievers. Are the participants in the MCFS (self) selected on the basis of their fecundability, and if so, is this selectivity related to age of woman or age of man? Hopefully, the decision to study first rather than all pregnancies minimizes any such selectivity.
The time origin for the waiting time to conception is entry into the MCFS rather than first exposure to the risk of conception (with the exception of the first five cycles just after stopping the contraceptive pill use, which were excluded). The more time exposed to the risk of having a first child before entry into the MCFS study, the greater the potential selectivity. Some couples who had intended to enrol in a natural family planning clinic might have become pregnant before entry and, therefore, ineligible for this study of first pregnancies. This possibility was investigated by including an additional variable in the model of the waiting time to conception. The time from marriage to entry into the study was calculated and this variable was categorized into the following categories: (1) same month as marriage; (2) 1–11 months after marriage; (3) 12 or more months after marriage; and (4) missing. This variable was not significantly related to the waiting time to conception. Hence, any such selectivity effects are probably unimportant.
Women must have had no sign of infertility as a precondition for enrolment, so enrolled women might have higher fecundability at entrance and/or be healthier than the general population. Couples with high fecundability would be more likely to be lost before entry into the MCFS than couples with lower fecundability. Such selectivity would have a tendency to reduce the estimated level of fecundability, but not necessarily the age pattern. Is any selectivity age related? It is presumed that older women are less fecund than younger women and, if selectivity is against older women, the estimated age of woman effect would presumably be stronger than the true effect.
Conclusion
This study of the age pattern of fecundability for childless women does not suffer from the various limitations of many other previous studies: (1) it uses individual-level data, rather than aggregate-level data; (2) it uses menstrual cycles as the unit of analysis, rather than months as a proxy or continuous time; (3) it uses prospectively collected daily diary data, which allows the day of ovulation to be estimated; (4) it uses recognizable conceptions rather than live births; and (5) it uses daily information on the number and timing of acts of intercourse within the menstrual cycle relative to the estimated day of ovulation. The Menstrual Cycle Fecundability Study data analysed in this study are unique.
The result of a gradual decline in fecundability from the early twenties was surprising as the authors expected an increase in fecundability to the middle 20s and then a decline. However, Larsen & Vaupel (Reference Larsen and Vaupel1993) found a similar result for parous Hutterite women with a continuous time hazard model, but didn't control for sexual behaviour as this information was not available. These results relate to nulliparous women, control for sexual behaviour relative to the estimated day of ovulation and use the proper discrete-time scale of menstrual cycles.
Can women wait until their early thirties to try for a first birth? The evidence is yes, providing they are not already sterile. The magnitude of the decline in fecundability is such that the increase in average waiting time to conception is very modest and of little practical importance.
Acknowledgments
The authors wish to express their appreciation for the work done by the general coordinators and local principal investigators of the Menstrual Cycle Fecundability Study. They also thank the study participants who made their data available to the authors, and the group of investigators at the Department of Statistics, University of Padua, Italy.









