1 Introduction
Green roofs are roofs that are partially or (almost) completely covered by vegetation as a result of planned action rather than neglect. Green roofs are an increasing feature of cities’ urban planning tool set. Local adaptation plans around the world list green roofs as a tool for both storm-water management and attenuation of the urban heat-island effect, as is the case for adaptation plans of Vancouver, Copenhagen, London, Melbourne, Singapore, Chicago and Barcelona (see Copenhagen, 2015, for a review and links). Green roofs also decrease the energy consumption in buildings (e.g., Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014) and are identified as a valuable strategy to make buildings more sustainable, and increase urban green in cities while avoiding the negative effects of lowering densities. The inclusion of green roofs to the urban planning tool set creates a high demand for cost-benefit studies to support decision-making with regards to choosing the right implementation strategy, for example, choice of plant cover, needed incentives and efficient scale (U.S. Government, 2011). This article aims to contribute to this increasing demand, and convert the green roof benefits into monetary terms, aggregate monetary values over time and compare benefits to the costs of green roof installation. We focus on the benefits and costs of thin, lightweight, left-sustaining green roofs with minimal maintenance requirements – often labeled as extensive green roofs in the literature (e.g., Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014).
The benefits and costs of green roofs have been studied for several sites, including New York (Rosenzweig, Gaffin & Parshall, Reference Rosenzweig, Gaffin and Parshall2006; Bianchini & Hewage, Reference Bianchini and Hewage2012), Toronto (Bantinget al., Reference Banting, Doshi, Li, Missios, Au, Currie and Verrati2005), Atlanta, Georgia (Carter & Keeler, Reference Carter and Keeler2008; Whatley, Reference Whatley2011), Michigan (Clark, Adriaens & Talbot, Reference Clark, Adriaens and Talbot2008) and Seoul, South Korea (Shin & Kim, Reference Shin and Kim2015). Additionally, the costs and benefits of green roofs have been studies in more general settings than a specific city context in Germany and Brazil by Porsche and Köhler (Reference Porsche and Köhler2003), in Belgium by Claus and Rousseau (Reference Claus and Rousseau2012), and in the USA by Porsche and Köhler (Reference Porsche and Köhler2003) and Sproul, Wan, Mandel and Rosenfeld (Reference Sproul, Wan, Mandel and Rosenfeld2013). All studies quantified benefits pertaining to membrane longevity, building energy savings, storm-water management and air-quality benefits, while many also quantified reduction of the heat-island effects, noise insulation and greenhouse gas reduction. Scenic benefits that include at least aesthetic and psychological benefits, and biodiversity benefits are usually left out of the analysis. The exceptions are a study by Rosenzweig et al. (Reference Rosenzweig, Gaffin and Parshall2006) in which aesthetic benefits were included by assuming a certain willingness to pay (WTP) for New York residents, and a study by Bianchini and Hewage (Reference Bianchini and Hewage2012) in which percentual (2%–5%) increases in the value of the nearby properties were assumed. Taking into account the state of the art, our main contributions to the literature are (1) ease the transferability of the value estimates by providing detailed information on the valuation methods and the roles of different assumptions and parameter values in the estimates of benefit and cost items and (2) inclusion of scenic value benefit item into the analysis based on a formal and trackable analysis rather than a guess.
The paper is structured as follows: We first discuss the valuation of benefits that people obtain from the consumption of ES, and explain the choice of discount rate. Next, we present all the building blocks and benefit items of a CBA of green roofs and the options to assess them. The presentation is based on an application in Helsinki, Finland, but with added information on how the same item can be treated for another location. In this way we intent to contribute to the spread of benefit-transfer approaches so as to make CBA of green roofs affordable. One section has been dedicated to the valuation of scenic benefits since previous measures of the scenic value individuals place on green roofs are weak at best. Subsequently, we review the costs of green roofs, and finally we discuss the net present value (NPV) of green roofs and present a green roof implementation scenario in which 10% of the city’s roof area is being greened, while a distinction is made between public and private costs and benefits. In the conclusion, we summarize the results and reflect on policy options such as needed incentives, and discuss the limitations of our approach.
2 Economic Background
Ecosystem services (ES) are benefits that people obtain from ecosystems (Millennium Ecosystem Assessment, 2005). The concept of ES is useful as it allows to separate different types of services provided by an ecosystem, in this case a collection of green roofs. This allows the valuation of each ecosystem service separately. Within urban areas, the primary issue from the perspective of human well-being is whether urban settlements are able to provide a healthy and satisfying living environment for residents. The emergence and growth of cities is (usually) based on the proximity of producers and consumers that creates common advantages in productions and consumptions. As a consequence, the productivity per acre in cities can get so high that it pushes up land and real estate prices (Brown, Reference Brown1974). This creates pressure for ecosystems in terms of high opportunity costs of urban green space, while the benefits of ES are not often explicitly valued. The trade-off between ES and urban economic activity is not evenly weighted in the absence of such assessments. Consequently, the interest in ES is rising also for urban environments, which ties in with the need of revising the concept of sustainable urban planning. This article focuses on valuation of benefits of ES of an ecosystem that is not yet a standard solution in most cities: green roofs. The addition of green roofs to the green infrastructure portfolio is promising, as green roofs can raise the supply of ES while avoiding the negative effects of lowering densities.
2.1 Defining the economic value of ecosystem services
Based on the preferences of an individual, the “equivalent in money” can be calculated for a change in the quantity or quality of ES, where the sum of money represents the equivalent effect on the welfare of an individual (Freeman, Herriges & King, Reference Freeman, Herriges and King2014). The valuation of urban planning realization effects, for example, trough changes in real estate value, is eventually based on the theoretical concepts of compensating variation and equivalent variation, first adapted to commodity (rather than the price) space by Mäler (Reference Mäler1974):
$$\begin{eqnarray}\displaystyle & v(\mathbf{p},q_{1},y-CV)=v(\mathbf{p},q_{0},y) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & v(\mathbf{p},q_{1},y)=v(\mathbf{p},q_{0},y+EV). & \displaystyle\end{eqnarray}$$
The compensating variation, CV in equation (1), is the maximum amount of money that an individual would be willing to pay (WTP), so as to achieve the higher supply of ecosystem service
$q_{1}$
as compared to
$q_{0.}$
The equivalent variation, EV in equation (2), is the minimum compensation that an individual would accept (WTA) to forgo the raise of supply of ES from
$q_{0}$
to
$q_{1}$
associated with the enhancement of an ecosystem. The difference between the concepts is that the monetary “value” is measured at different points, either at
$q_{1}$
or at
$q_{0}$
in the ES quantity/quality dimension. In the case of green roofs, the correct welfare measure is CV – based on the property rights argument, as the beneficiaries of green roofs do not yet possess the higher level of ES. (The property rights argument is explained, for example, in Boadway, Reference Boadway2006; Arrow et al., Reference Arrow, Solow, Portney, Leamer, Radner and Schuman1993).
Hanemann (Reference Hanemann1991) showed that in the case the good
$q$
has a perfect substitute
$x_{i}$
that can be bought at the market place for a price
$p_{i}$
, and assuming interior solution so that
$x_{i}>0,$
both at
$q_{0}$
and at
$q_{1}$
, there are no income effects and the CV can be calculated by
$\left(q_{1}-q_{0}\right)\ast p_{i}$
. Consequently, if the ES replaces a market good/service that would have been bought by the decision maker regardless, it is straightforward to use this avoided costs as a value measure. It should be noted that we do not claim that green roofs are a perfect substitute for conventional roofs but that some ES it provides are perfect substitutes for some market goods. In the subsequent chapters, we use this as a basis for our valuation methods and show that many of the benefits of green roofs are in the form of avoided costs, for example, energy costs or storm-water-related costs.
2.2 Applied valuation methods
There is a variety of methods developed for estimating the value of ES, discussed in detail in several articles (e.g., de Groot, Wilson & Boumans, Reference de Groot, Wilson and Boumans2002; Kaval, Reference Kaval2010). Valuation methods all share a target for attributing a monetized value to the benefits obtained from a change in quality or quantity of ES. We discuss only those we have applied in the green roof valuation. The choice of method is dependent on the function of the ecosystem service.
Green roofs are a technical solution that takes advantage of the regulating properties of the vegetation and substrate layers. Many of the ES they provide can be classified into regulating services. These services benefit people mainly by enabling avoidance of other costs. The natural choice of the valuation method is then “Avoided costs” as suggested by de Groot et al. (Reference de Groot, Wilson and Boumans2002) or on more theoretical terms by Hanemann (Reference Hanemann1991).
Green roofs, however, benefit people also in subtler ways. There is evidence that green roofs can provide urban habitat for wild species and help to increase the local biological diversity (Coffman & Waite, Reference Coffman and Waite2011; Madre, Vergnes, Machon & Clergeau, Reference Madre, Vergnes, Machon and Clergeau2014; Gabrych, Kotze & Lehvävirta, Reference Gabrych, Kotze and Lehvävirta2016). This “refugium” function of green roofs could be tackled with contingent valuation methods to some extent, but is left out of the scope of this study as it would suffer from lack of adequate quantitative input. Yet, green roofs can also provide aesthetic and psychological benefits for people in urban areas. These benefits have been grouped together in this article as “scenic benefits” for methodological reasons. Hartig, Mang and Evans (Reference Hartig, Mang and Evans1991) proved that experiencing naturel has restorative outcomes and the effect can last for several weeks after the experience. It is widely known that property prices are positively affected by the view and closeness of green space. In Finland Tyrväinen and Miettineni (Reference Tyrväinen and Miettineni2000) have shown the positive relationship between the urban green and property prices. We confirm this relationship in our analysis. Hauru, Lehvävirta, Korpela and Kotze (Reference Hauru, Lehvävirta, Korpela and Kotze2012) showed that changing the visual setting from urban built-up area to an urban forest offers restorative benefits, while Lee et al. (Reference Lee, William, Sargent, Farrell, Williams and Johnson2015) show that restorative benefits are even elicited by a small urban green roof and are comparable to that of a small urban park. We use the results from the hedonic regression analysis to indicate an upper limit for the scenic value of urban parks, expressed as mark-up of the square meter price of involved real estate.
The scenic value can also be studied by means of the contingent valuation (CV) methodology. Our choice in favor of hedonic pricing (HP) is explained by: (1) HP is the appropriate methodology for valuation of services and disservices that are intrinsically dependent on the location of households (Brander & Koetse, Reference Brander and Koetse2011); (2) we are able to avoid the bias of stated preferences contained in CV (Brander & Koetse, Reference Brander and Koetse2011); (3) there are only a couple of green roofs installed in Helsinki and people lack experience to the extent of turning stated preferences into mere guesses (Murphy, Allen, Stevens & Weatherhead, Reference Murphy, Allen, Stevens and Weatherhead2005); and (4) we would expect the results to be of the same magnitude in the case of a CV study (Blomquist, Reference Blomquist1988; Carson, Flores, Martin & Wright, Reference Carson, Flores, Martin and Wright1996; Shabman & Stephenson, Reference Shabman and Stephenson1996; Bateman, Lovett & Brainardi, Reference Bateman, Lovett and Brainardi2004; Ghermandi, van den Bergh, Brander, de Groot & Nunes, Reference Ghermandi, van den Bergh, Brander, de Groot and Nunes2010). Expected differences and uncertainties in the hedonic estimates and the use of the proxy are handled by using lower and upper bounds for the value.
2.3 Choice of discount rate
Weitzman (Reference Weitzman2001) concluded – based on a survey of more than 2000 economists – that the appropriate discount rates for environmental BCA can be summarized in the following simplified scheme based on the project’s lifetime: 4% for the immediate future (years 1–5), 3% for years 6–25, 2% for years 26–75 and 1% for years 76–300 and 0% for the benefits and costs for years after 300. The declining trend in the discount rates can be backed by the economic theory on uncertainty (see Gollier & Weitzman, Reference Gollier and Weitzman2010). However, for simplicity and to ease the interpretation of the results, we have applied a single interest rate of 3% which approximates the discount rate schedule above. This choice is also in line with the fixed long-term interest rates applied to mortgages and long-term investment loans. The same interest rate of 3% is also recommend by the U.S: Office of Management and Budget (2003) and by the German treasury. Slightly higher social interest rates are recommended by France (4%) and UK (3.5%) (EU, 2008).
3 The benefits of green roofs in Helsinki and the transferability of the results
In this section, we show how each benefit item of green roof CBA can be treated. We measure the benefits in Helsinki, the capital of Finland, with around 625 000 inhabitants, and a metropolitan area of around 1.1 million inhabitants. We compare our findings to results from the literature. We also divide the benefits between those that directly accrue to the property owner/resident and those that are shared by the wider public, such as savings on in public spending and health benefits. For each benefit, we also show how the results obtained from Helsinki change when changing the city-specific environmental or infrastructural parameters. Furthermore, the valuation methods described in this section can be applied to any other urban location. To ensure replicability and transferability, we take some space to describe the methods.
3.1 Membrane longevity
The historic experience built up with green roofs points at approximately doubling the lifespan of the roofing membrane. This amounts to an additional 20 years lifetime compared to a conventional roof. We use this assumption so that the life cycles are 20 and 40 years for conventional roofs and green roof respectively (Porsche & Köhler, Reference Porsche and Köhler2003; Liu & Baskaran, Reference Liu and Baskaran2003; TRC 2007). This is fairly conservative as 40 years is the minimum life cycle of a green roof in other cost-benefit analyses, for example, Bianchini and Hewage (Reference Bianchini and Hewage2012). The price of installing a regular bitumen roof in Finland is around 43€
$/\text{m}^{2}$
, which includes the value-added tax, as this is a private cost (taxes are removed when analyzing the social benefit and costs). Hence, the NPV of the benefit is 23.8€
$/\text{m}^{2}$
or the discounted price of the reference roof. The factor that determines this benefit is the local cost of the chosen reference roof that the green roof is compared to.
3.2 Energy cost savings
Green roofs have an effect on the heat transfer properties of the roof via three different phenomena (Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014): (1) substrate increases thermal capacity and decreases thermal transmittance through the roofs, (2) foliage shades, under the foliage convection provokes heat thermal exchange but foliage absorbs part of the thermal energy for photosynthesis and (3) substrate and vegetative layers induce evaporative and evapotranspiration cooling. These phenomena have the potential to reduce the energy consumption for heating in the winter and for cooling in the summer. The benefits of these processes are determined by the type of vegetation, substrate depth, availability of water, local climate and building type (Liu & Baskaran, Reference Liu and Baskaran2003). We employ the avoided cost method to estimate the savings in the energy costs for an extensive green roof in Helsinki. Our results below show that when moving toward warmer climates, the energy savings in total tend to increase as the cooling energy benefit increases considerably faster than the heating energy benefit decreases.
3.2.1 Energy cost savings for heating
We explore the impact of a green roof on the heating consumption of a building by comparing the heat loss of different types of roof. Green roofs reduce the thermal transmittance of a roof, thereby improving the insulation capacity. This effect is highly dependent on the building envelope characteristics on which the green roofs are placed. Generally, in non-insulated buildings, the impact of green roofs is much higher than in insulated ones, whereas the better the insulation of the roof, the lower the contribution of green roofs. In cold, heating dominated climates, the insulation properties of the roof carry the highest significance as the heating load benefits from a low U value (U is the coefficient of thermal transmittance). (Roche & Berardi, Reference La Roche and Berardi2014). More complex models have been developed, most notably by Sailor and Hagos (Reference Sailor and Hagos2011) but the use of these models requires a vast amount of input data from local conditions to building characteristics. Based on Sailor’s model, a web based calculator has been developed to quantify energy savings, but it is only available for U.S. cities. (Green Building Research Laboratory Websites, 2016). Here, we demonstrate the effects of added insulation of green roofs to reduce the heating load with a model suggested by a senior researcher in energy technology (personal communication, Jokisalo, Reference Jokisalo2012): We calculate the hourly heat losses of the green roof and the reference roof, and compare the differences between them. Hourly heat losses (q) are calculated as in equation (3), where
$U$
$=$
Coefficient of thermal transmittance, A
$=$
Roof area,
$T_{s}$
$=$
Target temperature
$^{\circ }\text{C}$
inside the building,
$T_{u}$
$=$
Hourly average temperature
$^{\circ }\text{C}$
outside (Seppänen, Reference Seppänen2001).
$$\begin{eqnarray}\displaystyle q=U_{1}\times A\times (T_{s}-T_{u}). & & \displaystyle\end{eqnarray}$$
Next, by taking the average of the difference in the annual heat losses of the chosen reference years, we get an estimate for the impact of the green roof on the annual heat loss of a building. To get the impact of the green roof on the energy consumption, we still need to divide the reduction in the heat loss by the combined efficiency of the heat supply and heat delivery system of the building, for example, 95% for a building with a radiator and 100% for an electric heating system (FEA, 2012). Finally, we get the annual savings on the energy use (kWh), converted into monetary savings by multiplication with the price of energy for those buildings heated by district heating (80% share) and with the price of electricity for those building heated by electricity (20% share). The average price of electricity per kWh in Helsinki is 0.115€ and the price of energy used for district heating is around 0.081€ (Energy Authority, 2016). The average price per kWh is then around 0.9€/kWh. Around 30% of the price (of both) are taxes (around 0.27€ per kWh).
We use the same price for both the private and the social benefits, albeit for different reasons. For private benefits, the taxes are included as costs for the private decision maker. On the other hand, external costs of energy production need to be accounted for in the social case. The district heat is produced for over 90% in fossil fuel power stations (
${\sim}$
40% coal;
${\sim}$
50 natural gas). The origin of the supplied electricity is 50% nuclear, 33% natural gas and the remainder is renewables (mainly biomass as supplementary fuel). Finland takes part in the EU Emission Trade System (ETS), which affects both the production of district heat and electricity (for units beyond a minimum size). The so-called pass through of the ETS prices into power prices is high in Finland (Honkatukia, Mälkönen & Perrels, Reference Honkatukia, Mälkönen, Perrels and Giulio2008), meaning that 50%–100% of the carbon price is captured in the end use price (with a higher percentage mostly during winter months). A similarly high pass through may be assumed for district heat, which is a regulated monopoly. This means that the external costs of carbon with respect to global warming are to a large extent captured in the energy price. Now the effects of NOx and SO2 remain to be included. The co-generation power stations are fitted with sulphur and nitrogen emission reduction technology, greatly reducing the emissions of these agents. The costs of these technologies are internalized in the energy prices. Nevertheless some emissions remain of which the costs may be in the order of magnitude 0.25 eurocent/kWh (EU eXterne study, 2005). The indicative external cost per kWh of nuclear power in the EU eXterné study is also rated at approximately 0.25 eurocent/kWh.
In Helsinki, we selected one year (2008) that was near to normal with respect to the observed climate, and one that was unusually warm (2010) to account for the warming of the climate and to be more conservative when estimating the benefits. For a new building (
$U=0.09$
for the reference roof,
$U=0.08$
for the green roof) we get a total discounted benefit of 2.9€
$/\text{m}^{2}$
. For an older building the benefit is much higher based on the poorer insulation properties of the roof (e.g., Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014).
Simulations with the heat loss model show that an increase in the average temperature (Helsinki average temperatures: summer 16.2
$^{\circ }\text{C}$
, winter
$-$
3.5
$^{\circ }\text{C}$
(FMI, 2015)) by 1 degree reduces the difference in the heat losses between the green roof and the reference roof around 7% compared to the initial level in Helsinki. This corresponds to around 0.1 kwh
$/\text{m}^{2}$
with thermal coefficient of heat loss
$U=0.09$
for the reference roof. The same trend continues when the average temperature is increased further.
The other determining factor on the heating energy savings is the energy insulation quality of the considered building stock, and more specifically the insulation properties of the roof. Each 0.01 increase in the coefficient of heat loss of the reference roof will increase the benefit by 100% compared to the original benefit when
$U=0.09$
, assuming that with a green roof
$U=0.08$
is achieved. Decrease in the thermal transmittance can be achieved by green roof design, as demonstrated in Roche and Berardi (Reference La Roche and Berardi2014). Consequently, the effect of the building regulation has much more relative weight compared to the changes in the outside temperature. The heating energy savings do not need to drastically decrease when moving south from Helsinki if the building code is less strict in relation to the insulation properties of the roof. As an example, for Madrid in Spain, with average winter temperature of 9.7
$^{\circ }\text{C}$
(Saiz, Kennedy, Bass & Presnail, Reference Saiz, Kennedy, Bass and Presnail2006) and heat loss coefficient U of 0.15, the benefit would translate into around 1.5€
$/\text{m}^{2}$
. However, the optimal design of a green roof in Spain would have less insulation to maximize the cooling benefits, as additional insulation could in fact increase the energy consumption by overheating the building. (Roche & Berardi, Reference La Roche and Berardi2014). Consequently, in reality the heating savings in a warm climate are close to zero.
3.2.2 Energy cost savings for cooling
The cooling savings are estimated using results from the cooling energy simulations by Saiz et al. (Reference Saiz, Kennedy, Bass and Presnail2006) and Roche and Berardi (Reference La Roche and Berardi2014). Saiz et al. (Reference Saiz, Kennedy, Bass and Presnail2006) obtained results from an eight-story residential building located in Madrid (average temperatures, summer 19.4
$^{\circ }\text{C},$
winter 9.7
$^{\circ }\text{C}$
) with a flat roof and total living area of 3381
$\text{m}^{2}$
and annual cooling energy use around 90,000 kWh or 27 kWh
$/\text{m}^{2}$
. The green roof was found to have a cooling impact on the five highest floors with a total effect of around 10% on these floors. For the highest floor or for a one-floor building, the cooling energy was reduced by around 25%. The green roof was a standard extensive green roof, with 9 cm substrate and plant types of sedum, cactus desert shrub. Roche and Berardi (Reference La Roche and Berardi2014) compared different types of green roofs in three different climate conditions for a one-story office building, and recorded annual cooling load reductions between 17% and 22% for optimal green roof designs in different climates.
In Finland, much more energy is used for heating buildings than for cooling them. Simulations show that a reference model building in southern Finland consumes around 3 kWh
$/\text{m}^{2}$
per year for cooling in the current climate with a small expected increase in the future to at most 3.5 kWh
$/\text{m}^{2}$
in 2030 (Jylhä et al., Reference Jylhä, Kalamees, Tietäväinen, Ruosteenoja, Jokisalo, Hyvönen, Ilomets, Saku and Hutila2012). The benefit would then translate to 1.5–2.2€/floor
$\text{m}^{2}$
(buildings are cooled with electricity) which in a building with one floor is roughly the same for the roof area for a flat roof. An example office building in Jylhä et al. (Reference Jylhä, Kalamees, Tietäväinen, Ruosteenoja, Jokisalo, Hyvönen, Ilomets, Saku and Hutila2012) uses relatively more energy for cooling than a residential building. The energy demand for cooling in southern Finland was estimated to be 7 kWh
$/\text{m}^{2}$
per year at 2010 and 7.5 kWh
$/\text{m}^{2}$
in 2030. For such a building, the reduction in the energy demand for cooling is then roughly 10%. The benefit is then 2€/floor
$\text{m}^{2}$
. For an office building with five floors, this roughly equates to 10€
$/\text{m}^{2}$
per installed green roof. This is close to the maximum benefit as addition of more stores to the building does not increase the benefit since the marginal benefit per store is decreasing and approaches zero at the sixth highest floor.
For comparison in Madrid, the eight-story residential building would have a total discounted benefit of around 24€
$/\text{m}^{2}$
. As the benefit is calculated for a residential building, the benefit would be even larger for a commercial building that tends to use more energy for cooling.
It must be noted that these benefits are likely for green roof designs optimized for cooling the building and the maximum benefits of heating and cooling are hard to realize at the same time. Roche and Berardi (Reference La Roche and Berardi2014) proposed “active green roofs” to partly solve this dilemma, in which the cooling in the summer is increased with a plenum fan and variable insulation can be achieved.
3.3 Noise insulation
Lightweight vegetated roofs may increase transmission loss up to 10 dB at low frequency and up to 20 dB at mid-range frequencies (Connelly & Hodgson, Reference Connelly and Hodgson2013). Connelly and Hodgson (Reference Connelly and Hodgson2013) show that the noise insulation benefits of green roofs are comparable or better to an additional, though unspecified, ceiling element. We use the cost of adding a plasterboard layer, a widely used technique to improve the noise insulation (personal communication, Helimäki, 2013), on a roof as the maximum sound insulation benefit of a green roof. We estimate that the benefit of a green roof is this avoided cost under flight routes. In other areas we assume that the benefit is zero, even though large amounts of green roofs in downtown areas may also affect the soundscape of the inner city, generally in the sense of attenuating mechanical noises (Irvine et al., Reference Irvine, Devine-Wright, Payne, Fuller, Painter and Gaston2009; Renterghem, Hornikx, Forssen & Botteldooren, Reference van Renterghem, Hornikx, Forssen and Botteldooren2013).
The total costs of plasterboard installation are around 20€
$/\text{m}^{2}$
in Finland, of which around 50% is attributable to labor costs (net costs 50€/h) (prices for materials and contracts e.g., Gyproc, 2015; Kodinremontit.fi, 2015).
3.4 Storm-water management
Green roofs can reduce the demand on sewer system capacity by delaying water flows and reducing total runoff by retaining part of the rainfall and releasing it back to the atmosphere by evapotranspiration. Results from Berlin suggest that a light (<100 mm substrate) low-growth green roof on 10% of the building stock would result in a reduction of 2.7% in runoff for the region and 54% for the individual buildings (Mentens, Raes & Hermy, Reference Mentens, Raes and Hermy2006). Rosenzweig et al. (Reference Rosenzweig, Gaffin and Parshall2006) showed that a similar green roof infrastructure in New York could produce a 2% reduction in total runoff.
In Helsinki, the storm-water management can be divided into two main categories: combined storm-water–sewer systems and separated systems. In the combined systems both the storm water and sanitation waters are conveyed through the same pipes to the water treatment facility. In a separated system the different types of water are conveyed through separate courses. In the downtown area of Helsinki (
${\sim}$
2200 hectares) the storm-water and sewer system is combined; in other parts of Helsinki mainly separate systems are in use. Of the over 1900 km of sewer pipes about 250 km are built as combined sewer system and 1650 km as separate system. The expansion of the sewer network (almost all new sewers are separate systems) incurs annual costs of 4 million € for the storm water alone. The repair of the existing storm-water pipes costs around 2 million € per year. The repair costs of combined systems are around 5–10 million € per year, of which 2–4 million € is allocated to storm-water-induced repair costs (personal communication Heinonen, Reference Heinonen2012). The discounted total costs of rain water purification are shown in Table 1.
In the future, repair costs are estimated to rise to double or triple the current level, as a consequence of (over)aging of the sewer systems. The annual expansion costs of the network are expected to rise about 20%, since the new pipes should have larger sizes to account for the effects of climate change. In several cost-benefit analyses it has been assumed that there is a linear relationship between the amount of reduced runoff and the reduction in the capital and purification expenditures (e.g., Rosenzweig et al., Reference Rosenzweig, Gaffin and Parshall2006). However, based on our interview (personal communication Heinonen, Reference Heinonen2012), some costs are fixed even in the long term and the amount of runoff has only a small effect on these costs.
Three kinds of capital expenditure are taken into account in our analysis: (1) the building of new (separate) sewer systems, (2) the repair of existing separate sewer infrastructure and (3) the repair of existing combined sewer system. We assume that at a 10% infrastructure scenario (10% of roof space is greened in Helsinki and uniformly distributed across the inner city), the resizing costs of the pipes would go down 10% (personal communication Heinonen, Reference Heinonen2012). As for the other cost reductions, we can also speculate that a 10% green roof scenario would reduce other costs by 2%–3% with the usual assumption of a linear runoff reduction–cost-reduction relationship (e.g., in Rosenzweig et al., Reference Rosenzweig, Gaffin and Parshall2006).
Our cost-reduction estimates based on the 10% infrastructure scenario are shown in Table 1.
Table 1 Expenditure categories and estimated avoided costs.
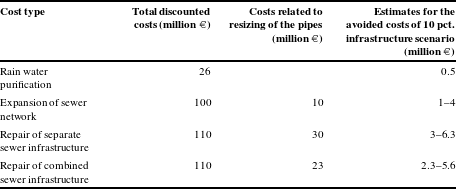
These assumptions would result into benefits between 6.8 and 16.4 million € . The range of the green roof benefit for storm-water reduction is then 3.9€–9.4€
$/\text{m}^{2}$
. It must be noted that compared to some earlier estimates (e.g., Bianchini and Hewage, 39$–100$
$/\text{m}^{2}$
), these figures are on relatively low level. The realization of the higher figures would mean that savings around 20%–30% should be achieved with 10% green roof infrastructure scenario. This does not seem plausible based on the literature or the interview (personal communication, Heinonen, Reference Heinonen2012).
Out of the different cost types in Table 1, only the annual water purification costs are directly related to the amount of precipitation and only in those areas where combined sewer system is used. The annual average precipitation is around 7000 mm in Helsinki (FMI, 2015).
The capital expenditure benefits are affected by more complicated relationships between rainfall patterns (e.g., return periods of extreme rainfall events) and city-specific storm-water and sewage system infrastructure. An important factor is the current state of the sewer infrastructure: the capacity is usually designed for a return period of a certain extreme rainfall event. In the future, sewer systems in many parts of the world will be under ever more stress due to expected increase in extreme rain events due to climate change (e.g., IPCC, 2014).
The storm-water benefit is then positively dependent on (1) the amount of precipitation (2) backlog of the current sewer system, the more outdated the system, the larger the benefit (3) occurrence and intensity of extreme rain events and (4) expected changes in extreme rainfall events due to climate change. All these need to be evaluated separately in each site. As mentioned, the figures in Helsinki are relatively low compared to other estimates, and the benefits are likely to be much higher in other cities.
3.5 Air-quality improvements
Tan and Sia (Reference Tan and Sia2005) found that the levels of fine particles (
$\mathit{PM}_{x}$
) and sulphur dioxide (
$\mathit{SO}_{2}$
) decreased by 6% and 37% in the immediate surrounding air space after a green roof was installed. Currie and Bass (Reference Currie and Bass2008) estimated that 109 ha of green roofs in Toronto could remove about 8 tons of unspecified air pollutants per year. Peck (Reference Peck2003) estimated that current roof greening in Toronto (cover over 6.5 million
$\text{m}^{2}$
) results in a 5–10% reduction in nitrogen dioxide (
$NO_{2}$
) and
$\mathit{SO}_{2}$
, and in a reduction of 30 tons of
$\mathit{PM}_{x}$
. Yang, Yu and Gong (Reference Yang, Yu and Gong2008) showed that a total of 1675 kg of air pollutants was removed by 19.8 ha of green roofs in one year in Chicago with the following distribution: 52% of ozone (
$0_{3}$
), 27% of
$NO_{2}$
, 14% of
$\mathit{PM}_{10}$
and 7% of
$\mathit{SO}_{2}$
. The annual total removal per ha of green roof was then 85 kg, of which 44 kg of
$0_{3}$
, 23 kg of
$NO_{2}$
, 12 kg of
$\mathit{PM}_{10}$
and 6 kg of
$\mathit{SO}_{2}$
. Yang et al. (Reference Yang, Yu and Gong2008) reported that their estimate was 18% higher compared to above cited estimates from Toronto (Currie & Bass, Reference Currie and Bass2008). In this article, we utilize proportions of gas reductions from Yang et al. (Reference Yang, Yu and Gong2008) and use their estimate of total removal as our high estimate and the result from Toronto (Currie & Bass, Reference Currie and Bass2008) as our low estimate for green roof air purification potential.
The average costs of different emissions were studied in a report by the Finnish Transport Agency (Tervonen & Ristikartano, Reference Tervonen and Ristikartano2010). The calculations include negative effects on health (e.g., cancer, heart and lung diseases), environment, infrastructure (e.g., corrosion) and climate change (of GHGs). The costs were significantly higher in urban areas since there pollutants have an effect on a higher number of people. Their valuation is based on methods dealing with valuing reduced mortality risks and valuing reduced morbidity risks (Freeman et al., Reference Freeman, Herriges and King2014). The results of the air-quality benefits are shown in Table 2. Summing up the effects regarding each agent in Table 2, the total air-quality benefit in Helsinki is between 4.8€ and 6.9€
$/\text{m}^{2}$
.
Table 2 Green roof emission reduction benefits.
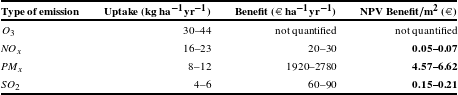
Results show, that at least 95% of the air-quality benefits can be attributed to the removal of particulate matter. Consequently, the air-quality benefit is positively dependent on the uptake potential of green roofs for
$\mathit{PM}_{x}$
and the (local) marginal cost of the
$\mathit{PM}_{x}$
. The exact concentration-response function for
$\mathit{PM}_{x}$
is unknown, but based on current evidence, the marginal social cost of
$\mathit{PM}_{x}$
is increasing with the concentration (Beelen et al., Reference Beelen2015; Wyzga & Rohr, Reference Wyzga and Rohr2015). Consequently, air-quality benefits are expected to be higher in those sites with higher concentration of particulate matter compared to Helsinki. Compared to most cities across Europe, Helsinki ranks as one of the lowest for concentrations of particulate matter (visualization and statistics available at EEA website, 2015). As the concentration-response function is unknown, local estimates of marginal costs need to be employed to give more accurate results. In Helsinki, a marginal social cost of 232 800€ for a ton of particulate matter was used (Tervonen & Ristikartano, Reference Tervonen and Ristikartano2010). The benefits of air-quality improvements are prone to changes in the transport fuel mix. The pace of change is however too speculative to take into account.
3.6 Heat-island effect
In urban environments, vegetation has largely been replaced by impervious and often dark surfaces. These conditions contribute to the urban heat-island effect, wherein urban regions are significantly warmer than the surrounding suburban and rural areas, especially in the nighttime. One of the benefits of green roofs is mitigation of the urban heat-island effect (Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014). A study by Santamouris (Reference Santamouris2014) reviewed urban heat-island mitigation techniques, and remarked that large-scale application of green roofs could reduce the ambient temperature by 0.3 K to 3 K.
The value of the benefits and costs of the heat-island effect in Helsinki or other cities in cold climates has not been estimated or even comprehensively qualitatively listed. Some impacts are positive (such as reduced energy demand in the winter) and some negative (increased mortality during heat waves is shown by Ruuhela, Lahtinen, Haga, Fronzek and Carter (Reference Ruuhela, Lahtinen, Haga, Fronzek and Carter2012)). The value of the urban heat-island benefit/cost is not included in the cost-benefit calculation of Helsinki.
By only considering the price of saved cooling energy, Bianchini and Hewage (Reference Bianchini and Hewage2012) considered that extensive green roofs could generate a benefit of 1.2$–3$ and Rosenzweig et al. (Reference Rosenzweig, Gaffin and Parshall2006) that the energy savings of the cooling costs could be in the range of 0.7–10%. As the difference between the low and high estimates is high, and only the decrease in energy consumption has been taken into account, it can be noted that the monetary benefit of green roofs for urban heat-island mitigation is still largely unknown.
4 Valuation of scenic benefits
All of the reviewed articles of green roof economics stated that green roofs offer amenity, aesthetic, psychological or other cultural benefits to urban residents. Nevertheless all but two left these benefits out of the cost-benefit calculations. The first exception was a study in New York (Rosenzweig et al., Reference Rosenzweig, Gaffin and Parshall2006) in which it was assumed that between 0.9 and 3.4 million residents of New York City would enjoy having half of city’s roofs greened, with each resident willing to pay $10, $25 or $50 for the installation. These estimates were not supported by any valuation study. The second exception was the study by Bianchini and Hewage (Reference Bianchini and Hewage2012) in which it was assumed that “the aesthetics benefit obtained from extensive green roofs varies from 2% to 5% of property value. For intensive green roofs the aesthetics benefit is considered that varies from 5% to 8% of the property.” These numbers were based solely on assumptions. A review article on green roof economic benefits by the U.S. Government (2011) stated that: “…studies are not specifically related to green roofs and the methodology is open to debate; productivity, absenteeism, aesthetics, and views were not accounted for in the cost-benefit analysis (CBA). The overall evidence, however, is that green roofs have the capacity to provide significant value in terms of productivity and absenteeism to the tenants (and thus the owner) as well as to the community at large who benefit from the improved aesthetics and views of the green roof.”
4.1 The study method and discussion of the proxy
White and Gatersleben (Reference White and Gatersleben2011) compared the aesthetic quality of different roof types and found that people prefer view to a nonvegetated roof. Fernandez-Cañero, Emilsson, Fernandez-Barba and Machuca (Reference Fernandez-Cañero, Emilsson, Fernandez-Barba and Machuca2013) argue that green roofs with similar appearances to conventional green areas are most valued by citizens and the closer their design is to that of conventional urban green, the more comparable the aesthetic quality is to conventional urban green. Jungels, Rakow, Allred and Skelly (Reference Jungels, Rakow, Allred and Skelly2013) showed that positive attitudes toward green roofs increased as the green roofs became more familiar. Lee, William, Sargent, Farrell and Williams (Reference Lee, William, Sargent, Farrell and Williams2014) confirm that green roofs carry aesthetic quality over concrete surfaces; aesthetic quality is however strongly dependent on green roof characteristics, such as choice of vegetation and diversity. Lee et al. (Reference Lee, William, Sargent, Farrell, Williams and Johnson2015) confirm in a later study that green roofs have restorative effects comparable to conventional urban green – a view to a green roof can restore attention in the same way as a view to conventional urban green. Based on the literature, the scenic quality of green roofs may be lower than that of conventional urban green, but with good design the scenic quality approaches that of small pockets of conventional urban green. Consequently, we use the scenic value of small urban areas with green cover (referred as “small parks” from here) as the high estimate and zero as the low estimate for the scenic value of green roofs. Even though this is quite a wide range, it will define the limits based on which the scenic value can be added to the CBA.
Next, we need to (1) find the value that inhabitants place on small parks (2) isolate the scenic value from other values of urban green, for example, recreational values. To this end, we use evidence from housing transactions in Helsinki and analyze the values that individuals have placed on different proximities to different types of parks and, based on this evidence, we infer the effects of increasing urban green in Helsinki. For robustness, we also repeated the analysis in another city in Finland (Table 4c)
A spatial hedonic specification was estimated on a sample of approximately 6500 apartment transactions that took place in Helsinki’s city center between 2008 and 2011. The observed dependent variable in this context is the purchase price/m
$^{2}$
of the property, which can be interpreted as the present value of the stream of expected rental values; rental price is a function of a vector of amenities, of which the view to urban green is one component (Freeman et al., Reference Freeman, Herriges and King2014). In our analysis, we define the scenic value to be the value that residents in the immediate vicinity (defined below) of urban green receive compared to those farther from it.
Previous work on the dataset showed that the value of urban green is highest in the city center and diminishes rapidly when moving away. For this reason, we focused on Helsinki’s center in which there is the greatest potential for incremental value. We defined the point of highest density of commercial establishments as Helsinki’s central business district (CBD) and then selected property transactions within 3 km from the CBD.
Urban parks are the predominant type of urban green in the study area; for Helsinki, the term refers to areas with a mix of trees, other vegetation, and artificial configurations like walkways and playgrounds. We split parks into two categories (“big parks” larger than 1 ha and “small parks” 1 ha or smaller), since we wanted to find out whether even small areas devoted to urban green can have positive effects on the housing market. Dummy variables were created for properties that are within 30, 50, and 70 meters from big and small parks. These alternative distances to a park were tested to see how varying the distance to a park affects the average WTP. Figure 1 displays the study area and park categories. The variables connected to each transaction are listed in Table 3.
Figure 1 Helsinki’s CBD and park categories.
Table 3 The variables of the analysis and their mean values in Helsinki’s CBD.
$^{\text{(a)}}$
Refers to loans undertaken by the housing committee for large maintenance tasks (e.g., roof, pipes or structural renovations), distributed to each property usually according to its size.
$^{\text{(a)}}$
Figures for the “within 30 m” category.
For this estimation, we have used a spatial error regression specification:
$$\begin{eqnarray}y_{i}=a+\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D6FD}S_{ki}+\mathop{\sum }_{j=1}^{n}\unicode[STIX]{x1D6FE}N_{\!ji}+\mathop{\sum }_{l=1}^{n}\unicode[STIX]{x1D6FE}E_{li}+\unicode[STIX]{x1D706}Wu_{i}+e_{i}.\end{eqnarray}$$
In equation (4),
$W$
is a spatial weights matrix (in this case produced by a 1st order Moore neighborhood rule), Wu a spatially autocorrelated error term,
$e$
a random error term,
$\unicode[STIX]{x1D6FC}$
the intercept, and
$\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D706}$
coefficients. The beta coefficients are interpreted as in nonspatial OLS regressions. The spatial error term lambda (
$\unicode[STIX]{x1D706}$
) is treated in this analysis as an uninterpretable instrument that clears residuals from spatial autocorrelation. Equation (4) includes structural, neighborhood, and environmental attributes of housing (Dubin, Reference Dubin1992):
S
is a vector of k structural attributes of a property,
N
is a vector of j attributes describing the neighborhood of the property, and
E
is a vector of l attributes describing aspects of the natural environment in the vicinity of the property. Vector E contains the target variables of this analysis (direct view to small and big parks). Equation (4) was estimated on the previously described sample and variables of Table 3. Pre- and post-estimation tests verified the assumption of spatially autocorrelated residuals and indicated that the spatial error model of equation (4) as the preferred specification as compared to a nonspatial OLS regression or alternative spatial specifications.
Table 4a–c Hedonic regression results for the CBDs of Helsinki and Pori (dependent variable: Price/m2 in € thousand, 2011 prices)
Significance ranges: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1.
4.2 Estimation results and interpretation
First, we estimated the value of any urban park, regardless of its size, within 30, 50 and 70 m of a building (Table 4a). The value of a presence of urban green is significant in all of the tested distances. The average marginal value is highest for buildings within the 30 m radius from a park and decreases when increasing the allowed distance from the park. The average values for the respective distances are 134€, 122€ and 94€ per m
$^{\text{2}}$
of living space. It has been empirically shown (Crompton, Reference Crompton2001) that the incremental of value attributable to the park significantly increases with the size of the park; for instance, in an early study by Coughlin and Kawasima (Reference Coughlin and Kawasima1973) it was found that a 5-acre park (2 ha) had almost five times the increase in the price of a dwelling unit than a 1-acre park (0.4 ha) and it was also found that the incremental value attributable to a small park decreased more quickly as the distance to the park increased. Our findings were similar regarding the effects of park size (Table 4b). The value of a big park for buildings within 30 m from the park was in average 200€ per square meter while the value of a small park was 130€. However, when increasing the distance radius including also buildings within 50 m from the parks, the average value of a big park was almost 250€ while the average value of a small park was around 50€. We interpret that this shows that the recreational value of a big park is still available when allowing a longer distance, but the presence of a small park bears mainly scenic value that goes down quickly as the view gets blocked.
Based on GIS analysis, small parks are mainly visible to those building within 30 m radius, and the view is more or less blocked when increasing the radius. However, all of the services related to recreational or other use values of the parks are still present and (almost) as easily available at the radius between 30 and 50 m from the small parks. Consequently, we take the value that is attached to small parks at 30–50 m radius and deduct that from the total value of the parks available between 0 and 30 m radii. We define the residual as the “scenic value” of small parks. This is around 110€ per square meter as the value of a small park decreases fast when increasing the distance as expected from the literature, and the mean value attached to a small patch of urban green is only around 20€ per square meter at the distance between 30 and 50 m from the park.
In percentage terms, the range for the scenic benefit of the green roofs is 0–2.3% without taking the vertical location of the green roof into account. However, this undermines the fact that compared to a park, the view to a green roof is limited, as only those neighbors that live on a higher floor compared to the green roof, are able to actually enjoy the view. Consequently, the building heights distribution needs to be taken into account. As in figure 2, around 37% of the buildings in the study area are buildings with 1–2 floors, and 63% of the buildings have three or more floors. If all the green roofs are installed on the buildings with either one or two floors, we assume that out of the buildings with 1–2 floors 25% of the residents live on a higher level than the green roofs, and 66% of the residents on a 3
$+$
building live on a higher level than the green roofs. In total, the vertical location of the green roof would limit the view from 46% of those apartments that would have had a view to an urban park. To take this into account, the high estimate for the value of having a green roof within 30 m from the building drops to 1.2%.
Figure 2 The distribution of building heights in Helsinki, Finland.
The only comparison in the literature is Bianchini and Hewage (Reference Bianchini and Hewage2012) in which the value of properties was assumed to be 2%–5% higher for extensive green roofs. Based on our results, we recommend to use value increases between 0% and 1.2% for those properties in the immediate vicinity (within 30 m) of a green roof.
4.3 Simulation of the scenic value in Helsinki
We analyze two scenarios (Figure 2): (1) high benefit simulation (Simulation 1) in which all the roofs that are greened are placed in the CBD, which would result in 50% of roofs in the CBD being green and would yield the highest pay-off and (2) low benefit simulation (Simulation (2) with equal distribution of green roofs across the broader urban area of Helsinki in which 10% of the CBD roof tops are greened. In both of the cases we assume that (i) the average marginal value of increase in urban green drops linearly to zero once the last simulated green roof has been installed, and (ii) the average marginal value of the scenic value of a green roof is between 0% and 1.2% as explained above.
Figure 3 The simulations (1) and (2) of green roof cover in Helsinki CBD.
We start by surveying the current green cover in Helsinki and adding green space to those areas with the least green space. Before the simulation (1) 26% or 629 buildings out of 2415 in our delineation of Helsinki’s CDB were situated within 50 m from a big park or within 30 m from a small park. The total amount of roof area in the city of Helsinki is around 1740 ha, approximately 19% of 334 ha of which is located in the study area (CBD). In simulation 1, 174 ha green roofs would all be located in the CBD. We simulated this additional green cover by placing green roofs in a GIS software in those areas that currently exhibit the highest distances to urban parks. We selected adjacent rooftops that would generate large green cover areas. Our selection for simulation (1) is shown in figure 3 on the left hand side. After the simulation, 68% of the buildings or 1652 of the buildings in the CBD had a presence of either a green roof or a small park within 30 meters, or a big park within 50 meters. The residential living area in the CBD is around 550 ha. (Helsinki Statistics). With assumptions (i) and (ii), the benefit of a green roof would be between 0 and 37€
$/\text{m}^{2}.$
The 37€
$/\text{m}^{2}$
can be seen as the upper limit for the value of the scenic benefit of green roofs in Helsinki as it relies on the assumptions that (1) green roofs are optimally placed in those areas with the least amount of urban green and highest property values, (2) green roofs carry the same scenic value as small urban parks and (3) they are optimally placed on the low-rise buildings.
The second simulation was done by assuming a uniform distribution of green roofs across the city of Helsinki, so that only 10% of the CDB roofs were greened. We again, simulated green roof cover by placing green roofs to those areas of CBD with the lowest proximity to urban green depicted in figure 3 on the right hand side. After the simulation, 38% of the buildings had either a green roof or a small park within 30 m, or a big park within 50 m from the building. With assumptions (i) and (ii), the value of the increase per installed green roof would be 0–17€
$/\text{m}^{2}$
. This range can be regarded as more realistic, as it relies only on assumptions that (1) green roofs would carry value on those areas with the lowest amount of urban green (CBD), (2) the scenic value would be close to that of a small park without its use values, and (3) the value of the green roofs last green installed last green roofs would approach zero as the supply of urban green is less scarce.
Out of the other benefits, only the air-quality benefits can be partly included twice if the scenic benefits are fully incorporated into the CBA. If air-quality benefits are conservatively – to avoid double counting – reduced from the scenic benefits of the green roofs, the scenic benefits of green roofs are between 0 and 10€
$/\text{m}^{2}$
5 Costs of green roofs
The main barrier for green roof implementation is the additional costs compared to standard roof solutions (e.g., Berardi et al., Reference Berardi, Hosein, Hoseini and Hoseini2014; Clark et al., Reference Clark, Adriaens and Talbot2008). The cost levels for extensive green roofs exhibit significant differences across the world. The high estimate of the literature can be found in Sproul et al. (Reference Sproul, Wan, Mandel and Rosenfeld2013) in which cost level of 150€
$/\text{m}^{2}$
for extensive green roofs is assumed. Almost as high figures were reported in Bianchini and Hewage (Reference Bianchini and Hewage2012) in which the costs of extensive green roofs were approximated to be 90€
$/\text{m}^{2}$
–113€
$/\text{m}^{2}$
in British Columbia, Canada. However, neither of the aforementioned studies elaborate whether the costs were additional costs compared to reference roof or total costs. Additional costs of 68€
$/\text{m}^{2}$
were applied in a study by Carter et al. (Reference Carter and Keeler2008) in City of Atlanta. In a literature review report from 2007, Toronto Region Conservation (Toronto Region Conservation (TRC), 2007) confirms the wide range of initial capital costs across the world. In North America, with very low implementation rates of green roofs across the continent, the additional costs of extensive green roofs ranged from 45€
$/\text{m}^{2}$
to 190€
$/\text{m}^{2}$
. However, in Germany with established green roofs industry and higher implementation rates, the additional costs were only around 13€
$/\text{m}^{2}$
–41€
$/\text{m}^{2}$
.
To get an appreciation of the cost level in Finland, green roof suppliers were interviewed. Our example roofs are built on a supporting structure and the cost estimates are based on the assumption that the roof will be built on an existing building or to a new building with sufficient loading capacity. This section is an updated version of chapter 5 of a project report by Nurmi, Votsis, Perrels and Lehvävirta (Reference Nurmi, Votsis, Perrels and Lehvävirta2013).
-
∙ The standard bitumen roof costs are around 35€
$/\text{m}^{\text{2}}$
(
$+$
VAT 24%,
$=$
43€
$/\text{m}^{\text{2}}$
). This includes rubber bitumen layers, waterproofing and installation. These installations are needed also under green roofs (with some modifications, the costs remain approximately the same). -
∙ The additional costs to install a green roof are on average around 50€
$/\text{m}^{\text{2}}$
(
$+$
VAT 24 %,
$=$
62€
$/\text{m}^{\text{2}}$
). The additional costs include the sedum mats (53% of the additional costs), the installation costs (around 24% of the additional costs) and taxes (23%).
The least expensive green roof is achieved by installing a drainage layer, filter fabric, substrate, and plants from cuttings and seeds. These green roofs may allow for more plant diversity if a deeper substrate is used, but require more structural capacity to hold the weight of the soil. They are generally at least 20% less expensive than ready-made green roof sedum mat systems, the total extra costs being around 40€
$/\text{m}^{\text{2}}$
(
$+$
VAT 24%).
Cost estimates from Finland are very high in comparison with estimates in those countries with established green roof industries, such as Germany. The low price level in Germany is a result of more than thirty years of market development. In Switzerland low cost solutions cost only around 20€
$/\text{m}^{\text{2}}$
(personal communication Brenneisen, Reference Brenneisen2013) despite the high price level of the country. In new markets competition is scarce and no economies of scale exist, labor is more expensive since installers lack experience, and there is a tendency to use custom-design systems. Obviously, adopting low cost techniques would support the proliferation of green roofs. The additional costs of a green roof have gone down by 33%–50% (Toronto Region Conservation (TRC), 2007) since the industry has established itself. In our scenarios we assume that the same would happen in Finland if 10% of roof top area in Helsinki was greened. For comparison in Basel, of which around 30% of flat roofs or 3% of total roof area is green, the additional costs have gone down from around 80 euros to only around 15 euros per square meter (ZHAW, 2013), making our cost-reduction estimate fairly conservative.
6 Results of the cost-benefit analysis
In this section, we wrap up the estimates of benefits and costs in Helsinki, Finland. First, we discuss the private incentives to build green roofs. Next, we take a look at the public benefits assuming that 10% of Helsinki’s roofs are converted to green roofs. By modifying the values of different ES based on the target cities characteristics as described in Section 4, it is then easy to see how the cost-benefit ratio would change when replacing Helsinki for another case-study location.
Table 5a Private Cost-benefit analysis, with 90%–110% sensitivity analysis.
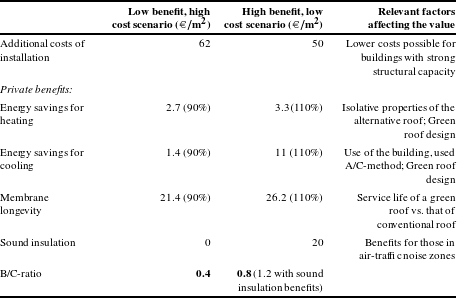
6.1 Private benefits versus private costs
Only a part of the aforementioned benefits accrue to the owner of the property where the green roof is installed, however all the costs are levied on the private decision maker (Table 5a). A higher price of the roof also increases the value-added tax burden on the investor. The private benefits and costs also include avoided and incurred tax costs (namely VAT) for the property owner.
In Table 5a we list the private costs and benefits. All of these benefits are of the same nature – they are avoided costs for the property owner and represent the WTP. These kinds of benefits can be summed together (as shown in Section 2) and are the same for any building owner. The analysis shows that the current level of costs is too high compared to the benefits for a private decision maker to have an incentive to install a green roof, the B/C-ratio is between 0.4 and 0.8 and the NPV is
$-$
36.5–
$-$
9.5€
$/\text{m}^{2}$
. The expected value for NPV is
$-$
257€
$/\text{m}^{2},$
assuming uniform distribution for other benefits except sound insulation (0 for 98.5%; 20€
$/\text{m}^{2}$
for 1.5% population under flight routes) and taking into account that both cooling and heating benefits are hard to achieve with the same design of the green roof. These results are in line with results from other cities as indicated by the literature review. We present both the lower and higher bounds for the benefits and vice versa for the costs.
Table 5b Social Cost-benefit analysis.
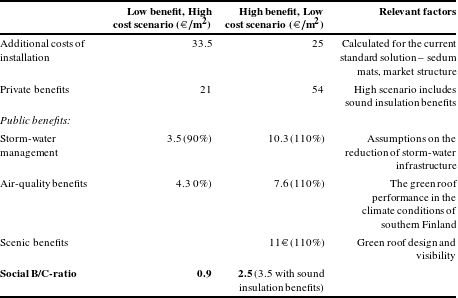
6.2 Social cost-benefit analysis with 10% installation scenario in Helsinki
Next, we take a look at the social costs and benefits in a scenario in which green roofs have been installed in 10% of the building tops in Helsinki. In addition to the private ones, public benefits are expected to emerge. We assume that higher implementation rates would lower the additional costs of green roofs by at least 33% and at most 50%, as explained in Section 5. In Table 5b we list the social benefits including both private and public. Here we also exclude taxes (from the membrane longevity and sound insulation benefits) from the calculations – unlike in Table 5a – as we are interested in the social benefits instead of private incentives. The social B/C-ratio is between 0.9 and 2.1, and NPV is between
$-$
4.7 and 37.9€
$/\text{m}^{2}$
and possibly even higher on those areas with air-traffic noise. The expected value for the social NPV is 13.4€
$/\text{m}^{2}$
with the same assumptions as for the private benefits. The focus of this study – the scenic benefits – represent 13% of the total benefits in the high estimate case, or around 13% of the expected value of the benefits. Consequently, while not insignificant, the addition of the scenic benefits only strengthens the conclusion that while the private benefits are not high enough to cover the installation costs, the social CBA shows positive results.
7 Conclusions
The aim of this article was to discuss the economic benefits and costs of thin, lightweight green roofs with special emphasis on the previously unmeasured benefit of the increase in the scenic value.
The main conclusions of green roof CBA in Helsinki are:
-
(1) As the reviewed literature would suggest, the private benefits are usually not high enough to cover the current level of additional private costs. In Helsinki, even in the low cost-high benefit scenario the private B/C-ratio is under 1. However, in some circumstances, in warm climates the cooling energy savings can drive even the private B/C-ratio slightly over 1. The most important parameters determining the private benefits are: (1) cost of the reference roof so that higher reference roof price increases the benefits, (2) temperature profile of the location so that higher temperatures increase the benefits, (3) energy price so that higher energy price increases the benefits and (4) building code of the roof so that higher coefficient of heat loss increases the benefit.
-
(2) When adding up private and public benefits, the benefits would surpass the costs in most of the cases, especially if a higher implementation rate drives down the costs. The factors that have a positive effect on the public benefits, which are at a relatively low level in Helsinki, are: (1) the average annual precipitation and frequency of extreme rainfall, (2) the maintenance backlog of the current sewer system and (3) the concentration of particulate matter. As also the cost level of green roofs is high in Finland, the social B/C-ratios can be expected to be higher than those reported in this study in most other cities of similar size or larger.
-
(3) Scenic benefits have a potential to be a significant factor in green roof CBA; the increase in the property values in the buildings within 30 m of a green roof was assessed to be between 0% and 1.2%. Helsinki is a green city compared to many other cities, thus benefits are likely to be higher in many other cities with less vegetation cover. Compared to other benefits, scenic benefits represent 13% of the total benefits of the high estimate case for social benefits, or around 13% of the expected value of the benefits.
In this study, we were able to quantify several green roof benefits, including membrane longevity, sound insulation, energy cost savings, air-quality, storm-water management and scenic benefits. Many studies also indicate that green roofs have the potential to increase urban biodiversity, but this benefit was not in the scope of this article. The level of benefits was found to be positively correlated with outside temperature (Section 3.2), level of precipitation and frequency of extreme downpours (Section 3.4), level of urbanization, and proximity to city center (Section 4). Presumably climate change and urbanization will drive the level of benefits higher in the future.
The costs of green roof installation were gathered by supplier interviews. The additional costs of a green roof in Finland are around 50–60€
$/\text{m}^{2}$
making them more than two times more expensive than the reference roof. Cost estimates were significantly higher than in countries with long traditions in green roof implementation, namely Switzerland and Germany. The cost-benefit calculations together with the reviewed literature show that private benefits are usually not high enough to justify a green roof installation for a private decision maker. It can be expected that the level of implementation stays low in most cities with comparable climatic and ambient conditions as Helsinki without corrective policy instruments. Policy instruments could include supportive policies that turn part of the public benefits into private ones (e.g., reduction in storm-water fee). In addition, research projects and demonstration projects could drive the benefits up and the costs down.
The two main limitations of this article are related to scarcity of evidence of the impacts of green roofs in different environments. First, many of the natural processes of green roofs have been studied only in a few sites, for example, we had to rely on figures of the emission uptake in Toronto and Chicago. More research is needed in local climate conditions to obtain more reliable figures. The second limitation is of the same nature: we had to estimate the upper limit of the scenic value of green roofs by indirect means by looking at the value people attach to the presence of an urban park. We assumed that the value of the presence of an urban park is comparable to that of a presence of a green roof but took into account the reduction in the visibility.
Supplementary material
To view supplementary material for this article, please visit http://dx.doi.org/10.10 17/bca.2016.18.
Acknowledgments
This article is based on the dissertation work of Väinö Nurmi funded by the Nessling Foundation and on the dissertation work of Athanasios Votsis funded jointly by the Finnish Academy and the Helsinki University Centre for Environment (HENVI).
