2 Model

The theoretical model closely follows Whitehead (Reference Whitehead1995). Suppose anglers have the utility function, $u(x_{j},q_{j})$ , where $x_{j}$ is the number of fishing trips at site $j$ and $q_{j}$ is fishing quality (e.g., catch rates) at site $j$ . The expenditure function is $e(p_{j},q_{j},u)$ , where $p_{j}$ is the price, measured by the travel cost, of fishing trips at site $j$ . Willingness to pay is the maximum amount of money anglers would give up for the improvement in fishing quality resulting from the stocking program at site $j=1$ , $q_{1}^{\ast }$ . Substitution of the indirect utility function, $v(p_{j},q_{j},y)$ where $y$ is income, yields $\text{WTP}=e[p_{1},p_{2},q_{1},q_{2},v(p_{1},p_{2},q_{1}^{\ast },q_{2},y)]-y$ , for $j=1,2$ . When the quality change at site $j=1$ is omitted and quality at site $j=2$ is constant, the linear willingness to pay function is $\text{WTP}=\unicode[STIX]{x1D6FC}_{0}+\unicode[STIX]{x1D6FC}_{1}p_{1}+\unicode[STIX]{x1D6FC}_{2}p_{2}+\unicode[STIX]{x1D6FC}_{3}y+e$ , where $e$ is the error term, $\unicode[STIX]{x1D6FC}_{1}<0$ if recreation trips to site $j=1$ increase with the quality improvement, $\unicode[STIX]{x1D6FC}_{2}>0$ if recreation trips to site $j=2$ decrease and $\unicode[STIX]{x1D6FC}_{3}>0$ if the quality change is a normal good.

We use the Cameron (Reference Cameron1988) censored logistic regression model to estimate $\text{WTP}$ and its determinants associated with the red drum stocking program. The dependent variable in the model is the dichotomous choice “yes” response. The logistic regression model estimates the probability that willingness to pay is greater than or equal to the bid amount, $\Pr [\mathit{yes}]=\Pr [(\boldsymbol{\unicode[STIX]{x1D6FE}}^{\prime }X-B)/\unicode[STIX]{x1D705}\geqslant e/\unicode[STIX]{x1D705}]$ , where $\boldsymbol{\unicode[STIX]{x1D6FE}}$ is a logit coefficient vector, $B$ is the bid and $-1/\unicode[STIX]{x1D705}$ is the logit coefficient on the bid amount. The means of the independent variables are used to estimate willingness to pay, $\widehat{\text{WTP}}=-(\hat{\boldsymbol{\unicode[STIX]{x1D6FE}}}/\hat{\unicode[STIX]{x1D705}})^{\prime }\bar{X}$ . Standard errors of $\text{WTP}$ and marginal effects are constructed using the Delta Method (Cameron, Reference Cameron1991; Greene, Reference Greene2003).

We investigate the convergent validity of the $\text{WTP}$ estimate by testing for the consistency of the value of the estimate of additional fishing trips as a result of the program from both CVM and travel cost method. The estimate is constructed using the consumer surplus estimate from the travel cost method and the own-price coefficient in the $\text{WTP}$ model. From the travel cost method, the demand for fishing trips is $x_{1}(p_{1},p_{2},q_{1},q_{2},y)$ . If this demand is estimated with the semilog functional form as is common with count data models such as the negative binomial (Parsons, Reference Parsons, Champ, Boyle and Brown2017), then the consumer surplus per fishing trip is $\text{CS}/x=-1/\unicode[STIX]{x1D6FD}_{1}$ , where $\unicode[STIX]{x1D6FD}_{1}<0$ is the coefficient on $p_{1}$ . The negative of the coefficient on the own-price variable in the $\text{WTP}$ model is an estimate of the change in the number of fishing trips that would result from the stocking program, $\unicode[STIX]{x1D6E5}x=-\hat{\unicode[STIX]{x1D6FC}}_{1}=x_{1}(q_{1}^{\ast })-x_{1}(q_{1})$ , assuming the marginal cost of utility across quality levels approaches one (Whitehead, Reference Whitehead1995). An estimate of the value of the change in trips that would result from the stocking program is $\unicode[STIX]{x1D6E5}\text{CS}=\unicode[STIX]{x1D6E5}x/\unicode[STIX]{x1D6FD}_{1}$ . The null hypothesis for the convergent validity of the contingent valuation and travel cost demand methods is $\widehat{\text{WTP}}=\hat{\unicode[STIX]{x1D6FC}}_{1}/\unicode[STIX]{x1D6FD}_{1}.$ The alternative hypothesis is the inequality.

4 Data

Respondents were excluded from the CVM analysis if their returned questionnaire had missing data for key response variables (e.g., income, fishing trips). The total respondents used in this analysis were 1,772. The willingness to pay yes responses are presented in Table 1. As the bid amount rises from $5 to $50 the probability of a yes response falls from 61% to 23%. When the yes responses are recoded so that only those who are certain at the level 7 and above are considered, then the probability falls from 50% to 17%. Most conservatively, when the yes responses are recoded so that only those who are certain at the level 10 are considered true yes responses then the probability falls from 31% to 15%.

The variables used in the logistic regression analysis are fishing trips, travel costs and income (Table 2). The average number of fishing trips for red drum was 6.Footnote ⁵ The average before taxes household income in 2003 was $81 thousand (Table 2) with 52% reported receiving a state tax refund for 2004. Travel costs, $tc$ , are measured including transportation and time costs, $tc=c\times d+\unicode[STIX]{x1D6FF}(w\times d/mph)$ , where $d$ is the round trip distance for each individual to each site. Transportation costs, $c$ , are calculated at $0.30 per mile traveled. Time costs are calculated using estimated travel times (assuming an average speed of 40 miles per hour) and the wage rate. The wage, $w$ , is measured as household income divided by 2080 hours worked. The average travel cost to the nearest South Carolina fishing site is $166. The average travel cost to the nearest Georgia site, a substitute, is $281.Footnote ⁶

Table 1 Willingness to pay responses.

Table 2 Data summary.

For variables used in analysis, average education was 15 years and average age was 47 years. The sample is 86% male and 96% Caucasian. Forty-seven percent own a boat. Eighty-two percent purchased an annual license, 33% are from the South Carolina coastal region and 39% are from the South Carolina noncoastal region.Footnote ⁷

5 Benefits

We separately estimate the recreation demand and the willingness to pay models (Table 3). All models are weighted by license type and the population of the three zones. The recreation demand model is a negative binomial regression that accounts for the count nature and overdispersion of the data (Parsons, Reference Parsons, Champ, Boyle and Brown2017). The number of days fished for red drum decreases with the own price and increases with the cross-price variables. Income has no statistically significant effect on days fished. In the willingness to pay model, we present estimates using the yes variable recoded for respondents who are certain at the level 7 or higher. As the bid increases the probability of a yes response decreases. As the own-price variable increases the probability of a yes response decreases. According to the theory described above, this indicates that fishing trips would increase with the stocking program. As income increases the probability of a yes response increases, indicating that the stocking program is a normal good. The cross-price variable has no statistically significant effect on the probability of a yes response, indicating that fishing trips in Georgia would not change. Similar qualitative results are found in the logit models for the unrecoded (Yes1) and recoded at 10 yes variables (Yes10).Footnote ⁸

Table 3 Recreation demand and contingent valuation regression models. ^a

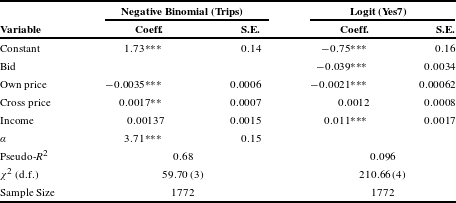
a Regression models are weighted.

*** Significant at $p=0.01$ .

** Significant at $p=0.05$ .

* Significant at $p=0.10$ .

In Table 4, we present $\text{WTP}$ and $\unicode[STIX]{x1D6E5}\text{CS}$ estimates. Since the probability of a yes response approaches 1 in the negative range of the bid values, we estimate willingness to pay over the nonnegative portion of the logistic distribution, $\text{WTP}=-ln(1+e^{\boldsymbol{\unicode[STIX]{x1D6FE}}^{\prime }\bar{X}})/\unicode[STIX]{x1D705}$ (Hanemann, Reference Hanemann1989). The mean willingness to pay from the unrecoded yes responses (Yes1) is $25. Mean willingness to pay with yes responses recoded at 7 (Yes7) and 10 (Yes10) are $19 and $8. The consumer surplus per fishing trip from the recreation demand model is $285 (standard error, s.e.  $=$  48). The change in fishing trip estimates from the Yes1, Yes7 and Yes10 willingness to pay models are 0.052 (s.e.  $=$  0.015), 0.053 (s.e.  $=$  0.016) and 0.0072 (s.e.  $=$  0.015), respectively. The consumer surplus for the change in fishing trips is $15, $15 and $2, respectively, in the Yes1, Yes7 and Yes10 models (Table 4). The difference in the change in consumer surplus ( $\unicode[STIX]{x1D6E5}\text{CS}$ ) and willingness to pay ( $\text{WTP}$ ) is not statistically significant in the Yes7 model since the 95% confidence intervals are overlapping. In the Yes1 model, the willingness to pay estimate is significantly greater than the change in consumer surplus estimate. In the Yes10 model the change in consumer surplus estimate is not statistically different from zero. We use these results to justify use of the Yes7 willingness to pay estimate, which is convergent valid with the travel cost demand model estimate, as our base case in the benefit-cost analysis. We conduct sensitivity analysis with the Yes1 and Yes10 willingness to pay estimates.

Table 4 Individual benefit estimates.

a Difference in $\unicode[STIX]{x1D6E5}\text{CS}$ and $\text{WTP}$ is not statistically different from zero $(p=0.05)$ .

6 Costs

Costs are the explicit government costs incurred by the SCDNR for the seasonal stocking (August through October) of red drum juveniles (20–50 mm TL) during 2005 (Table 5) and based upon the assumption that the maximum annual capacity output of juvenile red drum by SCDNR was needed for the seasonal stocking (Jenkins, Denson, Bridgham, Collins & Smith, Reference Jenkins, Denson, Bridgham, Collins and Smith2004b ). This assumption was based on existing SCDNR Marine Resources Division aquaculture facilities, mainly the Waddell Mariculture Center (WMC). Operating costs were estimated from actual facility activities specific to red drum juvenile cultivation and stocking research, such as electricity cost for juvenile pond aeration and broodstock tanks as well as personnel costs, including direct supervision and administration. Estimated annual administrative costs, an indirect cost category associated with personnel management, purchasing, accounting, etc., were calculated as 20% of direct personnel costs.

Table 5 Estimated costs of a South Carolina red drum stocking program in 2005 US $.

Initial investment costs were based on actual repair and construction costs associated with 2004–05 improvements in the WMC as well as the cost of equipment purchased for the red drum stocking program. Allocating major WMC improvement costs to the program was considered a conservative treatment of initial investment costs directly related to red drum stocking because WMC improvements also benefited other SCDNR programs. After the initial investment, replacement costs for durable items such as equipment needed in the harvest and transport of juveniles were also periodically added to the projected annual stocking program costs.

Based upon the use of existing MRD facilities used for mariculture programs, it was estimated that about 2.9 million red drum juveniles $({\sim}30.0~\text{mm}~\text{TL})$ (Personal communication, August 6, 2007, M. Denson, SCDNR, Marine Resources Division, Charleston, SC) could be produced and released at a total annualized operating cost including indirect administrative costs of approximately $372,000 or $0.13 per red drum juvenile stocked by SCDNR (Table 5).Footnote ⁹ Initial incremental investment, mainly total fixed costs of equipment and improvements in the WMC needed for the red drum stocking program, was approximately $558,000 (Table 5). Projected annual replacement costs for durable items after 2005, e.g., equipment (e.g., tractors) needed in the harvest and transport of juveniles, were also included in the projected annual stocking program costs (Table 5).

7 Net benefits

A standard BCA decision rule about whether a government program can be justified on economic principles is NPV, i.e., the discounted value of projected net economic benefits

(1) $$\begin{eqnarray}\text{NPV}=\mathop{\sum }_{t=0}^{T}\frac{(B_{t}-C_{t})}{(1+d)^{t}}\end{eqnarray}$$

where $B_{t}$ is the estimated willingness to pay values (the benefits of the project in year $t$ , $t=0$ to $T$ and year $2005=1$ ), $C_{t}$ are the government costs of the red drum stocking program in year $t$ and $d$ is the real social discount rate. As a simple rule, a positive $\text{NPV}$ in the context of a “stand-alone” program (i.e., a simple comparison to the status quo) would lead to the acceptance of a program, while a negative $\text{NPV}$ would signal a rejection of the program. All benefits and costs are standardized to constant 2005 dollars with the CPI. The social discount rate used in this study was 3.5% (Moore, Boardman, Vining, Weimer & Greenberg, Reference Moore, Boardman, Vining, Weimer and Greenberg2004). The time period of 10 years was based on the plan that the statewide hatchery release of red drum would be limited to a 5–10-year period (Smith et al., Reference Smith, Jenkins, Denson and Collins2004).

Individual benefit estimates were aggregated over the 110,579 (FY04) South Carolina license holders 20 years and older. Annual net benefits were extrapolated over a 10-year period starting in 2005 using the base case and upper and lower benefit levels (Table 6). For each benefit level, projected net benefits were positive for all years. The NPVs for the baseline benefit level is $14.6 million. The NPV using the low and high benefit levels is $4.5 million and $20 million.

Table 6 Estimated constant annual benefits and operating costs generated by the SC red drum stocking program (2005 US $ in thousands).

a Low, base and high are WTP estimates from Table 4 multiplied by 110,579 anglers.

The NPVs are considered conservative for several reasons. First, the extrapolation of licensee benefits was based on the applicable number of licenses sold remaining fixed at the FY04 level even though the number had increased an average of 4.9% per fiscal year during the FY04–FY08 period with 135,902 licenses sold in FY08. Second, saltwater shore-based anglers were not included in the projected aggregate benefit estimates because anglers fishing from shore-based sites were not required to purchase a saltwater recreational fishing license in FY04. In addition, the donation payment vehicle used in this study is also likely to elicit lower estimates of willingness to pay relative to a referendum vote (Champ et al., Reference Champ, Bishop, Brown and McCollum1997; Carson & Groves, Reference Carson and Groves2007). Lastly, benefits that might potentially stem from the utility of equipment and/or other improvements (i.e., horizon values) funded through the red drum stocking after 10 years, especially infrastructure improvements at the Waddell Mariculture Center, were not considered.