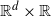1. Introduction
In the present paper we investigate the extremal behaviour of a space-time random field ![]() $(X_{v,t})_{{(v,t)\in B\times [0, T]}}$ defined by
$(X_{v,t})_{{(v,t)\in B\times [0, T]}}$ defined by
where M is an infinitely divisible, independently scattered random measure on ![]() ${\mathbb{R}}^{d+1}$,
${\mathbb{R}}^{d+1}$, ![]() $d\in\mathbb{N}$, f is some kernel function, and B and [0, T] are compact index sets. We think of v and t as the position in space and time, respectively. Similarly, the first d coordinates of M refer to the spatial position, while the last coordinate is interpreted as time. The random field defined in (1.1) is a causal model in the sense that
$d\in\mathbb{N}$, f is some kernel function, and B and [0, T] are compact index sets. We think of v and t as the position in space and time, respectively. Similarly, the first d coordinates of M refer to the spatial position, while the last coordinate is interpreted as time. The random field defined in (1.1) is a causal model in the sense that ![]() $X_{v,t}$ only depends on the noise, accounted for by M, up to time t, i.e. the restriction of M to
$X_{v,t}$ only depends on the noise, accounted for by M, up to time t, i.e. the restriction of M to ![]() ${\mathbb{R}^d}\times({-}\infty,t]$. We shall make continuity assumptions on f ensuring that X is continuous in the space direction. Discontinuities in the time direction will however be possible, and we therefore have to pay particular attention to the assumptions on f to obtain sample paths that are both continuous in space and càdlàg in time; see Definition 2.1, Assumption 2.2, and Theorem 5.3 below.
${\mathbb{R}^d}\times({-}\infty,t]$. We shall make continuity assumptions on f ensuring that X is continuous in the space direction. Discontinuities in the time direction will however be possible, and we therefore have to pay particular attention to the assumptions on f to obtain sample paths that are both continuous in space and càdlàg in time; see Definition 2.1, Assumption 2.2, and Theorem 5.3 below.
Lévy-driven moving average models, where a kernel function is integrated with respect to a Lévy basis, provide a flexible and tractable modelling framework and have been used for a variety of modelling purposes. Recent applications that include both time and space, similarly to (1.1), include modelling of turbulent flows [Reference Barndorff-Nielsen and Schmiegel5] and growth processes [Reference Jónsdóttir, Schmiegel and Jensen13]. Spatial models without an additional time axis have, for example, been used to define Cox point processes [Reference Hellmund, Prokešová and Jensen11] and have served as a modelling framework for brain imaging data [Reference Jónsdóttir, Rønn-Nielsen, Mouridsen and Jensen12, Reference Rønn-Nielsen, Sporring and Jensen22]. Lévy-based models for a stochastic process in time have gained recent popularity in finance. A simple example is a Lévy-driven Ornstein–Uhlenbeck process, with ![]() $f(t)={\mathrm{e}}^{-\lambda t}$, which has been used as a model for option pricing, for example, as illustrated in [Reference Barndorff-Nielsen and Shephard6]. In [Reference Rønn-Nielsen and Jensen21] estimators for the mean and variogram in Lévy-driven moving average models are proposed, and central limit theorems for these estimators are derived.
$f(t)={\mathrm{e}}^{-\lambda t}$, which has been used as a model for option pricing, for example, as illustrated in [Reference Barndorff-Nielsen and Shephard6]. In [Reference Rønn-Nielsen and Jensen21] estimators for the mean and variogram in Lévy-driven moving average models are proposed, and central limit theorems for these estimators are derived.
In this paper we will assume that the Lévy measure ![]() $\rho$ of the random measure M has a convolution equivalent right tail [Reference Cline8, Reference Cline9, Reference Pakes16] with index
$\rho$ of the random measure M has a convolution equivalent right tail [Reference Cline8, Reference Cline9, Reference Pakes16] with index ![]() $\beta >0$, with the notation
$\beta >0$, with the notation ![]() $\mathcal{S}_{\beta}$ for this class of probability measures; see (2.2) and (2.3) below. Measures with a convolution equivalent tail cover the important cases of an inverse Gaussian and a normal inverse Gaussian (NIG) basis, respectively; see [Reference Rønn-Nielsen and Jensen19] and in particular examples 2.1 and 2.2 therein. We show that certain functionals of the field will have a right tail that is equivalent to the tail of the underlying Lévy measure. More precisely, we show that for a functional
$\mathcal{S}_{\beta}$ for this class of probability measures; see (2.2) and (2.3) below. Measures with a convolution equivalent tail cover the important cases of an inverse Gaussian and a normal inverse Gaussian (NIG) basis, respectively; see [Reference Rønn-Nielsen and Jensen19] and in particular examples 2.1 and 2.2 therein. We show that certain functionals of the field will have a right tail that is equivalent to the tail of the underlying Lévy measure. More precisely, we show that for a functional ![]() $\Psi$ satisfying Assumptions 3.1–3.3 given below, there exist known constants C and c such that
$\Psi$ satisfying Assumptions 3.1–3.3 given below, there exist known constants C and c such that
We give three important examples of the functional ![]() $\Psi$ to illustrate the generality of the setting. The simplest is
$\Psi$ to illustrate the generality of the setting. The simplest is ![]() $\Psi(X)=\sup_{v,t} X_{v,t}$, where it is concluded that under appropriate assumptions on f it holds that
$\Psi(X)=\sup_{v,t} X_{v,t}$, where it is concluded that under appropriate assumptions on f it holds that ![]() $\sup_{v,t}X_{v,t}$ asymptotically has the same right tail as
$\sup_{v,t}X_{v,t}$ asymptotically has the same right tail as ![]() $\rho$.
$\rho$.
A second example (see Example 3.1) involves the spatial excursion set at level x and time t:
Under some further regularity conditions, we show that the asymptotic probability that there exists a t for which the excursion set at level x contains some rotation of an object D with a fixed radius has a tail that is equivalent to the tail of ![]() $\rho$. An asymptotic result for this probability will give information about the size of the excursion sets in the asymptotic scenario where
$\rho$. An asymptotic result for this probability will give information about the size of the excursion sets in the asymptotic scenario where ![]() $x\to\infty$. Study of the asymptotic behaviour of excursion sets has previously appeared in the literature in various contexts. In [Reference Spodarev26] an overview is given of central limit theorem results concerning the volume of the excursion set for a broad class of stationary processes. Note, however, that statements about the volume are different from statements about excursion sets given here. As explained in the paragraph on convolution equivalence below, the literature offers some, though different, asymptotic results for excursion sets in the Gaussian and the sub-exponential case.
$x\to\infty$. Study of the asymptotic behaviour of excursion sets has previously appeared in the literature in various contexts. In [Reference Spodarev26] an overview is given of central limit theorem results concerning the volume of the excursion set for a broad class of stationary processes. Note, however, that statements about the volume are different from statements about excursion sets given here. As explained in the paragraph on convolution equivalence below, the literature offers some, though different, asymptotic results for excursion sets in the Gaussian and the sub-exponential case.
In concrete applications with spatial data, possibly observed over time, it is often of interest to detect locations where the observations are significantly large. A result for the probability defined above will make it possible to detect whether a cluster of neighbouring locations, all with large observations, experienced at a certain time point within some period jointly constitutes an extreme observation. A specific application could be observations of temperatures in time and space. See e.g. [Reference Sommerfeld, Sain and Schwartzman25] for an application of excursion sets to climate data.
In the last example (see Example 3.2) we show a similar result for the probability that there is a time interval and a translation and rotation of some fixed spatial object D such that the field on average, over both the time interval and the resulting spatial object, exceeds the level x. While Example 3.1 studied the probability of the excursion set being large enough to contain (a rotation and translation of) the set D, the present example has a slightly different scope. Here we are concerned with the probability that the field in some area (in time or space) on average is large. In a climate application this could be the existence of a 24-hour average or a land area of a certain size with an average above a certain level.
In [Reference Braverman and Samorodnitsky7] sub-additive functionals of similar random fields, also with convolution equivalent tails, are studied. Here it is shown that under appropriate regularity conditions there exist constants ![]() $C_1{<}\,C_2$ and a constant c such that
$C_1{<}\,C_2$ and a constant c such that
Note that the functional ![]() $\Psi$ in the present paper is not necessarily required to be sub-additive. In particular, the functional corresponding to the excursion set framework is indeed not sub-additive.
$\Psi$ in the present paper is not necessarily required to be sub-additive. In particular, the functional corresponding to the excursion set framework is indeed not sub-additive.
In [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] the extremal behaviour of spatial random fields of the form
is studied, when M is assumed to have a convolution equivalent Lévy measure. Here assumptions are imposed on the kernel function f to ensure that ![]() $v\mapsto X_v$ is continuous. Under some further regularity conditions it is shown in [Reference Rønn-Nielsen and Jensen19] that
$v\mapsto X_v$ is continuous. Under some further regularity conditions it is shown in [Reference Rønn-Nielsen and Jensen19] that ![]() $\sup_{v\in B}X_v$ has a tail that is asymptotically equivalent to the tail of the underlying Lévy measure. In [Reference Rønn-Nielsen and Jensen20] this result is extended to the asymptotic probability that there exists a rotation of a fixed spatial object that is contained in the excursion set
$\sup_{v\in B}X_v$ has a tail that is asymptotically equivalent to the tail of the underlying Lévy measure. In [Reference Rønn-Nielsen and Jensen20] this result is extended to the asymptotic probability that there exists a rotation of a fixed spatial object that is contained in the excursion set ![]() $A_x=\{v\in B \colon X_v>x\}$. The present paper extends the results of [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] leading towards the generality of [Reference Braverman and Samorodnitsky7], as it includes time dependence in X and furthermore shows the asymptotic tail behaviour for a certain class of functionals
$A_x=\{v\in B \colon X_v>x\}$. The present paper extends the results of [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] leading towards the generality of [Reference Braverman and Samorodnitsky7], as it includes time dependence in X and furthermore shows the asymptotic tail behaviour for a certain class of functionals ![]() $\Psi$ acting on X, including those considered in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20]. By including the time dependence, time discontinuity and asymmetry are imposed on the kernel function, which necessitates particular care in the arguments. However, a few proofs are of a structure similar to those of [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] and are therefore found in the online supplementary material [Reference Stehr and Rønn-Nielsen27].
$\Psi$ acting on X, including those considered in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20]. By including the time dependence, time discontinuity and asymmetry are imposed on the kernel function, which necessitates particular care in the arguments. However, a few proofs are of a structure similar to those of [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] and are therefore found in the online supplementary material [Reference Stehr and Rønn-Nielsen27].
In [Reference Fasen10], results for a moving average process on ![]() ${\mathbb{R}}$ are derived, when the process is obtained as an integral with respect to a Lévy process with convolution equivalent tail. Here the process
${\mathbb{R}}$ are derived, when the process is obtained as an integral with respect to a Lévy process with convolution equivalent tail. Here the process ![]() $(X_t)_{t\in[0,T]}$ is given by
$(X_t)_{t\in[0,T]}$ is given by
where, again, M has a convolution equivalent Lévy measure. In agreement with the similar but more general result of the present paper for the field defined in (1.1), it is derived in [Reference Fasen10] that ![]() $\sup_{t}X_t$ has a tail that is asymptotically equivalent to this.
$\sup_{t}X_t$ has a tail that is asymptotically equivalent to this.
Note that convolution equivalent distributions, as studied in the present paper, have heavier tails than Gaussian distributions and lighter tails than those of sub-exponential distributions (including regularly varying), i.e. distributions in ![]() $\mathcal{S}_0$. For Gaussian random fields it is known that the distribution of the supremum of the field can be approximated by the expected Euler characteristic of an excursion set (see [Reference Adler and Taylor2] and references therein). The extremal behaviour of a non-Gaussian random field given by integrals with respect to an infinitely divisible random measure with a sub-exponential Lévy measure has already been studied in the literature. Results for the asymptotic distribution of the supremum are found in [Reference Rosinski and Samorodnitsky23], and these results are refined to results on asymptotics for higher-level geometric properties in [Reference Adler, Samorodnitsky and Taylor3] and [Reference Adler, Samorodnitsky and Taylor4]. The proofs rely heavily on the assumption of sub-exponential tails, where, asymptotically, the tail of a sum of independent variables is completely given in terms of that of one variable. For distributions in
$\mathcal{S}_0$. For Gaussian random fields it is known that the distribution of the supremum of the field can be approximated by the expected Euler characteristic of an excursion set (see [Reference Adler and Taylor2] and references therein). The extremal behaviour of a non-Gaussian random field given by integrals with respect to an infinitely divisible random measure with a sub-exponential Lévy measure has already been studied in the literature. Results for the asymptotic distribution of the supremum are found in [Reference Rosinski and Samorodnitsky23], and these results are refined to results on asymptotics for higher-level geometric properties in [Reference Adler, Samorodnitsky and Taylor3] and [Reference Adler, Samorodnitsky and Taylor4]. The proofs rely heavily on the assumption of sub-exponential tails, where, asymptotically, the tail of a sum of independent variables is completely given in terms of that of one variable. For distributions in ![]() $\mathcal{S}_{\beta}$ with
$\mathcal{S}_{\beta}$ with ![]() $\beta >0$ this is not the case, and the proofs therefore cannot be applied in this context.
$\beta >0$ this is not the case, and the proofs therefore cannot be applied in this context.
The paper is organized as follows. In Section 2 we formally define the random field (1.1) and introduce some necessary assumptions for the field to be well-defined and to have sample paths that are continuous in space and càdlàg in time. In Section 3 we state and prove the main result for a general functional ![]() $\Psi$ and introduce two specific examples of the functional. Some of the proofs in this section will apply many of the same techniques as in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] and are therefore deferred to the online supplementary material [Reference Stehr and Rønn-Nielsen27]. In Section 4 we state conditions for each of the two examples under which we afterwards show that the main result can be obtained. Section 5 is devoted to showing that under appropriate regularity conditions, the field defined in (1.1) is continuous in space and càdlàg in time.
$\Psi$ and introduce two specific examples of the functional. Some of the proofs in this section will apply many of the same techniques as in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20] and are therefore deferred to the online supplementary material [Reference Stehr and Rønn-Nielsen27]. In Section 4 we state conditions for each of the two examples under which we afterwards show that the main result can be obtained. Section 5 is devoted to showing that under appropriate regularity conditions, the field defined in (1.1) is continuous in space and càdlàg in time.
2. Preliminaries and initial assumptions
We define a Lévy basis to be an infinitely divisible and independently scattered random measure. Then the random measure M on ![]() ${\mathbb{R}}^{d+1}$ is independently scattered, such that for all disjoint Borel sets
${\mathbb{R}}^{d+1}$ is independently scattered, such that for all disjoint Borel sets ![]() $(A_n)_{n\in\mathbb{N}} \subseteq {\mathbb{R}}^{d+1}$ the random variables
$(A_n)_{n\in\mathbb{N}} \subseteq {\mathbb{R}}^{d+1}$ the random variables ![]() $(M(A_n))_{n\in\mathbb{N}}$ are independent and furthermore satisfy
$(M(A_n))_{n\in\mathbb{N}}$ are independent and furthermore satisfy ![]() $M(\cup_{n\in \mathbb{N}} A_n)=\sum_{n\in \mathbb{N}} M(A_n)$. Furthermore, M(A) is infinitely divisible for all Borel sets
$M(\cup_{n\in \mathbb{N}} A_n)=\sum_{n\in \mathbb{N}} M(A_n)$. Furthermore, M(A) is infinitely divisible for all Borel sets ![]() $A\subseteq {\mathbb{R}}^{d+1}$.
$A\subseteq {\mathbb{R}}^{d+1}$.
Moreover, in this paper we assume M to be a stationary and isotropic Lévy basis on ![]() ${\mathbb{R}}^{d+1}$. With
${\mathbb{R}}^{d+1}$. With ![]() $m(\!\cdot\!)$ denoting the Lebesgue measure, and
$m(\!\cdot\!)$ denoting the Lebesgue measure, and ![]() $C(\lambda \dagger Y ) = \log {\mathbb E} \mathrm{e}^{{\mathrm{i}}\lambda Y}$ the cumulant function for a random variable Y, this means that the random variable M(A) has Lévy–Khinchin representation
$C(\lambda \dagger Y ) = \log {\mathbb E} \mathrm{e}^{{\mathrm{i}}\lambda Y}$ the cumulant function for a random variable Y, this means that the random variable M(A) has Lévy–Khinchin representation
where ![]() $a\in {\mathbb{R}}$,
$a\in {\mathbb{R}}$, ![]() $\theta \ge 0$, and F is the product measure
$\theta \ge 0$, and F is the product measure ![]() $m \otimes \rho$ of the Lebesgue measure and a Lévy measure
$m \otimes \rho$ of the Lebesgue measure and a Lévy measure ![]() $\rho$. The notion of the so-called spot variable M ′ will be useful. It is a random variable equivalent in distribution to M(A) when
$\rho$. The notion of the so-called spot variable M ′ will be useful. It is a random variable equivalent in distribution to M(A) when ![]() $m(A) = 1$.
$m(A) = 1$.
We assume that the Lévy basis M has a convolution equivalent Lévy measure ![]() $\rho$ with index
$\rho$ with index ![]() $\beta>0$, by which we formally mean that the probability measure
$\beta>0$, by which we formally mean that the probability measure ![]() $\rho_1$, the normalized restriction of
$\rho_1$, the normalized restriction of ![]() $\rho$ to
$\rho$ to ![]() $(1,\infty)$, is in
$(1,\infty)$, is in ![]() $\mathcal{S}_{\beta}$. This means that
$\mathcal{S}_{\beta}$. This means that ![]() $\rho_1\in \mathcal{L}_{\beta}$, the class of probability measures with an exponential right tail
$\rho_1\in \mathcal{L}_{\beta}$, the class of probability measures with an exponential right tail ![]() $\beta$, that is,
$\beta$, that is,
for all ![]() $y\in {\mathbb{R}}$, and that it furthermore satisfies the convolution property
$y\in {\mathbb{R}}$, and that it furthermore satisfies the convolution property
where ![]() $*$ denotes convolution. To ease notation, we write
$*$ denotes convolution. To ease notation, we write ![]() $\rho \in \mathcal{S}_{\beta}$ when
$\rho \in \mathcal{S}_{\beta}$ when ![]() $\rho_1\in\mathcal{S}_{\beta}$.
$\rho_1\in\mathcal{S}_{\beta}$.
For later reference, we list the mentioned properties as part of Assumption 2.1 below.
We write the tail of ![]() $\rho$ as
$\rho$ as ![]() $\rho((x,\infty)) = L(x) \exp({-}\beta x)$, so for all
$\rho((x,\infty)) = L(x) \exp({-}\beta x)$, so for all ![]() $y\in{\mathbb{R}}$, (2.2) implies that
$y\in{\mathbb{R}}$, (2.2) implies that
Equation (2.4) implies that the mapping ![]() $x\mapsto L(\log(x))$ is slowly varying. A consequence (see formula (3.6) in [Reference Rønn-Nielsen and Jensen20]) is that for all
$x\mapsto L(\log(x))$ is slowly varying. A consequence (see formula (3.6) in [Reference Rønn-Nielsen and Jensen20]) is that for all ![]() $\gamma >0$ there exist
$\gamma >0$ there exist ![]() $x_0>0$ and
$x_0>0$ and ![]() $C_0>0$ such that
$C_0>0$ such that
Before we define the kernel function f and consequently the field X, we introduce a continuity property called t-càdlàg, which is of importance in this paper. Under assumptions on the basis M and the integration kernel f (appearing below), the entire field ![]() $X=(X_{v,t})$ exhibits this regularity, thus ensuring that the supremum of such fields on bounded sets behaves nicely; see e.g. the proof of Lemma 3.2 in the supplementary material [Reference Stehr and Rønn-Nielsen27]. Moreover, this continuity property will be explicitly used in the proofs of Section 4.
$X=(X_{v,t})$ exhibits this regularity, thus ensuring that the supremum of such fields on bounded sets behaves nicely; see e.g. the proof of Lemma 3.2 in the supplementary material [Reference Stehr and Rønn-Nielsen27]. Moreover, this continuity property will be explicitly used in the proofs of Section 4.
Definition 2.1. (t-càdlàg.) A field ![]() $(y_{v,t})_{{(v,t)}}$ is t-càdlàg if, for all (v, t), it satisfies
$(y_{v,t})_{{(v,t)}}$ is t-càdlàg if, for all (v, t), it satisfies
In defining the field ![]() $X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ below, we make the following assumptions on the Lévy basis M and the integration kernel f. The assumptions are stronger than needed to ensure the existence of the integral (2.10) defining
$X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ below, we make the following assumptions on the Lévy basis M and the integration kernel f. The assumptions are stronger than needed to ensure the existence of the integral (2.10) defining ![]() $X_{v,t}$. By [Reference Rajput and Rosinski18, Theorem 2.7] the integral is well-defined if only the stationary and isotropic basis has a Lévy measure
$X_{v,t}$. By [Reference Rajput and Rosinski18, Theorem 2.7] the integral is well-defined if only the stationary and isotropic basis has a Lévy measure ![]() $\rho$ satisfying
$\rho$ satisfying ![]() $\int_{|y|>1} \lvert{y}\rvert \rho ( \mathrm{d} y) < \infty$, and if the bounded integration kernel f is integrable in the sense of (2.8). However, we make the stronger assumptions below as these also guarantee the existence of a t-càdlàg version of X; see Theorem 5.3.
$\int_{|y|>1} \lvert{y}\rvert \rho ( \mathrm{d} y) < \infty$, and if the bounded integration kernel f is integrable in the sense of (2.8). However, we make the stronger assumptions below as these also guarantee the existence of a t-càdlàg version of X; see Theorem 5.3.
Assumption 2.1. The Lévy basis M on ![]() ${\mathbb{R}}^{d+1}$ is stationary and isotropic with a Lévy measure
${\mathbb{R}}^{d+1}$ is stationary and isotropic with a Lévy measure ![]() $\rho\in \mathcal{S}_{\beta}$,
$\rho\in \mathcal{S}_{\beta}$, ![]() $\beta > 0$. Moreover,
$\beta > 0$. Moreover, ![]() $\rho$ satisfies
$\rho$ satisfies
Note that the integrability along the right tail is already given from the exponential tail property, and since ![]() $\rho$ is a Lévy measure it also satisfies
$\rho$ is a Lévy measure it also satisfies ![]() $\int_{[-1,1]}y^2 \rho( \mathrm{d} y) < \infty$. Also, by [Reference Sato24, Theorem 25.3], (2.7) is equivalent to finite moments
$\int_{[-1,1]}y^2 \rho( \mathrm{d} y) < \infty$. Also, by [Reference Sato24, Theorem 25.3], (2.7) is equivalent to finite moments ![]() ${\mathbb E}|M'|^k<\infty$ of the spot variable. This is explicitly used when showing that there is a t-càdlàg version of X. Here we use a result from [Reference Adler1] which requires finite moments of a certain high order. In Sections 2, 3, and 4, it is assumed that Assumption 2.1 is satisfied.
${\mathbb E}|M'|^k<\infty$ of the spot variable. This is explicitly used when showing that there is a t-càdlàg version of X. Here we use a result from [Reference Adler1] which requires finite moments of a certain high order. In Sections 2, 3, and 4, it is assumed that Assumption 2.1 is satisfied.
Assumption 2.2. The kernel ![]() $f\colon[0,\infty) \times {\mathbb{R}} \to [0,\infty)$ is bounded, it satisfies
$f\colon[0,\infty) \times {\mathbb{R}} \to [0,\infty)$ is bounded, it satisfies ![]() $f(x,y)=0$ for all
$f(x,y)=0$ for all ![]() $x\in [0,\infty)$ and
$x\in [0,\infty)$ and ![]() $y<0$, it is integrable in the sense that
$y<0$, it is integrable in the sense that
and it is Lipschitz-continuous on ![]() $[0,\infty)\times [0,\infty)$, that is, there exists
$[0,\infty)\times [0,\infty)$, that is, there exists ![]() $C_L\in(0,\infty)$ such that
$C_L\in(0,\infty)$ such that
for all ![]() $(x_1,y_1),(x_2,y_2)\in[0,\infty)\times[0,\infty)$.
$(x_1,y_1),(x_2,y_2)\in[0,\infty)\times[0,\infty)$.
Let ![]() $B\subseteq {\mathbb{R}^d}$ be a compact set with strictly positive Lebesgue measure, and consider [0, T] for deterministic
$B\subseteq {\mathbb{R}^d}$ be a compact set with strictly positive Lebesgue measure, and consider [0, T] for deterministic ![]() $0<T<\infty$. For
$0<T<\infty$. For ![]() $r,\ell \ge 0$ fixed, define the expanded sets
$r,\ell \ge 0$ fixed, define the expanded sets ![]() $B^{\prime}=B\oplus C_r(0)=\{x+y \colon x\in B, |y|\le r\}$ and
$B^{\prime}=B\oplus C_r(0)=\{x+y \colon x\in B, |y|\le r\}$ and ![]() $T^{\prime}=[0,T+\ell]$. Here
$T^{\prime}=[0,T+\ell]$. Here ![]() $C_r(u)\subseteq {\mathbb{R}^d}$ is the d-dimensional closed ball with radius r and centre in
$C_r(u)\subseteq {\mathbb{R}^d}$ is the d-dimensional closed ball with radius r and centre in ![]() $u\in {\mathbb{R}^d}$. Under Assumptions 2.1 and 2.2 we define the random field
$u\in {\mathbb{R}^d}$. Under Assumptions 2.1 and 2.2 we define the random field ![]() $X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ by
$X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ by
Note that alternatively we can write
due to the assumptions on f. Thus X has a causal structure in the time direction in the sense that ![]() $X_{v,t}$ only depends on M restricted to the subset
$X_{v,t}$ only depends on M restricted to the subset ![]() ${\mathbb{R}^d} \times ({-}\infty,t]$.
${\mathbb{R}^d} \times ({-}\infty,t]$.
We are ultimately interested in extremal probabilities of the form
where ![]() $\Psi\colon {\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ is a functional satisfying some assumptions that will be given in Section 3. For notational convenience we usually write
$\Psi\colon {\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ is a functional satisfying some assumptions that will be given in Section 3. For notational convenience we usually write ![]() $\Psi(y_{v,t})$ when applying
$\Psi(y_{v,t})$ when applying ![]() $\Psi$ to a field
$\Psi$ to a field ![]() $(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$, but when it is necessary to clarify the indices of the field we write it out in full. For the type of functionals
$(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$, but when it is necessary to clarify the indices of the field we write it out in full. For the type of functionals ![]() $\Psi$ we shall consider, it will be convenient to make some further assumptions on the kernel. The following Assumption 2.3 clearly implies Assumption 2.2 above. In Sections 2, 3, and 4, Assumption 2.3 is assumed to be satisfied.
$\Psi$ we shall consider, it will be convenient to make some further assumptions on the kernel. The following Assumption 2.3 clearly implies Assumption 2.2 above. In Sections 2, 3, and 4, Assumption 2.3 is assumed to be satisfied.
Assumption 2.3. The kernel ![]() $f\colon[0,\infty)\times {\mathbb{R}} \to [0,\infty)$ satisfies
$f\colon[0,\infty)\times {\mathbb{R}} \to [0,\infty)$ satisfies ![]() $f(0,0)=1$ and
$f(0,0)=1$ and ![]() $f(x,y)=0$ for all
$f(x,y)=0$ for all ![]() $x\in[0,\infty)$ and
$x\in[0,\infty)$ and ![]() $y<0$. Moreover,
$y<0$. Moreover,
and f is Lipschitz on ![]() $[0,\infty)\times [0,\infty)$, i.e. it satisfies (2.9).
$[0,\infty)\times [0,\infty)$, i.e. it satisfies (2.9).
It turns out that the infinite divisibility of M is inherited to the field X. We shall spend the remainder of this section establishing this property and use it to obtain a useful representation of the field as an independent sum of a compound Poisson term and a term with a lighter tail than exponentials. The procedure is inspired by a similar technique used in [Reference Rønn-Nielsen and Jensen19], [Reference Rønn-Nielsen and Jensen20], and [Reference Rosinski and Samorodnitsky23]. Here we present the procedure in full to introduce all relevant notation.
The cumulant function of ![]() $X_{v,t}$ takes the form (see [Reference Rajput and Rosinski18, Theorem 2.7])
$X_{v,t}$ takes the form (see [Reference Rajput and Rosinski18, Theorem 2.7])
 \begin{align*}C(\lambda \dagger X_{v,t})& = {\mathrm{i}} \lambda a \int_{\mathbb{R}^d} \int_{\mathbb{R}} f(\lvert{v-u}\rvert, t-s) \,\mathrm{d}s \,\mathrm{d}u- \dfrac12 \theta \lambda^2 \int_{\mathbb{R}^d} \int_{\mathbb{R}} f(\lvert{v-u}\rvert, t-s)^2 \,\mathrm{d}s \,\mathrm{d}u \\[5pt]
&\quad\, + \int_{{\mathbb{R}^d}}\int_{\mathbb{R}} \int_{\mathbb{R}}( {\mathrm{e}}^{{\mathrm{i}}\, f(\lvert{v-u}\rvert, t-s) \lambda z} - 1 - {\mathrm{i}} f(\lvert{v-u}\rvert, t-s)\lambda z 1_{[-1,1]}(z) ) \rho(\mathrm{d} z) \,\mathrm{d}s \,\mathrm{d}u .\end{align*}
\begin{align*}C(\lambda \dagger X_{v,t})& = {\mathrm{i}} \lambda a \int_{\mathbb{R}^d} \int_{\mathbb{R}} f(\lvert{v-u}\rvert, t-s) \,\mathrm{d}s \,\mathrm{d}u- \dfrac12 \theta \lambda^2 \int_{\mathbb{R}^d} \int_{\mathbb{R}} f(\lvert{v-u}\rvert, t-s)^2 \,\mathrm{d}s \,\mathrm{d}u \\[5pt]
&\quad\, + \int_{{\mathbb{R}^d}}\int_{\mathbb{R}} \int_{\mathbb{R}}( {\mathrm{e}}^{{\mathrm{i}}\, f(\lvert{v-u}\rvert, t-s) \lambda z} - 1 - {\mathrm{i}} f(\lvert{v-u}\rvert, t-s)\lambda z 1_{[-1,1]}(z) ) \rho(\mathrm{d} z) \,\mathrm{d}s \,\mathrm{d}u .\end{align*}
A similar expression can be obtained for any finite linear combination of ![]() $X_{v,t}$ for varying v, t by replacing f with a relevant linear combination of f for varying v, t. Thus all finite-dimensional distributions of
$X_{v,t}$ for varying v, t by replacing f with a relevant linear combination of f for varying v, t. Thus all finite-dimensional distributions of ![]() $(X_{v,t})_{(v,t)\in B^{\prime}\times T'}$ are infinitely divisible, and consequently any countably indexed field
$(X_{v,t})_{(v,t)\in B^{\prime}\times T'}$ are infinitely divisible, and consequently any countably indexed field ![]() $(X_{v,t})$ is infinitely divisible. Define the countable set
$(X_{v,t})$ is infinitely divisible. Define the countable set ![]() $\mathbb{K}=(B^{\prime}\times T^{\prime}) \cap \mathbb{Q}^{d+1}$, and let
$\mathbb{K}=(B^{\prime}\times T^{\prime}) \cap \mathbb{Q}^{d+1}$, and let ![]() $\nu=(m \otimes m \otimes \rho)\circ H^{-1}$ be the measure on
$\nu=(m \otimes m \otimes \rho)\circ H^{-1}$ be the measure on ![]() $\big({\mathbb{R}}^{\mathbb{K}}, \mathcal{B}\big({\mathbb{R}}^{\mathbb{K}}\big)\big)$ defined as the image-measure of H on
$\big({\mathbb{R}}^{\mathbb{K}}, \mathcal{B}\big({\mathbb{R}}^{\mathbb{K}}\big)\big)$ defined as the image-measure of H on ![]() $ m \otimes m \otimes \rho $, where
$ m \otimes m \otimes \rho $, where ![]() $H\colon{{\mathbb{R}^d} \times {\mathbb{R}}}\times{\mathbb{R}} \to {\mathbb{R}}^{\mathbb{K}}$ is given by
$H\colon{{\mathbb{R}^d} \times {\mathbb{R}}}\times{\mathbb{R}} \to {\mathbb{R}}^{\mathbb{K}}$ is given by
Then direct manipulations show that ![]() $\nu$ is the Lévy measure of
$\nu$ is the Lévy measure of ![]() $(X_{v,t})_{(v,t)\in \mathbb{K}}$, and furthermore the Lévy–Khinchin representation is
$(X_{v,t})_{(v,t)\in \mathbb{K}}$, and furthermore the Lévy–Khinchin representation is
 \begin{align*}C(\beta \dagger (X_{v,t})_{(v,t)\in \mathbb{K}}) & = {\mathrm{i}} \sum_{{(v,t)}} \beta_{v,t}a_{v,t}- \dfrac12 \theta \int_{\mathbb{R}^d} \int_{\mathbb{R}} \biggl( \sum_{{(v,t)}} \beta_{v,t}\,f(\lvert{v-u}\rvert, t-s) \biggr)^2 \,\mathrm{d}s \,\mathrm{d}u \\* &\quad\,+ \int_{{\mathbb{R}}^\mathbb{K}} \biggl( \mathrm{e}^{{\mathrm{i}}\sum_{{(v,t)}}\beta_{v,t} z_{v,t}} - 1 - {\mathrm{i}}\sum_{{(v,t)}}\beta_{v,t}z_{v,t} 1_{[-1,1]^{\mathbb{K}}}(z) \biggr) \nu( \mathrm{d} z)\end{align*}
\begin{align*}C(\beta \dagger (X_{v,t})_{(v,t)\in \mathbb{K}}) & = {\mathrm{i}} \sum_{{(v,t)}} \beta_{v,t}a_{v,t}- \dfrac12 \theta \int_{\mathbb{R}^d} \int_{\mathbb{R}} \biggl( \sum_{{(v,t)}} \beta_{v,t}\,f(\lvert{v-u}\rvert, t-s) \biggr)^2 \,\mathrm{d}s \,\mathrm{d}u \\* &\quad\,+ \int_{{\mathbb{R}}^\mathbb{K}} \biggl( \mathrm{e}^{{\mathrm{i}}\sum_{{(v,t)}}\beta_{v,t} z_{v,t}} - 1 - {\mathrm{i}}\sum_{{(v,t)}}\beta_{v,t}z_{v,t} 1_{[-1,1]^{\mathbb{K}}}(z) \biggr) \nu( \mathrm{d} z)\end{align*}
for suitable ![]() $(a_{v,t})_{(v,t)\in \mathbb{K}} \in{\mathbb{R}}^{\mathbb{K}}$. Here
$(a_{v,t})_{(v,t)\in \mathbb{K}} \in{\mathbb{R}}^{\mathbb{K}}$. Here ![]() $\beta\in{\mathbb{R}}^{\mathbb{K}}$ with
$\beta\in{\mathbb{R}}^{\mathbb{K}}$ with ![]() $\beta_{v,t}\neq 0$ for at most finitely many
$\beta_{v,t}\neq 0$ for at most finitely many ![]() ${(v,t)\in \mathbb{K}}$. From the infinite divisibility,
${(v,t)\in \mathbb{K}}$. From the infinite divisibility, ![]() $(X_{v,t})_{(v,t)\in \mathbb{K}}$ can be represented as the independent sum
$(X_{v,t})_{(v,t)\in \mathbb{K}}$ can be represented as the independent sum
The field ![]() $(X_{v,t}^1)_{(v,t)\in \mathbb{K}}$ is a compound Poisson sum
$(X_{v,t}^1)_{(v,t)\in \mathbb{K}}$ is a compound Poisson sum
 \begin{equation*}X_{v,t}^1 = \sum_{n=1}^N V_{v,t}^n ,\end{equation*}
\begin{equation*}X_{v,t}^1 = \sum_{n=1}^N V_{v,t}^n ,\end{equation*}
where N is Poisson-distributed with intensity ![]() $\nu(A)<\infty$ and
$\nu(A)<\infty$ and
The finiteness of ![]() $\nu(A)$ follows from arguments similar to those of [Reference Rønn-Nielsen and Jensen19, Lemma A.1] using (2.12). The fields
$\nu(A)$ follows from arguments similar to those of [Reference Rønn-Nielsen and Jensen19, Lemma A.1] using (2.12). The fields ![]() $((V_{v,t}^n)_{(v,t)\in \mathbb{K}})_{n\in\mathbb{N}}$ are independent and identically distributed (i.i.d.) with common distribution
$((V_{v,t}^n)_{(v,t)\in \mathbb{K}})_{n\in\mathbb{N}}$ are independent and identically distributed (i.i.d.) with common distribution ![]() $\nu_1 = \nu_A / \nu(A)$, i.e. the normalization of the restriction of
$\nu_1 = \nu_A / \nu(A)$, i.e. the normalization of the restriction of ![]() $\nu$ to A. Also,
$\nu$ to A. Also, ![]() $(X_{v,t}^2)_{(v,t)\in \mathbb{K}}$ is infinitely divisible and has Lévy measure
$(X_{v,t}^2)_{(v,t)\in \mathbb{K}}$ is infinitely divisible and has Lévy measure ![]() $\nu_{A^c}$, the restriction of
$\nu_{A^c}$, the restriction of ![]() $\nu$ to
$\nu$ to ![]() $A^c$.
$A^c$.
It will be essential that there exist extensions of the fields ![]() $(X_{v,t}^1)$ and
$(X_{v,t}^1)$ and ![]() $(X_{v,t}^2)$ to
$(X_{v,t}^2)$ to ![]() $B^{\prime}\times T^{\prime}$ with t-càdlàg sample paths. In law, each of the fields
$B^{\prime}\times T^{\prime}$ with t-càdlàg sample paths. In law, each of the fields ![]() $(V_{v,t}^n)$ can be represented by
$(V_{v,t}^n)$ can be represented by ![]() $(Z\,f(|v-U|,t-S))_{(v,t)\in \mathbb{K}}$, where
$(Z\,f(|v-U|,t-S))_{(v,t)\in \mathbb{K}}$, where ![]() $(U,S,Z)\in {{\mathbb{R}^d} \times {\mathbb{R}}}\times{\mathbb{R}}$ has distribution
$(U,S,Z)\in {{\mathbb{R}^d} \times {\mathbb{R}}}\times{\mathbb{R}}$ has distribution ![]() $F_1$, the normalized restriction of F to the set
$F_1$, the normalized restriction of F to the set
Hence a t-càdlàg extension ![]() $(V_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ clearly exists, and it is represented by
$(V_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ clearly exists, and it is represented by ![]() $(Z\,f(|v-U|,t-S))_{(v,t)\in B^{\prime}\times T^{\prime}}$. As
$(Z\,f(|v-U|,t-S))_{(v,t)\in B^{\prime}\times T^{\prime}}$. As ![]() $X^1$ is a finite sum of such fields it also has an extension to
$X^1$ is a finite sum of such fields it also has an extension to ![]() $B^{\prime}\times T^{\prime}$ which is t-càdlàg. As mentioned above and shown in Theorem 5.3, the entire field
$B^{\prime}\times T^{\prime}$ which is t-càdlàg. As mentioned above and shown in Theorem 5.3, the entire field ![]() $(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ has a version with t-càdlàg sample paths, and hence
$(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ has a version with t-càdlàg sample paths, and hence ![]() $X^2$ also has an extension with such paths.
$X^2$ also has an extension with such paths.
3. Functional assumptions and main theorem
In this section we introduce assumptions on ![]() $\Psi$ and related functionals, and we derive the main theorem on the asymptotic behaviour of the extremal probability
$\Psi$ and related functionals, and we derive the main theorem on the asymptotic behaviour of the extremal probability ![]() $\mathbb{P}(\Psi(X_{v,t}) > x)$ as
$\mathbb{P}(\Psi(X_{v,t}) > x)$ as ![]() $x\to\infty$. As the proofs of some of the results follow the same ideas as in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20], we refer to the supplementary material for these [Reference Stehr and Rønn-Nielsen27].
$x\to\infty$. As the proofs of some of the results follow the same ideas as in [Reference Rønn-Nielsen and Jensen19] and [Reference Rønn-Nielsen and Jensen20], we refer to the supplementary material for these [Reference Stehr and Rønn-Nielsen27].
Throughout this section we shall assume the following.
Assumption 3.1. The functional ![]() $\Psi\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ satisfies the following.
$\Psi\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ satisfies the following.
(i) For all deterministic fields
 $(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ and all
$(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ and all  $a\ge 0$ and
$a\ge 0$ and  $b\in {\mathbb{R}}$ it holds that
$b\in {\mathbb{R}}$ it holds that
 \begin{equation*}\Psi(a\,y_{v,t} + b) = a\, \Psi(y_{v,t}) + b .\end{equation*}
\begin{equation*}\Psi(a\,y_{v,t} + b) = a\, \Psi(y_{v,t}) + b .\end{equation*}
-
(ii)
 $\Psi$ is increasing, that is,
whenever the field
$\Psi$ is increasing, that is,
whenever the field \begin{equation*}\Psi(y_{v,t} + z_{v,t}) \ge \Psi(y_{v,t})\end{equation*}
\begin{equation*}\Psi(y_{v,t} + z_{v,t}) \ge \Psi(y_{v,t})\end{equation*}
 $(z_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ satisfies that
$(z_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ satisfies that  $z_{v,t} \ge 0$ for all
$z_{v,t} \ge 0$ for all  ${(v,t)\in B^{\prime}\times T^{\prime}}$.
${(v,t)\in B^{\prime}\times T^{\prime}}$.
-
(iii) For all
 $x>0$,
$x>0$,  $u\in{\mathbb{R}^d}$ and
$u\in{\mathbb{R}^d}$ and  $s\in{\mathbb{R}}$, there is a functional
$s\in{\mathbb{R}}$, there is a functional  $\psi_{x,u,s,f}\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ such that
for all
$\psi_{x,u,s,f}\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}} \to {\mathbb{R}}$ such that
for all \begin{equation*}\Psi (a\, f(\lvert{v-u}\rvert, t-s) + y_{v,t} ) >x\quad \textit{if and only if}\quad\psi_{x,u,s,f}(y_{v,t})
< a\end{equation*}
\begin{equation*}\Psi (a\, f(\lvert{v-u}\rvert, t-s) + y_{v,t} ) >x\quad \textit{if and only if}\quad\psi_{x,u,s,f}(y_{v,t})
< a\end{equation*}
 $a\ge 0$ and all fields
$a\ge 0$ and all fields  $(y_{v,t})$.
$(y_{v,t})$.
Proposition 3.1. The functionals ![]() $\Psi$ and
$\Psi$ and ![]() $\psi_{x,u,s,f}$ satisfy the following.
$\psi_{x,u,s,f}$ satisfy the following.
(i)
 $\psi_{x,u,s,f}$ is decreasing, that is, for all
$\psi_{x,u,s,f}$ is decreasing, that is, for all  $x>0$,
$x>0$,  $u\in {\mathbb{R}^d}$, and
$u\in {\mathbb{R}^d}$, and  $s\in {\mathbb{R}}$, and all fields
$s\in {\mathbb{R}}$, and all fields  $(y_{v,t})$,
if
$(y_{v,t})$,
if \begin{equation*}\psi_{x,u,s,f}(y_{v,t}) \ge \psi_{x,u,s,f}(y_{v,t} + z_{v,t})\end{equation*}
\begin{equation*}\psi_{x,u,s,f}(y_{v,t}) \ge \psi_{x,u,s,f}(y_{v,t} + z_{v,t})\end{equation*}
 $z_{v,t}\ge 0$ for all
$z_{v,t}\ge 0$ for all  ${(v,t)\in B^{\prime}\times T^{\prime}}$.
${(v,t)\in B^{\prime}\times T^{\prime}}$.
-
(ii) For all fields
 $(y_{v,t})$ and any constant
$(y_{v,t})$ and any constant  $y\in {\mathbb{R}}$,
$y\in {\mathbb{R}}$,
 \begin{equation*}\psi_{x,u,s,f}(y_{v,t} + y) = \psi_{x-y,u,s,f}(y_{v,t}) .\end{equation*}
\begin{equation*}\psi_{x,u,s,f}(y_{v,t} + y) = \psi_{x-y,u,s,f}(y_{v,t}) .\end{equation*}
-
(iii) For all
 $x>0$,
$x>0$,  $u\in {\mathbb{R}^d}$, and
$u\in {\mathbb{R}^d}$, and  $s\in {\mathbb{R}}$, and all fields
$s\in {\mathbb{R}}$, and all fields  $(y_{v,t})$,
where
$(y_{v,t})$,
where \begin{equation*}\psi_{x,u,s,f}(y_{v,t}) \ge \psi_{x,u,s,f}(y^*) = \dfrac{x-y^*}{\Psi((f(\lvert{v-u}\rvert, t-s))_{(v,t)})} ,\end{equation*}
\begin{equation*}\psi_{x,u,s,f}(y_{v,t}) \ge \psi_{x,u,s,f}(y^*) = \dfrac{x-y^*}{\Psi((f(\lvert{v-u}\rvert, t-s))_{(v,t)})} ,\end{equation*}
 $y^* = \sup_{{(v,t)\in B^{\prime}\times T^{\prime}}} y_{v,t}$.
$y^* = \sup_{{(v,t)\in B^{\prime}\times T^{\prime}}} y_{v,t}$.
Proof. Statement (i) is seen as follows. Let x, u, s be fixed, and assume for contradiction the existence of ![]() $\varepsilon > 0$ such that
$\varepsilon > 0$ such that ![]() $\psi_{x,u,s,f}(y_{v,t}) + \varepsilon = \psi_{x,u,s,f}(y_{v,t} + z_{v,t}) .$ Now choose a such that
$\psi_{x,u,s,f}(y_{v,t}) + \varepsilon = \psi_{x,u,s,f}(y_{v,t} + z_{v,t}) .$ Now choose a such that ![]() $a-\varepsilon \le \psi_{x,u,s,f}(y_{v,t}) < a ,$ and therefore
$a-\varepsilon \le \psi_{x,u,s,f}(y_{v,t}) < a ,$ and therefore ![]() $\psi_{x,u,s,f}(y_{v,t} + z_{v,t}) \ge a .$ However, appealing to Assumptions 3.1 (ii) and 3.1 (iii) we also conclude that
$\psi_{x,u,s,f}(y_{v,t} + z_{v,t}) \ge a .$ However, appealing to Assumptions 3.1 (ii) and 3.1 (iii) we also conclude that
so also ![]() $\psi_{x,u,s,f}(y_{v,t} + z_{v,t}) < a$, a contradiction.
$\psi_{x,u,s,f}(y_{v,t} + z_{v,t}) < a$, a contradiction.
Parts (ii) and (iii) are seen using Assumptions 3.1 (i) and 3.1 (iii).
Before giving two examples of functionals easily seen to satisfy Assumption 3.1, we introduce some notation. Let ![]() $D \subseteq C_r(0) \subseteq {\mathbb{R}^d}$ be a fixed spatial object, and for all rotations
$D \subseteq C_r(0) \subseteq {\mathbb{R}^d}$ be a fixed spatial object, and for all rotations ![]() $R\in SO(d)$ and translations
$R\in SO(d)$ and translations ![]() $v\in {\mathbb{R}^d}$, define
$v\in {\mathbb{R}^d}$, define ![]() $D^R(v)=RD + v$. Similarly, let
$D^R(v)=RD + v$. Similarly, let ![]() $D(v)=D + v$. Furthermore, let
$D(v)=D + v$. Furthermore, let ![]() $I(t)=[t,t+\ell]$ for all
$I(t)=[t,t+\ell]$ for all ![]() $t\ge 0$. In Example 3.1 below we assume that the set D in fact has radius
$t\ge 0$. In Example 3.1 below we assume that the set D in fact has radius ![]() $r/2\ge 0$, by which we mean there exists
$r/2\ge 0$, by which we mean there exists ![]() $\alpha \in \mathbb{S}^{d-1}$ such that
$\alpha \in \mathbb{S}^{d-1}$ such that ![]() $\{-\alpha r/2, \alpha r/2\} \subseteq D \subseteq C_{r/2}(0)$.
$\{-\alpha r/2, \alpha r/2\} \subseteq D \subseteq C_{r/2}(0)$.
Example 3.1. Suppose we are interested in the probability that there exist a time point t, a translation ![]() $v_0$, and a rotation R of a given set D such that the field exceeds the level x on the entire set
$v_0$, and a rotation R of a given set D such that the field exceeds the level x on the entire set ![]() $\{t\} \times D^R(v_0)$. More formally, we assume that
$\{t\} \times D^R(v_0)$. More formally, we assume that ![]() $D \subseteq C_{r/2}(0) \subseteq {\mathbb{R}^d}$ has radius
$D \subseteq C_{r/2}(0) \subseteq {\mathbb{R}^d}$ has radius ![]() $r/2$ and study the probability
$r/2$ and study the probability
To put this within the more general framework introduced in (2.11), we define ![]() $\Psi$ by
$\Psi$ by
Consequently (obtained by straightforward manipulations),
Note that the probability above can be reformulated in terms of the excursion set ![]() $A_{x,t}$, defined in (1.2), as
$A_{x,t}$, defined in (1.2), as
Example 3.2. Suppose we are interested in the probability that there is a time interval and a location and rotation of the fixed spatial object D, in which the average of the field exceeds the level x. For this, let ![]() $D \subseteq C_r(0) \subseteq {\mathbb{R}^d}$ be given and consider the probability
$D \subseteq C_r(0) \subseteq {\mathbb{R}^d}$ be given and consider the probability
where ![]() $K=\int_D \int_0^\ell 1\,\mathrm{d} t \,\mathrm{d} v$. The set D can both be of full dimension in
$K=\int_D \int_0^\ell 1\,\mathrm{d} t \,\mathrm{d} v$. The set D can both be of full dimension in ![]() ${\mathbb{R}^d}$ and a subset of some lower-dimensional subspace. In either case,
${\mathbb{R}^d}$ and a subset of some lower-dimensional subspace. In either case, ![]() $\mathrm{d} v$ refers to the relevant version of the Lebesgue measure. The special cases of
$\mathrm{d} v$ refers to the relevant version of the Lebesgue measure. The special cases of
with a time point instead of an interval (and K defined appropriately), and
with a single spatial point, will be covered by the general formulation of the example, simply by defining ![]() $\int_{I(t_0)}X_{v,t} \,\mathrm{d} t = X_{v,t_0}$ when
$\int_{I(t_0)}X_{v,t} \,\mathrm{d} t = X_{v,t_0}$ when ![]() $\ell=0$ and
$\ell=0$ and ![]() $\int_{D^R(v_0)} X_{v,t} \,\mathrm{d} v = X_{v_0,t}$ when
$\int_{D^R(v_0)} X_{v,t} \,\mathrm{d} v = X_{v_0,t}$ when ![]() $D=\{0\}$ and hence
$D=\{0\}$ and hence ![]() $D^R(v_0)=\{v_0\}$. In the same spirit, the special case of
$D^R(v_0)=\{v_0\}$. In the same spirit, the special case of
corresponds to letting ![]() $\ell=0$ and
$\ell=0$ and ![]() $D=\{0\}$. Note that this probability could be formulated alternatively as
$D=\{0\}$. Note that this probability could be formulated alternatively as
To put this example into the framework of functionals, we define
leading to
 \begin{equation*}\psi_{x,u,s,f}(y_{v,t}) = \inf_{t_0\in [0,T]}\inf_{v_0\in B} \inf_{R\in SO(d)} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} .\end{equation*}
\begin{equation*}\psi_{x,u,s,f}(y_{v,t}) = \inf_{t_0\in [0,T]}\inf_{v_0\in B} \inf_{R\in SO(d)} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} .\end{equation*}
For the further arguments to hold it will be important that ![]() $\psi_{x,u,s,f}$ converges in a particular way as
$\psi_{x,u,s,f}$ converges in a particular way as ![]() $x\to\infty$. The following assumption is satisfied under further case-specific assumptions on the kernel f in each of the Examples 3.1 and 3.2, as illustrated in Section 4.
$x\to\infty$. The following assumption is satisfied under further case-specific assumptions on the kernel f in each of the Examples 3.1 and 3.2, as illustrated in Section 4.
Assumption 3.2. With the functionals ![]() $\Psi$ and
$\Psi$ and ![]() $\psi_{x,u,s,f}$ as in Assumption 3.1, there exists c such that
$\psi_{x,u,s,f}$ as in Assumption 3.1, there exists c such that
for all ![]() ${(u,s)\in B\times [0,T]}$ and
${(u,s)\in B\times [0,T]}$ and ![]() $\Psi((f(\lvert{v-u}\rvert, t-s))_{(v,t)})<c$ for all
$\Psi((f(\lvert{v-u}\rvert, t-s))_{(v,t)})<c$ for all ![]() ${(u,s)}\not\in B\times [0,T]$. Furthermore, for all
${(u,s)}\not\in B\times [0,T]$. Furthermore, for all ![]() ${(u,s)\in B\times [0,T]}$ there is a functional
${(u,s)\in B\times [0,T]}$ there is a functional ![]() $\lambda_{u,s}\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}}\to{\mathbb{R}}$, such that
$\lambda_{u,s}\colon{\mathbb{R}}^{B^{\prime}\times T^{\prime}}\to{\mathbb{R}}$, such that
as ![]() $x\to\infty$, holds for all t-càdlàg fields
$x\to\infty$, holds for all t-càdlàg fields ![]() $(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$.
$(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$.
The following proposition is easily seen from Assumption 3.1 and Proposition 3.1.
Proposition 3.2. With c and ![]() $\lambda_{u,s}$ as in Assumption 3.2, the following hold.
$\lambda_{u,s}$ as in Assumption 3.2, the following hold.
(i) If the field
 $(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ is constantly equal to
$(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ is constantly equal to  $y\in{\mathbb{R}}$, then
$y\in{\mathbb{R}}$, then
 \begin{equation*}\lambda_{u,s}(y_{v,t}) = \lambda_{u,s} (y) = \dfrac{y}{c} .\end{equation*}
\begin{equation*}\lambda_{u,s}(y_{v,t}) = \lambda_{u,s} (y) = \dfrac{y}{c} .\end{equation*}
-
(ii) For all constants
 $y\in{\mathbb{R}}$ and fields
$y\in{\mathbb{R}}$ and fields  $(y_{v,t})$,
$(y_{v,t})$,
 \begin{equation*}\lambda_{u,s}(y_{v,t} + y) = \lambda_{u,s}(y_{v,t}) + \dfrac{y}{c} .\end{equation*}
\begin{equation*}\lambda_{u,s}(y_{v,t} + y) = \lambda_{u,s}(y_{v,t}) + \dfrac{y}{c} .\end{equation*}
-
(iii)
 $\lambda_{u,s}$ is increasing.
$\lambda_{u,s}$ is increasing.
In the remainder of this section it is assumed that Assumption 3.2 is also satisfied.
The first step in proving the asymptotic behaviour of the extremal probability ![]() $\mathbb{P}(\Psi(X_{v,t})>x)$ is to consider the asymptotic behaviour of extremal sets of a single jump-field
$\mathbb{P}(\Psi(X_{v,t})>x)$ is to consider the asymptotic behaviour of extremal sets of a single jump-field
with distribution ![]() $\nu_1$.
$\nu_1$.
Theorem 3.1. Let ![]() $(V_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ have distribution
$(V_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ have distribution ![]() $\nu_1$ and let
$\nu_1$ and let ![]() $(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ be t-càdlàg. As
$(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ be t-càdlàg. As ![]() $x\to\infty$, it holds that
$x\to\infty$, it holds that
Proof. For sufficiently large ![]() $x>0$ we find
$x>0$ we find
 \begin{align} &\nu(A) \, \mathbb{P}(\Psi(V_{v,t} + y_{v,t}) > x) \notag \\*& \quad= F ( \{ (u,s,z)\in {\mathbb{R}^d} \times {\mathbb{R}} \times {\mathbb{R}}_+ \colon \Psi (z\,f(\lvert{v-u}\rvert, t-s) + y_{v,t} )> x \}) \notag \\*&\quad= F ( \{ (u,s,z)\in {\mathbb{R}^d} \times {\mathbb{R}} \times {\mathbb{R}}_+ \colon \psi_{x,u,s,f}(y_{v,t})<z \}) \notag \\& \quad = \int_{B\times [0,T]} L(\psi_{x,u,s,f}(y_{v,t})) \exp({-}\beta \psi_{x,u,s,f}(y_{v,t}) ) m(\mathrm{d}u,\mathrm{d}s) \notag \\ & \quad \quad\, + \int_{(B\times [0,T])^c} L(\psi_{x,u,s,f}(y_{v,t})) \exp({-}\beta \psi_{x,u,s,f}(y_{v,t}) ) m(\mathrm{d}u,\mathrm{d}s) .\end{align}
\begin{align} &\nu(A) \, \mathbb{P}(\Psi(V_{v,t} + y_{v,t}) > x) \notag \\*& \quad= F ( \{ (u,s,z)\in {\mathbb{R}^d} \times {\mathbb{R}} \times {\mathbb{R}}_+ \colon \Psi (z\,f(\lvert{v-u}\rvert, t-s) + y_{v,t} )> x \}) \notag \\*&\quad= F ( \{ (u,s,z)\in {\mathbb{R}^d} \times {\mathbb{R}} \times {\mathbb{R}}_+ \colon \psi_{x,u,s,f}(y_{v,t})<z \}) \notag \\& \quad = \int_{B\times [0,T]} L(\psi_{x,u,s,f}(y_{v,t})) \exp({-}\beta \psi_{x,u,s,f}(y_{v,t}) ) m(\mathrm{d}u,\mathrm{d}s) \notag \\ & \quad \quad\, + \int_{(B\times [0,T])^c} L(\psi_{x,u,s,f}(y_{v,t})) \exp({-}\beta \psi_{x,u,s,f}(y_{v,t}) ) m(\mathrm{d}u,\mathrm{d}s) .\end{align}
First we show that the latter integral is of order ![]() ${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ as
${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ as ![]() $x\rightarrow \infty$. Let
$x\rightarrow \infty$. Let ![]() $y^*=\sup_{(v,t)\in B^{\prime}\times T^{\prime}} y_{v,t}$. Using Proposition 3.1 (iii) and the fact that
$y^*=\sup_{(v,t)\in B^{\prime}\times T^{\prime}} y_{v,t}$. Using Proposition 3.1 (iii) and the fact that ![]() $x\mapsto L(x)\exp({-}\beta x)$ is decreasing, we obtain that the second integral in (3.4) is bounded from above by
$x\mapsto L(x)\exp({-}\beta x)$ is decreasing, we obtain that the second integral in (3.4) is bounded from above by
Let ![]() $h(u, s;\, x)$ denote the integrand. For all
$h(u, s;\, x)$ denote the integrand. For all ![]() $(u,s)\in (B\times [0,T])^c $ we have
$(u,s)\in (B\times [0,T])^c $ we have ![]() $\Psi( f(\lvert{v-u}\rvert,\break t-s)) < c$. In combination with (2.4) and (2.5), this implies the existence of
$\Psi( f(\lvert{v-u}\rvert,\break t-s)) < c$. In combination with (2.4) and (2.5), this implies the existence of ![]() $\gamma >0$ and
$\gamma >0$ and ![]() $C>0$ such that
$C>0$ such that
for sufficiently large x. Thus ![]() $h(u,s;\,x)$ is of order
$h(u,s;\,x)$ is of order ![]() ${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ at infinity. By dominated convergence, the integral is also of order
${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ at infinity. By dominated convergence, the integral is also of order ![]() ${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ if we can find an integrable function
${\mathrm{o}}(L(x/c)\exp({-}\beta x/c))$ if we can find an integrable function ![]() $g\colon{{\mathbb{R}^d} \times {\mathbb{R}}}\to{\mathbb{R}}$ such that
$g\colon{{\mathbb{R}^d} \times {\mathbb{R}}}\to{\mathbb{R}}$ such that
for all ![]() $(u,s)\in{{\mathbb{R}^d} \times {\mathbb{R}}}$. Returning to (2.5) we see that for all
$(u,s)\in{{\mathbb{R}^d} \times {\mathbb{R}}}$. Returning to (2.5) we see that for all ![]() $0<\gamma<\beta/c$ there exist
$0<\gamma<\beta/c$ there exist ![]() $C>0$ and
$C>0$ and ![]() $x_0>y^*$ such that
$x_0>y^*$ such that
for all ![]() $x\ge x_0$. Independent of (u, s) there is a constant
$x\ge x_0$. Independent of (u, s) there is a constant ![]() $\tilde C$ such that the right-hand side of (3.5) is bounded by
$\tilde C$ such that the right-hand side of (3.5) is bounded by
where we used Assumptions 3.1 (i) and 3.1 (ii). By Assumption 2.3, this is integrable.
It remains to show that the first integral in (3.4) has the desired mode of convergence. From (3.2), the representation of L, and the fact that ![]() $\rho$ has an exponential tail, we have that, for any
$\rho$ has an exponential tail, we have that, for any ![]() ${(u,s)\in B\times [0,T]}$,
${(u,s)\in B\times [0,T]}$,
as ![]() $x\to \infty$. Since
$x\to \infty$. Since ![]() $x\mapsto L(x)\exp({-}\beta x)$ is decreasing, we find using Proposition 3.1 (iii) that, for sufficiently large x,
$x\mapsto L(x)\exp({-}\beta x)$ is decreasing, we find using Proposition 3.1 (iii) that, for sufficiently large x,
for any ![]() ${(u,s)\in B\times [0,T]}$, where, according to (2.4), C is such that
${(u,s)\in B\times [0,T]}$, where, according to (2.4), C is such that
As ![]() $B\times [0,T]$ is compact, the upper bound is integrable over
$B\times [0,T]$ is compact, the upper bound is integrable over ![]() $B\times [0,T]$, and (3.3) then follows by dominated convergence.
$B\times [0,T]$, and (3.3) then follows by dominated convergence.
The next step is to extend the relation (3.3) to an asymptotic result for ![]() $\mathbb{P}(\Psi(V_{v,t}^1 + \cdots + V_{v,t}^n + y_{v,t}) > x)$, where, for
$\mathbb{P}(\Psi(V_{v,t}^1 + \cdots + V_{v,t}^n + y_{v,t}) > x)$, where, for ![]() $i=1,\ldots,n$,
$i=1,\ldots,n$, ![]() $V^i$ are i.i.d. with common distribution
$V^i$ are i.i.d. with common distribution ![]() $\nu_1$. Here it will be useful to recall that each
$\nu_1$. Here it will be useful to recall that each ![]() $V^i$ can be represented by
$V^i$ can be represented by ![]() $(Z^i f(|v-U^i|,t-S^i))_{(v,t)\in B^{\prime}\times T^{\prime}}$, where
$(Z^i f(|v-U^i|,t-S^i))_{(v,t)\in B^{\prime}\times T^{\prime}}$, where ![]() $(U^i,S^i,Z^i)$ has distribution
$(U^i,S^i,Z^i)$ has distribution ![]() $F_1$. Before being able to extend (3.3), we need a final assumption on the existence of a function
$F_1$. Before being able to extend (3.3), we need a final assumption on the existence of a function ![]() $\phi$ ensuring sufficient integrability properties.
$\phi$ ensuring sufficient integrability properties.
For the assumption we need some notation representing a deterministic version of the sum ![]() $V_{v,t}^1 + \dots + V_{v,t}^n$. Thus, for each
$V_{v,t}^1 + \dots + V_{v,t}^n$. Thus, for each ![]() $i=1,\ldots,n$, let the field
$i=1,\ldots,n$, let the field ![]() $(y_{v,t}^i)_{(v,t)\in B'\times T^{\prime}}$ be given by
$(y_{v,t}^i)_{(v,t)\in B'\times T^{\prime}}$ be given by
where all ![]() $z^i \ge 0$,
$z^i \ge 0$, ![]() $u^i\in {\mathbb{R}^d}$, and
$u^i\in {\mathbb{R}^d}$, and ![]() $s^i\in{\mathbb{R}}$.
$s^i\in{\mathbb{R}}$.
Assumption 3.3. There exists a Lebesgue-integrable function ![]() $\phi\colon{\mathbb{R}^d}\times {\mathbb{R}} \to [0,\infty)$ such that
$\phi\colon{\mathbb{R}^d}\times {\mathbb{R}} \to [0,\infty)$ such that
 \begin{equation}\phi(u,s)\begin{cases}= c & \textit{for $ {(u,s)\in B^{\prime}\times T^{\prime}}$,} \\
< c & \textit{for $ (u,s)\not\in B^{\prime}\times T^{\prime} $,}\end{cases}\end{equation}
\begin{equation}\phi(u,s)\begin{cases}= c & \textit{for $ {(u,s)\in B^{\prime}\times T^{\prime}}$,} \\
< c & \textit{for $ (u,s)\not\in B^{\prime}\times T^{\prime} $,}\end{cases}\end{equation}
where ![]() $c>0$ is the constant defined in (3.1).
$c>0$ is the constant defined in (3.1).
The function ![]() $\phi$ satisfies
$\phi$ satisfies
and
The definition of ![]() $\phi$ ensures that the tail of
$\phi$ ensures that the tail of ![]() $Z\phi(U,S)$ is asymptotically equivalent to
$Z\phi(U,S)$ is asymptotically equivalent to ![]() $\rho((x/c,\infty))$ and hence
$\rho((x/c,\infty))$ and hence ![]() $Z\phi(U,S)$ is convolution equivalent with index
$Z\phi(U,S)$ is convolution equivalent with index ![]() $\beta/c$; see Lemma 3.1 below. Equation (3.7) then provides a convolution equivalent upper bound of the extremal probability for the functional
$\beta/c$; see Lemma 3.1 below. Equation (3.7) then provides a convolution equivalent upper bound of the extremal probability for the functional ![]() $\Psi$ of a sum of jump-fields. Finally, finiteness of relevant exponential moments of
$\Psi$ of a sum of jump-fields. Finally, finiteness of relevant exponential moments of ![]() $\lambda_{u,s}$ applied to jump-fields is ensured by (3.8). This result is seen in Theorem 3.2 below.
$\lambda_{u,s}$ applied to jump-fields is ensured by (3.8). This result is seen in Theorem 3.2 below.
When showing the convolution equivalence of ![]() $Z\phi(U,S)$, we use the integrability of
$Z\phi(U,S)$, we use the integrability of ![]() $\phi$, although the weaker assumption that
$\phi$, although the weaker assumption that ![]() $\exp({-}\gamma/\phi(u,s))$ is integrable for some
$\exp({-}\gamma/\phi(u,s))$ is integrable for some ![]() $\gamma >0$ is sufficient; see the proof of Lemma 3.1 in the supplementary material [Reference Stehr and Rønn-Nielsen27]. However, as seen in Section 4, in practice
$\gamma >0$ is sufficient; see the proof of Lemma 3.1 in the supplementary material [Reference Stehr and Rønn-Nielsen27]. However, as seen in Section 4, in practice ![]() $\phi(u,s)$ is often bounded by
$\phi(u,s)$ is often bounded by ![]() $\sup_{(v,t)} f(\lvert{v-u}\rvert, t-s)$ and hence its integrability follows from that of
$\sup_{(v,t)} f(\lvert{v-u}\rvert, t-s)$ and hence its integrability follows from that of ![]() $\sup_{(v,t)} f(\lvert{v-u}\rvert, t-s)$.
$\sup_{(v,t)} f(\lvert{v-u}\rvert, t-s)$.
In the remainder of this section it is also assumed that Assumption 3.3 is satisfied. The proof of Lemma 3.1 below follows by arguments similar to the proof of Theorem 3.1 above, but for completeness the proof can be found in the supplementary material [Reference Stehr and Rønn-Nielsen27].
Lemma 3.1. Let (U, S, Z) have distribution ![]() $F_1$. Then, as
$F_1$. Then, as ![]() $x\to\infty$,
$x\to\infty$,
In particular, the distribution of ![]() $Z \phi(U,S)$ is convolution equivalent with index
$Z \phi(U,S)$ is convolution equivalent with index ![]() $\beta/c$ and
$\beta/c$ and
As mentioned, the convolution equivalence of ![]() $Z \phi(U,S)$ is translated into a convolution equivalent upper bound for the extremal probability of a sum of jump-fields. Here (3.7) is applied together with the relation
$Z \phi(U,S)$ is translated into a convolution equivalent upper bound for the extremal probability of a sum of jump-fields. Here (3.7) is applied together with the relation
when F is a convolution equivalent distribution with index ![]() $\beta$,
$\beta$, ![]() $F^{*n}$ is its n-fold convolution, and
$F^{*n}$ is its n-fold convolution, and ![]() $\overline F$ is its tail. For this relation see e.g. [Reference Cline9, Corollary 2.11].
$\overline F$ is its tail. For this relation see e.g. [Reference Cline9, Corollary 2.11].
In Theorem 3.2 below, a similar convolution equivalence for the sum of jump-fields is obtained.
Theorem 3.2. Let ![]() $V^1,V^2,\dots$ be i.i.d. fields with common distribution
$V^1,V^2,\dots$ be i.i.d. fields with common distribution ![]() $\nu_1$, and assume that
$\nu_1$, and assume that ![]() $(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ is t-càdlàg. For all
$(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ is t-càdlàg. For all ![]() $n\in\mathbb{N}$ it holds that
$n\in\mathbb{N}$ it holds that
 \begin{align*} &\dfrac{\mathbb{P}(\Psi(V_{v,t}^1 + \dots + V_{v,t}^n + y_{v,t}) > x)}{\mathbb{P}(\Psi(V_{v,t}^1) > x)} \\*
&\quad \to\dfrac{n}{m(B\times [0,T])} \int_B \int_0^T {\mathbb E} \big[\exp\big( \beta \lambda_{u,s}\big(V_{v,t}^1 + \dots + V_{v,t}^{n-1} + y_{v,t}\big) \big) \big] \,\mathrm{d}s \,\mathrm{d}u\end{align*}
\begin{align*} &\dfrac{\mathbb{P}(\Psi(V_{v,t}^1 + \dots + V_{v,t}^n + y_{v,t}) > x)}{\mathbb{P}(\Psi(V_{v,t}^1) > x)} \\*
&\quad \to\dfrac{n}{m(B\times [0,T])} \int_B \int_0^T {\mathbb E} \big[\exp\big( \beta \lambda_{u,s}\big(V_{v,t}^1 + \dots + V_{v,t}^{n-1} + y_{v,t}\big) \big) \big] \,\mathrm{d}s \,\mathrm{d}u\end{align*}
as ![]() $x \to \infty$.
$x \to \infty$.
Recall that the field ![]() $X^1$ is defined as the compound Poisson sum with i.i.d. jump-fields
$X^1$ is defined as the compound Poisson sum with i.i.d. jump-fields ![]() $V^1,V^2,\dots$ and an independent Poisson-distributed variable N with intensity
$V^1,V^2,\dots$ and an independent Poisson-distributed variable N with intensity ![]() $\nu(A)<\infty$. The following result on the extremal behaviour of
$\nu(A)<\infty$. The following result on the extremal behaviour of ![]() $X^1$ follows from Theorem 3.2 by conditioning on the value of N.
$X^1$ follows from Theorem 3.2 by conditioning on the value of N.
Theorem 3.3. For each ![]() $(u,s)\in B\times [0,T]$,
$(u,s)\in B\times [0,T]$,
For a field ![]() $(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ satisfying (2.6),
$(y_{v,t})_{{(v,t)\in B^{\prime}\times T^{\prime}}}$ satisfying (2.6),
as ![]() $x\to\infty$.
$x\to\infty$.
Now recall that we write the field ![]() $X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ defined in (2.10) as the independent sum
$X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ defined in (2.10) as the independent sum ![]() $X=X^1+X^2$, where
$X=X^1+X^2$, where ![]() $X^1$ is the compound Poisson sum of fields with distribution
$X^1$ is the compound Poisson sum of fields with distribution ![]() $\nu_1$. Also, the fields in the decomposition can be assumed to be t-càdlàg. One can show that the tail of
$\nu_1$. Also, the fields in the decomposition can be assumed to be t-càdlàg. One can show that the tail of ![]() $\sup_{{(v,t)}} X_{v,t}^2$ is lighter than that of
$\sup_{{(v,t)}} X_{v,t}^2$ is lighter than that of ![]() $\Psi(X_{v,t}^1)$, which is equivalent to the tail of
$\Psi(X_{v,t}^1)$, which is equivalent to the tail of ![]() $\rho$ by Theorem 3.3. Combining this fact with [Reference Pakes16, Lemma 2.1], an argument based on independence and dominated convergence can be used to conclude Theorem 3.4 below from Theorem 3.3.
$\rho$ by Theorem 3.3. Combining this fact with [Reference Pakes16, Lemma 2.1], an argument based on independence and dominated convergence can be used to conclude Theorem 3.4 below from Theorem 3.3.
Lemma 3.2. For all ![]() $(u,s)\in B\times [0,T]$ it holds that
$(u,s)\in B\times [0,T]$ it holds that ![]() ${\mathbb E} [\exp (\beta \lambda_{u,s}(X_{v,t}) )] < \infty$.
${\mathbb E} [\exp (\beta \lambda_{u,s}(X_{v,t}) )] < \infty$.
Theorem 3.4. Let the field X be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumption 2.3. Let the functionals ![]() $\Psi$ and
$\Psi$ and ![]() $\lambda_{u,s}$ satisfy Assumptions 3.1 and 3.2, respectively. Then
$\lambda_{u,s}$ satisfy Assumptions 3.1 and 3.2, respectively. Then
4. Example results
In this section we return to Examples 3.1 and 3.2 to show versions of Theorem 3.4 when ![]() $\Psi$ is specifically given as in the examples. We make further assumptions on the kernel f that guarantee Assumptions 3.2 and 3.3.
$\Psi$ is specifically given as in the examples. We make further assumptions on the kernel f that guarantee Assumptions 3.2 and 3.3.
In the setting of Example 3.1 we assume the following.
Assumption 4.1. The kernel ![]() $f\colon[0,\infty)\times {\mathbb{R}} \to [0,\infty)$ is decreasing in both coordinates on
$f\colon[0,\infty)\times {\mathbb{R}} \to [0,\infty)$ is decreasing in both coordinates on ![]() $[0,\infty) \times [0,\infty)$, and it is strictly decreasing in the point
$[0,\infty) \times [0,\infty)$, and it is strictly decreasing in the point ![]() $(r/2,0)$ in the sense that
$(r/2,0)$ in the sense that
Moreover, the derivative
exists for all ![]() $x \ge 0$, and there is a function g such that
$x \ge 0$, and there is a function g such that
for all ![]() $x\in [0,r]$, where also
$x\in [0,r]$, where also ![]() $f(x,0) \le g(x) $ for all
$f(x,0) \le g(x) $ for all ![]() $x\in [0,r]$.
$x\in [0,r]$.
Such a g exists in particular when f is concave on [0, r]. The following lemma shows that Assumption 3.2 is satisfied when the kernel satisfies Assumption 4.1.
Lemma 4.1. If ![]() $\Psi$ and
$\Psi$ and ![]() $\psi_{x,u,s,f}$ are given as in Example 3.1 and f satisfies Assumption 4.1, then Assumption 3.2 is satisfied with
$\psi_{x,u,s,f}$ are given as in Example 3.1 and f satisfies Assumption 4.1, then Assumption 3.2 is satisfied with ![]() $c=f(r/2,0)$. Furthermore, for a t-càdlàg field
$c=f(r/2,0)$. Furthermore, for a t-càdlàg field ![]() $y=(y_{v,t})_{(v,t)\in B^{\prime} \times [0,T]}$, the functional
$y=(y_{v,t})_{(v,t)\in B^{\prime} \times [0,T]}$, the functional ![]() $\lambda_{u,s}$ takes the form
$\lambda_{u,s}$ takes the form
for a functional ![]() $\lambda_u\colon{\mathbb{R}}^{B^{\prime}} \to {\mathbb{R}}$.
$\lambda_u\colon{\mathbb{R}}^{B^{\prime}} \to {\mathbb{R}}$.
Proof. From [Reference Rønn-Nielsen and Jensen20, Lemma 3.1] we have, for fixed ![]() $s\in [0,T]$ and for all
$s\in [0,T]$ and for all ![]() $u\in B$, a functional
$u\in B$, a functional ![]() $\lambda_{u}$ such that
$\lambda_{u}$ such that
as ![]() $x\to\infty$. With
$x\to\infty$. With ![]() $\lambda_{u,s}$ defined by
$\lambda_{u,s}$ defined by
we claim that Assumption 3.2 is satisfied. For notational convenience, we write ![]() $C=-\lambda_u(y_{v,s})$.
$C=-\lambda_u(y_{v,s})$.
For all sufficiently large x, we can choose ![]() $t_x\in [s,T]$,
$t_x\in [s,T]$, ![]() $v_x\in B$, and
$v_x\in B$, and ![]() $R_x \in SO(d)$ such that
$R_x \in SO(d)$ such that
With ![]() $y^* = \sup_{(v,t)\in B^{\prime} \times [0,T]} y_{v,t}$ and
$y^* = \sup_{(v,t)\in B^{\prime} \times [0,T]} y_{v,t}$ and ![]() $y_* = \inf_{(v,t)\in B^{\prime} \times [0,T]} y_{v,t}$, we then find
$y_* = \inf_{(v,t)\in B^{\prime} \times [0,T]} y_{v,t}$, we then find
 \begin{align*}\dfrac{x - y^*}{\inf_{v\in D^{R_x}(v_x)} f(\lvert{v-u}\rvert,t_x-s)} &\le \sup_{v\in D^{R_x}(v_x)} \dfrac{x - y_{v,t_x}}{f(\lvert{v-u}\rvert,t_x-s)} \\* &\le \sup_{v\in D^{R_x}(u)} \dfrac{x - y_{v,s}}{f(\lvert{v-u}\rvert,0)}\\*&\le \dfrac{x - y_*}{f(r/2,0)} .\end{align*}
\begin{align*}\dfrac{x - y^*}{\inf_{v\in D^{R_x}(v_x)} f(\lvert{v-u}\rvert,t_x-s)} &\le \sup_{v\in D^{R_x}(v_x)} \dfrac{x - y_{v,t_x}}{f(\lvert{v-u}\rvert,t_x-s)} \\* &\le \sup_{v\in D^{R_x}(u)} \dfrac{x - y_{v,s}}{f(\lvert{v-u}\rvert,0)}\\*&\le \dfrac{x - y_*}{f(r/2,0)} .\end{align*}
Going to the limit ![]() $x\to\infty$ and using that
$x\to\infty$ and using that ![]() $\inf_{v\in D^R(v_0)} f(\lvert{v-u}\rvert,t-s)\leq f(r/2,0)$ shows that
$\inf_{v\in D^R(v_0)} f(\lvert{v-u}\rvert,t-s)\leq f(r/2,0)$ shows that
Since in fact ![]() $\inf_{v\in D^R(v_0)} f(\lvert{v-u}\rvert,t-s)<f(r/2,0)$ for all
$\inf_{v\in D^R(v_0)} f(\lvert{v-u}\rvert,t-s)<f(r/2,0)$ for all ![]() $(v_0,t)\neq (u,s)$ and
$(v_0,t)\neq (u,s)$ and ![]() $R\in SO(d)$, the convergence implies that also
$R\in SO(d)$, the convergence implies that also ![]() $v_x \to u$ and
$v_x \to u$ and ![]() $t_x \to s$. We will show the desired convergence
$t_x \to s$. We will show the desired convergence
by contradiction. Since
we assume the existence of ![]() $\varepsilon >0$ and a sequence
$\varepsilon >0$ and a sequence ![]() $(x_n)$,
$(x_n)$, ![]() $x_n\to\infty$, such that
$x_n\to\infty$, such that
for all n, where ![]() $t_n = t_{x_n}$,
$t_n = t_{x_n}$, ![]() $v_n=v_{x_n}$ and
$v_n=v_{x_n}$ and ![]() $R_n = R_{x_n}$. By t-càdlàg properties of the y-field, we can find
$R_n = R_{x_n}$. By t-càdlàg properties of the y-field, we can find ![]() $n_0$ such that
$n_0$ such that
for all ![]() $n\ge n_0$. Consequently, and using that f is decreasing and (4.4),
$n\ge n_0$. Consequently, and using that f is decreasing and (4.4),
 \begin{align*} \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,s}}{f(\lvert{v-u}\rvert,0)} - \dfrac{x_n}{f(r/2,0)} & \leq \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,t_n}}{f(\lvert{v-u}\rvert,0)} - \dfrac{x_n}{f(r/2,0)} +\dfrac{\varepsilon}{2}\\* & \leq \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,t_n}}{f(\lvert{v-u}\rvert,t_n-s)} - \dfrac{x_n}{f(r/2,0)}+\dfrac{\varepsilon}{2}\\* &\leq C-\dfrac{\varepsilon}{2},\end{align*}
\begin{align*} \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,s}}{f(\lvert{v-u}\rvert,0)} - \dfrac{x_n}{f(r/2,0)} & \leq \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,t_n}}{f(\lvert{v-u}\rvert,0)} - \dfrac{x_n}{f(r/2,0)} +\dfrac{\varepsilon}{2}\\* & \leq \sup_{v\in D^{R_n}(v_n)} \dfrac{x_n - y_{v,t_n}}{f(\lvert{v-u}\rvert,t_n-s)} - \dfrac{x_n}{f(r/2,0)}+\dfrac{\varepsilon}{2}\\* &\leq C-\dfrac{\varepsilon}{2},\end{align*}
which contradicts the limit relation (4.3).
Theorem 4.1. Let the field X be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumptions 2.3 and 4.1. Let ![]() $D\subseteq C_{r/2}(0)$ have radius
$D\subseteq C_{r/2}(0)$ have radius ![]() $r/2>0$ and let
$r/2>0$ and let ![]() $\Psi$ be defined by
$\Psi$ be defined by
Furthermore, let ![]() $\lambda_{u,s}$ be the functional given in Lemma 4.1 and write
$\lambda_{u,s}$ be the functional given in Lemma 4.1 and write ![]() $c=f(r/2,0)$. Then
$c=f(r/2,0)$. Then
Proof. The result follows from Theorem 3.4 and Lemma 4.1 once we show the existence of a function ![]() $\phi$ satisfying Assumption 3.3. Now define
$\phi$ satisfying Assumption 3.3. Now define ![]() $\phi$ as
$\phi$ as
which is integrable by (2.12) and satisfies (3.6) by (4.1). Appealing to Lemma 4.1 and [Reference Rønn-Nielsen and Jensen20, Lemma 3.2],
for all ![]() ${(u,s)\in B\times [0,T]}$, if
${(u,s)\in B\times [0,T]}$, if ![]() $D=\{-\alpha r/2, \alpha r/2\}$ for some
$D=\{-\alpha r/2, \alpha r/2\}$ for some ![]() $\alpha \in \mathbb{S}^{d-1}$. Adapting the proof of [Reference Rønn-Nielsen and Jensen20, Lemma 3.3] to this time-dependent setting, it is seen using (4.5) that (3.7) and (3.8) follow when it is shown that
$\alpha \in \mathbb{S}^{d-1}$. Adapting the proof of [Reference Rønn-Nielsen and Jensen20, Lemma 3.3] to this time-dependent setting, it is seen using (4.5) that (3.7) and (3.8) follow when it is shown that
with ![]() $y_{v,t}^i$ defined as just before Assumption 3.3. Since f is decreasing in both coordinates,
$y_{v,t}^i$ defined as just before Assumption 3.3. Since f is decreasing in both coordinates,
Using the upper bound g assumed by (4.2), arguments as in [Reference Rønn-Nielsen and Jensen20, Lemma 3.3] show that (4.6) is satisfied when ![]() $(u^i,s^i)\in B^{\prime} \times [0,T]$. When
$(u^i,s^i)\in B^{\prime} \times [0,T]$. When ![]() $(u^i,s^i)\in (B^{\prime} \times [0,T])^c$ it is immediately seen that
$(u^i,s^i)\in (B^{\prime} \times [0,T])^c$ it is immediately seen that
This concludes the proof.
In the setting of Example 3.2 the following is assumed.
Assumption 4.2. For the set ![]() $D\subseteq C_r(0) \subseteq {\mathbb{R}^d}$ the kernel function f satisfies
$D\subseteq C_r(0) \subseteq {\mathbb{R}^d}$ the kernel function f satisfies
for all ![]() $(v_0,t_0) \neq (u,s) \in {{\mathbb{R}^d} \times {\mathbb{R}}}$.
$(v_0,t_0) \neq (u,s) \in {{\mathbb{R}^d} \times {\mathbb{R}}}$.
Lemma 4.2. Let ![]() $y=(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ be a t-càdlàg field. For all
$y=(y_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ be a t-càdlàg field. For all ![]() ${(u,s)\in B\times [0,T]}$ it holds that
${(u,s)\in B\times [0,T]}$ it holds that
 \begin{align} & \inf_{t_0\in[0,T]} \inf_{v_0\in B} \inf_{R\in SO(d)} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v} {{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \notag \\[5pt]
&\quad\, - \dfrac{x}{c} + \sup_{R\in SO(d)} \dfrac{1}{c} \dfrac{1}{K}\int_{D^R(u)}\int_{I(s)} y_{v,t} \,\mathrm{d} t \,\mathrm{d} v\to 0\end{align}
\begin{align} & \inf_{t_0\in[0,T]} \inf_{v_0\in B} \inf_{R\in SO(d)} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v} {{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \notag \\[5pt]
&\quad\, - \dfrac{x}{c} + \sup_{R\in SO(d)} \dfrac{1}{c} \dfrac{1}{K}\int_{D^R(u)}\int_{I(s)} y_{v,t} \,\mathrm{d} t \,\mathrm{d} v\to 0\end{align}
as ![]() $x\to\infty$, where
$x\to\infty$, where
That is, with ![]() $\Psi$ and
$\Psi$ and ![]() $\psi_{x,u,s,f}$ as in Example 3.2, and with
$\psi_{x,u,s,f}$ as in Example 3.2, and with
Assumption 3.2 is satisfied.
Proof. For all sufficiently large ![]() $x>0$, choose
$x>0$, choose ![]() $t_x\in[s,T]$,
$t_x\in[s,T]$, ![]() $v_x\in B$, and
$v_x\in B$, and ![]() $R_x\in SO(d)$ with
$R_x\in SO(d)$ with
 \begin{equation*}\inf_{t_0,v_0,R} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v}=\dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} .\end{equation*}
\begin{equation*}\inf_{t_0,v_0,R} \dfrac{x-{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^R(v_0)} \int_{I(t_0)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v}=\dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} .\end{equation*}
By definition of ![]() $t_x$ and
$t_x$ and ![]() $v_x$ we find that
$v_x$ we find that
 \begin{align*}\dfrac{x-y^*}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} &\le\dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&\le\inf_{R\in SO(d)}\dfrac{x-{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D(u)} \int_{I(s)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&= \dfrac{x-\sup_{R\in SO(d)}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c},\end{align*}
\begin{align*}\dfrac{x-y^*}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} &\le\dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&\le\inf_{R\in SO(d)}\dfrac{x-{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D(u)} \int_{I(s)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&= \dfrac{x-\sup_{R\in SO(d)}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c},\end{align*}
where ![]() $y^* = \sup y_{v,t}$. Rearranging and noting that
$y^* = \sup y_{v,t}$. Rearranging and noting that
for all ![]() $(v_0,t_0)\neq (u,s)$ and any
$(v_0,t_0)\neq (u,s)$ and any ![]() $R\in SO(d)$, we conclude that
$R\in SO(d)$, we conclude that
and consequently ![]() $v_x \to u$ and
$v_x \to u$ and ![]() $t_x \to s$ as
$t_x \to s$ as ![]() $x\to\infty$. Since the field
$x\to\infty$. Since the field ![]() $(y_{v,t})$ is t-càdlàg, we furthermore find that, as
$(y_{v,t})$ is t-càdlàg, we furthermore find that, as ![]() $x\to\infty$,
$x\to\infty$,
Recalling that
and turning to the inequalities above, we conclude (4.8) by
 \begin{align*}0 &\le\dfrac{x-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c}- \dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&\le\dfrac{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c} \\[4pt]
&\le\dfrac{\sup_R {{K}^{-1}}\int_{D^{R}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v} {c} \\* & \to 0\end{align*}
\begin{align*}0 &\le\dfrac{x-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c}- \dfrac{x-{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} f(\lvert{v-u}\rvert, t-s) \, \mathrm{d} t \,\mathrm{d} v} \\[4pt]
&\le\dfrac{{{K}^{-1}}\int_{D^{R_x}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v}{c} \\[4pt]
&\le\dfrac{\sup_R {{K}^{-1}}\int_{D^{R}(v_x)} \int_{I(t_x)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v-\sup_{R}{{K}^{-1}}\int_{D^{R}(u)} \int_{I(s)} y_{v,t} \, \mathrm{d} t \,\mathrm{d} v} {c} \\* & \to 0\end{align*}
as ![]() $x\to\infty$.
$x\to\infty$.
Theorem 4.2. Let the field X be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumptions 2.3 and 4.2. Let ![]() $D\subseteq C_r(0)\subseteq {\mathbb{R}^d}$ for
$D\subseteq C_r(0)\subseteq {\mathbb{R}^d}$ for ![]() $r\ge 0$ be given, and let
$r\ge 0$ be given, and let ![]() $\Psi$ be defined by
$\Psi$ be defined by
where ![]() $K=\int_D \int_0^\ell 1\,\mathrm{d} t \,\mathrm{d} v$. Furthermore, let
$K=\int_D \int_0^\ell 1\,\mathrm{d} t \,\mathrm{d} v$. Furthermore, let
Then
where ![]() ${(u,s)\in B\times [0,T]}$ is chosen arbitrarily.
${(u,s)\in B\times [0,T]}$ is chosen arbitrarily.
Proof of Theorem 4.2. The result follows from Theorem 3.4 and Lemma 4.2 once we show the existence of a function ![]() $\phi$ satisfying Assumption 3.3. Note that the integrand in the limit in Theorem 3.4 is constant due to the stationarity of X and
$\phi$ satisfying Assumption 3.3. Note that the integrand in the limit in Theorem 3.4 is constant due to the stationarity of X and ![]() $\lambda_{u,s}$. Define
$\lambda_{u,s}$. Define
which is integrable by (2.12) and satisfies (3.6) by (4.7). Now let ![]() $n\in\mathbb{N}$ be fixed, and let
$n\in\mathbb{N}$ be fixed, and let ![]() $(y_{v,t}^i)_{(v,t)\in B^{\prime}\times T^{\prime}}$ for
$(y_{v,t}^i)_{(v,t)\in B^{\prime}\times T^{\prime}}$ for ![]() $i=1,\ldots,n$ be t-càdlàg fields. Then
$i=1,\ldots,n$ be t-càdlàg fields. Then
 \begin{align*}\Psi\biggl( \sum_{i=1}^n y_{v,t}^i \biggr) &= \sup_{t_0\in [0,T]} \sup_{v_0\in B} \sup_{R\in SO(d)} \dfrac{1}{K}\int_{D^R(v_0)} \int_{I(t_0)} { \sum_{i=1}^n y_{v,t}^i} \, \mathrm{d} t \,\mathrm{d} v \\* &\le \sum_{i=1}^n \sup_{t_0\in [0,T]} \sup_{v_0\in B} \sup_{R\in SO(d)} \dfrac{1}{K}\int_{D^R(v_0)} \int_{I(t_0)} {y_{v,t}^i} \, \mathrm{d} t \,\mathrm{d} v\\* & = \sum_{i=1}^n \Psi(y_{v,t}^i) .\end{align*}
\begin{align*}\Psi\biggl( \sum_{i=1}^n y_{v,t}^i \biggr) &= \sup_{t_0\in [0,T]} \sup_{v_0\in B} \sup_{R\in SO(d)} \dfrac{1}{K}\int_{D^R(v_0)} \int_{I(t_0)} { \sum_{i=1}^n y_{v,t}^i} \, \mathrm{d} t \,\mathrm{d} v \\* &\le \sum_{i=1}^n \sup_{t_0\in [0,T]} \sup_{v_0\in B} \sup_{R\in SO(d)} \dfrac{1}{K}\int_{D^R(v_0)} \int_{I(t_0)} {y_{v,t}^i} \, \mathrm{d} t \,\mathrm{d} v\\* & = \sum_{i=1}^n \Psi(y_{v,t}^i) .\end{align*}
Furthermore, if ![]() $y_{v,t}^i = z^i f(\lvert{v-u^i}\rvert,t-s^i)$, it is easily seen that
$y_{v,t}^i = z^i f(\lvert{v-u^i}\rvert,t-s^i)$, it is easily seen that ![]() $\Psi(y_{v,t}^i) \le z^i \phi(u^i,s^i) ,$ and hence (3.7) is satisfied. Since
$\Psi(y_{v,t}^i) \le z^i \phi(u^i,s^i) ,$ and hence (3.7) is satisfied. Since
(3.8) is also satisfied, which concludes the proof.
As mentioned in Example 3.2, the case of ![]() $\mathbb{P}( \sup_{t\in [0,T]} \sup_{v\in B}X_{v,t}>x)$ follows from Theorem 4.2 by letting
$\mathbb{P}( \sup_{t\in [0,T]} \sup_{v\in B}X_{v,t}>x)$ follows from Theorem 4.2 by letting ![]() $\ell=0$ and
$\ell=0$ and ![]() $D=\{0\}$. In this case the constant
$D=\{0\}$. In this case the constant ![]() $c=f(0,0)=1$ and (4.7) translates into
$c=f(0,0)=1$ and (4.7) translates into ![]() $f(\lvert{v_0 - u}\rvert,t_0-s)< f(0,0)$ for all
$f(\lvert{v_0 - u}\rvert,t_0-s)< f(0,0)$ for all ![]() $(v_0,t_0)\neq (u,s)$, or equivalently
$(v_0,t_0)\neq (u,s)$, or equivalently ![]() $f(x,y)<f(0,0)$ for all
$f(x,y)<f(0,0)$ for all ![]() $(x,y)\neq (0,0)$.
$(x,y)\neq (0,0)$.
Theorem 4.3. Let the field X be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumption 2.3 and ![]() $f(x,y)< f(0,0)$ for all
$f(x,y)< f(0,0)$ for all ![]() $(x,y)\neq (0,0)$. Then
$(x,y)\neq (0,0)$. Then
where ![]() ${(u,s)\in B\times [0,T]}$ is chosen arbitrarily.
${(u,s)\in B\times [0,T]}$ is chosen arbitrarily.
5. Continuity properties
The main purpose of this section is to show that the field defined in (2.10) has a version with t-càdlàg sample paths. This result will be obtained in Theorem 5.3 below. However, the proof involves showing two other results on continuity properties of related random fields of independent value. Therefore these results are formulated as separate theorems; see Theorems 5.1 and 5.2 below. Only the main results, Theorems 5.1–5.3, are stated fully with all assumptions included in the statement. The rest are to be understood in relation to the context. As stated in Section 2, Assumption 2.1 on the Lévy basis is partly used to guarantee that the field is t-càdlàg. However, if the aim is solely to obtain the t-càdlàg property, we can relax the assumption. In this section we therefore consider Assumption 5.1 below. It will be referred to with the dimension of the Lévy basis being d and ![]() $d+1$. Thus both the assumption and the subsequent Theorem 5.1 will be formulated with
$d+1$. Thus both the assumption and the subsequent Theorem 5.1 will be formulated with ![]() $m\in\mathbb{N}$ indicating the dimension.
$m\in\mathbb{N}$ indicating the dimension.
Assumption 5.1. The Lévy basis M on ![]() ${\mathbb{R}}^{m}$ is stationary and isotropic satisfying (2.1). Moreover, the Lévy measure, denoted
${\mathbb{R}}^{m}$ is stationary and isotropic satisfying (2.1). Moreover, the Lévy measure, denoted ![]() $\rho$, satisfies
$\rho$, satisfies
For the first result in this section, consider a compact set ![]() $K\subseteq {\mathbb{R}}^{m}$ and define the random field
$K\subseteq {\mathbb{R}}^{m}$ and define the random field ![]() $Y=(Y_v)_{v\in K}$ by
$Y=(Y_v)_{v\in K}$ by
where M is a Lévy basis on ![]() ${\mathbb{R}}^{m}$ satisfying Assumption 5.1. It is shown in [Reference Rønn-Nielsen and Jensen19, Theorem A.1] that such a field has a continuous version when
${\mathbb{R}}^{m}$ satisfying Assumption 5.1. It is shown in [Reference Rønn-Nielsen and Jensen19, Theorem A.1] that such a field has a continuous version when ![]() $h\colon[0,\infty) \to {\mathbb{R}}$ satisfies certain properties including being differentiable. Under much less restrictive assumptions on the kernel function h, we show that this is still the case. We only assume that h is bounded and integrable,
$h\colon[0,\infty) \to {\mathbb{R}}$ satisfies certain properties including being differentiable. Under much less restrictive assumptions on the kernel function h, we show that this is still the case. We only assume that h is bounded and integrable,
and that h is Lipschitz-continuous. That is, there exist ![]() $C_L>0$ such that
$C_L>0$ such that
for all ![]() $x,y\ge 0$. Having Assumption 5.1 satisfied for the basis M and (5.3) and (5.4) satisfied for the bounded kernel function ensures in particular that the integral (5.2) exists; see [Reference Rajput and Rosinski18, Theorem 2.7].
$x,y\ge 0$. Having Assumption 5.1 satisfied for the basis M and (5.3) and (5.4) satisfied for the bounded kernel function ensures in particular that the integral (5.2) exists; see [Reference Rajput and Rosinski18, Theorem 2.7].
To show continuity, we appeal to a result in [Reference Adler1], in which finite moments and cumulants of the spot variable M′ of the basis M are needed. As already mentioned, (5.1) is equivalent to saying that M′ has finite moments and thus cumulants of any order; see [Reference Peccati and Taqqu17, Corollary 3.2.2] for the relation between moments and cumulants.
Theorem 5.1. If the field Y is given by (5.2) with the Lévy basis M on ![]() ${\mathbb{R}}^m$ satisfying Assumption 5.1, and if the kernel is bounded and satisfies (5.3) and (5.4), then the field has a continuous version.
${\mathbb{R}}^m$ satisfying Assumption 5.1, and if the kernel is bounded and satisfies (5.3) and (5.4), then the field has a continuous version.
Proof. For ![]() $r\in{\mathbb{R}}$ and
$r\in{\mathbb{R}}$ and ![]() $n\in\mathbb{N}$ we shall consider moments of the form
$n\in\mathbb{N}$ we shall consider moments of the form ![]() ${\mathbb E} [ (Y_{v+r}-Y_v)^n]$. Note that only indices in K are relevant, so in particular,
${\mathbb E} [ (Y_{v+r}-Y_v)^n]$. Note that only indices in K are relevant, so in particular, ![]() $0\le \lvert{r}\rvert \le\mathrm{diam}(K)$. By (5.4) and the triangle inequality, there is a finite C such that
$0\le \lvert{r}\rvert \le\mathrm{diam}(K)$. By (5.4) and the triangle inequality, there is a finite C such that
Now let ![]() $\kappa_n[{}\cdot{}]$ denote the nth cumulant of a random variable; for a brief overview of the relation between cumulants and moments we refer to [Reference Peccati and Taqqu17, Chapter 3] and in particular [Reference Peccati and Taqqu17, Corollary 3.2.2]. The cumulants
$\kappa_n[{}\cdot{}]$ denote the nth cumulant of a random variable; for a brief overview of the relation between cumulants and moments we refer to [Reference Peccati and Taqqu17, Chapter 3] and in particular [Reference Peccati and Taqqu17, Corollary 3.2.2]. The cumulants ![]() $\kappa_n$ of the difference
$\kappa_n$ of the difference ![]() $Y_{v+r} - Y_v$ satisfy
$Y_{v+r} - Y_v$ satisfy ![]() $\kappa_1[Y_{v+r} - Y_v]=0$ and, for
$\kappa_1[Y_{v+r} - Y_v]=0$ and, for ![]() $n>1$,
$n>1$,
 \begin{align*}\bigl|{ \kappa_n[Y_{v+r} - Y_v] }\bigr| &\le \lvert {\kappa_n[M^{\prime}]}\rvert \int_{{\mathbb{R}}^m} \bigl| { h(\lvert{v + r- u}\rvert)-h(\lvert{v - u}\rvert)}\bigr|^n \,\mathrm{d}u \\[4pt]
&\le \lvert {\kappa_n[M^{\prime}]}\rvert C^{n-1} |r|^{n-1} \int_{{\mathbb{R}}^m} \bigl| { h(\lvert{v + r- u}\rvert)-h(\lvert{v - u}\rvert)}\bigr| \,\mathrm{d}u\\[4pt]
&\le C_n |r|^{n-1} ,\end{align*}
\begin{align*}\bigl|{ \kappa_n[Y_{v+r} - Y_v] }\bigr| &\le \lvert {\kappa_n[M^{\prime}]}\rvert \int_{{\mathbb{R}}^m} \bigl| { h(\lvert{v + r- u}\rvert)-h(\lvert{v - u}\rvert)}\bigr|^n \,\mathrm{d}u \\[4pt]
&\le \lvert {\kappa_n[M^{\prime}]}\rvert C^{n-1} |r|^{n-1} \int_{{\mathbb{R}}^m} \bigl| { h(\lvert{v + r- u}\rvert)-h(\lvert{v - u}\rvert)}\bigr| \,\mathrm{d}u\\[4pt]
&\le C_n |r|^{n-1} ,\end{align*}
where ![]() $C_n\ge 0$ is a finite constant, chosen independently of r and
$C_n\ge 0$ is a finite constant, chosen independently of r and ![]() $v\in K$ by
$v\in K$ by
(see e.g. [Reference Rønn-Nielsen and Jensen21, Appendix A] for the cumulant formulas). Consequently, for all ![]() $n\in\mathbb{N}$ there exist finite constants
$n\in\mathbb{N}$ there exist finite constants ![]() $C^{\prime}_n$ and natural numbers
$C^{\prime}_n$ and natural numbers ![]() $n^{\prime} \ge n/2$ such that
$n^{\prime} \ge n/2$ such that
with the equality ![]() $n^{\prime}=n/2$ whenever n is even (see [Reference Peccati and Taqqu17, Corollary 3.2.2]). Using the fact that
$n^{\prime}=n/2$ whenever n is even (see [Reference Peccati and Taqqu17, Corollary 3.2.2]). Using the fact that ![]() $\lvert{r}\rvert\le\mathrm{diam}(K)$, we find finite
$\lvert{r}\rvert\le\mathrm{diam}(K)$, we find finite ![]() $C'\ge 0$ and
$C'\ge 0$ and ![]() $\eta > 4(m+1)$ such that
$\eta > 4(m+1)$ such that
for all ![]() $v\in K$. From a corollary to [Reference Adler1, Theorem 3.2.5] we conclude that
$v\in K$. From a corollary to [Reference Adler1, Theorem 3.2.5] we conclude that ![]() $(Y_v)_{v\in K}$ has a continuous version on K.
$(Y_v)_{v\in K}$ has a continuous version on K.
Next we consider a field indexed by ![]() ${{\mathbb{R}^d} \times {\mathbb{R}}}$ allowing for discontinuities in time, and we show that it has a t-càdlàg version. For compact sets
${{\mathbb{R}^d} \times {\mathbb{R}}}$ allowing for discontinuities in time, and we show that it has a t-càdlàg version. For compact sets ![]() $K\subseteq{\mathbb{R}^d}$ and [0, S],
$K\subseteq{\mathbb{R}^d}$ and [0, S], ![]() $S>0$, we let the random field
$S>0$, we let the random field ![]() $Z=(Z_{v,t})_{(v,t)\in K\times [0,S]}$ be given by
$Z=(Z_{v,t})_{(v,t)\in K\times [0,S]}$ be given by
where M is a Lévy basis satisfying Assumption 5.1 with ![]() $m=d+1$, and the integration kernel
$m=d+1$, and the integration kernel ![]() $g\colon[0,\infty) \to {\mathbb{R}}$ is assumed to be bounded, integrable, and Lipschitz-continuous, i.e. it satisfies (5.3) and (5.4) with
$g\colon[0,\infty) \to {\mathbb{R}}$ is assumed to be bounded, integrable, and Lipschitz-continuous, i.e. it satisfies (5.3) and (5.4) with ![]() $m=d$.
$m=d$.
Choose ![]() $0=t_0<\dots<t_n$ in [0, S] and
$0=t_0<\dots<t_n$ in [0, S] and ![]() $v\in K$. Arguing as in Section 2, the cumulant function for
$v\in K$. Arguing as in Section 2, the cumulant function for ![]() $(Z_{v,t_1}, Z_{v,t_2}-Z_{v,t_1},\ldots,Z_{v,t_n}-Z_{v,t_{n-1}})$ can be found to be
$(Z_{v,t_1}, Z_{v,t_2}-Z_{v,t_1},\ldots,Z_{v,t_n}-Z_{v,t_{n-1}})$ can be found to be
 \begin{align*}&C(\boldsymbol{\lambda} \dagger (Z_{v,t_1}, Z_{v,t_2}-Z_{v,t_1},\ldots,Z_{v,t_n}-Z_{v,t_{n-1}})) \\[3pt]
&\quad = \sum_{j=1}^n (t_j - t_{j-1})\biggl({\mathrm{i}} \lambda_j a \int_{\mathbb{R}^d} g(\lvert{v-u}\rvert) \,\mathrm{d}u- \dfrac12 \theta \lambda_j^2 \int_{\mathbb{R}^d} g(\lvert{v-u}\rvert)^2 \,\mathrm{d}u \\[3pt]
& \quad\quad\, + \int_{{\mathbb{R}^d}} \int_{\mathbb{R}} \mathrm{e}^{{\mathrm{i}} g(\lvert{v-u}\rvert) \lambda_j z} - 1 - {\mathrm{i}} g(\lvert{v-u}\rvert)\lambda_j z 1_{[-1,1]}(z) \rho(\mathrm{d} z) \,\mathrm{d}u\biggr)\end{align*}
\begin{align*}&C(\boldsymbol{\lambda} \dagger (Z_{v,t_1}, Z_{v,t_2}-Z_{v,t_1},\ldots,Z_{v,t_n}-Z_{v,t_{n-1}})) \\[3pt]
&\quad = \sum_{j=1}^n (t_j - t_{j-1})\biggl({\mathrm{i}} \lambda_j a \int_{\mathbb{R}^d} g(\lvert{v-u}\rvert) \,\mathrm{d}u- \dfrac12 \theta \lambda_j^2 \int_{\mathbb{R}^d} g(\lvert{v-u}\rvert)^2 \,\mathrm{d}u \\[3pt]
& \quad\quad\, + \int_{{\mathbb{R}^d}} \int_{\mathbb{R}} \mathrm{e}^{{\mathrm{i}} g(\lvert{v-u}\rvert) \lambda_j z} - 1 - {\mathrm{i}} g(\lvert{v-u}\rvert)\lambda_j z 1_{[-1,1]}(z) \rho(\mathrm{d} z) \,\mathrm{d}u\biggr)\end{align*}
where ![]() $\boldsymbol{\lambda} = (\lambda_1,\ldots,\lambda_n)\in {\mathbb{R}}^n$. By a change of measure, we see for fixed
$\boldsymbol{\lambda} = (\lambda_1,\ldots,\lambda_n)\in {\mathbb{R}}^n$. By a change of measure, we see for fixed ![]() $v\in\mathbb{K}$ that
$v\in\mathbb{K}$ that ![]() $(Z_{v,t})_{t\in [0,S]}$ is a one-dimensional Lévy process in law. In the following we shall extend this to a result concerning the process of random fields indexed by time.
$(Z_{v,t})_{t\in [0,S]}$ is a one-dimensional Lévy process in law. In the following we shall extend this to a result concerning the process of random fields indexed by time.
In this section we will often consider the field as being a collection of real-valued functions defined on space K or ![]() $\tilde K = K \cap \mathbb{Q}^d$, with the functions indexed by time in [0, S] or
$\tilde K = K \cap \mathbb{Q}^d$, with the functions indexed by time in [0, S] or ![]() $\tilde S = [0,S] \cap \mathbb{Q}$. As such we introduce the notation
$\tilde S = [0,S] \cap \mathbb{Q}$. As such we introduce the notation ![]() $\textbf{Z}_t = (Z_{v,t})_{v\in K}$, with the entire field denoted by
$\textbf{Z}_t = (Z_{v,t})_{v\in K}$, with the entire field denoted by ![]() $\textbf{Z} = (\textbf{Z}_t)_{t\in [0,S]}$ when considered as a collection of random functions. We use the same notation when space and time are indexed by
$\textbf{Z} = (\textbf{Z}_t)_{t\in [0,S]}$ when considered as a collection of random functions. We use the same notation when space and time are indexed by ![]() $\tilde K$ and
$\tilde K$ and ![]() $\tilde S$, respectively, although when it is unclear which is meant and it is necessary to distinguish the cases, we explicitly state it.
$\tilde S$, respectively, although when it is unclear which is meant and it is necessary to distinguish the cases, we explicitly state it.
Let ![]() $t\in[0,S]$ be fixed and choose
$t\in[0,S]$ be fixed and choose ![]() $v_1,\ldots,v_n\in K$. Then
$v_1,\ldots,v_n\in K$. Then ![]() $(Z_{v_1,t},\ldots,Z_{v_n,t})$ has cumulant function given by
$(Z_{v_1,t},\ldots,Z_{v_n,t})$ has cumulant function given by
 \begin{align} & C(\boldsymbol{\lambda} \dagger (Z_{v_1,t},\ldots,Z_{v_n,t})) \notag \\* &\quad = t{\mathrm{i}} a \int_{\mathbb{R}^d} \sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) \,\mathrm{d}u \notag \\* & \quad \quad\, - t\dfrac12 \theta \int_{\mathbb{R}^d} \biggl( \sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) \biggr)^2 \,\mathrm{d}u \notag \\* & \quad \quad\, + t \int_{{\mathbb{R}^d}} \int_{\mathbb{R}} \mathrm{e}^{{\mathrm{i}}\sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert)z} - 1 - {\mathrm{i}}\sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) z 1_{[-1,1]}(z) \rho(\mathrm{d} z) \,\mathrm{d}u .\end{align}
\begin{align} & C(\boldsymbol{\lambda} \dagger (Z_{v_1,t},\ldots,Z_{v_n,t})) \notag \\* &\quad = t{\mathrm{i}} a \int_{\mathbb{R}^d} \sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) \,\mathrm{d}u \notag \\* & \quad \quad\, - t\dfrac12 \theta \int_{\mathbb{R}^d} \biggl( \sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) \biggr)^2 \,\mathrm{d}u \notag \\* & \quad \quad\, + t \int_{{\mathbb{R}^d}} \int_{\mathbb{R}} \mathrm{e}^{{\mathrm{i}}\sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert)z} - 1 - {\mathrm{i}}\sum_{j=1}^n\lambda_j g(\lvert{v_j-u}\rvert) z 1_{[-1,1]}(z) \rho(\mathrm{d} z) \,\mathrm{d}u .\end{align}
Replacing ![]() $(a,\theta,\rho)$ with
$(a,\theta,\rho)$ with ![]() $(ta,t\theta,t\rho)$, we see from (5.6) that
$(ta,t\theta,t\rho)$, we see from (5.6) that ![]() $\textbf{Z}_t$ is the type of field defined in (5.2). Thus, by Theorem 5.1,
$\textbf{Z}_t$ is the type of field defined in (5.2). Thus, by Theorem 5.1, ![]() $(Z_{v,t})_{v\in \tilde K}$ is almost surely uniformly continuous. This holds jointly for all rational time points
$(Z_{v,t})_{v\in \tilde K}$ is almost surely uniformly continuous. This holds jointly for all rational time points ![]() $t\in\tilde S$, and therefore a version of
$t\in\tilde S$, and therefore a version of ![]() $(\textbf{Z}_t)_{t\in \tilde S}$ can be chosen with
$(\textbf{Z}_t)_{t\in \tilde S}$ can be chosen with ![]() $\textbf{Z}_t$ being continuous for all
$\textbf{Z}_t$ being continuous for all ![]() $t\in \tilde S$, i.e. it has values in the space of real-valued functions on the compact set K. It will be useful in the following that this space equipped with the uniform norm, here denoted
$t\in \tilde S$, i.e. it has values in the space of real-valued functions on the compact set K. It will be useful in the following that this space equipped with the uniform norm, here denoted ![]() $(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$, is a separable Banach space; see [Reference Kechris14, Theorem 4.19]. The following lemma concerns this specific version of
$(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$, is a separable Banach space; see [Reference Kechris14, Theorem 4.19]. The following lemma concerns this specific version of ![]() $(\textbf{Z})_{t\in \tilde S}$ taking its values in
$(\textbf{Z})_{t\in \tilde S}$ taking its values in ![]() $(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$.
$(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$.
Lemma 5.1. The process ![]() $(\textbf{Z}_t)_{t\in\tilde S}$ is a Lévy process in law, that is, each
$(\textbf{Z}_t)_{t\in\tilde S}$ is a Lévy process in law, that is, each ![]() $\textbf{Z}_t$ has an infinitely divisible distribution, the process has stationary and independent increments, and it is stochastically continuous with respect to the uniform norm.
$\textbf{Z}_t$ has an infinitely divisible distribution, the process has stationary and independent increments, and it is stochastically continuous with respect to the uniform norm.
Proof. As ![]() $\textbf{Z}_t$ is a version of the field studied in (5.6) for each
$\textbf{Z}_t$ is a version of the field studied in (5.6) for each ![]() $t\in \tilde S$, the cumulant function for
$t\in \tilde S$, the cumulant function for ![]() $(Z_{v_1,t},\ldots,Z_{v_n,t})$ will also be as in (5.6). With similar considerations but heavier notation, it can be realized that for
$(Z_{v_1,t},\ldots,Z_{v_n,t})$ will also be as in (5.6). With similar considerations but heavier notation, it can be realized that for ![]() $v_1,\ldots,v_n \in K$ and
$v_1,\ldots,v_n \in K$ and ![]() $0=t_0<t_1 < \dots < t_m \in \tilde S$, and defining
$0=t_0<t_1 < \dots < t_m \in \tilde S$, and defining ![]() $Z_{t_j}^n = (Z_{v_1,t_j},\ldots,Z_{v_n,t_j})$ for
$Z_{t_j}^n = (Z_{v_1,t_j},\ldots,Z_{v_n,t_j})$ for ![]() $j=1,\ldots,m$, it holds that
$j=1,\ldots,m$, it holds that
 \begin{align*}&C\big(\boldsymbol{\lambda} \dagger \big(Z^n_{t_1}, Z^n_{t_2}-Z^n_{t_1},\ldots,Z^n_{t_m}-Z^n_{t_{m-1}}\big)\big) = \sum_{j=1}^mC\big(\lambda_j \dagger Z^n_{t_j} - Z^n_{t_{j-1}}\big)= \sum_{j=1}^mC\big(\lambda_j \dagger Z^n_{t_j- t_{j-1}}\big) ,\end{align*}
\begin{align*}&C\big(\boldsymbol{\lambda} \dagger \big(Z^n_{t_1}, Z^n_{t_2}-Z^n_{t_1},\ldots,Z^n_{t_m}-Z^n_{t_{m-1}}\big)\big) = \sum_{j=1}^mC\big(\lambda_j \dagger Z^n_{t_j} - Z^n_{t_{j-1}}\big)= \sum_{j=1}^mC\big(\lambda_j \dagger Z^n_{t_j- t_{j-1}}\big) ,\end{align*}
where ![]() $\boldsymbol{\lambda} = (\lambda_1,\ldots,\lambda_n)$ and each
$\boldsymbol{\lambda} = (\lambda_1,\ldots,\lambda_n)$ and each ![]() $\lambda_j \in {\mathbb{R}}^n$, and the natural convention
$\lambda_j \in {\mathbb{R}}^n$, and the natural convention ![]() $Z_0^n=(0,\ldots,0)$ is applied. This shows that
$Z_0^n=(0,\ldots,0)$ is applied. This shows that ![]() $(\textbf{Z}_t)_{t\in\tilde S}$ has stationary and independent increments.
$(\textbf{Z}_t)_{t\in\tilde S}$ has stationary and independent increments.
To show stochastic continuity it suffices to show that
for any rational sequence ![]() $(t_n)$ satisfying
$(t_n)$ satisfying ![]() $t_n\downarrow 0$. As
$t_n\downarrow 0$. As ![]() $(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is a separable Banach space, this is equivalent to showing that
$(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is a separable Banach space, this is equivalent to showing that ![]() $\textbf{Z}_{t_n}$ converges to
$\textbf{Z}_{t_n}$ converges to ![]() $\delta_{\textbf{0}}$ in law in the uniform norm, where
$\delta_{\textbf{0}}$ in law in the uniform norm, where ![]() $\delta_{\textbf{0}}$ is the degenerate probability measure concentrated at
$\delta_{\textbf{0}}$ is the degenerate probability measure concentrated at ![]() $\textbf{0}$. For
$\textbf{0}$. For ![]() $t\in\tilde S$, let
$t\in\tilde S$, let ![]() $\nu_t$ denote the distribution of
$\nu_t$ denote the distribution of ![]() $\textbf{Z}_{t}$ and let
$\textbf{Z}_{t}$ and let ![]() $\hat \nu_{t_n}$ be its characteristic function defined on the dual space of
$\hat \nu_{t_n}$ be its characteristic function defined on the dual space of ![]() $\mathcal{C}(K,{\mathbb{R}})$; see [Reference Linde15, Section 1.7]. Since
$\mathcal{C}(K,{\mathbb{R}})$; see [Reference Linde15, Section 1.7]. Since ![]() $(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is separable,
$(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is separable, ![]() $\nu_t$ is a Radon measure [Reference Linde15, Proposition 1.1.3] and the results in [Reference Linde15, Chapters 2 and 5] apply. Due to the infinite divisibility,
$\nu_t$ is a Radon measure [Reference Linde15, Proposition 1.1.3] and the results in [Reference Linde15, Chapters 2 and 5] apply. Due to the infinite divisibility, ![]() $\nu_1 = \nu_{t_n}*\nu_{1-t_n}$ for any
$\nu_1 = \nu_{t_n}*\nu_{1-t_n}$ for any ![]() $n\in \mathbb{N}$ (assuming
$n\in \mathbb{N}$ (assuming ![]() $t_n\le 1$), and we conclude that
$t_n\le 1$), and we conclude that ![]() $\{\nu_{t_n}\}$ is relatively shift compact [Reference Linde15, Theorem 2.3.1]. Following the proofs of [Reference Linde15, Propositions 5.1.4 and 5.1.5] we obtain that
$\{\nu_{t_n}\}$ is relatively shift compact [Reference Linde15, Theorem 2.3.1]. Following the proofs of [Reference Linde15, Propositions 5.1.4 and 5.1.5] we obtain that ![]() $\lim_{n\to\infty} \hat \nu_{t_n} \to 1$ uniformly on bounded sets of the dual space. Combining [Reference Linde15, Propositions 2.3.9 and 1.8.2] shows that
$\lim_{n\to\infty} \hat \nu_{t_n} \to 1$ uniformly on bounded sets of the dual space. Combining [Reference Linde15, Propositions 2.3.9 and 1.8.2] shows that ![]() $\textbf{Z}_{t_n}$ converges in law to
$\textbf{Z}_{t_n}$ converges in law to ![]() $\delta_{\textbf{0}}$ as claimed.
$\delta_{\textbf{0}}$ as claimed.
The next theorem states that the field Z defined in (5.5) indeed has a t-càdlàg version.
Theorem 5.2. Let the field Z be given by (5.5) such that the Lévy basis M on ![]() ${\mathbb{R}}^{d+1}$ satisfies Assumption 5.1 with
${\mathbb{R}}^{d+1}$ satisfies Assumption 5.1 with ![]() $m=d+1$, and the bounded kernel g satisfies (5.3) and (5.4), with
$m=d+1$, and the bounded kernel g satisfies (5.3) and (5.4), with ![]() $m=d$. There is a field
$m=d$. There is a field ![]() $Z^{\prime}=(Z^{\prime}_{v,t})_{(v,t)\in K\times [0,S]}$ that is a version of Z, i.e.
$Z^{\prime}=(Z^{\prime}_{v,t})_{(v,t)\in K\times [0,S]}$ that is a version of Z, i.e. ![]() $\mathbb{P}(Z^{\prime}_{v,t}=Z_{v,t}) = 1$ for all
$\mathbb{P}(Z^{\prime}_{v,t}=Z_{v,t}) = 1$ for all ![]() ${(v,t)\in K\times [0,S]}$, and such that
${(v,t)\in K\times [0,S]}$, and such that ![]() $\lim_{s\downarrow t} \textbf{Z}^{\prime}_s(\omega)=\textbf{Z}^{\prime}_t(\omega)$ and
$\lim_{s\downarrow t} \textbf{Z}^{\prime}_s(\omega)=\textbf{Z}^{\prime}_t(\omega)$ and ![]() $\lim_{s\uparrow t} \textbf{Z}^{\prime}_s(\omega)$ exist with respect to
$\lim_{s\uparrow t} \textbf{Z}^{\prime}_s(\omega)$ exist with respect to ![]() $\|\cdot\|_{\infty}$ for all
$\|\cdot\|_{\infty}$ for all ![]() $\omega$. Furthermore, the map
$\omega$. Furthermore, the map ![]() $v \mapsto Z^{\prime}_{v,t}$ from K into
$v \mapsto Z^{\prime}_{v,t}$ from K into ![]() ${\mathbb{R}}$ is continuous for all
${\mathbb{R}}$ is continuous for all ![]() $t\in [0,S]$. In particular, Z′ has t-càdlàg sample paths.
$t\in [0,S]$. In particular, Z′ has t-càdlàg sample paths.
The desired t-càdlàg version will be an extension of the field ![]() $(\textbf{Z}_t)_{t\in \tilde S}$ studied in Lemma 5.1. Thus
$(\textbf{Z}_t)_{t\in \tilde S}$ studied in Lemma 5.1. Thus ![]() $(\textbf{Z}_t)_{t\in\tilde S}$ will still be a version chosen such that each
$(\textbf{Z}_t)_{t\in\tilde S}$ will still be a version chosen such that each ![]() $\textbf{Z}_t$ is a continuous random field. The result relies on a sequence of lemmas that are shown using an adaptation of the ideas of [Reference Sato24, Theorems 11.1 and 11.5] and [Reference Sato24, Lemmas 11.2–11.4] for Lévy processes on
$\textbf{Z}_t$ is a continuous random field. The result relies on a sequence of lemmas that are shown using an adaptation of the ideas of [Reference Sato24, Theorems 11.1 and 11.5] and [Reference Sato24, Lemmas 11.2–11.4] for Lévy processes on ![]() ${\mathbb{R}}$. Lemmas 5.2 and 5.3 are shown using similar techniques for the Lévy process
${\mathbb{R}}$. Lemmas 5.2 and 5.3 are shown using similar techniques for the Lévy process ![]() $(\textbf{Z}_t)_{t\in\tilde S}$, and therefore we omit the proofs here and refer to the supplementary material [Reference Stehr and Rønn-Nielsen27] for completeness.
$(\textbf{Z}_t)_{t\in\tilde S}$, and therefore we omit the proofs here and refer to the supplementary material [Reference Stehr and Rønn-Nielsen27] for completeness.
For the statement and proof of these lemmas, the following notation will be useful. We say that ![]() $\textbf{Z}(\omega)$ has
$\textbf{Z}(\omega)$ has ![]() $\varepsilon$-oscillation n times in a set
$\varepsilon$-oscillation n times in a set ![]() $M\subseteq\mathbb{Q} \cap [0,\infty)$ if there exist
$M\subseteq\mathbb{Q} \cap [0,\infty)$ if there exist ![]() $t_0<t_1<\dots < t_n \in M$ such that
$t_0<t_1<\dots < t_n \in M$ such that
for all ![]() $j=1,\ldots,n$. We say that
$j=1,\ldots,n$. We say that ![]() $\textbf{Z}(\omega)$ has
$\textbf{Z}(\omega)$ has ![]() $\varepsilon$-oscillation infinitely often in M if it has
$\varepsilon$-oscillation infinitely often in M if it has ![]() $\varepsilon$-oscillation n times in M for any
$\varepsilon$-oscillation n times in M for any ![]() $n\in\mathbb{N}$. Consider
$n\in\mathbb{N}$. Consider ![]() $\Omega_1$ given by
$\Omega_1$ given by
 \begin{align*}\Omega_1 = \Bigl\{\omega\in\Omega \mid& \lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s(\omega) \text{ exists with respect to $\|\cdot\|_{\infty}$ for all $t\in [0,S]$ and} \\*& \lim_{s\in\mathbb{Q},s\uparrow t} \textbf{Z}_s(\omega) \text{ exists with respect to $\|\cdot\|_{\infty}$ for all $t\in [0,S]$} \Bigr\} .\end{align*}
\begin{align*}\Omega_1 = \Bigl\{\omega\in\Omega \mid& \lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s(\omega) \text{ exists with respect to $\|\cdot\|_{\infty}$ for all $t\in [0,S]$ and} \\*& \lim_{s\in\mathbb{Q},s\uparrow t} \textbf{Z}_s(\omega) \text{ exists with respect to $\|\cdot\|_{\infty}$ for all $t\in [0,S]$} \Bigr\} .\end{align*}
Furthermore define the sets
and from these define ![]() $\Omega^{\prime}_1=\cap_{k\in\mathbb{N}} A_k$. Each
$\Omega^{\prime}_1=\cap_{k\in\mathbb{N}} A_k$. Each ![]() $A_k$ is measurable as each
$A_k$ is measurable as each ![]() $\textbf{Z}_t$ is continuous on K for
$\textbf{Z}_t$ is continuous on K for ![]() $t\in \tilde S$, such that
$t\in \tilde S$, such that ![]() $\|\cdot\|_{\infty} = \sup_{v\in K}|\cdot| = \sup_{v\in \tilde K}|\cdot| $.
$\|\cdot\|_{\infty} = \sup_{v\in K}|\cdot| = \sup_{v\in \tilde K}|\cdot| $.
Lemma 5.2. ![]() $\Omega^{\prime}_1 \subseteq \Omega_1$.
$\Omega^{\prime}_1 \subseteq \Omega_1$.
Lemma 5.3. ![]() $\mathbb{P}(\Omega^{\prime}_1)=1$.
$\mathbb{P}(\Omega^{\prime}_1)=1$.
Having established that ![]() $\lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s$ and
$\lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s$ and ![]() $\lim_{s\in\mathbb{Q},s\uparrow t} \textbf{Z}_s$ exist almost surely, we now prove the main result, Theorem 5.2, on the existence of a t-càdlàg version of Z.
$\lim_{s\in\mathbb{Q},s\uparrow t} \textbf{Z}_s$ exist almost surely, we now prove the main result, Theorem 5.2, on the existence of a t-càdlàg version of Z.
Proof of Theorem 5.2. We have ![]() $\mathbb{P}(\Omega^{\prime}_1)=1$ by Lemma 5.3. For all
$\mathbb{P}(\Omega^{\prime}_1)=1$ by Lemma 5.3. For all ![]() $t\in [0,S]$, define
$t\in [0,S]$, define ![]() $\textbf{Z}^{\prime}_t(\omega) =\textbf{1}_{\Omega_1^{\prime}}(\omega)(\lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s(\omega))$, where the limit is with respect to
$\textbf{Z}^{\prime}_t(\omega) =\textbf{1}_{\Omega_1^{\prime}}(\omega)(\lim_{s\in\mathbb{Q},s\downarrow t} \textbf{Z}_s(\omega))$, where the limit is with respect to ![]() $\|\cdot\|_{\infty}$, and exists according to Lemma 5.2. The càdlàg assertion is trivially true for
$\|\cdot\|_{\infty}$, and exists according to Lemma 5.2. The càdlàg assertion is trivially true for ![]() $\omega\not\in\Omega_1^{\prime}$. Now consider
$\omega\not\in\Omega_1^{\prime}$. Now consider ![]() $\omega\in\Omega_1^{\prime}$ but suppress
$\omega\in\Omega_1^{\prime}$ but suppress ![]() $\omega$ to ease notation. By definition of
$\omega$ to ease notation. By definition of ![]() $\textbf{Z}^{\prime}_t$, for all
$\textbf{Z}^{\prime}_t$, for all ![]() $\epsilon >0$ there exists N such that
$\epsilon >0$ there exists N such that
Let ![]() $(t_n)$ be any sequence satisfying
$(t_n)$ be any sequence satisfying ![]() $t_n\downarrow t$. Fix
$t_n\downarrow t$. Fix ![]() $\varepsilon > 0$, and let
$\varepsilon > 0$, and let ![]() $N\in\mathbb{N}$ satisfy (5.7) with the bound
$N\in\mathbb{N}$ satisfy (5.7) with the bound ![]() ${{\varepsilon}/{2}}$. There exists
${{\varepsilon}/{2}}$. There exists ![]() $n_0\in\mathbb{N}$ such that
$n_0\in\mathbb{N}$ such that ![]() $|t_n-t|<{{1}/{N}}$ for all
$|t_n-t|<{{1}/{N}}$ for all ![]() $n\ge n_0$. Now fix such n. By another application of (5.7) there exists
$n\ge n_0$. Now fix such n. By another application of (5.7) there exists ![]() $N_n$ such that
$N_n$ such that ![]() $t_n+{{1}/{N_n}}\le t+{{1}/{N}}$ and
$t_n+{{1}/{N_n}}\le t+{{1}/{N}}$ and ![]() $\|\textbf{Z}_{t_n}^{\prime}-\textbf{Z}_s\|_{\infty}<{{\varepsilon}/{2}}$ for all
$\|\textbf{Z}_{t_n}^{\prime}-\textbf{Z}_s\|_{\infty}<{{\varepsilon}/{2}}$ for all ![]() $s\in (t_n,t_n+{{1}/{N_n}})\cap \mathbb{Q}$. For any of those s we find in particular that
$s\in (t_n,t_n+{{1}/{N_n}})\cap \mathbb{Q}$. For any of those s we find in particular that
As this is true for all ![]() $n\ge n_0$, we conclude that
$n\ge n_0$, we conclude that ![]() $\textbf{Z}^{\prime}=(\textbf{Z}^{\prime}_t)_{t\in [0,S]}$ is right-continuous with respect to
$\textbf{Z}^{\prime}=(\textbf{Z}^{\prime}_t)_{t\in [0,S]}$ is right-continuous with respect to ![]() $\|\cdot\|_{\infty}$. Similar arguments show that
$\|\cdot\|_{\infty}$. Similar arguments show that ![]() $\textbf{Z}^{\prime}$ has limits from the left and that the limits are unique. The mapping
$\textbf{Z}^{\prime}$ has limits from the left and that the limits are unique. The mapping ![]() $v \mapsto Z^{\prime}_{v,t}$ is continuous because the space
$v \mapsto Z^{\prime}_{v,t}$ is continuous because the space ![]() $(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is complete, and
$(\mathcal{C}(K,{\mathbb{R}}),\|\cdot\|_{\infty})$ is complete, and ![]() $\textbf{Z}^{\prime}_t$ is defined as the limit of such functions.
$\textbf{Z}^{\prime}_t$ is defined as the limit of such functions.
We now argue that ![]() $\textbf{Z}^{\prime}$ is indeed a version of
$\textbf{Z}^{\prime}$ is indeed a version of ![]() $\textbf{Z}$. If
$\textbf{Z}$. If ![]() $(t_n)\subset \tilde S$ with
$(t_n)\subset \tilde S$ with ![]() $t_n\downarrow t$ then
$t_n\downarrow t$ then ![]() $Z_{v,t_n} \overset{\mathbb{P}}{\to} Z_{v,t}$ for all
$Z_{v,t_n} \overset{\mathbb{P}}{\to} Z_{v,t}$ for all ![]() $v\in K$ as
$v\in K$ as ![]() $(Z_{v,t})_{t\in [0,S]}$ is a Lévy process in law and thus especially stochastically continuous. Since
$(Z_{v,t})_{t\in [0,S]}$ is a Lévy process in law and thus especially stochastically continuous. Since ![]() $\mathbb{P}(\Omega^{\prime}_1)=1$ we have
$\mathbb{P}(\Omega^{\prime}_1)=1$ we have ![]() $Z_{v,t_n} \to Z^{\prime}_{v,t}$ almost surely, and by uniqueness of limits we conclude that
$Z_{v,t_n} \to Z^{\prime}_{v,t}$ almost surely, and by uniqueness of limits we conclude that ![]() $\mathbb{P}(Z^{\prime}_{v,t}=Z_{v,t}) = 1$ for all
$\mathbb{P}(Z^{\prime}_{v,t}=Z_{v,t}) = 1$ for all ![]() ${(v,t)\in K\times [0,S]}$.
${(v,t)\in K\times [0,S]}$.
It remains to show that Z′ is t-càdlàg. For given ![]() ${(v,t)\in K\times [0,S]}$ we can write
${(v,t)\in K\times [0,S]}$ we can write
for any choice of ![]() ${(u,s)} \in K\times [0,S]$, and thus we conclude that
${(u,s)} \in K\times [0,S]$, and thus we conclude that ![]() $\lim_{(u,s)\to(v,t^+)} Z^{\prime}_{u,s} = Z^{\prime}_{v,t}$, from the continuity of
$\lim_{(u,s)\to(v,t^+)} Z^{\prime}_{u,s} = Z^{\prime}_{v,t}$, from the continuity of ![]() $\textbf{Z}^{\prime}_t$ and the uniform càdlàg property of
$\textbf{Z}^{\prime}_t$ and the uniform càdlàg property of ![]() $(\textbf{Z}^{\prime}_t)_{t\in [0,S]}$. Similar arguments give that the limit
$(\textbf{Z}^{\prime}_t)_{t\in [0,S]}$. Similar arguments give that the limit ![]() $\lim_{(u,s)\to(v,t^-)} Z^{\prime}_{u,s}$ exists in
$\lim_{(u,s)\to(v,t^-)} Z^{\prime}_{u,s}$ exists in ![]() ${\mathbb{R}}$ and that it is unique.
${\mathbb{R}}$ and that it is unique.
Theorem 5.3 below is stated under Assumption 2.1. However, in order to establish t-càdlàg sample paths, the milder Assumption 5.1 would have been sufficient.
Theorem 5.3. Let the field ![]() $X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumption 2.2. Then X has a version with t-càdlàg sample paths.
$X=(X_{v,t})_{(v,t)\in B^{\prime}\times T^{\prime}}$ be given by (2.10), where the Lévy basis M satisfies Assumption 2.1 and the kernel function f satisfies Assumption 2.2. Then X has a version with t-càdlàg sample paths.
Proof. We decompose the field ![]() $(X_{v,t})$ as
$(X_{v,t})$ as
 \begin{align*}X_{v,t} & = \int_{{\mathbb{R}^d} \times[0,t]} f(\lvert{v-u}\rvert, t-s) - f(|v-u|,0) M(\mathrm{d}s,\mathrm{d}u) \\[5pt]
& \quad\, + \int_{{\mathbb{R}^d} \times({-}\infty,0)} f(\lvert{v-u}\rvert, t-s) M(\mathrm{d}s,\mathrm{d}u)+ \int_{{\mathbb{R}^d} \times[0,t]} f(|v-u|,0) M(\mathrm{d}s,\mathrm{d}u) .\end{align*}
\begin{align*}X_{v,t} & = \int_{{\mathbb{R}^d} \times[0,t]} f(\lvert{v-u}\rvert, t-s) - f(|v-u|,0) M(\mathrm{d}s,\mathrm{d}u) \\[5pt]
& \quad\, + \int_{{\mathbb{R}^d} \times({-}\infty,0)} f(\lvert{v-u}\rvert, t-s) M(\mathrm{d}s,\mathrm{d}u)+ \int_{{\mathbb{R}^d} \times[0,t]} f(|v-u|,0) M(\mathrm{d}s,\mathrm{d}u) .\end{align*}
By Theorem 5.2, choosing ![]() $g(\cdot) = f(\cdot,0)$, the third term has a t-càdlàg version. Due to continuity of the integrands, the first and second terms have continuous versions by arguments similar to those in the proof of Theorem 5.1: defining the continuous function
$g(\cdot) = f(\cdot,0)$, the third term has a t-càdlàg version. Due to continuity of the integrands, the first and second terms have continuous versions by arguments similar to those in the proof of Theorem 5.1: defining the continuous function ![]() $\phi\colon[0,\infty)\times{\mathbb{R}} \to {\mathbb{R}}$ by
$\phi\colon[0,\infty)\times{\mathbb{R}} \to {\mathbb{R}}$ by
the first term above reads
where ![]() $y_{v,t} = {\mathbb E} Y_{v,t}^{\prime}$ and
$y_{v,t} = {\mathbb E} Y_{v,t}^{\prime}$ and ![]() $Y_{v,t} = Y_{v,t}^{\prime} - y_{v,t}$. The field
$Y_{v,t} = Y_{v,t}^{\prime} - y_{v,t}$. The field ![]() $(Y_{v,t})$ is continuous by previous arguments, replacing assumptions (5.3) and (5.4) with the conditions
$(Y_{v,t})$ is continuous by previous arguments, replacing assumptions (5.3) and (5.4) with the conditions
and the Lipschitz continuity of ![]() $\phi$,
$\phi$,
for all ![]() $u_1,u_2\in {\mathbb{R}^d}$ and
$u_1,u_2\in {\mathbb{R}^d}$ and ![]() $t_1,t_2\in T^{\prime}$. These conditions are easily seen to be satisfied under Assumption 2.2. As
$t_1,t_2\in T^{\prime}$. These conditions are easily seen to be satisfied under Assumption 2.2. As
the deterministic field ![]() $(y_{v,t})$ is continuous by a dominated convergence argument using (5.8). The continuity of the second term follows similarly.
$(y_{v,t})$ is continuous by a dominated convergence argument using (5.8). The continuity of the second term follows similarly.
Supplementary material
Proofs of all the results in this article are furnished in the supplementary material [Reference Stehr and Rønn-Nielsen27].
Acknowledgements
This work was supported by the Centre for Stochastic Geometry and Advanced Bioimaging, funded by a grant from the Villum Foundation.