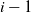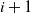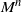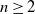1. Introduction
Motivated by genetic studies, Karlin and Tavaré [Reference Karlin and Tavaré11] introduced the class of continuous-time birth–death processes with killing (or CBDKs for short) and obtained explicit results on the killing time for the case of linear CBDKs. (Earlier, Puri [Reference Puri13] also discussed related processes.) Later, van Doorn and Zeifman [Reference Van Doorn and Zeifman17,Reference Van Doorn and Zeifman18] considered more general CBDKs and derived the eventual killing probability, among other things. (See also [1, Chapter 9] and [Reference Brockwell2–Reference Di Crescenzo, Giorno, Nobile and Ricciardi6,Reference Stirzaker16] for work on the closely related topic of birth–death processes with catastrophes.)
A CBDK
![]() $\{X_t\}$
is a continuous-time Markov chain with state space
$\{X_t\}$
is a continuous-time Markov chain with state space
![]() $\{0,1,\ldots\}\cup \{e\}$
, where e is an absorbing state and transitions from state
$\{0,1,\ldots\}\cup \{e\}$
, where e is an absorbing state and transitions from state
![]() $i \;(\ne e)$
may go to either
$i \;(\ne e)$
may go to either
![]() $i-1$
(if
$i-1$
(if
![]() $i>0$
) or
$i>0$
) or
![]() $i+1$
or e with respective transition rates
$i+1$
or e with respective transition rates
![]() $\mu_i$
(death rate),
$\mu_i$
(death rate),
![]() $\lambda_i$
(birth rate), and
$\lambda_i$
(birth rate), and
![]() $\gamma_i$
(killing rate). We assume that
$\gamma_i$
(killing rate). We assume that
![]() $\{X_t\}$
is non-explosive. See equations (2) and (3) of [Reference Van Doorn and Zeifman18] for conditions on
$\{X_t\}$
is non-explosive. See equations (2) and (3) of [Reference Van Doorn and Zeifman18] for conditions on
![]() $\lambda_i, \mu_i$
, and
$\lambda_i, \mu_i$
, and
![]() $\gamma_i$
under which
$\gamma_i$
under which
![]() $\{X_t\}$
is non-explosive.
$\{X_t\}$
is non-explosive.
Let
![]() $T_e\,:\!=\,\inf\{t\ge 0\colon X_t=e\}$
, the killing time. (By convention,
$T_e\,:\!=\,\inf\{t\ge 0\colon X_t=e\}$
, the killing time. (By convention,
![]() $\inf \emptyset \,:\!=\,\infty$
.) The distribution of
$\inf \emptyset \,:\!=\,\infty$
.) The distribution of
![]() $T_e$
and the probability of
$T_e$
and the probability of
![]() $T_e<\infty$
(the eventual killing probability) are of primary interest in the study of CBDKs. Let
$T_e<\infty$
(the eventual killing probability) are of primary interest in the study of CBDKs. Let
![]() $\mathcal{L}_i(T_e)$
denote the distribution of
$\mathcal{L}_i(T_e)$
denote the distribution of
![]() $T_e$
given
$T_e$
given
![]() $X_0=i$
. We write
$X_0=i$
. We write
![]() $\mathcal{L}_i(T_e)\leq_d \mathcal{L}_j(T_e)$
(or equivalently
$\mathcal{L}_i(T_e)\leq_d \mathcal{L}_j(T_e)$
(or equivalently
![]() $\mathcal{L}_j(T_e) \geq_d \mathcal{L}_i(T_e)$
) if
$\mathcal{L}_j(T_e) \geq_d \mathcal{L}_i(T_e)$
) if
![]() $\mathcal{L}_i(T_e)$
is stochastically smaller than
$\mathcal{L}_i(T_e)$
is stochastically smaller than
![]() $\mathcal{L}_j(T_e)$
, that is,
$\mathcal{L}_j(T_e)$
, that is,
CBDKs have found applications in medicine and biology. Nagylaki [Reference Nagylaki12] considered a stochastic model for a progressive chronic disease. For a patient with the disease, it is assumed that there is a useful prognostic indicator for the course of the disease and the survival of the patient. This indicator may be modeled as a birth–death process with killing. (In [Reference Nagylaki12], the indicator is modeled as a pure birth process with killing under the assumption that the condition of the patient cannot improve.) For example, a patient in a coma is given a score
![]() $i \in \{3,\ldots, 15\}$
(on the Glasgow Coma Scale) indicating the state of the patient’s consciousness. (A lower score corresponds to a more severe condition.) With the absorbing state e denoting the patient’s death, the killing time
$i \in \{3,\ldots, 15\}$
(on the Glasgow Coma Scale) indicating the state of the patient’s consciousness. (A lower score corresponds to a more severe condition.) With the absorbing state e denoting the patient’s death, the killing time
![]() $T_e$
is the patient’s survival time. A natural question is whether the survival time of the patient with score i is stochastically non-decreasing in i, i.e.
$T_e$
is the patient’s survival time. A natural question is whether the survival time of the patient with score i is stochastically non-decreasing in i, i.e.
![]() $\mathcal{L}_i(T_e) \leq_d \mathcal{L}_{j}(T_e)$
for
$\mathcal{L}_i(T_e) \leq_d \mathcal{L}_{j}(T_e)$
for
![]() $i<j$
. Theorem 1 in the next section answers this question in the affirmative provided the killing rate
$i<j$
. Theorem 1 in the next section answers this question in the affirmative provided the killing rate
![]() $\gamma_i$
is non-increasing in i, regardless of the values of
$\gamma_i$
is non-increasing in i, regardless of the values of
![]() $\lambda_i$
and
$\lambda_i$
and
![]() $\mu_i$
. In another application of CBDKs, Hadeler [Reference Hadeler and Tautu7] considered a situation where a host carries a finite number of parasites. Let
$\mu_i$
. In another application of CBDKs, Hadeler [Reference Hadeler and Tautu7] considered a situation where a host carries a finite number of parasites. Let
![]() $X^\prime_t$
denote the parasite population size within the host at time t, which may be modeled as a birth–death process. Let T denote the death time of the host, and define the process
$X^\prime_t$
denote the parasite population size within the host at time t, which may be modeled as a birth–death process. Let T denote the death time of the host, and define the process
![]() $\{X_t\}$
by
$\{X_t\}$
by
![]() $X_t=X^\prime_t$
for
$X_t=X^\prime_t$
for
![]() $t<T$
and
$t<T$
and
![]() $X_t=e$
for
$X_t=e$
for
![]() $t\geq T$
. Hadeler [Reference Hadeler and Tautu7] proposed modeling
$t\geq T$
. Hadeler [Reference Hadeler and Tautu7] proposed modeling
![]() $\{X_t\}$
as a CBDK. Note that
$\{X_t\}$
as a CBDK. Note that
![]() $T=T_e=\inf\{t\geq 0\colon X_t=e\}$
is the survival time of the host. Again, Theorem 1 shows that the survival time of the host carrying i parasites is stochastically non-increasing in i if the killing rate
$T=T_e=\inf\{t\geq 0\colon X_t=e\}$
is the survival time of the host. Again, Theorem 1 shows that the survival time of the host carrying i parasites is stochastically non-increasing in i if the killing rate
![]() $\gamma_i$
is non-decreasing in i.
$\gamma_i$
is non-decreasing in i.
The rest of this paper is organized as follows. Section 2 states the main results Theorem 1 for CBDKs and Theorem 2 for the discrete-time counterpart of CBDKs. The proofs of both theorems rely on Lemma 1 concerning the monotonicity of the row sums of powers of non-negative tri-diagonal matrices, which is of independent interest. Section 3 presents numerical examples. The proofs of Theorems 1 and 2 and Lemma 1 are relegated to Section 4.
2. Main results
For a non-negative matrix
![]() $M=(M_{i,j})$
, let
$M=(M_{i,j})$
, let
![]() $(M)_{i,+}$
denote the ith row sum of M, i.e.
$(M)_{i,+}$
denote the ith row sum of M, i.e.
![]() $(M)_{i,+}=\sum_j M_{i,j}$
. Before presenting the main results Theorems 1 and 2, we state Lemma 1 below, which is needed for the proofs of Theorems 1 and 2. All the proofs are given in Section 4.
$(M)_{i,+}=\sum_j M_{i,j}$
. Before presenting the main results Theorems 1 and 2, we state Lemma 1 below, which is needed for the proofs of Theorems 1 and 2. All the proofs are given in Section 4.
Lemma 1. Let
![]() $\mathbb{S}=\{0,1,\ldots, I\}$
(for some integer
$\mathbb{S}=\{0,1,\ldots, I\}$
(for some integer
![]() $I>0$
) or
$I>0$
) or
![]() $\mathbb{S}=\{0,1,\ldots\}$
or
$\mathbb{S}=\{0,1,\ldots\}$
or
![]() $\mathbb{S}=\mathbb{Z}\,:\!=\,\{0, \pm 1,\ldots\}$
. Suppose
$\mathbb{S}=\mathbb{Z}\,:\!=\,\{0, \pm 1,\ldots\}$
. Suppose
![]() $M=(M_{i,j})_{i,j \in \mathbb{S}}$
is a non-negative tri-diagonal matrix.
$M=(M_{i,j})_{i,j \in \mathbb{S}}$
is a non-negative tri-diagonal matrix.
-
(i) If, for some
 $i^{*}$
,
$i^{*}$
,
 $(M)_{i,+} \le (M)_{j,+}$
for all
$(M)_{i,+} \le (M)_{j,+}$
for all
 $i\leq i^{*}$
and
$i\leq i^{*}$
and
 $j>i^{*}$
, then we have
$j>i^{*}$
, then we have
 \begin{align}(M^{n})_{i^{*},+} \leq (M^{n})_{i^{*}+1,+} \quad for all n\geq 2.\end{align}
\begin{align}(M^{n})_{i^{*},+} \leq (M^{n})_{i^{*}+1,+} \quad for all n\geq 2.\end{align}
-
(ii) If, for some
 $i^*$
,
$i^*$
,
 $(M)_{i,+} \ge (M)_{j,+}$
for all
$(M)_{i,+} \ge (M)_{j,+}$
for all
 $i\leq i^{*}$
and
$i\leq i^{*}$
and
 $j>i^{*}$
, then we have
$j>i^{*}$
, then we have
 \begin{align}(M^{n})_{i^{*},+} \geq (M^{n})_{i^{*}+1,+} \quad for all n\geq 2.\end{align}
\begin{align}(M^{n})_{i^{*},+} \geq (M^{n})_{i^{*}+1,+} \quad for all n\geq 2.\end{align}
-
(iii) If the row sums of M are monotone, so are the row sums of
 $M^n$
for all
$M^n$
for all
 $n\ge 2$
.
$n\ge 2$
.
Theorem 1. Suppose
![]() $\{X_t\}$
is a non-explosive CBDK.
$\{X_t\}$
is a non-explosive CBDK.
-
(i) If, for some
 $i^* \in \{0,1,\ldots\}$
, the killing rates satisfy
$i^* \in \{0,1,\ldots\}$
, the killing rates satisfy
 $\gamma_i \le \gamma_{j}$
for all
$\gamma_i \le \gamma_{j}$
for all
 $i \le i^*$
and
$i \le i^*$
and
 $j>i^*$
, then we have
$j>i^*$
, then we have
 $\mathcal{L}_{i^*}(T_e) \geq_d \mathcal{L}_{i^*+1}(T_e)$
.
$\mathcal{L}_{i^*}(T_e) \geq_d \mathcal{L}_{i^*+1}(T_e)$
. -
(ii) If, for some
 $i^*$
,
$i^*$
,
 $\gamma_i \geq \gamma_{j}$
for all
$\gamma_i \geq \gamma_{j}$
for all
 $i \le i^*$
and
$i \le i^*$
and
 $j>i^*$
, then we have
$j>i^*$
, then we have
 $\mathcal{L}_{i^*}(T_e) \leq_d \mathcal{L}_{i^*+1}(T_e)$
.
$\mathcal{L}_{i^*}(T_e) \leq_d \mathcal{L}_{i^*+1}(T_e)$
. -
(iii) If
 $\gamma_i \leq \gamma_{i+1}$
for all
$\gamma_i \leq \gamma_{i+1}$
for all
 $i \geq 0$
, then we have
$i \geq 0$
, then we have
 $\mathcal{L}_{i}(T_e) \geq_d \mathcal{L}_{i+1}(T_e)$
for all
$\mathcal{L}_{i}(T_e) \geq_d \mathcal{L}_{i+1}(T_e)$
for all
 $i \geq 0$
.
$i \geq 0$
. -
(iv) If
 $\gamma_i \geq \gamma_{i+1}$
for all
$\gamma_i \geq \gamma_{i+1}$
for all
 $i \geq 0$
, then we have
$i \geq 0$
, then we have
 $\mathcal{L}_{i}(T_e) \leq_d \mathcal{L}_{i+1}(T_e)$
for all
$\mathcal{L}_{i}(T_e) \leq_d \mathcal{L}_{i+1}(T_e)$
for all
 $i \geq 0$
.
$i \geq 0$
.
Theorem 1 has a discrete-time analogue concerning a Markov chain
![]() $\{Y_n\}$
with state space
$\{Y_n\}$
with state space
![]() $\{0,1,\ldots\} \cup \{e\}$
in discrete time
$\{0,1,\ldots\} \cup \{e\}$
in discrete time
![]() $n=0,1,\ldots.$
Specifically,
$n=0,1,\ldots.$
Specifically,
![]() $\{Y_n\}$
has transition probabilities satisfying
$\{Y_n\}$
has transition probabilities satisfying
 \begin{align}\sum_{j=\max\{0, i-1\}}^{i+1} \mathbb{P}(Y_{n+1}=j \mid Y_n=i) +\mathbb{P}(Y_{n+1}=e \mid Y_n=i)=1,\quad i=0,1,\ldots,\end{align}
\begin{align}\sum_{j=\max\{0, i-1\}}^{i+1} \mathbb{P}(Y_{n+1}=j \mid Y_n=i) +\mathbb{P}(Y_{n+1}=e \mid Y_n=i)=1,\quad i=0,1,\ldots,\end{align}
and
![]() $\mathbb{P}(Y_{n+1}=e \mid Y_n=e)=1$
. (Note that
$\mathbb{P}(Y_{n+1}=e \mid Y_n=e)=1$
. (Note that
![]() $\mathbb{P}(Y_{n+1}=i \mid Y_n=i)>0$
is allowed.) We refer to
$\mathbb{P}(Y_{n+1}=i \mid Y_n=i)>0$
is allowed.) We refer to
![]() $\{Y_n\}$
as a discrete-time birth–death process with killing (or DBDK for short). Let
$\{Y_n\}$
as a discrete-time birth–death process with killing (or DBDK for short). Let
![]() $T_e^d\,:\!=\,\inf\{n\ge 0\colon Y_n=e\}$
, which is the discrete-time counterpart of
$T_e^d\,:\!=\,\inf\{n\ge 0\colon Y_n=e\}$
, which is the discrete-time counterpart of
![]() $T_e$
. (By convention,
$T_e$
. (By convention,
![]() $\inf \emptyset\,:\!=\,\infty$
.)
$\inf \emptyset\,:\!=\,\infty$
.)
Theorem 2. Let
![]() $p_{i,e}\,:\!=\,\mathbb{P}(Y_{n+1}=e \mid Y_n=i)$
,
$p_{i,e}\,:\!=\,\mathbb{P}(Y_{n+1}=e \mid Y_n=i)$
,
![]() $i=0,1,\ldots.$
$i=0,1,\ldots.$
-
(i) If, for some
 $i^*$
,
$i^*$
,
 $p_{i,e} \leq p_{j,e}$
for all
$p_{i,e} \leq p_{j,e}$
for all
 $i \le i^*$
and
$i \le i^*$
and
 $j>i^*$
, then we have
$j>i^*$
, then we have
 $\mathcal{L}_{i^*}(T^d_e) \geq_d$
$\mathcal{L}_{i^*}(T^d_e) \geq_d$
 $\mathcal{L}_{i^*+1}(T^d_e)$
.
$\mathcal{L}_{i^*+1}(T^d_e)$
. -
(ii) If, for some
 $i^*$
,
$i^*$
,
 $p_{i,e} \geq p_{j,e}$
for all
$p_{i,e} \geq p_{j,e}$
for all
 $i \le i^*$
and
$i \le i^*$
and
 $j>i^*$
, then we have
$j>i^*$
, then we have
 $\mathcal{L}_{i^*}(T^d_e) \leq_d$
$\mathcal{L}_{i^*}(T^d_e) \leq_d$
 $\mathcal{L}_{i^*+1}(T^d_e)$
.
$\mathcal{L}_{i^*+1}(T^d_e)$
. -
(iii) If
 $p_{i,e} \leq p_{i+1,e}$
for all
$p_{i,e} \leq p_{i+1,e}$
for all
 $i \geq 0$
, then we have
$i \geq 0$
, then we have
 $\mathcal{L}_{i}(T^d_e) \geq_d \mathcal{L}_{i+1}(T^d_e)$
for all
$\mathcal{L}_{i}(T^d_e) \geq_d \mathcal{L}_{i+1}(T^d_e)$
for all
 $i \geq 0$
.
$i \geq 0$
. -
(iv) If
 $p_{i,e} \geq p_{i+1,e}$
for all
$p_{i,e} \geq p_{i+1,e}$
for all
 $i \geq 0$
, then we have
$i \geq 0$
, then we have
 $\mathcal{L}_{i}(T^d_e) \leq_d \mathcal{L}_{i+1}(T^d_e)$
for all
$\mathcal{L}_{i}(T^d_e) \leq_d \mathcal{L}_{i+1}(T^d_e)$
for all
 $i \geq 0$
.
$i \geq 0$
.
Remark 1. By Theorem 1, we have
![]() $\mathcal{L}_i(T_e)$
stochastically monotone in i provided the killing rate
$\mathcal{L}_i(T_e)$
stochastically monotone in i provided the killing rate
![]() $\gamma_i$
is monotone in i, regardless of the birth and death rates
$\gamma_i$
is monotone in i, regardless of the birth and death rates
![]() $\lambda_i$
and
$\lambda_i$
and
![]() $\mu_i$
. The fact that the process
$\mu_i$
. The fact that the process
![]() $\{X_t\}$
is skip-free to the left and to the right (apart from jumping into the absorbing state e) is crucial for Theorem 1 to hold. In a different context, Irle and Gani [Reference Irle and Gani10] and Irle [Reference Irle9] obtained level-crossing stochastic ordering results for Markov chains and semi-Markov processes which are skip-free to the right.
$\{X_t\}$
is skip-free to the left and to the right (apart from jumping into the absorbing state e) is crucial for Theorem 1 to hold. In a different context, Irle and Gani [Reference Irle and Gani10] and Irle [Reference Irle9] obtained level-crossing stochastic ordering results for Markov chains and semi-Markov processes which are skip-free to the right.
Remark 2. He and Chavoushi [Reference He and Chavoushi8] considered queueing systems with customer interjections in which two parameters (denoted by
![]() $\eta_I$
and
$\eta_I$
and
![]() $\eta_C$
) are introduced to describe the interjection behavior. They investigated the effects of the two parameters on the customer’s waiting time, and derived some monotonicity properties of the distribution of the waiting time and its mean and variance in terms of the parameters. (The proof of their Lemma 2.2 contains a special case of our Lemma 1.) In particular, with
$\eta_C$
) are introduced to describe the interjection behavior. They investigated the effects of the two parameters on the customer’s waiting time, and derived some monotonicity properties of the distribution of the waiting time and its mean and variance in terms of the parameters. (The proof of their Lemma 2.2 contains a special case of our Lemma 1.) In particular, with
![]() $W_n(\eta_I,\eta_C)$
denoting the waiting time of a customer initially in position n in the queue, they showed that
$W_n(\eta_I,\eta_C)$
denoting the waiting time of a customer initially in position n in the queue, they showed that
![]() $W_n(\eta_I,\eta_C) \leq_d W_n(\eta_I',\eta_C')$
if
$W_n(\eta_I,\eta_C) \leq_d W_n(\eta_I',\eta_C')$
if
![]() $\eta_I \leq \eta_I'$
and
$\eta_I \leq \eta_I'$
and
![]() $\eta_C \leq \eta_C'$
. Note that two different pairs of parameter values
$\eta_C \leq \eta_C'$
. Note that two different pairs of parameter values
![]() $(\eta_I,\eta_C)$
and
$(\eta_I,\eta_C)$
and
![]() $(\eta_I',\eta_C')$
correspond to two different transition rate matrices (with the same state space). In contrast, our results are concerned with a single transition rate matrix with an absorbing state and compare the absorbing time distributions when the Markov chain starts from different states.
$(\eta_I',\eta_C')$
correspond to two different transition rate matrices (with the same state space). In contrast, our results are concerned with a single transition rate matrix with an absorbing state and compare the absorbing time distributions when the Markov chain starts from different states.
3. Numerical examples
In this section we illustrate Theorems 1 and 2 with numerical examples. We first consider a DBDK
![]() $\{Y_n\}$
with transition probabilities given by
$\{Y_n\}$
with transition probabilities given by
 \begin{align*}\mathbb{P}(Y_{n+1}=e \mid Y_n=i)&=0.01,\quad i=0,1,2,\\[3pt] \mathbb{P}(Y_{n+1}=e \mid Y_n=i)&=0.02,\quad i\geq 3,\\[3pt] \mathbb{P}(Y_{n+1}=1 \mid Y_n=0)&=0.99=1- \mathbb{P}(Y_{n+1}=e \mid Y_n=0),\\[3pt] \mathbb{P}(Y_{n+1}=i+1 \mid Y_n=i)&=0.5,\quad i\geq 1,\\[3pt] \mathbb{P}(Y_{n+1}=i-1 \mid Y_n=i)&=0.5-\mathbb{P}(Y_{n+1}=e \mid Y_n=i),\quad i\geq 1.\end{align*}
\begin{align*}\mathbb{P}(Y_{n+1}=e \mid Y_n=i)&=0.01,\quad i=0,1,2,\\[3pt] \mathbb{P}(Y_{n+1}=e \mid Y_n=i)&=0.02,\quad i\geq 3,\\[3pt] \mathbb{P}(Y_{n+1}=1 \mid Y_n=0)&=0.99=1- \mathbb{P}(Y_{n+1}=e \mid Y_n=0),\\[3pt] \mathbb{P}(Y_{n+1}=i+1 \mid Y_n=i)&=0.5,\quad i\geq 1,\\[3pt] \mathbb{P}(Y_{n+1}=i-1 \mid Y_n=i)&=0.5-\mathbb{P}(Y_{n+1}=e \mid Y_n=i),\quad i\geq 1.\end{align*}
Figure 1 plots the survival probabilities
 \begin{equation*}\mathbb{P}(T_e^d > n \mid Y_0= i)=(M^n)_{i,+}=\sum_{j=0}^\infty M^n_{i,j} \quad \text{for $0\leq n \leq 160$ and $i=0,1,2,3$,}\end{equation*}
\begin{equation*}\mathbb{P}(T_e^d > n \mid Y_0= i)=(M^n)_{i,+}=\sum_{j=0}^\infty M^n_{i,j} \quad \text{for $0\leq n \leq 160$ and $i=0,1,2,3$,}\end{equation*}
where the matrix
![]() $M=(M_{i,j})$
is given by
$M=(M_{i,j})$
is given by
![]() $M_{i,j}=\mathbb{P}(Y_1=j \mid Y_0=i)$
for
$M_{i,j}=\mathbb{P}(Y_1=j \mid Y_0=i)$
for
![]() $i,j=0,1,\ldots.$
It shows that
$i,j=0,1,\ldots.$
It shows that
![]() $\mathbb{P}(T_e^d > n \mid Y_0= i)$
decreases as i increases, as expected in view of Theorem 2(iii).
$\mathbb{P}(T_e^d > n \mid Y_0= i)$
decreases as i increases, as expected in view of Theorem 2(iii).

Figure 1: The survival probabilities
![]() $\mathbb{P}(T_e^d > n \mid Y_0= i)$
,
$\mathbb{P}(T_e^d > n \mid Y_0= i)$
,
![]() $i=0,1,2,3$
.
$i=0,1,2,3$
.
For a linear CBDK
![]() $\{X_t\}$
with
$\{X_t\}$
with
![]() $\mu_i=ai$
,
$\mu_i=ai$
,
![]() $\lambda_i=bi+\theta$
, and
$\lambda_i=bi+\theta$
, and
![]() $\gamma_i=ci$
, where a,b,c and
$\gamma_i=ci$
, where a,b,c and
![]() $\theta$
are positive constants, Karlin and Tavaré [Reference Karlin and Tavaré11] derived the explicit formula
$\theta$
are positive constants, Karlin and Tavaré [Reference Karlin and Tavaré11] derived the explicit formula
where
![]() $0<v_0<1<v_1$
are the two roots of the equation
$0<v_0<1<v_1$
are the two roots of the equation
![]() $bx^2 -(a+b+c)x + a=0$
and
$bx^2 -(a+b+c)x + a=0$
and
![]() $\sigma_t={\mathrm{e}}^{-b(v_1-v_0)t}$
. Since
$\sigma_t={\mathrm{e}}^{-b(v_1-v_0)t}$
. Since
![]() $\gamma_i$
is increasing in i,
$\gamma_i$
is increasing in i,
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
should be decreasing in i by Theorem 1(iii). Noting that
$\mathbb{P}(T_e>t \mid X_0=i)$
should be decreasing in i by Theorem 1(iii). Noting that
![]() $v_0(v_1-1)+v_1 \sigma_t (1-v_0)<v_1-1+\sigma_t (1-v_0)$
(since
$v_0(v_1-1)+v_1 \sigma_t (1-v_0)<v_1-1+\sigma_t (1-v_0)$
(since
![]() $0<\sigma_t<1$
), we see that
$0<\sigma_t<1$
), we see that
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
decays geometrically in i. Figure 2 plots
$\mathbb{P}(T_e>t \mid X_0=i)$
decays geometrically in i. Figure 2 plots
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
for
$\mathbb{P}(T_e>t \mid X_0=i)$
for
![]() $0<t<5$
and
$0<t<5$
and
![]() $i=0,2,4,6,8$
with
$i=0,2,4,6,8$
with
![]() $a=b=c=\theta=1$
.
$a=b=c=\theta=1$
.

Figure 2: The survival probabilities
![]() $\mathbb{P}(T_e > t \mid X_0= i)$
,
$\mathbb{P}(T_e > t \mid X_0= i)$
,
![]() $i=0,2,4,6, 8$
.
$i=0,2,4,6, 8$
.
While no explicit formula for
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
is available for general CBDKs, we may use the technique of uniformization (see [14, Section 5.10] and [15, Section 6.7]) to compute
$\mathbb{P}(T_e>t \mid X_0=i)$
is available for general CBDKs, we may use the technique of uniformization (see [14, Section 5.10] and [15, Section 6.7]) to compute
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
if
$\mathbb{P}(T_e>t \mid X_0=i)$
if
![]() $\{X_t\}$
is uniformizable (i.e.
$\{X_t\}$
is uniformizable (i.e.
![]() $\sup_i (\lambda_i+\mu_i+\gamma_i)\leq C<\infty$
for some constant
$\sup_i (\lambda_i+\mu_i+\gamma_i)\leq C<\infty$
for some constant
![]() $C>0$
). Specifically, with
$C>0$
). Specifically, with
![]() $\mu_0\,:\!=\,0$
, let
$\mu_0\,:\!=\,0$
, let
![]() $\{Z_n\}$
be a DBDK with transition probabilities satisfying
$\{Z_n\}$
be a DBDK with transition probabilities satisfying
![]() $\mathbb{P}(Z_{n+1}=e \mid Z_n=e)=1$
, and for
$\mathbb{P}(Z_{n+1}=e \mid Z_n=e)=1$
, and for
![]() $i\geq 0$
$i\geq 0$
 \begin{align*}&\mathbb{P}(Z_{n+1}=i-1 \mid Z_n=i)=\dfrac{\mu_i}{C},\quad \mathbb{P}(Z_{n+1}=i+1 \mid Z_n=i)=\dfrac{\lambda_i}{C},\\[3pt] &\mathbb{P}(Z_{n+1}=e \mid Z_n=i)=\dfrac{\gamma_i}{C},\quad \mathbb{P}(Z_{n+1}=i \mid Z_n=i)=1-\dfrac{\mu_i+\lambda_i+\gamma_i}{C}.\end{align*}
\begin{align*}&\mathbb{P}(Z_{n+1}=i-1 \mid Z_n=i)=\dfrac{\mu_i}{C},\quad \mathbb{P}(Z_{n+1}=i+1 \mid Z_n=i)=\dfrac{\lambda_i}{C},\\[3pt] &\mathbb{P}(Z_{n+1}=e \mid Z_n=i)=\dfrac{\gamma_i}{C},\quad \mathbb{P}(Z_{n+1}=i \mid Z_n=i)=1-\dfrac{\mu_i+\lambda_i+\gamma_i}{C}.\end{align*}
Let
![]() $\{N(t)\}$
be a Poisson process of constant rate C, independent of
$\{N(t)\}$
be a Poisson process of constant rate C, independent of
![]() $\{Z_n\}$
. Then we have the following result:
$\{Z_n\}$
. Then we have the following result:
In other words, the CBDK
![]() $\{X_t\}$
may be constructed by placing the transitions of the DBDK
$\{X_t\}$
may be constructed by placing the transitions of the DBDK
![]() $\{Z_n\}$
at Poisson arrival epochs. It follows from (2) that
$\{Z_n\}$
at Poisson arrival epochs. It follows from (2) that
 \begin{align}\mathbb{P}(T_e>t \mid X_0=i)&= \mathbb{P}(X_t \neq e \mid X_0=i) \notag\\[3pt] &=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(Z_n \neq e, N(t)=n \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \dfrac{{\mathrm{e}}^{-Ct}(Ct)^n}{n!} (M^{*n})_{i,+}, \notag\end{align}
\begin{align}\mathbb{P}(T_e>t \mid X_0=i)&= \mathbb{P}(X_t \neq e \mid X_0=i) \notag\\[3pt] &=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(Z_n \neq e, N(t)=n \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i) \notag\\[3pt] &=\sum_{n=0}^\infty \dfrac{{\mathrm{e}}^{-Ct}(Ct)^n}{n!} (M^{*n})_{i,+}, \notag\end{align}
where the matrix
![]() $M^*=(M^*_{i,j})$
is given by
$M^*=(M^*_{i,j})$
is given by
![]() $M^*_{i,j}=\mathbb{P}(Z_1=j \mid Z_0=i)$
. So
$M^*_{i,j}=\mathbb{P}(Z_1=j \mid Z_0=i)$
. So
![]() $\mathbb{P}(T_e>t \mid X_0=i)$
may be approximated by
$\mathbb{P}(T_e>t \mid X_0=i)$
may be approximated by
 \begin{equation*}\sum_{n=0}^{L(t)} \dfrac{{\mathrm{e}}^{-Ct}(Ct)^n}{n!} (M^{*n})_{i,+}\end{equation*}
\begin{equation*}\sum_{n=0}^{L(t)} \dfrac{{\mathrm{e}}^{-Ct}(Ct)^n}{n!} (M^{*n})_{i,+}\end{equation*}
for sufficiently large integer L(t) (depending on t). The distributional equivalence of
![]() $\{X_t\}$
and
$\{X_t\}$
and
![]() $\{Z_{N(t)}\}$
in (2) will be called for in the proof of Theorem 1 in the next section.
$\{Z_{N(t)}\}$
in (2) will be called for in the proof of Theorem 1 in the next section.
4. Proofs of Theorems 1 and 2 and Lemma 1
To prove Theorem 2, let
![]() $M=(M_{i,j})_{i,j\in \{0,1,\ldots\}}$
be the transition matrix of
$M=(M_{i,j})_{i,j\in \{0,1,\ldots\}}$
be the transition matrix of
![]() $\{Y_n\}$
restricted to the states
$\{Y_n\}$
restricted to the states
![]() $0,1,\ldots.$
That is,
$0,1,\ldots.$
That is,
By (1), we see that
![]() $M_{i,j}=0$
for
$M_{i,j}=0$
for
![]() $|i-j|>1$
and that
$|i-j|>1$
and that
 \begin{align} (M)_{i,+}=\sum_{j=\max\{0,i-1\}}^{i+1} M_{i,j}=1- \mathbb{P}(Y_{n+1}=e \mid Y_n=i)=1-p_{i,e}. \end{align}
\begin{align} (M)_{i,+}=\sum_{j=\max\{0,i-1\}}^{i+1} M_{i,j}=1- \mathbb{P}(Y_{n+1}=e \mid Y_n=i)=1-p_{i,e}. \end{align}
Moreover,
 \begin{align}\mathbb{P}(T_e^d>n \mid Y_0=i)=\sum_{j=0}^\infty \mathbb{P}(Y_n =j \mid Y_0=i)=(M^n)_{i,+}.\end{align}
\begin{align}\mathbb{P}(T_e^d>n \mid Y_0=i)=\sum_{j=0}^\infty \mathbb{P}(Y_n =j \mid Y_0=i)=(M^n)_{i,+}.\end{align}
In view of (3) and (4), Theorem 2 follows immediately from Lemma 1. To prove Theorem 1, one may approximate the CBDK
![]() $\{X_t\}$
by a sequence of DBDKs via time-discretization and argue that
$\{X_t\}$
by a sequence of DBDKs via time-discretization and argue that
![]() $T_e$
is the limit of the corresponding
$T_e$
is the limit of the corresponding
![]() $T^d_e$
. Instead of taking this approach, we first consider uniformizable
$T^d_e$
. Instead of taking this approach, we first consider uniformizable
![]() $\{X_t\}$
(i.e.
$\{X_t\}$
(i.e.
![]() $\sup_i\; (\lambda_i+\mu_i+\gamma_i)<\infty$
) for which the associated (embedded) discrete-time Markov chain is a DBDK, so that the desired results follow from Theorem 2. The general CBDK
$\sup_i\; (\lambda_i+\mu_i+\gamma_i)<\infty$
) for which the associated (embedded) discrete-time Markov chain is a DBDK, so that the desired results follow from Theorem 2. The general CBDK
![]() $\{X_t\}$
is then approximated by a sequence of uniformizable CBDKs. The details are given in the proof below.
$\{X_t\}$
is then approximated by a sequence of uniformizable CBDKs. The details are given in the proof below.
Proof of Theorem 1. We first prove part (i) under the additional assumption that
![]() $\{X_t\}$
is uniformizable, i.e.
$\{X_t\}$
is uniformizable, i.e.
![]() $\sup_i\; (\lambda_i+\mu_i+\gamma_i)\leq C<\infty$
for some
$\sup_i\; (\lambda_i+\mu_i+\gamma_i)\leq C<\infty$
for some
![]() $C>0$
. Let
$C>0$
. Let
![]() $\{Z_n\}$
and
$\{Z_n\}$
and
![]() $\{N(t)\}$
be, respectively, the DBDK and (independent) Poisson process of constant rate C as described in the last paragraph of Section 3. Letting
$\{N(t)\}$
be, respectively, the DBDK and (independent) Poisson process of constant rate C as described in the last paragraph of Section 3. Letting
we see that
![]() $\{Z_n\}$
is a DBDK with
$\{Z_n\}$
is a DBDK with
![]() $p^{(Z)}_{i,e} \leq p^{(Z)}_{j,e}$
for
$p^{(Z)}_{i,e} \leq p^{(Z)}_{j,e}$
for
![]() $i\leq i^*$
and
$i\leq i^*$
and
![]() $j>i^*$
, so that by Theorem 2(i),
$j>i^*$
, so that by Theorem 2(i),
 \begin{align} \mathbb{P}(Z_n \neq e \mid Z_0=i^*)&=\mathbb{P}(T_e^{d(Z)}>n \mid Z_0=i^*)\notag\\[3pt] &\geq \mathbb{P}(T_e^{d(Z)} >n \mid Z_0=i^*+1) \notag \\[3pt] &=\mathbb{P}(Z_n \neq e \mid Z_0=i^*+1). \end{align}
\begin{align} \mathbb{P}(Z_n \neq e \mid Z_0=i^*)&=\mathbb{P}(T_e^{d(Z)}>n \mid Z_0=i^*)\notag\\[3pt] &\geq \mathbb{P}(T_e^{d(Z)} >n \mid Z_0=i^*+1) \notag \\[3pt] &=\mathbb{P}(Z_n \neq e \mid Z_0=i^*+1). \end{align}
Consequently, for
![]() $t>0$
,
$t>0$
,
 \begin{align*} \mathbb{P}(T_e>t \mid X_0=i^*)&=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i^*)\quad (\text{by} ({2}))\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i^*)\\[3pt] &\geq \sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i^*+1)\quad (\text{by} ({5}))\\[3pt] &=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i^*+1)\\[3pt] &=\mathbb{P}(T_e>t \mid X_0=i^*+1).\end{align*}
\begin{align*} \mathbb{P}(T_e>t \mid X_0=i^*)&=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i^*)\quad (\text{by} ({2}))\\[3pt] &=\sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i^*)\\[3pt] &\geq \sum_{n=0}^\infty \mathbb{P}(N(t)=n)\, \mathbb{P}(Z_n \neq e \mid Z_0=i^*+1)\quad (\text{by} ({5}))\\[3pt] &=\mathbb{P}(Z_{N(t)}\neq e \mid Z_0=i^*+1)\\[3pt] &=\mathbb{P}(T_e>t \mid X_0=i^*+1).\end{align*}
This proves part (i) for uniformizable
![]() $\{X_t\}$
.
$\{X_t\}$
.
For general (non-explosive)
![]() $\{X_t\}$
, to prove
$\{X_t\}$
, to prove
for any (fixed)
![]() $t_0>0$
, let
$t_0>0$
, let
where
![]() $T_k\,:\!=\,\inf\{t\geq 0\colon X_t=k\}$
. For
$T_k\,:\!=\,\inf\{t\geq 0\colon X_t=k\}$
. For
![]() $X_t$
to reach a (large) state k starting from
$X_t$
to reach a (large) state k starting from
![]() $i^*$
or
$i^*$
or
![]() $i^*+1$
, at least
$i^*+1$
, at least
![]() $k-i^*-1$
transitions are required. Since
$k-i^*-1$
transitions are required. Since
![]() $\{X_t\}$
is non-explosive, we have
$\{X_t\}$
is non-explosive, we have
For each
![]() $k>i^*$
, let
$k>i^*$
, let
![]() $\{X_t^{(k)}\}$
be a CBDK whose birth, death, and killing rates in state i are given by
$\{X_t^{(k)}\}$
be a CBDK whose birth, death, and killing rates in state i are given by
![]() $\lambda_i^{(k)}\,:\!=\,\lambda_{i\wedge k}$
,
$\lambda_i^{(k)}\,:\!=\,\lambda_{i\wedge k}$
,
![]() $\mu_i^{(k)}\,:\!=\,\mu_{i\wedge k}$
, and
$\mu_i^{(k)}\,:\!=\,\mu_{i\wedge k}$
, and
![]() $\gamma_i^{(k)}\,:\!=\,\gamma_{i\wedge k}$
, where
$\gamma_i^{(k)}\,:\!=\,\gamma_{i\wedge k}$
, where
![]() $i \wedge k\,:\!=\,\min\{i,k\}$
. Clearly
$i \wedge k\,:\!=\,\min\{i,k\}$
. Clearly
![]() $\{X_t^{(k)}\}$
is uniformizable with the killing rates satisfying
$\{X_t^{(k)}\}$
is uniformizable with the killing rates satisfying
![]() $\gamma_i^{(k)}\leq \gamma_j^{(k)}$
for
$\gamma_i^{(k)}\leq \gamma_j^{(k)}$
for
![]() $i\leq i^*$
and
$i\leq i^*$
and
![]() $j>i^*$
. Let
$j>i^*$
. Let
![]() $\mathcal{L}_i(T_k)$
(
$\mathcal{L}_i(T_k)$
(
![]() $\mathcal{L}_i(T_e \wedge T_k)$
, respectively) denote the distribution of
$\mathcal{L}_i(T_e \wedge T_k)$
, respectively) denote the distribution of
![]() $T_k$
(
$T_k$
(
![]() $T_e \wedge T_k$
, respectively) given
$T_e \wedge T_k$
, respectively) given
![]() $X_0=i$
. Similarly, let
$X_0=i$
. Similarly, let
![]() $\mathcal{L}_i(T_k^{(k)})$
(
$\mathcal{L}_i(T_k^{(k)})$
(
![]() $\mathcal{L}_i(T_e^{(k)}\wedge T_k^{(k)})$
, respectively) denote the distribution of
$\mathcal{L}_i(T_e^{(k)}\wedge T_k^{(k)})$
, respectively) denote the distribution of
![]() $T_k^{(k)}$
(
$T_k^{(k)}$
(
![]() $T_e^{(k)}\wedge T_k^{(k)}$
, respectively) given
$T_e^{(k)}\wedge T_k^{(k)}$
, respectively) given
![]() $X_0^{(k)}=i$
, where
$X_0^{(k)}=i$
, where
![]() $T_r^{(k)}\,:\!=\,\inf\{t \geq 0\colon X_t^{(k)}=r\}$
for
$T_r^{(k)}\,:\!=\,\inf\{t \geq 0\colon X_t^{(k)}=r\}$
for
![]() $r=k,e$
.
$r=k,e$
.
For
![]() $k>i^*$
, given
$k>i^*$
, given
![]() $X_0=i^*$
or
$X_0=i^*$
or
![]() $i^*+1$
, the distributions of
$i^*+1$
, the distributions of
![]() $T_k$
and
$T_k$
and
![]() $T_e \wedge T_k$
depend only on the values of
$T_e \wedge T_k$
depend only on the values of
![]() $\lambda_i, \mu_i, \gamma_i$
for
$\lambda_i, \mu_i, \gamma_i$
for
![]() $i< k$
. Similarly, given
$i< k$
. Similarly, given
![]() $X_0^{(k)}=i^*$
or
$X_0^{(k)}=i^*$
or
![]() $i^*+1$
, the distributions of
$i^*+1$
, the distributions of
![]() $T_k^{(k)}$
and
$T_k^{(k)}$
and
![]() $T_e^{(k)} \wedge T_k^{(k)}$
depend only on the values of
$T_e^{(k)} \wedge T_k^{(k)}$
depend only on the values of
![]() $\lambda_i^{(k)}, \mu_i^{(k)}, \gamma_i^{(k)}$
for
$\lambda_i^{(k)}, \mu_i^{(k)}, \gamma_i^{(k)}$
for
![]() $i< k$
. Since
$i< k$
. Since
![]() $\lambda_i=\lambda_i^{(k)}$
,
$\lambda_i=\lambda_i^{(k)}$
,
![]() $\mu_i=\mu_i^{(k)}$
, and
$\mu_i=\mu_i^{(k)}$
, and
![]() $\gamma_i=\gamma_i^{(k)}$
for
$\gamma_i=\gamma_i^{(k)}$
for
![]() $i\leq k$
, we find that
$i\leq k$
, we find that
implying that for
![]() $k>i^*$
,
$k>i^*$
,
Since
![]() $\{X_t^{(k)}\}$
is uniformizable with
$\{X_t^{(k)}\}$
is uniformizable with
![]() $\gamma^{(k)}_i \leq \gamma^{(k)}_j$
for
$\gamma^{(k)}_i \leq \gamma^{(k)}_j$
for
![]() $i \leq i^*$
and
$i \leq i^*$
and
![]() $j>i^*$
, we have shown that
$j>i^*$
, we have shown that
Also for
![]() $k>i^*$
and
$k>i^*$
and
![]() $i=i^*$
,
$i=i^*$
,
![]() $i^*+1$
,
$i^*+1$
,
 \begin{align*}\mathbb{P}(T_e>t_0 \mid X_0=i)&\geq \mathbb{P}(T_e \wedge T_k>t_0 \mid X_0=i)\\[3pt] &=\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)\quad (\text{by} ({9})),\end{align*}
\begin{align*}\mathbb{P}(T_e>t_0 \mid X_0=i)&\geq \mathbb{P}(T_e \wedge T_k>t_0 \mid X_0=i)\\[3pt] &=\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)\quad (\text{by} ({9})),\end{align*}
and
 \begin{align*}\mathbb{P}(T_e>t_0 \mid X_0=i)&\leq \mathbb{P}(T_e \wedge T_k>t_0 \mid X_0=i)+ \mathbb{P}(T_k\leq t_0 \mid X_0=i)\\[3pt] &=\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)+\mathbb{P}(T_k\leq t_0 \mid X_0=i) \quad (\text{by} ({9}))\\[3pt] &\leq \mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)+ a_k \vee b_k,\end{align*}
\begin{align*}\mathbb{P}(T_e>t_0 \mid X_0=i)&\leq \mathbb{P}(T_e \wedge T_k>t_0 \mid X_0=i)+ \mathbb{P}(T_k\leq t_0 \mid X_0=i)\\[3pt] &=\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)+\mathbb{P}(T_k\leq t_0 \mid X_0=i) \quad (\text{by} ({9}))\\[3pt] &\leq \mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)+ a_k \vee b_k,\end{align*}
where
![]() $a_k$
and
$a_k$
and
![]() $b_k$
are as defined in (6) and
$b_k$
are as defined in (6) and
![]() $a_k \vee b_k\,:\!=\,\max\{a_k,b_k\}$
. Consequently, for
$a_k \vee b_k\,:\!=\,\max\{a_k,b_k\}$
. Consequently, for
![]() $k>i^*$
,
$k>i^*$
,
Furthermore, for
![]() $k>i^*$
and
$k>i^*$
and
![]() $i=i^*$
,
$i=i^*$
,
![]() $i^*+1$
,
$i^*+1$
,
 \begin{align*}0&\leq \mathbb{P}(T_e^{(k)}>t_0 \mid X_0^{(k)}=i)-\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)\\[3pt] &\leq \mathbb{P}(T_k^{(k)} \leq t_0 \mid X_0^{(k)}=i)\\[3pt] &=\mathbb{P}(T_k \leq t_0 \mid X_0=i)\quad (\text{by} ({8}))\\[3pt] &\leq a_k \vee b_k,\end{align*}
\begin{align*}0&\leq \mathbb{P}(T_e^{(k)}>t_0 \mid X_0^{(k)}=i)-\mathbb{P}(T_e^{(k)} \wedge T_k^{(k)}>t_0 \mid X_0^{(k)}=i)\\[3pt] &\leq \mathbb{P}(T_k^{(k)} \leq t_0 \mid X_0^{(k)}=i)\\[3pt] &=\mathbb{P}(T_k \leq t_0 \mid X_0=i)\quad (\text{by} ({8}))\\[3pt] &\leq a_k \vee b_k,\end{align*}
which together with (11) implies that for
![]() $k>i^*$
and
$k>i^*$
and
![]() $i=i^*$
,
$i=i^*$
,
![]() $i^*+1$
,
$i^*+1$
,
It follows from (7), (10), and (12) that
completing the proof of part (i).
Part (ii) can be proved by using a similar argument and invoking Theorem 2(ii). Parts (iii) and (iv) follow immediately from parts (i) and (ii), respectively. □
Proof of Lemma 1. Note that part (ii) follows from part (i) by reversing the ordering of the rows and that of the columns, and that part (iii) is a consequence of parts (i) and (ii). It remains to prove part (i). It suffices to deal only with the case
![]() $\mathbb{S}=\mathbb{Z}$
, since the cases
$\mathbb{S}=\mathbb{Z}$
, since the cases
![]() $\mathbb{S}=\{0,1,\ldots, I\}$
and
$\mathbb{S}=\{0,1,\ldots, I\}$
and
![]() $\mathbb{S}=\{0,1,\ldots\}$
can be treated as special cases of
$\mathbb{S}=\{0,1,\ldots\}$
can be treated as special cases of
![]() $\mathbb{S}=\mathbb{Z}$
. More precisely, for
$\mathbb{S}=\mathbb{Z}$
. More precisely, for
![]() $M=(M_{i,j})_{i,j \in \{0,1,\ldots,I\}}$
satisfying
$M=(M_{i,j})_{i,j \in \{0,1,\ldots,I\}}$
satisfying
![]() $(M)_{i,+}\le (M)_{j,+}$
for
$(M)_{i,+}\le (M)_{j,+}$
for
![]() $i \le i^*<j$
, define
$i \le i^*<j$
, define
![]() $\widetilde{M}=(\widetilde{M}_{i,j})_{i,j \in \mathbb{Z}}$
by
$\widetilde{M}=(\widetilde{M}_{i,j})_{i,j \in \mathbb{Z}}$
by
where
![]() $\textbf{1}_A$
denotes the indicator function of a set A and
$\textbf{1}_A$
denotes the indicator function of a set A and
![]() $\delta_{i,j}=1$
if
$\delta_{i,j}=1$
if
![]() $i=j$
and
$i=j$
and
![]() $\delta_{i,j}=0$
otherwise. We have
$\delta_{i,j}=0$
otherwise. We have
![]() $(\widetilde{M})_{i,+}\le (\widetilde{M})_{j,+}$
for
$(\widetilde{M})_{i,+}\le (\widetilde{M})_{j,+}$
for
![]() $i\le i^*<j$
. Moreover,
$i\le i^*<j$
. Moreover,
![]() $(\widetilde{M}^n)_{i,+}=(M^n)_{i,+}$
for
$(\widetilde{M}^n)_{i,+}=(M^n)_{i,+}$
for
![]() $i=0,1,\ldots,I$
.
$i=0,1,\ldots,I$
.
We now prove part (i) for
![]() $\mathbb{S}=\mathbb{Z}$
. Without loss of generality, we assume
$\mathbb{S}=\mathbb{Z}$
. Without loss of generality, we assume
![]() $i^*=0$
, so that the tri-diagonal matrix M satisfies
$i^*=0$
, so that the tri-diagonal matrix M satisfies
![]() $M_{i,j}\ge 0$
for
$M_{i,j}\ge 0$
for
![]() $i,j \in \mathbb{Z}$
,
$i,j \in \mathbb{Z}$
,
![]() $M_{i,j}=0$
if
$M_{i,j}=0$
if
![]() $|i-j|>1$
, and
$|i-j|>1$
, and
![]() $(M)_{i,+}\le (M)_{j,+}$
for
$(M)_{i,+}\le (M)_{j,+}$
for
![]() $i \le 0<j$
. To show that
$i \le 0<j$
. To show that
![]() $(M^{n})_{0,+} \leq (M^{n})_{1,+}$
for any (fixed)
$(M^{n})_{0,+} \leq (M^{n})_{1,+}$
for any (fixed)
![]() $n\geq 2$
, note that
$n\geq 2$
, note that
![]() $(M^{n})_{0,+}$
and
$(M^{n})_{0,+}$
and
![]() $(M^{n})_{1,+}$
do not depend on the values of
$(M^{n})_{1,+}$
do not depend on the values of
![]() $M_{i,i-1}$
,
$M_{i,i-1}$
,
![]() $M_{i,i}$
, and
$M_{i,i}$
, and
![]() $M_{i,i+1}$
for
$M_{i,i+1}$
for
![]() $i\leq -n$
or
$i\leq -n$
or
![]() $i\geq n+1$
. Thus
$i\geq n+1$
. Thus
![]() $(M^{n})_{0,+}=(\overline{M}^{n})_{0,+}$
and
$(M^{n})_{0,+}=(\overline{M}^{n})_{0,+}$
and
![]() $(M^{n})_{1,+} = (\overline{M}^{n})_{1,+}$
, where
$(M^{n})_{1,+} = (\overline{M}^{n})_{1,+}$
, where
![]() $\overline{M}=(\overline{M}_{i,j})$
is defined by
$\overline{M}=(\overline{M}_{i,j})$
is defined by
Note that
![]() $\overline{M}$
has bounded row sums and satisfies
$\overline{M}$
has bounded row sums and satisfies
![]() $(\overline{M})_{i,+}\le (\overline{M})_{j,+}$
for
$(\overline{M})_{i,+}\le (\overline{M})_{j,+}$
for
![]() $i\leq 0<j$
. If we can show part (i) of the theorem for non-negative tri-diagonal matrices with bounded row sums, then we have
$i\leq 0<j$
. If we can show part (i) of the theorem for non-negative tri-diagonal matrices with bounded row sums, then we have
So it suffices to establish part (i) with M having bounded row sums. We may further assume that the row sums of M are bounded by 1.
To show that
![]() $(M^{n})_{0,+} \leq (M^{n})_{1,+}$
for
$(M^{n})_{0,+} \leq (M^{n})_{1,+}$
for
![]() $n\geq 2$
, we introduce a Markov chain
$n\geq 2$
, we introduce a Markov chain
![]() $\{X_{n}\colon n=0,1,\ldots \}$
with state space
$\{X_{n}\colon n=0,1,\ldots \}$
with state space
![]() $\mathbb{Z}\cup \{e\}$
and transition probabilities given by
$\mathbb{Z}\cup \{e\}$
and transition probabilities given by
 \begin{align*}\mathbb{P}(X_{n+1}&=j \mid X_{n}=i) = M_{i,j} ,\quad i,j\in \mathbb{Z} ,\\[3pt] \mathbb{P}(X_{n+1}&=e \mid X_{n}=i) = 1-(M)_{i,+} ,\quad i\in \mathbb{Z} ,\\[3pt] \mathbb{P}(X_{n+1}&=e \mid X_{n}=e) = 1 .\end{align*}
\begin{align*}\mathbb{P}(X_{n+1}&=j \mid X_{n}=i) = M_{i,j} ,\quad i,j\in \mathbb{Z} ,\\[3pt] \mathbb{P}(X_{n+1}&=e \mid X_{n}=i) = 1-(M)_{i,+} ,\quad i\in \mathbb{Z} ,\\[3pt] \mathbb{P}(X_{n+1}&=e \mid X_{n}=e) = 1 .\end{align*}
Note that the state e is absorbing. Let
![]() $T_{1}=\inf \{n\geq 0\colon X_{n}=1\}$
and
$T_{1}=\inf \{n\geq 0\colon X_{n}=1\}$
and
![]() $T_{e}=\inf \{n\geq 0\colon X_{n}=e\}$
. (In Theorem 1,
$T_{e}=\inf \{n\geq 0\colon X_{n}=e\}$
. (In Theorem 1,
![]() $T_e$
is defined with respect to the continuous-time process
$T_e$
is defined with respect to the continuous-time process
![]() $\{X_t\}$
. Here the same notation
$\{X_t\}$
. Here the same notation
![]() $T_e$
is used with respect to the discrete-time process
$T_e$
is used with respect to the discrete-time process
![]() $\{X_n\}$
. This proof does not involve the continuous-time process
$\{X_n\}$
. This proof does not involve the continuous-time process
![]() $\{X_t\}$
.)
$\{X_t\}$
.)
We write
![]() $\mathbb{P}_{i}( \cdot )=\mathbb{P}( \cdot\mid X_{0}=i)$
, and claim that for
$\mathbb{P}_{i}( \cdot )=\mathbb{P}( \cdot\mid X_{0}=i)$
, and claim that for
![]() $n=1,2,\ldots,$
and
$n=1,2,\ldots,$
and
![]() $j=1,2,\ldots,$
$j=1,2,\ldots,$
 \begin{align}\mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j}(T_{e}>n-\ell) \leq \mathbb{P}_{j}(T_{e}>n). \end{align}
\begin{align}\mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j}(T_{e}>n-\ell) \leq \mathbb{P}_{j}(T_{e}>n). \end{align}
Note that for
![]() $1 \leq \ell < n$
,
$1 \leq \ell < n$
,
 \begin{align}\mathbb{P}_0(T_{1}=\ell,\, T_{e}>n) &=\mathbb{P}(T_{1}=\ell,\, T_{e}>n\mid X_{0}=0)\notag \\[3pt] &=\mathbb{P}(T_{1}=\ell \mid X_{0}=0)\, \mathbb{P}(T_{e}>n\mid T_{1}=\ell,\, X_{0}=0)\notag \\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}(T_{e}>n\mid X_{\ell}=1)\notag\\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}(T_{e}>n-\ell \mid X_{0}=1)\notag\\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>n-\ell)\,. \end{align}
\begin{align}\mathbb{P}_0(T_{1}=\ell,\, T_{e}>n) &=\mathbb{P}(T_{1}=\ell,\, T_{e}>n\mid X_{0}=0)\notag \\[3pt] &=\mathbb{P}(T_{1}=\ell \mid X_{0}=0)\, \mathbb{P}(T_{e}>n\mid T_{1}=\ell,\, X_{0}=0)\notag \\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}(T_{e}>n\mid X_{\ell}=1)\notag\\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}(T_{e}>n-\ell \mid X_{0}=1)\notag\\[3pt] &=\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>n-\ell)\,. \end{align}
By (14), the left-hand side of (13) with
![]() $j=1$
equals
$j=1$
equals
 \begin{align*}& \mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>n-\ell)\\[3pt] &\quad =\mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell,\, T_{e}>n)\\[3pt] &\quad =\mathbb{P}_{0}(T_{e}>n) .\end{align*}
\begin{align*}& \mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>n-\ell)\\[3pt] &\quad =\mathbb{P}_{0}(T_{1}\geq n,\, T_{e}>n) + \sum^{n-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell,\, T_{e}>n)\\[3pt] &\quad =\mathbb{P}_{0}(T_{e}>n) .\end{align*}
Thus the inequality (13) with
![]() $j=1$
is equivalent to
$j=1$
is equivalent to
Since
![]() $\mathbb{P}_{i}(T_{e}>n) =\mathbb{P}(X_{n}\in \mathbb{Z} \mid X_{0}=i) = (M^{n})_{i,+}$
, (15) is equivalent to
$\mathbb{P}_{i}(T_{e}>n) =\mathbb{P}(X_{n}\in \mathbb{Z} \mid X_{0}=i) = (M^{n})_{i,+}$
, (15) is equivalent to
![]() $(M^{n})_{0,+} \leq (M^{n})_{1,+}$
.
$(M^{n})_{0,+} \leq (M^{n})_{1,+}$
.
We now prove (13) by induction on n. For
![]() $n=1$
, the left-hand side of (13) equals
$n=1$
, the left-hand side of (13) equals
while the right-hand side equals
![]() $\mathbb{P}_{j}(T_{e}>1)=(M)_{j,+}$
. Thus the inequality (13) with
$\mathbb{P}_{j}(T_{e}>1)=(M)_{j,+}$
. Thus the inequality (13) with
![]() $n=1$
follows from the assumption that
$n=1$
follows from the assumption that
![]() $(M)_{0,+}\leq (M)_{j,+}$
for
$(M)_{0,+}\leq (M)_{j,+}$
for
![]() $j>0$
.
$j>0$
.
For
![]() $m \geq 1$
, suppose (13) holds for
$m \geq 1$
, suppose (13) holds for
![]() $n=1,\ldots,m$
and
$n=1,\ldots,m$
and
![]() $j=1,2,\ldots.$
In particular, the induction hypothesis (see (15)) implies that
$j=1,2,\ldots.$
In particular, the induction hypothesis (see (15)) implies that
We need to show that for
![]() $j=1,2,\ldots,$
$j=1,2,\ldots,$
Note that for
![]() $j=1,2,\ldots,$
$j=1,2,\ldots,$
 \begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j-1}(T_{e}>m-\ell) \leq \mathbb{P}_{j-1}(T_{e}>m) , \end{align}
\begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j-1}(T_{e}>m-\ell) \leq \mathbb{P}_{j-1}(T_{e}>m) , \end{align}
 \begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j}(T_{e}>m-\ell) \leq \mathbb{P}_{j}(T_{e}>m) , \end{align}
\begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j}(T_{e}>m-\ell) \leq \mathbb{P}_{j}(T_{e}>m) , \end{align}
 \begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j+1}(T_{e}>m-\ell) \leq \mathbb{P}_{j+1}(T_{e}>m) . \end{align}
\begin{align}\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m)\ &+ \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\ \mathbb{P}_{j+1}(T_{e}>m-\ell) \leq \mathbb{P}_{j+1}(T_{e}>m) . \end{align}
Except for
![]() $j=1$
in (18), (18)–(20) follow immediately from the induction hypothesis. By (16),
$j=1$
in (18), (18)–(20) follow immediately from the induction hypothesis. By (16),
![]() $\mathbb{P}_{0}(T_{e}>m-\ell) \leq \mathbb{P}_{1}(T_{e}>m-\ell) $
for
$\mathbb{P}_{0}(T_{e}>m-\ell) \leq \mathbb{P}_{1}(T_{e}>m-\ell) $
for
![]() $\ell=1,\ldots,m-1$
, so the left-hand side of (18) with
$\ell=1,\ldots,m-1$
, so the left-hand side of (18) with
![]() $j=1$
equals
$j=1$
equals
 \begin{align*}& \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{0}(T_{e}>m-\ell) \\[3pt] & \quad \leq \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>m-\ell) \\[3pt] & \quad = \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell,\, T_{e}>m) \quad (\text{by} ({14})) \\[3pt] & \quad = \mathbb{P}_{0}(T_{e}>m) ,\end{align*}
\begin{align*}& \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{0}(T_{e}>m-\ell) \\[3pt] & \quad \leq \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{1}(T_{e}>m-\ell) \\[3pt] & \quad = \mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) + \sum^{m-1}_{\ell=1} \mathbb{P}_{0}(T_{1}=\ell,\, T_{e}>m) \quad (\text{by} ({14})) \\[3pt] & \quad = \mathbb{P}_{0}(T_{e}>m) ,\end{align*}
establishing (18) for
![]() $j=1$
.
$j=1$
.
Note that for
![]() $\ell=m$
,
$\ell=m$
,
 \begin{align*}& \mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{j-1}(T_{e}>m-\ell) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=m)\ \mathbb{P}_{j-1} (T_{e}>0) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=m) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) ,\end{align*}
\begin{align*}& \mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=\ell)\, \mathbb{P}_{j-1}(T_{e}>m-\ell) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=m)\ \mathbb{P}_{j-1} (T_{e}>0) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1) +\mathbb{P}_{0}(T_{1}=m) \\[3pt] & \quad =\mathbb{P}_{0}(T_{1}\geq m,\, T_{e}>m) ,\end{align*}
so (18) is equivalent to
Similarly, (19) and (20), respectively, are equivalent to
Letting
![]() $a_j=M_{j,j-1}$
,
$a_j=M_{j,j-1}$
,
![]() $ b_j=M_{j,j}$
, and
$ b_j=M_{j,j}$
, and
![]() $c_j=M_{j,j+1}$
, we have
$c_j=M_{j,j+1}$
, we have
 \begin{align}\mathbb{P}_{j}(T_{e} > m+1) & =\mathbb{P}(T_{e}>m+1 \mid X_{0}=j) \notag \\[3pt] & =\mathbb{P}(X_{1}\neq e,\, T_{e}>m+1\mid X_{0}=j) \notag \\[3pt] & = \sum^{j+1}_{r=j-1} \mathbb{P}(X_{1}=r,\, T_{e}>m+1\mid X_{0}=j) \notag \\[3pt] & = a_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j-1) + b_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j) \notag \\[3pt] &\quad+ c_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j+1) \notag \\[3pt] & = a_{j} \mathbb{P}_{j-1}(T_{e}>m) + b_{j} \mathbb{P}_{j}(T_{e}>m) + c_{j} \mathbb{P}_{j+1}(T_{e}>m) . \end{align}
\begin{align}\mathbb{P}_{j}(T_{e} > m+1) & =\mathbb{P}(T_{e}>m+1 \mid X_{0}=j) \notag \\[3pt] & =\mathbb{P}(X_{1}\neq e,\, T_{e}>m+1\mid X_{0}=j) \notag \\[3pt] & = \sum^{j+1}_{r=j-1} \mathbb{P}(X_{1}=r,\, T_{e}>m+1\mid X_{0}=j) \notag \\[3pt] & = a_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j-1) + b_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j) \notag \\[3pt] &\quad+ c_{j} \mathbb{P}(T_{e}>m+1\mid X_{1}=j+1) \notag \\[3pt] & = a_{j} \mathbb{P}_{j-1}(T_{e}>m) + b_{j} \mathbb{P}_{j}(T_{e}>m) + c_{j} \mathbb{P}_{j+1}(T_{e}>m) . \end{align}
Similarly, for
![]() $1 \leq \ell \leq m$
,
$1 \leq \ell \leq m$
,
In view of (24) and (25), it follows from (21)–(23) that
Note that, given
![]() $X_0=0$
,
$X_0=0$
,
and
We have
 \begin{align}&\mathbb{P}_{0}(T_{1} \geq m+1,\, T_{e}>m+1) \notag \\[3pt] &\quad = \mathbb{P}(X_{1}<1,\ldots,X_{m}<1,\, X_{m+1}\neq e\mid X_{0}=0) \notag \\[3pt] &\quad =\mathbb{P}(X_{1}<1,\ldots,X_{m}<1\mid X_{0}=0)\, \mathbb{P}(X_{m+1}\neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \notag \\[3pt] &\quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1)\, \mathbb{P}(X_{m+1}\neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \notag \\[3pt] &\quad \leq\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1)\ (a_{j}+b_{j}+c_{j}). \end{align}
\begin{align}&\mathbb{P}_{0}(T_{1} \geq m+1,\, T_{e}>m+1) \notag \\[3pt] &\quad = \mathbb{P}(X_{1}<1,\ldots,X_{m}<1,\, X_{m+1}\neq e\mid X_{0}=0) \notag \\[3pt] &\quad =\mathbb{P}(X_{1}<1,\ldots,X_{m}<1\mid X_{0}=0)\, \mathbb{P}(X_{m+1}\neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \notag \\[3pt] &\quad =\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1)\, \mathbb{P}(X_{m+1}\neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \notag \\[3pt] &\quad \leq\mathbb{P}_{0}(T_{1} \wedge T_{e} \geq m+1)\ (a_{j}+b_{j}+c_{j}). \end{align}
The above inequality follows since
 \begin{align*}& \mathbb{P}(X_{m+1} \neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i,\, X_{m+1} \neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\, \mathbb{P}(X_{m+1} \neq e\mid X_{m}=i) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\ (a_{i}+b_{i}+c_{i}) \\[3pt] & \quad \leq \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\ (a_{j}+b_{j}+c_{j}) \\[3pt] & \quad = a_{j}+b_{j}+c_{j} ,\end{align*}
\begin{align*}& \mathbb{P}(X_{m+1} \neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i,\, X_{m+1} \neq e\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\, \mathbb{P}(X_{m+1} \neq e\mid X_{m}=i) \\[3pt] & \quad = \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\ (a_{i}+b_{i}+c_{i}) \\[3pt] & \quad \leq \sum_{i \leq 0} \mathbb{P}(X_{m}=i\mid X_{0}=0,\, X_{1}<1,\ldots,X_{m}<1)\ (a_{j}+b_{j}+c_{j}) \\[3pt] & \quad = a_{j}+b_{j}+c_{j} ,\end{align*}
where the inequality is due to the assumption that
![]() $a_{i}+b_{i}+c_{i} \leq a_{j}+b_{j}+c_{j}$
for
$a_{i}+b_{i}+c_{i} \leq a_{j}+b_{j}+c_{j}$
for
![]() $i \leq 0 < j$
.
$i \leq 0 < j$
.
Finally (17) follows from (26) and (27). The proof is complete. □
Acknowledgements
The authors are grateful to the Editor and two reviewers for their helpful comments leading to an improved presentation. The authors also gratefully acknowledge support by the Ministry of Science and Technology, Taiwan, ROC.