Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-19T11:49:54.848Z Has data issue: false hasContentIssue false
  • English
  • Français

On a characterization property of finite irreducible Markov chains

Published online by Cambridge University Press:  14 July 2016

I. V. Basawa
I. V. Basawa*
Affiliation:
University of Sheffield
Get access Rights & Permissions [Opens in a new window]

Extract

Let {Xk}, k = 1, 2, ··· be a sequence of random variables forming a homogeneous Markov chain on a finite state-space, S = {1, 2, ···, s}. Xk could be thought of as the state at time k of some physical system for which 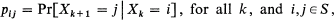are the (one-step) transition probabilities. It is assumed that all the states are inter-communicating, so that the transition matrix P = ((pij)) is irreducible.

Type
Short Communications
Information
Journal of Applied Probability , Volume 7 , Issue 3 , December 1970 , pp. 771 - 775
Copyright
Copyright © Applied Probability Trust 1970 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhat, B. R. (1960) Maximum likelihood estimation for positively regular Markov chains. Sankhya 22, 339–344.Google Scholar
Gani, J. (1955) Some theorems and sufficiency conditions for the maximum likelihood estimator of an unknown parameter in a simple Markov chain. Biometrika 42, 342–359.Google Scholar
Kingman, J. F. C. (1963) Poisson counts for random sequences of events. Ann. Math. Statist. 34, 1217–1232.CrossRefGoogle Scholar