Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T22:09:54.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Hitting probabilities for random ellipses and ellipsoids

Part of: Geometric probability and stochastic geometry General convexity

Published online by Cambridge University Press:  14 July 2016

Andrei Duma  and
Marius Stoka
Andrei Duma*
Affiliation:
University of Hagen
Marius Stoka*
Affiliation:
University of Torino
*
∗ Postal address: Fachbereich Mathematick, Postfach 940, DW-5800 Hagen, Germany.
∗∗ Postal address: Dipartimento di Matematica, Via Principe Amadeo 8, I-10123 Torino, Italy.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 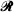denote a rectangular lattice in the Euclidean plane E2, generated by (a × b) rectangles. In this paper we consider the probability that a random ellipse having main axes of length 2α and 2ß, with 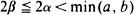intersects 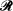. We regard the lattice 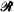as the union of two orthogonal sets 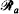and 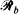of equidistant lines and evaluate the probability that the random ellipse intersects 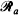or 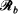. Moreover, we consider the dependence structure of the events that the ellipse intersects or 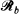. We study further the case when the main axes of the ellipse are parallel to the lines of the lattice and satisfy 2ß = min (a, b) < 2α = max (a, b). In this case, the probability of intersection is 1, and there exist almost surely two perpendicular segments in within the ellipse. We evaluate the distribution function, density, mean and variance of the length of these segments. We conclude with a generalization of this problem in three dimensions.

Keywords

GEOMETRIC PROBABILITYSTOCHASTIC GEOMETRYRANDOM SETSRANDOM CONVEX SETS AND INTEGRAL GEOMETRY

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry
Type
Short Communications
Information
Journal of Applied Probability , Volume 30 , Issue 4 , December 1993 , pp. 971 - 974
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Deltheil, R. (1926) Probabilités géométriques. Gauthier-Villars, Paris.Google Scholar
[2] Pettineo, M. (1989) On some random variables associated with random hyperspheres in the euclidean space En. Rend. Circ. Mat. Palermo (II) 38, 494–499.Google Scholar
[3] Schuster, E. F. (1974) Buffon's needle experiment. Amer. Math. Monthy 81, 26–29.CrossRefGoogle Scholar
[4] Stoka, M. (1989) Sur quelques problèmes de probabilités géométriques pour les réseaux dans l'espace euclidien. En. Publ. Inst. Stat. Univ. Paris 34 (3), 31–50.Google Scholar