Hostname: page-component-6dbcb7884d-cm8hq Total loading time: 0 Render date: 2025-02-14T08:52:30.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast mixing of a randomized shift-register Markov chain

Part of: Communication, information Markov processes

Published online by Cambridge University Press:  02 September 2022

David A. Levin  and
Chandan Tankala
David A. Levin*
Affiliation:
University of Oregon
Chandan Tankala*
Affiliation:
University of Oregon
*
*Postal address: Department of Mathematics, Fenton Hall, University of Oregon, Eugene, OR, 97403-1222 USA.
*Postal address: Department of Mathematics, Fenton Hall, University of Oregon, Eugene, OR, 97403-1222 USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a Markov chain on the n-dimensional hypercube 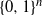$\{0,1\}^n$ which satisfies 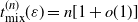$t_{{\rm mix}}^{(n)}(\varepsilon) = n[1 + o(1)]$ . This Markov chain alternates between random and deterministic moves, and we prove that the chain has a cutoff with a window of size at most 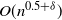$O(n^{0.5+\delta})$ , where $\delta>0$ . The deterministic moves correspond to a linear shift register.

Keywords

Markov chainsfast mixingcutoffhypercube

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 94A55: Shift register sequences and sequences over finite alphabets
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 1 , March 2023 , pp. 253 - 266
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, H. C. and Diaconis, P. (2007). Hit and run as a unifying device. Journal de la société française de statistique 148, 5–28.Google Scholar
Ben-Hamou, A. and Peres, Y. (2018). Cutoff for a stratified random walk on the hypercube. Electron. Commun. Prob. 23, 1–10.CrossRefGoogle Scholar
Ben-Hamou, A. and Peres, Y. (2021). Cutoff for permuted Markov chains. Preprint, arXiv:2104.03568.Google Scholar
Bierkens, J. (2016). Non-reversible metropolis-hastings. Statist. Comput. 26, 1213–1228.CrossRefGoogle Scholar
Boardman, S., Rudolf, D. and Saloff-Coste, L. (2020). The hit-and-run version of top-to-random. Preprint, arXiv:2009.04977.Google Scholar
Boucheron, S., Lugosi, G. and Massart, P. (2013). Concentration Inequalities. Oxford University Press.CrossRefGoogle Scholar
Chatterjee, S. and Diaconis, P. (2020). Speeding up Markov chains with deterministic jumps. Prob. Theory Relat. Fields 178, 1193–1214.CrossRefGoogle Scholar
Chen, F., Lovász, L. and Pak, I. (1999). Lifting Markov chains to speed up mixing. In Proc. 31st Ann. ACM Symp. Theory of Computing, pp. 275–281.CrossRefGoogle Scholar
Diaconis, P. and Graham, R. (1992). An affine walk on the hypercube. J. Comput. Appl. Math. 41, 215–235.CrossRefGoogle Scholar
Diaconis, P., Graham, R. L. and Morrison, J. A. (1990). Asymptotic analysis of a random walk on a hypercube with many dimensions. Random Structures Algorithms 1, 51–72.CrossRefGoogle Scholar
Diaconis, P., Holmes, S. and Neal, R. M. (2000). Analysis of a nonreversible Markov chain sampler. Ann. Appl. Prob. 10, 726–752.CrossRefGoogle Scholar
Diaconis, P. and Ram, A. (2000). Analysis of systematic scan Metropolis algorithms using Iwahori–Hecke algebra techniques. Michigan Math. J. 48, 157–190.CrossRefGoogle Scholar
Golomb, S. W. (2017). Shift Register Sequences, 3rd edn. World Scientific, Singapore.CrossRefGoogle Scholar
Guo, B.-N. and Qi, F. (2013). Refinements of lower bounds for polygamma functions. Proc. Amer. Math. Soc. 141, 1007–1015.CrossRefGoogle Scholar
Jensen, S. and Foster, D. (2014). A level-set hit-and-run sampler for quasi-concave distributions. Proc. Mach. Learn. Res. 33, 439–447.Google Scholar
Levin, D. A. and Peres, Y. (2017). Markov Chains and Mixing Times, 2nd edn. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Wilson, D. B. (1997). Random random walks on $\mathbb{Z}_2^d$ . Prob. Theory Relat. Fields 108, 441–457.CrossRefGoogle Scholar