Mathematical modelling and animal nutrition before 1925

This section summarizes rather than explains the state of knowledge prior to 1925. The reader should therefore consider each paragraph as a snapshot of a particular aspect of mathematics or animal nutrition.

Just over a century ago, major progress was being made in animal nutrition, especially regarding feed requirement systems. Feeding standards, nowadays referred to as feed evaluation systems or nutrient requirements, served to calculate daily rations for various farm animals on the basis of composition (proteins, carbohydrates, fat, non-nitrogenous material and total organic matter) of feedstuffs (e.g. clover-hay, oats, pumpkins, dried blood, birch foliage and pine needles) and were usually expressed per 1000 lbs liveweight (Wolff Reference Wolff1895). These feeding standards served as a stepping stone in the development of mathematical modelling in animal nutrition. Murray (Reference Murray1915) helped foster this transition by stressing the importance of mathematics when he wrote that feeding standards should be superseded by formulae in order to determine energy and nutrient (mostly protein and starch) requirements of animals at any given liveweight.

Animal nutritionists considered, primarily, chemicals rather than energy to study the conversion of food into biomass. Chemical (water, nitrogen, fat, ash and carbon) and physical (bone, muscle, adipose tissue, blood, skin, hair and offal) compositions of carcass and chemical composition of feedstuffs were estimated for farm animals at the very beginning of the twentieth century (Wolff Reference Wolff1895). Wolff (Reference Wolff1895) stands apparently as the first to adopt a factorial method to describe relatively and in detail the fate of dietary nitrogen, carbon and fat with consideration of intake, losses through faeces and urine and recovery as body fat and body flesh in the carcass.

Biological evaluation of dietary proteins was in the development stage at that time (e.g. Osborne et al. Reference Osborne, Mendel and Ferry1919). The concept of biological value of protein was borrowed from human nutrition and extended to animal studies presumably by Mitchell (Reference Mitchell1924) who, a few years later, hosted Kenneth Lyon Blaxter in his laboratory. This concept, still widely applied to approximate protein requirements of animals and humans, is based on direct determinations of the amount of nitrogen (N) in the faeces and in the urine, and indirect estimates of endogenous losses of N (Mitchell Reference Mitchell1924; Blaxter & Mitchell Reference Blaxter and Mitchell1948; Brody Reference Brody1999). For further details on the historical perspective of biological evaluation of proteins, the reader is referred to Mitchell (Reference Mitchell1952, Reference Mitchell1964).

The limiting effect of dietary proteins and amino acids, especially lysine and tryptophan, on growth was known before 1925 (Wolff Reference Wolff1895; Osborne & Mendel Reference Osborne and Mendel1912; McCollum et al. Reference McCollum, Simmonds and Pitz1917; Mitchell Reference Mitchell1918). Essential fatty acids had not been identified at that point in time, but unknown essential constituents were suspected in dietary fats and held responsible for growth performance (McCollum Reference McCollum1916). Utilization of body lipid reserves to support growth under feed restriction and the phenomenon of compensatory growth had already been demonstrated by Waters (Reference Waters1917).

Principles of bioenergetics along with the starch equivalent (SE) theory (considered further in the section on feed evaluation systems) were introduced into animal nutrition early in the twentieth century by Atwater (Reference Atwater1902), Armsby (Reference Armsby1903) and Kellner (Reference Kellner and Goodwin1905) (see also Wood & Yule Reference Wood and Yule1914; Halnan Reference Halnan1915; Nichols Reference Nichols1994). Unlike the chemical approach and the SE theory, bioenergetics gained in popularity despite evidence that dietary nutrients rather than energy stood as the basis of animal nutrition (McCollum Reference McCollum1916). Bioenergetics remains widely applied in animal science (Kleiber Reference Kleiber1975; Blaxter Reference Blaxter1989).

In bioenergetics, the factorial scheme is the most common way of describing the fate of energy intake and was adopted at the very beginning of energy requirement systems. Graphical representation of metabolizable energy (ME) requirements for maintenance and production (e.g. work and growth) was first proposed by Armsby (Reference Armsby1903), who did not, however, use equations to describe the linear segments. Moulton (Reference Moulton1918) also adopted the factorial approach and, unlike his contemporaries, discriminated between body protein and lipid gains in recovered energy.

Equations to estimate energy requirement of fasting animals were well established. Rubner (Reference Rubner, Markoff and Sandri-White1902) and, to a lesser extent, Armsby (Reference Armsby1903, Reference Armsby1917) popularized the surface law by showing that fasting metabolism is, in general, a function of the body surface (S; cm²) or the two-thirds power of body weight (S=kW ^2/3, where k and W are a scalar and body weight in g, respectively). From there, the surface law became a common way of representing energy requirements for maintenance and basal metabolism (Murray Reference Murray1914; Moulton Reference Moulton1918; Kleiber Reference Kleiber1937; Brody Reference Brody1945).

Unlike nutrition, mathematical modelling evolved later in the animal sciences. No differential and growth equations, simulation models, nor even regressions, were apparently being applied prior to 1910. Growth functions of Gompertz and Verhulst (i.e. logistic equation) were used in human population studies by actuaries and demographers (Gompertz Reference Gompertz1825; Verhulst Reference Verhulst1838; Winsor Reference Winsor1932), whereas the monomolecular (also referred to as the Mitscherlich equation) and saturation kinetic equations were confined to crop science and biochemistry, respectively (Mitscherlich-Königsberg Reference Mitscherlich-Königsberg1909; Hill Reference Hill1910; Michaelis & Menten Reference Michaelis and Menten1913). Although probable error (i.e. 0·67×standard deviation) was introduced presumably into animal nutrition in 1895 (Robinson & Halnan Reference Robinson and Halnan1912), statistics was confined mostly to the natural sciences and eugenics, and consisted of probable error, correlation, regression analysis, normal law assessment and the chi-squared test (Pearson Reference Pearson1920; Kevles Reference Kevles1985; Porter Reference Porter2004).

The period from 1910 to 1925 flourished with regard to many aspects of mathematical modelling in animal nutrition. An attempt to estimate milk yield from dairy cows using regression coefficients was proposed by Gavin in 1913 with the help of Mr G. U. Yule, a former assistant of Karl Pearson (Gavin Reference Gavin1913; Pearson Reference Pearson1920). Probably the first nutritionist and mathematician to work together, Wood & Yule (Reference Wood and Yule1914) stressed the usefulness of statistics in feeding trials and certainly contributed to introducing this branch of mathematics into animal nutrition.

Samuel Brody, one of the most influential scientists to have implemented mathematics in animal nutrition, arrived on the scene in the 1920s and published numerous bulletins on growth and development of farm animals (Brody & Ragsdale Reference Brody and Ragsdale1921; Ragsdale et al. Reference Ragsdale, Elting and Brody1926; Morgan Reference Morgan1960).

Concomitantly, the basis of allometry was taking place (Gayon Reference Gayon2000) and the equation y=bx ^c was proposed by Huxley (Reference Huxley1924), who used it to describe the differential growth rate between the chelae and remaining body parts of Fiddler crabs. Huxley (Reference Huxley1924) even hypothesized that the value of c adheres to the surface law and could equal two-thirds. This supposition of Huxley (Reference Huxley1924) hints that he had been inspired by Rubner (Reference Rubner, Markoff and Sandri-White1902) and used the equation of the surface law as a convenient tool to describe differential growth, later referred to as allometry (Huxley & Teissier Reference Huxley and Teissier1936).

The next three sections invite the reader to delve more deeply into the historical development of growth functions, feed requirement systems and animal response models.

From visual appraisal to meaningful equations: the development of growth functions and other time-related equations

Growth functions and other time-related equations are models where an outcome of interest (dependent variable, y) is determined using time, t, as the predictor (independent variable) taking the form y=f(t), where f represents some functional relationship. Growth functions are generally analytical solutions to differential equations that can be fitted by means of nonlinear regression analysis (Thornley & France Reference Thornley and France2007). These types of equations were introduced into animal science in the early 1920s to describe growth trajectory (sometimes currently referred to as ontogenetic growth), indicating that feed evaluation systems rather than growth modelling engrossed the mind of nutritionists. It is not surprising therefore that most of the scientists who introduced and developed animal growth equations were biologists rather than nutritionists per se.

Graphical representation of animal growth was current prior to 1925 where early fast growth rate, point of inflection and slow approach to final asymptotic weight were obvious based on visual appraisal of growth curves (e.g. Ritzman Reference Ritzman1917). However, mathematical descriptions of these curves were almost non-existent. The sigmoidal shape of the trajectory indicated that linear regression was not suitable for describing growth, unless small portions of the curve only are considered or data are transformed.

The description and prediction of growth using equations emerged in agriculture from two different directions: equations were either borrowed from human population studies or developed specifically for animals and plants. Since a large number of growth functions were proposed in the last century, only those that have been widely studied and applied in animal nutrition are discussed here. For a broader description of existing growth functions and theories, the reader is referred to Parks (Reference Parks1982), Ratkowski (Reference Ratkowski1990), Seber & Wild (Reference Seber and Wild2003) and Thornley & France (Reference Thornley and France2007).

Growth functions are presented here in the chronological order of their application in animal science. The logistic equation, developed by the mathematician Verhulst (Reference Verhulst1838), was applied to animals by Robertson (Reference Robertson1916, Reference Robertson1923), a mentor of Samuel Brody at the dawn of his outstanding career, and thereafter by Pearl (Reference Pearl1925) who described the growth of mammals, plants and yeast cells. Robertson (Reference Robertson1908) had originally applied the logistic to plants in studying autocatalysis.

The Gompertz equation (Gompertz Reference Gompertz1825) was first used as a growth function in animal science by Wright (Wright Reference Wright1926; Winsor Reference Winsor1932), a geneticist, who stated that growth curves of individual organisms display an asymmetrical S-shape which is better described by the equation log log (k/y)=a(b−x) than by the logistic. Wright (Reference Wright1926) never referred to Gompertz in his paper, but the equation he brought forward was, in reality, the linearized form of the Gompertz equation (cf. Wright Reference Wright1926; Winsor Reference Winsor1932). Two years later, Davidson (Reference Davidson1928) described the growth of Jersey cows using the Gompertz. He was arguably one of the first to note that the point of inflection of the Gompertz is fixed and corresponds to maximum asymptotic body weight divided by the base of natural logarithms (W _f/e). The Gompertz equation was used soon after to describe the growth of molluscs (Weymouth et al. Reference Weymouth, McMillin and Rich1931). Winsor (Reference Winsor1932) probably contributed to the popularization of the Gompertz equation in biology through his paper read at the US National Academy of Sciences.

Earlier in 1909, Mitscherlich-Königsberg (Reference Mitscherlich-Königsberg1909) proposed an equation with no accelerating phase to describe the effect of chemical fertilizers on crop yields. The growth response obeyed the law of diminishing returns, meaning that growth rate decreased continually and that the curve had no point of inflection. Wood & Yule (Reference Wood and Yule1914) referred to the law of diminishing returns in describing the relationship between liveweight gain and swede (rutabaga) intake in oxen, but did not mention explicitly whether they used the Mitscherlich-Königsberg equation. Weight gain as a function of feed intake had also been described using the law of diminishing returns by Jull & Titus (Reference Jull and Titus1928) and Hendricks (Reference Hendricks1931) in chickens. The Mitscherlich-Königsberg equation, also known as ‘monomolecular’ because of the equation's association with chemical reaction kinetics, is inadequate to describe the sigmoidal growth trajectory of juvenile animals with respect to time. Therefore, some scientists (e.g. Brody Reference Brody1945) brought the exponential and the monomolecular equations together to generate a curve having a sigmoidal shape. The monomolecular function is still used to represent the relationship between weight gain and energy intake in various farm animals (e.g. Darmani Kuhi et al. Reference Darmani Kuhi, Kebreab, Owen and France2001).

Although not a growth function per se, the simple Michaelis-Menten equation, which was intended originally for enzyme kinetics, has been used to describe weight gain of animals, effect of substrate on bacterial growth rate and fluxes of biochemicals in mechanistic models pertaining to ruminant and non-ruminant metabolism (Michaelis & Menten Reference Michaelis and Menten1913; Monod Reference Monod1942; Pirt Reference Pirt1975; López et al. Reference López, France, Gerrits, Dhanoa, Humphries and Dijkstra2000).

The rise of systemics – a collection of organized and interrelated concepts to explain causality – in science between 1920 and 1950 probably fostered the mechanistic representation of growth. Growth functions that attempt to include biologically meaningful parameters and circumvent concerns about a fixed point of inflection as assumed in the Gompertz and logistic equations arose mostly during this time period.

Pütter (Reference Pütter1920) conceptualized growth as anabolism prevailing over catabolism. The biologist von Bertalanffy (von Bertalanffy Reference von Bertalanffy1950; François Reference François1999), a pioneer of systemics, borrowed the concept proposed by Pütter (Reference Pütter1920) and formalized it (von Bertalanffy Reference von Bertalanffy1957; Ricker Reference Ricker, Hoar, Randall and Brett1979), incorporating various assumptions:

(1)

Here W is body weight, time t is measured as age, η and κ are constants of anabolism and catabolism, respectively, and the allometric exponent for anabolism m is dimensionless. Moreover, anabolism and catabolism are size-dependent (von Bertalanffy Reference von Bertalanffy1957). The equation has an asymptote, W _f, and a flexible point of inflection (Thornley & France Reference Thornley and France2007).

Prior to von Bertalanffy (Reference von Bertalanffy1957), Murray (Reference Murray1921) considered growth as a metabolic process and applied Eqn (1) to farm animals using a value of 2/3 for m. Murray (Reference Murray1921) did not refer to Pütter, nor differentiate between anabolism and catabolism in its mathematical expression, and therefore gave no biological interpretation of the parameters η and κ. However, it was assumed that metabolism adheres to the surface law and, for this reason, adopted the value two-thirds for m. Lotka (Reference Lotka1925), another pioneer of systemics, proposed a similar equation, but overlooked the metabolic processes in play.

Richards (Reference Richards1959), a botanist, starting with the von Bertalanffy equation, developed a flexible function that accommodates values of the allometric exponent for anabolism above unity:

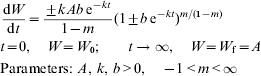
Here W is body weight, time t is measured as age, k is a rate parameter that corresponds to (1−m)κ in von Bertalanffy's equation, A is the upper asymptote, and the allometric exponent for anabolism m is dimensionless.

Richard's equation has four parameters and encompasses the von Bertalanffy, Gompertz, logistic and monomolecular growth functions. The inflection point can thus occur at various fractions of the maximum asymptotic weight. The function is highly flexible and accommodates various growth patterns (Black et al. Reference Black, Davies, Bray, Giles, Chapple, Danfaer and Lescoat1995; Thornley & France Reference Thornley and France2007).

Most of these growth functions are now routinely applied to predict animal growth (e.g. Mignon-Grasteau & Beaumont Reference Mignon-Grasteau and Beaumont2000). Furthermore these, along with chemical kinetic equations (e.g. the Michaelis–Menten equation), have been proved appropriate for describing complex dynamics and metabolic fluxes in recent mechanistic simulation models for pigs (Halas et al. Reference Halas, Dijkstra, Babinsky, Verstegen and Gerrits2004), poultry (Koehler et al. Reference Koehler, Pahle, Gruhn, Zander, Jeroch and Gebhardt1988), ruminants (Dijkstra et al. Reference Dijkstra, Neal, Beever and France1992) and fish (Lupatsch & Kissil Reference Lupatsch and Kissil2005), because they can exhibit a wide array of dynamic behaviour (May Reference May1976). For example, the Gompertz equation has been used to estimate protein growth of pigs, broiler chickens and turkeys (Gous et al. Reference Gous, Moran, Stilborn, Bradford and Emmans1999; Schinckel Reference Schinckel and Kyriazakis1999; Sakomura et al. Reference Sakomura, Longo, Oviedo-Rondon, Boa-Viagem and Ferraudo2005) as well as glucose oxidation in broiler chickens (Buyse et al. Reference Buyse, Geypens, Malheiros, Moraes, Swennen and Decuypere2004) and excretion of β-carotene by fish (Boyce et al. Reference Boyce, Murray and Peck2006). Variations of the von Bertalanffy equation have served to assess growth targets of fish in bioenergetic models (Cho & Bureau Reference Cho and Bureau1998; Lupatsch & Kissil Reference Lupatsch and Kissil2005). Finally, diminishing returns and sigmoidal functions were proposed as alternatives in current energy requirement systems to determine efficiencies of utilization of ME for maintenance, growth and milk production (Mercer et al. Reference Mercer, Flodin and Morgan1978; France et al. Reference France, Dhanoa, Cammel, Gill, Beever and Thornley1989; Kebreab et al. Reference Kebreab, France, Agnew, Yan, Dhanoa, Dijkstra, Beever and Reynolds2003).

Over the last century, various equations have been developed to estimate processes other than growth, such as digestion flow (Ewing & Smith Reference Ewing and Smith1917; Blaxter et al. Reference Blaxter, Graham and Wainman1956), milk yield (Blaxter & Ruben Reference Blaxter and Ruben1954a, Reference Blaxter and Rubenb), methanogenesis (Kriss Reference Kriss1930; Blaxter & Clapperton Reference Blaxter and Clapperton1965), volatile fatty acid (VFA) synthesis (Emery et al. Reference Emery, Smith and Huffman1956) and poultry egg production (Gavora et al. Reference Gavora, Liljedahl, McMillan and Ahlen1982; Yang et al. Reference Yang, Wu and McMillan1989). Hungate (Reference Hungate1966) also provided equations to estimate the rate of passage of food and fermentation in the rumen. These biological processes have been described either using time-related equations often formalized as differential equations or as functions of feed intake.

Ewing & Smith (Reference Ewing and Smith1917) showed discernment by considering the rate of passage of food residue in steers as a function of quality and amount of feed ration. They noticed the effect of size of feed particles on the rate of passage but they only included in their equation the dry matter content of the gastrointestinal tract and dry matter contents of the ration and faeces. Effects of volume of meal and gastrointestinal tract on the rate of passage of food residue were confirmed in humans a few decades later (Hunt & Spurrell Reference Hunt and Spurrell1951; Hunt & MacDonald Reference Hunt and MacDonald1954).

Effect of the interval between meals and state of emptiness of the proximate portions of the small intestine represented new variables to look at when computing the rate of passage of food residues in pigs, according to Laplace & Tomassone (Reference Laplace and Tomassone1970). The model of Blaxter et al. (Reference Blaxter, Graham and Wainman1956) was a preliminary step in that direction. It estimates rates of passage of dried grass in compartments of the digestive tract of sheep using differential equations. This time-dependent equation has been widely applied thereafter (Waldo et al. Reference Waldo, Smith and Cox1972; Baldwin Reference Baldwin1995). France et al. (Reference France, Thornley, Dhanoa and Siddons1985, Reference France, Gill, Dhanoa and Siddons1991a) examined existing mathematical models with reference to digesta flow kinetics and, inspired by the model of Blaxter et al. (Reference Blaxter, Graham and Wainman1956), extended their compartmental model to include supplementary compartments (e.g. caecum) with consideration for delays or time lags in the flow of materials.

Models became gradually more specific and attempted to predict rate of passage of particular feed constituents. For instance, Waldo et al. (Reference Waldo, Smith and Cox1972) represented the rates of passage and digestion of cellulose in the rumen. Ørskov & McDonald (Reference Ørskov and McDonald1979) and McDonald (Reference McDonald1981) proposed a mathematical model based on differential equations to estimate protein degradability in the rumen incorporating rate of passage of protein particles.

With reference to describing milk yield, the gamma function proposed by Wood (Reference Wood1967) has gained wide acceptance. This equation has many similarities to some of those suggested by Blaxter, a nutritionist, and Ruben, a mathematician (Blaxter & Ruben Reference Blaxter and Ruben1953, Reference Blaxter and Ruben1954a, Reference Blaxter and Rubenb), but Wood (Reference Wood1967) was apparently unaware of these previous comprehensive reports that were unpublished. The Wood equation is still commonly used for dairy cows and sheep (Grzesiak et al. Reference Grzesiak, Błaszczyk and Lacroix2006), but more mechanistic alternatives are available (e.g. Dijkstra et al. Reference Dijkstra, France, Dhanoa, Maas, Hanigan, Rook and Beever1997).

From hay equivalents to nutrient requirements: the development of feed evaluation systems

Feed evaluation systems are methods for describing the effect of the plane of nutrition (i.e. feed composition and feeding level) on animal performance (Dijkstra et al. Reference Dijkstra, Kebreab, Mills, Pellikaan, López, Bannink and France2007). Systems to evaluate feeds should predict with sufficient accuracy the performance of an animal based on knowledge of effects of body weight (or age), composition of biomass gain, activity, environment and rate of production and on knowledge of the amount of each feedstuff in the diet and its nutritive value (Baldwin Reference Baldwin1995). Since feed evaluation is concerned with quantitative prediction, feed evaluation systems comprise one or more equations and thus are models in themselves. A brief description of the development of feed evaluation or feed requirement systems is presented, with emphasis on energy evaluation in ruminants.

The initial development of feeding standards was by German workers, particularly Albrecht Thaer, the father of scientifically based agriculture in Germany. He developed the ‘hay value theory’ to express the nutritive value of a feed in relation to a standard feed, viz. ‘good meadow hay’. Based originally on weight changes in cattle fed with different feeds, hay values were subsequently based on the sum of ingredients extractable with water, alcohol, dilute acid and alkali. Although Thaer (Reference Thaer1809) was the first to put on record tables showing the relative values of different feeds, he was probably far more interested in the production of manure that, obviously in current intensive farming systems, has become a major issue as well, although not from a deficit (as in Thaer's days) but surplus point of view. Indeed, Thaer aimed for as much manure as possible (there was no artificial fertilizer at that time), so he wrote that an accurate knowledge of the nutritive value of feeds for animal production would enable the calculation of the quantity of manure the animals would produce on that feed.

Boussingault (Reference Boussingault1845) in France expressed the opinion that the N-containing compounds in the feed were the most important, drawing on observations that N-rich feeds such as lucerne and clover gave better milk production and horse muscle tissue reparation than traditional feedstuffs. Boussingault (Reference Boussingault1845) thus devised tables comparing feeds on their N content, but at the same time stated that information on other substances was also required.

Henneberg & Stohmann (Reference Henneberg and Stohmann1864) devised a scheme for routine description of animal feedstuffs referred to as Weende analysis, named after the Weende Experimental Station in Germany. Weende analysis is still used and is, or has been, the basis of various feed evaluation systems. In this analysis, the organic matter (OM) is analysed as well as crude protein (CP; N×6·25), crude fat (CFAT) and crude fibre (CF). The remainder of the OM is calculated by difference and termed nitrogen-free extract (NFE). Tyler (Reference Tyler1975) reviewed in detail the development of early feeding standards based on Weende analysis.

The next step was recognition that not all feed components are digestible in the gastrointestinal tract. Digestibility is a measure of disappearance of feed constituents following their passage through the gastrointestinal tract and corresponds to the intake minus the excreted (solid form). Wolff (Reference Wolff1874) devised standards based on digestible CP (DCP), digestible CFAT (DCFAT) and digestible carbohydrates. The digestible carbohydrates may be assumed to be the sum of digestible CF (DCF) and digestible NFE (DNFE). Lehmann (Reference Lehmann1899) further modified the standards of Wolff (Reference Wolff1874) in view of the concepts that, firstly, food has two functions to fulfil, viz. maintenance and production and, secondly, animals have a limited capacity for dry matter intake.

Principles of bioenergetics were introduced into feed evaluation systems at the turn of the twentieth century. Atwater & Bryant (Reference Atwater and Bryant1900) proposed elements of a system comprising physiological fuel values (PFV) to measure food energy in human nutrition. The PFV is based on average heat combustion values (gross energy (GE) of 5·7, 9·4 and 4·2 kcal/g of protein, fat and carbohydrate, respectively. Assuming fixed digestibility coefficient values of 0·91, 0·96 and 0·96 for protein, fat and carbohydrate, respectively, and accepting a fixed value of 1·25 kcal/g of dietary protein as energy losses in urinary N-containing compounds, PFV is calculated as:

This procedure imposes an average GE content and constant digestibility on all dietary proteins, fats and carbohydrates in foods for human nutrition. Determination of the heat of combustion for each food is thus not required. The system also assumes absence of interactions in digestibility between different components and different feed ingredients. As described previously, the most important, but also most variable, difference between feeds and feed components is digestibility in the gastrointestinal tract. For farm animals, the combination of proximate analysis and digestible nutrient values (all in g/kg) combined with Atwater's PFV scheme resulted in the total digestible nutrients (TDN; g/kg) system:

In the TDN system, all nutrients are scaled to the energy equivalent of carbohydrate. Although the term ‘total digestible nutrients’ implies that digestion losses only are taken into account, the energetic value for digestible protein is actually adjusted for losses in urine (see Maynard Reference Maynard1953, for a full discussion on the meaning of TDN). Thus, particularly in non-ruminant animals having minimal fermentation gas losses, TDN is not a measure similar to digestible energy (DE) but to ME. TDN requirements of animals are estimated by summing tabular values of TDN required for maintenance (as a function of body weight (W); kg), TDN required per unit weight gain, TDN required per unit of fat-corrected milk (FCM; kg/day), etc.

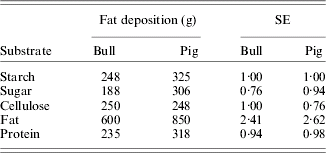
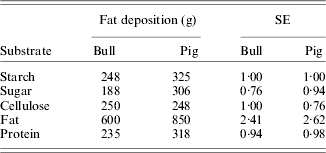
In ruminants, it was soon recognized that TDN from forages supported lower rates of production than TDN from concentrates. For example, 1 kg of Lehmann's total nutrients (similar to TDN, but factor 2·25 replaced with 2·3) in straw and in concentrates resulted in net energetic production values of 1112 and 2171 kcal, respectively (Kellner & Becker Reference Kellner and Becker1966). Part, but not all, of this discrepancy is related to higher losses of methane and fermentation heat with roughages. As a result, net energy (NE) systems originated based on studies by Kellner (Reference Kellner and Goodwin1905) in Germany on the fat-producing potential of feeds and on studies by Armsby (Reference Armsby1903, Reference Armsby1904) in USA using respiration calorimeters. Armsby (Reference Armsby1904) recognized that energy losses occurred in addition to the losses accounted for in arriving at ME. He measured the heat increment in a respiration calorimeter as the difference in heat resulting from ingested feed at two intake levels. The NE was calculated as ME minus the heat increment. The NE system proposed by Armsby did not gain wide acceptance, however. Whereas Armsby measured NE near maintenance, Kellner obtained the net fat-producing potential of pure substrates or feeds on top of a maintenance ration by measuring the carbon and nitrogen balance in adult oxen and other farm animals. Fat-producing power was expressed in terms of the kg of starch that would be required to produce the same amount of fat as 100 kg of the test feed and these values were called SEs (per kg). Fat production and SE in oxen and pigs of digestible pure substrates are presented in Table 1. Based on these values, the SE of the feeds for cattle is calculated from the Weende components as:

Table 1. Fat deposition and starch equivalents (SEs) of 1 kg of digestible substrates for mature bulls and pigs (Kellner & Becker Reference Kellner and Becker1966)

The value of 2·41 for DCFAT depends on the type of feed and varies between 1·91 and 2·41. In addition, a factor that ranges from 0·30 to 1·00 is applied to correct for ‘work of digestion’ related to the fibre content. SE requirements of animals are estimated by summing SE required for maintenance (as a function of W), weight gain, FCM, etc. For example, the SE required for maintenance and milk production of dairy cattle in the Dutch SE system is calculated as (Van der Honing & Alderman Reference Van der Honing and Alderman1988):

The SE system and systems derived from it (fodder unit systems) have been used widely in many European countries.

However, the development of feed evaluation systems has been influenced to a greater extent by bioenergetics – the quantitative study of the energy exchanges induced by metabolic processes in living organisms to stay alive, to grow and to reproduce (Nelson & Cox Reference Nelson and Cox2000). Although they were not concerned primarily with developing feeding standards, it is worth noting the contributions of Brody and Kleiber which provided substantial information on animal bioenergetics that subsequently proved most useful in formulating feeds. Their classic books (Brody Reference Brody1945; Kleiber Reference Kleiber1961, Reference Kleiber1975) showed that these scientists went beyond their predecessors and contemporaries in explaining energy utilization in farm animals. Brody (Reference Brody1945) played a major role by describing extensively the energetic efficiencies of growth, work and production of milk and eggs with numerous illustrations, tables and equations. Kleiber (Reference Kleiber1932, Reference Kleiber1937, Reference Kleiber1961) suggested that basal metabolism is more related to the 3/4 than to the 2/3 power of body weight, and facilitated determination of true digestibility by developing an isotopic technique for assessing endogenous loss of nutrients from the animal.

Blaxter & Graham (Reference Baxter, Kleiber and Black1955), influenced by Brody and Kleiber, moved from the SE theory to the NE concept based on calorimetry formerly proposed by Armsby (Reference Armsby1903). Partition of energy with consideration of losses through faeces, urine, gas and heat (specific dynamic action) in order to estimate ME and NE was represented using differential equations by Blaxter & Graham (Reference Baxter, Kleiber and Black1955).

Not all feeding systems considered the effect of metabolizability of the diet (q; ME/GE) on the efficiency of utilization of feedstuffs. With reference to the TDN system, the TDN of all feedstuffs is assumed to be used equally efficiently for maintenance and lactation, regardless of TDN composition. Similarly, in the various SE systems, it is assumed that efficiencies of use of SE for maintenance, growth and milk production are proportional to each other. However, the research of Blaxter & Wainman (Reference Blaxter and Wainman1961) in particular, indicated that efficiency of ME utilization for NE as maintenance, milk or body weight gain depends on q. These efficiencies are calculated nowadays using the coefficients k _m, k _l and k _g for maintenance, lactation and body weight gain, respectively. Linear regression equations that relate these efficiency coefficients to q are presented graphically in Fig. 1 based on AFRC (1993). More recently, linear regression equations to analyse energy balance data have been evaluated and compared with nonlinear alternatives using a large data set (Kebreab et al. Reference Kebreab, France, Agnew, Yan, Dhanoa, Dijkstra, Beever and Reynolds2003). The monomolecular equation with a constrained fasting metabolism value was preferred based on statistical and biological reasons. Application of the monomolecular to obtain estimates of maintenance requirements and efficiency coefficients based on data for cows in the late 1960s and early 1970s appeared to differ from those based on data from the 1990s. This probably reflects genetic differences in body composition of cows or in true efficiency of nutrient utilization.

Fig. 1. Efficiency of utilization of metabolizable energy (ME) for maintenance (k _m), lactation (k _l) and body weight gain (k _g) in relation to the metabolizability (q; ME/GE) of the diet.

The concept of variable efficiency of ME to NE for various purposes (maintenance, lactation, growth, etc.) has been adopted in most current energy systems in Europe. The common basis is the calculation of the ME of feeds. A number of systems use the equation from Schiemann et al. (Reference Schiemann, Nehring, Hoffmann, Jentsch and Chudy1971) or equations derived from it to estimate the ME content (kcal/kg) of feeds for cattle:

Owing to the limits associated with conventional digestibility experiments (e.g. time and resource requirements), Tilley & Terry (Reference Tilley and Terry1963) developed a simple in vitro technique and described the relationship between in vivo and in vitro digestibility using linear regression. Their rapid method has been used widely and has served as a basis to measure, for example, gas production in vitro in ruminants (Menke et al. Reference Menke, Raab, Salewski, Steingass, Fritz and Schneider1979). The system comprises incubation of forage samples in a buffered ruminal inoculum for 48 h followed by 24 h digestion in acid pepsin. The in vivo digestible OM at maintenance level (DOMD; g/kg) is calculated from this in vitro digestibility using feed-specific regression equations based on a comprehensive in vivo database of forage digestibilities. The GE content and the ME/DE ratios are quite constant for roughages and therefore the ME content of forages can be calculated as:

Actual ME available to the animal depends on level of feeding. High feeding levels decrease retention time in the gastrointestinal tract and thus reduce the coefficient of digestibility, on average 0·03 units per feeding level. At the same time, methane and urine energy losses as a fraction of the GE decrease at higher levels, on average 0·02 units per feeding level. Therefore, the decline in q at higher feeding levels is generally assumed to be 0·01 units per feeding level (Van Es Reference Van Es1975). ME values of feeds in feed tables are usually presented as a single value applicable to maintenance level and corrections for higher feeding levels need to be made when calculating requirements. For example, in the UK system the correction factor (C) varies with feeding level (L, multiple of maintenance requirements) according to (AFRC 1993):

The factor 0·018 is derived from the 0·01-unit value at a mean q of 0·57. The new Feed into Milk system in the UK, however, assumes a small and fixed correction factor of 0·02 to adjust ME values measured at maintenance independently of feed intake level (Thomas Reference Thomas2004). An independent comparison of various energy evaluation systems against grass-based diets fed to dairy cattle did not, however, show large improvements in prediction accuracy of the Feed into Milk system as compared with the AFRC ME system (Dijkstra et al., Reference Dijkstra, Kebreab, Bannink, Crompton, López, Abrahamse, Chilibroste, Mills and Francein press).

Energy requirements are calculated based on a factorial approach, summing the various requirements for maintenance, growth, pregnancy and milk production. For example, the requirements for maintenance and milk production (NE_mm; kcal/day) in the Dutch NE system defined at a feeding level of 2·38 (15 kg FCM/day) are (Van Es Reference Van Es1978):

where W is in units of kg.

Similar to the UK system, the requirements at other feeding levels are calculated using a correction factor of 0·018 per feeding level. Others have also adopted a factorial approach based on principles of bioenergetics to determine nutrient requirements (NRC 1998; Fox et al. Reference Fox, Tedeschi, Tylutki, Russell, Van Amburgh, Chase, Pell and Overton2004).

The factorial approach was illustrated by graphical representation involving linear segments early in the twentieth century (Armsby Reference Armsby1903) and such a representation apparently fell into oblivion for almost 60 years. The use of linear segments to describe the relationships between animal responses (e.g. retained energy and weight gain) and various inputs (e.g. energy intake and lysine intake) with consideration of requirements below and above maintenance was revived by Blaxter & Wainman (Reference Blaxter and Wainman1961). Unlike Armsby (Reference Armsby1903), Blaxter & Wainman (Reference Blaxter and Wainman1961) had access to advanced regression methods to describe the linear segments statistically.

More mathematically sophisticated methods for formulating diets and rations appeared in the 1960s, along with the development of computers and the increase in number of available nutrient sources. Linear programming (LP) became popular for computing the best combination of ingredients to meet the nutrient requirements of animals at the least cost (Dent & Casey Reference Dent and Casey1967; Glen Reference Glen1987). A limitation of the LP approach was the need to solve the model every time the ration needed to be changed. In order to overcome this drawback, Glen (Reference Glen1980) modified the LP method by describing the relationship between cost and ME of the ration using a piecewise linear analysis and solving for the least cost ration with differential equations. Flexible formulation systems using LP were also developed in which users can interact with the program and explore different scenarios (Crabtree Reference Crabtree1982). For further details of the use of LP in ration formulation, see Thornley & France (Reference Thornley and France2007).

With reference to the development of feeding systems based on rates of protein and lipid deposition, several modelling studies were initiated in the 1970s aimed at describing nutrient partitioning as a function of protein and energy intake. Wenk & Schürch (Reference Wenk, Schürch, Menke, Lantzsch and Reichl1974) were probably the first authors to observe an upper limit to retained protein in pigs (Whittemore & Fawcett Reference Whittemore and Fawcett1976). In a symposium held in 1973, they reported a levelling or plateau of protein deposition (later referred to as PD_max) even though energy intake was enhanced. They noticed also that lipid deposition kept increasing after animals have reached PD_max. Further studies such as those from Black & Griffiths (Reference Black and Griffiths1975) led to the concept of protein- and energy-dependent phases in protein deposition rate (PD). These phases were proposed to designate the portion of the curve where PD increases linearly with protein and energy intake, respectively. In the protein-dependent phase, PD is unaffected by energy intake, whereas in the energy-dependent phase, PD is not affected by protein intake (Black & Griffiths Reference Black and Griffiths1975). However, the concept of protein- and energy-dependent phases in body protein deposition is not applicable in some other animal species (e.g. Gerrits et al. Reference Gerrits, Tolman, Schrama, Tamminga, Bosch and Verstegen1996).

PD was a topic of interest in animal nutrition prior to Wenk & Schürch (Reference Wenk, Schürch, Menke, Lantzsch and Reichl1974). An increase in daily protein deposition in small growing pigs followed by a decline in larger animals had been previously reported by Thorbek (Reference Thorbek, Blaxter, Kielanowski and Thorbek1969) and Oslage & Fliegel (Reference Oslage, Fliegel and Blaxter1965), respectively. Oslage & Fliegel (Reference Oslage, Fliegel and Blaxter1965) acknowledged that they were not the first researchers to observe a decrease in daily protein deposition in older animals, but they omit to cite earlier references.

Modelling nutrient deposition (output) as a function of energy or protein intake (input) by means of regression using the linear-plateau concept (see the next section) or quadratic equations remains a common way of estimating nutrient requirements of farm animals (Garrett Reference Garrett, Moe, Tyrrell and Reynolds1987; NRC 1996, 1998). However, Morgan et al. (Reference Morgan, Mercer and Flodin1975) showed that a saturation kinetic equation was more flexible for representing such input–output relationships.

It has been shown that feed evaluation systems and animal growth models based on bioenergetics have limitations (Bajer Reference Bajer, Whitledge and Hayward2004; Dijkstra et al. Reference Dijkstra, Kebreab, Mills, Pellikaan, López, Bannink and France2007). For example, the concept of energy requirement for maintenance remains debatable and affected by body composition and feeding level (Le Dividich et al. Reference Le Dividich, Vermorel, Noblet, Bouvier and Aumaitre1980; Bureau et al. Reference Bureau, Kaushik, Cho, Halver and Hardy2002). As a consequence, several modelling efforts have moved away from bioenergetics and returned to more nutrient or biochemically oriented approaches (e.g. Machiels & Henken Reference Machiels and Henken1986; Halas et al. Reference Halas, Dijkstra, Babinsky, Verstegen and Gerrits2004) just as Wolff (Reference Wolff1895) was doing more than a century ago. Some nutritionists (e.g. Maynard Reference Maynard1937) remained primarily concerned with nutrients and metabolites. Even in his chapter on bioenergetics in the sixth edition of his classic book, Maynard (Maynard & Loosli Reference Maynard and Loosli1969) insisted on biochemical molarities and ATP rather than, for instance, ME and the calorie or joule. Currently, nutrient-based models that describe animal responses and nutritional requirements by considering nutrients and metabolites stand as more biologically sound alternatives to bioenergetic models, as animals metabolize chemicals rather than energy per se.

Concern over the adequacy of present feed evaluation systems has been expressed by several authors (e.g. Dijkstra et al. Reference Dijkstra, Kebreab, Bannink, France and Lopez2005). In particular, current systems are devised to meet animal requirements rather than to predict animal response.

From description to prediction: the development of animal response models

Apart from meat, milk and egg production, animal responses of interest prior to 1950 were growth of the whole animal and different body parts or organs, the latter being also referred to as differential or relative or allometric growth (Murray Reference Murray1921; Huxley Reference Huxley1931; Huxley & Teissier Reference Huxley and Teissier1936; Brody Reference Brody1945). Responses were expressed generally as a function of time, size of the animal, or both. Modelling animal response moved gradually towards more explanatory variables (e.g. ME intake and protein deposition) concomitantly with the progress made in science and technology. Nowadays, animal response models may be defined as mechanistic systems designed to simulate responses to intake of nutrients with consideration of the synthesis and utilization of metabolites (Dijkstra et al. Reference Dijkstra, Kebreab, Mills, Pellikaan, López, Bannink and France2007). This section looks at the development of animal response models and attempts to illustrate, among other things, how animal nutritionists needed to consider other scientific disciplines in order to progress.

Three main approaches have been adopted over the last century to describe and predict animal responses (Fig. 2). These were introduced to varying degrees in the previous sections. Each approach has its own method of representing a system and relies more or less exclusively on particular branches of mathematics. The classification in Fig. 2 is somewhat arbitrary since numerous variations and hybrid models exist in the literature. For instance, bioenergetics along with nutrient-based approaches are often mixed within the same model (NRC 1998) or include nonlinear regression as well as stoichiometric equations (Machiels & Henken Reference Machiels and Henken1986).

Fig. 2. A classification of animal response models. System descriptions (biological trend, bioenergetics, nutrient-based), approaches (curve fitting, factorial, compartmental) and mathematics (growth functions, regression, differential and stoichiometric equations) are sometimes mixed within a model (hybrid model).

Prior to 1970, biological trends or response curves (e.g. weight gain) to feeding level, time or other dependent variables were considered simply linearly or sigmoidally (Almquist Reference Almquist1953; Westerfield Reference Westerfield1956). Curnow (Reference Curnow1973) popularized the linear-plateau response curve and showed its relevance in animal nutrition by applying it to the description of egg production of chickens fed with varying amounts of methionine. The linear-plateau model has been used widely, especially within the factorial framework, along with linear and sigmoidal equations to predict animal responses (Mercer Reference Mercer1980; ARC 1981; Black et al. Reference Black, Davies, Bray, Giles, Chapple, Danfaer and Lescoat1995; NRC 1998).

The factorial approach is common in bioenergetic and some nutrient-based models but another approach, namely compartmental analysis, was introduced into animal nutrition over half a century ago. Compartmental analysis subdivides a given level of organization (e.g. whole-animal, tissue and cell levels) into different compartments or pools (e.g. amino acids in the blood, and intracellular glucose). Pools are referred to as state variables (i.e. a quantity that defines the size of the pool at a given point in time) and can be under steady state (e.g. blood volume in mature farm animals) or non-steady state (e.g. absolute protein content in a growing animal). Flows of substrates (e.g. lysine and metabolites) between pools are represented as terms within differential equations which are based ideally on principles of stoichiometry and saturation kinetics. The compartmental approach overcomes to a certain extent the lack of flexibility and theoretical basis associated with the underlying assumptions of the factorial method (AFRC 1991; Beever et al. Reference Beever, France, Alderman, Theodorou and France2000) but can require comprehensive data sets.

Compartmental analysis has been common in physiological and pharmacokinetic studies with tracers since 1950, especially to study drug distribution in the body, nutrient metabolism and protein turnover (Mazanov & Nolan Reference Mazanov and Nolan1976; Zierler Reference Zierler1981; Waterlow Reference Waterlow2006). Glucose turnover in animals was measured using ¹⁴C-labelled glucose as early as 1950 and the investigators were assuming the existence of three pools, namely body (i.e. extravascular), plasma and red blood cells (Feller et al. Reference Feller, Strisower and Chaikoff1950). However, dynamic transactions between pools were apparently not represented using differential equations before 1955 (Baxter et al. Reference Baxter, Kleiber and Black1955; Steele et al. Reference Steele, Wall, de Bodo and Altszuler1956). The simple model proposed by Bolie (Reference Bolie1961) on blood glucose regulation influenced modelling studies on glucose-insulin kinetics and likely fostered compartmental analysis of glucose metabolism (e.g. Bergman et al. Reference Bergman, Ider, Bowden and Cobelli1979; Cobelli et al. Reference Cobelli, Federspil, Pacini, Salvan and Scandellari1982).

A rudimentary form of the compartmental approach was applied in animal nutrition by Blaxter et al. (Reference Blaxter, Graham and Wainman1956) who subdivided the overall processes of passage of dried grass in ruminants into four compartments: rumen, abomasum, duodenum and faeces. Flows of digesta were described using differential equations as mentioned previously. Prior to Blaxter et al. (Reference Blaxter, Graham and Wainman1956), Armsby (Reference Armsby1917, p. 182) had proposed a scheme of nutrient metabolism which adheres to the compartmental approach, but he provided no equations to describe transactions between pools.

Inspired by a compartmental simulation model of brain metabolism (Garfinkel Reference Garfinkel1966), Baldwin & Smith (Reference Baldwin and Smith1971) further introduced the approach into animal nutrition and were the first to propose a metabolic simulation model at the whole-animal level. The model of Baldwin & Smith (Reference Baldwin and Smith1971) was dynamic and included differential equations based on principles of saturation kinetics and stoichiometry. Their model assumed that blood flow rate limits the utilization of blood metabolites. They did not represent explicitly (i.e. using equations) the effect of feeding on the concentration and utilization of these metabolites. Effects of feeding on rates of utilization of metabolites was accounted for by Gill et al. (Reference Gill, Thornley, Black, Oldham and Beever1984), who proposed a series of differential equations to simulate nutrient metabolism in growing sheep.

In addition to glucose metabolism (Feller et al. Reference Feller, Strisower and Chaikoff1950; Steele et al. Reference Steele, Wall, de Bodo and Altszuler1956; Bolie Reference Bolie1961; Kronfeld et al. Reference Kronfeld, Ramberg and Shames1971), tracer studies and compartmental analysis with further considerations of nutritional effects were conducted on ruminants to assess nitrogen metabolism (Nolan & Leng Reference Nolan and Leng1972) and the production of VFA and methane (Gray et al. Reference Gray, Weller, Pilgrim and Jones1966; Leng & Brett Reference Leng and Brett1966; Weller et al. Reference Weller, Gray, Pilgrim and Jones1967; Murray et al. Reference Murray, Bryant and Leng1975, Reference Murray, Bryant and Leng1976). Production of VFA using a three-pool scheme, similar to the compartmental analysis of steroids metabolism proposed by Vande Wiele et al. (Reference Vande Wiele, MacDonald, Gurpide, Lieberman and Pincus1963), was assessed apparently for the first time by Bergman et al. (Reference Bergman, Reid, Murray, Brockway and Whitelaw1965) with labelled acetate, propionate and butyrate in sheep. Extension of compartmental models along with their mathematical solutions was suggested for tracer kinetic studies on protein turnover in animals and served to circumvent the need to measure the specific radioactivity of the precursor pool (France et al. Reference France, Calvert, Baldwin and Klasing1988).

The first computer-simulated models using a compartmental approach with sometimes up to nine pools were published after 1970 with reference to ruminants (Baldwin & Smith Reference Baldwin and Smith1971; Morris et al. Reference Morris, Baldwin, Maeng and Maeda1975; Mazanov & Nolan Reference Mazanov and Nolan1976). An attempt to describe a whole agricultural production system was made by Rice et al. (Reference Rice, Morris, Maeda and Baldwin1974) who proposed an extensive model giving consideration to forage growth and intake as well as ruminant digestion and metabolism. A more recent and noteworthy example is the grassland simulator by Thornley (Reference Thornley1998), which comprises plant, animal, soil and water sub-models.

Increasing the number of compartments gives concerns about mathematical formalization and interpretation. To resolve these issues, unifying mathematical analyses and procedures to identify critical compartments have been proposed to describe, among others, mineral metabolism and VFA production (e.g. Boston & Weber Reference Boston and Weber1984; France et al. Reference France, Gill, Dhanoa and Siddons1987a, Reference France, Siddons, Dhanoa and Thornley1991b; Schneider et al. Reference Schneider, Boston and Leaver1987). Moreover, computer simulation software, which is virtually indispensable to modellers using the compartmental approach, has become available (e.g. Boston et al. Reference Boston, Greif and Berman1981, Reference Boston, Granek, Sutton, Weber, Greif and Zech1986; Baldwin Reference Baldwin1995; Kebreab et al. Reference Kebreab, Mills, Crompton, Bannink, Dijkstra, Gerrits and France2004).

Compartmental models have been designed for a wide variety of purposes in animal nutrition since 1980: (i) to simulate the metabolism of nutrients in sheep (Gill et al. Reference Gill, Thornley, Black, Oldham and Beever1984), pigs (Black et al. Reference Black, Campbell, Williams, James and Davies1986), pre-ruminant calves (Gerrits et al. Reference Gerrits, Dijkstra and France1997), dairy cows (Baldwin et al. Reference Baldwin, France and Gill1987a, Reference Baldwin, Thornley and Beeverb, Reference Baldwin, France, Beever, Gill and Thornleyc) and beef cattle (France et al. Reference France, Gill, Dhanoa and Siddons1987b), with sometimes special emphasis on the dynamics of microbial populations (e.g. Dijkstra et al. Reference Dijkstra, Neal, Beever and France1992; Dijkstra Reference Dijkstra1994; Baldwin Reference Baldwin1995) and metabolic processes in the rumen (e.g. France et al. Reference France, Thornley and Beever1982); (ii) to calculate the uptake and partition of amino acids in the mammary gland or other tissues (e.g. Baldwin Reference Baldwin1995; France et al. Reference France, Bequette, Lobley, Metcalf, Wray-Cahen, Dhanoa, Backwell, Hanigan, MacRae and Beever1995); (iii) to describe feed degradation in the rumen (e.g. Dhanoa et al. Reference Dhanoa, France, Siddons, López and Buchanan-Smith1995); and (iv) to predict voluntary forage intake (e.g. Imamidoost & Cant Reference Imamidoost and Cant2005). Given increasing concerns about greenhouse gases, models have been developed to estimate methane production from digestive processes in ruminants (e.g. France et al. Reference France, Dhanoa, Theodorou, Lister, Davies and Isac1993; Mills et al. Reference Mills, Dijkstra, Bannink, Cammell, Kebreab and France2001; Kebreab et al. Reference Kebreab, Mills, Crompton, Bannink, Dijkstra, Gerrits and France2004). The use of compartmental analysis to simulate whole-animal or specific tissue responses is less common in non-ruminants, and occurred later in fish (Machiels & Henken Reference Machiels and Henken1986; Conceicão et al. Reference Conceição, Verreth, Verstegen and Huisman1998), pigs (Pettigrew et al. Reference Pettigrew, Gill, France and Close1992; Halas et al. Reference Halas, Dijkstra, Babinsky, Verstegen and Gerrits2004) and poultry (Koehler et al. Reference Koehler, Pahle, Gruhn, Zander, Jeroch and Gebhardt1988).

One of the animal responses that has received much attention over the last half-century is voluntary feed intake (VFI). Inability to eat sufficient amounts of feed to satisfy animal requirements results in lower production levels in domesticated farm animals or failure to survive in wild habitats. A large amount of research has therefore been devoted to the study of control of feed intake and choices made when various feed sources are available (Forbes Reference Forbes1995).

Feed intake, which was based firstly on energy requirements for maintenance and growth as discussed in previous sections, is often deduced from the DE content of diets (e.g. ARC 1981; NRC 1998). Headley et al. (Reference Headley, Miller, Ullrey and Hoefer1961) considered energy intake (EI) as a function of body weight (W) and used the monomolecular equation to describe the relationship between the two variables. Thereafter, Cole et al. (Reference Cole, Duckworth and Holmes1967) proposed an allometric equation where EI became a function of metabolic body weight (EI=bW ^c). The latter form is still widely applied in animal nutrition (e.g. NRC 1998).

The effect of numerous exogenous (e.g. temperature and stocking density) and endogenous (e.g. genotype and gender) factors on VFI was increasingly recognized (Braude Reference Braude1967; NRC 1987; Forbes & Blundell Reference Forbes, Blundell, Forbes, Varley and Lawrence1989; Riley Reference Riley, Forbes, Varley and Lawrence1989) and the prediction of VFI moves concomitantly towards more explanatory models and theories (e.g. NRC 1987; Kyriazakis Reference Kyriazakis, Cole, Wiseman and Varley1994). For instance, different equations were proposed for predicting VFI as a function of temperature (Verstegen et al. Reference Verstegen, Brascamp and Van der Hel1978; Forbes Reference Forbes1995; NRC 1998), life stage (NRC 1998), energy stored in the body (Parks Reference Parks1982), season (Iason & Mantecon Reference Iason and Mantecon1991) and rates of protein and lipid deposition (Whittemore et al. Reference Whittemore, Kerr and Cameron1995). In addition, VFI was viewed from the short-term perspective (individual meal patterns) and from the long-term perspective. In ruminants, prediction of feed intake is based on two different quantitative theories. The first theory, developed over more than three decades, assumes that animals eat a certain amount of feed that will meet nutrient requirements unless some limiting factor prevents them from achieving this (Hubbell, Reference Hubbell1971). The main constraint in ruminants is assumed to be the limitation of forage intake by rumen capacity. In the other theory, more than one factor affecting intake is simultaneously taken into account and feed intake is controlled by a process of optimization of factors (e.g. Poppi et al. Reference Poppi, Gill and France1994). The reader is referred to Yearsley et al. (Reference Yearsley, Tolkamp and Illius2001) for a review of food intake models in animal nutrition.

The last aspect of animal response modelling covered in the present review relates to body composition, but is also relevant to milk composition. Predicting the composition of biomass gain is one of the major subjects of attention in animal nutrition and production because of increasing concern about product quality (e.g. fatness, fatty acid composition and bioaccumulation of various constituents) (Hocquette et al. Reference Hocquette, Ortigues-Marty and Vermorel2001). The importance of assessing meat quality in animal production and addressing the requirements of specific markets was actually stressed more than 60 years ago by McMeekan (Reference McMeekan1941) who recognized the technical difficulty, high cost and time requirement associated with chemical analysis and insisted on the need to develop indices of composition, i.e. mathematical equations. McMeekan (Reference McMeekan1941) proposed linear regression equations to predict contents of not only body fat, but also muscle and bone in bacon pigs. Equations were of the form Y _i=β₀+β₁x _i where Y _i is the ith fitted value of the outcome (i.e. skeleton, muscle or fat) in units of g, β₀ is the intercept, β₁ is the slope and x _i is the ith value of a given predictor (e.g. the length of the carcass). McMeekan (Reference McMeekan1941) overlooked the effect of body weight on carcass composition. Moreover, he did not describe body composition using allometric equations (y=bx ^c) even though, in his days, the concept of allometry was commonly applied in biology and animal nutrition to describe the rate of change between different anatomical characteristics of an organism (see the section ‘Mathematical modelling and animal nutrition before 1925’ and Gayon Reference Gayon2000). Furthermore, the allometric equation had already been used in animal science to examine the rate of fat deposition in different body parts of poultry (Lerner Reference Lerner1939). Almost 30 years after McMeekan (Reference McMeekan1941), Kotarbińska (Reference Kotarbińska1969) related body protein to fat-free lean mass and body water to body protein using linear regressions of allometric form. Kotarbińska (Reference Kotarbińska1969) also related body ash to body protein assuming an isometric (Y _i=β₀+β₁x _i) rather than an allometric relationship. Such relationships still prevail in estimating body composition of farm animals (Pomar et al. Reference Pomar, Harris and Minvielle1991; de Lange et al. Reference de Lange, Morel and Birkett2003).

From looking back to looking forward

Use of growth functions will most probably remain widespread in animal nutrition modelling. These functions along with chemical kinetic equations often stand as candidate tools in nutrition modelling because of the almost universal asymptotic responses in biology and their capability to describe different behaviour at various levels of organization (whole-animal, tissue, cell, etc.) (Westerfield Reference Westerfield1956; May Reference May1976). However, the high level of aggregation inherent in growth functions impairs their ability to represent causality in growth processes. These relatively simple equations should be used cautiously by considering their underlying assumptions and their selection should be based on sound statistical inference (Ratkowski Reference Ratkowski1983). Until now, history has proved wrong the prediction of Williams (Reference Williams, Solomon and Walter1977) that models based on differential equations will be replaced. On the contrary, the calculus has found a wide variety of applications in modern animal nutrition and other fields of biology, and continues to be the best alternative for describing the dynamics of a system.

Models based on the factorial approach to nutrient or energy utilization are still published and suggest that animal nutrition remains in the adoptive/dissemination phase (Johnson et al. Reference Johnson, Ferrell and Jenkins2003). The approach has hardly proposed revolutionary and original concepts over the last century. In contrast, simulation models based on a compartmental analysis, although sometimes more complex, have much to offer for they can be less aggregated and more flexible by considering different levels of organizations. They are at the same time capable of addressing specific outputs of direct interest (e.g. content and composition of milk fat and protein). Furthermore, their level of aggregation allows incorporation of new concepts and data continuously emerging from research at lower aggregation levels, thus enabling the essential link between experimental and modelling research.

Animal response models need to be adapted further if increasing concerns about product quality, traceability of feed ingredients and animals, environmental sustainability and climate change are to be addressed effectively. Access to simulation models enabling prediction of growth, body composition, feed requirements and production costs for various scenarios (e.g. effects of global warming on cereal supplies and, unavoidably, feed ingredient costs) could help agriculture improve its efficiency, face uncertainties and meet further the expectations of consumers and regulatory authorities. These challenges are more likely to be met if experiments are designed accordingly for the purpose of simulation rather than just description.

Recent advances in the -omic disciplines (genomics, transcriptomics, proteomics and metabolomics) will lead to refinement of animal response models. Nutritional effects on gene expression, protein translation and metabolite pathways and fluxes at different physiological states are likely to become responses of interest (Go et al. Reference Go, Nguyen, Harris and Lee2005). In other words, responses such as weight gain and rate of protein deposition might be superseded in future by the expression of mRNA (coding for a particular protein) and translation of a given protein. Knowledge of the interactions between nutrients and genomics, transcriptomics, proteomics and metabolomics should serve, in turn, to prevent disease, elucidate probiotic effects and estimate nutrient requirements, growth and body composition for a particular genotype with more accuracy (Arab Reference Arab2004; Bendixen Reference Bendixen2005; Kussmann et al. Reference Kussmann, Affolter and Fay2005). The large-scale data sets generated by each -omic technology enhance the role of mathematical modelling in describing and predicting cellular responses (Tyers & Mann Reference Tyers and Mann2003).

Increasing complexity in the disciplines of animal nutrition and mathematics pave the way to possible defeat if models are not constructed properly. Risks of failure of a model are inversely related to the understanding of both the system under study and the mathematical tools that are being used to describe it. In other words, the success of a model depends on the biological expertise of the mathematician and the mathematical expertise of the nutritionist (van der Vaart Reference Van der Vaart, Solomon and Walter1977). Too many assumptions are indices of ignorance and may indicate that further research is needed before disclosing a model.