INTRODUCTION
Bovine viral diarrhoea (BVD) is a common but avoidable disease that, in UK dairy farms, can account for over 0·20 of disease-free farm income (Gunn et al. Reference Gunn, Saatkamp, Humphry and Stott2005). Losses in beef suckler herds are less certain but are likely to be underestimated (Gunn et al. Reference Gunn, Stott and Humphry2004). This is because the main effects of the disease are non-specific (scouring, infertility, abortion and reduced growth) and include illness associated with immuno-suppression, which may not be attributed to BVD. Better estimates of the wide-ranging economic impacts of this disease in beef suckler herds are therefore needed to raise the profile of BVD with farmers and encourage greater investment in BVD prevention and control. This need is particularly acute in Scotland, where beef suckler cows account for approximately 0·70 of the national herd (Scottish Government 2005b).
Gunn et al. (Reference Gunn, Stott and Humphry2004) developed an epidemiological model of BVD in beef suckler herds and used it to estimate economic losses. It was concluded that reproductive losses accounted for 0·53 of total expected losses. However, the estimates of reproductive losses were based on fixed, conservative estimates averaged over a 10-year simulated epidemic. In practice, BVD epidemics will interact with the cyclical processes of reproduction and breeding management, leading to a range of outcomes depending on the nature and timing of infection. This hypothesis was tested by combining outputs from the epidemiological model of Gunn et al. (Reference Gunn, Stott and Humphry2004) with an aligned simulation model of herd dynamics and reproduction. In this way, the possible impacts of BVD on reproduction in different phases of an epidemic were explored, highlighting the range and extent of the likely financial impacts.
MATERIALS AND METHODS
Simulating herd dynamics
A state transition model, sometimes known as Markov Chain methodology (Agrawal & Heady Reference Agrawal and Heady1972), was developed to simulate the reproductive performance of beef suckler herds. Time steps of 21 days were selected to reflect the potential for cows to conceive every oestrus cycle. A similar methodology to the model developed by Azzam et al. (Reference Azzam, Kinder and Nielsen1990) was used to distinguish females with differing abilities to conceive in beef herds and to use, as states, the key physiological stages cows may pass through (oestrus, pregnancy, parturition or post-partum interval) during their reproductive life. In an important extension to the model described by Azzam et al. (Reference Azzam, Kinder and Nielsen1990), three values for conception rates (CRs), the ability of cows to conceive and perform successful implantation, were included. These three values were set to represent different probabilities of conceiving at first, second, third or successive oestrus appearances after parturition, based on the observations of Sinclair et al. (Reference Sinclair, Yildiz, Quintans and Broadbent1998). In the current model, cows conceive exclusively during a discrete breeding season, which is represented by switching the CR from nil to typical values during the time steps of the breeding season (Table 1).
Table 1. Important parameter values and assumptions employed in the fertility model

CR, conception rate, ability to conceive, including successful implantation.
The simulation model of herd dynamics was parameterized to represent the main characteristics and performances of typical Scottish beef suckler herds. These parameters were assumed to represent the performance of a BVD-free herd, i.e. they formed a representative baseline for the current study. This was achieved using data collected in a survey of 106 beef suckler farms carried out in 2004 by Varo Barbudo (Reference Varo Barbudo2005, reported by Stott et al. Reference Stott, Gunn and Varo Barbudo2008) and relevant data from the literature. A spring calving herd was represented, in which bulls had access to the cows from 30 April (onset of the breeding season) during a period of 126 days (length of the breeding season (LBS)). The approximate average Scottish beef suckler herd size of 57 females per holding (Varo Barbudo Reference Varo Barbudo2005) was considered, of which 0·85 were adult cows (older than 24 months) and 0·15 were young females new to the herd (12–24 months), i.e. heifers (in line with Gunn et al. Reference Gunn, Stott and Humphry2004). The approximate weighted average number of beef cows per holding across all regions and size groups in Scotland in the Agricultural Census of June 2004 as reported by Scottish Government (2005a) was 50, i.e. close to the assumption. The total herd size was kept constant and the herd run together as a management unit. Culling took place annually. The culling rate chosen (Table 1) was based on reproductive performance (all infertile cows were annually culled) together with an additional allowance to cover other typical reasons for culling among Scottish beef suckler farms such as trauma, lameness and poor performance of the calf (Varo Barbudo Reference Varo Barbudo2005). It was assumed that there were no spontaneous abortions in the BVD-free beef suckler herd. Table 1 shows other important parameter values and assumptions used in the fertility model.
A diagrammatic representation of the model is given in Fig. A1 of the Appendix.
Simulating BVD epidemics
A description of the epidemiology and economic importance of BVD are given by Houe (Reference Houe1999). For further details and recent developments including control strategies applied throughout Europe, see EU (2006). The model of Gunn et al. (Reference Gunn, Stott and Humphry2004) used in the current study is also based on a Markov Chain methodology but with annual time steps. Transitions between states: animal type (calves, heifers and cows), disease status (susceptible, transiently infected, immune or persistently infected (PI)) and herd exit (replacement or death) were tracked using a matrix of transition probabilities derived as explained in Gunn et al. (Reference Gunn, Stott and Humphry2004) and represented in Fig. A2 of the Appendix. A key transition probability is that of susceptible individuals becoming transiently infected in any one year (P), which was based on the Reed–Frost relationship (Abbey Reference Abbey1952):
where Ct is the number of PIs in the herd at time t (years) and Q the probability of avoiding effective contact, set to 0·4 throughout. The value for Q employed was within the range of values tested by Gunn et al. (Reference Gunn, Stott and Humphry2004), who found that the financial impact of BVD was insensitive to variation in this parameter. All calves born were assumed to be susceptible unless born to a PI cow (all PI) or a transient cow (susceptible, immune or PI according to stage of pregnancy at time of infection based on Houe et al. Reference Houe, Pedersen and Meyling1993). Sufficient female calves were retained to ensure a closed herd operated. Replacement rate was adjusted to maintain constant herd size throughout the course of each simulated epidemic.
Effects of BVD on the reproductive parameters
The epidemiological model of Gunn et al. (Reference Gunn, Stott and Humphry2004) is based on the premise that PI animals spread the virus. Such animals are infected in utero. Some may die at that point, resulting in increased but undiagnosed infertility and associated economic losses, and other facets of infection lead to still more reproductive loss (Fray et al. Reference Fray, Paton and Alenius2000). Others survive and may live normally in the herd, spreading the virus to susceptible individuals, which become transiently infected and then immune. Animals so infected may show few clinical signs of disease but, if pregnant, may again abort or give birth to more PIs.
The reproductive failure caused by BVD was represented as a reduction in the value of CR of the herd from the typical values of BVD-free herds and by the appearance of abortions (abortion rate (ABR)). In estimating these reproductive parameters for alternative BVD levels of infection, the importance of timing of transient BVD infection was considered relative to the stages of reproduction discussed above. If cows are infected during the ovary follicular phase or early pregnancy period, CR may suffer due to the disruption of the capacity of the ovulatory follicle to form a competent corpus luteum (Fray et al. Reference Fray, Mann, Bleach, Knight, Clarke and Charleston2002), or from the embryo-foetal deaths that may occur (McGowan et al. Reference Mcgowan, Kirkland, Richards and Littlejohns1993). However, if cows are infected at a later stage of pregnancy, then abortion may occur (Done et al. Reference Done, Terlecki, Richardson, Harkness, Sands, Paterson, Sweasey, Shaw, Winkler and Duffell1980).
The effect that the susceptibility of female animals to BVD has on the CR and ABR for different levels of the infection was explored based on the proportions of the herd in each of the four cow infective states for BVD (susceptible, PI, transient and immune). The epidemiological model of Gunn et al. (Reference Gunn, Stott and Humphry2004) was used to calculate the proportion of the herd in each of these states at different stages (reference points) of a simulated epidemic. The epidemiological assumptions of this model were unaltered from those used in Gunn et al. (Reference Gunn, Stott and Humphry2004). An intermediate value (0·6) was chosen to represent the probability of transmission (probability of a susceptible individual making effective contact with a PI during a period of a year: 1−Q (Gunn et al. Reference Gunn, Stott and Scanlon1998). The BVD epidemic starting scenario was as in Gunn et al. (Reference Gunn, Stott and Humphry2004), based on field data and experience of veterinary consultants in the field, and reflected a hypothetical, but probable, breakdown in biosecurity with 0·05 of the herd already seroconverted and the accidental introduction of a single PI cow. However, the parameters representing managerial practices, herd size and proportion of heifers in the herd were switched to the values used in the fertility model (57 females/holding of which 0·15 are heifers) so that both models were synchronized to represent the same herd. The average proportions of the herd within the different BVD states in years 1, 4 and 9 of a typical simulated BVD epidemic (Table 2) were selected to represent alternative infection levels to use in the exploration of the range of effects of BVD on reproductive performance at different points of a simulated BVD epidemic. These reference points were chosen based on observations of outputs from the epidemiological model, which show a peak of infection in the early years followed by a trough in the middle years when the majority of the herd has become immune and finally a later period of renewed infection once a pool of susceptible animals has re-established (Humphry et al. Reference Humphry, Stott and Gunn2005).
Table 2. Predicted proportions of a typical beef suckler herd in alternative BVD states in different years of a 10-year simulated epidemic

Source: based on Gunn et al. (Reference Gunn, Stott and Humphry2004).
Figures for year 1 are before introduction of one PI cow that seeds the epidemic.
As the model of Gunn et al. (Reference Gunn, Stott and Humphry2004) has annual time steps, it had to be assumed that there was a constant rate of infection at all stages of pregnancy and assumptions were made about the development of the BVD epidemic within the year in order to apply these to the 21-day time step model of reproduction in the same herd. At the start, in year 1, before the epidemic, no transiently infected individuals were present but one PI cow had been introduced (Table 2). A default assumption was that 0·40 of the susceptible animals (P=0·4) would become transiently infected with BVD during year 1, and the CR and ABR estimates employed reflected the associated drop in reproductive performance. Given that susceptible animals may be exposed to PIs all year, the assumption of only 0·40 of them becoming infected is conservative. However, this low level of transmission is supported by the observations of Taylor et al. (Reference Taylor, Janzen, Ellis and Van Donkersgoed1997), who suggested that the use of management practices such as segregated housing or pastures (typical among beef suckler farms) may reduce the risk of transmission between PI and susceptible animals. Even so, this is clearly an area of considerable uncertainty and likely variation in practice (Gunn et al. Reference Gunn, Stott and Humphry2004). It was therefore used as the basis for sensitivity analysis.
It is believed that typical management practices on beef suckler farms contribute to a constant level of exposure that results in equal chances throughout the year for susceptible individuals to become infected. Since the reproductive processes in the cow take approximately a year, it was therefore assumed that 0·50 of the newly BVD-infected females became infected during the post-partum and/or breeding periods (approximately half a year), i.e. during the follicular and early pregnancy phases. These cows (denoted SIC for susceptible to infected with reduced CR, see Table 3) therefore present a reduction of the ovulatory follicle to form a competent corpus luteum (Fray et al. Reference Fray, Mann, Bleach, Knight, Clarke and Charleston2002) and embryo-foetal deaths (McGowan et al. Reference Mcgowan, Kirkland, Richards and Littlejohns1993), which is denoted by a marked reduction in CR (40%) but no abortions (McGowan et al. Reference Mcgowan, Kirkland, Richards and Littlejohns1993). The remaining 0·50 of the newly infected cows became infected during later gestation (approximately half a year) and hence 0·4 ABR although no modification in the CR (Done et al. Reference Done, Terlecki, Richardson, Harkness, Sands, Paterson, Sweasey, Shaw, Winkler and Duffell1980) (denoted SIA for susceptible to infected with abortion, see Table 3).
Table 3. Reproductive performance assumed for each BVD state of cows and heifers

Reproductive disruptions based on McGowan et al. (Reference Mcgowan, Kirkland, Richards and Littlejohns1993) and Done et al. (Reference Done, Terlecki, Richardson, Harkness, Sands, Paterson, Sweasey, Shaw, Winkler and Duffell1980).
CR1, CR2 and CR3: conception rate of the adult cows at first, second, third and successive oestrus after parturition. CRH, CR for the heifer group; ABR, abortion rate. SNF, non-infected susceptible animals (equivalent to a BVD-free herd). SIA, susceptible animals that become infected during pregnancy and present abortions. SIC, susceptible females that become infected during pregnancy and present reduction in the CR and no abortions. Transients are acutely infected animals.
The reproductive performance of the transient animals was also based on the phase of the cow reproductive state in which these animals became infected. In order to represent the average value for the financial impact of transient animals via its effects on fertility, it was considered that animals in this infected state became infected during the period of re-establishment of ovarian activity or in early pregnancy. Hence, their expected reproductive performance was represented as a reduction in CR, based on the observations of McGowan et al. (Reference Mcgowan, Kirkland, Richards and Littlejohns1993).
The reproductive performance of PI cows was reflected by a reduction of the reproductive parameter CR, an increase of ABR to reflect the typical ovarian hypoplasia present in PI cows (Grooms et al. Reference Grooms, Ward and Brock1996) and the general weakness that this type of animal may present (Houe Reference Houe1993). Since the range of variation of the reproductive performance of PI animals is not well defined, for the purpose of the current study the reduction of CR of these animals was assumed to be the same as in SIC or transient individuals (0·40 from the base value) and their ABR to be the same as in SIA individuals (0·40). Immune animals are assumed to be no longer susceptible to BVD, hence the reproductive performance in this group of animals was considered to be the same as expected from BVD-free herds. Table 3 shows the reproductive performance that would be expected from each group of animals according to their infective state.
CR and ABR for the whole herd at each reference point in the simulated BVD epidemic (Table 4) were estimated as the weighted average of the CR and ABR for each group of animals (shown in Table 3) according to their susceptibility to BVD and the stage of reproduction when the infection occurred as explained above. The weighting factor was the proportion of the animals expected in each group for the given period of the epidemic (Table 2). These reproductive parameters were used in the herd dynamic model to represent the reproductive performance expected in the reference years.
Table 4. Estimated weighted average reproductive parameters at different stages of a 10-year simulation of a BVD epidemic based on the proportion of the herd in each BVD state (Table 2) at each stage and their assumed reproductive performance (Table 3)

CR1, CR2, CR3, ability to conceive at first, second and third or successive oestrus appearance after parturition. ABR, abortion rate, Based on McGowan et al. (Reference Mcgowan, Kirkland, Richards and Littlejohns1993) and Done et al. (Reference Done, Terlecki, Richardson, Harkness, Sands, Paterson, Sweasey, Shaw, Winkler and Duffell1980).
The herd dynamic Markov Chain is stationary and therefore reaches a steady state in the long run. As in Stott et al. (Reference Stott, Veerkamp and Wassell1999), the state variables of the stationary Markov Chain were used to evaluate the economic consequences of alternative reproductive performance scenarios. The model for each scenario was run for a sufficiently long period of time (number of years) until the steady state was reached. The number of years to reach the steady state varied and was dependent on the initial set of assumption parameters. State variables representing the reproductive performance of the herd in the steady state over a period of a year (number of calves, calving pattern, number of infertile cows and culled cows) were used to explore the financial consequences resulting from the reproductive performance associated with each period of the simulated epidemic investigated in the current study.
The financial model
A budget model in gross margin (GM) form (Table 5) was used to quantify the financial effects of BVD via impaired reproduction in beef suckler farms. This was built using a similar structure to SAC (2003). The data about the herd performance needed to calculate the financial result of the herd were obtained from the model of the herd dynamics as parameterized for each situation under study. In calculating the gross output, the estimation of the output achieved from the calf crop played an important role in the accuracy of the estimations. As in Naazie et al. (Reference Naazie, Makarechian and Hudson1997), a growth curve (Richards Reference Richards1959) was used to estimate the growth of the calves from their date of birth to their sale date (as weaned calves):
where Y is the current weight (kg), a is the mature weight (kg), b is an integration constant, k is the maturing index, m is the inflection parameter and t is time (age of animal in days). Parameters were as given by Naazie et al. (Reference Naazie, Makarechian and Hudson1997) ; 610·8, 0·9836, 1·006 and 0·63739 for a, b, k and m, respectively.
Table 5. Schematic representation of the budget in GM form used to calculate the financial performances of beef suckler herds under alternative reproductive impairment implied by BVD infection

Source: SAC (2003).
With respect to the variable costs, the feeding costs were estimated using a commercial computer-based ration formulation programme called Feed-Byte® (Schofield et al. Reference Schofield, Calder, Fraser, Lewis, Oldham, Offer and Rooke1999), which calculates the minimum cost ration per day based on the weight (600 kg, Angus×Charolais) and milk yield (Jenkins & Ferrell Reference Jenkins and Ferrell1984) during the lactation periods of cows, as well as their reproductive states. Cows were grouped based on which part of the calving season they had calved (early, middle and late) so that animals in each group were assumed to have similar nutritional requirements. Feeds used varied with the time of year and included barley at £76/tonne (SAC 2003) and silage at £19/tonne (Stott et al. Reference Stott, Jones, Humphry and Gunn2005). Full details are given by Varo Barbudo (Reference Varo Barbudo2005).
Reproductive indicators
The fertility indicators were calculated at herd level. Total calving rate (TCR), the number of calves born per cow present in the herd (Ponzoni Reference Ponzoni1992), was selected as the first indicator of reproductive performance. To account for variations in calving pattern, an additional measure of fertility was also included (MacGregor & Casey Reference Macgregor and Casey1999), ‘days to conception’ (DCON). The average calving date (CALD) was defined as the average of the mid points of each of four successive 21-day calving periods starting from the date of birth of the first calf and weighted by the proportion of the herd calving in each of these periods. The average conception date (AVC) was defined as the date resulting from subtracting the length of a typical gestation period, i.e. 280 days (Yavas & Watson Reference Yavas and Watson2001), from CALD. The DCON was then defined as the number of days from the onset of the breeding season (OB) to the AVC (DCON=OB−AVC). Thus, DCON measures the number of days on average that a herd needs to conceive.
Sensitivity analysis
By estimating the financial impact of BVD on infertility of beef suckler herds at different stages of a simulated epidemic, some indication of the variation of the effects of this disease in this context is produced. To complement this, the additional impact of a greater proportion of susceptible animals becoming transient within the year of study was examined (default P=0·4). The economic impact assessment was therefore repeated with P set to 0·6 and 1·0, i.e. assuming that either 0·60 or all of susceptible animals become transiently infected within the year rather than just 0·40. This range approximately reflected the variation in P reported in the literature as reviewed by Gunn et al. (Reference Gunn, Stott and Humphry2004).
LBS was also included in the sensitivity analysis. Instead of the default setting of 126 days (6 oestrus cycles), which was based on a survey of commercial farms (Varo Barbudo Reference Varo Barbudo2005) the assessment was repeated using an LBS of 63 days (three oestrus cycles). This latter figure is a target suggested by Riddell & Caldow (Reference Riddell and Caldow2007) for beef suckler farmers to improve fertility and hence increase profit and reduce labour. The use of this target figure allowed an exploration of the extent to which BVD might disrupt such improvement programmes.
Computational details
Both models were developed using proprietary spreadsheet software. Extensive use was made of macros written in Visual Basic (Oliver & Kantaris Reference Oliver and Kantaris2001) to facilitate multiple runs of these stochastic models.
RESULTS
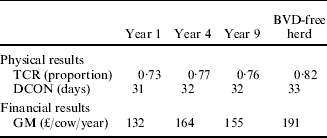
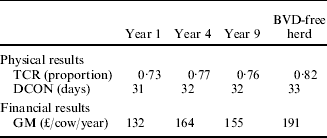
Results from the model of herd dynamics are shown in Table 6. In comparison with the reproductive performance of Scottish BVD-free beef suckler herds, TCR was depressed and DCON extended by BVD in all reference years and particularly in year 1.
Table 6. Reproductive performance and associated financial results based on reproductive parameters (Table 4) implied by different years of a simulated BVD epidemic (Table 2)

Key: TCR, total calving rate – calves born per year as a proportion of cows present; DCON, days to conception; GM, gross margin. Years 1, 4 and 9 refer to the performance of a BVD-infected herd during these years since introduction of a cow PI with BVD. BVD-free herd refers to the expected reproductive performance of a BVD free-herd in any year.
With respect to the financial consequences of the infestation, results from the model showed that in an average Scottish BVD-free herd, the expected GM was £187/cow. For the first year of BVD, the GM was reduced by 23% as a result of the reproductive losses caused by BVD. For the fourth reference year, BVD reduced GM by 12% whereas, in year 9, the reduction was 18% from the result expected from a BVD-free herd.
The above costs of infertility caused by BVD at different stages of an epidemic are shown graphically in Fig. 1 (black bars). These results are compared there with alternative assumptions regarding the probability of susceptible individuals becoming transiently infected with BVD within the year (P). Sensitivity to variation in P was high, especially in year 1 of the simulated epidemic, where the cost of infertility at P=1·0 at £125/cow was almost three times greater than the default value. The effect of reducing LBS on the cost of infertility due to BVD was much less (Fig. 1) at a maximum of 36% higher than default in year 1, falling to just 5% higher in year 9. Further results for the shorter LBS are shown in Table 7. Only in year 1 did the shorter LBS give an appreciably lower GM per cow than that under the default settings (Table 6). The shorter LBS gave a greater GM under BVD free assumptions despite no differences in CRs and hence a very low TCR.

Fig. 1. Results of sensitivity analysis: cost of infertility due to BVD (measured as the reduction in GM compared with BVD-free herds) assuming that the probability (P) of susceptible individuals become transiently infected within the given year of a simulated BVD epidemic is either 0·4 (black bars, default), or 0·6 (grey bars) or 1·0 (white bars). The hatched bar shows the effect of reducing breeding season length from 126 days to 63 days when P and all other assumptions are at the default settings.
DISCUSSION
The results presented in the current study provide an estimate of the effects of BVD on reproductive performance and the associated losses caused by this virus via impaired fertility in typical Scottish beef suckler herds at three different stages of BVD infection. The fertility model presented may be re-parameterized to reflect other conditions of production and BVD status. The current model may therefore aid understanding of the reproductive disruption and associated losses caused by BVD on Scottish beef suckler farms and hence support decision-making relating to management of fertility under the effects of this disease. The current herd dynamic model not only simulated the calving rate resulting from a BVD-infected beef herd under a defined set of managerial parameters but also it simulated the calving pattern in which calves were born. As a result, the effects on reproduction (calving rates and calving patterns) resulting from alternative fertility management strategies under different disease situations could be explored.
The results of the herd dynamics model for a BVD-free herd were compared with the data about reproductive performance obtained from a survey among a sample of 106 Scottish beef suckler farms (Varo Barbudo Reference Varo Barbudo2005). When the data from the survey were used as input parameters to the model (LBS of 118 days with its onset on 25 May), the model resembled closely the reproductive performance found in the survey (TCR 0·90 v. 0·89; DCON 40 v. 40 days). However, further analysis of data from 66 spring calving herds in the survey of Varo Barbudo (Reference Varo Barbudo2005) by Stott et al. (Reference Stott, Gunn and Varo Barbudo2008) highlighted the wide variability in reproductive performance and demonstrated no significant relationship between LBS and indicators of reproductive performance. The current study suggests that more research is needed to understand the complex relationships between decision making, reproductive performance and the economics of beef suckler farming. Models such as those described here are useful tools in this on-going research.
The models used in the current study modelled either the disease or reproduction at the herd level using a Markov Chain methodology. Humphry et al. (Reference Gunn, Saatkamp, Humphry and Stott2005) compared the BVD model used here with an alternative working at the level of the individual animal. The individual model may be expected to better reflect the biological reality because infection occurs at the animal level. These authors concluded that, for decision support, there was little benefit in the more complex individual model due to reasonable agreement between the models at current levels of understanding of the disease and the advantage of relative simplicity and transparency for the herd-based model. The same arguments apply to the model of reproduction and re-breeding presented here.
Results from the model simulating the herd dynamics suggest that the TCR for a typical Scottish beef suckler farm is approximately 90%, which compared closely with the expected 92% for this type of farm in Scotland (SAC 2003). The expected GM for this type of farm was forecast as £196 (SAC 2003) which compares closely with the GM (£187/cow) obtained from the current model. The slightly better reproductive and financial performances (TCR and GM) in the forecasts from SAC (2003) may reflect the superior performance of recorded herds compared with the ‘typical’ farm simulated by the current model.
The GMs presented include the £196 per cow that a Scottish beef suckler farmer was entitled to claim for during the year that this study was performed (2003). Although a new EU Common Agricultural Policy (CAP) regime was launched in Scotland in January 2005 (Scottish Government 2007) and the subsidy payments have therefore been modified, figures from 2003 were included based on old subsidy payments to allow validation against currently published performances and comparison with published BVD costing. As the old subsidies were largely in the form of mixed headage payments per breeding cow, their inclusion does not affect the marginal effects of BVD reported. As market prices respond to changes caused by CAP reform (Oglethorpe Reference Oglethorpe2005), the current model can be re-run and the effects of BVD on farm profits via its effect on reproduction re-assessed. Without the cushion of headage payments, such effects are likely to have more impact on farm business viability than they did in the past.
Results from the combined models suggested that, in the first year of the BVD infestation, there was a 10% drop in TCR, which resulted in the greatest financial losses of the three scenarios under study. This was due to the higher proportion of cows susceptible to BVD in the herd at this time. Losses were the lowest in the fourth year of the infestation, which coincided with the smallest reduction of TCR from the optimum and a very small variation of DCON. This was due to the lower proportion of susceptible cows and the higher proportion of immune animals at this stage in the BVD epidemic. This resulted in fewer cows becoming infected; hence, the overall ability of the herd to become pregnant was reduced to a lesser extent and fewer abortions occurred. By the ninth BVD epidemic year, the herd had time to recover partially, presenting intermediate values of susceptible animals and one PI, which resulted in intermediate reduction of TCR and intermediate increases of abortion rate in the herd.
Sensitivity analysis demonstrated how important it is to try and limit the spread of BVD virus to susceptible animals within the herd (reduce P). If the marginal change in relative risks of transmission associated with various husbandry practices can be estimated, then the current model will provide an associated cost or benefit. This could help guide and prioritize changes in farm practices. For example, keeping animals of unknown BVD status such as newly purchased replacements separate from the rest of the herd may be expensive and inconvenient. The current models could estimate the benefits of these costs. The farmer's veterinarian or other expert may be able to provide an estimate of the marginal change in P. This estimate may only be subjective, but subjective assessment of probabilities is an accepted part of managing risk (Hardaker et al. Reference Hardaker, Huirne, Anderson and Lien2004).
In the current study, high ABR had a greater effect on GM than the reduction in CR and/or embryo losses (Tables 4 and 6). This was probably due to the mitigation of some of the negative effects that BVD may have due to the use of a very long breeding season. As a result, the TCR of the herd did not differ excessively from the value estimated for the BVD-free herd, suggesting that the reproductive losses caused by BVD in many antibody positive herds may be hidden by the common use of long LBS among Scottish beef suckler farms. The sensitivity analysis supported this hypothesis by showing that shorter LBS can result in higher financial impact of BVD due to greater vulnerability to impaired fertility. However, the financial impact was relatively small and would have been smaller still if the assumed CR had been increased to match published fertility targets (Riddell & Caldow Reference Riddell and Caldow2007) alongside the shift to a target LBS. This issue provides another example of how the models might support practical decision making by predicting the change in physical and financial indicators that might arise from action to improve a particular target such as LBS. Using the models to support a more holistic approach to improving fertility might avoid the danger of concentrating on just one target that leads to deterioration elsewhere. In the example, reducing LBS without improvements elsewhere gave a very low TCR in year 1 of a BVD epidemic. This interaction between BVD states and farm management is likely to create great variation in the impact of BVD and hence heterogeneity of experience of the disease in the farming community. This may affect collective responses to disease and may, for example, hinder regional eradication programmes unless properly understood.
The modelling approach presented combined two state-transition models dealing with stochasticity in terms of transition probabilities between states. The BVD simulation model also includes Monte Carlo simulation, which was used to generate expected outcomes, i.e. means at three points in the 10-year simulated epidemic. The aim was to explore the variation in the mean impact of BVD on fertility through the variation that occurs through time during the course of the average epidemic. However, by taking averages from the Monte Carlo simulations, by having a fixed starting scenario for the BVD model and by leaving many other assumptions fixed it is probable that the amount of variation in BVD epidemics that occurs in practice was underestimated. The current approach reflects the uncertainty associated with these assumptions and the importance of establishing an average value for the financial impact of BVD via its effect on fertility. To examine the range of impacts that might occur in practice and hence establish the farm business risk posed by BVD a different approach would be required. Such an approach is described by Stott et al. (Reference Stott, Lloyd, Humphry and Gunn2003) based on the same BVD model used currently. In that example a linear programming framework was used, within which BVD control was incorporated. Here, the model of reproduction to provide the wider context was used. Both approaches offer the potential to combine decisions directly associated with the disease control with those indirectly associated with the disease control (management of reproduction here, choice of enterprise mix in the case of Stott et al. (Reference Stott, Lloyd, Humphry and Gunn2003) ). This allows the interaction between management of animal health and other farm management decisions to be explored. Such an approach is essential for decision support at farm level where disease control is one activity of many competing for scarce resources. The current paper establishes that taking a wider perspective based on the decision maker concerned rather than on the disease involved, alters the economic result and hence justifies further development of this approach to disease control assessment.
The current approach also highlights the importance of modelling interactions between disease spread and other interrelated events on the farm (which could include other diseases). These interactions go beyond the immediate issues of managing reproduction dealt with here. For example, wider calving patterns (perhaps caused by BVD) alter group dynamics within the herd and disrupt the match of energy demand with energy (grass) supply, leading to altered stocking and supplementary feeding decisions, further complicating the disease risk factor mix over time.
The simplified approach of the current paper represents a step forward on the way to wider systems modelling in this context. It provides a first insight into the potentially important influence of this approach on economic estimates of BVD and hence the need to explore it more fully to encourage better BVD control from farmers within the context of improved farm management. A similar approach was used by Santarossa et al. (Reference Santarossa, Stott, Woolliams, Brotherstone, Wall and Coffey2004) to bring in grass, soil and hence environmental dimensions to the management of fertility in dairy herds. By combining this approach with a disease model as in the current study, it will be possible to study the impact of disease on the sustainability of farming systems via the impact of disease on fertility. This example illustrates an important role for epidemiology in the quest for a balance from agriculture in the provision of food and environmental goods.
The study of Gunn et al. (Reference Gunn, Stott and Humphry2004) estimates the total losses caused by BVD at £37/cow/year, with £20 (0·53) of them allocated to reproductive losses. The current study estimated the reproductive losses caused by BVD at a maximum of £43/cow/year (BVD status for year 1 of an epidemic), and at a minimum of £22/cow/year (year 4). The latter estimate is therefore very close to that of Gunn et al. (Reference Gunn, Stott and Humphry2004) and in line with the conservative assumptions of Gunn et al. (Reference Gunn, Stott and Humphry2004). The results therefore build on those of Gunn et al. (Reference Gunn, Stott and Humphry2004) by demonstrating the importance of the interaction between BVD and reproductive management in the estimate of the average cost of BVD. The model deals in more detail with the reproductive losses resulting from alternative management practices and the specific impact of different BVD disease states on the reproductive process. In addition, the effects on total herd GM of a wider spread in the calving pattern and hence the wider spread of calf sale values (calf sale weights) are captured in the current model but not in that of Gunn et al. (Reference Gunn, Stott and Humphry2004). Other details of farm performance are absent from both models. For example, disruption to the calving pattern may have fixed cost implications such as poorer utilization of buildings and machinery. Thus, even the current study provides a conservative estimate of the direct reproductive losses caused by BVD in Scottish beef suckler herds and yet is in some circumstances much greater than previous cost estimates.
Results from the current study highlight the important area of loss that reproductive failure represents and that is often ignored in this field. The economic impact of reproductive failure must not be ignored (Gunn Reference Gunn2002). The current results indicate how costly, in the short run, a BVD infection can be in herds that had little previous contact with the virus. However, the current results also suggest that even when there are some antibody positive (immune) animals in the herd, an outbreak can be costly although these losses may be hidden by the use of low risk management practices such as a long breeding season. Therefore, costs may be underestimated if it is assumed that only herds with no evidence of BVD antibodies are at risk of a serious outbreak (Bennett et al. Reference Bennett, Christiansen and Clifton-Hadley1999). Overall, despite conservative costing, our results suggest that BVD is certainly of economic importance at farm level, probably more so than originally reported but likely to vary considerably due to the interaction with reproductive management.
We would like to express our thanks to Scottish Executive Environment and Rural Affairs Department for funding this project and Professor K. J. Thomson of Aberdeen University for comments on earlier versions of this work.
APPENDIX

Fig. A1. Diagrammatic representation of the state transition model of reproduction in beef suckler herds. Rectangular boxes represent the vectors of states that cows and heifers can occupy at any point in time (stage, t). After each 21-day stage, cows move between states as shown by the arrows. Movement is dictated by multiplying the state vectors by a transition matrix of probabilities derived from parameters in Table 1 (for uninfected herds) or as modified by BVD (Tables 3 and 4). During the breeding season animals may enter the pregnancy state according to the CR, which depends on time since parturition and BVD status. Unless BVD induces abortion, animals occupy the pregnancy state for 13 stages (273 days) plus an extra stage for parturition. Full details are given by Varo Barbudo (Reference Taylor, Janzen, Ellis and Van Donkersgoed2005).

Fig. A2. Diagrammatic representation of the state transition model of BVD transmission in beef suckler herds (Gunn et al. Reference Gunn, Stott and Humphry2004). Rectangular boxes represent the vectors of states that cattle can occupy at any point in time (stage, t). After each annual stage, animals move between animal and disease states as shown by the arrows. Movement from susceptible (calf, heifer or cow) at stage t to transient (cow or heifer) in stage t+1 is dependent upon the number of PI animals in the herd at stage t and the probability of effective contact (P=1−Q=0·4) as explained in the text. A transient cow at stage t can give birth to either a susceptible, immune or PI calf with a probability of 0·105, 0·656 and 0·239, respectively, based on Houe et al. (Reference Houe, Pedersen and Meyling1993).