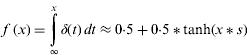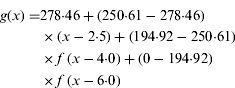INTRODUCTION
Dairy farming, along with other agricultural activities, is facing important changes such as public policy change and/or climate change (Thornton et al. Reference Thornton, Van de Steeg, Notenbaert and Herrero2008). Anticipating these changes and evaluating them is critical for appropriate exploration of the future possibilities for dairy farming. In contrast to farming systems based only on annual crops or short cycle animal species, the functioning of dairy farming depends on complex interactions between past and present decisions, the consequences of which are extended into the future. For instance, changes resulting from decisions regarding fodder improvement or the replacement of breeding stock will be seen within a short time frame, while the impacts of changes in agricultural policy might only be seen in the long term. Therefore, a combination of top-down and bottom-up approaches is needed to improve the decision-making processes, both at the farm (bottom-up) and the sector (top-down) levels. It is also critical to consider the consequences of environmental and agricultural policy measures.
The current paper focuses on the development of a regional dairy sector model for the island of La Réunion, France. The model ‘Ksheera’ was developed as a follow-up to earlier farm-scale modelling work (Alary Reference Alary2004). The objective of the current study was to scale up analysis of the dairy sector to regional level by developing a discussion support tool for regional decision makers. The strength of the regional dairy model ‘Ksheera’ is that it integrates the complexities of dairy herd dynamics, animal nutrition, labour use, environmental impacts, financial variables and policy (in terms of land allocation, subsidies and quotas). The resultant model supports discussion and evaluation of economic, environmental and social aspects in the broader context of sustainability for the island's dairy sector. The current paper focuses on the economic (income) and social dimensions (working hours). In the model, multiple and diverse datasets from different sources have been integrated, such as the dairy cooperative, the pasture cooperative, the concentrate cooperative, animal scientists, animal nutritionists and economists. The primary objective of the dairy industry is to achieve the allotted ‘quota’ of production within the effective constraints such as the EU Nitrate Directive, for example, which would lead to higher income and increased employment opportunities.
The dairy sector in La Réunion is relatively new, having started in the early 1970s. It expanded rapidly, from a milk production of 1 million litres in the 1970s to more than 23 million litres in 2010. The rapid growth during the 1970s can be attributed to institutional and organizational factors (cooperative implementation in 1962, dairy processing unit in 1972), the political involvement with the regional hillside development plan, and the social interest in developing milk supply and processing (Louhichi et al. Reference Louhichi, Alary and Grimaud2004). According to the EC treaty, Réunion is an outermost region (of the EU) where the European Commission (EC) objective 1 support applies. The subsidies have been put in place to encourage farmers to take up dairying for both social and economic reasons, such as employment generation, food self-sufficiency and reducing population pressure in the coastal areas by encouraging settlement at higher altitudes. These subsidies are also aimed at reducing the dependency of Réunion on imports of milk powder and dairy products (D'Haese et al. Reference D'Haese, Speelman, Alary, Tillard and D'Haese2009). While the milk quota for Réunion is currently 40 million litres, this quota is far from being achieved. It is worth noting that the EC is currently phasing out the milk quota; therefore it might become a less relevant target for milk production in Réunion. However, the quota remains important for the governmental support that is paid per litre of milk as long as this quota has not been reached (D'Haese et al. Reference D'Haese, Lecomte, Alary, D'Haese and Schipper2008). At the same time, the external driver is the competition for scarce land between urban development/arable farming and horticulture and dairy uses to expand the dairy sector to reach its quota of 40 million litres/yr. This is a complex setting and the model can be used as a discussion support tool to investigate ‘what if?’ scenarios in reaching the allotted milk production quota in the context of subsidy policy changes, land availability, social and environmental impacts.
The model was developed in close collaboration with the Dairy Cooperative (SICA Lait) who contributed key technical coefficients and data. The SICA Lait consults this model to generate ‘what if ?’ scenarios as a policy discussion tool and exploring potential impacts of expanding the dairy sector in a changing subsidy regime.
MATERIALS AND METHODS
Study area
Réunion is one of the overseas departments of France Département d'Outre-Mer (DOM). It is a volcanic tropical island, located in the Indian Ocean (21°S, 55°E), c. 800 km east of Madagascar. It covers an area of 2512 km2, of which c. 1004 km2 is located above an altitude of 1000 m asl. In 2008, agriculture occupied c. 0·19 of the available land area (47 479 ha). Sugarcane is the main crop with an area of 24 528 ha in the lowlands (<800 m asl); permanent grassland covers 11 150 ha in the highlands and the remaining 11 801 ha are used for diverse cropping systems (INSEE-RÉUNION 2008).
There are four agro-climatological zones on the island: (1) Plaine des Cafres (Cafre), (2) Plaine des Palmistes (Palm), (3) Hauts de St. Joseph (consisting of Plaine des Grègues, Jean Petit, Grand Coude and La Créte) (Joseph) and (4) Hauts de l'Ouest (Ouest) (Fig. 1). Mean annual rainfall and mean annual temperature for the four sub-regions are: Cafre – 1700 mm and 13·88°C; Palm – 3720 mm and 16·8°C; Joseph – 2240 mm and 16·3°C; Ouest – 860 mm and 19·2°C. For livestock systems on the island, the key differences between these zones are types of fodder grown, fodder yields and fertilizer application rates. Temperate forages, such as ryegrass (Lolium perenne), are grown at altitudes above 1000 m asl, with tropical grasses such as chloris (Chloris gayana) and fodder sugarcane (Pennisetum purpureum) dominating at lower altitudes. One tropical species, kikuyu grass (Pennisetum clandestinum), covers a wide range of altitudes (800–1500 m asl).

Fig. 1. Agro-climatic zones of Réunion. (1) Hauts de l'Ouest. (2) Plaine des Palmistes. (3) Plaine des Cafres. (4) Hauts de St. Joseph.
A regional model that can incorporate these diverse crop and animal production conditions therefore becomes very relevant to support discussion on the dairy sector on an island scale. In the current model, these diverse agro-climatic factors are incorporated through relevant co-efficient matrices.
In 2007, the dairy sector consisted of 119 dairy farms with c. 5700 dairy animals (4100 are dairy cows). The Cafre is the main dairy area of the island, with more than half of the dairy farms located in this sub-region, while the sub-region Ouest has the smallest number of farms. Average annual milk yield is c. 5500 litres/cow. The main dairy cattle breed on the island is Holstein, with a genetic potential of c. 8000 litres/lactation.
The model
The regional dairy model was developed within the General Algebraic Modelling System (GAMS) that utilizes an Interactive Multiple Goal Linear Programme (IMGLP) approach (Fig. 2). The basic structure of the linear programme (LP) model has the form of a standard linear programming model, as given by Berentsen & Giessen (Reference Berentsen and Giessen1995) and discussed by Van Calker et al. (Reference Van Calker, Berentsen, De Boer, Giesen and Huirne2004):
where x is a vector of activities, c is the vector of gross margins per unit activity, A is the matrix of technical coefficients and b is the vector of constraints. The constraints, as given by Eqn (2), consist of resource and policy constraints. The objective function (Z) maximizes returns on inputs (capital, labour, etc.). Z is maximized at the sub-regional level (considering each sub-region as whole farm). The heterogeneity in agro-climatic conditions in the study area, represented by the Cafre, Palm, Joseph and Ouest sub-regions, has explicitly been incorporated in the model. This heterogeneity is specifically reflected in the values of the technical coefficients relating to fodder type, fodder yields, fodder nutritional values and fertilizer application, which have been derived from previous studies in the region. The model contains a set of activities for dairy farming in Réunion (fodder production, milk production and animal feeding). Technical constraints, in terms of available land area, herd size, feed requirements, fodder yields and labour requirements, are used as links between activities. Environmental policy is included in terms of nitrogen (N) management and the indicator chosen is N emission/ha from the dairy farms.

Fig. 2. IMGLP model for the regional dairy sector.
The model gives the best allocation of factors between the different sub-regions to maximize the net regional income. It is implicitly supposed that this allocation will address the main preoccupations and individual constraints of dairy farmers. The model helps to generate ‘what if?’ scenarios, which are based on quantified input–output relations for current and alternative production activities with the formulation of constraints as mathematical functions. Optimization results (goal achievements) reveal the extent to which various objectives can be achieved given the technical and physical constraints, thus providing trade-offs between costs and benefits incurred in attaining the various goals (Van Keulen Reference Van Keulen, Rabbinge, Goudriaan, Van Keulen, Penning de Vries and Van1990; Laborte et al. Reference Laborte, Nuñez, Dreiser and Roetter2001; Jansen & van Ittersum Reference Jansen and Van Ittersum2007). The IMGLP model presented in the current paper is interactive by design. The parameters of the model are input into the model via an easy to use graphical user interface (GUI) and users can interactively change the input values to generate different scenarios. Therefore, the results of the model are dependent on the data, resources and constraints that are defined. By changing these, a number of scenarios can be generated, as discussed in the results section.
Description of model components
The model (Fig. 3) is built around the nutritional balance of dairy cows. It takes into account the genetic potential for milk production (MILK COWS (MC)) of the local cows (Hassoun et al. Reference Hassoun, Paillat, Mandret, Brunschwig, Bigot, Latchimy, Blanfort, Hassoun, Mandret, Paillart and Tillard2000) (4000–8000 litres/cow/yr – the term MC40, for example, refers to cows with a potential of 4000 litres/cow/yr, etc.). The young non-milking cows (calves and heifers) are categorized in age groups from Heif1 (calves ⩽6 months) to Heif5 (heifers 25–30 months old). These different categories of animals have different nutritional requirements, as derived from weekly ‘monitoring’ of intake conducted in 1998–2000 (Hassoun et al. Reference Hassoun, Paillat, Mandret, Brunschwig, Bigot, Latchimy, Blanfort, Hassoun, Mandret, Paillart and Tillard2000). Nutrient contents are expressed in forage units for milk production (FU); 1 FU=7·1 MJ/kg of dry matter (DM) (Barrière et al. Reference Barrière, Dias Gonçalves, Emile and Lefèvre2004). Potentially digestible protein based on nitrogenous components of the feed (PDIN), potentially digestible protein based on energy components of the feed (PDIE), calcium (CA), phosphorus (PHO) and crude cellulose (CB) are defined for both roughage and concentrate rations. The nutritive value of the available fodder types and concentrates has been derived from monthly feed analyses (Grimaud & Thomas Reference Grimaud and Thomas2002).

Fig. 3. Model components.
Forage types and yields (kg/ha) vary for the different sub-regions. This variation across sub-regions is included in the model. Fertilization and mechanization requirements for each forage type, in terms of both labour and costs, are quantified on the basis of (1) information collected in an exhaustive household survey conducted in 2000 (Alary Reference Alary2004) and (2) data collected by the Pasture Cooperative (UAFP) in the study area. Labour requirements for fodder and dairy cow management are considered from both a labour utilization and a cost point of view. Costs for fertilizers, concentrate supplements, machinery, pasture establishment and maintenance, labour, interest and loan repayment, veterinary services, insurance and other inputs are taken into account. Revenue (income) in the model comprises proceeds from sales of milk, transactions with regard to animals (including the sale of male cows), together with subsidies for maintaining a herd (as a function of animal density), milk production, farm efficiency, establishment of new pastures and pasture maintenance.
Activities, resources and constraints
The main resources considered in the model include land area, initial animal stocks, labour and capital. The various activities classified by type are listed in Table 1.
Table 1. Activities in the model

One of the key constraints for the dairy sector in Réunion is the shortage of suitable land to expand. In addition to the limited availability of land on the island, the land use policy limits the expansion of the dairy sector below 800 m asl, with subsidies only being given to farms at this altitude or above. One of the reasons for this policy is to encourage people to move to upland areas and reduce pressure on the coastal belt. In addition, the temperate climate in the highlands is suitable for high-yield-potential breeds like the Holstein. The availability of additional land is constrained in the model, by fixing the upper limit to that used in the current situation. Given this backdrop for land availability for the dairy sector, to aid policy discussion, one of the options explored in the model scenarios is expansion of the available land area by 25% assuming that land is made available to the dairy sector from other uses.
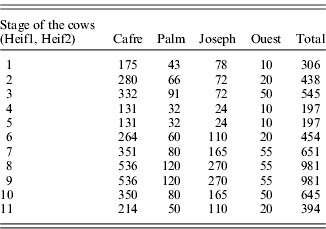
Initial stocks specify the numbers of animals present in all categories (Heif and MC) (Table 2) at the start of the calculations. In Table 2, numbers 1–5 represent non-milking cows (between 6 months and 2·5 years old), while numbers 6–11 represent milk cows (3–5·5 years old). Cows in period 11 are removed from the system in the subsequent period and new-born cows enter into the system in the category 1 as Heif1 each period. The model then calculates animal progression for the subsequent periods. Heifers that can start milk production within 6 months (Heif5) are generally purchased to augment the numbers of dairy cows. This purchase option is included in the model.
Table 2. Initial stocks (source: SICALait 2005)
Dairy farms in Réunion are managed mainly by family labour. Hiring outside labour is not very common and where it occurs it is to help out with various farm activities such as milking, feeding and slurry removal, among others. On average, about 2·5 persons are assumed to be working for 10 h/day on a farm. Additional hired labour has been limited to 10 h/day. The model accounts for labour time (h/day) for each of the activities to manage the dairy farm.
Capital is available for the dairy farmers from sources such as banks and cooperatives. Capital investments account for farm establishment, sheds, milking machines, fodder stores, manure store and farm machinery. About 0·20 of the initial capital is contributed by the farmer and the remainder is taken as a loan. Capital for setting up a farm is not considered a constraint in the model, as credit to start a farm is readily available. Interest at 5% per year is charged on the loan, which is completely repaid within the 6-year time horizon of the model.
Objective functions
Based on the context and hypothesis drawn in the preceding paragraphs, the objectives specified in the model are:
• Maximize revenue (profit)
• Minimize labour use
• Minimize surplus N
Profit objective
The objective of the local dairy cooperative is to maximize milk production to eventually reach the milk production quota of 40 million litres allocated to Réunion Island (SicaLait 2005). This objective is directly related to the objective of maximizing profit. Therefore, this objective has been specified in the model:
Profit objective function
Social objective (labour input)
One of the objectives of the farmers is to reduce working time to 8–10 h/day. Total direct employment of farm labour in the dairy sector is of the order of c. 300 persons and hence labour maximization is not an objective of the model. Indeed, reducing labour hours to achieve an acceptable work–leisure balance is an important social objective of the farmers.
Environmental objective (nitrogen)
Nitrogen (N) input in dairy farms is through purchase of chemical fertilizer for application on the forage areas, while manure is transferred from the animal component to the pasture component. It is assumed that all manure is applied on the farm. The model calculates total N applied per ha as the sum of mineral fertilizer-N and manure-N. The environmental calculations do not influence the model results directly but are used to evaluate the N/ha in different scenarios. This aspect of the model is not presented here and will appear as a separate publication.
Technical coefficients
Technical coefficients for the study were derived from studies in the region between 1994 and 2004 (Hassoun et al. Reference Hassoun, Paillat, Mandret, Brunschwig, Bigot, Latchimy, Blanfort, Hassoun, Mandret, Paillart and Tillard2000; Tillard et al. Reference Tillard, Lanot, Bigot, Nabeneza, Pelot, Blanfort, Hassoun, Mandret, Paillart and Tillard2000; Alary et al. Reference Alary, Messad and Tillard2001; Grimaud & Thomas Reference Grimaud and Thomas2002; Alary Reference Alary2004), obtained through household surveys conducted in the framework of Centre de Coopération Internationale en Recherche Agronomique pour le Développement (CIRAD) research projects. Complementary data were collected from sector-specific agencies including the Dairy Cooperative that conduct regular surveys on milk production, feed balances and annual profit and loss accounts.
Large livestock unit (LLU) subsidy calculation
LLU is the unit used to quantify animal density and stocking rate. In the present model, each heifer (Heif) is equivalent to 0·6 LLU and each milking cow (MC) to 1·0 6 LLU. Since a discontinuous, non-linear (land and number of animals are dynamic and calculating LLU/ha becomes non-linear) relationship cannot be implemented in LP programming, the calculation of the animal density-dependent subsidy per LLU (Table 3) for each half-year period within the IMGLP model was approximated by a continuous, linear function (see (iii) below). This function, consisting of a combination of the functions (i) and (ii) given below, follows the approach of Harris & Stöcker (Reference Harris and Stöcker1998), where x=LLU/ha. The coefficients of the equations are estimated based on the real data of LLU and subsidies on the island with reference to Table 3.
(i) Definition hyperbolic tangent:
(4)
(ii) The (logistic) ‘Help’ smoothing function is an analytic approximation of the Heaviside step function (Weisstein Reference Weisstein2008):
(5)The value of s determines the steepness of curve transitions, where a larger value of s corresponds to a sharper transition at x=0. In the model, s was set to 50 iteratively to achieve the best fit to the real data to achieve a sharper transition.
(iii)
(6)The form of the final function defines the approximation for the LLU subsidies calculation, for which function (ii) is used thrice to define the three curve transition parts. The outcome of the resulting function (iii) is less accurate if a curve transition occurs; therefore it is important to keep such transitions as steep as possible. Based on the current LLU subsidies, the following equation was developed: (7)
(7)
Table 3. Relationship between LLU/ha and LLU subsidy

MODEL VALIDATION
According to Hazell & Norton (Reference Hazell and Norton1986), model calibration aims to set parameters specific to each farm type, while validation assumes that the model reflects the base year situation (i.e. to check that the model reproduces the real activities and bio-economic conditions observed). 2006 was taken as the base year and the model time step is 6 months. Validation was attempted for the first 6 months of that year, i.e. January–June. The model results are close to the observed values (Table 4). The larger forage area in the model is the consequence of the maximizing profit objective that results in selection of the upper bound of animal density (6 LLU/ha) and of the fact that in reality the animals may not all meet the theoretical nutrient requirements used in the model.
Table 4. Comparison of observed data and model results (first time step of 6 months of the model) for the base run in 2006
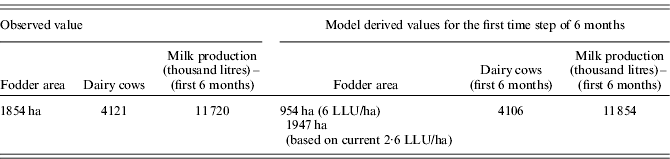
Note: The LLU/ha in the observed data is 2·61, while the model achieves the maximum upper bound (i.e. 6LLU/ha) to maximize profit. The fodder area in the simulated data therefore is re-calculated to reflect 2·61LLU/ha for comparing with the observed data. The values in this table may not be directly compared with values in Table 5.
RESULTS
The results of the modelling exercise are presented in the form of scenarios. The scenario analysis aims to characterize the response of model endogenous variables to changes in exogenous conditions, such as prices, policy instruments and technologies, i.e. they refer to the outcomes of the process of optimizing an objective function such as income. The modelling system allows the user to formulate his/her own scenarios interactively, characterized by different indicator values, and reformulate these scenarios by ‘playing’ with the model (Romero & Rehman Reference Romero and Rehman1989; Pitel Reference Pitel1990). The dairy industry in Réunion is sensitive to the price subsidy. Scenario 2 (S2) was chosen to explore the aspect of subsidy reduction. Réunion dairy is also constrained by availability of land. Therefore, Scenario 3 (S3) explored the option of ‘what if?’ there is more land available (e.g. from other agricultural sectors). Scenario 4 (S4) focused on technical improvement via genetic improvements, which lead to cows with higher milk yields. Scenario 5 (S5) focused on dairy cow imports and explored the trade-off between importing mature heifers and the cost of rearing young calves.
A sample set of scenarios is given in Table 5. In Scenario 1 (S1), the base scenario, the available land area for dairy farming is set to the current area of 1854 ha. The price of milk is €0·40 per litre and the subsidy is €0·083 per litre. Genetic progression for milk production is assumed to be normally distributed, with the mean around 5500 litres/yr. The fertility rate is set to 0·83. In Scenario 2 (S2), the price of milk has been set to €0·38. Profit in year 1 is 18% lower than in S1, while there is no significant change in other variables. This scenario corresponds to the situation in which the dairy sector looses a part of the regional price support on milk. This is assumed in the case where the quota systems are gradually removed, which may lead to reduced support for the dairy sector. In Scenario 3 (S3), the maximum land area that can be utilized for the dairy sector has been increased by 25% compared to S1. Milk production is c. 10% higher, as is the number of milking cows, while profit is 14% higher than in S1. This scenario responds to the demand of the dairy cooperative to extend the availability of land to increase fodder area, to reduce the stocking rate. In S4, the genetic progression (in terms of annual milk yield) is skewed towards higher genetic potential, assuming that introduction of new breeding techniques and/or of higher yielding breeds is possible in the following years. As can be expected, this results in 5% higher milk production and c. 14% higher profits. This scenario is aimed at keeping the current stock rates but increasing milk production. There is no change in the number of milking cows or land area compared to the base scenario.
Table 5. Simulated results for a sample set of scenarios (yearly values are a sum of two 6 months time-step runs of the model)

S1: Land area 1854 ha; milk price 0·40 €/l; subsidy 0·083 €/l; concentrate price 0·26 €/kg (avg); interest rate 5%; genetic progression normally distributed; rate of fertility 0·83.
S2: Land area 1854 ha; milk price 0·38 €/l; subsidy 0·083 €/l; concentrate price 0·26 €/kg (avg); interest rate 5%.
S3: Land area 2317 ha; milk price 0·40 €/l; subsidy 0·083 €/l; concentrate price 0·26 €/kg (avg); interest rate 5%.
S4: Land area 1854 ha; milk price 0·40 €/l; subsidy 0·083 €/l; concentrate price 0·26 €/kg (avg); interest rate 5%; genetic progression skewed towards higher genetic potential.
S5: Land area 1854 ha; milk price 0·40 €/l; subsidy 0·083 €/l; concentrate price 0·26 €/kg (avg); interest rate 5%; rate of fertility 0·50 (new born are lower, however, more Heif5 cows, which become productive earlier, are bought to maximize profit and still maintain the 6 LLU/ha upper bound as the objective is to maximize profit).
In Scenario 5 (S5), the fertility rate of the milking cows on the island is reduced to 0·50. This results in a smaller land area being used, a smaller number of milking cows and lower milk production, with only marginally higher profits than in S1 in year 1. However, from year 3 onwards, each of these characteristics assumes significantly higher values (Fig. 4). These increases are the result of the model augmenting animal resources by purchasing more Heif5 cows for replacement of cows removed from the system at the end of their productive life cycle. Heif5 cows are productive sooner than new-born calves and are cost-effective in terms of feed costs. Therefore, in the model, it is profitable to import Heif5 cows for replacement when the supply of new-born calves is low.

Fig. 4. Impact of a change in fertility rate on selected dairy sector characteristics on La Réunion (Scenario 5).
The model results can support discussion on the trade-off between achieving work-life balance v. profits forgone for reduced working hours. In order to approach the social dimension of sustainability in the dairy sector, the number of hours worked by the farm family is considered. Currently, farmers work on average 10–12 h/day. One of their objectives is to reduce the number of working hours to develop a healthier work–leisure balance. In the model, this aspect is explored by considering the labour requirements on the farm to maintain both the animals and the fodder areas. Two scenarios are explored, Labour Scenario 1 (LS1) and Labour Scenario 2 (LS2), using the parameter set of Scenario 1 but with labour input restricted to 10 and 8 h/day, respectively. Model results indicate that both options are feasible. However, the profit decreases by c. 2% in the first year and c. 16% in the sixth year if the working time is reduced from 10 to 8 h/day (Fig. 5).

Fig. 5. The impact of a change in (family) labour input from 10 to 8 h/day in the Scenario S1 context.
DISCUSSION
Economic developments, environmental degradation and maintenance of a social infrastructure are some of the reasons why policy makers at (inter-)national, regional and/or local levels actively pursue formulation and implementation of land use and environmental policies (Sterk et al. Reference Sterk, van Ittersum, Leeuwis, Rossing, van Keulen and van de Ven2006). The regional dairy model for Réunion in this study was developed to analyse the impact of changing technical and economic measures on the dairy sector in the context of changing future agricultural policies and is complementary to the farm-scale models developed in earlier studies (Alary 2004; Louhichi et al. Reference Louhichi, Alary and Grimaud2004). Livestock and forage in the dairy system of Réunion have a strong and complex inter-relationship that has been integrated in this regional modelling approach. The time-step of the model was set to 6 months, which is suitable for following the progression of dairy animals based on studies of Grimaud & Thomas (Reference Grimaud and Thomas2002) and Hassoun et al. (Reference Hassoun, Paillat, Mandret, Brunschwig, Bigot, Latchimy, Blanfort, Hassoun, Mandret, Paillart and Tillard2000). All relevant income and expenditure components have been retained from the farm-scale models (Louhichi et al. Reference Louhichi, Alary and Grimaud2004). The ‘Ksheera’ is data- and coefficient-intensive, and the effort required to generate the technical coefficients, and to gather and organize relevant datasets, has been significant. The model draws significantly on earlier work in the island for both data and the coefficients (Hassoun et al. Reference Hassoun, Paillat, Mandret, Brunschwig, Bigot, Latchimy, Blanfort, Hassoun, Mandret, Paillart and Tillard2000; Grimaud & Thomas Reference Grimaud and Thomas2002; Alary et al. 2004; Louhichi et al. Reference Louhichi, Alary and Grimaud2004).
The scenarios presented serve as an illustration of the capabilities of the model. A large number of scenarios can be generated by changing the data inputs in the model. In Fig. 6, it is observed that with reference to the base scenario, the number of milking cows gradually increases in the course of the simulation period of 6 years. Consequently, milk production increases. This is due to the fact that the objective of the dairy cooperative introduced in the model is to reach the milk production quota of 40 million litres for the island. Hence, a number of incentives are available to increase milk production on the island through the intensification of the dairy sector. The price support for milk guarantees the viability of the sector and cash availability for expansion.

Fig. 6. Simulation of milk cows and milk production over the time horizon of the model run.
The trend in revenue in the course of the model run of 6 years is in line with the increasing trend in milk production. It is based on the assumption that the financial regime in terms of pricing and subsidies remains identical to that of the base year. Milk production, and thus revenue, increases in time, and stabilizes from the 4th year onwards (Table 5), because at that time the maximum area available for the dairy sector (one of the key model constraints) is almost completely utilized. Based on the LLU/ha upper bound (currently fixed at six), a further increase in dairy cows is not allowed.
In terms of reducing labour hours, prioritizing tasks and improved management of farmer's time could be part of the solution. For example, Vayssières et al. (Reference Vayssières, Lecomte, Guerrin and Nidumolu2007) define a number of tasks for the functioning of a dairy farm. These tasks are categorized as ‘Non-deferrable and routine technical operations’ taking place at specified times during each day such as milking, feeding, green harvest, mulching and slurry removal; ‘Urgent and contextual technical operations’, performed in a day, such as ensiling, changing of pasture, manure spreading, mineral fertilizer spreading; ‘Non priority technical operations’, which are realized in a 2-week planning horizon and can generally be anticipated by the farmers. These include solid manure removal, buying of concentrate feed, mineral fertilizer and forage, buying and selling of animals and selling of solid manure. Depending on their situation farmers' need to prioritize tasks and optimize their time to achieve their goal of shorter day tasks.
In accordance with Sterk et al. (Reference Sterk, van Ittersum, Leeuwis, Rossing, van Keulen and van de Ven2006), the current study has shown that regional-scale modelling can make a valuable contribution to the process of reframing policies, enabling discussion of potential consequences before the policies are implemented. In the context of the current project, the main objective of the dairy cooperative is to achieve the milk production quota allotted to the island, while concurrently adhering to the environmental regulations that are in place and ensuring maximum revenue for the farms. The model provides a framework for analysing possible pathways for reaching these goals. For example, the objective of the milk cooperative to produce 40 million litres of milk can be achieved in c. 4 years by increasing the total herd size of milking cows from the current level of c. 4000 to c. 7000, i.e. increasing animal density from the current 2·6 to 6 LLU/ha, given that no additional land is available. This would mean further intensification of the dairy sector and expansion of the farms from the current 40 head of milking cows to about 60. Another option would be to increase the genetic potential of cows from the current average of 5500 litres/yr to 6000 or 6500 litres/yr. However, as illustrated in Scenario S4, this only offers a partial solution, and an increase in total herd size appears necessary to reach the 40 million litres production objective. The implication of the increase in herd size is fodder availability and the environmental impact in terms of amount of N/ha. The model has raised interesting questions on the advantage of accessing cane fodder from the sugarcane industry and exporting the excess manure to the sugarcane fields as a way of meeting the additional requirement of fodder and managing excess N from the dairy sector. This area of interactions of the dairy and the sugarcane sector is being developed as a separate study. In this context, it is relevant to refer to D'Haese et al. (Reference D'Haese, Speelman, Alary, Tillard and D'Haese2009) who, using a data envelopment analysis, suggest that dairy production on the island has potential area of efficiency gains with reference to milk production to land ratio.
The modelling work in part was user driven particularly by the Dairy Cooperative (SICALait). They have provided insights into the complex interactions of various players of the dairy sector on the island, made available key datasets and participated in the model evaluation and provided valuable feedback. The base scenario of the model for the first time step of 6 months closely mimics the current situation and the modelled future scenarios were extensively discussed with both the CIRAD researchers and the staff of the Dairy Cooperative SICALait. SICALait have requested an easy to use interface to the model that indicates their continued interest in the model. A user-friendly GUI has been developed for easy access and application of the model.
The work reported in the current paper has been funded under European Union Marie Curie Actions as a Transfer of Knowledge (ToK) Project (EU FP6 MTKD-CT-2004-509256) and hosted by CIRAD. Both the institutions are thankfully acknowledged. The enthusiastic participation of key stakeholders, viz., the local dairy cooperative SICALait, l'Union Réunionnaise des Coopératives Agricoles (Urcoopa) and Union de Associations Foncières Pastorales (UAFP) is gratefully acknowledged. Ted Wolfe helped in improving an earlier version of the manuscript. Thanks to the comments of anonymous referees which helped to significantly improve the manuscript.