It is commonly thought that there is an inverse relationship between
“broader” and “deeper” in international
multilateral agreements—that is, multilaterals that are more
inclusive in their memberships will necessarily be shallower in their
level of cooperation. When there is a broader-deeper trade-off, a given
member's treaty-mandated cooperative policy would be more
cooperative if some other member of the treaty were excluded from it.
Or to put it another way, adding a particular state to an agreement
necessitates reducing the level of cooperation of the other members.
The idea often arises in discussion of European integration. One reason
why the European Community (EC) was created with six states rather than
all of (Western) Europe was that some European states were unwilling to
integrate their economies as much as the original EC six were.
Presumably if those states had been included the extent of integration
embodied in the Treaty of Rome would have been lessened, because those
less integration-inclined states would never have agreed to a treaty
with such a “deep” level of integration. Excluding those
states allowed the original six to cooperate (that is, integrate) to a
greater extent.
The same argument has been applied to other areas of international
cooperation. For instance Downs, Rocke, and Barsoom claim, “large
multilaterals that start out small will tend to become deeper in a
cooperative sense than those that start out with many
members.”1
The idea is the same. By
excluding states that are not committed to cooperation, the level of
cooperation of the members that do join—reductions in pollution
for instance—can be greater (deeper). Including those less
cooperation-minded states will make the treaty broader (it will have
more members), but each state's level of cooperation (reduction in
pollution) will be lessened because those states will not sign a treaty
that requires such deep levels of cooperation. Thus by excluding less
cooperation-minded states the states that do join can engage in deeper
cooperation.
The claim that there is a broader-deeper trade-off produces a puzzle
though. A brief review of the creation of some multilaterals reveals
that, in many cases, issues of broader versus deeper simply did not
arise. Certainly the proposer of some of the most important
multilaterals in the early postwar era (the United States) was
concerned with making them as expansive as possible, not with limiting
their membership to “hard core” members. Kahler put it this
way: “Postwar multilateralism … expressed an impulse
toward universality that implied relatively low barriers to
participation in these instruments.”2
The creation of the General Agreement on Tariffs and Trade (GATT) is
an example of an important postwar institution in which one finds no
references to a “broader versus deeper” debate. The GATT
was created in 1947 with twenty-three members, not a large organization
by today's standards, but it comprised about 60 percent of the
states with market economies at the time, and a much larger share of
world trade. States were invited widely. No state was excluded by the
treaty's core members because they thought that state was too
protectionist and would limit the depth of cooperation of the other
members. Indeed some early members of the GATT were some of the most
protectionist states in the world (India, which was admitted when it
became independent in 1948, is a good example). Much of the
“evolution” of the GATT—meaning the addition of
states after the forming of the agreement—was pro forma as former
colonies of GATT members were given easy membership in the
organization.3
The same could be said of the Bretton Woods
system. The framers of the system hoped that it would be as expansive
as possible. They did not seem to be concerned with restricting
membership to those states that supported a stable fixed exchange rate
system.
4 The International Monetary Fund (IMF) opened its
doors in 1946 with thirty-nine members, about 89 percent of the
world's market economies at the time, and an even larger
percentage global GDP or world trade. A more recent example might be
the Montreal Protocol, which limited emission of ozone-depleting
chlorofluorocarbons (CFCs). The treaty came into force in 1989 with a
membership of twenty-nine states and the EC, not a large number of
states, but it did account for 82 percent of world CFC consumption.
5 If the broader-deeper trade-off is not a general phenomenon, what
determines when it will arise? I show that the broader-deeper trade-off
occurs when members of the multilateral choose a single policy that is
applicable to all members, that is when all members of the agreement
must set their policy at the same level. The assumption that states
must set their cooperative policies at an identical level is
appropriate in some contexts and not appropriate in others. The purpose
of this article is to show that when this assumption is relaxed the
broader-deeper trade-off disappears. The multilateral agreement modeled
in this article allows states to set their policies at different
levels. Once this change is made, there is no broader-deeper trade-off.
Indeed once the “identical-policy” assumption is relaxed,
broader multilateral agreements can actually engage in deeper
cooperation than narrower ones.
The findings in this article have obvious empirical and policy
implications. Empirically, the model offers an explanation for why some
agreements seem to exhibit a broader-deeper trade-off and others do
not. From a policy standpoint this article calls into question policy
recommendations in favor of adopting multilateral agreements with
relatively small exclusive memberships. The analysis in this article
shows that the claim that “multilaterals that start out small
will tend to become deeper” is not true for a large class of
cooperation problems. For the types of cooperation problems modeled in
this article, excluding states from the agreement only lessens the
benefits of cooperation by reducing the number of states that set their
policies cooperatively while offering no increase (and perhaps even
some reduction) in the depth of cooperation. Thus creators of
multilateral agreements should in fact strive for inclusiveness in
these cases.
A further purpose of this article is to show that modeling
multilateral bargaining is not so complex as to be avoided altogether.
To date there has been little or no effort at modeling the creation of
multilateral agreements formally. One reason for the lack of formal
study of multilateral agreements is that the problem has been thought
to be too complex analytically. One of the best formal studies of this
topic avoids the multilateral bargaining issue stating: “The
[multilateral institution] creation decision in its purest
form is an unstructured bargaining problem of enormous complexity. For
example in a world of fifty states there are over two million
combinations by which a five state multilateral might form.”6
This article shows that that statement makes
the problem seem rather more complicated than it needs to be and takes
a first step at filling this gap in the formal international relations
literature.
The article is organized as follows. In the following section I
review a model of the creation of a multilateral agreement in which
members choose an identical cooperative policy level, and I show how
that assumption leads to the conclusion that there is a broader-deeper
trade-off. In the next section I present informally my model of
multilateral bargaining. The following section offers an informal
discussion of the major findings that follow from the model. The next
section illustrates the findings with a few empirical examples. The
final section concludes. The Appendix contains the formal model and
proofs of the propositions that are discussed in the body of the
article.
The Identical-Policy Assumption
In this section I illustrate how the assumption that states set their
cooperative policies at identical levels produces a broader-deeper
trade-off. Downs, Rocke, and Barsoom provide the clearest example in
the published literature of this line of reasoning, so I will use their
model as the basis for my discussion. A more formal treatment of their
model, including proofs for the claims that I mention here, is
available in their paper. Figure 1
illustrates the policy space. One might think of the space as a
continuum of the amount of pollution states pump into a common body of
water with the left side corresponding to more cooperative
policy—one that creates less pollution. I have depicted a world
of eleven states. One can obviously generalize these claims to apply to
a world of more states. States' ideal points for the policy in
question are arrayed along a continuum—x1 is
state 1's ideal point, x2 is state 2's
ideal point, and so forth.7
See ibid.,
400, for the setup of their model.
Members of the organization
vote on the level of policy that they want set for the group as a
whole. With simple majority voting, the ideal point of the median of
the admitted members will be the equilibrium policy in the sense that
it will win a majority of votes in a pairwise vote against any other
policy.
8 Downs, Rocke, and Barsoom assume
two-thirds majority voting but this does not change the substantive
point.
If all the states are allowed to become members, the
cooperative policy would be state six's ideal point. If instead a
subset of states—for example, states one through
five—created a more exclusive agreement, the cooperative policy
would be state three's ideal point—much deeper cooperation
than if the full group were admitted. This argument by itself does not
definitively show that “deeper is better than broader,”
because excluding states achieves greater cooperation from states with
low ideal points but completely forgoes cooperation with states with
higher ideal points. It is, however, the basis for the recommendation
that multilateral agreements should be relatively exclusive in their
early stages and admit members only as they become more willing to set
their policies at a low level such as
x3.
Voting on a single cooperative policy with eleven countries
London, Slantchev, and Stone offer a different model that also
produces a broader-deeper trade-off. In their model, states do not vote
on the single cooperative policy. Instead a hegemon proposes
contribution levels for the provision of some international public
good. The authors assume that the hegemon requires each member to
contribute an identical percentage of its gross national product (GNP)
to the provision of this good. Although the model is quite different
from that of Downs, Rocke, and Barsoom the results in terms of the
broader-deeper trade-off are similar. Small states are unwilling to
contribute as large a percentage of their GNP as large states are, and
so a broader-deeper trade-off is produced. The hegemon may exclude some
of the smaller states from the organization, because including them
would reduce the percentage of GNP that the remaining states would
contribute.9
There are fundamental
differences between these two models—Downs, Rocke, and
Barsoom's is a voting model and London, Slantchev, and
Stone's is not. Despite this difference, both models predict a
broader-deeper trade-off because both models make the identical-policy
assumption.
The identical-policy assumption that drives these results is
questionable in a variety of contexts. Multilateral agreements do not
generally require that their members set their policies at exactly the
same level, as is assumed by these models. For example, membership in
the Montreal Protocol did not require that each state set the same
level of ozone depleting substances. The U.S. level of pollution was
different from Japan's, which was different from Canada's
level and so on.10
Similarly the Kyoto
protocol set different levels of greenhouse gas emissions for each of
the members.
11 Information about the
Kyoto Protocol, including the treaty text that lists the abatement
levels, is available at the United Nations Framework Convention on
Climate Change Web site, 〈http://unfccc.int〉.
Accessed 24 March 2004.
Furthermore, the identical-policy assumption can produce odd side
effects. Assuming that the states' noncooperative equilibrium
policies are their national ideal points, this model implies that
states with ideal points below the median of the members of the
multilateral would actually be allowed to increase their policy level
and still be in compliance with the treaty. In other words, their
cooperative policy could be higher (less cooperative) than their
noncooperative policy had been. For instance, even in the more
exclusive treaty containing only states 1 through 5, states 1 and 2
will actually be allowed to increase their policy level up to
x3 and still be compliant with the treaty.
The other assumption that might be questionable in this analysis is
the assumption concerning voting. This assumption does not drive the
broader-deeper trade-off, so I will not focus on it here except to say
that in the international context bargaining models seem more
appropriate.12
Adopting a legislative
voting approach does not take into account two important problems in
the creation of international multilateral agreements. The first of
these concerns states' incentive to participate in the agreement,
and the second concerns compliance. Legislative districts that lose the
vote on a national policy issue must still abide by that policy. They
cannot opt out. States that lose a “vote” in a multilateral
organization, on the other hand, can simply refuse to sign the
agreement, in which case they will not be bound by its provisions.
Furthermore, even if a state does sign the agreement, it can still
cheat. Because there is no international authority to force states to
participate in and comply with an international agreement, that
agreement must offer its members sufficient incentive to sign it and it
must be self-enforcing. The model presented in the next section will
explicitly address the problems of participation and enforcement.
In summary, the identical-policy assumption is crucial to the
conclusion that there is a broader-deeper trade-off. That conclusion is
an artifact of the assumption that adding a less cooperative member
increases every member's policy level because it raises the median
or average policy level. This assumption is not generally appropriate.
As I discuss below, it may have its place in certain contexts such as
policy making within the European Union (EU) where states really do
often adopt a single policy for the whole Union (the establishment of a
single currency being the most prominent recent example) but it is not
a close match for many multilaterals. In the next section, I informally
present a model of multilateral bargaining in which states are allowed
to set different levels of the policy in question and the cooperative
solution is arrived at via bargaining. In that model the broader-deeper
trade-off disappears.
The Model
Some complications arise in the multilateral setting that are not
present in bargaining over a bilateral agreement. One of the more
important complications is whether the benefits of cooperation are
excludable or not. By excludable benefits I mean that nonsignatories
can be prevented from receiving the benefits of cooperation among
signatories. The key to excludability is whether or not a state can
target its policies toward other states. Some types of policies can be
set differently toward different states. Trade policy is one example.
State A's tariff on products from state B can be different than
its tariff on products from state C. Extradition treaties and treaties
on the granting of visas are other examples. Policies that are
targetable in this way will allow members of a multilateral treaty to
exclude nonmembers from the benefits of cooperation, because they can
have different (presumably less cooperative) policies toward nonmembers
than they have toward members.
In some cases, however, a state can only set its policy at one level.
A state can only emit one amount of CFCs, for instance. State A cannot
emit one level of CFCs toward state B and a different level toward
state C. Similarly a state can only have one amount of biological
weapons in its stockpile. In these cases, members of a multilateral
agreement will not be able to set different policies toward members
than they do toward nonmembers. Nonmembers will be able to enjoy the
benefits of cooperation even when they do not participate in the
agreement.
For modeling purposes excludable benefits treaties are quite
different from nonexcludable benefits treaties. The two most important
differences are (1) the punishments for cheating on the agreement, and
(2) whether states that are invited to join the agreement have an
unambiguous incentive to do so or whether they have incentive to free
ride. The first of these differences concerns whether or not
punishments can be targeted to states that cheat on the agreement. The
latter of these differences has important implications for what states
should do if some subset of them refuses to join the multilateral in
the hope of free riding. This problem has implications for the number
of ratifications that should be required for the treaty to come into
force as I discuss below. These differences between the two types of
cooperation problems are sufficient to require discussing each of them
separately. In this article, I discuss a treaty in which benefits are
nonexcludable because I regard it as the harder case for international
cooperation. The main result should also apply to excludable-benefits
treaties.
N is the set of states in the model, cardinality n.
Although it is not an essential feature of the model, substantively it
makes sense to think of N as the set of states that are
relevant to the issue in question rather than all of the states in the
world. For instance, an agreement to clean up the Black Sea would have
no reason to include all of the states in the world. The agreement is
only relevant to states that border that body of water. Even an
agreement that regulates a global issue, such as protecting the ozone
layer, would not necessarily include all states in the world, because
many states' consumption of ozone-depleting substances is
negligible.
Each state i ∈ N sets a policy
xi > 0. One can think of this as a
policy that produces negative externalities such as the amount of
pollution produced by the state. Each state has an ideal level for its
own policy, which I denote zi > 0. I
assume that i's ideal level for the other states'
policies is zero. This assumption greatly reduces the amount of
notation in the model and is not unreasonable substantively. If, for
instance, one is discussing an environmental treaty, the assumption
implies that states do not want other states to pollute at all.
Although there are cases that violate this assumption, it seems
reasonable for many cases and offers substantial gains in the
tractability of the model. Each state's utility is characterized
by a standard quadratic loss function. Given this setup, each state
will set its policy at its ideal point
(zi) in the absence of an agreement, and
this outcome is globally suboptimal (this is a standard result, so I
omit the proof). Each state would be willing to trade some reduction in
its policy for some reduction in other states' policies. To
accomplish this the states can agree to a treaty that reduces their
policies. I will now discuss a game of bargaining over such a treaty
and the subsequent enforcement of the agreement.
The game form can be described as follows. The game is divided into
two phases, a bargaining phase and an enforcement phase. Each player
can take actions at discrete times t∈{1, 2, 3, …}
that correspond to the stages of the relevant phase of the game. I will
begin by describing the bargaining phase. “Nature” chooses
a proposer from N according to some rule (more on this rule
later). The chosen proposer then makes a proposal Π1
that includes a list of states to be invited along with cooperative
policies, ci ≥ 0, for each of them. The
proposal does not specify policies for uninvited states (that is, if
Π1 is accepted, those states may set their policies
wherever they like.) The set of states that the proposer invites is
allowed to be empty. The invited states either accept or reject
Π1. If one or more of these rejects Π1,
the proposal fails and bargaining proceeds to the next stage (stage 2)
and the stage game repeats. Nature picks the next proposer from
N according to the rule. The proposer that nature has just
chosen then makes a proposal Π2 that includes a list of
the states invited and their policies. This list can include states
that were not invited in the previous proposal. The invited states
either accept or reject Π2. If one or more of them
rejects it, the game goes on to stage three. The bargaining stage game
repeats in this way until all states accept the current proposal. Once
this occurs the bargaining phase of the game ends and the accepted
proposal is implemented. The game then proceeds to an enforcement phase
in which the members of the agreement play a multilateral repeated
prisoners' dilemma. In each stage of this phase of the game,
members of the agreement either set their policies no higher than those
mandated by the agreement or they do not (that is, they cheat). If a
member cheats, the other members of the agreement punish the cheater by
reverting to “punishment levels” of their respective
policies (more on these later) for a specified period of time. After
punishing the cheater for this specified period of time, states return
to their cooperative policies as specified by the agreement. Nonmembers
are allowed to set their policies wherever they like without
punishment.
The empirical record does not suggest a clear answer to the question,
“Who proposes?” While the United States may have had a
dominant role in proposing many multilateral agreements during the
early postwar years, a cursory review of the more recent history of the
creation of multilateral agreements reveals that it no longer does. For
the purposes of this model it is only necessary to assume that each
state i is chosen to be the proposer with some probability
ri and that this probability does not
change from period to period.13
Obviously
0 ≤ ri ≤ 1 for all i ∈
N and [sum ]i∈N
ri = 1.
Note that, if chosen
twice in succession, states may make counterproposals to their
(previous) proposals.
I now return to the issue of punishments. The treaty must be
self-enforcing. Each state must receive utility from complying with the
treaty that is at least as high as it would receive from cheating on
the agreement and being punished for it. The proposer's problem is
to put forward a treaty that maximizes its utility subject to the
constraint that all the signatories will comply with it. One must
specify the punishments to be able to determine this constraint. For
simplicity I assume the members of the treaty will punish cheating by
returning to their noncooperative Nash equilibrium policy levels (that
is, set their policies at their ideal levels) for p periods.
Note that in punishing a cheater, the members of the agreement also
“punish” each other. This is unavoidable given the
nonexcludability assumed here.14
See
Pahre 1994 for further discussion of
enforcement in a multilateral setting.
I would like to highlight one final feature of the game form.
Agreement requires unanimity. If any invited state rejects the treaty,
no treaty is implemented in that period and the bargaining continues.
Without this feature some nonproposers may have an incentive to reject
the treaty in order to free ride on the cooperation of those that
signed it. This is a step-level public goods problem with incentives
similar to those of the well-known “paradox of (not)
voting.”15
A sufficient
number of states must ratify the treaty for it to come into force.
States may prefer that other states ratify the treaty, so that it would
come into force and they could free ride on the cooperation of the
other members. However, if too many states play this strategy, the
treaty will not come into force in which case states will regret their
decision not to ratify the treaty. The game form I have described
allows one to ignore these complications by effectively taking away the
nonproposers' incentives to reject the treaty to free ride on the
cooperation of the other members. Admittedly this assumption is a
limitation of the model. In practice, treaties do not require that all
relevant states ratify them before coming into force, although treaties
usually do require that some substantial number of them do. Indeed the
treaty's ratification requirement is typically part of the
equilibrium—that is the number of ratifications required for the
treaty to enter into force is decided as part of the negotiations.
Unfortunately, endogenizing the ratification requirement is beyond the
scope of this article.
To give an intuitive idea of how the model works, I turn to the
proposer's problem. The proposer wants to put forward an agreement
that both makes it as well off as possible and will be accepted by the
other states. Indeed the proposer wants to make the other states an
offer that just makes them indifferent between accepting and rejecting
it. If the proposer gives the invited states a better offer, then it
will have given them more than it had to do to get them to sign the
treaty. If the proposer offers the invited states less than that
amount, they will reject the treaty, no agreement will occur in that
period, and a new, potentially different, proposer will be chosen in
the next period. Thus the proposer will make a proposal that equates
the other states' utility from accepting it to their utility from
rejecting it. I call this constraint the “participation
constraint,” because this constraint must be met if the invited
state is to participate in the agreement.
There is a complication, however. The proposal must offer each member
sufficient utility to keep them compliant with the agreement. Clearly,
it does the proposer no good to obtain a treaty that the members will
certainly cheat on. Therefore, if the proposal that just meets the
invited states' participation constraints does not offer
sufficient rewards to keep a state compliant with the agreement, the
proposer must offer that state a better proposal—one just
sufficient to ensure that state's compliance. I will call this
constraint the “compliance constraint.” See the Appendix
for details.16
See Fearon 1998 for a discussion of the contradictions
between bargaining and enforcement in the context of a different
model.
Here too there is no reason for the proposer to offer
such a state more than that amount because doing so is unnecessary to
ensure that state's compliance and only offers the proposer lower
utility.
I call the set of states for whom the compliance constraint binds
C and the set of states for whom the participation constraint
binds P. I show in the Appendix that both of these constraints
cannot bind, so a state is either a member of C or P
or neither. If neither constraint binds for some state, that state will
sign and comply with the given agreement for any cooperative level of
its policy that the proposer offers, so the proposer will set that
policy at zero (see the Appendix for more details). In this case the
state's participation and compliance constraints are not binding
so it will actually receive more from the agreement than is necessary
to get it to sign and comply with the agreement.
Results
As shown by Proposition 1, which is presented in the Appendix, the
equilibrium proposal in this model possesses some standard features of
complete information alternating offers bargaining games: the outcome
is unique, bargaining ends in the first period, and the proposer
receives a larger share of the gains, ceteris paribus. The
reason for these features is the same as in the more standard
two-person game so I do not dwell on them here.17
Instead I focus on the main substantive point of this
article, namely that there is no broader-deeper trade-off in the
situation described by this model.
First, one must establish the equilibrium policies. Without loss of
generality, I index the proposer as state 1. As proved in Proposition
1, the proposer's equilibrium cooperative policy is:
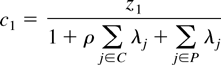
Proposition 1 also shows that the nonproposers' equilibrium
cooperative policies are:
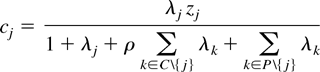
The λs in Equations (1) and (2) are the Kuhn-Tucker multipliers
on the members' relevant constraints and ρ is analogous to a
discount rate (see the Appendix for more details).18
I show in the Appendix that the proposer's
participation and compliance constraints do not bind.
In the
discussion that follows it will be convenient to refer to the
cooperative equilibrium policies in Equations (1) and (2) as
percentages of the respective state's ideal level, which I will
call α
j, so that
cj = α
j
zj.
The main difference between this model and one that produces a
broader-deeper trade-off is that states are allowed to set different
policies. Equations (1) and (2) illustrate how states' policies
will differ. States that have less cooperative policies (for example,
more pollution) in the noncooperative equilibrium will also have less
cooperative policies in the equilibrium treaty. There are two effects
that produce this result. First, each state's cooperative policy
is some percentage of its noncooperative policy,
zj, so that states with high
zjs will also have higher treaty-mandated
policies. Second, states with higher noncooperative policies will have
larger λs, and thus these states will also reduce by smaller
percentages. λj is the multiplier on state
j's relevant constraint and will be larger the more
binding the constraint is. States in P with large
zjs will have larger λs because their
participation constraints are more binding. The reason for this is that
these states receive relatively higher utility from the status quo so
they have to be given a better deal, (for example, allowed to pollute
more than other states) to get them to sign the agreement. States with
low zjs, by contrast, receive lower
utility from the noncooperative status quo and therefore their
participation constraints are less binding. These states are willing to
accept less lucrative deals, and so the proposer offers them less in
equilibrium. States in C with large
zjs will have more binding compliance
constraints for a similar reason—their utility from the status
quo, which is the utility that they will receive when punished, is
higher. Punishment is not so harmful for them so they must be given
higher utility from cooperation to induce them to comply. The proposer
accomplishes this by reducing their policy by less.
A numerical example will help illustrate these effects. Imagine a
five-state multilateral in which each state's ideal level for its
own policy is 1 and for the other states' policies is 0, the
states' common discount rate is 0.98 and
ri = 0.2 for all states. State 1 is the
proposer. Solving for the equilibrium policies shows that all
nonproposers are in group P (the compliance constraint does
not bind but the participation constraint does) and the
λis are approximately 0.514. Plugging these
multipliers into (1) and (2) reveals that the equilibrium policy for
the proposer is approximately 0.486 and for the nonproposers is 0.25.
Incidentally this example shows the substantial benefits of being
proposer in this model.
Now suppose instead that state 5's ideal level for its own
policy was not 1 but 2, and all other parameters were kept the same. In
this case state 5 is still in P but λ5
increases to 1.302 and λ2 = λ3 =
λ4 falls to 0.214. The states' policies in this
case would be 0.514 for state 1, 1.34 for state 5, and 0.11 for the
other states. State 5 would only have to reduce its policy to about
two-thirds of its noncooperative level while state 1 (the proposer)
would have to reduce to 51 percent and the other states would have to
reduce to about eleven percent of their noncooperative level.
Why the difference? In the first example all three states received
the same level of utility from the noncooperative status quo, namely
−4. In the second example, states 1 through 4's utility from
the noncooperative status quo is −7 while state 5's utility
from the noncooperative status quo is −4. States 1 through 4 are
disadvantaged by the status quo relative to state 5 in the second
example and, therefore, they are willing to accept a worse cooperative
deal than state 5 is. Decreasing marginal returns play a role as well.
In the second example, state 5's policy is farther away from state
1 through 4's ideal level than state 1 through 4's policies
are from state 5's ideal level. Therefore, a small change in
5's policy generates large gains for 1 through 4. Because state 1
through 4's policies are already relatively close to state
5's ideal level for their policies (zero), states 1 through 4 have
to change their policies by more to generate sufficient gains for state
5 to be willing to sign the agreement.
I now turn to the absence of a broader-deeper trade-off. Proposition
1 shows that the equilibrium treaty will include all N states.
I have not yet established the absence of a broader-deeper trade-off in
this model. To do so I must show that a treaty with fewer than
N members would not be more cooperative (specify lower
policies) than a treaty that included more members. Because the
equilibrium of the model in this article is a treaty among all members
of N, answering the question of whether or not there is a
broader-deeper trade-off necessitates comparing the policies of two
treaties at least one of which is not an equilibrium because it does
not include all n states. Discussing out-of-equilibrium
behavior opens a Pandora's box because there are an infinite
number of such equilibria. Therefore to discuss the broader-deeper
trade-off in a theoretically meaningful way, one needs to put some
additional structure on the discussion.
As I understand it, the claim that a broader-deeper trade-off exists
is a counterfactual claim about what the policies in a particular
agreement would be if somehow the membership of that treaty could be
changed. More precisely, the claim that there is a broader-deeper
trade-off, as I understand it, is that if some proper subset of
N, which I will call M, could commit to excluding the
states in N[setmn ]M from the agreement, the
equilibrium policies from such an agreement would be lower (more
cooperative) than the equilibrium policies in the treaty with more
members. This exogenous commitment device, while admittedly artificial,
is necessary in this model because, as I mentioned, without such a
commitment device a treaty among a proper subset of N will not
occur. For the purposes of this article, I assume that such a
commitment device exists. Proposition 2, which is presented in the
Appendix, shows that in such a case the treaty among M is not
deeper than a more inclusive treaty. More formally:
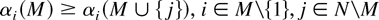
where αi(M) is state
i's cooperative policy from an agreement with some given
set of states M, cardinality m < n, as a
percentage of its ideal level, zi.
Equation (3) simply states that the policies of the nonproposing
states will not be larger (less cooperative) for a treaty with more
members. Adding an extra member can only change a member's policy
by lowering it.19
Note that Proposition 2
says nothing about the effect of adding more members on the
proposer's policy. The proposer's policy will typically be
higher from a more inclusive treaty than a less inclusive one, but it
will not be so much higher as to completely offset the lower policies
of the nonproposers. In no case would the proposer's policy be
higher than z1.
In this sense, broader
treaties exhibit at least as much cooperation as narrower ones, and can
actually be deeper. This statement is proven in Proposition 2 in the
Appendix.
This result is perhaps best explained by thinking through the
proposer's incentives. Imagine the proposer has already determined
its optimal proposal for an agreement among the members of M
and is deciding if it would prefer to propose its optimal treaty among
the members of M ∪ {j}, j ∈
N[setmn ]M instead. In other words, the proposer is
deciding if it would prefer to make a proposal that includes some extra
state j in the agreement. For the sake of argument, I take a
look at the effect of some small negative change on this additional
state's policies as a result of it being added to the agreement.
Suppose the additional state's policy is reduced from
zj to something slightly less than that,
and the policies of the states in M[setmn ]{1} remain fixed at
their levels from a treaty without the additional state (that is, a
treaty just among the members of M). All of these policies
will in fact change in equilibrium—this is just for the sake of
argument. Such an agreement obviously increases the utility of the
states in M, because it reduces the additional state's
policy from zj to something less than
that.
The policies of the invited states (that is, M[setmn ]{1}) in
an agreement among the members of M had been chosen to give
each of them just enough utility to get them to sign that agreement
(unless they needed more to keep them compliant with it). The proposer
has no incentive to give them any more than that amount, because doing
so only offers them more utility than necessary and the proposer less
utility than possible. Now with the reduction in the added state's
policy these states are in fact receiving more utility than necessary
to sign the treaty and remain compliant with it, and so adding the
extra state provides the proposer an opportunity to increase its own
utility while keeping the invited states' utility at the level
necessary for them to sign the agreement and remain compliant.
The proposer can do this in one of three ways: (1) increase its
policy toward its ideal level, z1, (2) reduce the
policies of the invited states (M[setmn ]{1}) toward the
proposer's ideal level for them (zero) or (3) some combination of
(1) and (2). Consider option (1) first. If the proposer increases its
policy toward its ideal level, it will increase its utility and
decrease the utility of the invited states (recall that their ideal
level for the proposer's policy is 0). The proposer can do this up
to the point that the invited states are indifferent between accepting
the agreement and rejecting it (unless they need greater utility to
remain compliant with the agreement), but there is only this
“first order” effect on the proposer's utility.
Compare this to option (2) where the proposer reduces the invited
state's policies toward zero. It is immediately apparent that this
is a more fruitful approach. There are more states whose policies the
proposer can change in this option. In option (1) the proposer was only
able to change one state's policy (its own), while in option (2)
the proposer can change m − 1 states policies (that is,
the number of states in M besides itself). But there is also a
second-order effect in adopting option (2). Consider the effect of
reducing the policy of state 2 ∈ M. The proposer can
reduce 2's policy to the point at which state 2 is indifferent
between accepting the agreement and rejecting. Doing so increases the
utility of all states in M[setmn ]{2}—the proposer as
well as the other invited states. Similarly reducing state 3's
policies in this way increases the proposer's utility and that of
all the other states in M. The proposer can reduce the
policies of every member of M[setmn ]{1} in this way and in the
process generate second-order increases in utility for the other
members of M. What will the proposer do with these
second-order increases in the invited states' utility? The same
logic applies, so the proposer will do the same thing—reduce
their policies even further to generate even more gains. Adopting
option (2) creates a second round of utility increases for each
state—utility increases that the proposer can exploit by reducing
the invited states' policies even further. For this reason the
reductions in the invited states' policies will be greater in
option (2) than the increase in state 1's policy could be in
option (1). In short, option (2) allows the proposer to move more
policies toward its ideal point, and it allows the proposer to change
each of those policies by a larger amount. Eventually, however, the
effects of decreasing marginal gains from this approach will set in and
the proposer will want to use some of the added gains in cooperation to
increase its own policy. Thus the proposer will adopt option (3).20
Once again this discussion applies to
states whose compliance or participation constraints bind. States for
whom neither constraint binds in a treaty with M will also
have nonbinding constraints in a treaty with M ∪
{j}. The treaty-mandated policies of these states are zero in
a treaty with M and zero in a treaty with M ∪
{j}, because their policy cannot go below zero.
I now present some numerical examples to illustrate the features of
this model, using an example I discussed previously: five states,
zi = 1, i ∈{1,…,4},
z5 = 2, δ = 0.98. I compare the characteristics
of two treaties in this world—one that includes all five states
and a second in which the state with the largest ideal level is
excluded. State 1 is the proposer in both examples. Several features of
the equilibria from these two treaties are summarized in Table 1. The first column indicates the membership
of the treaty. The second and third columns list the Kuhn-Tucker
multipliers for states 2 and 5 respectively. The equilibrium policies
of states 1, 2, and 5 are indicated in the next three columns; and the
utility obtained from the treaty by states 1, 2, and 5 are indicated in
columns 7, 8, and 9 respectively. The Kuhn-Tucker multipliers,
policies, and utilities of states 3 and 4 are identical to those of
state 2 in these two examples. The final column presents the total
amount of “pollution” (that is the total amount of the
policy) in the world. The first row lists these results for the treaty
among all five members, assuming that ri =
0.2. The second row shows the result if the states with lower ideal
levels, states 1 through 4, could somehow commit to excluding state 5
from their agreement. Doing so necessitates a change in
ri which I assume is 0.25 for all four
states.
The results in Table 1 clearly indicate the
absence of a broader-deeper trade-off. The cooperative policies of the
nonproposing members are larger (less cooperative) in the four-state
treaty than they are in the five-state treaty. The proposer's
policy is reduced somewhat in the four-state treaty but not
sufficiently to offset the increase in the policies of states 2 through
4. State 5's policy obviously remains fixed at its ideal point of
2 in the four-member treaty. The last column shows that the total
amount of the pollution increases in the four-state treaty compared to
the one with all five states. In addition to the increased pollution of
country 5, the total amount of pollution produced by countries 1
through 4 rises from about 0.84 to 1.465.
Table 1 also illustrates why it is
necessary to make the assumption that there is some exogenous mechanism
that allows states 1 through 4 to commit to this four-member treaty.
Without such an assumption, state 1 would never propose this treaty
because its utility is higher from the five-member treaty. Furthermore,
even if state 1 did propose the four-member treaty, states 2 through 4
would reject it because it does not meet their participation
constraint. The utility that they receive from the five-member treaty,
−2.87, is the level that meets this constraint. The utility that
they receive from the four-member treaty is lower than that level so
they would be better off, in expectation, rejecting such a proposal and
taking the negotiations to the next round.
Finally notice that state 5 is actually better off by being excluded.
It would prefer to free ride. Why then would it ever accept the treaty
in equilibrium? This is where the unanimity assumption comes in. If
state 5 rejects the treaty, no treaty will occur in that period and the
negotiations will go to the next round. In such a case, state 5 would
not in fact receive the free-riding utility because states will
continue to set their policies at the noncooperative level while the
bargaining continues. Thus by rejecting the treaty state 5 does not get
the free-ride value. Instead it only prolongs the negotiations.
I have asserted that the identical-policy assumption is crucial to
producing a broader-deeper trade-off. To illustrate the importance of
this assumption I now look at what would happen in this model if all
states are required to set the same cooperative policy level,
c*. The equilibrium policy in that case would be:
Notice the difference between this cooperative policy and the ones
described in Equations (1) and (2). The policies in Equations (1) and
(2) are functions only of each individual state i's ideal
level for its own policy, zi. The single
cooperative policy in Equation (4) by contrast is a weighted average of
all members' ideal levels. It is easy to construct
examples where there are no feasible agreements that both restrict all
members to identical policy levels and contain all members of
N. In such cases, agreements can only be created if the states
with the largest ideal points are excluded. The purpose of this article
is to question the general appropriateness of that restriction.
In summary, the key to the absence of a broader-deeper trade-off in
the model is allowing states to set their policies at different levels.
Imagine a case of three states—1, 2, and 3—deciding to
create a multilateral agreement to reduce pollution of a common body of
water. Two of the states, 1 and 2, are quite committed to this
environmental project, but state 3 is not at all committed. If states 1
and 2 can come to an agreement with relatively low amounts of pollution
between them, why should adding the third state in any way require them
to increase their pollution from that level? Increasing their (1's
and 2's) pollution in no way makes the agreement more palatable to
state 3. On the contrary, state 3 wants to keep its pollution levels
high; it does not want the other two states' pollution levels to
be high. An agreement in which the two “environmentalist”
states set relatively low pollution limits and the third state sets a
relatively high pollution limit (but still lower than the pretreaty
level) makes all three states better off. The broader-deeper trade-off
is an artifact of the often unspoken assumption that all members of a
treaty must set their policy at the same level, so that a lower level
of cooperation for everyone is required to coax the more intransigent
states into the agreement. But, this assumption is not applicable to
many multilateral institutions and as such should not always guide
one's prescriptions about the proper size of multilaterals.
Examples
One does not have to look hard to find examples of bargaining over
multilaterals where concerns about a broader-deeper trade-off simply
did not surface. I have already discussed the cases of the GATT, the
Bretton Woods system, and the Montreal Protocol.21
One has to be cautious in interpreting the history of
trade policy cooperation in terms of the model presented here, because
trade policy cooperation is clearly a case where benefits are
excludable. I expect the results to translate to excludable benefits
treaties, although I have not actually modeled it.
These
treaties did not require their members to set their policies at an
identical level and they did not seem to exhibit a broader-deeper
trade-off.
One can compare these agreements to EU institutions that often seem
to meet the identical-policy assumption more closely. For instance, the
EU (then EC) has set external trade policy as a unit since the late
1950s, which required that some states actually raise their tariffs on
trade with states outside the EC. Indeed this was the cause for some
trade frictions between the United States and the EC as some members of
the EC raised tariffs on some products (notably frozen chicken) to
comply with the Common External Tariff (CET). The United States argued
that as states raised their tariff rates on frozen chicken to comply
with the CET, they were violating their GATT commitments. The United
States retaliated, starting “The Chicken War.”22
European monetary union is another example where the identical-policy
assumption is appropriate because a single money supply is set for all
states in the monetary union. Issues of “broader versus
deeper” did arise in the creation of monetary union. There were
discussions of a “multi-speed” Europe in which “hard
core” states would proceed with monetary union while “soft
core” states waited.23
Furthermore, the
stringent conditions placed on states' macroeconomic policies
(size of budget deficit, inflation, and so on) before they could join
the union might be interpreted as an attempt to exclude states that
would have had overly inflationary preferences on macroeconomic
policy.
I should add, though, that even in the EU context the
identical-policy assumption and the broader-deeper trade-off that it
induces is not universally appropriate. Interestingly, cooperation has
actually deepened in the EU even as its membership has broadened. Pahre
offers one explanation for this phenomena. He presents a model of joint
provision of a club good. Enlarging the membership increases the number
of states that can contribute to the cooperative provision of this
good, thus “deepening” cooperation in the sense of greater
provision of it.24
In the context of the model in this article, it might be possible to
interpret the move in the EU away from harmonization and in favor of
mutual recognition in some circumstances as an attempt to get around
the broader-deeper trade-off that the identical-policy approach
induces. In other words, as the membership of the EU has grown and
become more diverse in terms of policy preferences, the members have
been forced to abandon their identical-policy approach in favor of
flexibility as a way of getting around the broader-deeper
trade-off.25
I am indebted to Lisa Martin
for these points.
In summary, the EU provides an example in which (1) the
identical-policy assumption is sometimes appropriate, (2) there were
concerns about “broader versus deeper,” and (3) some
potential members were effectively excluded as a result of it. The
point of this article is that these conditions are not universal
(indeed it was fairly easy to come up with examples where these
conditions were not met). In other words, the identical-policy
assumption and the tension between broader and deeper that it generates
is not appropriate for the general class of multilateral agreements. As
such, the normative conclusion that those treaties should be exclusive
does not necessarily follow.
Conclusion
The claim that there is a trade-off between broader and deeper in
international multilateral agreements flows from the assumption that
the members of such agreements must set their policy at identical
levels. This assumption is not appropriate for many important
multilateral agreements, because states are allowed to set their
policies at different levels. In multilateral agreements where each
state sets a different policy level, the broader-deeper trade-off does
not exist and the policy implication that membership in such agreements
should be exclusive to a “hard core” of committed
cooperators does not follow. The model in this article explains the
historical patterns of the creation of some important multilateral
agreements better than the “narrower and deeper is better”
model does. In particular, it explains why the United States was
interested in making the GATT and the Bretton Woods system as expansive
as possible. It explains the same pattern in negotiations over more
recent multilateral agreements such as the Montreal and Kyoto
Protocols. It also explains why those agreements included (or at least
attempted to include) states that did not appear to be particularly
committed to the principles of liberal world trade, stable exchange
rates, environmentalism, and so on.
The model also generates several interesting empirical implications.
For instance, agreements that require members to adhere to a single
cooperative policy are more likely to exhibit a broader-deeper
trade-off and, therefore, should be more exclusive than agreements that
allow greater flexibility in states' cooperative policies. There
are many avenues for future theoretical work as well. One of the more
prominent areas to research would be explaining why some treaties
require an identical policy and some do not. Looking at different types
of cooperation problems may provide one answer. In this model the
purpose of cooperation is to limit policies with negative
externalities, but for some types of agreements arriving at a single
policy on which the members will coordinate is the whole point. This
would be the case if there were some kind of network externalities
associated with the policy. A second explanation may be that some
subset of states may find that if they first unify their policymaking
process they will have greater bargaining leverage in a larger
bargaining game with the rest of the world. This may be part of the
reason why Europe decided to unify its trade and monetary policy.
Obviously, there is still much work to be done in understanding
bargaining over multilateral agreements. I make no claims about the
generality of the game form presented in this article. Indeed it would
be impossible to do so because so little is known about the
“general” case of bargaining over multilateral agreements.
For this reason, empirical work on how past agreements were negotiated
will be very useful. Beyond the few most famous agreements, there is
not a great deal of available data on which states proposed agreements,
how long bargaining over them took, and so on. Gathering such data will
be time consuming but very important.
I hope to accomplish three goals with publication at this stage.
First, I would like to convince those who research the creation of
multilateral treaties that modeling is not so difficult as to be
avoided altogether, and I offer a simple model as a starting point.
Second, I would like to call into question the appropriateness of the
identical-policy assumption for many important multilateral agreements.
Finally, I would like to caution that the policy recommendations that
follow from that assumption, namely excluding states that would
generate substantial cooperative gains, are questionable.
Appendix: Formal Presentation of the Model
The game form is described in the main text. There are N
relevant states, cardinality n. Each of these states receives
utility from its own and other states' policies according to the
following quadratic loss function.
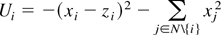
Equation (A1) implies that states have a dominant strategy to set
their policy at zi when they are not
members of an agreement. Other choices of utility function might imply
that states increase their policies when other states reduce theirs. I
have chosen the utility function in equation A1 because it is
reasonable and simplifies the model.
Call the set of members of the agreement M, cardinality
m ≤ n. X =
[sum ]h∈N[setmn ]M
xh2. All of the states have a
common discount rate δ. The proposer wants to ensure that the other
states accept its proposal and comply with the resulting agreement.
Compliance requires:
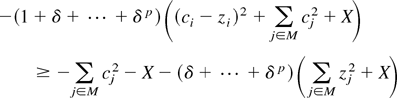
for all i ∈ M, which simplifies to:
where ρ = (δ + … + δp)/(1
+ δ + … + δp) and p is the
number of punishment periods.
As in other models of international cooperation, if the “shadow
of the future” is not long enough there will not be sufficient
gains from cooperation to ensure the compliance of the members of the
agreement. In this model the shadow of the future is captured by ρ,
which is a combination of the discount rate and the number of
punishment periods (ρ acts like the usual discount rate,
ρ(p) < ρ(p + 1) and
limp→∞ ρ = δ). I assume that
ρ is not “too low” by this criterion throughout the
article.
Notice that, as long as there is some bilateral treaty with some
state j with which the proposer will comply, the proposer will
always comply with a multilateral treaty that contains state j
and maximizes the proposer's utility. To see why, notice that
proposer i will comply with a bilateral treaty with state
j if the following is true:
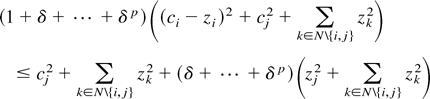
The worst-case scenario for the proposer is that it could add another
state k to this agreement with cooperative policies
ck = zk and
not change its policies or those of state j. Doing so will not
lower the proposer's utility. Thus, the proposal that includes
state k and maximizes the proposer's utility cannot lower
that utility and therefore adding some state k to the treaty
will either not alter the above inequality relation or will strengthen
it. Obviously if no such bilateral treaty with some state j
exists, then there is no possibility of any treaty. Therefore, for the
remainder of the Appendix, I will assume that such a treaty exists,
which, by the argument above, implies that the proposer will comply
with the treaty it proposes.
To ensure participation proposer i must offer the
nonproposing state j per period utility
Vji such that:
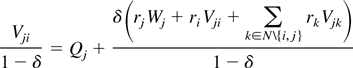
where Qj is state j's per
period utility from the noncooperative equilibrium,
Wj is the per period utility that state
j would receive from the equilibrium agreement when it is
proposer, and rj is state
j's probability of being chosen proposer.
There is an equation like (A3) for each state indexed by k
in Equation (A3). These equations form a system that can be solved
recursively to yield the level of utility that will meet state
j's participation constraint solely as a function of the
ris, δ,
Qj, and Wj. I
call this value Vj*. The importance of
Vj* is that unlike
Vji it does not depend on the identity of
the proposer but only on the parameters mentioned above. Furthermore,
Vj* is clearly less than
Wj because it is a weighted average of
Wj and Qj,
which is less than Wj.
State j's per period utility from i's
proposed agreement must be at least equal to
Vj* if j is to accept the
agreement. In other words:
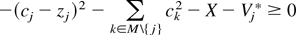
Because Vi* <
Wi, the proposer's own participation
constraint will not bind. Notice also that the proposer will want to
ensure that all states' participation constraints are met because
if they are not states will reject the proposal and the bargaining will
continue to the next period giving the proposer expected utility
Vi* <
Wi.
If δ and/or rj is small,
Vj* may be insufficient to keep state
j compliant, in which case the proposer will have to choose
policies that satisfy state j's compliance constraint as
defined in Equation (A2). More formally the proposer must choose
policies for state j such that:
C is the set of states for which the compliance constraint
binds, and P is the set of states for which the participation
constraint binds. The proposer will choose a proposal so as to maximize
its utility subject to the compliance and participation constraints.
That is, the chosen proposer will propose the agreement that
maximizes:
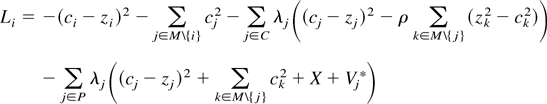
The λs in Equation (A5) are Kuhn-Tucker multipliers on the
constraints in Equations (A2) and (A4).
Maximizing this equation with respect to each
ci and cj and
solving for ci and
cj yields the policies mentioned in
Equations (1) and (2) in the main text. Complementary slackness from
the Kuhn-Tucker conditions requires:
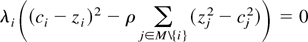
for all i ∈ C, and
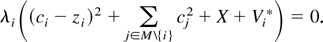
for all i ∈ P. This implies that if
constraints do not bind on state j, λj
is zero. Equations (1) and (2) in turn imply that state
j's cooperative policy will be zero in that case.
For the remainder of this Appendix and without loss of generality, I
will index the proposer as state 1.
Proof of Proposition 1
The equilibrium to the game described above has the following features.
1. Equation (A5) has a unique maximum.
2. The proposer's cooperative policy will be:
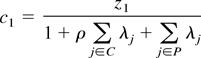
and the cooperative policy of the other states j ∈
M will be:
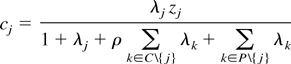
3. Bargaining will end in the first period.
4. The agreement will include all states in
N.
5. All members will comply with the
agreement.
I prove the proposition part by part.
1. Define E as the set of all points
(x1,
x2,…,xm) such
that 0 ≤ xi ≤
zi ∀ i ∈ M.
E is a compact subset of Rm. The
constraints define a closed subset of E, E*, such
that all the constraints are satisfied and E* is nonempty (the
constraints are satisfied at the Nash equilibrium, for example). Thus a
maximum exists. Furthermore, because Equation (A5) is monotonically
increasing in ci and monotonically
decreasing in cj, j ∈
M[setmn ]{i} that maximum is unique.
2. Equations (A6) and (A7) are derived from the first-order
conditions for a maximum to Equation (A5).
3. The proposer chooses the policies of states in P to
ensure their participation. The compliance constraints of states in C
are more binding than their participation constraints. Since the former
constraints are met, the latter will be met as well.
4. Part (3) has already shown that all invited states will accept
their invitations. Furthermore, the proposer has a weakly dominant
strategy to invite all states in N, because the proposer can
always propose a cooperative policy cj =
zj and be no worse off than if it did not
invite state j.
5. The policies of states in C are chosen to ensure their
compliance. For states in P their participation constraints
are more binding than their compliance constraint. The former
constraints are met, insuring the compliance of these states. As shown
above, the proposer will always comply with the equilibrium treaty it
proposes.
Proof of Proposition 2
To recap Proposition 2:
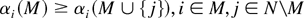
where αi(M) refers to state
i's cooperative policy in an agreement with some given
set of states M as a percentage of state i's
ideal level for its policy, zi.
It is only necessary to discuss the case when
αi(M ∪ {j}) > 0,
because if this condition does not hold the proposition is immediate
because αi(M) ≥ 0.
The proof is by contradiction. Suppose, contrary to Proposition 2,
that ∃ αi(M) <
αi(M ∪ {j}), for some
i ∈ M[setmn ]{1}, j ∈
N[setmn ]M.
I proceed in three steps. The first of these steps will prove that if
one of the αis, i ∈
M[setmn ]{1} increases with the inclusion of state j
∈ N[setmn ]M, all such
αis do. The second step will establish that, if
the proposition is false, the proposer's policy will be reduced as
a result of adding the additional member. The third step will establish
the contradiction that completes the proof.
Step 1
If αi(M) <
αi(M ∪ {j}), for some
i ∈ M[setmn ]{1}, then
αi(M) <
αi(M ∪ {j}) for all
i ∈ M[setmn ]{1}.
Because I am only discussing the case where
αi(M ∪ {j}) > 0, one
can ignore cases where αi(M) = 0. When
αi(M) > 0, the claim is true
because the complementary slackness condition for states in C
requires:
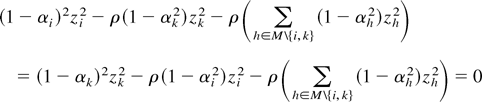
for any two states i and k in C with
nonzero cooperative policies. Rearranging reveals that:
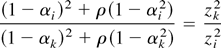
The right side of Equation (A8) is a constant, which means that any
change in αi must be matched by a proportional
change in αk in the same direction. A similar
calculation using the complimentary slackness conditions for states in
P shows that their policies must also move in the same
direction.
Step 2
Show that if αi(M) <
αi(M ∪ {j}), then
α1(M) ≥ α1(M ∪
{j})
It follows from the first-order conditions that:
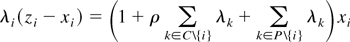
Combining the λs on the right side and solving for
λi yields:
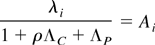
where ΛC = Σi
λi i ∈ C,
ΛP = Σi
λi i ∈ P and
Ai is either
[αi /(1 −
αi)]/{1 +
ρ[αi /(1 −
αi)]} if i ∈ C or
[αi /(1 −
αi)]/{1 +
[αi /(1 −
αi)]} if i ∈ P.
Note that Ai is strictly increasing in
αi. Summing the left and right side of Equation
(A10) over all i ∈ N produces the following
relations:
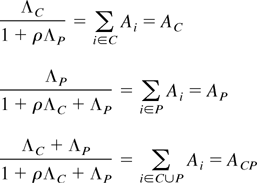
Returning to the earlier discussion, if one of the
Ais on the right side increases with the
addition of the extra member, j, all the
Ais do. Because, by assumption,
αi(M) <
αi(M ∪ {j}), it must be
true that Ai(M) <
Ai(M ∪ {j}),
i ∈ {C, P, CP}. This fact in
turn implies ΛC(M) <
ΛC(M ∪ {j}) and
ΛP(M) <
ΛP(M ∪ {j}). To see this
note that ΛC and ΛP
cannot both decrease with the addition of another state, because if
they did it would imply a decrease in ACP.
Furthermore, ΛC cannot decrease as a result of
adding another state because if it did while ΛP
increased (or did not change), it would imply a decrease in
AC. A similar argument shows that
ΛP cannot decrease while
ΛC increases (or does not change). Thus I have
shown that ΛC(M) <
ΛC(M ∪ {j}) and
ΛP(M) <
ΛP(M ∪ {j}).
Recall from the first order conditions that:
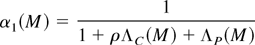
and
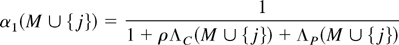
Using Equations (A11) and (A12), the fact that
ΛC(M) <
ΛC(M ∪ {j}) and
ΛP(M) <
ΛP(M ∪ {j}) implies that
α1(M) > α1(M ∪
{j}).
Step 3
In this final step I establish a contradiction. The discussion in
Step 2 has indicated that if it is true that
αi(M) <
αi(M ∪ {j}), then the
effect of adding another state j is to decrease the policy of
state 1. By assumption, this is the agreement that state 1 proposes in
equilibrium (that is, the agreement that maximizes state 1's
utility). Call this agreement Θ(M ∪ {j}),
and call Θ(M) the equilibrium agreement with M.
Consider instead an agreement among the members of M ∪
{j} in which the policies of the states in
M[setmn ]{1} are kept at the levels for the equilibrium treaty
with M, while the policies of state 1 and the extra state,
j, are kept at their levels for an equilibrium treaty among
the members of M ∪ {j}. Call this agreement
Ω. If states 1 and the extra state, j, will comply with
Θ(M ∪ {j}), they will surely comply with
Ω because their policies are the same as those in
Θ(M ∪ {j}) and
αi(M) <
αi(M ∪ {j}), i
∈ M[setmn ]{1}. If the states in M[setmn ]{1} will
comply with Θ(M), they will surely comply with Ω
because their policies are the same as those in Θ(M) and
α1(M ∪ {j}) <
α1(M), and
αj(M ∪ {j})< 1. Ω
offers state 1 unambiguously greater utility than agreement
Θ(M ∪ {j}) does, but Θ(M ∪
{j}) supposedly maximized the proposer's utility. This
contradiction completes the proof.
