During the last days of September 1950, the U.S. administration faced a momentous decision about what to do in Korea: should American forces stop at the 38th parallel, as originally planned, or should they continue into North Korea, and turn the conflict from a war of liberation into a war of unification? The North Koreans could effect no organized resistance to the onslaught of the UN forces, and the only uncertainty clouding the issue had to do with the behavior of the Chinese Communists: would the People's Republic of China (PRC) intervene to forestall unification of Korea on American terms or not?
After some hesitation and an effort to ascertain Chinese intent, the U.S. administration concluded that the risk of Chinese intervention was negligible and therefore the gamble was worth taking. One crucial factor in that estimate was the lack of obvious military preparations that China would have to undertake had it seriously intended to wage war on the United States. In particular, the PRC had not sent troops in significant numbers south of the Yalu River, it had not prepared Beijing for possible aerial raids, it had not mobilized economic or manpower resources, and it had failed to move when it made best sense to do so from a military standpoint—right after General Douglas MacArthur's landing at Inchon. All the Chinese appeared to have done was issue propaganda statements in government-controlled media, send somewhat contradictory messages through a diplomatic channel known to be distrusted by the Americans, fail to make a direct statement to the United Nations, and move some token forces of “volunteers” into North Korea. Even in late November, the Far East Command estimated that there were no more than about 70,000 of these “volunteers” to face over 440,000 UN troops of “vastly superior firepower.”Footnote 1 Confident of success, General MacArthur launched the “home by Christmas” offensive on November 24.
This UN offensive was shattered in a mass Chinese counterattack. Unbeknownst to UN Command, the Chinese had managed to move more than 300,000 crack troops into North Korea. As Appleman documents, their armies had marched in complete secrecy “over circuitous mountain roads” with defense measures that required that during the day “every man, animal, and piece of equipment were to be concealed and camouflaged… When CCF [Chinese Communist Forces] units were compelled for any reason to march by day, they were under standing orders for every man to stop in his tracks and remain motionless if aircraft appeared overhead. Officers were empowered to shoot down immediately any man who violated this order.”Footnote 2 This discipline had enabled the PRC to deploy vast numbers of troops in Korea without being discovered by aerial reconnaissance prior to actual contact.
But if the Chinese wanted to deter the Americans, why did they not make their mobilization public? When they knew the Americans doubted their resolve, why did they not choose an action that would reveal it? Whereas it is doubtless true that the Chinese benefitted from the tactical surprise once fighting began, they practically ensured that the Americans would not believe their threats. As Schelling puts it:
It is not easy to explain why the Chinese entered North Korea so secretly and so suddenly. Had they wanted to stop the United Nations forces at the level, say, of Pyongyang, to protect their own border and territory, a conspicuous early entry in force might have found the U.N. Command content with its accomplishment and in no mood to fight a second war, against Chinese armies, for the remainder of North Korea. They chose instead to launch a surprise attack, with stunning tactical advantages but no prospect of deterrence.Footnote 3
This behavior is indeed puzzling, especially when we consider the logic of costly signaling in crisis bargaining. When two opponents face each other with conflicting demands, the only way to extract concessions is by persuading the other that rejecting the demand would lead to highly unpleasant consequences such as war. The focus is on credible communication of one's intent to wage war should one's demands not be met. As is well known, to achieve credibility, an actor must engage in an action that he would not have taken if he were unresolved, even if the act of taking it would cause the opponent to become convinced that he is resolved. In other words, the action must be sufficiently costly or risky (or both) to make bluffing unattractive. Because a weak actor would not attempt to bluff his way into concessions with such an action, the act of taking it signals strength. Conversely, the absence of such an act can be taken as prima facie evidence of weakness.
In this light, the American administration was justified in drawing what turned out to be a wildly incorrect assessment about Chinese intent. The Chinese had not backed up their threats with any costly or risky actions, and even their demands had been somewhat watered down. For instance, at one point they said that it would be acceptable for South Korean troops to cross the parallel as long as the American forces remained south of it. This unwillingness by the Chinese to take actions that were available to them, and that they could have expected to produce concessions from the United States at an acceptable cost provided they were resolved to forestall unification, eventually persuaded the Americans that the threats were not serious, causing them to embark on unification.Footnote 4
Since the Chinese goal was to deter unification, the logic of crisis bargaining suggests that the Chinese should not have concealed their preparations, and should have made the (admittedly much riskier) public demand for UN forces to remain south of the parallel. The fact that concealment had significant tactical advantages cannot, by itself, explain the decision to mobilize in secret because such an argument presupposes that the Chinese preferred to fight over Korea rather than prevent unification through deterrence, which is a highly dubious assumption.
In this article, I propose a development of our crisis bargaining models that could help shed some light on the puzzling failure to signal strength. First, I show that in a war, a strong player can obtain serious tactical advantage from an opponent who mistakenly believes him to be weak. This is intuitive and unsurprising although there is merit in having this emerge as a result of optimal behavior by both actors instead of assuming it. Second, I consider a crisis model of the type in which strong actors can obtain better negotiated outcomes when their opponent correctly infers that they are strong. I show that when bargaining in a crisis can end in war, a strong actor has contradictory incentives. On one hand, he wants to obtain a better negotiated deal, which requires him to convince his opponent that he is strong. On the other hand, should persuasion fail and war break out, he wants his opponent to believe that he is weak. Somehow, this actor must simultaneously signal strength and weakness.
I show that this contradiction is resolved in equilibrium by the strong actor sometimes feigning weakness during the crisis bargaining phase itself. He pretends to be weak by mimicking the smaller demand of a weak type. Even though this puts him at a disadvantage at the negotiation table, the loss is offset by the gain of tactical surprise on the battlefield that he can achieve if war follows anyway. This explanation also provides a rationale for the Chinese decision to forego the potential benefits of deterrence in order to gain tactical advantages in case deterrence failed.Footnote 5
Signaling Strength in Crises
When two actors with conflicting interests lock horns in a crisis, the only way to secure concessions is for one to convince the other that such concessions, however painful, are preferable to the consequences of failing to comply with demands. In an interstate crisis, the threatened consequences are in the form of a costly and risky war. The stronger an actor is, the worse the expected war outcome for the adversary, and the more that adversary should be prepared to concede in order to avoid it. If there is one conclusion that emerges from studies of crisis bargaining, it is that actors must signal credibly their strength if they are to obtain better deals from their opponents. Pretending to be weak does not pay.
Loosely speaking, the logic goes as follows. If an actor's expected payoff from war is high, his minimally acceptable peace terms are more demanding relative to what they would have been if he were weak. Because actors are loath to concede more than what is absolutely necessary, they need to ascertain what the minimally acceptable terms of the opponent might be. A simple assertion from an actor that he expects to do well in war will not do. If the opponent were to believe it and concede, there would be no risk or cost in making that statement. But then even a weak actor can make such an assertion, which means that the opponent cannot take the assertion at face value. The only way to persuade the opponent that one is strong is by taking an action that is so costly or risky that even if it were to succeed, the weak type could not benefit from imitating it.
We have studied many mechanisms that allow a strong actor to distinguish himself from a weak one by taking some such action. For instance, an actor could make public statements that increase the domestic political costs of backing down, allow his domestic political opponents to contradict him for political gain, put his international reputation on the line, engage both domestic and international audiences, or generate an autonomous risk of inadvertent war.Footnote 6 As Banks has proven for a general class of models, strong types can expect to obtain better negotiated deals but only at the cost of taking actions that are too risky for the weak types to imitate.Footnote 7
The crisis bargaining models that are central to these studies rely on a conceptualization of war as a costly lottery. Both actors must pay to participate in it but only one can win it. The expected payoff from war, usually referred to as the distribution of power, is a fundamental primitive in these models and is assumed to be exogenous. This assumption is carried over to the crisis bargaining models that treat war as a process rather than a costly lottery.Footnote 8
Why does it matter that the distribution of power is assumed to be exogenous? For one, if one maintains this assumption, one cannot study military investment decisions because these presumably change the distribution of capabilities, and as such influence the distribution of power. Powell shows that when the expected payoff from war depends on strategic decisions about how to allocate resources between consumption and arming, the necessity to spend on mutual deterrence creates a commitment problem that may lead to war when peace becomes too expensive to maintain.Footnote 9
More directly related to crisis bargaining, this assumption excludes any actions that might alter the distribution of power. I have argued that military moves—mobilization and deployment of troops, for instance—must necessarily affect it, thus their use as instruments of coercion may have effects that do not obtain in models that do not take this into account.Footnote 10 I have shown that strong types do not, in fact, have to run higher risks in order to obtain better deals: the costliness of increasing military capability discourages bluffing while the concomitant improvement in the distribution of power reduces the opponent's expected war payoff and makes her more likely to concede.
These are theoretical reasons for treating the distribution of power as endogenous. The puzzle of Chinese intervention in the Korean War suggests at least one substantive reason to do so. As the admittedly cursory sketch of that episode illustrates, the PRC concealed its military preparations so thoroughly to gain tactical surprise. It was well known at the time that the superior air power of the UN forces put the Chinese at a serious disadvantage, which is why they tried so hard to obtain Soviet air cover for their land action.Footnote 11 If the Chinese were to expose their preparations, they risked having their forces annihilated before getting a chance to engage the enemy. If the U.S. administration had decided on unification, the revelation of the extent of Chinese mobilization could have also caused the United States to increase its effort in the war, which would similarly have jeopardized the PRC's chances of success.Footnote 12 The upshot is that for both actors, the expected payoff from war depended on the behavior they thought their opponent might engage in. If the Chinese revealed their mobilization, they might have succeeded in deterring the United States but they might have also considerably reduced their payoff from war if deterrence failed. If, on the other hand, they concealed their mobilization, they might not have been able to deter the United States but they would have increased their payoff from war. In other words, the expected distribution of power depended on the actions taken during the crisis.
This episode not only provides a rationale for treating the distribution of power as endogenous, it also suggests a particular timing of decisions that is useful in investigating analogous cases. In Powell's and Slantchev's models, actors make military allocation decisions that fix the distribution of power for the duration of the war before the actual choice to attack.Footnote 13 The decision to fight is then taken after they observe each other's military preparations in light of the distribution of power that results from their actions. The Chinese tactic in the Korean War intervention, on the other hand, was to conceal the actual distribution of power until after the battle was joined. That is, they managed to lull the Americans into a false sense of security that was designed to prevent them from formulating an even more formidable offensive plan that would have attacked whatever vulnerability the Chinese revealed. In that sense, the episode suggests that we might want to think about war-fighting decisions made after bargaining breaks down but in light of information revealed during the bargaining phase.
One simple model with a structure that could address this situation would be an ultimatum crisis bargaining game in which the distribution of power is endogenously determined by actions taken after the ultimatum is rejected. This means that the expected payoff from war will depend on what the actors do when they go to war but that these decisions will be based on the information they obtain during the crisis. This structure allows me to investigate the contradictory incentives the Chinese faced in November: on one hand, they wanted to signal that they were serious and the Americans should not advance to the Yalu River, but on the other hand, they wanted to keep the Americans in the dark about their actual military preparations. As I shall show, this dilemma appears in the model in the following terms: should the strong actor choose a demanding ultimatum that would reveal his strength but put him at a fighting disadvantage if the demand is rejected, or should he choose a middling demand that is not very attractive and will cause the opponent to think he might be weak but that would give him a tactical advantage if it is rejected?
The Model
The model is designed as a simple setting that captures the contradictory incentives of strong players, and has three characteristics: (1) bargaining—an ultimatum to distribute an infinitely divisible benefit; (2) endogenous distribution of power—military effort determines the expected payoff from war; and (3) signaling—military effort can be contingent on information obtained from the crisis bargaining phase.
Two risk-neutral players, i ∈ {1,2} are disputing the two-way partition of a continuously divisible benefit represented by the interval [0,1]. An agreement is a pair (x,1 − x), where x ∈ [0,1] is player 1's share and 1 − x is player 2's share. The players have strictly opposed preferences with u 1(x) = x and u 2(x) = 1 − x. Player 1 begins by making a take-it-or-leave-it demand, x ∈ [0,1], that player 2 can either accept or reject.Footnote 14 If she accepts, the game ends with the agreement (x,1 − x). If she rejects, she decides whether to mobilize additional resources, at cost k 2 > 0, or fight with what she already has. In any case, war occurs and each player pays costs c i > 0. The winner obtains the entire benefit.
The outcome of the war depends on the distribution of power summarized by the probability that player 1 will win. This probability itself depends on player 2's arming choice: if she mobilizes additional resources, player 1's chances of victory decrease. I shall leave the precise functional form of the relationship between arming and victory unspecified. Instead, assume that player 1 can be either weak or strong. If player 2 does not arm, the weak type prevails in the war with probability w n and the strong type prevails with probability s n > w n. If player 2 arms, the weak type prevails with probability w a < w n, and the strong type prevails with probability s a < s n, such that s a > w a (that is, player 2's additional mobilization cannot make the strong type's chance of winning lower than the weak type's). If player 1 is weak, his expected war payoffs are W wn = w n − c 1 if player 2 does not arm, and W wa = w a − c 1 if she does. If player 1 is strong, his expected war payoffs are W sn = s n − c 1 if player 2 does not arm, and W sa = s a − c 1 if she does.
Player 2's war payoff against a weak opponent is 1 − w n − c 2 without arming, and 1 − w a − c 2 − k 2 with arming. Hence, she will not arm against a weak type when k 2 > w n − w a. Analogously, her war payoff against a strong opponent is 1 − s n − c 2 without arming, and 1 − s a − c 2 − k 2 with arming. Hence, she will arm against the strong type when k 2 < s n − s a. To make the model interesting, make the following:
Assumption 1. The marginal effect of building arms on the probability of winning can only justify its cost if the opponent is strong: w n − w a < k 2 < s n − s a.
To ensure that this interval exists, we require that s n − w n > s a − w a. Although this specifies what player 2 would do if she knew her opponent's type, she is unsure about it. Player 1 knows whether he is weak or strong, but player 2 believes that he is strong with probability p and weak with probability 1 − p, and this belief is common knowledge.
Analysis
Under the assumptions, player 2 will certainly arm if she believes her opponent is strong, and will not if she believes he is weak. In between these certainties, her arming decision depends on the posterior belief that she acquires after player 1's ultimatum. Let q denote the (possibly updated) belief that player 1 is strong after his demand. Player 2's war payoffs are W 2n(q) = q(1 − s n) + (1 − q)(1 − w n) − c 2, and W 2a(q) = q(1 − s a) + (1 − q)(1 − w a) − c 2 − k 2, where the superscript denotes her arming choice. Since player 2 will arm when W 2a(q) > W 2n(q), it follows that she will arm when:
The assumptions ensure that q a ∈ (0,1). Therefore, player 2 will arm if q > q a and will not arm otherwise.
I assumed that player 2's arming will reduce player 1's expected payoff from war, and I found that her decision to do so depends on her belief that player 1 is strong. In the “tactical game” that follows the rejection of the crisis ultimatum, player 1's incentives are clear: he wants player 2 to believe that he is weak. (As I shall show in an extension of the model, these incentives also arise in exactly the same way if I model the arming decisions of both sides explicitly.)
The question that we really wish to investigate is whether these incentives extend to the crisis game itself: after all, the only way for player 1 to obtain better deals through bargaining is by convincing player 2 that he is strong. I show that this game has feint equilibria. In these, player 1 always makes a low-value, low-risk demand if he is weak. If he is strong, however, he sometimes makes a high-value, high-risk demand (which credibly signals his strength) but sometimes pretends to be weak by making the low-value, low-risk demand. The risks and the intensity of fighting are endogenous: player 2 rejects the low-value demand with lower probability than the high-value demand, but she arms only when rejecting the high-value demand. Hence, the strong player 1 foregoes some of the bargaining benefit that would arise from revealing his type to obtain some of the fighting benefit that would arise should negotiations fail and player 2 mistakenly believes he is weak.
The Feint Equilibria
The construction of feint equilibria proceeds in several steps. First, I show that the separating demand that only the strong type is willing to make must be larger, risker, and costlier than the demand that both he and the weak type are willing to pool on. Second, I show that player 2 would reject very large demands and accept very small demands regardless of her beliefs. This renders meaningless attempts to manipulate her beliefs (through feints or signaling) with demands in those ranges. Third, I specify intuitive beliefs for demands where player 2's reaction does depend on her beliefs: the more player 1 demands, the more player 2 is convinced that he is strong. Fourth, I show that when the fighting benefit from deceiving player 2 is not much greater than the low-value demand, the feint could be riskless (that is, the low-value demand might carry no risk of war). I then derive a sufficient condition—the fighting advantage from a feint is very large compared to the low-value demand—that guarantees that the feint must carry a strictly positive risk of war.
Let x denote the demand that both types are willing to make, and let x denote the demand that only the strong type is willing to make. Let r denote the probability with which player 2 rejects x without arming, and r denote the probability with which she rejects x with arming. Incentive-compatibility equilibrium conditions require that x is the low-value demand, and r is the low risk associated with it, as the following lemma demonstrates.
Lemma 1. In any feint equilibrium, x < x and r < r.
Proof.
In a feint equilibrium,
Adding these inequalities gives r(s n − w n) ≤ r(s a − w a), but from the assumptions we know that s n − s a > w n − w a, which implies that s n − w n > s a − w a, so this condition requires that r < r, as claimed. Furthermore, because W sn > W sa, this implies that if x ≥ x, the indifference condition for the strong type cannot be satisfied. Therefore, x < x.
Player 2 does not arm for any q ≤ q a, so the best war payoff (without arming) is W2 = 1 − w n − c 2. She arms for any q > q a, so the worst war payoff (with arming) is W2 = 1 − s a − c 2 − k 2. Thus, in any equilibrium, if player 1 demands x < x 1 = 1 − W2, player 2 will accept, and if he demands x > x 2 = 1 − W2, she will reject. The only belief-contingent responses are to demands in [x 1,x 2]. Since player 2 must reject some offers with positive probability, I am interested in beliefs that leave her indifferent between accepting the demand, and rejecting it. Let q solve x = 1 − W 2n(q) if q ≤ q a, and solve x = 1 − W 2a(q) otherwise. This yields the cut-point demand x a = x 1 + q a(s n − w n) where x a = 1 − W 2n(q a) = 1 − W 2a(q a). Define the posterior beliefs as follows:
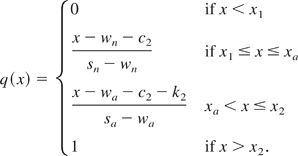
It is clear from inspection that q(x) is continuous because W 2n(q a) = W 2a(q a) and strictly increasing (which implies the belief is unique). These beliefs are intuitively appealing: the more player 1 demands, the higher the probability that player 2 will assign to him being strong. The low-value demand is the largest demand player 2 would accept without arming: x = x a. The high-value demand is the largest demand she would accepting with arming: x = x 2.
The weak type strictly prefers player 2 to accept even the low-value demand: x − W wn = C + q a(s n − w n) > 0, where C = c 1 + c 2. The strong type, on the other hand, might actually prefer player 2 to reject the low-value demand and fight unprepared. In particular, if this demand is worse than fighting even a prepared opponent, then its risk must be strictly positive or else the strong type would not be willing to make it. Observe that (ICs) gives us the risk of the high-value demand:
Since r < 1 must be satisfied, r > 0 will hold whenever x ≤ W sa, or:
In this situation, the strong type attempts to deceive player 2 into incorrectly rejecting the low-value demand and entering the war unprepared. It is always possible to construct a feint equilibrium with a riskless low-value demand when (D) is not satisfied. Although one can also construct equilibria with a strictly positive risk, these are all Pareto inferior. When (D) is satisfied, however, the low-value demand must be risky. In this case, the risk should not be too high or the weak type would not be willing to run it, preferring to deviate to the largest possible riskless demand, x 1. The upper bound on the risk that makes such a deviation unprofitable is r ≤ (x − x 1)/(x − W wn). Since r should be neither too large nor too small, the necessary condition that admits the existence of such values is that the upper bound is at least as large as the lower bound, or
It is worth emphasizing that (4) is not binding when (D) is not satisfied because in this case the lower bound is at 0, which trivially satisfies the requirements.
Proposition 1. If p > q a ≥ q, there are perfect Bayesian equilibria in which the weak player 1 demands x = x a, and the strong player 1 demands x with probability φ = (1 − p)q a /[p(1 − q a)] and x = x 2 with probability 1 − φ. Player 2 accepts any x ≤ x 1, rejects any x ∈ (x 1,x] with probability r, rejects any x ∈ (x,x] with probability r, and rejects any x > x for sure. The rejection probabilities are r = 0 if (D) is not satisfied, and r ∈ (1 − (s n − s a)/(W sn − x),(x − x 1)/(x − W wn)) otherwise, and r is as defined in (3). On and off the path, beliefs are defined in (2).
The intuition for this result is as follows. If player 1 is strong, he can credibly reveal this provided he is willing to run higher risks of war in which the opponent is prepared. The mechanism is the same as in the standard costly signaling models. To prevent bluffing from weak types, the strong types must incur costs and risks that the weak ones would not be willing to incur even if doing so would convince the opponent they are strong. Bluffing, however, is not the only strategic problem player 2 faces: sandbagging is another.
Player 2 reacts to the low-value demand by accepting it with a higher probability. On one hand, this is unattractive to the strong type: the terms are worse than the separating high-value demand, and there is a good chance that it will be accepted. On the other hand, this is attractive: the risk of war is lower, and even when it is positive the war that follows will be against an unprepared opponent. In equilibrium, the strong type balances these trade-offs and sometimes feigns weakness.
When (D) is satisfied, the low-value demand is too unattractive to the strong type: he will only feign weakness if there is a chance that it will be rejected. In this situation, minimizing the risk associated with this demand has ambiguous social welfare implications, which is why Proposition 1 specifies the range of risks that can be supported in equilibrium.
Selection of a Signaling Equilibrium
Like most signaling games, this one has many equilibria. Of particular interest are ones in which the strong type either fully or partially reveals his type. The claim of Lemma 1 holds for any fully or partially separating equilibrium where the weak type demands some x and the strong type demands some x, with player 2 rejecting the former with probability r and the latter with probability r.Footnote 15
Separating equilibria
In a separating equilibrium, q(x) = 0 and q(x) = 1, which immediately implies that the high-value demand will be exactly the same as in the feint equilibria, or x = x 2. The low-value demand is the highest demand the weak player 1 can make provided that making it leads player 2 to infer that he is weak, or x = x 1. Because preventing deviations would require positive probabilities of rejection of demands in [x,x], it follows that the equilibrium beliefs over that range would have to be exactly the same as in the feint equilibria as well. Thus, one substantive difference between the separating and feint equilibria is that in the former, the weak type gets a strictly lower payoff because the low-value demand is smaller.
The intuition is that because player 2 would conclude that the opponent is weak after seeing this demand in the separating equilibrium, her expected payoff from rejecting it and fighting without arming will be much higher than the corresponding payoff in a feint equilibrium where she believes there might be a chance that her opponent is strong. This implies that her expected payoff from rejection is strictly larger in the separating equilibrium, so the acceptable low-value demand will be correspondingly smaller. This is particularly evident in the case where the low-value demand is riskless in the feint equilibria as well. Observe that in a separating equilibrium, the low-value demand would reflect the most player 2 would be willing to concede when she is certain that her opponent is weak. In a feint equilibrium, on the other hand, the corresponding low-value demand reflects what she would be willing to concede when she suspects her opponent might actually be strong.
Recall that the high-value demand is the same in both types of equilibrium. The fact that a riskless low-value demand is strictly better in a feint equilibrium where the strong type is indifferent between the two demands implies that the risk of the high-value demand must be lower in the feint equilibrium. This is so because the strong type's expected payoff from the high-value demand is strictly decreasing in the risk of war, so if the low-value demand increases, the risk of the high-value demand must decrease if he is to remain indifferent. This implies that the expected payoff for player 1 is strictly higher in the feint equilibria, which gives one possible reason for selecting them in situations where both equilibrium types exist.
When the conditions stated in Proposition 1 are not satisfied, feint equilibria will not exist. In particular, when q a < q, the weak type would want to make the highest possible riskless demand, x 1, that would reveal his weakness. In other words, this is where the separating equilibrium would still exist. In fact, separating equilibria can be supported with the assessment used in the proof of Proposition 1 with appropriate minor adjustments.
Semi-separating (bluffing) equilibria
In a semi-separating equilibrium, the weak type sometimes demands x but occasionally bluffs by demanding x, and the strong type demands x for sure. Because the weak type is the only one demanding x with positive probability, it follows that in such equilibria, x = x 1. The high-value demand has to be such that the strong type would be unwilling to separate by making a larger demand. The most straightforward way to accomplish that is to use the same belief system as in the feint equilibria, but require that player 2 certainly reject any x > x. (Since player 2 is indifferent for any x ∈ [x 1,x 2] and rejects any x > x 2 regardless of beliefs, this is clearly possible.)
For instance, x = x a can be supported in a bluffing equilibrium as follows. Let r > r = 0 be such that the weak type is indifferent between x and x = x 1, or r = (x a − x 1)/(x a − W wn). Consider a strategy for player 2 such that she accepts any x ≤ x 1, rejects any x ∈ (x 1,x] with probability r, and rejects any x > x with certainty. This strategy is sequentially rational with the assessment in (2). As in the feint equilibrium, deviation to x ∈ (x 1,x) merely produces peace terms that are worse than x with the same risks and same type of war (without player 2 arming), so it cannot be profitable. Any deviation to x > x results in a certain war. The strong type cannot profit if rW sn + (1 − r)x a ≥ W sa. Since W sn > W sa, the sufficient condition for this is x a ≥ W sa, or (D) not being satisfied. Recall that this means that the peace terms are at least as good for the strong type as fighting an armed opponent. When this is not the case, the peace terms are so bad that the strong type's only incentive to demand them is in the possibility that player 2 might reject them and fight a war unprepared. This means the risk of war should be sufficiently high, or r ≥ (W sa − x a)/(W sn − x a). There are ranges for the parameters that satisfy this requirement.
It is always possible to satisfy the weak type's indifference condition for a sufficiently low risk for x. This risk will also deter deviations that cause certain war when (D) is not satisfied, and for some parameter configurations even when (D) is satisfied. In either case, the binding condition for the existence of bluffing equilibria is in the high risk associated with making large demands. This risk dampens the strong type's ability to separate and keeps him locked into making a demand so low that even the weak type is willing to mimic it. If we are willing to preserve the substantively more appealing monotonicity exhibited by the rejection probability in the feint equilibria, then this artificial constraint will disappear, and so will the bluffing equilibria. In other words, there are strong substantive reasons to select the feint equilibria over the fully revealing or bluffing equilibria when these types coexist.
The Likelihood of Feints
The probability with which the strong type feigns weakness is φ = (1 − p)q a /[p(1 − q a)], so:
![\[
\frac{\partial\phi}{\partial p} = \frac{-q_a}{p^2(1-q_a)}<0,
\quad\text{and}\quad
\frac{\partial\phi}{\partial q_a} = \frac{1-p}{p(1-q_a)^2}>0.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU001.gif?pub-status=live){kind=small}
The more pessimistic player 2 is, the more likely the strong player 1 is to feign weakness. The second comparative static is more interesting: since the feint probability is strictly increasing in the critical belief q a, we can conduct additional comparative statics on this belief as defined in (1). It is immediate that the higher the marginal cost of arming to player 2, the more likely is player 1 to feign weakness (because even relatively low probabilities of him being weak can discourage her from arming when doing so is costly).
The benefit of arming
Player 2's marginal benefit from arming depends on player 1's type and the technology of fighting implicit in the definition of the probabilities of winning. Let b w = w n − w a < k 2 be her benefit from arming against a weak opponent, and b s = s n − s a > k 2 be the benefit from arming against a strong opponent. Since q a = (k 2 − b w)/(b s − b w), it follows that:
![\[
\frac{\partial q_a}{\partial b_w}=\frac{k_2-b_s}{(b_s-b_w)^2}<0
\quad\text{and}\quad
\frac{\partial q_a}{\partial b_s}=\frac{b_w-k_2}{(b_s-b_w)^2}<0.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU002.gif?pub-status=live){kind=small}
As player 1's benefit from player 2's failure to arm (for example, b s) goes up, the probability of a feint goes down. This is surprising because it says that as the benefit of successful deception increases, the likelihood that player 1 will attempt to deceive player 2 decreases.
At first glance, it would appear that the converse should be true: after all, the strong type can benefit from deception most when his war payoff against an unprepared opponent is much higher than his payoff from an armed one. This logic, however, does not consider player 2's response. If the marginal benefit from arming increases (whether against a weak or a strong opponent), then player 2 would arm even if she is less convinced that the opponent is strong. In other words, when player 2 expects to get a significantly worse payoff if she fails to arm and can mitigate this disaster by arming, she will arm as a precaution even though she might not assign a great probability to her opponent being strong. Because larger demands cause her to revise her beliefs upward, this implies that the largest demand player 1 can make without provoking arming upon rejection decreases. This reduces the strong type's incentives to feign weakness.
Relative power
One can think of s n − w n as the strong type's power relative to the weak type's when player 2 is unprepared, and s a − w a as the analogous relative power when she is prepared. This results in:
![\[
\frac{\partial q_a}{\partial s_n}=\frac{b_w-k_2}{(b_s-b_w)^2}<0,
\quad
\frac{\partial^2 q_a}{\partial s_n\partial w_n}=\frac{b_s+b_w-2k_2}{(b_s-b_w)^3} \gtrless 0
\Leftrightarrow
b_s-k_2\gtrless k_2-b_w.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU003.gif?pub-status=live){kind=small}
The interpretation of the partial derivative is straightforward: an increase in the strong type's probability of winning against a disarmed opponent increases the risks from rejecting the low-value offer, and increases player 2's propensity to arm. This reduces the value of the feint to the strong type, and he feints less often. The cross-partial shows that the magnitude of this effect depends on the expected war-time performance of the weak type as mediated by the marginal cost of arming for player 2. The cross-partial is positive when the marginal cost of arming is relatively small (b s − k 2 > k 2 − b w). In that case, an increase in relative power of the strong type due to a drop in w n magnifies the detrimental effect of s n and leads to a sharp decline in the desirability of the low-value offer. In other words, because player 2 finds it cheaper to arm, she counters this increase in the strong type's relative power more readily. If, on the other hand, the cross-partial is positive because her marginal costs of arming are high, then an increase in relative power due to a drop in w n, although unpleasant, does not lead to very drastic revisions of player 2's arming propensity. Even though she still arms more readily in response to an increase in relative power, the effect is muted because of the high costs of doing so.
Turning now to the effect of relative power against an armed opponent, the partial derivatives are:
![\[
\frac{\partial q_a}{\partial s_a}=\frac{k_2-b_w}{(b_s-b_w)^2}>0,
\quad
\frac{\partial^2 q_a}{\partial s_a\partial w_a}=\frac{b_s+b_w-2k_2}{(b_s-b_w)^3} \gtrless 0
\Leftrightarrow
b_s-k_2\gtrless k_2-b_w.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU004.gif?pub-status=live){kind=small}
The direct effect of an increase in the strong type's probability of winning against a prepared opponent is perhaps surprising: the better this type expects to do in such a war, the more likely is he to feign weakness! To understand this, consider how player 2 responds to such an increase. Her benefit from war, even when fully prepared, decreases, which means that the terms she is prepared to concede in the high-value demand become more attractive to player 1. The strong type will thus be willing to feign weakness either because the risk of making this demand increases or because the terms of the low-value offer improve considerably. Because player 2 expects to do rather poorly in a war against the strong type, the relative value of arming in effect declines and she becomes more willing to make concessions. The improvement in the terms of the low-value demand makes it more attractive to the strong type, and makes him more likely to attempt a feint.
The cross-partial is the same as for the relative power against an unarmed opponent but because the effect of s a is different, so is the overall interpretation. The cross-partial is positive when player 2's marginal cost of arming is small. With such costs, player 2 tends to arm even while relatively optimistic; that is, while she still believes with a relatively high probability that her opponent is weak. Thus, a decline in her expected war payoff due to an increase in the weak type's strength, w a, affects her propensity to arm and she becomes less willing to do so. This increases the threshold belief for arming and magnifies the effect of increase in the strong type's relative power. In other words, even though the strong type's power relative to the weak type is not that pronounced when the latter is only moderately weak, the increase in his relative strength has a disproportionately large effect on player 2's incentive to arm when her costs are low. Conversely, when her cost of arming is high (and the cross-partial is negative), player 2 only arms when relatively pessimistic. This means that increases in the weak type's strength have a smaller marginal impact on her expected war payoff, and so her incentive to arm does not increase nearly as dramatically. This dampens the overall effect of an increase in the strong type's relative power.
Luring into war
When (D) is satisfied, the strong type prefers fighting an unprepared opponent to the peace terms from the low-value demand. The feint under these conditions can be interpreted as an attempt to lure the opponent into fighting by lulling him into a false sense of optimism. Not surprisingly, decreasing the costs of war makes this condition easier to satisfy. Somewhat less predictably, a decrease in player 2's marginal cost of arming does so as well. To see why this should be so, observe that lowering k 2 effectively lowers the barrier to preventive arming, which in turn makes player 2 less willing to make concessions. This reduces the peace benefit from the low-value demand, and if the decline is sufficiently large, makes fighting an unprepared opponent more attractive to the strong type. Gauging the effect of s n in this context is slightly more involved because q a, q d, and q are all decreasing in s n. However, it can be shown that q a decreases at a faster rate than q, which means that for high enough values of s n that satisfy (D), the necessary condition for the existence of the feint equilibria, q a ≥ q, will be violated. The logic is as follows. As we have seen, increasing s n lowers the arming threshold for player 2, which in turn lowers the terms of the low-value demand. If the strong type is to feign weakness, the risk associated with this demand must increase (so he can reap the benefits of war against an unprepared opponent). However, this makes the demand less attractive to the weak type, and when the risk is sufficiently high, (4) will fail, and he will not be willing to make the low-value demand, opting instead for a riskless x 1. In other words, as the advantages of deceiving player 2 increase for the strong type, he becomes less able to mislead her successfully.
Endogenous Tactical Incentives
The model I analyzed is tractable and transparent, which makes the exposition easier to follow. It is also generic because it leaves the functional form of the technology of war unspecified. However, player 1 does not have an opportunity to react to player 2's expected behavior once a demand is rejected. To study the problem with fully endogenous tactical incentives, it is necessary to model the technology of war explicitly. Although this limits the results somewhat, the importance of the question justifies the cost.
The Extended Model
The crisis game is the same as in the original model, the difference is what happens when players go to war. As before, player 1 makes an ultimatum demand x. If player 2 accepts, players receive (x,1 − x), if she rejects a costly contest (war) occurs. The contest is a simultaneous-move game in which each player chooses a level of effort m i ≥ 0 at cost c i > 0. The probability of winning is determined probabilistically by the ratio contest-success function πi(m 1,m 2) = m i /(m 1 + m 2) if m 1 + m 2 > 0 and πi = 1/2 otherwise.Footnote 16 The winner obtains the entire benefit, so player i's expected payoff from a contest is πi(m 1,m 2) − m i /c i.
The game has one-sided incomplete information.Footnote 17 Player 2 knows her cost of effort, c 2, but is unsure about player 1's cost. Specifically, player 2 believes that player 1 is strong, c1 with probability p, and weak, c1 < c1, with probability 1 − p. These beliefs are common knowledge. If the costs of effort are too high, then war is prohibitively costly and the game will carry no risk of bargaining breakdown. We thus make the following
Assumption 2. The uninformed player's costs are not too high: 
.
Since the strategies for the crisis bargaining game would have to form an equilibrium in the contest continuation game, I analyze that first.
The Contest Endgame
There are only two possibilities in the continuation game following player 1's demand: either player 2 will infer his type or not. If she infers the type, as she would after the separating high-value high-risk demand that only the strong type makes, the contest is one of complete information. If she can only partially infer it, as she would do after the low-value low-risk demand that the strong and the weak type pool on, the contest is one of asymmetric information where her posterior belief that player 1 is strong is q ∈ (0,1). I derive the expected equilibrium war payoffs for both situations, and then show that the more convinced player 2 becomes that player 1 is strong, the more intense her fighting effort gets. This worsens the strong type's war payoff, and gives him an incentive to mislead player 2 that he is weak. That is, I show that the incentive to feign weakness can arise fully endogenously.
Complete information
Players optimize maxm i{m i /(m i + m j) − m i /c i}, which yield the best responses 
and 
in an interior equilibrium. Solving the system of equations then gives us the equilibrium effort levels: m 1* = c 2(c 1 /(c 1 + c 2))2 and m 2* = c 1(c 2 /(c 1 + c 2))2. The equilibrium expected payoffs are:
Fighting is inefficient: W 1 + W 2 < 1 ⇔ 0 < 2c 1c 2. Players always have an incentive to negotiate a division of the good instead of fighting to win it all. Moreover, a mutually acceptable peaceful division always exists. The rationalist puzzle that arises from war's inefficiency remains intact.Footnote 18
One-sided asymmetric information
Player 2, whose cost c 2 is common knowledge, believes that player 1 is strong with probability q and weak with probability 1 − q. Player 1 knows his own cost, and optimizes as he would under complete information, which yields:
which eliminates some contests from consideration.
Lemma 2. In equilibrium, either both types of player 1 exert positive effort in the contest, or only the strong type does.
This means that there are only two possibilities to consider: either both types of player 1 spend strictly positive effort (skirmish), or only the strong type does (war). The fanciful names are meant as reminders that contests in which the weak type participates are lower in intensity than conflicts in which only the strong type participates.
The skirmish equilibrium
Let m1 = m 1(m 2;c1) and m1 = m 1(m 2;c1) denote the effort levels of the weak and strong types, respectively. Because player 2 is unsure about player 1's type, her optimization problem is maxm 2 {qm 2 /(m1 + m 2) + (1 − q)m 2 /(m1 + m 2) − m 2 /c 2}. Her equilibrium effort level is
![\begin{equation}
m_2^* = \ul{c}_1\ol{c}_1\left[\frac{f(q)}{g(q)}\right]^2,
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqn009.gif?pub-status=live){kind=small}
where 
and g(q) = c1c1 /c 2 + q c1 + (1 − q)c1 > 0. The expected equilibrium war payoffs are:
![\[
W_1(q;c_1)=\left(1-\frac{f(q)}{g(q)}\sqrt{\frac{\ul{c}_1\ol{c}_1}{c_1}}\right)^2
\quad\text{and}\quad
W_2(q) = \Big(q\ul{c}_1+(1-q)\ol{c}_1\Big)\left[\frac{f(q)}{g(q)}\right]^2.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU010.gif?pub-status=live){kind=small}
In the skirmish equilibrium, m1 > 0, which means that m 2* < c1, or:
is the necessary condition for this equilibrium to exist.
The war equilibrium
In this case, the weak type does not exert any effort in equilibrium, so m1 = 0. The strong type's optimal effort is still defined by (5). Player 2's maximization problem, maxm 2{qm 2 /(m1 + m 2) + (1 − q) − m 2 /c 2}, is simpler because whatever positive effort she expends, she will win outright if her opponent happens to be the weak type. The solution is:
The expected equilibrium war payoffs are:
![\[
W_1(q;\ol{c}_1)=\left(\frac{\ol{c}_1}{\ol{c}_1+qc_2}\right)^2
\quad\text{and}\quad
W_2(q)=1-q+q\left(\frac{qc_2}{\ol{c}_1+qc_2}\right)^2.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU011.gif?pub-status=live){kind=small}
It is not difficult to verify that q ≥ q s is the condition for the war equilibrium to exist. The two cases characterize the complete solution to the one-sided incomplete information contest.
The Sun Tzu Principle of Feigning Weakness
Lemma 3 (Sun Tzu). When player 1 exerts positive effort in the contest, his equilibrium payoff is decreasing in player 2's belief that he is strong.
The logic behind the principle is straightforward. Player 2's equilibrium effort level is increasing in q: the more pessimistic she is, the higher the effort she will exert. This leads player 1 to compensate by increasing his effort, leading to an overall decrease in his expected payoff because of the higher costs he incurs in the process. This parallels Sun Tzu's principle of feigning weakness, which he stated as follows: “If your opponent is of choleric temper, seek to irritate him. Pretend to be weak, that he may grow arrogant.”Footnote 19
This result provides the microfoundations for Assumption 1 in the original model. It is worth noting that Sun Tzu's principle is here derived as the result of optimal rational behavior in a contest under uncertainty. The upshot of this analysis is that the strong type's incentive to mislead player 2 in the strategic game arises in this model as well.
The Crisis Ultimatum
As it turns out, the method for constructing feint equilibria in this model is analogous to what we did in the simple one. I will only sketch the steps here.
Equilibrium beliefs
The belief-contingent responses are limited by the best and worst war payoffs that player 2 can expect.
Lemma 4. Let x 1 = 1 − W2 and x 2 = 1 − W2, where W2 = W 2(c1,c 2) is player 2's expected payoff from a full information contest against a strong opponent and W2 = W 2(c1,c 2) is her analogous payoff against a weak opponent. In any equilibrium, player 2 will accept any x ≤ x 1 and reject any x > x 2 regardless of her beliefs.
Since only the strong type ever demands x in equilibrium, rejection leads to a complete-information war against a strong opponent. With such a belief, player 2 accepts any x such that 1 − x ≥ W2, and because player 1 has no incentive to demand less than what she is willing to accept, it follows that in equilibrium,
which is exactly the same as in the simple model.
Since both types make the low-value demand with positive probability, rejection leads to war with incomplete information with a posterior belief q(x). Player 2's optimal effort is then given by (6) if the contest admits the skirmish equilibrium and by (8) otherwise. I use W 2(q(x)) to denote the expected payoff with the understanding that this notation refers to the appropriate payoff.Footnote 20 With such a belief, player 2 will accept any demand such that 1 − x ≥ W 2(q(x)). Because player 1 has no incentive to offer more than the absolute minimum necessary to obtain acceptance, it follows that in equilibrium,
Because the low-value demand results in a belief-contingent response, x ∈ [x 1,x 2] with q(x) satisfying (9). The following lemma proves that it is always possible to find such a belief.
Lemma 5. For any x ∈ [x 1,x 2], there exists a unique q(x) ∈ [0,1] that satisfies (9). Moreover, q(x) is strictly increasing in x.
I conclude that in any equilibrium, player 2 will accept any x < x 1, will reject any x > x 2, and can randomize between accepting and rejecting any x ∈ [x 1,x 2] when her posterior beliefs are defined by Lemma 5. This is the exact analogue to the (on and off the path) beliefs I constructed in the simple model.
The feint equilibria
It is not difficult to verify that the analogue to the incentive-compatibility conditions in Lemma 1 obtains in this model as well. Letting r and r be the probabilities with which player 2 rejects x and x, respectively, we know that r < r and x < x in any feint equilibrium.
As before, there are conditions that permit r = 0. The low-value demand can be riskless only when the incentives of the weak and the strong types are aligned given these peace terms: W 1(q(x);c1) ≤ x. This implies that the low-value demand cannot be smaller than 
. Hence, the lower bound on the low-value demand is ![$x^*=\max\left[\wt{x},x_1\right]$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU014.gif?pub-status=live){kind=small}
.
Finally, Bayes rule yields the feint probability: φ = q(x)(1 − p)/[p(1 − q(x))], which requires p > q(x). Because q(x) is increasing and q(x) = 1 > p, this puts an upper bound on the low-value demand. In particular, there exists x** < x such that q(x**) = p, so that only x < x** can be supported as a low-value demand in a feint equilibrium. Observe in particular that x* = x 1 ensures that x** > x*.
Proposition 2. Any x ∈ [x*,x**] can be supported in a feint equilibrium with a riskless low-value demand and x = x 2. Player 2 accepts any x ≤ x, rejects any x ∈ (x; x] with probability r(x) = (x − x)/(x − W 1(q(x);c1)), and rejects any x > x with certainty. On and off the path, her beliefs are defined in Lemma 5.
Although it is possible to construct feint equilibria with r > 0 when the low-value demand can be riskless, a social welfare argument would select the Pareto-optimal equilibrium with r = 0. There is, however, a major difference between this model and the original one. When the conditions that permit r = 0 are not met (for example, (D) is satisfied), the original model admits feint equilibria with a risky low-value demand. This is not the case here: with this particular technology of war it is not possible to induce the weak type to run a risk of war under conditions that make fighting more beneficial than the peace terms for the strong type. (The proof of this is a bit involved and is omitted.) I conjecture that this is an artifact of the particular functional form chosen for the technology of conflict. This is why Proposition 2 restricts attention to feint equilibria with a riskless low-value demand. Substantively, these equilibria are equivalent to the ones in the original model.
Discussion
Although the framing of the model might make it look like the feint mechanism applies only narrowly to situations where a player might derive a tactical fighting advantage, the substance of the claim is more general. At the most abstract level, the mechanism applies to any setting where an attempt to influence a player's behavior with a threat might trigger a counter response that would diminish the effectiveness of executing the threat if the attempt fails. As described, this is a very generic phenomenon and it is somewhat surprising that the formal study of coercion has neglected it. If I were to venture a guess as to the reason, it would have to be that scholars have only recently begun to study the distribution of power as an endogenous variable rather than something fixed by observable capabilities. As a result, studies have only recently pointed out that some of our general conclusions depend on the assumption of a fixed distribution of power.Footnote 21
It is possible to use this mechanism to study the puzzle of secret defensive alliances.Footnote 22 One prominent vein in the alliance literature explains them as valuable signaling and commitment devices.Footnote 23 A defensive alliance, by its very nature, is supposed to enhance state A's capability against state C by adding the capabilities of state B to A's. This should improve A's defensive posture against C, and deter C from attacking. Abstracting away from how credible B's commitment to A is, concluding such an alliance in secret cannot increase A's deterrent threat for the simple reason that C is unaware of B's promise to aid A in war. So what is the point of concluding such an alliance?
The feint mechanism offers one possible answer: since a defensive alliance increases A's strength, making it public would alert C that she would have to be better prepared if she wants to coerce A. This would impel C to increase her capabilities, either by arming or by searching for allies of her own. If C succeeds, the overall benefit of the alliance might actually decrease. Hence, A might take his chances with a secret alliance: although C is less likely to agree to terms beneficial to A, if war occurs A will fight with B's help against an opponent who did not have the opportunity to prepare.
The Disadvantages of Democracy in Crisis Bargaining
There is an ongoing debate about the advantages democracies enjoy over other political systems when it comes to crisis bargaining or war fighting. One especially prominent argument is that democracies are better able to signal the resolve of their leaders in crises, perhaps because of audience costs, the interaction of opposition and incumbent parties, or other institutional features. The (somewhat simplified) core of these arguments is that democracies constrain the leaders' ability to bluff because open public debate and reselection incentives force them to issue threats only when they are resolved to follow through on them. In other words, it might be much more difficult for democratic leaders to conceal their resolve than for an autocrat. This makes threats more credible, which is held to be a good thing.Footnote 24
The problem with the exclusive focus on credibility is that it neglects the consequences a believable threat might have for the threatener if the target fails to comply. The tactical game here shows one possible reaction a target might have to a threat that is more credible: she might start preparing for a fight. In other words, enhancing credibility might actually diminish capability. The trade-off between communicating one's resolve without provoking a countervailing response is a difficult one. As such, even if one grants the argument that democracies can communicate resolve better than nondemocracies, it is not at all clear that this will enable them to obtain better peace terms or enjoy lower risks of war. In fact, the present model suggests that the opposite might well be true.
It is generally the case that military capabilities are much more readily observable than the will to use them. This means that a country with a well-trained and well-supplied army that it is unwilling to commit to a fight is “weaker” than an opponent whose objective capabilities are not as great but who is ready to use them all in that fight. This is why indicators based on observable capabilities might not be very good predictors of how a crisis will end: the driving force behind the outcome is the contest of will rather than of brute numerical strength.
Consider now a democracy whose leader cannot feign weakness because the interaction of domestic political groups reveals the political will to use the observable capabilities. In the context of our model, this leader will either make the high-value demand when he is resolved or the low-value demand when he is not. This means that a democratic leader is more likely to be forced into a separating equilibrium than a nondemocratic leader who can conceal his resolve. As I have shown, in a separating equilibrium the weak type's peace terms are worse than the peace terms he can obtain in a feint equilibrium with a riskless low-value demand. While the terms of the high-value demand are the same for the resolved type in both cases, the risk he has to run to obtain them is strictly greater in the separating equilibrium. In other words, an unresolved democratic leader will obtain worse peace terms than an unresolved nondemocratic leader, and a resolved democratic leader must run higher risks of war to obtain the same peace terms as a resolved nondemocratic leader. This suggests that the openness of democracies might put them at a disadvantage in crisis bargaining precisely because it communicates resolve better.
Shows of Strength and the Fostering of False Optimism
One of the most prominent causal mechanisms that explains war as the result of bargaining failure due to asymmetric information is the risk-return trade-off.Footnote 25 The essence of the mechanism is a screening logic: a player who is uncertain about his opponent's expected payoff from war makes a demand that balances the risk of rejection should its terms prove unacceptable to the opponent with the extra gain from peace these terms represent should they prove acceptable. Although one can always ensure peace by making a demand that even the strongest type of opponent would accept, this strategy is generally suboptimal because it involves large concessions that might well be unnecessary if the opponent is actually weak. The optimal strategy trades the gain from making a demand that is slightly less favorable to the opponent against the slightly higher risk that such a demand entails. The risk of war therefore arises from not knowing precisely what kind of demand that opponent would find agreeable.
The mechanism that explains war in the present model is different even though the basic ultimatum game is the same. In contrast to the traditional screening setting in which player 1 is uncertain about player 2's expected payoff from war, the crisis here is a signaling setting in which it is player 1 who has private information. In fact, I did not need to assume any sort of uncertainty about player 2's type at all. The interaction is dominated by the informed player's attempt to signal his type in a credible manner: when the strong type succeeds in separating from the weak type, player 2 becomes much more amenable to concessions. The risk of war is a necessary feature of a separating strategy that aims to achieve credible communication.
The feint equilibria exhibit this costly signaling dynamics common to crisis bargaining behavior. The strong player 1 can obtain the high-value demand x only if he takes the high risk of a costly war with a fully prepared, strong player 2. This discourages the weak type from attempting to bluff with the same demand. Endogenizing the war contest does not alter the basic logic of costly signaling. The only way a strong player can obtain a better deal is by revealing credibly that he is strong, which requires him to engage in behavior that the weak type would not want to mimic.
The interesting new feature of the feint equilibria is that the strong type of player 1 might mimic the behavior of the weak instead. One reason for this comes from the incentives the strong player 1 has to keep private his information about his own strength in the event of war. In the exogenous specification of the distribution of power, a player's expected war payoff may depend on his opponent's private information but not on her beliefs about the information that he knows but she does not. This means that with exogenous war payoffs, it does not matter to the player whether he fights an adversary that is fully informed or one that is uncertain about his strength. There is no reason for the player to manipulate the belief with which his opponent would enter the war, only the belief she has when deciding what to do about his demands. In these cases, the strong player is better off whenever his opponent knows that he is strong.
With endogenous war payoffs, the player does care about the beliefs with which his opponent begins the war. The informed strong type's expected payoff under uncertainty is strictly better than his payoff when his opponent is fully informed. (As q → 1 the payoff under uncertainty converges to the complete-information payoff but by Lemma 3, it is strictly decreasing in q.)
This gives the strong type a potent reason not to reveal his strength during the crisis itself. He may deliberately leave his opponent in a state of false optimism to exploit the advantages of surprise in case war breaks out. Unlike the usual scenario in which strong types always attempt to overcome the optimism of the opponent with costly or risky shows of strength, the feint equilibrium dynamic suggests that they may not be willing to do so even if such actions are potentially available to them. This creates a serious problem for peaceful crisis resolution because mutual optimism is regularly blamed as a major cause of war.Footnote 26
In the classic formulation of the mutual optimism argument, “war is usually the outcome of a diplomatic crisis which cannot be solved because both sides have conflicting estimates of their bargaining power.”Footnote 27 One problem is overconfidence about the likely development of the war: its duration (short), outcome (victory), and costs (low). In the model with endogenous war effort, the expected outcome depends on how hard the actors fight. Their joint efforts determine the probability of victory, and their uncertainty about the behavior of the opponent induces uncertainty in these estimates.
The resulting expectations about the war may well be incompatible. In the skirmish equilibrium, the strong type expects to win with probability 
, and player 2 expects to win with probability π2(q) = f (q)2/g(q;c 2). These players are too optimistic because π1(q;c1) + π2(q) > 1. Similarly, in the war equilibrium the strong type expects to win with probability π1(q;c1) = c1 /(c1 + qc 2), whereas player 2 expects to win with probability π2(q) = [(1 − q)c1 + qc 2]/(c1 + qc 2). As in the skirmish equilibrium, these expectations are incompatible: it is easily verified that π1(q;c1) + π2(q) > 1. These optimistic expectations about victory translate into optimistic estimates about the expected payoffs from war.
It is crucial to understand that these disagreements are not about some fundamental underlying “true” probability of winning. Instead, they are disagreements about how war will “play out,” and this, of course, depends to a large extent on the opponent's likely behavior. That behavior in turn depends on what the opponent expects the player to do, and these expectations are profoundly influenced by the opponent's belief about some aspect that is privately known by the player. This is where deliberate falsification enters the picture.
When mutual optimism is a possible cause of war, credible signaling might be some sort of imperfect cure. When players have exaggeratedly optimistic expectations about their chances in war because they are not aware of private information the opponents posses, the only way to arrive at a peaceful settlement is to reduce this mutual optimism. Crisis bargaining studies have shown that the only way to do so is through costly signaling. The cure is imperfect because the attempt to impart credibility to one's message forces the actor to behave in ways that increase the probability of war. Scholars are well aware of this paradox inherent in crisis bargaining, and it is perhaps best summarized by Schelling: “Flexing of muscles is probably unimpressive unless it is costly or risky… Impressive demonstrations are probably the dangerous ones. We cannot have it both ways.”Footnote 28
The results here suggest that the difficulty with settling peacefully may go beyond the risk generated by signaling efforts. When unwarranted optimism arises from lack of information to which the opponent has access, it can be dispelled only when the opponent chooses to reveal it. Unfortunately, the logic of feigning weakness suggests that an actor may choose instead to obfuscate inferences in order to gain advantage in the war that follows. In other words, the actor may deliberately foster false optimism even though this may make it very unlikely that his opponent would concede enough to make that actor willing to forego fighting.Footnote 29
Private information can remain private not for lack of means to reveal it but because the only type who can afford to send the credible signal may have no incentive to do so. It is this intentional and strategic concealment of information that is so troubling for resolving crises peacefully. To see how matters can come to a head, consider a crisis in which side A has deliberately fostered optimism in side B. Because side B (incorrectly) believes herself strong, she engages in very risky actions designed to cause side A to revise his war expectation downward. Unfortunately, side A cannot use side B's willingness to run risks as evidence that side B is strong, not when he misled B into believing that she is strong. In other words, when a state has gone to great lengths to convince the opponent to be optimistic, that state cannot very well use that optimism as evidence that its own assessment is faulty. Side B's signaling behavior then will be more likely to cause war because A is essentially dismissing it, because B is unwilling to offer the necessary concessions, and because B's exaggerated optimism is prompting her to take large risks. In this situation, mutually incompatible crisis expectations cannot be reconciled without the actual resort to arms. As Blainey puts it, “The start of war is … marked by conflicting expectations of what that war will be like. War itself then provides the stinging ice of reality.”Footnote 30
Conclusion
Consider the Chinese options in the fall of 1950. On one hand, they could openly threaten with intervention and demand that the UN forces remain south of the 38th parallel. If this worked, the outcome would have been excellent. However, making this high demand is also risky: if the United States happened to be resolved to unify Korea, this demand would simply have alerted it to prepare better for fighting the PRC. The resulting war would have been of very high intensity and the Chinese would certainly have lost the tactical advantage that would have secured a first morale-boosting victory. On the other hand, the Chinese could have demured and asked that only U.S. troops desist from crossing the parallel. Although permitting the occupation of North Korea by South Korean troops would not have been as good as keeping it free of UN forces, there is some chance that the United States would have agreed to this and war would have been averted. Had the United States been bent on unification, the absence of a credible signal could have been expected to increase American confidence and possibly cause the United States to march into a war without the type of preparation it would have engaged had it known the Chinese were going to intervene in strength. These are unpalatable choices, certainly, and no wonder Chairman Mao vacillated for so long before making up his mind on the strategy to pursue.
This stylized description of the situation seriously abstracts from the complex domestic dynamics in both countries, and it may well have been the case that by the time Mao resolved to intervene, the United States had become undeterrable by the Chinese without open Soviet support. In November, war may have been already unavoidable.Footnote 31 However, the logic of feigning weakness developed in this article can help explain why the Chinese did not pursue more vigorous signaling actions when they were resolved not to permit unification.
The crisis bargaining literature focuses on how strong actors can signal their strength and reduce the possibility of bluffing. When weak types can mimic their actions, messages will not be believed, and when threats are not credible, they are unlikely to influence the behavior of the opponent. This basic mechanism also obtains in the model presented here. This article, however, also points out some perverse incentives that strong types may face that may make them unwilling to send costly signals even when they could have done so.
One implication of this result is that it is not safe to infer that one's opponent is weak when he fails to engage in some costly action that is available to him and that could persuade one that he is strong. One should carefully consider the incentive to feign weakness for tactical purposes. This, of course, may be harder than it sounds because, after all, it could be the case that the opponent is not signaling because he really is weak.
The logic of the feint also suggests that overcoming mutual optimism in crises may be very difficult for two reasons. First, when a strong opponent who could reveal his strength to reduce an actor's optimism decides to feign weakness, then that actor may persist in her incorrect beliefs and blunder into disaster. Second, the possibilities for peaceful resolution of the crisis may diminish because the feigning opponent himself may be unable to correct his optimistic beliefs. Because he has purposefully misled the other actor, he cannot take her costly signals as evidence that he should revise his expectations: after all, she is signaling precisely because she believes that she is strong, which is the false belief he has taken great care to induce. In this rather unfortunate scenario, war may be the only way to inject a dose of reality into these beliefs.
Proofs
Proof of Proposition 1.
Since the strong type is mixing, rW sn + (1 − r)x = rW sa + (1 − r)x, which gives r in (3). Note that x < W sn yields:
If (10) is not satisfied, r ∈ (0,1) regardless of the value of r, so we can take r = 0. Suppose now that (10) is satisfied. Then r < 1 yields r > 1 − (s n − s a)/(W sn − x) ≡ r′. Taking r′ ≥ 0 yields (D), which ensures that the low-value demand must be risky, otherwise r = 0 can work. Also, r > 0 yields r < 1 − (s n − s a − k 2 − C)/(W sn − x) ≡ r′′. Since r′′ − r′ > 0 ⇔ k 2 + C > 0, such r exist.
Since the weak type should not have an incentive to demand x, it follows that rW wn + (1 − r)x ≥ rW wa + (1 − r)x, which simplifies to:
It is readily verifiable that r ∈ (0,1) regardless of r. Since both (3) and (11) must hold, we require that:
![\[
\frac{\ul{r}\left(\ul{x}-W_s^n\right)+\ol{x}-\ul{x}}{\ol{x}-W_s^a}
\geq\frac{\ul{r}\left(\ul{x}-W_w^n\right)+\ol{x}-\ul{x}}{\ol{x}-W_w^a}.
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU016.gif?pub-status=live){kind=small}
At r = 0, the inequality reduces to s a ≥ w a, which holds. Recall that if (D) is not satisfied, there are no lower-bound restrictions on r to guarantee valid r values, which means that in this case I may use r = 0.
I now derive the range of low risks that can be supported in equilibrium when (D) is satisfied. The weak type should not deviate to the best possible riskless demand, x 1, so 
.
reduces to (4).
Let r(x) denote player 2's rejection probability. Since r(x) = 0 for any x ≤ x 1, if r = 0, then player 1 cannot profit from deviating to a riskless x regardless of type. If r > 0, the derivation ensures that the weak type cannot profit by deviating to x 1 ≥ x, which also means that the strong cannot profit either. Since r(x) = r for any x ∈ (x 1,x), such a demand only produces peace terms worse than x, so a deviation cannot be profitable. Since r(x) = r for any x ∈ (x,x), such demands result in peace terms worse than x and the same risk of war against armed player 2. The strong type cannot profit from deviating and since our construction ensures that the weak cannot profit from x, he will not deviate either. Since r(x) = 1 for any x > x, the strong type cannot profit from deviations to certain war because W sa < x. Neither can the weak type: W wa < W wn < x.
Proof of Lemma 2.
Let m 2* ≥ 0 denote player 2's equilibrium effort, and m 1*(c 1) = m 1(m 2*;c 1) player 1's effort. There can be no equilibrium in which player 1 makes no effort regardless of type. Suppose, to the contrary, that m 1*(c1) = m 1*(c1) = 0 in some equilibrium. Since m 1(c 1) > 0 whenever c 1 > m 2*, this implies that m 2* ≥ c1 > 0. This cannot be optimal because she can deviate to a lower effort and still win for sure. Therefore, in any equilibrium at least one type of player 1 must be exerting a strictly positive effort. This cannot be the weak type by himself. Suppose, to the contrary, that m 1*(c1) > 0 and m 1*(c1) = 0 in some equilibrium. Since m 1*(c1) > 0 implies that m 2* < c1, it follows from c1 < c1 that m 2* < c1, and so m 1*(c1) > 0 as well, a contradiction.
Proof of Lemma 3.
Note that m 2* is increasing in q when Assumption 2 is satisfied: in the skirmish equilibrium, 
, where the inequality follows from Assumption 2; in the war equilibrium, ∂m 2*/∂q = 2q c12c 22/((c1 + qc 2)3) > 0. Turning now to the claim of the lemma, observe that in the skirmish equilibrium, 
because the bracketed term is positive by (7) and because m 2* is increasing in q. Since only the strong type participates in the war equilibrium, inspection of his payoff is sufficient to establish the claim.
Lemma 6. W 2(q) is continuous and strictly decreasing.
Proof.
(Continuity.) Since W 2(q) is continuous for each equilibrium, it is enough to show that it is continuous at q s where the equilibrium switch occurs: 
.
(Monotonicity.) In the war equilibrium, dW 2w(q)/dq = −(c12(c1 + 3qc 2))/((c1 + qc 2)3) < 0. In the skirmish equilibrium, dW 2s(q)/dq = (g′f 2/g 2) + (2f (q c1 + (1 − q)c1))/g 3(f′g − g′f) < 0. To see this, note that f > 0, g > 0, f′ < 0, g′ < 0, and 
by Assumption 2. The last requirement is that gg′f + 2(q c1 + (1 − q)c1)(f′g − g′f) < 0, which can be shown but it takes three pages of algebra.
Proof of Lemma 4.
Lemma 6 implies that to get the best and worst payoffs for player 2, I only need to consider q = 0 and q = 1. So, limq→0W 2s(q) = (c 2 /(c1 + c 2))2 = W2, and limq→1W 2s(q) = limq→1W 2w(q) = (c 2 /(c1 + c 2))2 = W2, with W2 < W2.
Proof of Lemma 5.
By Lemma 6, W 2(q) is continuous, and the intermediate value theorem implies that for any y ∈ [W2,W2], there exists q such that W 2(q) = y. By Lemma 6, W 2(q) is strictly decreasing, so q(y) = W 2−1(y) is unique and strictly decreasing in y. Letting x = 1 − y establishes the claim.
Proof of Proposition 2.
Let W1 = W 1(1;c1) = W 1(c1,c 2). Since the strong player 1 is willing to mix, U 1(x;c1) = U 1(x;c1), or
Using the definitions of x and x, I can rewrite this as:
![\begin{equation}
\ol{r} = \frac{\ul{r}\left[1-W_1(q(\ul{x});\ol{c}_1)-W_2(q(\ul{x}))\right]
-\ul{W}_2+W_2(q(\ul{x}))}{1-\ul{W}_1-\ul{W}_2}
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqn015.gif?pub-status=live){kind=small}
Since r > 0 and 1 > W1 + W2, it follows that:
![\[
\ul{r}\left[1-W_1(q(\ul{x});\ol{c}_1)-W_2(q(\ul{x}))\right]
>\ul{W}_2-W_2(q(\ul{x}))
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqnU024.gif?pub-status=live){kind=small}
must hold. Since W 2(q(x)) > W2 for any q(x) < 1, the right-hand side is negative, so r = 0 certainly satisfies this condition. Since r < 1 as well,
![\begin{equation}
\ul{r}\left[1-W_1(q(\ul{x});\ol{c}_1)-W_2(q(\ul{x}))\right]
<1-\ul{W}_1-W_2(q(\ul{x}))
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007081401668-0001:S002081831000010Xjra_eqn016.gif?pub-status=live){kind=small}
must hold. There are two cases to consider. First, suppose
Since W 1(q(x);c) > W1 for any q(x) < 1, it follows that (13) is satisfied for any r, so for r = 0 in particular. Now suppose that (Z) is not satisfied. Both sides of (13) are negative, which implies that only r > 0 can possibly satisfy it. Thus, if (Z) is not satisfied, the low-value demand cannot be riskless. Because I am looking for equilibria with such a demand, assume that (Z) holds for the rest of the proof. I labeled this condition to indicate the zero-risk associated with the low-value demand, and it is the analogue to the converse of (D) in the simple models.
Consider now the rejection probability specified in the proposition. For any x ∈ (x,x], r(x) = (x − x)/[x − W 1(q(x);c1)] solves U 1(x;c1) = x. That is, player 2's rejection probability leaves the strong type indifferent between any demand in that range and the equilibrium riskless low-value demand. Note in particular that 
implies that r(x) is a valid probability. Moreover, r(x) = r from (12) because r = 0 and q(x) = 1. Since x ≥ x 1, taking 
yields the lower bound on the riskless demand that can be supported in equilibrium. The upper bound x** follows from Bayes rule and is derived in the text.
I now check that deviations are unprofitable. Since player 2 accepts any x < x, such deviation from x is not profitable. Any x ∈ (x; x] is rejected with probability that leaves the strong type indifferent between x and x. But since x is also the weak type's payoff and the weak type's payoff from war is strictly worse than the strong type's, this deviation is strictly worse for the weak type. Finally, any x > x is rejected for sure, and the resulting war is one in which player believes she is facing the strong type. This is clearly worse for the strong type (at x he fights such a war with positive probability but also obtains x > W1 with positive probability), and this implies it is also worse for the weak type.
