A widespread approach to explaining international cooperation that has emerged over the past twenty-five years is based on insights from the analysis of repeated games.Footnote 1 This cooperation theory typically assumes that the underlying preferences of governments have the structure of a Prisoners' Dilemma (PD), which makes defection from any agreement the dominant strategy, and then shows how cooperative behavior can be sustained in the long run despite the absence of an agent that can enforce agreements.Footnote 2 The answer this theory provides is invariably the same: reciprocal threats to punish deviations from the desired behavior can be used to coerce the cooperation of the actors.Footnote 3 Cooperation is a within group problem that the collective solves by appropriate group enforcement against individual members.
Such an approach explains how cooperation can emerge “spontaneously” under anarchy and make agreements self-enforcing, but it is poorly suited as a guide to understanding many interesting cases of international collective action. One reason for this is that actors may often have heterogeneous preferences over the outcome of an international collective action (for instance, many actions generate both positive and negative externalities), and so disagree about the desirability of undertaking it. This splits the actors into supporters and opponents of that particular collective endeavor.Footnote 4 Whereas free-riding incentives might still arise within each group, a second important problem is that of one group overcoming the opposition of the other. In this setting, cooperation is also a between groups problem that the collective must solve by an appropriate distribution of benefits to the groups of supporters and opponents of the collective action.
In this article, we conceive of international cooperation in terms of competition between groups and analyze its effects on the types of organization that individuals choose to solve the collective action problem. We develop a theoretical model in which actors can disagree about the desirability of the collective action and can choose to spend their resources either in its support or in opposition. The actors' preferences are private information that they must communicate to each other (through, for example, voting). Since there is no exogenous enforcement to ensure that individual actors abide by that outcome, the collective faces two serious problems: how to induce its members to communicate truthfully, and how to get them to behave in accordance with the collective vote.
We analyze two institutions that can solve both problems, and compare their relative merits. These institutional solutions, however, rely on coercion and long shadows of the future, both of which are arguably problematic empirically.Footnote 5 What is needed, then, is an institution that does not require either. One possible venue is to shift the enforcement mechanism to the realm of domestic politics.Footnote 6 While we believe this is essentially the right way to go, we want to show that noncoercive cooperation is quite possible even in the existing framework with an alternative organization form, where the actors hire an agent who implements the action if the vote clears an agreed-upon threshold. We show that this organizational form, which is independent of the shadow of the future, could be quite attractive and actors might be willing to spend very large portions of their endowments to maintain it when none of the alternatives are viable. This is so even though we assume no special informational or expertise advantages for the agent over the actors and even though delegation involves a cost that each country has to pay. Thus, we uncover a novel rationale for delegation that has nothing to do with facilitating cooperation in coercive environments—indeed it is useful precisely because it makes coercion unnecessary, and thus renders the shadow of the future irrelevant. Overall then, we show that even if international cooperation is conceived as a sequence of ad hoc collective actions, it is possible to design self-enforcing institutions that improve individual and collective welfare. Moreover, it is possible to design an institution that can accomplish this at some additional cost but without coercing its members.
Avoiding the Costs of Anarchy
The following discussion is primarily intended to provide some basic definitions and to motivate the assumptions of our model by substantiating three major claims. First, most international actions have both supporters and opponents. “Cooperation” among those that want a particular collective action to take place might well mean “conflict” from the perspective of those that do not. Second, these groups of supporters and opponents can “invest” resources either to facilitate that action or hinder its implementation. Third, the memberships in these two groups can be unstable over time. Based on these assumptions we develop a model that shows how certain institutional arrangements can help mitigate the problems for collective action that arise within this “anarchic” situation.
The standard approach to collective action problems is to model them as arising among actors who have the same collective goal but who attempt to free ride on the efforts of others. International collective action, however, often involves actors who have heterogeneous preferences about the collective outcome itself. Increasing trade cooperation through enlargement of the World Trade Organization (WTO) might mean very different things to existing WTO members. Some states (those with strong import or export interests in the newcomers) gain from the enlargement. Others (those that experience stiffening of export competition to major export markets after accession) lose from that cooperative action. International peacekeeping missions can produce negative externalities for governments with strategic interests in the target of intervention (or those who prefer another form of international pressure because they disagree with the leaders of the action).
The heterogenous preferences over the outcomes can lead to conflict between supporters and opponents, and this conflict might be quite costly. Soon we will address institutional solutions that aim at preventing conflict between the two groups. But to understand why both supporters and opponents have a basic incentive to find institutional solutions, it is important to understand what can happen when actors fail to avoid a costly confrontation—that is, when they fail to find institutional arrangements that allow them to coordinate some mutually acceptable outcome, and must instead resort to brute-force “fighting” by spending resources in an attempt to impose their preferred outcome on each other. One illustration is furnished by the attempts to regulate trade of genetically modified organisms (GMOs). The unilateral regulation of GMOs in the EU led to a decline of American GM corn imports from $211 million in 1997 to merely $0.5 million in 2005. The United States openly criticized the EU's actions as a strategy to protect its agricultural sector and vetoed the adoption of regulations. It also initiated a WTO trade dispute and put serious pressure on countries to abide by that position. In Africa, it threatened to cut off aid completely unless the recipients abandoned existing regulations on GMO imports. When the Egyptian government, which had initially supported the United States, decided to withdraw from the WTO complaint, the United States retaliated by pulling out of the free trade agreement talks. The EU itself had to invest heavily in institution-building projects in African countries to offset the potential loss of American aid. It also threatened to ban imports of agricultural products from countries that used GMOs, and it conditioned many of the trade benefits it offered to developing countries, such as the General System of Preferences Plus agreements, on the implementation of the precautionary principle. The conflict between the United States and the EU about the desirability of the international collective action regarding trade in GMOs proved quite costly to both sides.Footnote 7
When there is conflict over the desirability of collective action, the success of international cooperation depends on the ability of its supporters to overcome its opponents. The task is complicated by preferences over that action being heterogeneous over the particular issue, varying over time, and only privately known. It is in this environment plagued by asymmetric information and uncertainty that actors must identify each other's preferences through some form of communication. Only then can they organize into groups of supporters and opponents that can then coordinate on some policy according to a rule that would benefit the collective. A serious additional problem is that once these groups are identified, one can use its superior resources to impose a solution on the other irrespective of what the rules say. As the GMO case shows, this type of conflict can be very costly, which provides strong incentives to find a way to avoid it.
The GMO case, then, demonstrates what can happen in the “anarchic” context when actors fail to organize themselves in order to avoid the costs of conflict. We study three “ideal-type” self-enforcing institutional arrangements that can help coordinate the actors, mitigate (and even avoid) the dissipation of resources, and provide large benefits for the members of the collective. The first two institutions rely on coercive enforcement, which requires long shadows of the future, but the third does not. We begin by studying the organizing principle we label a coalition of the willing, in which after an affirmative collective decision, only members who have voted in support of the action must contribute to its implementation.Footnote 8 Some collective security institutions can be organized this way. The Concert of Europe, for instance, provided for formal consultation among its members, but after a collective decision was reached, only the interested parties would undertake the authorized action.Footnote 9 Along similar lines, UN peacekeeping operations provide members in support of intervention with the opportunity to contribute (financially or otherwise) above and beyond their assessments. The principle is not limited to security: in the UN Framework Convention on Climate Change implementation of regulations is usually required only of those who supported the measures in the first place.
Second, we study the organizing principle we label universal burden-sharing, in which after an affirmative collective decision, all members must contribute to the implementation of the action regardless of whether they voted for or against it. For example, members of the WTO and other regional trade agreements have to implement any rules once they are agreed upon regardless of their position during the negotiations. Similarly, in many policy areas—such as the common market or environmental issues—the EU expects that all members contribute toward the collective action once a decision has been reached (whether it is to provide financial resources or to implement certain rules).Footnote 10 The International Whaling Commission might be the clearest example of a universal burden-sharing organization where the supporters and opponents of whaling commit themselves to majority decisions within the same organization. In the realm of security, the North Atlantic Treaty Organization (NATO) requires that all members respond (although not necessarily militarily) to an attack on a member once the alliance agrees to invoke article 5, as it did after the 9/11 attacks on the United States.
Third, we study the organizing principle we label an agent-implementing organization, where the actors delegate resources to an agent who is neutral with respect to the outcome of the action and implements the action only if the vote clears the agreed-upon threshold. In the International Monetary Fund (IMF), for example, each bailout is preceded by a vote of its members. If they vote in favor of a bailout, the Executive Board implements it and manages it. In the World Bank and other multilateral and regional development institutions, foreign aid projects are similarly implemented by a bureaucratic agent after the member states vote in their favor. Finally, in many policy areas—such as development, structural policies, and external trade policies—the EU is an example in which members have delegated implementation to a supranational agent.Footnote 11
The Model
There are N actors, each endowed with 1 unit of resource, who might want to take a collective action in each of discrete time periods indexed by t, (t = 0,1,2,…). The action produces a public outcome, a ≥ 2, and actors differ in their valuation of that outcome. The action succeeds only if at least θ > 1 resources are dedicated to it, and fails (if attempted) otherwise. If the action is taken, the individual payoff is:
$$
u_{it} = 1-x_{it}+\pi
av_{it}.
$$In this specification, x it ∈ [0,1] is i's period-t spending in support or opposition of the action, v it ∈ {−1,1} is i's period-t valuation of the benefit, and π is the probability that a is produced. Observe that if v it = −1, the actor prefers that the action is not taken, so we shall call this actor an opponent; and if v it = 1, the actor prefers that the action is taken, so we shall call this actor a supporter. Since individual actors might have opposing preferences over the desirability of the action, they can dedicate their resources either in support of its success or against it. We assume a simple technology of conflict, in which the success of the action depends on the difference between the resources dedicated in its support and the resources dedicated against it. To ease notation, we shall label individual spending in support of the action with x, and individual spending against the action with y. Let X t = ∑x it denote the total resources devoted in support of the action in period t, and Y t = ∑y it denote the total resources devoted against the action in period t. The probability that a is produced is
$$
\pi = \begin{cases}
1 &\text{if } X_t-Y_t\geq \theta\\
0 &\text{if } X_t-Y_t<\theta.
\end{cases}
$$If the resources devoted to support the action can meet its costs and overcome the opposition produced by resources devoted against it, then the action will take place. We say that the action is implemented at cost whenever X t = θ. With this specification and the assumption that a ≥ 2, it always pays for an individual to spend the entire resource if doing so meant obtaining the preferred outcome on a. Assume that θ ≤ N or else the action is infeasible because it is beyond the means of the entire collective.
In each period t, the preferences of the actors with regard to the action to be taken in that period are randomly and independently drawn from a common knowledge distribution with p ∈ (0,1) being the probability of being a supporter, and 1 − p being the probability of being an opponent.Footnote 12 Actors privately observe their own valuation, v it, only. From this perspective, the probability that there are exactly k supporters among the remaining N − 1 actors is: 
$f(k)=\binom{N-1}{k}p^k(1-p)^{N-1-k}$. Since the private values are independently drawn, learning one's own value tells an actor nothing about the other actors. Similar to other work in this area we assume that preferences are not correlated either between periods or within a period.Footnote 13
It is perhaps useful to pause at this point to clarify our assumptions about the structure of uncertainty and heterogeneity of preferences in our model. First, we assume that actors do not have complete information about the preferences of other actors within each period, and that they are also uncertain about their own future preferences, which means that today's preferences are no indication about where an actor will stand on some future action. Since international organizations deal with multiple possible actions in varied contexts rather than repeatedly revisiting the same problem over time, this is a natural way to model this environment. The uncertainty can arise for various reasons. For example, it might be due to variation within the same issue area.Footnote 14 A government could support the collective bailout of one country this year, but object to a bailout of another country two years later (perhaps because they believe that the latter country is likely to use the resources provided ineffectively or because they cannot afford it or even because of geopolitical conflict of interests). Since one cannot forecast which countries would require bailouts years down the line or one's own financial situation at that time, one's position on a collective action (bailout) today may not be very informative about one's position on a similar action in the future. The uncertainty might also be due to variation across issue areas. A government might support prosecution of violators of human rights and yet be opposed to intervention in a civil war where such abuses are known to occur. Preferences over some collective actions may also vary over time because of changes in domestic governing coalitions, which represent different interests. They may also vary because of changing public opinion that forces governments to reconsider prior positions. All of these changes are difficult, if not impossible, to predict and are thus ready sources of uncertainty that can decouple present preferences from future ones.Footnote 15 Second, we assume that knowing one's own standing cannot help an actor infer where others currently stand. This is clearly more demanding: actors who see how a shock to the environment has affected their standing on an issue might use this information to infer how this shock might have affected other actors who share relevant characteristics with them. However, in our model actors are symmetric and there is nothing that can anchor a subset of actors who are similar in the way they are affected within any given realization of the preference profile.Footnote 16
The timing of play in each period is as follows: actors observe their own valuations, engage in a round of costless and nonbinding communication, and then simultaneously decide how to spend their resources.Footnote 17 Because the relevant bit of information concerns the preferences of the actor over the collective action, we will consider the simplest possible form of communication: actors simultaneously announce whether they support the action or oppose it—they vote. That is, we have a straightforward reason to consider voting if we conceptualize it as a method of communicating privately known preferences. If resources spent after the vote in support of the action satisfy the threshold X t ≥ θ + Y t, the action takes place, otherwise the status quo prevails. The period ends and actors receive their payoffs. Each actor i maximizes his overall payoff, which is the time-discounted sum of his period payoffs: ∑t=0∞ δtu it, where δ ∈ (0,1) is the common discount factor.
To establish a welfare benchmark, consider the case where actors' preferences become known after they are realized. Let S t denote the number of supporters and N − S t denote the number of opponents in period t. Suppose there existed a planner who simply maximized social welfare and who could implement the action at cost while (costlessly) enforcing her decision. Since she can always maintain the status quo, society is guaranteed the income from private consumption whenever she chooses not to implement the action. The social welfare then will be N. When would he implement the action? The planner could choose to tax either supporters only or everyone, at a flat rate that collects just enough resources to pay for the action. Social welfare from implementation will be the same, N + a(2S t − N) − θ, in either case.Footnote 18 The planner will act when doing so is at least as good as remaining with the status quo, or whenever:
$$
S_t\geq\left\lceil\frac{N+\theta/a}{2}\right\rceil\equiv Q^*$$That is, the action will take place in every period in which S t ≥ Q*, and the status quo will prevail otherwise. For obvious reasons, we shall refer to Q* as the social optimum in our comparisons to the optimal quotas under uncertainty.
Inefficiencies in the Stage Game
We begin our analysis by considering the stage game in an arbitrary period t and ignore any previous or subsequent interactions for the moment (and so we suppress the timing subscripts on variables). If actors vote sincerely, the subsequent investment stage would proceed as if under complete information. As it turns out, however, this results in a highly inefficient interaction:
Proposition 1. The stage game has a pure-strategy Nash equilibrium in which all actors consume privately and the status quo prevails. Moreover, unless all actors are supporters, this is the unique pure-strategy equilibrium and there is no Nash equilibrium in which the action takes place with certainty.Footnote 19
One immediate consequence of this result (whose proof, as all others, is in the appendix) is that any mixed-strategy equilibrium will be quite inefficient in two ways: (1) the action will fail to take place with positive probability whenever it is socially optimal for it to be implemented; and (2) resources are dissipated by both groups (supporters spend X > 0 and the action fails to take place or opponents spend Y > 0 and it takes place anyway). This brute-force resolution of the problem of collective action is the type of “solution” that can arise when actors do not coordinate to avoid it (for example, the GMO case).
This result is important because it tells us that in a single-shot interaction with asymmetric information voting is of no help. Even if it were to work in the sense of being truthful, the best actors can expect is that they end up in the situation with complete information where the above conclusion would immediately hold. Since voting is costless and nonbinding, any subgame-perfect equilibrium (SPE) would require that actors play a Nash equilibrium in the investment stage. There is no way to implement the action at cost or avoid the other types of inefficiencies. For this, we need to consider some sort of institutional arrangement. We now show that the traditional approach to overcoming some inefficiencies through endogenous enforcement that relies on punishment strategies can be employed to ensure that (1) voting is sincere, and (2) the actors can implement the action at cost whenever it is socially efficient to do it.
Coercive Cooperation
Consider the repeated game and suppose that actors have selected a quota, Q, which is the minimum number of supporting votes before an action can take place. We will derive the optimal quota momentarily. For now, we note that the choice of voting rule is made once at the outset, and the rule remains in place for the rest of the interaction. Since actors do not know where they will stand on issues that come up for decisions by the collective in the future, the choice of voting rule is done “behind a veil of ignorance.”Footnote 20 This constitutional choice reduces to selecting a decision-making procedure that is both optimal ex ante and enforceable ex post. Because the actors are ex ante symmetric, the optimal quota is the same for all actors, and thus we can focus on the quota that maximizes the expected payoff of an arbitrary actor and satisfies any constraints necessary to enforce the behavior it implies. In the sections that follow, we first derive the conditions that make any given quota self-enforcing, and then identify the payoff-maximizing quota that we expect actors to coordinate on.
After the constitutional choice, the game proceeds as follows: in each period actors observe their private values, communicate by casting a public, costless, and nonbinding vote, observe the outcome of the collective vote, and simultaneously implement their investment decisions. Since the private consumption equilibrium exists in the stage game even with voting (actors simply ignore the outcome of the vote), the repeated game has a SPE, which is independent of the discount factor, and in which actors always consume privately. The expected payoff in this private consumption equilibrium is 1/(1 − δ) for each actor. We shall use this SPE as the threat that might enforce the desirable properties of the institutional SPE. This grim-trigger reversion SPE allows us to find the lowest discount factor that can sustain the institutional SPE—if the cooperation cannot be induced with the most severe threat, then it would be impossible with milder forms of coercion.Footnote 21
What are the desirable properties of the institutional SPE? We shall look for SPE in which (1) the voting is sincere—supporters vote to implement the action, and opponents vote not to; (2) the voting outcome is meaningful—actors condition their behavior on it; and (3) there is no resource dissipation—the action is implemented at cost and no resources are spent opposing it when it is not implemented. The first requirement is that it should not be optimal for actors to falsify their votes. This is a natural component that supports the second requirement, which is that voting actually means something because it can affect how actors behave. One of our goals is to rationalize voting in IOs by showing that even when it does not cost anything to cast a vote and actors are not bound by the voting outcomes, voting can meaningfully alter behavior. The final requirement embodies the raison d'être of IOs in our framework—avoiding the costs of conflict—we aim to show that institutions can enable actors to do just that.
Coalitions of the Willing
The first institution we examine is the coalition of the willing: whenever an action is to be implemented, only the (self-identified) supporters contribute toward it. Since contributions are limited to supporters, the quota must be feasible, Q ≥ θ, or else there would exist groups of supporters whose size satisfies the quota but that cannot implement the action using only their own contributions. The following proposition states informally the result from Proposition A2 in the appendix, which establishes the existence of an SPE, in which the threat of reverting to private consumption sustains sincere voting and at-cost implementation through contributions by the self-identified supporters.
Proposition 2. For any feasible quota, a coalition of the willing can be implemented provided actors are sufficiently patient, and provided no supporter can benefit by concealing his support. In this SPE, actors vote sincerely, and if the votes in support meet the quota, the supporters share the cost of implementation equally, and the opponents consume privately; otherwise everyone consumes privately. If the action ever fails when it is supposed to take place or gets implemented when it is not supposed to, actors revert to unconditional private consumption.
As we shall show, it is always possible to find a quota that can satisfy all conditions. Repeated interaction can coerce sincere voting by threatening retaliation for acting contrary to one's vote. Although this institution can support cooperation, it has at least two deficiencies even in the highly permissive environment that ignores monitoring and coordination costs. First, the institution must guard against opponents derailing the action at the implementation stage. This deviation is observable, so actors can implement the conditional punishment to deter it. Second, the institution must guard against supporters trying to free ride by pretending to be opponents and enjoying the benefits without incurring the costs. This deviation is far harder to deter because the supporter's behavior is identical with that of opponents, making the deviation impossible to detect. There is no threat-based solution for this problem—it must be voluntaristic. The sincerity constraint (defined in (SC) in the appendix), states what it takes for actors to remain sincere even when they could deviate without being found out. The benefit of voting sincerely is that the action will be implemented if the actor turns out to be pivotal. In all other cases, that vote merely results in costs should the action be voted for implementation (the actor would still contribute in those cases because otherwise the action would fail). The constraint ensures that the benefit of sincere voting outweighs the expected costs for a supporter.
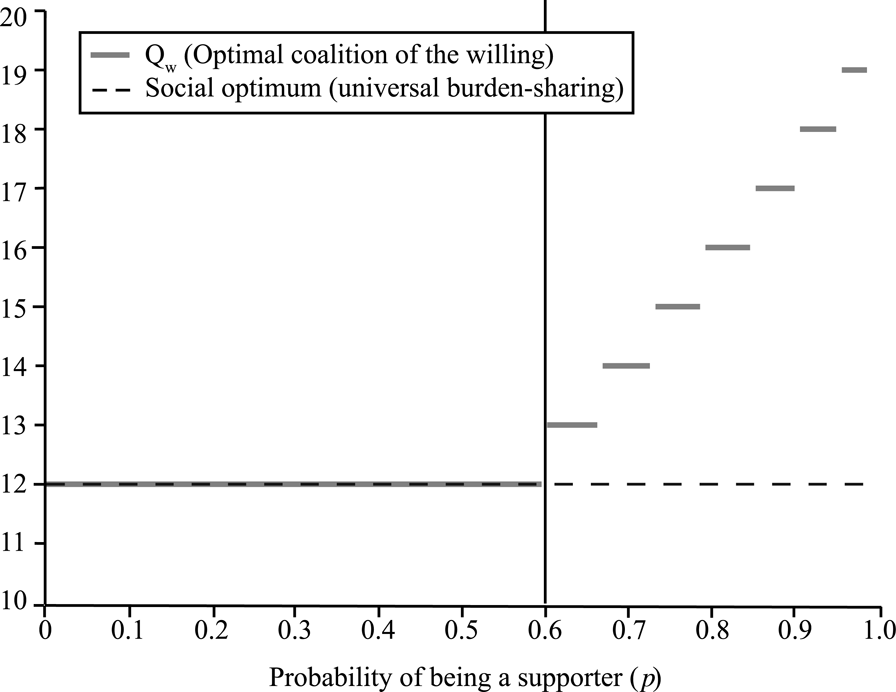
As it turns out, this constraint can be severely binding, especially when the probability of being a supporter is moderate to high. To show this, we now examine the optimal quota, which maximizes the equilibrium period payoff under the feasibility and sincerity constraints. The optimal quota for the coalition of the willing, Q w, is formally defined in Lemma A1. Figure 1 shows how it varies with p, the probability of being a supporter.
FIGURE 1. Coalitions of the willing and the social optimum (N = 20, a = 3, θ = 11).
When p is sufficiently low, the optimal quota is either at the social optimum, Q*, provided a group of that size can implement the action, or at θ—the smallest group that can do so. (This constraint would also bind if the social planner taxed only supporters.) However, as p increases, so does the optimal quota, in a stepwise manner with discontinuous jumps. In these cases, the sincerity constraint binds and forces the quota up and away from the social optimum. The vertical line marks the smallest value for p for which the constraint binds.
What explains these upward jumps? As the probability of support increases, the likelihood that any one actor would be pivotal for any given quota decreases. This increases the temptation to free ride. The only way to overcome this problem is to increase the quota: doing so reduces the expected benefit of free riding because it decreases the probability that the action would take place without one's vote. This restores the incentive to vote sincerely but as p increases further, the problem reappears and the quota must be adjusted again. In this way, the sincerity constraint drives the optimal quota further away from what is socially desirable. Somewhat paradoxically, as the number of actors that might be supportive of the action increases, the institution, in which only the coalition of the self-identified willing contributes to the action, becomes ever less socially efficient.
This social inefficiency suggests that it might be beneficial to organize cooperation differently. The first problem is that concentrating the costs on the group of cooperators precludes socially desirable outcomes because doing so puts expensive actions out of reach. The second problem is that a supporter might have incentives to distort his vote in an attempt to conserve his resources. An institution with universal burden sharing might help with both problems: it spreads the costs among all actors, and since one has to contribute whenever the action is voted to take place regardless of whether one voted for or against it, there should be no incentive to distort a supporting vote.
Universal Burden Sharing
We now consider an institution with universal burden sharing: one, where each member—supporter and opponent alike—is supposed to contribute whenever the agreed-upon quota is met. This changes nothing in the single-shot interaction: there is no reason to abide by the outcome of the vote. However, since every relevant deviation is now observable, it can be subjected to collective punishment when the interaction is repeated. The following proposition states informally the result from Proposition A3, which establishes the existence of an SPE with sincere voting and at-cost implementation through universal contributions.
Proposition 3. For any quota, universal burden sharing can be implemented provided actors are sufficiently patient. In this SPE, actors vote sincerely, and if the votes in support meet the quota, all actors share the cost of implementation equally; otherwise everyone consumes privately. If some actor fails to contribute the required amount or if the action gets implemented when it is not supposed to, actors revert to unconditional private consumption.
Observe that there is no analogue to the sincerity constraint because we no longer need a special condition to prevent hidden free riding by supporters. The reason is simple: a supporter who votes against the action lowers the probability of implementation (by the probability of being pivotal) but does not save on the contribution for all those cases where the action will go forward regardless of this actor's vote. Furthermore, since everyone contributes once the action is voted for implementation, there is no constraint implied by its costliness. In other words, there should be nothing to force the quota of the universal burden-sharing institution away from the social optimum.
Indeed, Lemma A2 shows that the optimal quota for universal burden sharing, Q u, is always the same as the social optimum. The lemma thus establishes that Q u is not merely independent of the uncertainty, but that it is socially optimal even after the uncertainty is removed by the act of voting. It is worth emphasizing this finding because asymmetric information usually induces serious ex post inefficiencies (as it does with the coalition of the willing). The universal burden-sharing institution does not have to suffer from this problem. The intuition is that the quota for this institution is selected to maximize the difference between the private consumption outcome and the expected outcome when everyone chips in to pay for the action. In the latter, each actor expects to pay the cost when the action is taken, removing any incentive to consider the likelihood of being a supporter. The only relevant consideration is how many members will find the action beneficial (precisely what the value of Q* gives us). Does this mean that actors would always opt for universal burden sharing over a coalition of the willing? Surprisingly, the answer turns out to be negative.
The Organization of Coercive Cooperation
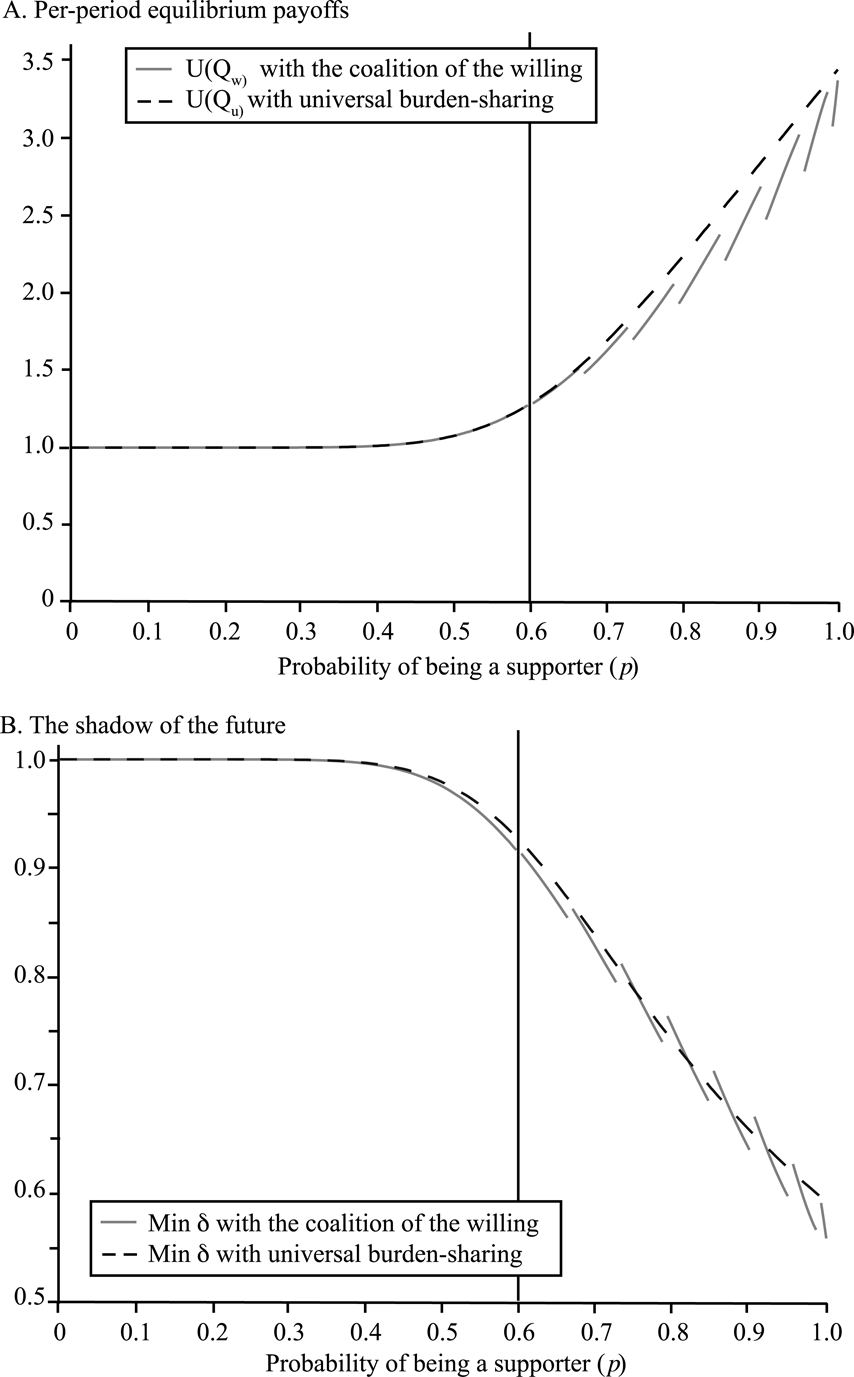
Since universal burden sharing is socially optimal ex post and because actors are symmetric ex ante, one might think that they would never choose to organize as coalitions of the willing. Indeed, when it comes to the expected payoff, universal burden sharing is always at least as good as the coalition of the willing, and often strictly better (Lemma A3). Figure 2A illustrates this.
FIGURE 2. Coalitions of the willing and universal burden-sharing (N = 20, a = 3, θ = 11).
The problem is that when the optimal quota for both institutions is at the social optimum (and so both yield the same expected payoffs), universal burden sharing is more difficult to implement because it requires a longer shadow of the future to coerce cooperation (Lemma A4).Footnote 22 If actors are not sufficiently patient, then this institution might simply be out of reach. Moreover, this problem might crop up even when universal burden sharing is strictly preferable. As Figure 2B shows, the relationship between the minimum discount factors necessary to implement the institutions can be quite involved once p forces Q w away from the social optimum: for some values of p the coalition of the willing is easier to implement, and for others it is universal burden sharing. The overall picture, however, is clear: if actors are patient enough, then universal burden sharing is the way to go, especially if the probability of support is not too low.
The Limits of Self-Enforcement
We have now identified two solutions to the problem of meaningful communication. They both make sincere voting self-enforcing with the threat to abandon cooperation if any actor deviates from the required behavior given the voting outcome. These solutions suffer from the familiar host of problems associated with this approach to endogenizing enforcement.
First, we assumed away transaction costs, which might be problematic in the asymmetric information setting. Actors can vote, observe voting outcomes, monitor each other's compliance, and then coordinate their contributions, all without paying any transaction costs. Introducing any of these considerations in the model will make the institutions harder to sustain because they will lower the expected payoff from participation.
Second, we assumed that actions (for example, contributions) are perfectly observable, that there is no noise, and that the action succeeds whenever actors contribute enough to it. These assumptions permit actors to identify those who attempt to free ride or purposefully derail implementation. If we relax this assumption, deviations will be harder to detect and therefore become more attractive. The institution would have to account for these problems by relaxing the trigger somewhat. It is not a priori clear whether the overall impact on the expected value of the institutions would be detrimental, but at any rate, the institutions would have to be far more involved, which in turn would increase the transaction costs and make them less valuable.
Third, we used a grim trigger strategy to sustain cooperation. The problem is that this type of punishment might be too severe for the other actors to execute. This gives them incentives to coordinate on restoring cooperation, which might make the SPE not renegotiation-proof. This would reduce the costs of deviating, and make cooperation harder to sustain. Any punishment that is immune to renegotiations would necessarily be less severe than the grim trigger, which means that it would require higher discount factors to work, exacerbating the already onerous demands on the shadow of the future.
The fundamental problem with these solutions is that they all require actors to be sufficiently patient. Transaction costs, monitoring and noise, the credibility of punishment strategies—all of these issues require investments or behaviors that reduce the expected value along the cooperative path. Since compliance is enforced with threats to revert to private consumption, the lower value of cooperation makes it harder to sustain the institutions because they require even longer time horizons to deter deviations. Ultimately, any institution that coerces cooperation with conditional threats of future punishment would be vulnerable in this way. Thus, we want to know if it is possible to sustain cooperation without coercion: if it can be done, then there would be no need for threats, and no need to worry about how valuable the future is.
Cooperation without Coercion
We now analyze whether it is possible to maintain cooperation regardless of the actors' time preferences. To this end, we begin with the single-shot game: if we can find a way to obtain a cooperative equilibrium here, then we automatically obtain the result in the repeated setting by simply having actors choose the stage-game equilibrium unconditionally in each period.
We propose the following formal organization. At the constitutional stage, the actors hire an agent whose wage is W > 0, select the quota (Q), and set the individual contributions (x 0) that they will be making to that agent. Just as before, this choice is made “behind a veil of ignorance” and the symmetry of the actors with respect to their future expectations and resource endowments implies that the optimal quota is the same for all of them and that their contributions will be symmetric as well. The only information available at this point is about the costs of agency and the action itself.
We conceptualize the wage, W, as transaction costs that arise when delegating implementation to an agent. Such costs may stem from the process of finding and hiring an agent (creating the IO), the agent's fees (maintaining the IO), or the potential costs of agency slippage (losses from imperfect monitoring of the IO's execution). The agent's wage is exogenous and is shared equally so that each actor contributes w = W/N toward it. Since the action must be feasible at the maximum that the actors can contribute toward it, we require that (1 − w)N > θ, which we can express as w < w, where w = 1 − θ/N, or else the combined cost of the formal organization and the action exceed the total resources available to the actors (that is, the organization is not feasible). Assume that the agent has no preferences regarding the action and cannot use any of the entrusted resources other than his wage for private gain. Further assume that the agent has the capacity to implement the action whenever it is authorized to act provided the subsequent behavior of the actors does not block it.
Following the constitutional choice, but before observing the realization of the preference profile, actors simultaneously contribute a portion of their resources, x 0 ∈ (w,1], to the agent. If any actor contributes less, the agent returns the contributions and the game continues as it would without him. After learning their preferences, actors engage in costless and nonbinding voting about the action the agent should take. The agent is committed to investing R = (x 0 − w)N toward action if the number of votes in support is at least Q, and to returning x 0 − w to each actor otherwise. After the agent's move, the actors simultaneously choose their investments.
Several things about this scenario are worth noting. First, all actors contribute to the agent's war chest. Since ex ante they are all the same, we focus on symmetric contributions. Second, this contribution is made “behind a veil of ignorance.” Thinking ahead to the repeated setting, this is a natural way to model organizations in which members agree on periodic (for example, annual) fixed contributions that the organization would then use in accordance with the wishes of its members to deal with whatever issues arise within its domain. In this setting, actors make their contributions in each period before they know what issues might come up or where they will stand on those that do. Third, the voting outcome is still not binding for the actors, only for the agent. Since the agent is assumed to have no preferences for the action, she can commit to invest according to the agreed-upon voting outcome. Actors, on the other hand, can still choose how to spend their resources. Fourth, the assumption that the agent returns the contributions (net her fee) if the action fails to garner the minimum required support stacks the model against sincere voting because it might allow the actors to use the information obtained at the voting stage after a failed vote to force the action with the resources they obtain. Fifth, we have not assumed any special expertise or informational advantages for the agent relative to the other actors. That is, none of the usual rationales for delegation apply here.Footnote 23
The Agent-Implementing Equilibrium
The first feature of this organization we must decide upon is whether actors should contribute anything over their initial investment when the vote goes in favor of implementing the action. Suppose that after the vote the agent did not have enough resources to implement the action without additional contributions from the actors. Since the voting outcome is not binding on the actors themselves, this effectively only lowers the cost of the action, and thus puts the actors back in the original situation where there is no way to implement the action without additional dissipation. Hence, in any equilibrium in which the agent's move implements the action with certainty, it must be that x(q) = 0 for all q ≥ Q: supporters (and opponents) consume privately their remaining resources when the action takes place.Footnote 24
When there are no additional contributions after the vote, it must be the case that the resources the agent controls are sufficient to overcome any opposition that might arise. Moreover, it must be the case that the supporters cannot impose the action if the vote fails and the agent returns some of the initial investments to the actors. We impose a strong requirement, one that is much stronger than what is necessary for a Nash equilibrium: we require that neither the supporters nor the opponents would be able to overturn the outcome of the vote even if they could coordinate costlessly to act as groups. In other words, instead of ensuring that the equilibrium is immune to individual deviations, we also ensure that it is immune to group deviations; that is, we require that the Nash equilibrium be coalition-proof.Footnote 25 Whereas this requirement is strong, the findings will be more persuasive if the equilibrium satisfies it.
The first possible group deviation we must guard against is by the opponents who might coalesce to derail the action in spite of the favorable vote. The largest opponent group that needs to be deterred from doing so occurs at the quota Q, so it is sufficient to ensure that the agent's resources can overcome their opposition. Since there is no need to give the agent any more resources than absolutely necessary for that, it follows that x 0(Q) must solve R − (1 − x 0)(N − Q) = θ, which pins down the optimal initial “no-blocking” contribution (NBC) to:
$$x_0(Q)=\frac{(1+w)N-Q+\theta}{2N-Q}.
$$Note that x 0(Q) ≤ 1 for any w ≤ w, so this contribution is feasible whenever the organization itself is. Since the group of opponents cannot overturn the voting outcome when the condition is satisfied, no single opponent would be able to derail the action either. Since the initial investment is sufficient for the action to take place after the affirmative vote, we shall call this an agent-implementing equilibrium.
Although x 0(Q) is sufficient to ensure that opponents would not attempt to block the action whenever it is supposed to take place, we must also make sure that supporters do not attempt to impose the action whenever it is not supposed to take place. Note that this is not necessary for a Nash equilibrium: if no supporter is expected to contribute toward the action after a failed vote, no individual supporter would have an incentive to contribute himself. Thus, the following condition is only required to make the Nash equilibrium immune to deviations by supporters acting as a group. For this to be the case, there should exist no q < Q such that the self-identified group of q supporters can impose the action using the resources that the agent returns to the collective after the failed vote. Given any quota Q, the largest such group is Q − 1: if this group can be deterred from imposing the action after reimbursement, then all smaller groups will be deterred as well. Since the agent always keeps his fee and the opponents spend Y = 0 after a failed vote, the no-imposition constraint (NIC) can be expressed as (1 − w)(Q − 1) < θ, which we can rewrite as:
$$
Q\leq\left\lceil 1+\frac{\theta}{1-w}\right\rceil-1\equiv{\bar{Q}_{\mathrm{a}}}.
$$Thus, any quota that does not exceed Qa will be such that the remaining opponents can always successfully block imposition attempts by the supporters who are not numerous enough to get the agent to implement the action. This means that together (NBC) and (NIC) guarantee that both opponents and supporters will abide by the outcome of the vote and will consume privately whatever resources they have after the agent moves. The following proposition shows that this is also sufficient to guarantee that they vote sincerely without coercion, so an equilibrium with delegation exists.
Proposition 4. For any quota that satisfies (NIC), there exists an agent-implementing subgame-perfect equilibrium. Each actor contributes according to (NBC) and votes sincerely. The agent invests toward the action if the supporting votes meet the quota, and reimburses the actors (net her fee) otherwise. Actors consume privately the resources they have after the agent's move.
Although this result tells us that there exists an SPE with delegation, it says nothing about the optimal quota actors would use, and indeed nothing whatsoever about whether they would even choose to delegate. Lemma A5 shows that there exists a unique optimal quota, Q a(w,p), for delegating to the agent, and that it is nondecreasing in the probability of being a supporter. To see whether actors would choose to delegate, we need to consider the alternative that they do not. We know what happens in that case: the action will not take place because sincere voting cannot be supported (Proposition 1). The alternative to no delegation in the single-shot interaction is private consumption with a payoff of 1. This implies that actors would choose to delegate if, and only if, doing so gives them something better.
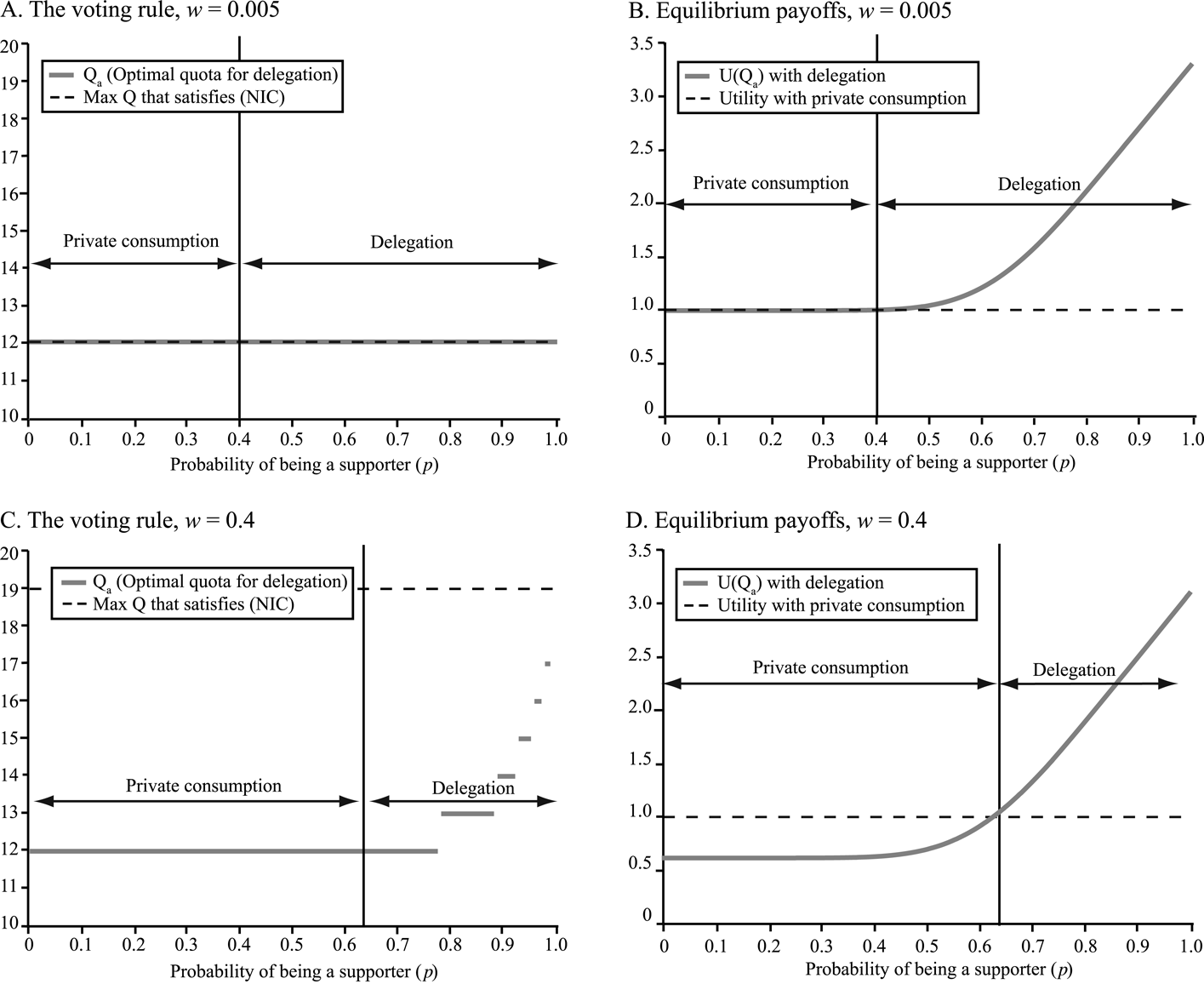
Figure 3 shows when delegation is preferable to private consumption for two organizational cost scenarios: relatively modest costs (each actor pays 0.5 percent of his resource endowment in agent fees, shown in the top row, where the (NIC) constraint binds) and somewhat exorbitant ones (each actors pays 40 percent of his resource endowment in agent fees, the bottom row, where it does not). All the other parameters are held at the values we used in the previous figures for the coalition of the willing and universal burden sharing. The vertical lines separate the values of p for which private consumption is preferable from those for which delegation is.
FIGURE 3. Delegation and private consumption (N = 20, a = 3, θ = 11).
As we know from Lemma A5, the optimal quota is a nondecreasing discontinuous step-function of p. Figure 3C shows a pattern reminiscent of the optimal quota for the coalition of the willing in Figure 1, which might be surprising. Recall that in coalitions of the willing the quota is forced upward by the sincerity constraint. Delegation is more like universal burden sharing in that respect: since all actors contribute, there is no incentive to vote insincerely when one is a supporter. So what forces the quota to increase?
The upward pressure on the quota under delegation comes from the unconstrained optimization itself: the quota increases because doing so produces better expected payoffs, not because it must or else an equilibrium condition would fail. Setting aside the ex ante probability that the quota is met for a moment, it is clear that actors prefer larger quotas: a large quota means that when it is met, the lingering opposition group will be small, which in turn means fewer resources must be wasted on deterring its potential attempt to undermine the collective decision to implement the action.Footnote 26 Since the amount contributed to the agent in itself does not affect the probability that the action takes place in equilibrium, it follows that actors prefer to conserve as much as possible for private consumption. Thus, for any given probability of the action taking place, actors would prefer the largest possible quota in order to minimize excess spending on deterrence.
The ceiling on how high this quota can be, of course, comes from the fact that for any given probability of being a supporter, a larger quota means a lower probability that the action will take place. This decreases the expected benefits, especially when actors expect to be supporters with high probability. The trade-off actors face, then, is that the lower cost of implementation must come at the expense of its lower probability. As p increases, the probability that any given quota will be met increases as well, which makes the trade-off less and less salient. At some point, it becomes beneficial to increase the quota and get the lower implementation cost because the probability that it will be met is high enough. Continuing in this way, we can see that the optimal quota will increase in step-wise fashion as p increases. Even though the behavior of the quota under delegation is superficially the same as its behavior in a coalition of the willing, the causes are radically different. This is clearly seen in Figures 3B and 3D, which show that the expected equilibrium payoff is strictly increasing in p under delegation, whereas it is nonmonotonic in the coalition of the willing, as revealed by Figure 2A.
Another noteworthy result is that there are circumstances under which delegation appears to be preferable even when the agent demands an excessive fee—in this case, up to 40 percent of each actor's budget! The wastage reflected by this fee does reduce the expected payoff from delegation, as one can see by comparing Figure 3D with Figure 3B. This in turn means that delegation will not become attractive until p is sufficiently high. The plots do, however, raise a question: is it the case that delegation is always preferable if p is high enough no matter how large the organizational costs (provided, of course, they retain the feasibility of implementation)? As it turns out, the answer is affirmative, as the following result shows.
Proposition 5. If the probability of being a supporter is sufficiently high, then actors strictly prefer to delegate for any feasible agent fee.
As Figure 3 shows, delegation becomes optimal (relative to private consumption) at much lower values of p than the sufficient condition in Proposition 5 might suggest. This is especially pronounced when the agent's wage is not too high. At any rate, we have shown that there exist conditions under which actors would delegate even though it is costly. They prefer to create a formal organization that would enable them to cooperate even in a single-shot interaction even though voting in such an organization is nonbinding and even though they must pay organizational costs and dissipate additional resources (to ensure that whatever opposition to implementation remains, it cannot block the action).
Why Delegate with Repeated Play?
Consider now the repeated game with the possibility of delegation. In each period t (t = 0,1,2,…), actors contribute the pre-set amounts to the agent, observe privately the realization of their preferences, and engage in costless nonbinding voting. If the supporting vote clears the quota, the agent invests toward implementation of the action and if it does not, he reimburses the actors net his operating fees. The key feature of this institutional setup is that the pre-set per-period contributions are made before actors observe their preferences for the action in that period, as they would be in organizations with subscriptions. We now show that delegation is easily supported in SPE in the repeated game whenever it can be supported in equilibrium of the single-shot game.
Proposition 6. If delegation is preferable in the single-shot interaction at Q a(w,p), then the following strategies constitute a SPE of the repeated game regardless of the discount factor: actors choose delegation with Q a(w,p), and use the stage-game equilibrium strategies from Proposition 4 in every period of the game.
This is an important result because it suggests one way in which actors can overcome the limits of self-enforcement inherent in organizing as coalitions of the willing or in a universal burden sharing institution. These institutional arrangements are very attractive because they can implement the action at cost and avoid the wastage inherent in the delegated environment where the resources must be sufficient to overcome any lingering opposition. However, these coercive environments are fundamentally constrained by the shadow of the future: it has to be long enough so that the long-term costs of failing to cooperate today outweigh any gains that actors might obtain by doing so. This requirement could be quite severe, as Figure 2B shows. For p ≈ 0.4, for instance, the minimum discount factor required to enable cooperation is close to 1. It stays above 0.8 for p up to 0.75. In other words, even when there is a 75 percent chance of each actor being supportive of the action, the coercive institutions require them to discount the future by no more than 20 percent or else cooperation will be impossible.
Maggi and Morelli find that when the discount factor is not high enough to sustain the socially optimal voting rule, the optimal self-enforcing rule is unanimity.Footnote 27 This is natural in their model where the action can take place only when all actors agree to it. In our model, unanimity would entail serious inefficiencies and might not even be enforceable if we allow for group deviations: if sincere voting reveals that there is enough support to implement the action but the vote is not unanimous, the supporters can impose it. Coercive threats can deter this but they would require high discount factors as well. Thus, the problem that low discount factors pose for cooperation in our model must be overcome through delegation rather than unanimity.
The great advantage of the noncoercive environment is that cooperation requires no threats of future punishment, which makes the shadow of the future irrelevant. For instance, as Figure 3B shows, cooperation with delegation is preferable to private consumption for any p > 0.4, which means that it can be implemented in situations where the tough demands of the discount factor would make the other arrangements impossible. Even with the relatively exorbitant agency fees in Figure 3D, delegation might work where nothing else would (for example, at p around 0.65). The key to this advantage is that the institution creates a “veil of ignorance,” which provides a commitment mechanism that allows actors to relinquish conditionally their ability to undermine the action before they know whether they will support or oppose this specific project. The condition is that the agreed-upon quota for support is met—this provides a buffer against imposition of the will of even large groups of supporters and opponents, and makes the institution attractive. The fact that delegation is noncoercive has other positive implications: there is no need to monitor compliance, and the problems of noise, involuntary defection, and renegotiation do not arise. Deviations are simply ignored: the play continues as if nothing has happened and there is no need to destroy cooperation if someone defects (or is believed to have defected). Finally, note that there is no special expertise required of the agent when it comes to the action. Delegation in this case does not occur because the agent can implement the action at lower cost or because he knows something others do not. This, in fact, strengthens our result: any of the traditional reasons to delegate would increase the value of this organizational form relative to the two others, making it even more likely that actors would choose it.
Although no international organization corresponds fully to the simple theoretical model, the findings already illuminate some of the fundamental differences between traditional coercive cooperation and agent-implementation. A full empirical study requires the theory to be extended in several nontrivial ways, as we note in the conclusion. It might still be instructive to consider the case of multilateral aid institutions. First, the staff of multilateral aid agents (for example, the World Bank) does not possess more expertise relative to the staff of governmental aid organizations (for example, USAID). In both cases, the staff comprises mainly economists with similar backgrounds and training. Second, the coercive mechanisms are very weak and only rarely employed.Footnote 28 Third, the shadow of the future tends to be relatively short because allocation decisions diffuse the interests of many members and because the political circumstances in members states sometimes shift quite dramatically. Thus, the existence (and proliferation) of multilateral aid institutions is puzzling in the traditional context since they neither provide special expertise to encourage delegation nor can they rely on coercion to enforce contributions. The noncoercive commitment mechanism we provide here can help us understand this phenomenon. Moreover, the case of multilateral aid institutions points to the importance of accounting for between-groups conflicts in addition to within-groups conflicts when analyzing the strategic logic of international organizations since the persistent bargaining over how aid should be allocated indicates that members often disagree with particular policies and are sometimes in support and sometimes in opposition to the action the agent takes.
Conclusion
This article analyzed international cooperation as between-group conflict between supporters and opponents of a collective action. Our model is premised on two fundamental aspects of collective action. First, and as usual, such action might be difficult to achieve because of incentives to free ride on the efforts of others. Second, and innovatively, whereas international collective action might be beneficial for some, it might be detrimental for others. This can give rise to highly conflictual situations where significant resources can be wasted on imposing one group's preferred outcome on the other. Whereas most existing work focuses on ways of overcoming the contributor dilemma, we focus on the problem of avoiding dissipation in attempts to implement some collective action.
This perspective of collective action is not meant as a contradiction to extant approaches but as a refinement, an extension that can provide new insights for our understanding of international cooperation. First, we offer an analysis of the rationale for diverse organizational forms for cooperation in a unified theoretical framework. The most important advantage of coalitions of the willing and universal burden sharing is their ability to avoid conflict and implement the action without any dissipation at all. The great advantage of agent-implementing organizations is that they do not require a long shadow of the future and do not depend on coercive threats to function.
Second, we uncover a novel rationale for delegation. The traditional explanation of why states delegate relies almost exclusively on the assumption that the agent has better information or superior expertise. Our model does not require any such asymmetry between the agent and the other actors. Instead, delegation eliminates the need for coercive enforcement mechanisms and works even when the shadow of the future is not long enough to render coercive solutions effective.
Third, our model helps explain why voting takes place despite the lack of external enforcement, and how the voting rule interacts with the structure of the organization itself. Empirically, voting is very common in IOs and there are considerable resources devoted to deciding on the voting rule.Footnote 29 Both are puzzling if IOs merely implemented informal institutions. We show that the need to ensure that actors truthfully reveal their preferences through voting can be a major driving force behind alternative organizational solutions to collective action problems. Whereas we identify two coercive mechanisms that can promote self-enforced voting (and in this we are consistent with the existing literature's emphasis on endogenous enforcement), we also identify a solution that requires no threats. In contrast to Maggi and Morelli, who were the first to study the endogenous enforcement of voting in IOs,Footnote 30 we do not find that unanimity is the optimal voting system within any of the three organizational forms. Moreover, we show that the different forms have varying pros and cons, and that there exist circumstances that make each of them preferable to the other two. This helps rationalize the empirical existence of all three types.
Fourth, these findings can shed more light on the question of why states tend to comply with international agreements. Whereas most of the literature either treats compliance as epiphenomenal (members comply because they want to and would have done so even without the organization) or attributes it to the enforcement capabilities of the organization (members comply because they are punished if they do not), we show that it is possible to design an institution in which neither is the case. In the agent-implementing organization, members contribute even though they would have not done so without it, but are not punished by others for deviating from prescribed behavior (beyond the failure to take action, that is).
The conceptual shift toward analyzing international cooperation as a phenomenon that involves, at least in part, between-group conflict is merely one step toward a theory of international organizations. We have abstracted away from many important aspects of international interaction that are highly relevant for the outcomes we observe. For instance, it would be important to relax the assumption of symmetry in resource endowments and valuation of the action for the actors. Doing so would introduce more interesting voting rules (for example, some types of weighted voting) in the design of international organizations. Another important extension would allow actors to make side payments in order to “buy” votes. In addition, bringing in security concerns might well introduce the need to admit veto power for some members of the collective. The model is readily adaptable to these types of extensions. In the delegated solution we have also ignored the possibility that the agent might have preferences regarding the action, and in doing so we have not considered the usual agency problems directly although bureaucratic politics and agency slippage are partially reflected in the agent “fee” that members must bear for having access to the agent; the more pronounced these problems, the higher the sunk costs they would have to pay, and the less attractive the delegated solution will be. The model can be extended to consider how agents with preferences about the action itself can be disciplined for failing to comply with the outcome of the collective vote (for example, by replacing it or by cutting its wage) although doing so would necessarily move us back into the dynamic setting, and bring the shadow of the future back into play.
Appendix
Proof of Proposition 1. The first part is easy to verify. For the second, suppose π = 1 in equilibrium. This implies Y = 0 or else any opponent with y > 0 could profit by reducing his spending. But then X = θ or else any supporter with x > 0 can reduce spending as long as the action can still be implemented. But if X = θ, then any opponent can block the action.
Proposition A2. Fix some Q (θ ≤ Q ≤ N), let x(q) = θ/q, and let
$$
{\underline{\delta}}_{\,\mathrm{w}}(Q)=\frac{a}{a+\zeta _{\rm w}(Q)},
$$where ζw(Q) = p(a − x(Q)) f (Q − 1) + ∑k=QN−1[(2p − 1)a − px(k + 1)] f (k). The following strategies constitute an SPE for all δ ≥ δw(Q) if, and only if, ζw(Q) > 0 and
$$
\underset{\text{benefit of sincerity}}{\underbrace{af(Q-1)}}
\geq\underset{\text{cost of sincerity}}{\underbrace{\sum_{k=Q-1}^{N-1}x(k+1)f(k)}}.
$$In each period actors vote sincerely; if there are q ≥ Q votes in favor of the action, supporters spend x(q) each and opponents consume privately; otherwise everyone consumes privately. If the action ever fails when it is supposed to take place (because some actor who voted for it fails to contribute or because it is blocked by opponents) or gets implemented when it is not supposed to be, actors revert to the unconditional SPE with private consumption. The equilibrium period payoff is 1 + ζw(Q).
Proof. Fix Q and consider the ex ante per-period equilibrium payoff for some player i:
$$
u_i (\sigma ) = \underbrace {\sum\limits_{k = 0}^{Q - 2} {(1)f(k)} }_{{\rm no\ action\ regardless\ of\ }i{\rm 's\ vote}} + \underbrace {[p(1 + a - x(Q)) + (1 - p)(1)]f(Q - 1)}_{{\rm action\ occurs\ only\ if\ }i{\rm \ votes\ in\ favor}} + \underbrace {\sum\limits_{k = Q}^{N - 1} {[p(1 + a - x(k + 1)) + (1 - p)(1 - a)]f(k)} }_{{\rm action\ occurs\ regardless\ of\ }i{\rm 's\ vote}},
$$which simplifies to u i(σ) = 1 + ζw(Q).
Consider the implementation stage. Suppose that q ≥ Q so the action should take place. Any supporter who deviates from x(q) will cause the action to fail, making this unprofitable. Furthermore, there is no need to contribute more than the minimum necessary to implement it. Since this is an at-cost implementation, any opponent who invests against the action some y arbitrarily close to 0 can derail it but then the game will revert to the unconditional SPE. Doing so would not be profitable if
$$
1-y+\frac{\delta(1)}{1-\delta}\leq 1-a+\frac{\delta u_i(\sigma)}{1-\delta}$$for y → 0. We can rewrite this as (1 − δ)a ≤ δζw(Q). The necessary condition for this inequality to work is ζw(Q) > 0. This condition is also sufficient to ensure that there exists δ high enough to satisfy the inequality. In that case any δ ≥ δw(Q) will work.
Suppose now that q < Q so the action is not supposed to take place. If q < θ then the action cannot be imposed because the supporters do not have enough resources to do so. Any attempt to do so would fail and would be unprofitable. If, on the other hand, q ≥ θ, then the (self-declared) supporters can implement the action if they wish to (because opponents are not spending anything against it) but doing so would result in the reversion to the unconditional SPE. This deviation will not be profitable if
$$1+a-x(q)+\frac{\delta(1)}{1-\delta}\leq 1+\frac{\delta u_i(\sigma)}{1-\delta},
$$which we can rewrite as (1 − δ)(a − x(q)) ≤ δζw(q). Recall now that the condition that prevents the deviation of an opponent is (1 − δ)a ≤ δζw(q). Thus, if an opponent will not deviate, then supporters certainly would not do so in the implementation phase.
We now turn to the voting stage. Consider now a player who learns that he opposes the action. If he votes sincerely, then his expected payoff in this period will be
$$
u_o(\sigma) = \sum_{k=0}^{Q-2}(1)f(k)+(1)f(Q-1)+\sum_{k=Q}^{N-1}(1-a)f(k)
=1-a(1-F(Q-1)).
$$If he votes, falsely, in support of the action and then behaves as a supporter (so the action gets implemented), his payoff in this current period will be
$$
\sum\limits_{k = 0}^{Q - 2} {(1)f(k) + (1 - a - x(Q))f(Q - 1) + \sum\limits_{k = Q}^{N - 1} {(1 - a - x(k + 1))f(k) < u_o (\sigma ).} }
$$Since this deviation will not be detected (and would not have been punished if it had), the game will continue as before. Thus, this deviation cannot be profitable. Suppose he votes for the action but then derails it. The optimal way of doing so would be to just consume privately—the other supporters, incorrectly expecting him to contribute x(q) toward the “at cost” implementation would end up with X < θ. Thus, his best possible payoff from a deviation for the current period will be 1. However, this deviation is observable and will be punished. This deviation will not be profitable if 1 + δ/(1 − δ) ≤ 1 − a(1 − F(Q − 1)) + δu i(σ)/(1 − δ). This reduces to (1 − δ)a(1 − F(Q − 1)) ≤ δζw(Q). However, since (1 − F(Q − 1))a < a, this condition will be satisfied whenever the condition that prevents an opponent (who has voted sincerely) from derailing the implementation.
Finally, consider a player who learns that he supports the action. If he votes sincerely, then his expected payoff will be
$$
u_s(\sigma) = \sum_{k=0}^{Q-2}(1)f(k)+(1+a-x(Q))f(Q-1)+\sum_{k=Q}^{N-1}(1+a-x(k+1))f(k).
$$If he deviates and votes insincerely and then does not derail the action (he has no incentive to vote insincerely and derail it), his payoff would be
$$
u_s(\sigma^\prime)=\sum_{k=0}^{Q-2}(1)f(k)+(1)f(Q-1)+\sum_{k=Q}^{N-1}(1+a)f(k).
$$Since this deviation will go undetected, the game continues as before. Thus, the necessary and sufficient condition for this deviation to be unprofitable is u s(σ) − u s(σ′) ≥ 0, or
$$
(a-x(Q))f(Q-1)\geq\sum_{k=Q}^{N-1}x(k+1)f(k),
$$which we can rewrite as (SC). This exhausts the possible deviations and completes the proof.
Lemma A1. The optimal quota for a coalition of the willing is Q w = max{θ,Q* + n(p)}, where n(p) ≥ 0 is the smallest integer such that Q* + n(p) satisfies the sincere voting constraint in (SC). The stepping function n(p) is nondecreasing.
Proof. Recall that U(Q) = 1 + ζw(Q) and that in SPE two constraints, Q ≥ θ and (SC), must be satisfied. We begin by showing that unconstrained maximization selects the complete information social optimum; that is Q u = Q*. The payoff function will be increasing at Q if, and only if, U(Q + 1) − U(Q) = ζu(Q + 1) − ζu(Q) > 0, and decreasing if the difference is negative. We now obtain:
$$
\zeta _{\rm u} (Q + 1) - \zeta _{\rm u} (Q) = (1 - p)af(Q) - p\left( {a - {\theta \over Q}} \right)f(Q - 1) > 0 \Leftrightarrow Q < {{N + \theta /a} \over 2} \equiv \tilde Q.
$$Thus, the payoff is strictly increasing for all 
$Q < \tilde Q$, and strictly decreasing for all 
$Q > \tilde Q$, which implies that the unconstrained optimum is at 
$Q_{\rm u} = \lceil\tilde Q\rceil = Q^*$. Clearly, if θ ≤ Q*, then the first constraint will not be binding; otherwise, Q u = θ as long as the second constraint is not binding. We now turn to investigating the conditions under which it will.
We can rewrite (SC) as
$$
\frac{a}{\theta}\geq\sum_{k=0}^{N-Q}\left[\frac{(N-Q)!(Q-1)!}{(Q+k)!(N-Q-k)!}\right]\left(\frac{p}{1-p}\right)^k
\equiv T(p,Q).
$$Note that a/θ > 0, but since
$$
{{\partial T} \over {\partial p}} = \sum\limits_{k = 0}^{N - Q} {\left[ {{{(N - Q)!(Q - 1)!} \over {(Q + K)!(N - Q - k)!}}} \right]} \left( {{p \over {1 - p}}} \right)^k \equiv T(p,Q).
$$the inequality must be violated for p sufficiently high (limp→1T(p,Q) = ∞ for any Q < N). On the other hand, limp→0T(p,Q) = 0, and the inequality is satisfied for any Q.
Take now Q u = max{Q*,θ} so that the first constraint is satisfied. For p sufficiently low condition (SC) will be met (with n(p) = 0), but as we increase p, it must eventually fail. Since T(p,Q) is continuous in p, there must exist some 
where (1) is satisfied with equality, so that the condition will fail for any 
$p > \hat p$. We now show that it is necessary to increase Q to restore the condition. First, note that T(p,Q) is strictly decreasing in Q. Since Q changes in discrete jumps, we can rewrite T(p,Q + 1) − T(p,Q) = D(p,Q) as
$$
D(p,Q)=\sum_{k=0}^{N-Q}\left[\frac{(N-Q-1)!(Q-1)!}{(Q+k+1)!(N-Q-k)!}\right]\left(\frac{p}{1-p}\right)^k
\left[Q-(k+1)N\right]<0,
$$where the inequality follows from the fact that the first two terms in the summation are positive but the third is negative for any k ≥ 0.
We now show that it is possible to satisfy (1) at 
$p > \hat p$ by choosing some Q > Q u. For this, it is sufficient to establish that there exists ε > 0 such that 
$T(\hat p + \varepsilon ,Q_{\rm u} + 1) < T(\hat p,Q_{\rm u} )$. Since T(p,Q) = T(p,Q + 1) − D(p,Q), we can write this as
$$
T(\hat{p}+\varepsilon,{Q_{\mathrm{u}}}+1)-T(\hat{p},{Q_{\mathrm{u}}})
=T(\hat{p}+\varepsilon,{Q_{\mathrm{u}}}+1)-T(\hat{p},{Q_{\mathrm{u}}}+1)+D(\hat{p},{Q_{\mathrm{u}}}).
$$But since 
$\lim_{\varepsilon\rightarrow
0}\left[T(\hat{p}+\varepsilon,{Q_{\mathrm{u}}}+1)-T(\hat{p},{Q_{\mathrm{u}}}+1)\right]=0$ but 
$D(\hat{p},{Q_{\mathrm{u}}})<0$, the fact that this difference is continuous in ε implies that that there exists 
$\hat{\varepsilon}>0$ such that 
$T(\hat{p}+\varepsilon,{Q_{\mathrm{u}}}+1)-T(\hat{p},{Q_{\mathrm{u}}}+1)+D(\hat{p},{Q_{\mathrm{u}}})<0$ for all 
$\varepsilon<\hat{\varepsilon}$. In other words, (1) must be satisfied at 
$T(\hat{p}+\varepsilon,{Q_{\mathrm{u}}}+1)$. Thus, the optimal quota for these values of p will be Q u + 1, or n(p) = 1. Continuing in this way, we find that as p increases, n(p) must increase by one unit in a step-wise manner as well until the quota reaches unanimity, in which case the condition will be satisfied regardless of the value of p because then T(p,N) = 1/N < a/θ.
Proposition A3. Fix some quota Q (1 ≤ Q ≤ N), let x = θ/N, and let
$$
\underline{\delta}(Q)=\frac{a+x}{a+x+{\zeta_{\mathrm{u}}}(Q)},
$$where ζu(Q) = p(a − x) f (Q − 1) + [(2p − 1)a − x](1 − F(Q − 1)). The following strategies constitute an SPE for any δ ≥ δu(Q) if, and only if, ζu(Q) > 0. In each period actors vote sincerely; if there are q ≥ Q votes in favor of the action, then each actor spends x and it gets implemented, otherwise everyone consumes privately. If some actor fails to contribute what they are supposed to or if the action gets implemented when q < Q, actors revert to the unconditional SPE with private consumption. The equilibrium period payoff is 1 + ζu(Q).
Proof. Fix Q and consider the voting phase assuming that players will contribute if the quota is met. With everyone contributing when they have to there is no incentive not to vote sincerely. If a supporter votes against the action, it will fail if he happens to be pivotal, and he will contribute if it gets implemented even without his vote. Clearly such a deviation cannot be profitable. If an opponent votes for the action, he will cause it to be implemented only if he happens to be pivotal, an unprofitable deviation. Thus, it is only necessary to ensure that the contribution is properly enforced.
Consider now the phase in which players have voted and there are q ≥ Q in support so the action should take place under the equilibrium strategies. Since x = θ/N, any player who fails to contribute will derail the action. The consequences of not contributing x are the same regardless of how one has voted, so we can analyze the deviation in this phase of the stage game without reference to the vote of the player. It is easy to see that if an opponent can be induced to contribute, then a supporter will surely do so: the continuation game is the same for both and the current payoff from the equilibrium strategy is lower for the opponent. Thus, it is sufficient to provide an incentive to the opponent. If he does not contribute, the action will fail to take place, and the game will revert to the noncooperative equilibrium. If the player follows the equilibrium strategy σ and contributes x, the action will take place now and in every future period in which the quota is met. To calculate the latter, we need the ex ante expected payoff to an arbitrary player (that is, the expected payoff before he learns his preferences). Since the action takes place for any q ≥ Q, the per-period expected payoff is
$$
u_i (\sigma ) = \underbrace {\sum\limits_{k = 0}^{Q - 2} {(1)f(k)} }_{{\rm no action regardless of }i{\rm 's vote}} + \underbrace {[p(1 + a - x) + (1 - p)(1)]f(Q - 1)}_{{\rm action occurs only if }i{\rm votes in favor}} + \underbrace {\sum\limits_{k = Q}^{N - 1} {[p(1 + a) + (1 - p)(1 - a) - x]f(k)} }_{{\rm action occurs regardless of }i{\rm 's vote}},
$$which simplifies to
$$
u_i(\sigma) = 1 + p(a-x)f(Q-1)+\sum_{k=Q}^{N-1}\left[(2p-1)a-x\right]f(k).
$$Thus, the condition for an opponent to follow the equilibrium strategy and invest for the action today is
$$
1-a-x + \frac{\delta u_i(\sigma)}{1-\delta} \geq 1 + \frac{\delta(1)}{1-\delta},
$$which we can rewrite as δu i(σ) ≥ δ + (1 − δ)(a + x), or δζu(Q) ≥ (1 − δ)(a + x). Since a + x + ζu(Q) > 0, this yields δ ≥ δu(Q), with δu(Q) defined in (2). To ensure that δu(Q) < 1, we require that ζu(Q) > 0, as stated.
Finally, we need to consider q < Q when the action will not take place. Clearly, no opponent would contribute anything if the supporters follow the equilibrium strategy, so we need to make sure only that the supporters do so. If q < θ, then the action is beyond the combined capabilities of the group. This deviation would result in wasted spending and no action, so it cannot be profitable. The only possibly tempting deviation is for them to implement the action, which they can do when q ≥ θ (since the opponents are spending Y = 0). In this case, the action can take place now (with opponents consuming privately) but the game will revert to the private consumption SPE from the following period. The condition for supporters to follow their equilibrium strategy and not impose the action today is
$$
1+\frac{\delta u_i(\sigma)}{1-\delta}\geq 1+a-x(q)+\frac{\delta(1)}{1-\delta},
$$which simplifies to δζu(Q) ≥ (1 − δ)(a − x(q)). Since this inequality must hold for all realizations of q < Q ≤ N and because the RHS is increasing in q (since x(q) = θ/q is decreasing), it is necessary that it be satisfied at q = N. Thus, we end up with δζu(Q) ≥ (1 − δ)(a − x). Recalling that the condition that prevents deviation by opponents is δζu(Q) ≥ (1 − δ)(a + x), we conclude that whenever the latter is satisfied, the supporters will have no incentive to impose the action either.
Lemma A2. The optimal quota for the universal institution is Q u = Q* regardless of p, and is always socially optimal even ex post.
Proof. Since U(Q) = 1 + ζu(Q), the payoff function will be increasing at Q if, and only if, U(Q + 1) − U(Q) = ζu(Q + 1) − ζu(Q) > 0, and decreasing if the difference is negative. We now obtain:
$$
\zeta _{\rm u} (Q + 1) - \zeta _{\rm u} (Q) = \left[ {{{p^Q (1 - p)^{N - Q} (N - 1)!} \over {(Q - 1)!(N - Q - 1)!}}} \right]\left[ {{{a + x} \over Q} - {{a - x} \over {N - Q}}} \right].
$$Since the first bracketed term is always positive, it follows that
$$
{\zeta_{\mathrm{u}}}(Q+1)-{\zeta_{\mathrm{u}}}(Q)>0 \Leftrightarrow \frac{a+x}{Q}-\frac{a-x}{N-Q}>0.
$$Solving the second inequality yields (a + x)N > 2aQ, which, after substituting x = θ/N ends in
$$
Q < \frac{N+\theta/a}{2}\equiv\tilde Q.
$$Thus, if 
$Q<\tilde{Q}$, then U(Q + 1) > U(Q), and the payoff function is increasing; but if 
$Q>\tilde{Q}$, then U(Q + 1) < U(Q), so it is decreasing. Since for any 
$Q<\tilde{Q}$ we would pick Q + 1 for a higher payoff, it follows that the best possible payoff is at 
$Q_\mathrm{u}=\lceil\tilde{Q}\rceil\,=Q^*$.
Lemma A3. The expected payoff in both institutions is the same under the same quota, and is strictly better under universal burden-sharing when the optimal quotas differ.
Proof. We first establish that the payoffs are the same when the optimal quotas are the same. We need to show that U w(Q) = U u(Q) ⇔ ζw(Q) = ζu(Q). We can rewrite this equation as
$$
\sum_{k=Q}^{N-1}\left(\frac{1}{N}-\frac{p}{k+1}\right)f(k)=p\left(\frac{1}{Q}-\frac{1}{N}\right)f(Q-1).
$$We need to prove equation (3) for an arbitrary Q, which we now do by induction. First, we show that it holds for Q = N. Since the summation term is 0 (the lower bound exceeds the upper bound), it is sufficient to show that the right-hand side is 0 too:
$$
p\left(\frac{1}{N}-\frac{1}{N}\right)f(N-1)=0.
$$For the inductive step, assume that (3) holds for some Q > 1. We now prove that the claim holds for Q − 1 as well. Rewriting the claim at Q − 1 yields
$$
p\left(\frac{1}{Q-1}-\frac{1}{N}\right)f(Q-2)
= \left(\frac{1}{N}-\frac{p}{Q}\right)f(Q-1)
+\sum_{k=Q}^{N-1}\left(\frac{1}{N}-\frac{p}{k+1}\right)f(k),
$$and since the claim is assumed to hold at Q, we substitute the second term using equation (3):
$$
=\left(\frac{1-p}{N}\right)f(Q-1).
$$Using the definition of the probability mass function, the equality is easily verifiable, so the claim holds at Q − 1. By induction, it must hold for all Q = 1,2,…, N.
Turning to the second part of the claim, recall from Lemma A1 that the social optimum Q* can be supported in a coalition of the willing whenever the cost and sincerity constraints do not bind. Since this is the equilibrium quota for universal burden-sharing, the first part of this lemma immediately implies that actors will be indifferent between the two in these circumstances. Since in all other situations the coalition of the willing requires a quota that is worse than the unconstrained social optimum but universal burden sharing does not, it follows that the latter must be strictly better.
Lemma A4. If Q w = Q*, then δu(Q*) > δw(Q w).
Proof. Observe that δu(Q*) > δw(Q w) ⇔ ζw(Q w) > (a/(a + x))ζu(Q*), where x = θ/N. If Q w = Q*, then ζw(Q*) = ζu(Q*) by Lemma A3, which immediately implies that the inequality holds. Thus, in these situations the discount factor required to sustain the universal burden sharing is strictly higher than what is required to sustain a coalition of the willing.
Proof of Proposition 4. Consider first the continuation game after the vote. Whenever the agent invests toward the action, it will succeed because x 0(Q) ensures that any groups of opponents at q ≥ Q does not have enough resources left to derail it (even though supporters consume privately). If q < Q, the agent reimburses the players. Since everyone consumes privately, no supporter can benefit by deviating and attempting to implement the action. Thus, neither opponents nor supporters have an incentive to deviate after the vote.
We now examine the voting stage given that the continuation game after the vote will be played according to the equilibrium strategies. Consider a player who learns that he is an opponent. If he votes sincerely, the action will be implemented if there are q ≥ Q supporters among the remaining N − 1 players. If, on the other hand, he votes insincerely in support of the action, the agent would implement it when there are q ≥ Q − 1 supporters among the remaining players. Since the player would not be able to block the action whenever implementation is attempted, this deviation simply increases the likelihood of implementation and decreases the likelihood that he will get back some of his payment to the agent, making him strictly worse off.
Consider now a player who learns that he is a supporter. If he votes sincerely, the action will be implemented if there are q ≥ Q − 1 supporters among the remaining players, and his payoff would be
$$
U_s = \sum_{k=0}^{Q-2}(1-w)f(k)+\sum_{k=Q-1}^{N-1}(1-x_0(Q)+a)f(k)
= 1 - w + (a-\hat{x}(Q))\sum_{k=Q-1}^{N-1}f(k).
$$If he deviates and votes against the action, then the agent will attempt implementation when there are q ≥ Q supporters among the remaining players. Since he will not even try to implement the action with fewer votes, there is no point in the supporter spending anything toward it. Since the action will succeed in all other cases, his payoff will simply be
$$
\hat{U}_s = \sum_{k=0}^{Q-1}(1-w)f(k)+\sum_{k=Q}^{N-1}(1-x_0(Q)+a)f(k) = 1 - w + (a-\hat{x}(Q))\sum_{k=Q}^{N-1}f(k) < U_s
$$making this deviation unprofitable. Thus, any supporter has strict incentives to vote sincerely as well.
Lemma A5. There exists a unique Q a(w,p), which maximizes the delegation payoff. Moreover, this optimal quota is nondecreasing in p.
Proof. Delegating with Q means that every player contributes x 0(Q), votes sincerely after observing his preference, and consumes privately. The agent commits the resources toward the action if there are q ≥ Q supporting votes and reimburses the players (net her fee) otherwise. The expected payoff to an opponent from a sincere vote is
$$
U_o = \sum_{k=0}^{Q-1}(1-w)f(k)+\sum_{k=Q}^{N-1}(1-x_0-a)f(k)
= 1 - w - (a+\hat{x}(Q))\sum_{k=Q}^{N-1}f(k),
$$where we used (NBC) to obtain
$$
x_0(Q)-w = \frac{(1-w)(N-Q)+\theta}{2N-Q}\equiv\hat{x}(Q).
$$That is, 
$\hat{x}(Q)=x_0(Q)-w$ is the portion of the contribution that can be used for implementation. For any agreed-upon Q, the ex ante expected payoff to player i is
$$
U_{\mathrm{a}} =1-w+p(a-\hat{x}(Q))f(Q-1)+\left[(2p-1)a-\hat{x}(Q)\right]\sum_{k=Q}^{N-1}f(k),
$$where we used equation (4) for the payoff in case he turns out to be a supporter (with probability p), equation (5) for the payoff in case he turns out to be an opponent (with probability 1 − p). Some rather tedious algebra shows that U a(Q + 1) − U a(Q) ⪌ 0 if, and only if,
$$
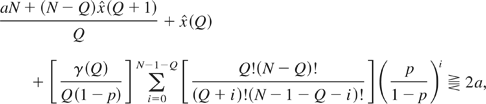\frac{aN+(N-Q)\hat{x}(Q+1)}{Q}+\hat{x}(Q) + \left[\frac{\gamma(Q)}{Q(1-p)}\right]\sum_{i=0}^{N-1-Q}\left[\frac{Q!(N-Q)!}{(Q+i)!(N-1-Q-i)!}\right]
\left(\frac{p}{1-p}\right)^i\gtreqqless 2a,
$$where
$$
\gamma(Q) = \frac{(1-w)N-\theta}{(2N-Q)(2N-Q-1)}>0.
$$Observe now that all three terms on the left-hand side of equation (6) are positive. Furthermore, at Q = 1 the left-hand side is strictly larger because it reduces to aN plus three nonnegative terms and N ≥ 2. Thus, at Q = 1, the difference is strictly positive, so the payoff function is increasing. More tedious algebra shows that all three terms on the left-hand side are decreasing in Q. Thus, the payoff function is concave, which implies that it has a unique maximizer, which we denote Q a*(w,p). It is immediate that the optimal quota must be Q a(w,p) = min(Q a*(w,p),Qa). Finding this quota numerically is straightforward: it is the smallest integer such that the left-hand side of equation (6) is less than the right-hand side.
We finally show that Q a(w,p) is nondecreasing in p. Since only the interior solution depends on p, we only need to prove the claim for Q a*(w,p). From the FOC given by equation (6), it is sufficient to show that the summation term (the only one involving p) is increasing in p. Taking the derivative of that term with respect to p produces
$$
\left[\frac{\gamma(Q)}{Q}\right]\sum_{i=0}^{N-1-Q}\left[\frac{Q!(N-Q)!}{(Q+i)!(N-1-Q-i)!}\right]
\left[\frac{p^i}{(1-p)^{2+i}}\right]\left(1+\frac{i}{p}\right)>0,
$$so the claim holds. To see why this is so, fix some p and consider the optimum Q a*(w,p), which is the smallest integer for which the left-hand side of equation (6) is less than the right-hand side (that is, increasing the quota would make the payoff worse). If increasing p causes the left-hand side to increase, it will eventually exceed the right-hand side for some 
$\hat{p}>p$. But then 
$Q_{\mathrm{a}}^*(w,\hat{p})$ will no longer be the smallest integer that makes the left-hand side less than the right-hand side (that is, it will no longer be optimal). Since the left-hand side is decreasing in Q, the requirement for optimality can be restored by increasing the quota to 
$Q_{\mathrm{a}}^*(w,\hat{p})=Q_{\mathrm{a}}^*(w,p)+1$, which will make the left-hand side less than the right-hand side again. Continuing in this manner, we see that increasing p causes the quota to increase in step-wise fashion until it reaches the ceiling Qa.
Proof of Proposition 5. Note now that 
$\lim_{p\rightarrow 1}U_{\mathrm{a}} = 1-w+a-\hat{x}(Q_{\mathrm{a}})$. This is strictly preferable to private consumption whenever this is greater than 1, or, after rearranging terms, whenever aN + (a − 1)(N − Q a) > wN + θ. Since N ≥ Q a and a − 1 > 0, the second term on the left-hand side is nonnegative at the optimum quota. It then follows that it is sufficient to establish that aN > wN + θ holds. Since the right-hand side is increasing in w, we only need to establish the claim at w, where it reduces to aN > wN + θ = N ⇔ a > 1, which holds.
Proof of Proposition 6. Since the strategies are unconditional, deviation does not affect future play, and the discount factor is irrelevant. The only possibly profitable deviation is therefore limited to the stage-game. Since delegation with Q a is preferable to private consumption and the strategies from Proposition 4 specify an equilibrium in the stage-game, no such deviation exists.
