Cost-effectiveness analysis (CEA) compares the costs and health outcomes of interventions to determine which intervention or policy is optimal given society's willingness to pay (WTP) for health outcomes. It is one of several criteria that should be used in decision making to inform the decision to adopt a technology, or not, given current knowledge. However, in the case of new technologies analyzed at an early stage in their cycle, considerable uncertainty about parameter values is likely when estimating cost-effectiveness. Decision makers need both to consider the uncertainties while making an immediate decision about adoption and to decide whether further research should be undertaken to reduce uncertainty in that decision. The expected value of information (EVI) theory in medical decision making is one such analytical technique that can identity the priorities for further research. The expected cost of making decisions under uncertainty can be referred to as the expected value of perfect information (EVPI) as it is the maximum a decision maker should be willing to pay to remove uncertainty concerning a decision (1). It is determined jointly by the probability that a decision based on existing information will be wrong and the consequences of the wrong decision. Within decision analysis, all parameters contribute to decision uncertainty. Estimating the expected value of partial perfect information (EVPPI) provides information on which parameters contribute most to this uncertainty and can provide the basis from which to determine future research priorities.
Total knee replacement (TKR) itself is a well-proven procedure. The demand for TKR is increasing mainly because of longer life expectancies and rising public expectations for quality of life and mobility in later years. TKR usually produces excellent results, although serious complications occur in around 5 percent of cases because of loosening, instability, dislocation, infection, or fracture (13). In 20–60 percent of patients, less serious complications such as anterior knee pain or limited movement are reported at approximately 3 years after operation (9–11). The surgeon's experience in patient selection, soft-tissue balancing, the alignment of the leg, the restoration of the joint line, and also the prosthetic design are all possible factors influencing the success of TKR (7).
Computer-assisted surgery (CAS) systems have been developed to improve limb and component alignment in TKR. However, as yet there is limited evidence of its contribution to the cost-effectiveness of TKR, although some studies of effectiveness have been undertaken (2–4;16). A Markov model had previously been used to make a preliminary assessment of the cost-effectiveness of computer-assisted TKR with that of conventional TKR (8). That study found, based on evidence from short-term radiographic studies demonstrating an improvement in the accuracy and precision of component and mechanical axis alignment with CAS and studies linking implant survival outcomes to these same alignments, that compared with conventional TKR, computer-assisted TKR is highly likely to be cost-saving and to offer a small quality-adjusted life-year (QALY) advantage.
However, there are multiple sources of uncertainty (e.g., utility values, costs, transition probabilities, and the effect of CAS) in the model. This finding is accentuated by the lack of long-term evidence from randomized clinical trials, which would provide a more definitive assessment of cost-effectiveness. Thus, in this study, value of information analysis is applied to measure the upper limit on returns to future research and to identify parameters for which future research may be warranted.
METHODOLOGY
Markov Model and Monte Carlo Simulation
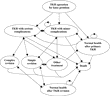
In our previous study (8), we designed a nine-state Markov model (Figure 1). A 10-year cohort simulation with a starting number of 1,000 TKRs was carried out. We selected a time horizon of 10 years given the average age of patients at operation was 70. Effectiveness was expressed by QALYs. Both costs and QALYs were discounted at 3.5 percent in line with 2003 Treasury guidelines (12). The differences between CAS and the conventional technique were expressed by the incremental cost-effectiveness ratio (ICER).

Markov state transition model for total knee replacement (TKR).
The model was made probabilistic using Monte Carlo simulation (MCS). We refined the model not only by keeping the hierarchical relationship between the utilities of states “Normal health after primary TKR,” “TKR with serious complications,” and “TKR with minor complications” in our previous study (8), but also by retaining the hierarchical relationship between the costs of states “Complex revision,” “Simple revision,” and “TKR operation for knee problem” in the simulation. We ran 10,000 120-cycle (a cycle length is 1 month) cohort simulations trials, randomly sampling from the distributions of transition probabilities, costs, and utilities. The assumed parameter distribution was showed in Table 1. In each of the 10,000 simulated trials, we calculated the net benefits of both CAS and conventional techniques at the level of £30,000 per QALY, the upper value suggested by the National Institute for Health and Clinical Excellence (15).

EVPI
EVPI is the difference between “the average of the maximized net-benefits” and “the maximum of the averages.” It refers to the expected value of information per individual presenting at the decision point. This value can be calculated as follows: (i) Conduct an MCS by sampling from the probability density functions for all parameters. (ii) Calculate the mean net benefits for each treatment option, and identify the optimal option as that with the maximum net benefits. (iii) For each replication within the MCS, calculate the difference between the net benefits of the optimal treatment and the maximum net benefits across all treatments. (iv) EVPI is the expected value from step iii.
Population EVPI
Population EVPI reflects the effective EVI that is relevant to a decision about further research. Population EVPI equals individual EVPI multiplied by the discounted effective population over a time horizon of the technology. The effective “population” of TKR operations per year was assumed as 44,898 in England and Wales (14). The time horizon over which the information on CAS-TKR would be relevant to decision makers was assumed as 5, 10, 15, and 20 years, so that we could see the change of population EVPI in quantity as the increase of the time horizon of a technology. The discount rate is 3.5 percent.
EVPPI and Population EVPPI
The EVPPI is the difference between the expected value of a decision made with perfect information about a particular parameter and the current optimal decision. Several methods for estimating individual EVPPI have been suggested (5;6). For this analysis, we adopted a two-stage MCS approach, which is calculated as follows: (i) Single values are randomly selected from the probability density functions of the parameters for which we wish to estimate EVPPI. (ii) The parameters are fixed at the values selected in step i, and the net benefit for all treatment options is estimated by conducting MCS by sampling from the probability density functions of all other parameters. (iii) For each simulation conducted in step ii, the net benefit of the optimum therapy from the base analysis is subtracted from the maximum net benefit over all therapeutic options. (iv) Steps i–iii are repeated numerous times with different sets of values for the parameters of interest. (v) EVPPI is then the expectation of values obtained from repeating step iii.
Population EVPPI equals the individual EVPPI multiplied by the discounted effective population over a time horizon of the technology. Population EVPPI is a function of the chosen time horizon of a technology. However, the rank order of EVPPIs will be the same regardless of the different time horizon.
RESULTS
Markov Model and Distributions of Parameters
Figure 1 shows the nine-state Markov model and the transition relationship between the health states. Table 1 shows the distributions of the parameters in the Markov model. Uncertainties around the cost-related parameters were characterized by Gamma distribution function, making the distributions skewed with a lower bound of 0. Uncertainties around the utility values were characterized by a Beta distribution function, which has bounds of 0 and 1. Uncertainties around the transition probabilities were characterized by the Dirichlet distribution function—the multinomial equivalent to the Beta distribution (8).
Individual and Population EVPI
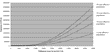
Figure 2 shows the EVPI for the UK population with TKR for different assumed time horizons of the technology, from 5 years to 20 years. In this instance, the population EVPI increase with the amount of WTP for one QALY is shown. If the WTP for one QALY were £30,000, the population EVPI assuming a 10-year time horizon for CAS-TKR would be £8.3 million, while the individual EVPI would be £21.4.

EVPI for UK population with TKR. EVPI, expected value of perfect information; TKR, total knee replacement; QALY, quality-adjusted life-year.
EVPPI
The overall EVPI for the model is a useful upper limit on returns to future research. However, of crucial importance is which particular parameters (or groups of related parameters) are most important in terms of representing the greatest value of information. In the EVPPI analyses (10-year time horizon of the technology), all individual parameters had an EVPPI of 0. However, three groups of parameters had positive EVPPIs (Table 2). Population EVPPI was £5.6 million for utility parameters, £20,000 for transition probabilities relating to CAS-TKR, and £5,000 for transition probabilities related to conventional TKR.

DISCUSSION
In our earlier study (8), based on short-term evidence from the studies that have compared the clinical effectiveness of CAS with that of conventional TKR in terms of correct alignment of components, we found that compared with conventional TKR, computer-assisted TKR is a cost-saving technology in the long-term and may offer small additional QALYs.
Our analysis here of the value of additional information related to specific parameters or parameter groups confirms the results of parameter importance analysis from our early study (8). Using the analysis of covariance approach to explore the proportion of the total model sum of squares that is explained by each individual input parameter, it was found that utility-related parameters and transition probabilities were the most important.
However, population EVPI and EVPPI are more informative measures of parameter importance as they measure the maximum possible payoff to additional research. The population partial EVPI can help to focus research priorities as it allows identification of the parameters contributing most to decision uncertainty (5). In our earlier study (8), it was found that, at £30,000 per QALY, there was a 92 percent probability that CAS was the more cost-effective technology. Given this high degree of certainty, it is not surprising that individual EVPI is not high, although given the high use of the technology population EVPI is of more interest.
The key assumption in the earlier study was that CAS surgery, due to improving alignment of components, could reduce complication rate and revision rate. This assumption is associated with a high degree of uncertainty because of the lack of direct longer-term evidence in support. However, despite this degree of uncertainty, the partial value of perfect information showed that transition-related parameters have only limited information value, and to be justified, future research related to these parameters would have to have value for decision making relating to a large number of patients outside the UK setting.
In the value of information analysis, the annual size for the relevant patient population and the time horizon over which the evidence is relevant (and, hence, the size of the total patient population who might benefit from a reduction in uncertainty) are critical parameters and can only be a matter of judgment. Moreover, these two parameters may well differ for different items of information. For example, reducing the uncertainty around the effectiveness of CAS will only be relevant as long as the specific technology does not change or develop—which is likely to be a relatively short time period. However, during this short period, well-conducted studies of relative effectiveness would probably have relevance to patients in a range of countries where the technology might be adopted (our analysis only considers patients in England and Wales).
On the other hand, better estimates of patient utilities in different health states might have longer-term relevance (for the evaluation of future developments in TKR surgery) in the United Kingdom but might not necessarily be seen as generalizable to patients from all other countries interested in the technology. UK cost data are likely to be of interest only in the United Kingdom and to be relatively rapidly outdated. Thus, comparison of (UK) population EVPPI for different parameters judged under a single time horizon may be misleading in terms both of the value beyond the UK population and for different time horizons.
Furthermore, special attention should be paid to generalizing the results of the current study to other countries. We did the analysis from the UK National Health Service point of view in terms of the relevant costs. Other countries will have different cost structures for these procedures, which would influence the mean value and variance of the cost in each health state. Thus, our results can only provide information for UK decision makers and may not be applicable in other countries. It is encouraged that other countries repeat the analysis applying their own cost and size of relevant patient patients.
In addition, population EVPI and EVPPI are the upper limit for additional research in one country. If analysis were repeated in other countries, the EVPI for parameters that are common across countries would be greater, providing greater rationale for a coordinated program of future research.
CONCLUSION
Based on the value of information analysis, from a UK perspective, it is likely to be worthwhile to have additional research related to patient utilities at different health states. Further research related to transition probabilities may be of value, but only from a more global perspective.
CONTACT INFORMATION
Hengjin Dong, MD, PhD (dong@uni-heidelberg.de), Junior group of International Health Economics and Technology Assessment, Department of Tropical Hygiene and Public Health, Heidelberg University, INF 324, D-69120, Heidelberg, Germany
Doug Coyle, PhD (dcoyle@uottawa.ca), Associate Professor, Epidemiology and Community Medicine, University of Ottawa, 451 Smyth Road, Ottawa, Ontario K1H 4H5, Canada
Martin Buxton, BA (Soc Sci), (martin.buxton@brunel.ac.uk), Professor of Health Economics, Health Economics Research Group, Brunel University, Cleveland Road, Uxbridge, Middlesex UB8 3PH, UK
The authors acknowledge support of this work through the MATCH Programme (EPSRC Grant GR/S29874/01), although the views expressed are entirely their own. Financial support to MATCH comes from several public and private sources including DePuy International Ltd. The authors have no personal conflict of interest with regard to this project.