When developing an economic model, a reference technology is compared with one or more comparators. A key element is the estimate of relative clinical effectiveness of the reference technology. The clinical effectiveness is frequently evaluated by pooling data from multiple trials, preferably using a meta-analysis approach in the framework of a systematic review. When carrying out a meta-analysis there is a choice between using a fixed effect or random-effects statistical model. More often than not, the choice between fixed and random-effects is driven by an assessment of the heterogeneity, generally summarized by the I2 statistic.
A fixed effect meta-analysis assumes that all the studies are measuring the same common treatment effect with differences in observed treatment effect between studies purely due to chance. In a random-effects meta-analysis, it is assumed that the estimate of treatment effect will vary across studies due to both chance differences and real differences in treatment effect. A random-effects meta-analysis estimates the average treatment effect and the confidence bound applies to that average effect. However, the confidence bounds for the average treatment effect might not give a good indication of what the treatment effect could be in a new study. The prediction interval was developed as a means of estimating the bounds within which the potential treatment effect could fall (Reference Higgins, Thompson and Spiegelhalter1;Reference Higgins2). With high heterogeneity the prediction interval tends to be much wider than the confidence bounds of the average treatment effect. The prediction interval does not affect the point estimate of average treatment effect.
In economic modeling, it is routine to vary treatment effect in a probabilistic sensitivity analysis. When incorporating a treatment effect estimate derived from a random-effects meta-analysis, it is tempting to use the confidence bounds of the average treatment effect to determine the range of potential treatment effects. However, in these cases it would be more correct to use the prediction interval as an economic model should reflect the potential effect of a technology rather than the more narrowly defined average treatment effect. The use of confidence bounds rather than prediction intervals can lead to a spuriously precise estimate of the effect of a technology and fail to show the decision maker the true uncertainty around the treatment effect. Indeed, confidence bounds may indicate a statistically significant treatment effect when prediction intervals may show a substantial probability of no effect.
The aim of this study is to investigate the impact on a cost-utility analysis of using clinical effectiveness derived from a random-effects meta-analysis presented as confidence bounds and prediction intervals, respectively. The impact is illustrated using a case study of robot-assisted surgery for radical prostatectomy.
METHODS
The analysis in this study uses an economic model that was developed for a health technology assessment of robot-assisted surgery for radical prostatectomy and hysterectomy (3). The model for prostatectomy combines information on both operative and functional outcomes, and hence was carried out as a cost-utility analysis, and is used as the case study in this study.
Model
To determine the cost-utility of robot-assisted surgery, an economic model was developed using a combination of international evidence on clinical effectiveness and local cost and health service information. Robotic-assisted surgery is a form of minimally invasive surgery carried out with a device that comprises a computer console, patient-side cart, and detachable instruments. The surgeon controls the robotic arms with hand controls and pedals on the console, potentially giving greater control and ease of use than conventional laparoscopic surgery. The comparator was current routine care, which comprises a mix of open and laparoscopic surgery. The target population was men requiring radical prostatectomy with a life expectancy of at least 10 years. As per the Irish national guidelines, costs were assessed from the perspective of the publicly-funded health and social care system in Ireland and restricted to direct costs (4).
Meta-analysis of Clinical Effectiveness
The clinical effectiveness of robot-assisted surgery compared with open and conventional laparoscopic surgery was estimated using meta-analysis of peer-reviewed publications (3). A systematic review was carried out with Medline, Embase, and the Cochrane library being searched for relevant studies using a previously published search strategy (Reference Ho, Tsakonas and Tran5). Randomized controlled trials (RCTs), controlled clinical trials and observational studies with historic or concurrent controls were considered for inclusion. Data were found for the following effects: operative time, hospital length of stay, conversion to open surgery, blood transfusion, positive surgical margin (PSM) for two pathological stages (pT2 and pT3), sexual function, and urinary continence.
Heterogeneity was assessed using the I2 statistic. It was assumed that treatment effect would vary across studies not only due to sampling variability but also due to differences between surgical teams in terms of ability (e.g., experience or skill). Random-effects meta-analysis was used to pool effect estimates using a restricted maximum-likelihood estimator to determine study weights. For continuous variables, the weighted mean difference was pooled while for binary outcomes the relative risk was pooled and presented as an odds ratio. For binary outcomes, a continuity correction of 0.5 was applied to all cells of any study with zero cases. Meta-regression was used to determine if differences in outcomes could be partly explained by reported surgeon experience as measured by the number of operations a surgeon carried out using the robot before the start of the study. Prediction intervals were generated to give the range of treatment effect that might be observed in a future study (Reference Riley, Higgins and Deeks6). The formula for the upper and lower prediction intervals is given by (Reference Higgins, Thompson and Spiegelhalter1):
$$\widehat\mu \pm t_{k - 2}\sqrt {\widehat\tau ^{\rm 2} + SE(\widehat\mu )^2 }$$
$\widehat\mu$
; the estimate of between study standard deviation is given by
$\widehat\tau$
; the standard error of
$\widehat\mu$
is given by SE(
$\widehat\mu$
); finally tk–2
is the 100(1− α/2) percentile of the t distribution with k–2 degrees of freedom, where k is the number of studies in the meta-analysis. Typically α is set at 0.05 to give a 5 percent significance level and generate a 95 percent prediction interval. Given the number of degrees of freedom, prediction intervals cannot be computed when there are fewer than 3 studies included in the meta-analysis.
Model Structure
A patient cohort was modeled for each year of the robot lifespan. A robot was assumed to have a median lifespan of 7 years. Each cohort was characterized by the age, pathological stage of the tumor, and life expectancy of each patient. For both the current standard of care and for robot-assisted surgery, each patient was given operative characteristics (e.g., operative time, length of stay, number of units transfused). Outcomes for sexual function, urinary function, and positive surgical margin were simulated along with the implications for further treatment (i.e., use of continence pads, phosphodiesterase type 5 [PDE5] inhibitors, adjuvant radiotherapy). The operative characteristics and outcomes were used to compute the total incremental cost and outcomes of robot-assisted surgery for the cohort.
The model was run for 10,000 simulations for each of two scenarios: defining the distributions around the effect estimates using confidence bounds and prediction intervals, respectively. The point estimate for the incremental cost-effectiveness ratio (ICER) was computed as both the mean incremental cost divided by the mean incremental benefit, and as the median ICER across simulations. The confidence bounds for the ICER were computed as the 2.5th percentile and 97.5th percentile using the Fieller method (Reference Wang and Zhao7). Stable estimates of the median ICER and associated confidence bounds were achieved after approximately 6,000 simulations.
Model Parameters
A range of other parameters were included in the model relating to the characteristics of the target population, service delivery, and utilities associated with functional outcomes. These parameters were estimated from a mixture of data sources and were validated by expert opinion (3). None of these parameters were estimated using meta-analysis; hence, they were not altered by the use of confidence bounds or prediction intervals. The model was fully probabilistic, allowing all parameters with uncertainty to vary in each simulation. A univariate sensitivity analysis was also carried out for the parameters that were derived from the meta-analyses. The univariate sensitivity analysis involved setting each parameter in turn to its upper and lower bound values, running the model, and extracting the median ICER. For presentation of the costs and benefits, density ellipses were computed that, assuming a bivariate normal distribution, contain 95 percent of the simulated points. The ellipses show the difference between using confidence bounds and prediction intervals in the extent of simulated costs and benefits.
The alpha level was set at 0.05 for all statistical tests. The model was developed and run in R 2.13.1 (Reference Foundation8) and the metafor (v. 1.6–0) package was used for meta-analyses (Reference Viechtbauer9).
RESULTS
The eight meta-analyses of robot-assisted surgery compared with open surgery had between seven and nineteen studies. Only two of these meta-analyses had I2 values below 50 percent. The nine meta-analyses of robot-assisted surgery compared with conventional laparoscopic surgery had between two and nine studies. Five of these meta-analyses had I2 values below 50 percent.
The treatment effects and associated confidence bounds and prediction intervals are provided in Table 1. In the comparison of robot-assisted versus open surgery, six of the seven outcomes showed a statistically significant treatment effect. Based on the prediction intervals, six of the seven outcomes could show a negative treatment effect. Comparing robot-assisted to conventional laparoscopic surgery, one of the outcomes showed a statistically significant treatment effect, but that outcome could show a negative treatment effect based on prediction intervals.
Table 1. Outcomes and Associated Confidence Bounds and Prediction Intervals
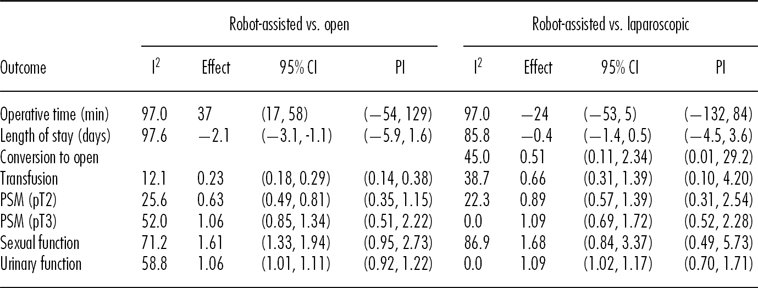
CI, confidence interval; PI, prediction interval; PSM, positive surgical margin.
Meta-regression using surgeon experience as a covariate was applied to all of the outcomes comparing robot-assisted to open surgery. In all cases, the covariate was not a significant explanatory variable and there was no change in the observed heterogeneity.
Using the confidence bounds approach, the mean and median ICER was estimated as €24,193 and €26,731/QALY (95%CI: €13,752 to €68,861/QALY), respectively. This is compared with the prediction interval approach which produced an equivalent mean and median ICER of €26,920 and €26,643/QALY, respectively, but a 95 percent CI of -€135,244 to €239,166 per QALY. With the use of prediction intervals, there is the possibility that robot-assisted surgery will result in a loss of utilities. In 4.2 percent of simulations, there was an incremental loss of utilities. This has to be counterbalanced by the fact that the prediction interval method also resulted in simulations with higher gains in utilities. A wider range of costs are observed for the prediction interval method because of costs related to the performance of the technology (adjuvant radiotherapy, length of stay, operative time).
The 95 percent density ellipses around the ICERs for the two scenarios are presented in Figure 1. The density ellipse for the confidence bound approach is fully encompassed by the ellipse for the prediction interval method.
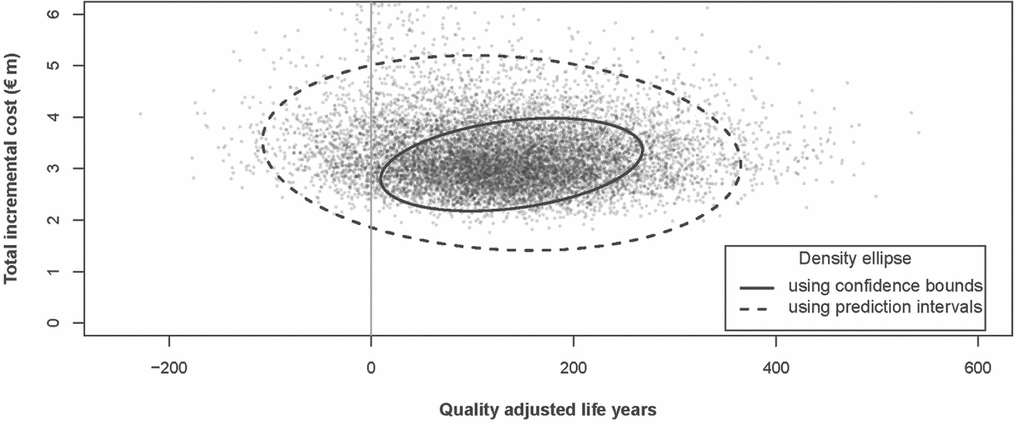
Figure 1. ICERs with 95 percent density ellipses. Note: the density ellipses indicate the area that encompasses 95 percent of the simulations. The density ellipse for the prediction interval approach is much larger indicating the greater uncertainty around estimated costs and benefits using that approach.
The impact of widening the range of ICER values can be anticipated to affect the cost-effectiveness acceptability curves. Both methods reach a probability of cost-effectiveness of 0.5 at an approximate willingness to pay of €26,700 per QALY. At lower willingness to pay thresholds, the prediction interval approach has a higher probability of cost-effectiveness although the reverse applies at higher thresholds, see Figure 2.
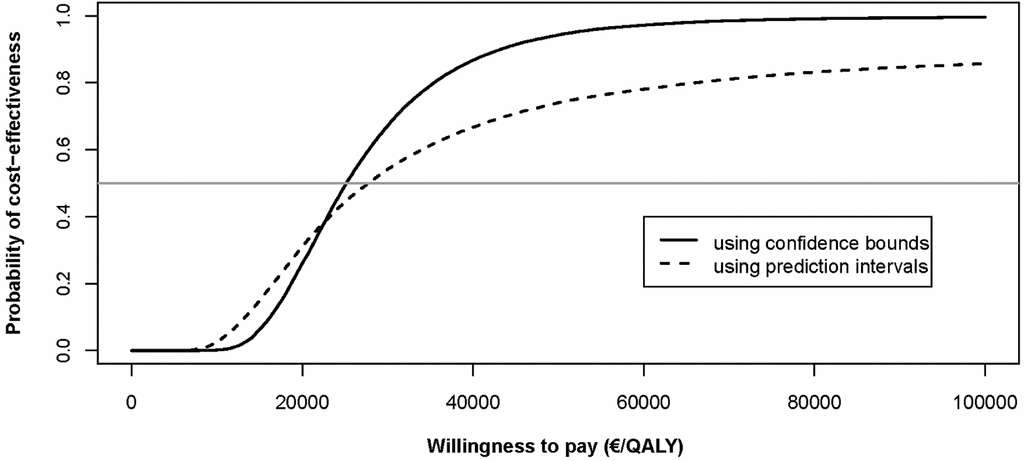
Figure 2. Cost-effectiveness acceptability curve for two methods. Note: the horizontal line indicates a probability of 0.5. Up to a willingness-to-pay threshold of €23,000 per QALY, the prediction intervals approach results in an equal or higher probability of robot-assisted surgery being cost-effective. Above €23,000 per QALY, the probability of being cost-effective is always higher based on the confidence bounds approach due to the fact that it does not result in simulations where robot-assisted surgery is less effective than open and laparoscopic surgery.
The univariate sensitivity analysis was carried out by setting each parameter at its upper and lower bounds based on confidence bounds and prediction intervals, respectively. The resulting tornado plot shows substantial differences depending on how the bounds are defined (Figure 3). Irrespective of approach, the parameter that causes the greatest fluctuation is urinary function. When prediction interval data are used, the upper bound is negative due to negative utilities. The impact of fluctuating length of stay is much greater when prediction interval data are used, reflecting the substantial heterogeneity in the meta-analysis data. The influence of conversion to open surgery is also highly sensitive to how the bounds are defined.
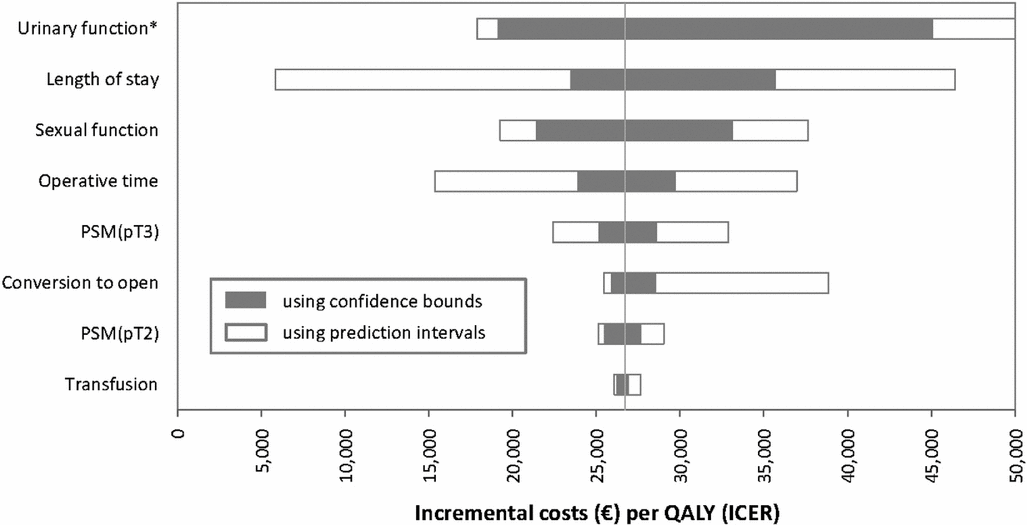
Figure 3. Impact on univariate sensitivity analysis. *Upper bound for urinary function based on prediction intervals is -€57,796 due to negative utilities. Abbreviations: PSM, positive surgical margin; pT, pathological stage; QALY, quality adjusted life year. Note: using the wider bounds generated by prediction intervals results in a much greater impact on the estimate of the ICER. This is particularly noticeable for length of stay, where at the lower extreme the ICER would be below €6,000 per QALY (based on an average 6 day reduction in length of stay) compared with €23,478 per QALY using the confidence bounds approach (based on average reduction of 3 days in length of stay).
DISCUSSION
Prediction intervals are suggested as a method of identifying potential treatment effect in a random-effects meta-analysis. The use of prediction intervals rather than confidence bounds does not impact on the point estimate of treatment effect generated by the meta-analyses. In meta-analyses with significant heterogeneity the prediction interval will produce wider ranges of treatment effect than those defined by the confidence bounds. If prediction intervals are used to define treatment effect in a subsequent economic evaluation, the confidence bounds of the ICER will be increased.
In the case study presented, the use of prediction interval data substantially increased the confidence bounds around the ICER, and also increased the probability of the intervention leading to reduced effectiveness compared with current practice. Depending on the context, and how risk-averse the decision maker is, a marked probability of reduced effectiveness may force a decision not to introduce a technology. The likelihood of this happening in practice is probably limited, as the confidence bounds of pooled data from very heterogeneous studies will tend to be wide to start with. Given how prediction intervals are computed, they will typically increase the distribution in both directions although this depends on the parameter and whether it is computed as a mean difference, or on the log scale as a relative risk or odds ratio. A very rare outcome, for example, is lower bounded by zero but the upper bound may increase substantially when prediction intervals are used. This is illustrated in Figure 3 with the parameter for conversion from robot-assisted to open surgery. Approximately 1 percent of operations convert to open; with such low numbers the range for relative risk is very wide and has a skewed impact on the bounds of ICER. The mean ICER was increased when using the prediction intervals approach, owing to the more skewed distribution of some of the effectiveness parameters. The median ICER was, however, unaffected by the approach used.
The extent to which the choice of confidence bounds or prediction intervals will impact on results is directly related to how much influence parameters derived from meta-analysis have on the model. Some clinical parameters may only impact on effectiveness without making any substantive contribution to costs. Alternatively, they may add to cost without altering benefit. In the case study, urinary function had little impact on costs but had a major impact on benefits. Transfusion of red blood cells was not associated with any change in utilities but did have an associated monetary cost. As rates of transfusion were low and the cost was low relative to the cost of surgery, it can be seen from the univariate sensitivity analysis that varying transfusion had little impact on the ICER (Figure 3). For the univariate sensitivity analysis presented here, only the clinical effectiveness parameters were included. In the original HTA, the most influential parameters were the utilities associated with sexual and urinary function (3).
Two cost-utility analyses of robot-assisted prostatectomy have been published previously (Reference Hohwü, Borre, Ehlers and Venborg Pedersen10;Reference O'Malley and Jordan11). In both cases, clinical effectiveness was drawn from a single study thereby avoiding the issues associated with pooling data. However, given the substantial heterogeneity observed across studies, such a restrictive approach to evidence gathering may greatly underestimate the uncertainty of how effective a program of robot-assisted surgery might be in practice.
For a systematic review, substantial heterogeneity may be used as justification for not pooling data. However, from an economic modeling perspective, a decision maker seeks advice and it may be difficult not to develop a model on the grounds that the data are heterogeneous. The resulting economic model should take into account the uncertainty or imprecision of the underlying data. Poor quality or heterogeneous evidence is often used, accompanied with the appropriate caveats and limitations. Sensitivity analysis is commonly used to test the impact of incorporating poor quality or suspect evidence, giving some indication of how different the cost-effectiveness might be if the data were different. It is for the modeling team to decide how to analyze and present the data to the decision maker. A key part of this process is assessing the uncertainty around the costs and benefits associated with a technology. Where applicable, using prediction intervals gives a better reflection of the potential effect of a technology than confidence bounds.
Strengths and Limitations
The case study presented in this analysis is perhaps unusual in that random-effects meta-analysis was used for all of the outcomes. Justification was not on the basis of the observed I2, although in many cases it was high, but rather on the fact that between study heterogeneity could be expected due to differences in surgical teams in terms of experience or skill. Where studies are largely homogeneous there is little difference between confidence bounds and prediction intervals; thus, there will be little impact on the bounds of the estimated ICER. Where a common effect is assumed and fixed effect analyses are justifiable, prediction intervals are not an issue as the confidence bounds reflect the uncertainty around the parameter estimate. However, experience suggests that when data are available for multiple studies, the estimates are rarely homogeneous for even some of the outcomes required for an economic model.
The case study used here is also a costly technology with limited evidence of long-term effectiveness. However, uncertainty around the benefits of a technology should always be adequately addressed irrespective of the cost of the technology, and the possibility that a technology is less effective than the comparator is an important consideration when deciding whether or not to adopt it.
CONCLUSIONS
When estimating the cost-effectiveness of a health intervention, the potential treatment effect rather than the average treatment effect should be considered. Where clinical effectiveness data are derived from a random-effects meta-analysis, this can be achieved by the calculation of prediction intervals. Such intervals tend to increase the uncertainty around the estimate of effect, but more adequately reflect the heterogeneity of the data being pooled.
CONTACT INFORMATION
Conor Teljeur, PhD (cteljeur@hiqa.ie), Michelle O'Neill, MSc, Patrick Moran, MSc, Linda Murphy, PhD, Patricia Harrington, PhD, Máirín Ryan, PhD, Health Information and Quality Authority, Dublin Ireland
Martin Flattery, MSc, Baxter Healthcare Corporation, Sydney, Australia
CONFLICTS OF INTEREST
Martin Flattery is employed by Baxter Healthcare Corp which has a wide portfolio in medical technology including infusion devices and solutions. The other authors report they have no potential conflicts of interest.
