A major issue within prospective payment systems (PPS) is how to take into account new technologies involving learning effects. The diffusion of innovative health technologies is often characterized by learning effects. Performance and skills improve with experience. At first, the technology is developed by one or a few leading teams, and once its feasibility has been demonstrated, new medical teams learn how to perform the surgical procedure or how to use the new equipment. The cost of a new technology may initially be high because of a learning curve. In calculating the baseline payment rate for a new technology, the regulator may be uncertain about the slope of the learning curve. We aimed at illustrating this issue through the example of a new type of radiation therapy.
Intensity modulated radiation therapy (IMRT) is an advanced form of three-dimensional conformal radiation therapy that involves carefully shaping and modulating treatment beams to maximize the dose delivered to the tumor and minimize exposure of healthy tissues (Reference Webb10). The advantage of IMRT is that any dose distribution can be achieved in a given target while sparing normal adjacent structures. This technique is appropriate for several types of tumors that surround organs-at-risk such as the brain, salivary glands, and the prostate (Reference Bolsi, Fogliata and Cozzi1;Reference Eisbruch3;Reference Khoo5). Implementing IMRT requires hands-on experience and extensive training involving colossal institutional costs (Reference Galvin, Ezzell and Eisbrauch4;Reference Miles, Clark and Urbano6).
Our aim was to study the impact of learning effects in IMRT on the variability of the mean cost per treatment. It was also to highlight funding implications of learning effects in a PPS. We addressed these issues using data from a prospective observational study.
DATA AND METHODS
Study Design and Cost Computation
Between July 2003 and April 2005, a series of consecutive patients with head and neck cancer was enrolled into a prospective study of IMRT. Nine French medical centers participated in the study (eight comprehensive cancer centers and one teaching hospital). Three centers began using IMRT at the initiation of the study, and the remaining six centers had previously treated patients using IMRT for either head and neck cancer or cancer at other sites. The IMRT process was divided into treatment planning steps and radiation fractions. Schematically, planning consisted of volume contouring, acquiring patient-specific parameters, and dose calculation. After planning, IMRT treatment was delivered daily. A daily dose of approximately 2 Gray (Gy) was delivered. During fractions, periodic checks were performed to verify patient positioning and dosimetry adequacy. The periodicity of these checks was related to the center's experience. For example, it was recommended that positioning be verified at the start of each course of treatment for the first patients treated with IMRT.
The use of resources was prospectively collected for each treatment. Following a micro-costing process, we performed a detailed inventory and measurement of resources used (manpower, imaging and radiation equipment, software, and supplies). Direct costs of IMRT were assessed from the perspective of the healthcare providers. The valuation of the resources was based on financial data provided by the centers. Ranges of unit costs observed in the centers are summarized in Table 1. To compare the cost of IMRT and its prospective payment, logistics costs and overhead were included using a coefficient of indirect charges. All costs are expressed in 2005 euros.
Table 1. Site-Specific Cost Information

IMRT, intensity modulated radiation therapy.
Model Specification
To explain the variation of the direct cost of IMRT between patients and centers, we used a two-level model with a random intercept: patients (level 1) nested within centers (level 2). For details on multilevel models, see Singer and Willett's book (Reference Singer and Willett8).
The dependent variable was the direct cost of IMRT for a patient i treated in a center j. To explain cost variability, emphasis was placed on learning effects. The learning process was modeled using a fixed rate of learning and random initial levels. Centers had different initial levels. The slope (i.e., the difference in treatment cost between two consecutive patients) was modeled using the order of inclusion of patients in the study within each center. To place patients in a given order, we used the initiation of the study as a shared date of origin for all centers. The order was a sequence number corresponding to the position of a patient within the series of cases recruited by a center. Although the order variable has a longitudinal dimension (it counts the number of patients treated by a given center), one should note that, in a center with previous experience with IMRT, a patient with an order value of 1 was not in fact the first patient treated by the center. Finally, we tested the interaction between the order of inclusion of the patient and the experience of the center at the initiation of the study to investigate whether or not the rate of learning was different in centers with experience and in centers implementing IMRT for the first time. Covariates were introduced to explain the patterns of variation in terms of patient and center characteristics. Covariates introduced at the patient level were the order of inclusion, the total radiation dose, and a variable for severity combining the cancer site and staging. Previous experience in IMRT was the sole variable considered at the second level. We used the logarithmic transformation for all the continuous variables (cost, inclusion order, and radiation dose) for fitting patterns. The two remaining variables of the model (experience and a combination of the cancer site and staging) were dichotomous: the experience value was 1 in centers with previous experience and 0 otherwise, the staging value was 1 for advanced nasopharyngeal lesions (stages III and IV) and 0 for other stages or oropharynx sites. Model specification was as follows:
Level 1 equation:
Level 2 equation:
![\begin{equation}
\[
\left\{
\begin{array}{@{}l@{}}
\Pi_{\rm 0j}=\gamma_{00}+\gamma_{01}.{\rm experience}_{\rm j}+{\rm u}_{\rm j}\\[3pt]
\Pi_{\rm 1j}=\gamma_{10}+\gamma_{11}.{\rm experience}_{\rm j}\\[3pt]
\Pi_{\rm 2j}=\gamma_{20}\\[3pt]
\Pi_{\rm 3j}=\gamma_{30}
\end{array}\right.
\]
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160316080901703-0773:S026646230707033X_eqnU2.gif?pub-status=live)
SAS PROC MIXED was used to fit the model. The maximum likelihood method and robust variance were used (empirical option) (Reference Singer9). Deviations from the mean initial value were estimated for each center. Confidence intervals were computed using the residual from the random effects.
RESULTS
Study Population
Ninety-nine patients with head and neck cancer were included in the study. Eighteen patients were treated in centers that began using IMRT at the initiation of the study, and the remaining eighty-one patients were treated in centers that had previous experience of using the technique. The study population included twenty-six women and seventy-three men who were 53 years old on average (range, 18–83 years). The mean total radiation dose was 68 Gy (standard deviation [SD]=4) and was delivered in thirty-three fractions (SD=2).
Cost of IMRT
The mean direct cost per treatment was €5,962 (SD=€3,735). It was characterized by a bimodal and a skewed distribution. The cost per treatment was significantly higher in the centers initiating IMRT. We plotted the costs of treatment for each center against the inclusion order of each patient in the study (Cf. Figure 1). The mean direct cost per treatment consisted of €3,174 (SD=€2,877) for manpower, €1,693 (SD=€529) for equipment, €927 (SD=€692) for IMRT-specific software, and €168 (SD=111) for supplies. Manpower accounted for 53 percent of the direct cost of treatment.

Figure 1. Observed cost per patient according to the inclusion order. IMRT, intensity modulated radiation therapy.
Modeling Learning Effects
The unconditional means model is a model with no predictors at either level (Cf. Table 2). The random intercept is the sole regressor variable. This model gives the partitioning of the variability of cost between centers effects and within centers effects and provides a baseline against which the multilevel model can be compared. The unconditional means model indicates that 88 percent of the variability was attributable to differences between centers. Patient characteristics explained 46 percent of the variation of costs within centers and experience explained 42 percent of the variation of costs between centers. All parameter estimates were statistically significant. As expected, the coefficient of the initial cost level in centers with previous IMRT experience was negative (−.81), indicating a lower base cost for these centers. For the first patient included in the study by a center initiating IMRT, with a stage value of 0, receiving the mean radiation dose, the direct cost of treatment was estimated at €14,192 (exponential of the intercept). For the first patient with the same characteristics included by an experienced center, it was €6,332 (exponential of the sum of the intercept and the coefficient estimate for previous experience). The rate of learning was also negative (−.32): as the number of patients treated within a center increased, so the cost of treatment decreased. The coefficient of the interaction parameter was positive (.18), indicating that the decrease in cost between two consecutive patients was smaller in centers with previous experience in IMRT. The total radiation dose had a substantial positive impact on the cost of IMRT, because it directly determined the number of fractions required to deliver this dose. The effect of the cancer site/stage was significant but weak: stage III and IV nasopharynx lesions resulted in a slightly higher predicted cost.
Table 2. Estimates of Model Parameters

Note. Dependent variable: logarithm of treatment cost. Standard deviations are reported in parentheses.
ap < .05.
bp < .01.
cp < .0001.
For each center, the deviation estimate after adjustment for patient-level variables is shown in Figure 2. When the confidence interval does not cross the zero line, the initial cost level in the center considered is significantly different from the mean initial level across centers. Thus, the initial cost level was significantly above average in two centers and significantly below average in three centers.
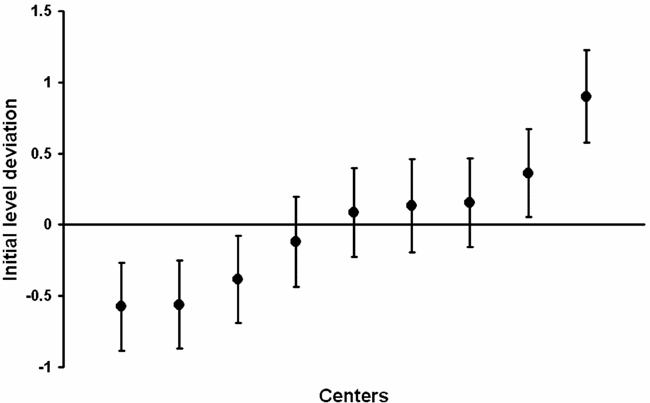
Figure 2. Estimates of initial cost level deviation and 95 percent confidence intervals.
Full Cost and Prospective Payment of IMRT
The full cost of treatment, including logistics costs and overhead, was estimated at €10,916 (SD=€6,454): €2,773 (SD=€2,249) for IMRT planning and €247 (SD=€170) per each treatment session. In 2006, no specific reimbursement existed for IMRT in France. Current reimbursement is based on conformational radiation therapy lump sums of two diagnosis-related groups: €850 for a three-dimensional planning and €184 per each radiation fraction in case of complex treatment delivery. The resulting mean reimbursement per treatment in our study was €6,987 (SD=€452). Reimbursement did not offset the cost of treatment for 70 percent of the patients of the study, and average net loss per treatment borne by hospitals was €3,929.
DISCUSSION
Assessment of the Learning Curve
In this study, we attempted to explain the variability of costs of a new type of radiation therapy by the experience of care providers in the use of the technique. We used a multilevel model with the cost of treatment as a performance measure and the number of patients treated within a center as the experience variable. We demonstrated a statistically significant relationship between experience and the cost of IMRT. We found that learning effects explained 42 percent of cost variability. It is, therefore, a strong confounding factor in the analysis of costs of innovative health technologies involving learning effects. Major issues in learning curve studies are the measures chosen to appraise performance and experience, and the statistical methods used. Performance measures identified in the medical literature are of two types. On the one hand, proxies are based on a clinical process or task efficiency such as the time required to complete an operation. On the other hand, patient outcome such as the rate of complications or quality assurance are used (Reference Ramsay, Grant and Wallace7). Although we used a different measure in our study, it is noteworthy that the direct cost of treatment is in fact highly correlated with the time to complete an IMRT treatment. As far as experience is concerned, the universal measure is the number of patients in a case series or in a clinical trial. Statistical methods used to assess learning curves are frequently suboptimal (Reference Cook, Ramsay and Fayers2). The two most common approaches are the split group method and curve fitting. The split group approach consists in dividing a series of consecutive cases into categories. However, it raises the problem of dichotomization of the experience variable, which is not straightforward. In the curve fitting approach, studies aim at estimating the correct slope of the learning curve using various shapes (polynomial, logarithmic, exponential, and so on). However, it is often difficult to provide a rationale for the choice of a particular shape. Multilevel modeling is a more sophisticated approach that enables one to estimate the rate of learning taking into account patterns of variation at different levels.
Study Limitations
There are, however, some limitations in our study. First, the study population consisted of patients with head and neck cancer. This cancer site was selected because it is a complex planning case where the learning curve is, therefore, a major issue. However, results are likely to be sensitive to the cancer site. Therefore, as far as the absolute level of the cost of IMRT and the rate of learning are concerned, all cancer sites should be included. Second, parameter estimates could be biased, as residual variation was still unexplained. Some predictors may have been omitted and/or the sample size was too limited. At the patient level, we tested the influence of age, sex, tumor dimension, and the lymph node status. However, these variables did not explain the variability of costs and worsened model fitting. At the second level, the number of centers involved in the study was limited. In 2003, only twelve hospitals had IMRT capabilities in France. Therefore, the number of variables that could be introduced at the second level was limited, and we chose to present the model with experience as the sole second level variable. A larger data set would allow one to test the impact of variables likely to be involved in the variability of costs simultaneously: unit costs of labor (radiation oncologist, physicist, and radiation therapist), unit costs of equipment (IMRT software), IMRT delivery techniques (dynamic multileaf collimation versus the step and shoot technique), and the periodicity of checks during treatment delivery. Finally, we did not study the impact of the learning process on the clinical outcomes following IMRT. For feasibility reasons, the economic study was interrupted in July 2005, but the clinical study was still ongoing. Up to that point, only medical data were recorded. Inclusions were closed in December 2005, and 147 patients were enrolled in the study. Early and late complications and local control at 18 months will be studied based on the whole study population.
POLICY IMPLICATIONS
As in other industries, experience effects can result in a decrease in unit costs and a reduction of variability can be observed for a new healthcare technology. In market-driven sectors, the risk of an innovation is borne solely by the first firm to adopt it. If the innovation is successful, the first adopter will be in a favorable position as a price-maker, and eventually keep a competitive edge over late-comers because it will be sooner on the learning curve, thus combining both advantages of temporary monopoly and cost-efficiency. In the healthcare sector, this scenario could happen in countries with a high degree of competition among providers and payers, such as in the United States, although it is plausible that large payers, such as HMOs, would wait for a stabilization of a technology and the demonstration of its cost-effectiveness before accepting to put it on their reimbursement list. Policy implications are more important for countries with public funding and provision of care. In countries where the purchasing/providing split has not been achieved, the risk of innovation is borne both by the payer and the provider. If the payer is willing to adopt the innovation, then it will have to provide funding to cover the risk of adoption, and pay for the learning process, on a retrospective basis, until the technology is stabilized. The aim of splitting purchasing from provision is usually to put an incentive on providers through competition, albeit their public status. Regulated prospective tariffs per case are usually used with this goal. In principle, in such systems, providers should bear alone the risk of innovation, like in a market-driven sector. The public payer must then decide whether or not it is ready to pay for a new service, and if so at what rate. In this case, the payer cannot observe the actual costs of the innovation. Two options are possible: one option is that the payer can delay price setting, wait until second adopters provide the new service, and set up a competitive bid among providers to force them to reveal cost information. In this case, providers bear alone the cost of the learning process, but there is a risk of collusion among providers, if the innovation requires specific skills that restrict competition. The other option is that the payer can decide to share the risk of the learning process, to gain access to cost information. A secondary benefit of this decision is to ensure a more rapid access of the innovation to patients. In this case, at the initial stages of learning, it may be adequate to use a retrospective payment scheme based on observed costs, with some form of risk sharing: costs could be covered fully or partially, and centers experiencing the new technology could make a commitment concerning the formal implementation of the learning process, and set up training programs for other later adopters. They would also agree to reveal their costs, so that the payer can set a final price, taking into account the lowering of costs with the learning process. This solution suggests higher transaction costs than the former one, but with the added benefit of a better control of the learning and diffusion process and, thus, ultimately of the quality of care delivered.
CONTACT INFORMATION
Julia Bonastre, Msc (bonastre@igr.fr), Researcher, Eric Noël, MSc (noel@igr.fr), Junior Health Economist, Julie Chevalier, MSc (chevalier@igr.fr), Junior Health Economist, Health Economics Department, Gustave Roussy Institute, 39 rue Camille Desmoulins, Villejuif, France 94805
Jean Pierre Gerard, MD (jean-pierre.gerard@nice.fnclcc.fr), Director, Department of Radiation Oncology, Antoine Lacassagne Centre, 33 avenue de Valombrose, Nice, France 06189
Dimitri Lefkopoulos, PhD (lefko@igr.fr), Chief, Department of Physics, Jean Bourhis, MD (bourhis@igr.fr), Head, Department of Radiation Oncology, Gustave Roussy Institute, 39 rue Camille Desmoulins, Villejuif, France 94805
Rene Jean Bensadoun, MD (rene-jean.bensadoun@nice.fnclcc.fr), Radiation Oncologist, Department of Radiation Oncology, Antoine Lacassagne Centre, 33 avenue de Valombrose, Nice, France 06189
Gerard de Pouvourville, PhD (pouvourville@essec.fr), Professor, Chair of Health Economics, ESSEC Business School, Avenue Bernard Hirsch, BP 50105 Cergy, 95021 Cergy, Pontoise Cedex, France






