Although definitive assessment of cost-effectiveness may require long-term evidence from randomized trials, it is important early in the life-cycle of new technologies to begin to estimate likely cost-effectiveness (49). Such estimates can help prioritize internal development plans, indicate which parameters must need further research, and inform early adopters of the technology.
Computer-assisted total knee replacement (TKR) is one such new technology. The demand for TKR is increasing mainly because of longer life expectancies and rising public expectations for quality of life and mobility in later years. In the United Kingdom, 20 percent of the population is over 60 years old, and it is estimated that between 1995 and 2025 the number of people over 80 will increase by around 50 percent and the number of people over 90 will double (22). Currently, approximately 2 percent of the population 55 years of age and over are so disabled that they need TKR, and this rate increases with age. The estimated prevalence in women is nearly twice as high as in men (51).
TKR is a well-proven procedure. The number of replacements has increased steadily (3;16;52). The average age of patients at operation is 70; two-thirds are women. TKR usually produces excellent results, although serious complications occur in around 5 percent of cases because of loosening, instability, dislocation, infection, or fracture (36). In 20–60 percent of patients, less serious complications such as anterior knee pain or limited movement are reported at approximately 3 years after operation (25;28;31). Total revision rates 2–5 years after TKR are reported as being around 2 percent (36).
The complication rate is related to a surgeon's experience. The average surgical complication rate and mortality rate, adjusted for hospital size, decline as TKR volume increases (30). The surgeon's experience in patient selection, soft-tissue balancing, the alignment of the leg, the restoration of the joint line, and also the prosthetic design are all possible factors influencing the success of TKR (21).
The patients' age, sex, and type of disease also affect the results. After controlling for the follow-up period, the greater the age of patients at the primary operation, the lower the overall revision rate as activity levels decrease (47). The overall cumulative revision rate after TKR is similar in both sexes for patients with osteoarthrosis, whereas in patients with rheumatoid arthritis, men have a higher revision rate (47).
Component misalignment in any anatomical plane can cause complications. Minor malpositioning and varus or valgus misalignment of the limb mechanical axis can lead to early loosening, increased polyethylene wear, or poor function (27;44;55). Malrotation of either the femoral or tibial component will affect patellar tracking and can lead to patellar subluxation or dislocation (8). Alterations in the joint line usually lead to limited movement (25). Anteroposterior (AP) malpositioning of the femoral component by as little as 2.5 mm could reduce the range of knee's movement by up to 20 degrees (27). Soft-tissue balancing and the range of movement are strongly influenced by the tibial slope (24;45;53). In principle, either misalignment of any of the components or incorrect soft-tissue balancing can lead to failure of the implant (37).
Computer-assisted surgery (CAS) systems have been developed to improve limb and component alignment in TKR. “Their aim is to provide more accurate implantation by digital mapping based on standard anatomical landmarks and kinematic analysis” (18). However, as yet, there is limited evidence of its effectiveness. In a prospective randomized study, the radiological outcomes of 120 TKRs using a navigation system were compared with that of 120 conventional cases (50). By using AP radiographs to diagnose the misalignment, the results revealed a highly significant difference between the two groups in favor of navigation with regard to the mechanical axis, the frontal and sagittal femoral axis, and the frontal tibial axis. In a separate randomized study, radiographs also showed that computer-assisted TKR gave a better alignment of the leg and orientation of the components compared with the conventional technique (6). In another randomized prospective trial, postoperative computed tomographic (CT) scans showed that CAS had a significant improvement in the alignment of components with regard to femoral varus/valgus, femoral rotation, tibial varus/valgus, tibial posterior slope, tibial rotation, and femorotibial mismatch (17;18).
Some studies of TKR have included cost analyses or cost-effectiveness analyses. Total hospital cost per patient was approximately US$11,500 for conventional TKR in Finland (46). The cost per “quality well year” (defined by the Quality of Well Being Index) compared with before operation was approximately $6,656 at 2-year after operation in the United States (39). To our knowledge, however, there are as yet no studies comparing the cost-effectiveness of conventional TKR with that of computer-assisted TKR.
This study uses a Markov model to make a preliminary assessment of the cost-effectiveness of computer-assisted TKR with that of conventional TKR. It includes both a deterministic analysis with one-way sensitivity analysis and a probabilistic analysis, as is increasingly recommended (43), to better characterize the uncertainty in analysis.
METHODOLOGY
Structure of the Markov Model
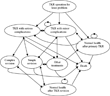
The key components of a Markov model are Markov health states, transition probabilities, and corresponding cost and outcome data (10). Based on the natural history of the clinical problem and the outcomes of the surgical intervention, nine Markov health states were identified (Table 1). These are represented by ovals in Figure 1. Entry into the model was by means of the state “TKR operation for knee problem.” From all states, other than the entry state, patients could die. The full pattern of potential transitions (shown by arrows) and the states in which patients could remain for multiple periods (indicated by backward bending arrows returning to the state that they left) are shown in Figure 1.

Markov state transition model for total knee replacement (TKR).

Parameter Estimation for Initial Deterministic Analysis
A structured search was carried out to identify evidence relating to the clinical outcome and cost-effectiveness of TKR. This approach included an electronic search of MEDLINE, Health Economic Evaluation Database, the UK Department of Health Database, the U.S. Department of Health and Human Services Database, the Cost-Effectiveness Analysis Registry Database, and relevant National Joint Replacement Registry Databases in Sweden, Australia, and Canada. For example, a total of 623 articles was found from MEDLINE between 2000 and 2004 using the key words of “TKR” and “English,” from which we further identified articles relating to systematic reviews, randomized clinical trials, or follow-up studies. From the references of identified articles, we enlarged the search. In total, we reviewed approximately 200 articles or reports and drew on data from approximately 40 studies.
The transition probabilities for conventional TKR were estimated from a variety of sources as indicated and were weighted by the relevant sample size (Table 2). The principal “effect of CAS” was assumed to be to reduce the transition probabilities to the state “TKR with serious complication.” The mean of three randomized control trial studies suggested that CAS could reduce the misalignment rate by approximately 48 percent (6;18;50). Given that it was estimated that 70.4 percent of complications are due to misalignment (3), we assumed that CAS could reduce the serious complications by 34 percent.

A cycle length of 1 month was chosen; therefore, the transition probabilities between states were all expressed as 1-month probabilities. Given the different follow-up periods in the various sources, a two-step calculation was used: first, the 1-month rate (r) was calculated by the formula r =−ln(1−P)/t(1), where P is the probability at the original follow-up period and t is the time in months of the follow-up. The 1-month probability (P1-month) was calculated from the 1-month rate (r) using the formula: P1-month= 1−exp(−r) (2).
The death probability related to a primary TKR and a TKR revision was calculated from in-hospital mortality (3;13–16;35;38), and the death probability related to all causes was converted from the UK death rate of age group 70–79 years of age (42). The transition probabilities from “Complex revision” to “TKR with serious complication” and from “Simple revision” to “TKR with serious complication” or to “TKR with minor complication” were estimated based on the information of second and subsequent revisions from the Australian or Canadian TKR registries (3;14–16). The same source and methodology were used to estimate the transition probabilities from “Normal health after primary TKR” to the state “Simple revision,” or “Complex revision.”
Costs were estimated from the perspective of the National Health Services (NHS) and in accordance with the UK National Institute for Clinical Excellence (NICE) guidance, we did not include productivity loss (43). All costs were in 2003 UK pounds sterling. A cost was estimated for each Markov state, but we assumed that there were no costs for the states “Normal health after primary TKR,” “Normal health after TKR revision,” and “Death” (Table 3). The cost for conventional primary TKR, revision, and other treatment was the hospital costs, calculated on the basis of a Finished Consultant Episode. Hospital cost includes all costs incurred in the hospital, such as the operation itself, examinations, drugs, tests, consumables, staff time and salaries, ward costs, and overhead costs.

The costs of conventional TKR, revision, and other treatments were taken from NHS Reference Costs 2003 (23), which reports data by Health Related Groups (HRGs). Primary TKR has its individual code (HRG H04). Unfortunately, the HRG codes combine together costs for both “complex” and “simple” revisions and include both knee and hips (HRGs H05 and HO6, respectively). These costs were used, but their lack of differentiation leaves some uncertainty as to the specific cost of knee revision surgery. The state “Other treatments” was given the cost of HRG H30 (infections of bones or joints), because most of the other treatments are to control infections.
We assumed that a TKR patient with any complication has one surgeon visit and a CT examination before receiving further treatment. For simplicity, these costs have been added to the HRG costs of the subsequent treatment.
When CAS is considered, its costs affect three Markov states: “TKR operation for knee problem,” “Complex revision,” and “Simple revision.” For CAS, extra costs per use (CASec), including that of the CAS system (CASs), warranty (CASw), disposables (CASd), and added length of surgery were added to the costs of the conventional procedure. An annual equivalent cost of the system was calculated assuming 5 years of useful equipment life and a 3.5 percent of discount rate (32). The system cost and warranty cost were then estimated, assuming an average trust would carry out 250 CAS procedures per year (throughput) (41).
On average, computer-assisted TKR takes 15 minutes more than the conventional operation (6;17). We estimated the extra surgery time cost per use (including personnel and operation theatre) (CASt) based on this 15 minutes and the unit cost of hospital consultants and nurses (20). Thus, CASec= CASs + CASw + CASd + CASt (3).
No ideal set of utility values was available, and the estimates used were drawn from different sources. To increase consistency, we used values reflecting Knee Society Scores, where available (Table 3). No utility value was available for the states “TKR operation for knee problem” and “Other treatments.” We assumed that the utility values of these two states were lower than the utility for “Normal health after primary TKR” (0.78) and higher than that for “TKR with minor complications” (0.66). Thus, we assigned them a value equal to the mean of these two utilities (0.72).
Cohort Simulation and Cost-Effectiveness Analysis
A 10-year cohort simulation with a starting number of 1,000 TKRs was carried out. Effectiveness was expressed by QALYs (Quality Adjusted Life Years). Both costs and QALYs were discounted at 3.5 percent in line with 2003 Treasury guidelines (32). The differences between CAS and the conventional technique were expressed by the incremental cost-effectiveness ratio (ICER).
One-Way Sensitivity Analysis
One-way sensitivity analysis focuses on the “effect of CAS,” utility values, and the additional cost of CAS. The solver function in Excel was used to find the value of key parameters above or below which the baseline conclusions would change.
Making the Model Probabilistic
To generate a logical multi-Markov state probabilistic transition matrix from the initial point estimates, the Dirichlet distribution was used (11). We estimated a count for each Markov state by the transition probabilities (we assumed that the total counts equalled 1,000). We used random number and Gamma distribution formulae to generate a one-parameter (standard) Gamma distribution for each cell of the transition matrix. The one-parameter Gamma distribution in Excel was obtained by setting the first (alpha) parameter equal to the estimated count and the second (beta) parameter equal to 1. The final step was to “normalize” the realizations from the Gamma distribution back to the 0–1 scale by dividing each realization through by the corresponding row total.
Lognormal function was used to generate a random “effect of CAS.” The variance of the “effect of CAS” was estimated from the clinical trials (6;17;18;50).
The NHS Reference Costs provide means and cost ranges (23). Variance for the Gamma distribution was estimated from the ranges. A Gamma function was used to generate a random cost for each Markov state (12). No measure of variance was available for the estimates of the extra cost of CAS. We assumed that the ratio of its standard deviation over mean was four times as large as that of conventional primary TKR, so generating a distribution for the extra cost of CAS.
A Beta function, with the mean equal to the point estimate and a high variance to reflect the uncertainty, was used to generate a random utility for each Markov state (12). To ensure a plausible relationship between the utilities of states “Normal health after primary TKR,” “TKR with minor complications,” and “TKR with serious complications,” the process was structured so that the hierarchical relationship was retained but the differences between the utilities were randomly drawn from the distribution.
We ran ten thousand 120-cycle cohort simulations trials, randomly sampling from the distributions of transition probabilities, costs, and utilities. The results of the simulations were analyzed using the cost-effectiveness plane and cost-effectiveness acceptability curves.
Parameter Importance
The analysis of covariance approach was used to explore the proportion of the total model sum of squares that was explained by each individual model input parameter. Both the incremental costs and the incremental QALYs were analyzed separately as the dependent variable.
RESULTS
Transition Probabilities
For conventional surgery, approximately 4.3 percent of patients with primary TKR would have minor complications and 1.5 percent serious complications during the first month after operation: 94.2 percent of them would have “Normal health after primary TKR.” The patients who have “Normal health after primary TKR” would have a 1.4 percent chance of minor complications and a 0.9 percent chance of serious complications every subsequent month. The patients with serious complications would have a 3.0 percent chance of complex or simple revisions every month (2.469 percent + 0.523 percent). The patients after primary TKR would have a risk of 0.5 percent of death per month, and the patients after TKR revision would have a risk of 1.5 percent of death per month (Table 2).
Approximately 2.5 percent of the patients with “Complex revision” would transfer to the state “TKR with serious complications” every month, and 2.4 percent (1.59 percent + 0.816 percent) of the patients with “Simple revision” would transfer to the state “TKR with serious complications” or “TKR with minor complication.” On this basis, we estimated that 3.0 percent (2.003 percent + 1.038 percent) of the patients being “Normal health after TKR revision” would transfer to the state “Complex revision” or “Simple revision” every month.
Costs and Utilities
For the conventional technology, the average NHS cost for elective primary TKR was £5,197; the costs of “Complex revision,” “Simple revision,” and “Other treatments” were £7,326, £6,234, and £2,844, respectively (Table 3). The additional CAS cost was estimated as £235 per case. The utility values for the Markov states ranged from 0.78 for “Normal health after primary TKR” down to 0.354 for the state “TKR with serious complications” (Table 3).
Simulated Complication, Revision, and Death Rate
The deterministic analysis shows that, by the end of the 10 years after conventional TKR, the cumulative serious complication rate would be 87.3 percent, the minor complication rate 135.9 percent, the complex revision rate 5.1 percent, and the simple revision rate 2.6 percent. For patients with computer-assisted TKR, the cumulative rates would be 58.1 percent, 136.5 percent, 3.6 percent, and 1.9 percent, respectively (Table 4). The cumulative mortality of conventional TKR is 4.3 percent and of revision 0.24 percent. The cumulative mortality of computer-assisted TKR is unaffected at 4.3 percent, but that of revision falls to 0.17 percent. The cumulative total mortality is 37.1 percent for both cohorts (Table 4).

The probabilistic analysis shows, as expected, very similar mean values for rates. For example, the serious complication rate of conventional TKR is 87.3 percent (point estimate) and 88.1 percent (simulated); revision rate is 5.1 percent (point estimate) and 5.2 percent (simulated) (Tables 4, 5). Compared with conventional TKR, computer-assisted TKR had a lower serious complication rate, complex or simple revision rate, and death rate related to revision but had a similar death rate related to primary TKR; it also had lower variances for each indicator (Table 5).

Incremental Cost-Effectiveness Ratio
Compared with conventional TKR, the use of CAS is, after the first 2 years, the dominant strategy reducing cost considerably and offering a small increase in QALYs. After 10 years, CAS reduced costs per patient by approximately 7.5 percent (−£583) and increased QALYS by 0.3 percent (0.0148). The probabilistic analysis also produced almost identical mean estimates of incremental costs (−£637) and QALYs (0.0164).
Parameters Influencing the ICER
The one-way sensitivity analysis indicates that CAS would remain dominant at 10 years, providing its assumed effect (i.e., in reducing the transition probabilities to the state “TKR with serious complications”) exceeded 10.3 percent (compared with the original estimate of 34 percent). The ICER was sensitive to the utility for patients of “Normal health after primary TKR.” CAS remained dominant unless the utility for this state fell from the assumed 0.78 to less than 0.58. The results were not sensitive to the utilities from any other individual state. Similarly, CAS remained dominant at 10 years providing the additional CAS costs did not exceed £789 per use.
Probabilistic Representation of Uncertainty
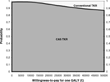
The standard cost-effectiveness plane shows that almost all of the 10,000 trials (all but 147) are located below the x-axis. More than two-thirds (7,589/10,000) were located on the southeast quadrant (Figure 2). It means that CAS TKR dominated. It offered a small increase in QALYs, but the main advantage of CAS lies in its cost-reduction.

Cost-effectiveness plane. QALY, quality-adjusted life year.
The cost-effectiveness acceptability curve again shows the dominance of CAS (Figure 3). Only as the health system places increasing values on a QALY does any real uncertainty about the cost-effectiveness of CAS arise, reflecting the near certainty within this model that CAS is cost-reducing but the greater uncertainty as to whether it produces additional QALYs. But even at £30,000 per QALY, the upper value suggested by NICE (43), there is a 92 percent probability that CAS is the more cost-effective technology.

Probability of alternative being cost-effective. TKR, total knee replacement; CAS, computer-assisted surgery.
Parameter Importance
The main contributors to the total model sum of squares for incremental costs were the “effect of CAS” (57.76 percent), the transition probability from “Normal health after primary TKR” to “Serious complications” (23.19 percent), and the cost for “Other treatments” (11.97 percent) (Figure 4). The contribution of the additional cost of CAS was only 1.58 percent. By far the most important parameter in determining incremental QALYs was the utility of the state “Normal health after TKR revision” (33.74 percent) (Figure 5).

Individual parameter contributions to model sum of squares (increment costs). TKR, total knee replacement; CAS, computer-assisted surgery.

Individual parameter contributions to model sum of squares (increment quality-adjusted life years [QALYs]). TKR, total knee replacement; CAS, computer-assisted surgery.
DISCUSSION
Whereas three studies have compared the clinical effectiveness of CAS with that of conventional TKR in terms of correct alignment of components and found that CAS could improve alignment, there have been no studies looking at longer-term outcomes, such as complications and revision rates, as this is a newly introduced technology. In these circumstances, this analysis uses available short-term evidence to model likely cost-effectiveness in terms of the ICER.
The model exhibits good internal and external consistency. The results of the one-way sensitivity analysis follow logical expectations, and the results, such as the cumulative revision rate, are reasonably consistent with data from the Swedish National Knee Register (52), which was not an input to our model. In that registry, the 10-year cumulative revision rate is approximately 9 percent; our model shows a 10-year cumulative revision rate of 7.7 percent. For simplicity and given the paucity of evidence, the model assumes that the transition probabilities remain constant over the 10 years. This assumption should be treated with caution.
A critical parameter for this technology is the assumed mean “effect of CAS” on the need for revision surgery and the uncertainty around that. This is estimated indirectly from trials showing radiologically evident reductions in misalignment. This analysis allows for considerable uncertainty for the combined extent of reduction in misalignments and the proportion of these that would require revision. The results indicate that the technology is likely to be cost-effective even if the “effect of CAS” is much less than might reasonably be assumed from existing data.
The data available to estimate utilities for the Markov states was particularly weak. Using simple one-way sensitivity analysis, the ICER is insensitive to the utilities, except to the utility of the state “Normal health after primary TKR.” It is the proportion of patients in this state to which CAS makes the greatest increase. This result is confirmed with parameter importance analysis. In the probabilistic analysis, we assumed a large variance for each utility to reflect the uncertainty in the values from the literature, while maintaining a logical hierarchy. This strategy may overestimate the range of uncertainty surrounding utilities, and a priority for future research would be to improve the estimates of utility.
Within the analysis, we more generally compared the additional information provided by the probabilistic analysis to that of the deterministic one. Probabilistic analysis is part of the Reference Case for technology submissions to NICE (19), but it increases analytical complexity. There is little predictable difference between the means estimated by both analyses, so in terms of a decision to adopt the technology or not, given available information, the probabilistic analysis adds little. However, it provides additional information about the distribution of ICERs, confirms the much higher probability of CAS being the more cost-effective technology at a range of values for a QALY, and provides the basis for parameter importance analysis. Overall, it adds to the clarity of the conclusions without providing any major additional insight over and above those from the deterministic analysis; it would provide, however, the basis for a formal value of information analysis.
Even a probabilistic analysis does not address the issue of “structural” uncertainty arising from the model specification, nor to the key issue of interpretation and relevance of evidence garnered from a variety of sources. It is important to remember that the uncertainty surrounding parameter estimates is not the only source of uncertainty in a cost-effectiveness model.
When estimating mortality, we considered not only the mortality related to primary TKR and revision, but also mortality of all causes. We recognize that this strategy involves a small level of double counting, because all causes include primary TKR and revision.
CONCLUSION
On the basis of evidence from short-term radiographic studies demonstrating an improvement in the accuracy and precision of component and mechanical axis alignment with CAS and studies linking implant survival outcomes to these same alignments, compared with the conventional TKR, computer-assisted TKR is highly likely to be cost-saving and to offer a small QALY advantage. As with all such models, in the absence of long-term clinical trials, the conclusion should be treated with appropriate caution, but it demonstrates clearly that such an outcome is probable. Indeed it might be taken as suggesting that this issue should not be a priority for scarce trial funding. Such a conclusion is informed by the analysis of parameter importance.
This example also demonstrates the feasibility of undertaking such modeling at an early point in the life-cycle of a new technology, when clinical trial data do not exist. It shows the added information available from a probabilistic analysis, although in this case, the dominance of the new technology is such that the probabilistic analysis may add less valuable insights than might be the case in other less clear circumstances.
POLICY IMPLICATIONS
Based on early short-term results, the model suggests that, in the longer term, computer-assisted TKR is highly likely to be cost-saving and to offer a small QALY advantage. Investing in CAS systems may well reduce costs for health care, providing that the throughput of cases of TKR is sufficiently high.
CONTACT INFORMATION
Hengjin Dong, MD. PhD (Hengjin.dong@brunel.ac.uk), Senior Research Fellow, Martin Buxton, BA (Soc Sci) (martin.buxton@brunel.ac.uk), Professor and Director, Health Economics Research Group (HERG), Brunel University, Uxbridge Middlesex UB8 3PH, UK
This research was part of the MATCH (Multidisciplinary Assessment of Technology Centre for Healthcare) Project funded in the United Kingdom by the EPSRC, with other sponsors including the DTI, Invest Northern Ireland, and the National Patient Safety Agency, and commercial parties including DePuy International Ltd. The authors are academic researchers and have no personal conflict of interest with regard to this project. Many thanks for the invaluable assistance and comments from Mick Boroff and Michael Etter from DePuy International Ltd; and comments from Boyka Stoykova from HERG; Andrew Briggs from the University of Oxford; and Terry Young, Nicholas Botterill, Hywel Williams, and Alan Girling from MATCH.