I. INTRODUCTION
Time-varying movement causes lots of non-linear influences in communication and radar systems [Reference Dakovicć, Thayaparan and Stankovicć1, Reference Bidon, Savy and Deudon2]. The background usually is non-stationary [Reference Gui and Yang3]. It is crux to process and compensate the negative influences produced by time-varying targets in radar systems.
In the communication system, the time-varying terminals can result in the changes of communication distances and the frequency of subcarrier waves. Then the quality of communication servers is reduced. Time-varying targets in radar systems are encountered widely also. The location and velocity of targets are changing. The ambiguities of distance and Doppler should be considered in this situation. The fast coherent integration is exploited for migrating targets with velocity ambiguity [Reference Gui4]. A continuous wave radar is considered in the time-varying situation with a linear frequency modulation and a very short chirp duration [Reference Gui and Yang5]. The radar with frequency modulation continuous wave (FMCW) system should transmit the FMCW radio wave repeatedly for enhancing the signal-to-noise ratio (SNR). Usually the target is treated as the same position during the coherence integration time. The process is illustrated by Fig. 1. The Radar transmits the radio wave of FMCW repeatedly; the radio wave can be reflected by the target. For the static target, the receiving signal can be accumulated by the same time delay for the same position. However, for the moving target, the receiving signal cannot be accumulated, because of different delay caused by the different distance.
Fig. 1. Detection of the moving target with the FMCW radar.
The radar echo consists of a sequence of chirp signals related with targets' echo during the range and Doppler frequency measurement. The maximum unambiguously measurable radial velocity is limited by minimum chirp duration in this case. Therefore the fast moving targets will cause measurement results ambiguous that should be solved.
The techniques of overcoming the ambiguities are compared on the basis of several subsequent measurements with different ambiguity interval lengths [Reference Tigrek and van Genderen6]. Performance bounds and angular resolution are limited for the multi-input multi-output (MIMO) Radar [Reference Kronauge, Schroeder and Rohling7]. The fully adaptive processing is utilized in the radar with MIMO antenna array for solving fast time-varying movement [Reference Boyer8]. The method extends the availability of narrowband delay-Doppler processing to a wider range of waveform and target parameters.
For detecting target simply, we usually assume that the velocity of target is invariable and the value of velocity cannot be extremely great. However, the velocity of target is not fixed but it is variable. Targets such as moving vehicle, naval vessel, missile, and airplane in low space move toward radar with variable velocity. The signals of those targets are instable signals. If the conventional method is exploited, the Doppler spectrum is spread. So the loss of coherent relative process will appear because of instable signal. At this time, it is difficult to detect and locate target.
Target detection based on synthetic aperture radar (SAR), the hot topic, includes numerous methods such as texture based method [Reference Lu, Zhang, Zhou and Gao9], size method, and intensity method. High-order statistics includes more abundant information than low-order statistics, so it is widely applied in all kinds of situations such as: non-stationary distribution, non-minimum phase, colored noise, non-linear system, and non-stationary [Reference Shearman10]. The second-order statistic applied in signal analyzing can extract enough information and identify parameters with the variety of processes, by treating signal and noise as Gaussian distribution. For non-stationary signal, the second-order statistic is just one kind of information [Reference Zhang and Bao11], which does not contain phase information, so the second-order statistic is unable to process non-minimum phase system. High-order statistics contains more abundant information than the second-order statistics [Reference Raney12, Reference Soumekh13], so it not only can restrain colored noise, but also can suppress the effects of non-stationary noise occasionally. High-order statistics is widely applied in signal detection, frequency estimation, and feature extraction [Reference Xue, Jung and Zhang14]. Georgios B. Giannakis and Miehail K. Tsatsanis can classify the target signals contained noise using matched filter and the third accumulation [Reference Grandi, Lee and Schuler15]. Recognition rate could achieve more than 95%, which was twice higher than the second-order moment [Reference Aiazzi, Alparone and Baronti16]. Ajay N. Balan and Mahmood R. Azimi-Sadjadi in the USA extracted the features of ground radar and background echo signals through bi-spectrum analyzing, and then the features was recognized in neural network. The recognition rate could achieve more than 93%.
Vittorio Murino in Italy utilizes the third moment to classify materials with different organizational structure based on minimum distance criterion. The classifier's recognition rate could be more than 90% when SNR > −5 dB [Reference Greco and Gini17, Reference Chen, Haddar and Lechleiter18].
High-order statistics includes high-order accumulation and high-order moment. High-order accumulation is widely used in radar target detection. High-order moment, which contains variety of information about target that is not found in the second-order moment, is a useful measure to detect target. Vehicle has more reflectors and their reflections are stronger than the clutters'. The middle positions of probability density function (PDF) graphics are different between the vehicle target chip and the clutter chip. The middle position of the vehicle target chip's PDF locates at the right side of normal PDF graph, because the vehicle chip contains more and brighter pixels [Reference Gui19]. Additionally, the pixels lied in the vehicle position become brighter. The ones around the vehicle are affected by multiple reflections. The shadow can be shown in the features of SAR imaging. High-order moment should make it easier to detect target from clutter than detecting with the second-order moment.
II. FIX ACCELERATION ECHO WAVES ANALYSIS
We assume the target with velocity ν and radial acceleration a. The target signal which is processed with the mixing frequency and low-pass filter in the receiver of the radar based on the system of FMICM（frequency-modulated interrupting continuous wave） is described as follows.
Suppose the transmitting signal of the radar is expressed with
$$S\lpar t\rpar =\cos \left({2\pi \left({{f_0} - \displaystyle{{Kt} \over 2}} \right)t} \right){\kern 1pt} {\kern 1pt}\comma \; \quad 0 \leq t\lt T\comma \;$$where f 0 is the carrying frequency,
$$K=B/T$$is the rate of scanning frequency, B is the bandwidth of scanning frequency, and T is the time-width of scanning frequency.
The transmitting signal S(t) is modulated with gate-control signal g(t) to form the transmitting signal of FMICW
$${S_T}\lpar t\rpar =S\lpar t\rpar g\lpar t\rpar =S\lpar t\rpar \cdot \sum\limits_{p=0}^{P - 1} {\hbox{rect}\left[{\displaystyle{{t - pq - \lpar {T_0}/2\rpar } \over {{T_0}}}} \right]}\comma \;$$where P is the number of gate-control pulses in the time-width T; T 0, q express the pulse-width and pulse-period, respectively; rect(t/T 0) is the pulse rectangle, which middle is origin and which width is T 0.
Suppose that the target locates in the distance r and its radial velocity and acceleration toward radar site are ν and a, respectively, the delay time of target echo is expressed with the formula
$$\tau=\displaystyle{{2\lpar r - vt - \lpar 1/2\rpar a{t^2}\rpar } \over {c+v}} \approx \displaystyle{{2r} \over c} - \displaystyle{{2v} \over c}t - \displaystyle{{a{t^2}} \over c}\comma \; \quad v \ll c\comma \;$$where c is the velocity of light. At this time, the echo signal of this target is expressed with
$${S_r}\lpar t\rpar ={S_T}\lpar t - \tau \rpar =g\lpar t - \tau \rpar S\lpar t - \tau \rpar .$$The echo signal that enters into receiver is controlled with the T/R switch pulse. So the receive signal is expressed with
$${S_R}\lpar t\rpar =\lsqb 1 - g\lpar t\rpar \rsqb g\lpar t - \tau \rpar S\lpar t - \tau \rpar .$$This signal is mixed with the transmitting signal, and then we eliminate the parts of high frequency and modulating pulse with the low-pass filter. Thus, the baseband signal is attained. It is expressed as
$$\eqalign{S_I \lpar t\rpar &= \hbox{lowpass} \lcub S\lpar t\rpar \cdot S_R \lpar t\rpar \rcub = \cos \left(2\pi \left(K\tau t - f_0 \tau - \displaystyle{K \tau^2 \over 2} \right)\right)\cr & = \cos \left\{2\pi \left[\matrix{ - \displaystyle{2r f_0 \over c} + \displaystyle{2Kr \over c}t + \displaystyle{2f_0 v \over c}t + \displaystyle{f_0 a \over c} t^2 \hfill \cr - \displaystyle{2Kv \over c} t^2 - \displaystyle{aK \over c} t^3 - \displaystyle{1 \over 2} K \left(\displaystyle{2r \over c} - \displaystyle{2v \over c}t - \displaystyle{a t^2 \over c} \right)^2 \hfill} \right]\right\}\cr &=\cos \lpar \varphi_{\tau}\rpar .}$$The last item is neglected for its small value caused by the extremely great denominator. The instantaneous frequency of baseband signal is expressed as
$${f_\tau }\lpar t\rpar =\displaystyle{1 \over {2\pi }}\displaystyle{{\hbox{d}{\varphi _\tau }} \over {\hbox{d}t}}=\displaystyle{{2Kr} \over c}+\displaystyle{{2{f_0}v} \over c}+\displaystyle{{2{f_0}at} \over c} - \displaystyle{{4Kvt} \over c} - \displaystyle{{3aK{t^2}} \over c}.$$At this time, because the target has one acceleration, the first two items in formula (7) are not enough to describe the movement of target. The resolution of distance
$$\Delta R={C \over {2B}}$$is decided with the bandwidth of radar. The resolution of Doppler frequency is
$$\Delta {f_d}=\displaystyle{1 \over {m{T_s}}}=\displaystyle{1 \over t}\comma \;$$which is decided by coherent integration time (CIT). The echo signal of the target with the same radial velocity is sinusoidal signal after processing with eliminating slope. Its Doppler spectrum is a vertical line. The signal of the target becomes more and more strong along with the increase of the CIT. So the radar can detect the weak signal by increasing the CIT. But we can see that the Doppler spectrum of the target which moves with one acceleration is spread with (2f 0 at/c). Moreover, the spread is more and more serious, along with the increase of the CIT. In other words, when the target moves with one acceleration, the conventional method which improves SNR by increasing the CIT is ineffective.
Then the radar echo should include the noise from background. The non-linear processing method is exploited to suppress noise and detect the target with the model mentioned above.
III. HIGH-ORDER MOMENT DETECTION
Detecting the vehicle target should be confronted with all kinds of noises in SAR image. The multiplicative noise exists widely. The multiplicative noise, whose strength obeys the units mean and exponent distribution, modulates the actual radar cross-section (RCS) with specific distribution. The multiplicative noise model is the supposed ideal model in the background with constant RCS, which simplifies the analyzing of image statistics features and is more suitable than the additive noise model. So this paper considers multiplicative noise situation.
For target t and attitude θ image, the multiplicative noise model is:
$$\hbox{I}\lsqb m\comma \; n\rsqb ={S_{t\comma \theta }}\lsqb m\comma \; n\rsqb w\lsqb m\comma \; n\rsqb \comma \;$$where w[m, n] is mean units noise with the same independent distribution. The mean image for target t and attitude θ is:
$$\eqalign{E\lcub I\lsqb m\comma \; n\rsqb \rcub & =E\lcub {S_{t\comma \theta }}\lsqb m\comma \; n\rsqb w\lsqb m\comma \; n\rsqb \rcub \cr& =E\lcub {S_{t\comma \theta }}\lsqb m\comma \; n\rsqb \rcub E\lcub w\lsqb m\comma \; n\rsqb \rcub \cr& ={S_{t\comma \theta }}\lsqb m\comma \; n\rsqb .}$$The mean image is the corresponding template image. The STD image for target t and attitude θ is:
$$\eqalign{\sqrt {E\lcub {{\lpar I\lsqb m\comma \; n\rsqb - E\lcub I\lsqb m\comma \; n\rsqb \rcub \rpar }^2}\rcub }& =\sqrt {S_{t\comma \theta }^2 \lsqb m\comma \; n\rsqb E\lcub {w^2}\lsqb m\comma \; n\rsqb - 1\rcub } \cr& ={S_{t\comma \theta }}\lsqb m\comma \; n\rsqb \sqrt {E\lcub {w^2}\rcub - 1} \cr& =C \bullet {S_{t\comma \theta }}\lsqb m\comma \; n\rsqb .}$$That is the corresponding multiplicative noise model. The multiplicative noise in image can be estimated with the following formula.
$$\mathop w\limits^ \wedge \lsqb m\comma \; n\rsqb =\displaystyle{{I\lsqb m\comma \; n\rsqb } \over {\mathop {{S_{t\comma \theta }}\lsqb m\comma \; n\rsqb }\limits^ \wedge }}.$$Suppose random variable x has PDF, then the characteristic function is
$$\phi \lpar \omega \rpar =\vint_{ - \infty }^{+\infty } {f\lpar x\rpar } \, {e^{j\omega x}}\, dx=E\lsqb {e^{jwx}}\rsqb .$$In other words, characteristic function is the Fourier transform of the density function. As f(x) ≥0, characteristic function has the maximum at the origin
$$\vert {\phi \lpar \omega \rpar } \vert \leq \phi \lpar 0\rpar =1.$$Random variable's K-order moment is the k-order derivative of the characteristic function at the origin
$${m_k}={\phi ^k}\lpar \omega \rpar \vert {_{\omega=0} } =E\lsqb {x^k}\rsqb =\vint_{ - \infty }^{+\infty } {{x^k}f\lpar x\rpar \, dx} .$$This paper is focused on the fourth-order moment. The fourth-order moment called kurtosis is a measure of the thickness in PDF graphics. The defined formula of the fourth order moment is expressed as
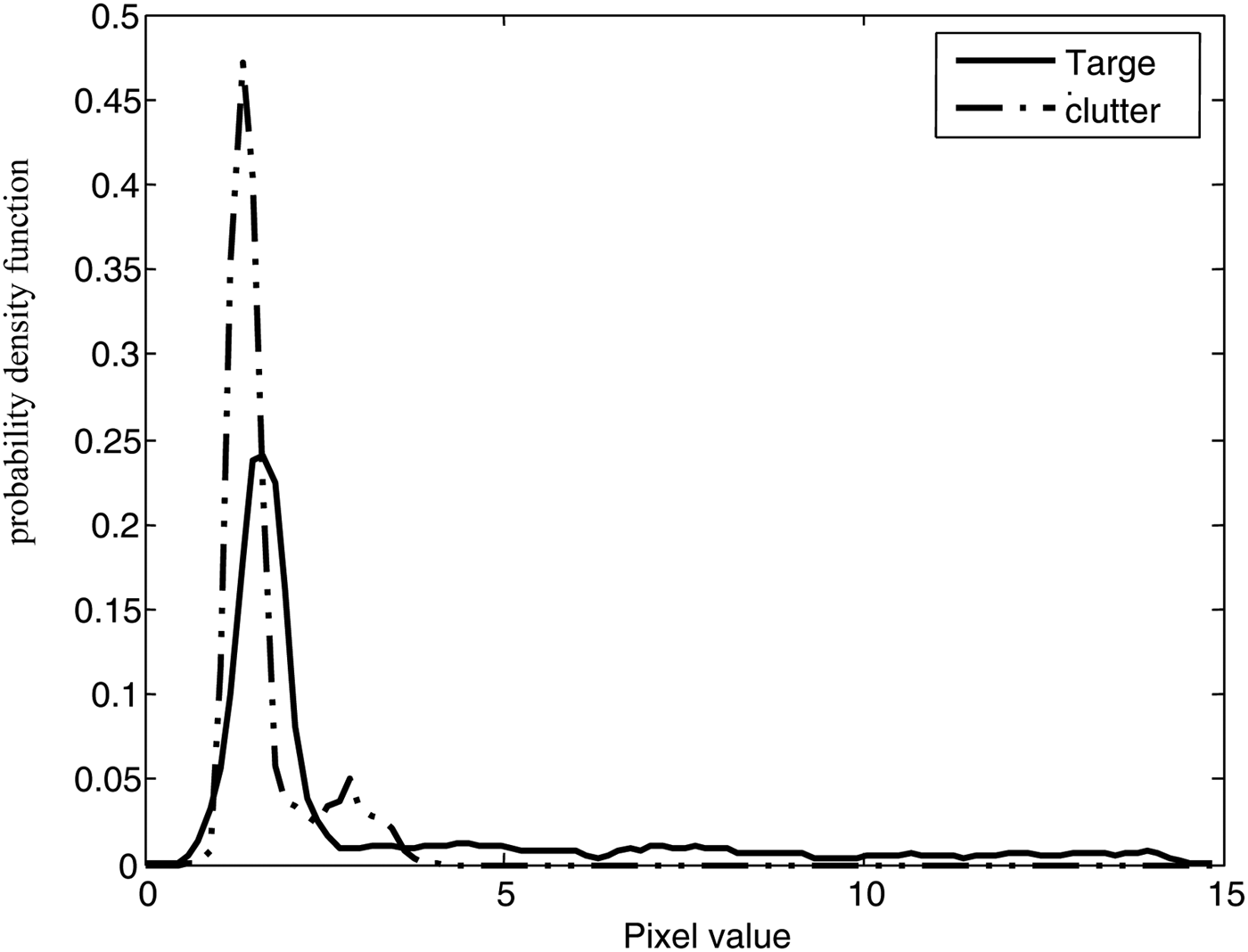
$${m_4}={\phi ^4}\lpar \omega \rpar \vert {_{\omega=0} } =\vint_{ - \infty }^{+\infty } {{x^4}f\lpar x\rpar \, dx}=E\lsqb {x^4}\rsqb .$$The target and clutter chip's PDF graphics are illustrated in Fig. 2. By processing lots of SAR data from Sandia National Laboratories for detecting the TN72 tank, we found that thicker the tail is, the higher amplitude the fourth-order moment has in PDF graphics, and generally the vehicle target chip's tail is much thicker than the clutter chip's. So the target chip can be distinguished from the clutter chip by setting up suitable threshold.
Fig. 2. Target and Clutter chip's PDF graphic.
We can see clearly that the vehicle target chip's tail is much thicker than the clutter one.
IV. PROCESSING ACTUAL RADAR ECHO DATA
The actual data are selected from Sandia National Laboratories to extract the vehicle target chip from the deserted field. The SAR image contained the target is shown in Fig. 3. It is cut from the whole SAR strip image. The target is TN72 tank moved with time-varying velocity during the coherent integration time. The radar parameters are set as follows: carrying frequency is Ku-band, 0.1 m resolution, 3.3 km range and 30º grazing angle. We extract the target chip and the clutter chip from the real data.
Fig. 3. SAR Image with target.
In the selection of window size, if the size is too large, the consume time of calculation is too big, too small size, information cannot be fully effectively included. The size of 128 × 128 is selected by comparing the processing results of different window sizes. First, we select the different window sizes to calculate the second-order moment and the fourth-order moment, and draw their PDF graphic. Then the threshold can be calculated after giving the false alarm probability. According to the threshold, the detection probability can be acquired.
The different conditions are listed as follows: noise models, noise variance value, and window size. Figures. 4–6 show the results related with different situations. The fourth-order moment is better than the second-order moment in different conditions by comparing the detection probabilities of the two methods.
Fig. 4. Multiplicative noise sized 7 × 7pixels.
Fig. 5. Multiplicative noise sized 15 × 15pixels.
Fig. 6. Multiplicative noise sized 21 × 21pixels.
The two methods are utilized to detect the target chip with the corresponding detection probability in different conditions. In every figure mentioned above, it can be visible clearly that detection probability becomes higher with the given bigger false alarm probability. The detection probability is proportional to change large with the increase of window size taken in both methods. When the noise variance value gets larger, the detection probability of the fourth-order moment declines more slowly than the one of the second-order moment, although both are all declining. Detection probability of the fourth-order moment is higher than the second-order moment in the same condition.
V. CONCLUSION
We have compared the fourth-order moment method with the second-order moment method in this paper. In view of the unique features of higher-order statistics moment applied in SAR image, we note that the fourth-order moment method is more stable and robust than the second-order moment through a large number of real SAR data processing. During the experiment process, we also found that the detection probability of the fourth-order moment method is not higher than the second-order moment when we only add Gaussian noise. Besides, we can also study and explore the features of other high-order moments to extend this issue, such as the third-order and fifth-order moments. These need to be studied further.
ACKNOWLEDGEMENTS
This work was supported by the National Natural Science Foundation of China (Grant no. 61271351) and the Fundamental Research Funds for the Central Universities
Renzhou Gui was born in 1973. He is a Ph.D. and a professor in Tongji University. His research interests are in wireless communication, optics communication, signal detection and estimation, signal processing, and radio wave propagation. During September 2000–July 2003, he got master degree from School of Electronic Information, Wuhan University. During September 2003– July 2006, he got Doctorate degree from Radiowave Propagation Laboratory in School of Electronic Information, Wuhan University. During July 2006–December 2007 he taught in Tongji University. During December 2007– December 2008 he was Krupp researcher in Erlangen Nuernberg University, Germany. From December 2008, he is teaching in Tongji University.
