Introduction
The introduction of “time” as an additional parameter to control antenna array radiation patterns was originated with the pioneering work of Shanks and Bickmore [Reference Shanks and Bickmore1]. “Time” is often considered as the fourth dimension, which can be accurately controlled by inserting rapid switches in the array feeding network [Reference Haupt2]. Time-modulated arrays (TMAs) have evolved as unconventional alternatives to phased arrays due to their reconfiguration capabilities [Reference Rocca, Oliveri, Mailloux and Massa3]. The simple periodic on–off sequence also increases the architectural simplicity by eliminating the phase shifters for a profitable solution [Reference Rocca, Yang, Poli and Yang4]. The adaptabilities of time-domain arrays have further been explored with electronic scanning [Reference Shanks5] and also validated experimentally for nearly ultra-low sidelobe levels (SLLs) [Reference Kummer, Villeneuve, Fong and Terrio6]. The interest in TMAs has been accelerated with emerging optimization algorithms as a means to control the beam pattern through optimized pulse driving sequences [Reference Fondevila, Brégains, Ares and Moreno7, Reference Yang, Gan and Qing8]. The reliability of periodic time sequence to obtain the desired radiation characteristics has also come with the inherent generation of sideband radiations (SRs) at multiples of modulated frequencies usually considered as power loss in undesired directions [Reference Brégains, Fondevila-Gómez, Franceschetti and Ares9]. Several studies have been carried out with optimized time sequences to reduce SRs [Reference Yang, Gan, Qing and Tan10, Reference Poli, Rocca, Manica and Massa11]. The sideband levels (SBLs) have been minimized with optimized shifted pulses [Reference Poli, Rocca, Manica and Massa12], sub-sectioned time steps [Reference Zhu, Yang, Zheng and Nie13, Reference Tong and Tennant14], and nonuniformly excited thinned arrays [Reference Aksoy and Afacan15]. The joint optimization approach using convex programing and evolutionary techniques are also studied for the synthesis of large-scale heterogeneous TMAs [Reference Yang, Yang, Chen and Qu16, Reference Yang, Yang, Chen, Qu and Hu17]. Research on TMAs has further been extended by proposing iterative convex optimization algorithms for efficient pencil beam synthesis [Reference Yang, Yang, Member, Chen and Member18]. Some hybridized approaches to generate pencil beam patterns as well as shaped beam patterns have been investigated by constraining dynamic range ratios (DRRs) of TMAs [Reference Yang, Yang, Chen and Guo19]. An optimal pulse shifting approach has also been introduced to minimize the SLL and SBL of linear TMAs at the same time [Reference Chakraborty, Ram and Mandal20]. The optimization of shifted on-off time sequences required to generate the desired radiation patterns, decreases the efficiency of TMA as the off-states account for energy absorption. Several methods for the simultaneous reduction of SLLs and SBLs have also been discussed with different switching configurations to enhance the gain [Reference Zhu, Yang, Yao and Nie21], directivity [Reference Rocca, Poli and Massa22], and the overall efficiency [Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23] of the array. Pulse-shaped strategies [Reference Bekele, Poli, Rocca, D'Urso and Massa24] and other unified time and frequency domain studies have been performed to explore different switching schemes [Reference Zhu, Yang, Yao, Huang and Nie25]. The accurately modeled circuit-level analysis of TMAs considering the dynamic behavior of nonlinear switching elements has also been investigated [Reference Rocca, Masotti, Costanzo, Salucci and Poli26, Reference Masotti, Poli, Salucci, Rocca and Costanzo27]. A different perspective by exploiting the undesired SRs has unfolded the use of TMAs for the direction of arrival estimation [Reference Li, Yang and Nie28]. The multiple independent harmonic patterns generated at different frequencies have also been enhanced for secure communication [Reference Guo, Yang, Qu, Hu and Nie29, Reference Maneiro-Catoira, Brégains, García-Naya and Castedo30]. The potentialities of TMAs for beamforming [Reference Poli, Rocca, Oliveri and Massa31, Reference Li, Chen and Yang32] and beam steering [Reference Gassab, Azrar, Dahimene, Bouguerra and He33, Reference Chakraborty, Mandal and Ram34] applications have been addressed with appropriate time sequences. TMAs for monopulse sum-difference patterns [Reference Chakraborty, Ram and Mandal35] and multi-harmonic steered patterns [Reference Chakraborty, Ram and Mandal36, Reference Chakraborty, Ram and Mandal37] have been discussed with controlled radiation properties. Multiple optimized patterns of TMAs [Reference Poli, Masotti, Hannan, Costanzo and Rocca38] have also been generated for cognitive radios [Reference Rocca, Zhu, Bekele, Yang and Massa39, Reference Poli, Rocca, Oliveri, Chuan, Mazzucco, Verzura, Lombardi and Massa40] and multiple-input multiple-output systems [Reference Bogdan, Godziszewski and Yashchyshyn41, Reference Ni, Yang, Chen and Guo42], which further enhances the diversity and multifunctional capabilities.
Most of the already reported literature related to SLL and SBL reduction in TMAs have considered either conventional or analytical techniques to achieve a desired solution. The time sequences are optimized in [Reference Yang, Gan, Qing and Tan10] to suppress the SLL and SBLs as low as possible. An optimized pulse-shifted time scheme has been derived in [Reference Poli, Rocca, Manica and Massa12] by considering total ON-times of each element equal to a −30 dB Chebyshev distribution. The sub-sectional optimized time scheme has also been proposed for SLL and SBL reduction [Reference Zhu, Yang, Zheng and Nie13]. A different approach of deriving the shifted time scheme has been proposed in [Reference Zhu, Yang, Yao and Nie21] by setting the target SLL to −30 dB. The optimal time scheme for the desired radiation pattern generation with a target SLL and SBL of – 30 and −25 dB, respectively has also been discussed in [Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23]. Two different examples have been proposed in [Reference Guo, Yang, Qu, Hu and Nie29], where a certain number of elements are kept in switched-on condition and the on-times for the rest of the elements are optimized. The first example has proposed a time scheme with at least two elements switched-on for every instant of the modulation period, whereas, in the second example at least 10 elements are kept in switched-on condition for every instant of the total modulation period [Reference Guo, Yang, Qu, Hu and Nie29]. The target SLLs for both the methods have been selected as −20 dB, and then tried to minimize the SBLs as low as possible [Reference Guo, Yang, Qu, Hu and Nie29]. Because of the conflicting nature of SLLs and SBLs, either lowered SLLs or lowered SBLs have been obtained with these methods, so far. A balance between these two has also been achieved in some cases by lowering the SLLs and SBLs simultaneously to some extent. The scope of minimizing the SLL and SBLs simultaneously is still a serious research concern for TMAs. These challenging issues are addressed in this paper by proposing a unique method where ultra-low SLL (<–40 dB) and a simultaneous reduction in SBLs as low as possible is targeted. The method proposed here is completely different from the already reported literature and unique in the sense that a joint optimization of excitations and time sequences of only the four outer elements are performed, whereas in all the reported literature, only the time sequences were considered.
The aim of this paper is to minimize the SLL and SBLs of the time-modulated linear array (TMLA) while improving the directivity and the overall efficiency of the array at the same time. Toward this purpose, the time sequences of outer elements of the array are optimized along with the spacing between elements and the array excitations for the desired solution. To achieve the proposed time scheme, the on-time durations and the starting instants of the edge elements of the TMLA are taken into account for optimization within the specified modulation period. The remaining elements are switched on for the entire time period, which also reduces the computational burden. The off-states in a time scheme bear a resemblance to the energy consumed in the array feeding network due to the absorptive nature of high-speed switches. The proposed time scheme also gets the better of this problem to a great extent and increases the power handling capability as well as the efficiency of the array. Other methods of suppressing the SLL and SBLs by optimally shifted time schemes and sub-sectioned time schemes with uniform excitations are also demonstrated for a fair comparison. The optimization process is carried out with modified versions of the particle swarm optimization (PSO). In this framework, a wavelet mutation-based novel PSO (NPSOWM) strategy is employed to get the optimal results. The conventional PSO and a modified novel PSO (NPSO) based results are also presented and compared with NPSOWM-based results. Sixteen-element TMLAs with isotropic radiating elements are used throughout this discussion, and the representative results obtained from exhaustive numerical analysis are assessed with state-of-the-art literature results.
This paper is organized with the discussion of theoretical and mathematical insights of TMLA in section “Theory and mathematical insights.” The generalized time schemes associated with TMLA are also described in this section. The objectives of simultaneously suppressed SLL and SBLs and the improvements in directivity and efficiency are identified as the problem statement, and the proposed method to address these is presented in section “Problem formulation.” The advantages and limitations of the proposed method compared to other SLL and SBL reduction methods are also discussed. The results obtained from the exhaustive numerical analysis are reported and assessed with other published works in section “Numerical assessment” before concluding the paper in section “Conclusion.”
Theory and mathematical insights
The generalized architecture of an N-element TMLA equipped with attenuators and high-speed switching devices for controlling the array excitations and time sequences is shown in Fig. 1. The isotropic radiating elements are aligned toward the positive z-axis with uniform spacing d. The time-averaged response of the TMLA in the far-field can be expressed as [Reference Rocca, Yang, Poli and Yang4]:
where the array excitations are denoted with I n (n = 1, 2, …, N), β = 2π/λ 0 is the wavenumber with λ 0 being the wavelength at the operating frequency f 0, signals are impinging at a direction θ from the array main axis, and the time modulating function to control the switches connected with each array element is described as U n(t). Due to the periodic nature of time sequences within the modulation period T p, the time modulating function U n(t) can be expanded into Fourier series as:
where f p is the modulation frequency $( f_{p}\ll f_{0})$
, and the complex Fourier coefficient a mn for the n th element at m th frequency (m = 0, ±1, ±2, …, ±∞) is described as [Reference Rocca, Yang, Poli and Yang4]:
The time-averaged array factor response can now be expanded as [Reference Rocca, Yang, Poli and Yang4]:
The time-domain array factor response for m th frequency component can further be simplified as:
The array factor for the fundamental pattern at operating frequency f 0 can be obtained with m = 0, whereas the inherently generated harmonic patterns due to time-modulation can be expressed with m = ±1, ±2, …, ±∞. These harmonic radiations are usually considered as loss of power in undesired directions, which can be controlled with appropriately designed switching sequences.
Fig. 1. Standard N-element TMLA architecture with high-speed RF switches and attenuators.
The radiated power used by the fundamental pattern (P 0), and the power radiated (P T) by undesired sidebands, including the fundamental pattern, can be expressed as:
The directivity of the TMLA for the desired pattern can be given as [Reference Yang, Yang, Chen and Qu16]:
where the fundamental pattern pointing toward θ = θ 0, ϕ = ϕ 0 is denoted as AF 0(θ 0, ϕ 0), and the undesired sideband patterns at m th order frequency are presented with AF m(θ, ϕ).
Switching configuration
The modulating function U n(t) can be defined with different time sequences, shown in Fig. 2. The simple on-off time scheme for the n th element is shown in Fig. 2(a), where the element is on for a period of τ n within the modulation period T p (0 ≤ τn ≤ Tp). The rise time and fall time of the pulse are denoted as t 1 (t 1 = 0) and t 2, respectively. The modulating function for the simple on-off time scheme can be expressed as:
Fig. 2. Time sequences with (a) simple on-off pulse, (b) shifted pulse, and (c) sub-sectioned pulse.
The Fourier excitation coefficient of the simple on-off time sequence can be derived as [Reference Zhu, Yang, Zheng and Nie13]:
where the normalized on-time duration of the n th element is denoted as ξ n ( = τ n/T p).
A modified time scheme with shifted pulse behavior is presented in Fig. 2(b), where the starting instant or the rise time of the pulse is shifted. For this shifted time scheme, the modulating function can be presented as:
The corresponding complex excitation for the pulse-shifted time sequence can be derived as [Reference Zhu, Yang, Zheng and Nie13]:
which can further be simplified as:
where the normalized starting instant of the n th element is denoted as δ n ( = t 1/T p). The reduction in SRs can be achieved with modified time sequences without altering the properties of the desired fundamental pattern. The starting instants and closing instants of array elements account for the simple on-off configuration of switches associated with each element of TMLA. Different possible combinations of time schemes can be generated to address different applications of TMLA.
Toward this purpose, a combined sub-sectional time sequence for the n th element is also presented in Fig. 2(c), where the on-time period of each element is split up into two sub-pulses with an off-state in between. The element is switched on at t 1 (t 1 = 0) and remain in on-state up to t 2 with an on-time duration of τ n1 ( = t 2 − t 1). Then the element is switched off from t 2 to t 3 before going into an on-state again for the duration of τ n2 ( = t 4 − t 3). The modulating function of sub-sectioned time scheme can be expressed as:
The corresponding Fourier excitation for the sub-sectioned time sequence can be given as [Reference Zhu, Yang, Zheng and Nie13]:
The complex excitation coefficient for the time scheme shown in Fig. 2(c) can be simplified as:
where ξ n1 and ξ n2 are the normalized on-time durations of the sub-pulses shown in Fig. 2(c). The normalized starting instants of the sub-pulses are denoted as δ n1 ( = t 1/T p) and δ n2 ( = t 3/T p). It is clear from equations (10), (13), and (16) that an additional degree of freedom in terms of δ n is available for modified time schemes compared to simple on-off time scheme. This additional freedom can be suitably explored to control the harmonic radiations without affecting the fundamental pattern.
Problem formulation
The objectives of simultaneous suppression of SLL and SBLs, as well as directivity enhancement of 16-element TMLA, is addressed in this paper by proposing a unique outer-element controlled time sequence along with optimized excitations (I n). The normalized starting instants (δ n) and the on-time periods (ξ n) of only four outer elements are optimized to get the proposed time sequence. The SLL and all the undesired harmonic radiation patterns (SBLs) are minimized with a constraint on beamwidth to achieve a high-directive radiation pattern.
Other SBL reduction methods using shifted and sub-sectioned optimized time sequences are also presented, and the outcomes of these methods are compared with the proposed method. For an optimally shifted time sequence, the normalized switch-on instants (δ n) of each array element are optimized along with the duration of on-states (ξ n) by considering uniform excitations (I n = 1). Another method of SBL reduction is also demonstrated with a sub-sectioned optimal time scheme, where the switching instants (δ n1, δ n2) and the normalized on-times (ξ n1, ξ n2) of the sub-pulses are simultaneously optimized by keeping the static excitations uniform (I n = 1). For all these methods, the uniform spacing between the radiating elements is also optimized.
The cost function (CF) for the minimization problem is designed as:
where SLL 0 and SBLm are the maximum level of sidelobe for the fundamental pattern at f 0 and the maximum level of sidebands for the harmonic patterns at f 0 + mf p (m = ±1, ±2, …, ±∞), FNBW denotes the beamwidth between the first nulls, and w 1, w 2, w 3 represent the contributing weights. The contributing factors are equally weighted (w 1 = w 2 = w 3 = 1 ) for the simultaneous suppression of SLL and SBLs. The target is to lower the maximum SLL of the fundamental pattern below −40 dB and all the higher sidebands as low as possible at the same time. For higher order SBLs, first 20 harmonic patterns (|m| = 20) are considered in the optimization process. The power dispersed in higher order sidebands are also calculated to show the decaying nature of SBLs.
Different cases of SLL and SBL reduction approaches are explored by using the modified versions of PSO. The optimal solutions are achieved by employing a NPSOWM. The numerical results obtained from traditional PSO and NPSO-based strategies for different SLL and SBL reduction methods are also presented to show the performance superiority of the NPSOWM-based approach. PSO is a familiar swarm intelligence-based computational technique used to solve diverse electromagnetic problems [Reference Robinson and Rahmat-Samii43]. To enhance the global search ability of traditional PSO, a modified version of PSO termed as novel PSO has been proposed [Reference Mandal, Ghoshal and Bhattacharjee44]. Further modifications have been made to PSO for fine-tuning of a solution by introducing a wavelet theory-based mutation process [Reference Ling, Iu, Leung and Chan45]. The wavelet mutation (WM) differs from the conventional mutation of PSO by incorporating a balance between the exploration and exploitation of the search space. A broader search space at the initial stages of optimization process for the better exploration, and a relatively narrower search space at the final stages for the fine-tuning of the desired solution can be attained by NPSOWM. In this way, a global optimum solution for the above-mentioned optimization problem is achieved by outperforming the solutions from NPSO and PSO. A detailed discussion of NPSOWM, NPSO, and PSO can be found in [Reference Ram, Mandal, Kar and Ghoshal46]. For the SLL and SBL reduction problems discussed in this work, the search ranges of the modeling parameters are predefined. The search ranges for the normalized on-time duration (ξ n), switch-on instants (δ n), and inter-element spacing (d) are considered as [0.01, 1], [0.1, 1], and [0.5λ 0, λ 0]. The best-proven values of control parameters for the applied optimization strategies, obtained after several runs, are presented in Table 1.
Table 1. Control parameter values of different optimization strategies
Numerical assessment
Three different cases of SLL and SBL reduction methods are discussed in this section. The first two cases of SLL and SBL reduction with optimally shifted and sub-sectioned pulses are presented for an exhaustive comparison of different approaches with the employed optimization algorithms. Shifted pulses within the modulation period generally considered beneficial for the SBL reduction. Dividing the total on-time periods into multiple sub-sections further decreases the SBLs. The proposed method demonstrated in the third case has extended this idea by incorporating an outer-element controlled optimized time sequence for SLL and SBL reduction. The results obtained by this method is also assessed for all the employed optimization techniques, and also compared with other two methods to show the superiority of the proposed method. The first case is concerned with an optimally shifted time scheme where the starting instants of each element and the total on-time periods are optimized. The spacing between elements is also considered for optimization by keeping the amplitude excitations uniform. The second case is devoted to a sub-sectioned time scheme with uniform excitation where the starting instants and on-time durations of each sub-pulses are simultaneously optimized along with the uniform element spacing of the array. The discussion of the outer-element controlled time scheme in the third case is considered as the proposed method to get the desired solutions. In this case, an optimal time sequence, along with optimized excitation coefficients, is developed to suppress the SLL and SBLs simultaneously. The results obtained from the first two cases are compared with this case to show the performance superiority of the proposed method. For all three cases, PSO- and NPSO-based results are presented along with the optimal solutions obtained from NPSOWM.
The proposed method is also compared with a −30 dB reference Chebyshev pattern to show the improvements in terms of SLLs and SBLs. The time sequence of a −30 dB Chebyshev pattern for the 16-element TMLA is shown in Fig. 3. The normalized power patterns for the fundamental (m = 0), first positive (m = 1), and second positive (m = 2) sidebands are presented in Fig. 4. The array is uniformly spaced with 0.5λ 0, and operating at 3 GHz (f 0) along with a modulating frequency of 1 MHz (f p). The first two SBLs of the reference Chebyshev pattern is obtained as SBL 1 = –12.39 dB and SBL 2 = –18.25 dB. The directivity is calculated as 10.8819 dB. The radiation properties of a uniform 16-element TMLA is also calculated using MATLAB. The SLL, half-power beamwidth (HPBW), FNBW, and directivity of uniform TMLA are −13.15 dB, 6.48°, 14.4°, and 12.04 dB.
Fig. 3. Normalized on-time sequence of a −30 dB Chebyshev pattern for 16-element TMLA.
Fig. 4. Normalized radiation patterns of the fundamental and first two positive sidebands using a −30 dB Chebyshev time scheme.
Case 1: time scheme with optimally shifted pulses and uniform excitations
The first approach of suppressing SLL and SBLs is concerned with an optimal pulse-shifted time scheme, where the normalized starting instants (δ n) of radiating elements, as well as the duration of on-times (ξ n), are optimized within the specified search ranges. The number of variables used in the optimization are the starting instants of 10 elements (δ 1, δ 2, …, δ 5 and δ 12, δ 13, …, δ 16). The on-time duration of each element (ξ 1, ξ 2, ξ 3, …, ξ 16) along with the uniform spacing (d) between them (d 1 = d 2 = d 3 = ⋅ ⋅ ⋅ = d 16 = d) are also optimized. Thus, a total number of 27 variables are considered for optimization against the selected total number of particles of 100. The ratio between the number of particles to the total number of variables are calculated as 3.70 : 1 for all the applied optimization algorithms. The excitations are considered uniform (I n = 1), and the optimization processes are performed with PSO, NPSO, and NPSOWM. The uniform element spacings of the array for PSO-, NPSO-, and NPSOWM-based approaches are optimized as 0.8169λ 0, 0.7892λ 0, and 0.8692λ 0. The reduced SLLs obtained with PSO, NPSO, and NPSOWM are −26.94, −27.59, and −31.04 dB, respectively. The SBLs are suppressed simultaneously, and the values of SBL1 and SBL2 obtained with PSO, NPSO, and NPSOWM are −18.30, −18.25, −18.15 , and −22, −21.22, −21.02 dB, respectively. The directivities of the 16-element TMLA optimized with PSO, NPSO, and NPSOWM are reported as 12.3776, 12.2325, and 12.2127 dB. All the numerical outcomes obtained with the employed optimization techniques are presented in Table 2 for a fair comparison. It is evident from Table 2 that the NPSOWM-based result is better than PSO and NPSO-based results in terms of SLLs. The NPSOWM technique also improves the SLL with −31.04 dB contrasted to −13.15 and −30 dB of the uniform and Chebyshev patterns, respectively. The SBLs of −12.39 and −18.25 dB of the reference Chebyshev pattern is also reduced to −18.15 and −21.02 dB with NPSOWM. The directivities are also enhanced to 12.2127 dB from 10.8819 and 12.04 dB of the Chebyshev and uniform patterns.
Table 2. Numerical results obtained with different optimization algorithms for case 1
The optimal on-time sequence derived with NPSOWM is presented in Fig. 5. The corresponding optimal power patterns for the fundamental (m = 0) and first two sidebands (m = 1, 2) are shown in Fig. 6. The higher-order sidebands (m > 2) are also reduced, and the first 20 positive SBLs obtained with different optimization techniques are presented in Fig. 7. All the SBLs are reduced below the level of the first two SBLs, which implies that simultaneous reduction of SLLs and SBLs is achieved. The radiated power by fundamental and first 10 sideband patterns obtained with all three optimization processes is shown in Fig. 8. The power in fundamental patterns is reported as 64.04, 59.65, and 60.04% with PSO, NPSO, and NPSOWM-based strategies. The radiated power in the first and second sidebands is also suppressed below 12 and 5% of the total power radiated with all three optimization techniques. The wasted power in all the sidebands is reported as 35.95, 40.34, and 39.95% obtained with PSO, NPSO, and NPSOWM.
Fig. 5. Normalized on-time sequence obtained by NPSOWM for 16-element TMLA (case 1).
Fig. 6. Normalized radiation patterns of the fundamental and first two sidebands obtained by NPSOWM (case 1).
Fig. 7. First twenty SBLs for 16-element TMLA obtained by different optimization strategies (case 1).
Fig. 8. Radiated power in the fundamental and first ten positive sidebands obtained by different optimization strategies (case 1).
Case 2: time scheme with optimal sub-sectioned pulses and uniform excitations
The second approach of SLL and SBL reduction is discussed in this section by an optimally derived sub-sectioned time scheme, where the normalized on-time durations (ξ n1, ξ n2) and the normalized on-time instants (δ n1, δ n2) of the sub-pulses are optimized within the specified search ranges. The number of variables considered in this case are the on-time instants of the second pulse (n = 2) for 14 elements (δ n1, δ n2, …, δ n7 and δ n10, δ n11, …, δ n16) where the starting instants of the first pulse (n = 1) for all the elements are considered 0 (as all the elements are switched on at the starting). The sub-sectioned (in two parts) on-time duration of each element except for the central two elements i.e. 28 number of variables and the uniform spacing (d) between them are also optimized. Thus, a total number of 43 variables are considered for optimization. The swarm size or the total number of particles for PSO, NPSO, and NPSOWM are 100. So, the ratio between the number of particles to the total number of variables are calculated as 2.32 : 1 for all the optimization algorithms. The excitations are considered uniform (I n = 1), and the optimized inter-element spacings are obtained as 0.7442λ 0, 0.7607λ 0, and 0.8012λ 0 with PSO, NPSO, and NPSOWM. The SLL, SBL1, SBL2, and directivity attained with NPSOWM are −34.57, −22.18, −19.23, and 12.6857 dB, respectively. The SLLs of −30.67 and −31.89 dB are obtained with PSO and NPSO. The values of SBL1 and SBL2 are reported as −21.59, −20.36 , and −21.79, −19.95 dB with PSO and NPSO-based strategies, respectively. The directivities obtained by PSO and NPSO are 12.6046 and 12.6258 dB, respectively. The numerical results attained with all three employed optimization techniques are presented in Table 3. The NPSOWM-based approach shows better results in terms of SLL and SBL1. The optimal results achieved by all three optimization strategies outperform the results obtained with the reference Chebyshev pattern.
Table 3. Numerical results obtained with different optimization algorithms for case 2
The optimal sub-sectioned time scheme obtained by NPSOWM is presented in Fig. 9. The optimal radiation patterns achieved by NPSOWM-based time scheme for the fundamental pattern (m = 0) and the first two sidebands (m = 1, 2) are presented in Fig. 10. The higher-order sidebands (m > 2) up to the first 20 positive SBLs for different versions of PSO are shown in Fig. 11. The power in the fundamental pattern and first 10 positive sidebands obtained by PSO, NPSO, and NPSOWM are presented in Fig. 12. The radiated power in fundamental patterns is reported as 66.83, 66.05, and 64.27% with PSO, NPSO, and NPSOWM, respectively. The power radiated by individual sidebands is reduced below 6% with all three optimization strategies. The wasted power in undesired sidebands is calculated as 33.16, 33.94, and 35.72% obtained with PSO, NPSO, and NPSOWM.
Fig. 9. Normalized on-time sequence obtained by NPSOWM for 16-element TMLA (case 2).
Fig. 10. Normalized radiation patterns of the fundamental and first two sidebands obtained by NPSOWM (case 2).
Fig. 11. First twenty SBLs for 16-element TMLA obtained by different optimization strategies (case 2).
Fig. 12. Radiated power in the fundamental and first ten positive sidebands obtained by different optimization strategies (case 2).
Case 3: outer-element controlled time scheme and optimized excitations
This section is devoted to analyzing and assessing the proposed SLL and SBL reduction method with optimally controlled outer elements and optimized nonuniform excitations (I n ≠ 1). Toward this purpose, the normalized starting instants (δ n) and on-time durations (ξ n) of four edge elements of the array (element nos. 1, 2, 15, and 16) are optimized along with the uniform element spacing. For the remaining radiating elements, uniform duration of on-times (ξ n = 1) are considered, which also implies that element nos. 3–14 is switched on for the entire modulation period. The variables considered for optimization are the excitations of 16 elements ((I 1, I 2, I 3, …, I 16)), the total on-time duration and on-time instants of outer elements (δ 1, δ 2, δ 15, δ 16 and ξ 1, ξ 2, ξ 15, ξ 16) along with the uniform spacing (d). Thus, a total number of 25 variables are used in the optimization process and the swarm size or the total number of particles are selected as 100. So, the ratio between the number of particles to the number of variables is calculated as 4 : 1 for the proposed case. This also implies that a better solution is obtained with the proposed method by reducing the computational burden as a smaller number of variables need to be optimized compared to the other two methods. The optimized element spacings obtained by PSO, NPSO, and NPSOWM are 0.8416λ 0, 0.8507λ 0, and 0.8812λ 0. The SLLs obtained with PSO, NPSO, and NPSOWM-based strategies are −38.98, −40.90, and −43.29 dB. The SBL1 is reduced to −29.13, −29.96, and −30.97 dB with PSO, NPSO, and NPSOWM. The values of SBL2 obtained with PSO, NPSO, and NPSOWM-based approaches are −33.06, −33.45, and −34.13 dB, respectively. The directivities of the array are also enhanced to 13.0584, 13.0592, and 13.1439 dB with all three optimization techniques. The results achieved with case 3 improve the SLLs and SBLs compared to the corresponding reference Chebyshev pattern and uniform pattern. The numerical results are reported in Table 4, which shows that the NPSOWM-based approach outperforms other results. The simultaneously reduced values of SLLs and SBLs obtained in case 3 also shows superior performance than the other two cases (cases 1 and 2) discussed earlier in this work.
Table 4. Numerical results obtained with different optimization algorithms for case 3
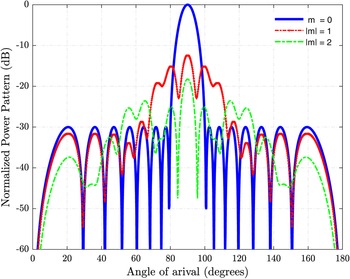
The optimized excitations and the proposed optimal time scheme derived by NPSOWM are shown in Figs 13 and 14. The corresponding optimal power patterns at the fundamental (m = 0) and first two sidebands (m = 1, 2) obtained with the proposed method are presented in Fig. 15. The higher-order sidebands (m > 2) are also suppressed with the proposed method, and the nature of the first twenty SBLs obtained with PSO, NPSO, and NPSOWM are shown in Fig. 16. The radiated power in optimally derived patterns up to the first ten harmonics is presented in Fig. 17. The power radiated by the desired fundamental patterns is obtained as 91.75, 93.07, and 94.37% with PSO, NPSO, and NPSOWM-based approaches. The total amount of wasted power in sidebands are reduced to 8.24, 6.92, and 5.62% with PSO, NPSO, and NPSOWM.
Fig. 13. Normalized excitation amplitudes for 16-element TMLA obtained by NPSOWM (case 3).
Fig. 14. Normalized outer-element controlled time sequence obtained by NPSOWM for 16-element TMLA (case 3).
Fig. 15. Normalized radiation patterns of the fundamental and first two sidebands obtained by NPSOWM (case 3).
Fig. 16. First twenty SBLs for 16-element TMLA obtained by different optimization strategies (case 3).
Fig. 17. Radiated power in the fundamental and first ten positive sidebands obtained by different optimization strategies (case 3).
The optimal time sequences with periodic on-off states are beneficial for SLL and SBL reduction. But it also comes with an inherent limitation of gain reduction as the off-states in a time sequence accounts for energy absorption by high-speed switches in the feed network. The reductions in gain for case 1 due to PSO, NPSO, and NPSOWM-based time schemes are 3.3920, 3.4874, and 3.7980 dB. The gain reductions in case 2 due to PSO, NPSO, and NPSOWM-based time schemes are reported as 3.1109, 3.2094, and 3.4047 dB. The outer element-controlled proposed time schemes have shown considerable improvements in terms of gain reduction compared to the other two cases. The reductions in gain for case 3 due to PSO, NPSO, and NPSOWM-based time sequences are achieved as 0.2353, 0.1948, and 0.1567 dB. Comparisons of different cases in terms of gain reduction are presented in Fig. 18. The NPSOWM-based result for case 3 outperforms all other results with a minimal reduction in gain. The power handling capability is also enhanced to a great extent, with 94.37% power radiated in the desired pattern. The power in undesired sidebands is also reduced below a minimum level of 5.62%, which implies that the most efficient solution is achieved with this method compared to all other approaches discussed in this paper. The DRRs calculated for case 3 with PSO, NPSO, and NPSOWM are 4.40, 4.34, and 4.21, respectively. The DRRs obtained with other two cases can be considered 1 because of the uniform amplitude distribution. The NPSOWM-based approach with case 3 is considered as the proposed method to achieve the desired objectives and also compared with other published works to show the potency of the method. The comparisons with other published results are presented in Table 5. The convergence profiles for all the cases are shown in Figs 19–21, respectively.
Fig. 18. Comparisons of gain reduction in case1, case 2, and case 3 due to optimized time sequences.
Fig. 19. Convergence profiles of all the employed optimization algorithms for case 1.
Fig. 20. Convergence profiles of all the employed optimization algorithms for case 2.
Fig. 21. Convergence profiles of all the employed optimization algorithms for case 3.
Table 5. Comparative analysis of the proposed method with other published literature works for SLL and SBL reduction
NR, not reported.
The reduction in SLL observed with the proposed technique has shown a substantial improvement with −43.29 dB over −30 dB of the best-published literature results reported in [Reference Poli, Rocca, Manica and Massa12, Reference Zhu, Yang, Zheng and Nie13, Reference Zhu, Yang, Yao and Nie21, Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23]. The SBL1 is suppressed to −30.97 dB in comparison with −18 dB [Reference Guo, Yang, Qu, Hu and Nie29], −19.50 dB [Reference Poli, Rocca, Manica and Massa12], −20 dB [Reference Zhu, Yang, Yao and Nie21], −21 dB [Reference Guo, Yang, Qu, Hu and Nie29], −24.60 dB [Reference Yang, Gan, Qing and Tan10], −25.53 dB [Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23], and −27.80 dB [Reference Zhu, Yang, Zheng and Nie13] of already reported results. The SBL2 is also minimized to −34.13 dB compared to −21.70 dB [Reference Poli, Rocca, Manica and Massa12] and −25.01 dB [Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23] of the reported literature works. The power handling capability is also enhanced with 94.37% power radiated in the desired pattern compared to 77.58% [Reference Chen, Liang, He, Fan, Zhu, Geng and Jin23], 78% [Reference Zhu, Yang, Zheng and Nie13], and 78.20% [Reference Poli, Rocca, Manica and Massa12] reported in published literature works. The power radiated in unintended sidebands is also suppressed, and the directivity of the array is simultaneously improved with the proposed method.
Conclusion
An efficient design method for the simultaneous suppression of sidelobe and SRs in a TMLA is introduced in this paper. A unique outer-element controlled optimal time scheme along with optimized excitations is generated for this purpose. The proposed time scheme is derived by suitably exploiting the on-time instants and on-time durations of outer elements of the 16-element TMLA. Other sidelobe and sideband reduction methods with optimally shifted and sub-sectioned time sequences are also presented for comparative analysis. Furthermore, the obtained numerical results are assessed with a −30 dB Chebyshev pattern to show the efficacies of this approach. Multiple objectives with controlled radiation features are addressed by using modified versions of the PSO algorithm. In this regard, an NPSOWM algorithm is utilized to get the optimal solutions. The optimal NPSOWM-based results are also compared with NPSO and conventional PSO-based results to show its performance superiority over the others. The numerical assessment shows that a much-improved performance is achieved with the proposed method by reducing the SLL and SBLs to −43.29, −30.97, and −34.13 dB compared to −30, −27.8, and −25.01 dB of the already reported works. Thus, a considerable improvement of 44.3, 11.4, and 36.46% in terms of SLL, SBL1, and SBL2 is achieved. The directivity of the TMLA is also enhanced by 28.86% from the best-published result. As compared to the reference Chebyshev pattern, the proposed TMLA has reduced the SLL and SBLs by 13.29, 18.58, and 15.88 dB. The power handling capability of the TMLA is increased to 94.37%, implying an enhanced performance by 16.17% from the best-published work. The SRs due to higher-order harmonics are suppressed, and the power wasted in sidebands is also reduced to a marginal level. Moreover, the computational load of the optimization procedure is also mitigated as only the outer four elements are optimized for the desired time scheme. Thus, an efficient solution with multiple desired objectives is achieved in a 16-element TMLA with the proposed approach.
Acknowledgements
This research work is part of a project funded by Science and Engineering Research Board (SERB), Department of Science and Technology (DST), Government of India (GoI) under the project grant no. EEQ/2017/000519, dated March 23rd, 2018.
Avishek Chakraborty obtained his B.Tech. degree in electronics and communication engineering. He received his M.Tech. degree in radio physics and electronics with a specialization in space science and microwaves from the University of Calcutta, West Bengal, India, in 2017. He is presently working as a senior project fellow in a DST-SERB funded project at the National Institute of Technology, Durgapur, West Bengal, India. He is also pursuing the Ph.D. degree as a full-time research scholar in the Department of Electronics and Communication Engineering, National Institute of Technology, Durgapur. His current research interests include antenna array synthesis, application of soft computing in antenna array optimization, and radar signal processing.
Gopi Ram obtained his B.E. degree in “electronics and telecommunication engineering,” from Government Engineering College, Jagdalpur, Chhattisgarh, India in 2007. He received his M.Tech. degree in “telecommunication engineering” from the National Institute of Technology, Durgapur, West Bengal, India in 2011. He joined as a full-time institute research scholar in 2012 at the National Institute of Technology, Durgapur to carry out research for the Ph.D. degree. He received the scholarship from the Ministry of Human Resource and Development (MHRD), Government of India for the period 2009–2011 (M.Tech.) and 2012–2015 (Ph.D.). His research interest includes analysis and synthesis of antenna arrays via bio-inspired evolutionary algorithms and antenna array optimization of various radiation characteristics. He has published more than 50 research papers in international journals and conferences.
Durbadal Mandal obtained his B.E. degree in electronics and communication engineering, from Regional Engineering College, Durgapur, West Bengal, India in 1996. He received his M.Tech. and Ph.D. degrees from the National Institute of Technology, Durgapur, West Bengal, India in 2008 and 2011, respectively. Presently, he is attached with the National Institute of Technology, Durgapur, West Bengal, India, as associate professor in the Department of Electronics and Communication Engineering. His research interest includes array antenna design and filter optimization via evolutionary computing techniques. He has published more than 350 research papers in international journals and conferences.
