I. INTRODUCTION
High resolution in synthetic aperture radar (SAR) is essential in detection and for the imaging quality. Different solutions to attain this high resolution have been proposed such as an augmentation of the number of antennas for the transmission multiple input single output (MISO) [Reference Kim, Ossowska and Wiesbeck1] or an augmentation of the number of receptors single input multiple output (SIMO) [Reference Yuan, Huilian, Hui, Da, Qingsong and Peiqiang2]. In these cases, only one waveform is sent for the transmission. Thus, another configuration has been proposed from digital communication: the multiple input multiple output (MIMO) radar [Reference Li and Stoica3]. It is based on the same principle as digital communication such as the use of different waveforms in transmission and, each of these waveforms will be orthogonal with the others or at least, will have their cross-correlation really low.
Two types of MIMO radars exist and they are currently investigated: The statistical MIMO and the colocalized MIMO. The statistical MIMO is based on the angular diversity [Reference Fishler, Haimovich, Blum, Chizhik, Cimini and Valenzuela4]. In this case, the radar cross section seen by each transmitting antenna is unique and by coupling these unique views of the scene, we can have a gain in resolution and have better detection capability. The second MIMO radar configuration is the colocalized MIMO radar where the distance between the antennas on transmission is close enough, so we can approximate the radar cross section seen by each transmitting antenna as the same for all of them [Reference Ma, Yeo, Feng and Tan5]. This configuration, considering the localization of the transmitting and receiving antennas along the cross-range direction, is based on the principle of the virtual antenna. Also, on one hand, the azimuth resolution is slightly improved, even with a large number of antennas. On the other hand, this configuration achieves a good robustness against interference [Reference Chen6].
The main motivation of this work is the development of our own airborne SAR system. This SAR system must be dedicated to our remote sensing applications and especially in C-band frequency. One of the principal problem of having our own system is to obtain the permission to emit in this frequency band. This difficulty is mainly due to the possible interference between our system and the other systems operating in the C-band frequency. Thus our main objective is to be as discreet as possible by using specific transmitted waveform. In this way, we propose to investigate the well-known MIMO configuration in order to reduce the transmitted power. However the reduction of power must not affect the performances we could obtain with an equivalent SISO SAR system.
In this paper we synthesize the different approaches of the MIMO radar in a colocalized configuration which is described above. Thus, the azimuth resolution will be slightly improved. In the first part of the paper, simulations of different approaches of the reception design are proposed. Those methods are based on SAR signal processing using the Stolt interpolation [Reference Cumming and Wong7]. Thus, we evaluate the performances of the different methods by analyzing the effect of different configurations on the resolutions and the robustness based on the peak sidelobe ratio (PSLR) and on the integrated sidelobe ratio (ISLR). As we consider the same bandwidth for the transmitted signals, only azimuth resolution is analyzed and discussed. We present different methods to manage the signals received before and after the Stolt interpolation. The results of those methods will be compared with an equivalent SISO SAR system. In the second part of the paper, we describe the experimental ground-based system we use to process SAR images. Resolutions on real data will be analyzed as well as the robustness of the different methods in order to validate the simulation results.
II. SYSTEM MODEL
We consider an MIMO configuration with M antennas in transmission and N antennas in reception. Each antenna is close enough to each other to view the scene with the same radar cross section in transmission. In reception, the antennas are separated by λ/2 to avoid ambiguities. The M antennas transmit different waveforms Φ = [ϕ1(t) ϕ2(t) ⋯ ϕM (t)]T with
where t is the time-range domain, and (.)T and (.)* are the transpose and conjugate operator, respectively. If the different waveforms are not orthogonal, they will be chosen, such as the correlation operation between ϕm (t) and ϕn (t) is really small.
The received signal s R (t) is defined by
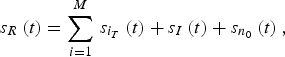
where s i T (t) is the signal sent from the ith antenna with the waveform ϕi (t), s I (t) is the different possible interference (for instance, jammer or other signals in the same frequency band), and s n0 (t) is the noise. By using a bank of matched filters in distance (MF distance), we can separate the different transmitted signals at the reception as
Thus, after the matched filter, M × N independent signals or with a low cross correlation are available.
Our work is based on the use of two chirp (linear modulated pulse) signals. Thus the configuration chosen for the MIMO SAR is composed of two transmitters spaced by a distance dt and two receivers by distance dr, as shown in Fig. 1(a). Each antenna transmits a chirp with the same bandwidth B, at the same frequency carrier f c. One chirp is an increasing function of the frequency (up-chirp) and the other one is a decreasing function of the frequency (down-chirp). We can define these chirps with
![s_i \left(t\right)= rect\left({\displaystyle{t \over {T_p }}} \right)\exp \left\{{j \pi\, \left[{2f_{si} t + k_i t^2 }\right]} \right\}\comma \; \eqno\lpar 4\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151130141431726-0178:S175907871200044X_eqn4.gif?pub-status=live){kind=small}
Fig. 1. Simulated (a) antenna configuration and (b) overview of the MIMO system.
Where f si is the starting frequency of the chirps at the beginning of the pulse, k i = ±B/T p is the chirp rate (+ and − stand for the up-chirp and down-chirp, respectively) and T p is the chirp length.
Although these chirps, defined in equation (4), are not orthogonal, the cross correlation, described in equation (1), of the two chirps is low enough compared to the main lobe of the autocorrelation. Thus, the use of those two signals is possible for the MIMO configuration [Reference Wang, Peng and Cai8]. Indeed, the cross-correlation level of the two chirps is −10 dB compared to the maximum of the auto-correlation level. This cross-correlation level is enough to produce an image of the scene. However with this cross-correlation level, we can note that artifacts appear on the final SAR image. By using strictly orthogonal waveforms, these artifacts would disappear.
III. RECEIVER DESIGN
On the receiver part of the MIMO radar, each antenna receives the combination of all transmitted signals coupled with interference and noise, as described in equation (2). The common model of the receptor [Reference Zhang and Suppappola9] gives the standard procedure of the MIMO SAR in reception. However we propose to study the different types of procedure in order to optimize the MIMO SAR processing regarding the spatial resolution and the image quality parameters. In this section we compare three different methods for the receiver using matched filters in distance, described in (3), matched filters in azimuth, and the Stolt interpolation. The Stolt interpolation is considered as an exact method in the frequency domain to compensate the range migration. Moreover, the range–Doppler coupling is compensated by taking into account the real position of the transmitted and received antenna, e.g. the middle point of the different couple transmitter/receiver.
A) Methods
Method #1, shown in Fig. 2(a), results from the sum of all the complex signals after the matched filter in azimuth. A Stolt interpolation [Reference Soumekh10] is carried out on the result of the sum, in order to correct the range migration. Method #2 is based on the gathering of all the complex signals in a single matrix, after the matched filter in azimuth, as shown in Fig. 2(b). So, we adapt the Stolt interpolation to the new size of the matrix image so as to correct the range migration. Method #3 uses the fact that the MIMO SAR has M × N couple transmitter/receiver available. For each of these couples, an SAR image can be created using the basic SAR processing with the Stolt interpolation. Finally, the scalar sum of these images gives us the final MIMO SAR image. This process is described in Fig. 2(c).
Fig. 2. MIMO SAR imaging methods.
B) Robustness
The comparison of the robustness for the SISO and MIMO configuration is based on the PSLR and the ISLR measurements, defined in equations (5) and (6) (see [Reference Davis, Fante and Perry11]). These parameters are defined by considering the impulse response of the system of the scene modelized by one scatterer. Thus, considering the obtained radar image of this scatterer, one can write the PSLR and ISLR with
![PSLR = \displaystyle{{\mathop {\left\vert {\lpar y_n \rpar _{psl} } \right\vert }\nolimits^2 } \over {\mathop {\left\vert {y_0 } \right\vert }\nolimits^2 }} = \mathop {\left[{\lpar y_n \rpar _{psl} } \right]}\nolimits_{db} - \mathop {\left[{y_0 } \right]}\nolimits_{db} \eqno\lpar 5\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151130141431726-0178:S175907871200044X_eqn5.gif?pub-status=live)
and
where |(y n)psl|2 is the intensity of the highest sidelobe outside the mainlobe, |y n|2 is the intensity of each pixel of the image outside the mainlobe, and |y 0|2 is the energy contained in the mainlobe.
Moreover, we measure the azimuth resolution by evaluating the width of the mainlobe at −3 dB of the response of the scatterer point along the azimuth axis.
IV. SIMULATION RESULTS
The configuration chosen is a MIMO SAR composed of two transmitters and two receivers, each transmitter sending a chirp waveform. The frequency carrier is 5 GHz and the bandwidth of the chirp is 100 MHz. Thus, we can define the angular spread ϕd = 0.51 rad of each transmitted antenna that gives us the optimum azimuth resolution R az = 0.0606 m. Moreover, the range resolution is derived from the bandwidth of the transmitted signal, i.e. R rg = 1.5 m. As shown in Fig. 1(a), the antennas are separated by (λ/2) for the reception and (42 × λ/2) for the transmission. The distance between the antennas and the center of the scene is X c = 5 m. Finally, we consider a radar data collection along a 3 m azimuth distance.
Firstly, the resolution in distance is unchanged and remains at 1.5 m irrespective of the imaging method. Secondly, depending on the configuration, the resolution in azimuth is modified as shown in Fig. 3.
Fig. 3. Azimuth cut of the response of one scatterer for the different methods.
In method #1, the azimuth resolution is equal to 0.0606 m and is the same as the one obtained in an SISO configuration. In the second and third methods, we can note that a small amelioration is visible: the azimuth resolutions are equal to 0.05 m for method #2, and 0.048 m for method #3. For method #2, we can not that grating lobes appear which limit the azimuth resolution. By adding a specific processing [Reference Zhuang and Liu12], this azimuth resolution can be improved. As for the robustness of the SISO and MIMO configuration, we define the noise as a white Gaussian noise with a variance σ2 of 60.
The results we obtained for the ISLR and PSLR are given in Table 1. For method #1 and method #2, the values of the PSLR and ISLR are higher than the values obtained for the SISO configuration. As for method #3, we have obtained lower PSLR and ISLR levels than the SISO configuration. Thus, we can consider that this MIMO configuration provides a better robustness against the noise.
Table 1. Simulation results of the azimuth resolution, PSLR and ISLR for the different methods.
V. EXPERIMENTAL SETUP AND MEASUREMENTS
The experimental system is shown in Fig. 1(b). The experiment setup is based on a vector network analyzer (VNA) which transmits a step frequency continuous waveform (SFCW) during a finite time in a stop & go configuration. Thus, we can compare this SFCW transmitted signal to a chirp signal used in a basic SAR system. The different parameters of the experimental setup are defined as follows: the carrier frequency is 5 GHz and each transmitted signal has a bandwidth of 500 MHz. The VNA and the antennas are placed on a rail of 3 m long that gives the deplacement necessary for the SAR processing. The MIMO radar system is composed of four antennas: two transmitters and two receivers, as described in the simulation part. The transmitters are separated by 1 m and the receivers are separated by 12 cm. Also these antennas are placed at a height of 2.56 m with the incidence angle of 45°. The considered target is a trihedral corner placed on the scene at 5 m from the nadir of the antennas (in the slant range, the target is located at 5.63 m). The scene is composed of grass that gives the noise speckle of the scene. Finally, the two transmitted signals are assumed to be orthogonal.
Depending on the imaging method, different values for the azimuth resolution, PSLR, and ISLR are obtained and shown in Table 2. Also, the azimuth cuts for each method are shown in Figs 4(a)–(c). Thus for method #1, we obtain a gain of 6.17 and 9.33% in comparison with the SISO configuration for the PSLR and the ISLR, respectively. As for the azimuth resolution, the measured value is 0.084 m. For method #2, the corresponding values obtained for the ISLR and the resolution are 10.06% and 0.05 m, respectively. Finally for method #3, the same kind of measurements gives the values for 38%, 16%, and 0.053 m for the PSLR, ISLR, and azimuth resolution, respectively.
Fig. 4. Azimuth cut of the different methods compared with the SISO configuration.
Table 2. Measurement results of the azimuth resolution, PSLR, and ISLR for the different methods.
VI. DISCUSSION
The different methods have been validated by the results obtained on simulation and experimental measurements. Method #1 has shown that a gain has been obtained for the ISLR. This is mainly due to the summation of different complex phases which represent the response of a scatterer point. Thus, no gain in resolution was to be expected and the level of the ISLR is improved due to the number of antennas (transmission and reception). As for method #2, a gain in resolution and ISLR was measured. This behavior is due to the different signals regrouped in a single matrix, as shown in Fig. 2(b), which is equivalent to make a periodicity of the received signal in the frequency domain. This periodicity induces a phenomena of grating lobes in the temporal domain and thus on the final image. Method #3 provides a gain for the azimuth resolution, ISLR and PSLR. These results are due to the coherent summation of the image intensities.
The different results obtained with the experimental setup confirm those obtained with the simulations. However the different values are slightly different in the measurements than the simulated ones. This is mainly due to the environment factor and the measurements conditions. Method #1 achieves a better robustness but at the cost of the resolution. Method #2 has a lower ISLR and a gain in the resolution but the cost is the apparition of artifacts that increase the value of the PSLR. Finally method #3 has a better PSLR and ISLR than the other methods and a small gain for the azimuth resolution. Thus method #1 has two drawbacks: the azimuth resolution has no gain and the results for the ISLR and PSLR are higher than the ones obtained in method #3. Method #2 is most appropriate to optimize only the azimuth resolution. Method #3 is most suitable if the main objective is that the transmission has to be as discrete as possible.
VII. CONCLUSION
In this paper, we have proposed a review of different receiver designs in a MIMO SAR configuration. We have simulated different MIMO SAR processings in order to quantify the gain we can obtain by using an MIMO configuration rather than an SISO one. On the simulation part, we have shown that depending on the receiver design an improvement in azimuth resolution can be attained. Consequently in the second and the third configuration of the receiver, an amelioration in azimuth has been observed. The simulation part has been validated by experimental measurements. Methods #1 and #2 achieve to obtain either a better robustness or a good azimuth resolution. Method #3 achieves to obtain the best gain for the PSLR and the ISLR compared to the SISO configuration. These encouraging results allow us to study further works dedicated to the development of an airborne system.
Vishal Riché received the M.S. in Signal and Circuit from the University of Bretagne Occidentale, Brest, France, in 2009. He is currently a Ph.D. student in electronics and working on synthetic aperture radar imaging in a MIMO configuration.
Stéphane Méric received the B.S degree in electrical engineering from the National Institute of Applied Sciences (INSA), Rennes, France, in 1991, the M.S. degree in signal processing and telecommunications from the University of Rennes1, Rennes, in 1991, and the Ph.D. degree in electronics from INSA in 1996. Since 2000, he has been an assistant professor with INSA, where he joined the SAPHIR Team, Institute of Electronics and Telecommunication of Rennes (CNRS UMR 6164), in 2005. He is currently working on radar systems (continuous-wave and frequency-modulated wave radar system) dedicated to SAR application (radar imaging in motorway context, remote sensing, MIMO configuration, and passive radar imaging).
Éric Pottier received the M.S. and Ph.D. degrees in signal processing and telecommunication from University of Rennes 1, Rennes, France, in 1987 and 1990, respectively, and the Habilitation from the University of Nantes, Nantes, France, in 1998. Since 1989, he has supervised more than 30 students to graduation (Ph.D.) in radar polarimetry covering areas from theory to remote sensing applications. Since 1999, he has been a full professor with the University of Rennes1, where he is currently the Deputy Director of the Institute of Electronics and telecommunications of Rennes (CNRS UMR 6164) and also the Head of the Image and Remote sensing Group, SAPHIR TEAM.
