Misell algorithm

The method of reconstructing wave-front phase distribution by intensity distribution was first proposed by Gerchberg–Saxton in 1972, and the algorithm (Gerchberg–Saxton, GS algorithm) solves the phase distribution of the wave function by the iterative method from the intensity distribution on the known plane and diffraction plane. In 1973, D. Misell modeled the GS algorithm and proposed the Misell algorithm to reconstruct the phase distribution of the wave function from the intensity distribution of the two defocused images with different defocusing values. Below we introduce the principle of the Misell algorithm [Reference Misell7].

In the small angle far field region, which is the intersection of the small angle and far-field regions, the field distribution satisfies the following equation:

(1)$$F(u,v) = \displaystyle{i \over \lambda} \displaystyle{{e^{ - ikR}} \over R}\int {\,f\,(x,y)\exp \{ - ik(ux + dy)\}} \,dx\,dy,$$

where f(x, y) represents the aperture distribution, R is the distance from the far-field point to the center of the aperture, λ is the wavelength, and k is the wave number, which equals 2π/λ . It is illustrated that there exists a Fourier transform relationship between the aperture distribution and far-field distribution. For the convenience of discussion, i/λ and e ^−ikR/R are ignored, and the aperture distribution and far-field distribution are expressed as the following equation in the form of amplitude and phase:

(2)$$f\,(x,y) = \vert f\,(x,y) \vert \exp [i\varphi _f\,(x,y)],$$

(3)$$F(u,v) = \vert F(u,v) \vert \exp [i\varphi _F(u,v)].$$

In the case of defocus operation, it is assumed that there is an additional phase difference Δφ in the aperture field, and the defocused aperture distribution is changed to

(4)$$f_d(x,y) = f\,(x,y)\exp (i\Delta \varphi ).$$

The relationship between the defocused and infocus far-field distributions can be expressed as follows:

(5)$$F_d(u,v) = ft\{ \exp (i\Delta \varphi )\cdot ift[F(u,v)]\} = G[F(u,v)],$$

(6)$$F(u,v) = ft\{ \exp ( - i\Delta \varphi )\cdot ift[F_d(u,v)]\} = G^{ - {\rm 1}}[F_d(u,v)],$$

where ft represents Fourier transform, ift represents inverse Fourier transform, G and G ⁻¹ are defined as

(7)$$G = ft[\exp (i\Delta \varphi )\cdot ift],$$

(8)$$G^{ - {\rm 1}} = ft[\exp ( - i\Delta \varphi )\cdot ift].$$

The iterative equation of the Misell algorithm is expressed as follows:

(9)$$F_d^k (u,v) = ft\{ \exp (i\Delta \varphi )\cdot ift[F^k(u,v)]\} = GF^k(u,v),$$

(10)$${F}^{\prime k}_d (u,v) = \vert F_d^k (u,v) \vert \exp [i\Delta \varphi _{Fd}^k (u,v)],$$

(11)$${F}^{\prime k}(u,v) = ft\{ \exp ( - i\Delta \varphi )\cdot ift[{F}^{\prime k}_d (u,v)]\} = G^{ - 1}{F}^{\prime k}_d (u,v),$$

(12)$$F^{k + 1}(u,v) = \vert {F}^{\prime k}(u,v) \vert \exp [i\Delta {\varphi} ^{\prime k}_F (u,v)].$$

The Misell algorithm starts from an estimation of the aperture distribution, and repeats (9)–(12) over and over until it satisfies the convergence criterion. The advantage of the Misell algorithm is that it can converge to the final solution with a high speed because the “projection” in (10) and (12) is an error reduction operation, which means the solution error at the k + 1th iteration is always lower than that at kth. On the other hand, if the initial estimation of the aperture distribution is far from the global minimum, the Misell algorithm will easily converge to the local minimum. The goal of this paper is to find an initial estimation near the global minimum to avoid local stagnation.

MVFSA–Misell algorithm

To find an appropriate initial estimation of the Misell algorithm, this paper constructs a hybrid MVFSA–Misell global optimization algorithm. The algorithm is based on the MVFSA, which is an improved form of very fast simulated annealing (VFSA) by enhancing the traversal capability of the algorithm at the initial stage of iteration. Below, we introduce the principles of the VFSA and MVFSA.

In a traditional SA, a given model state with energy E ₁ is compared to a state which is affected by a given perturbation. The perturbation displaces one of the particles of the state to another location on a small scale. The new state, with energy E ₂, is accepted if E ₂ − E ₁ ≤ 0. However, if E ₂ − E ₁ >0, it does not mean the new state is rejected. It can be accepted if exp[ − (E ₂ − E ₁)/T]>u, where T is the model temperature and u is a random number between 0 and 1. The receiving criterion is called the Metropolis criterion, which is the essence of the algorithm. The acceptance of the “deterioration” keeps the solution not stagnate at a local minimum. By repeating this process, the model temperature gets lower by a given annealing scheme. The global minimum of the state energy can be approached at a lower temperature. The SA method has been widely used because no specific information about the cost function is needed and it is easy to put into practice. However, the major problem of SA is that it costs a tremendous amount of time and computational efforts, which restricts its application in industry.

To speed up the convergence rate of SA, VFSA chooses a new perturbation model—a Cauchy-like distribution function, which is expressed as

(13)$$\eqalign{{{g}^{\prime}}_i(x,y) = \; & g_i(x,y) - y_i\left( {B_i - A_i} \right) \cr y_i = \; & T(u - 0.5)\left[ {{\left( {1 + \displaystyle{1 \over T}} \right)}^{\left \vert {2u - 1} \right \vert} - 1} \right],} $$

where g _i(x, y) represents the current model, ${g}^{\prime}_i(x,y)$ represents the perturbed model, [A _i, B _i] is the value range of g _i(x, y) , T represents the model temperature and u is a random number between 0 and 1 [Reference Zhao, Sen, Stoffa and Frohlich13]. The perturbation model is able to realize a narrower search as the iterative solution approaches optimum solution, which accelerates the convergence speed, but the traversal capability of the algorithm at the initial stage of iteration is sacrificed at the same time, which means there is a little risk of falling into the local minimum.

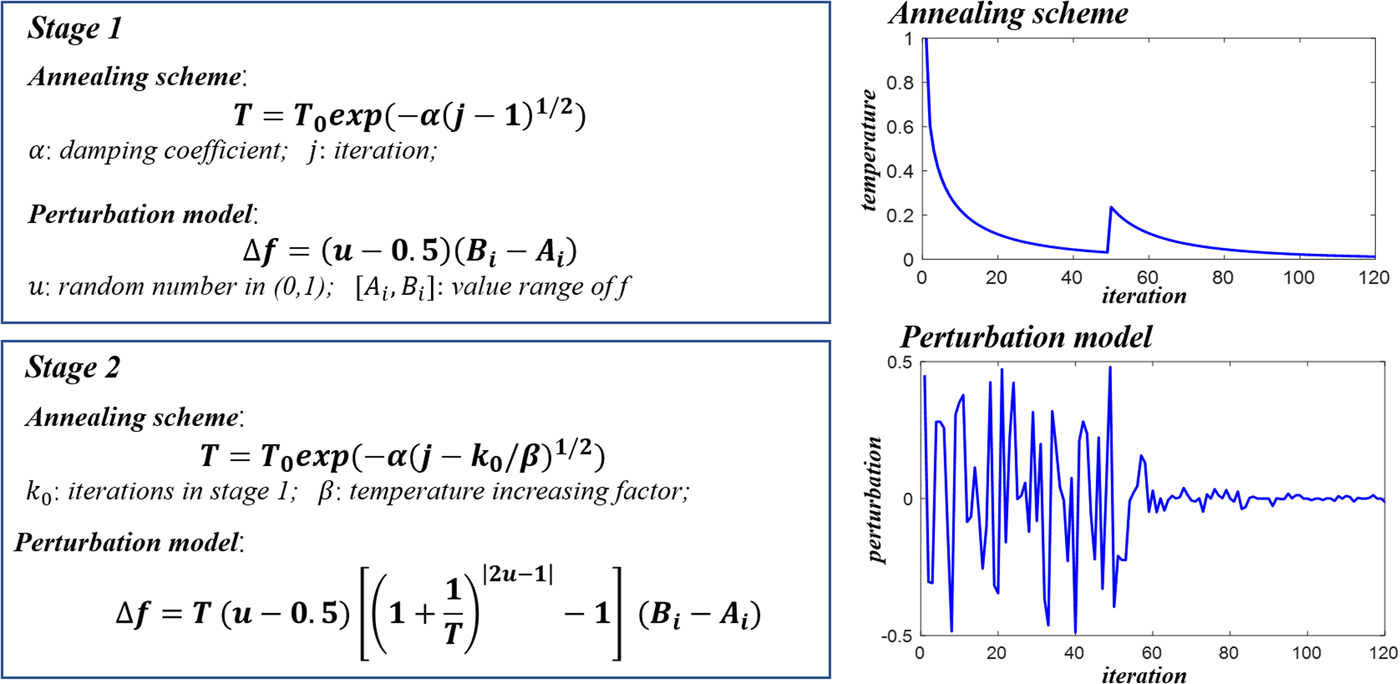
To enhance the global search capability of VFSA, we propose the MVFSA, which improves the VFSA in the following two aspects:

1. (1) An additional iterative stage is added to examine the global solution at high temperature. The initial temperature of this extra stage is slightly higher than the final temperature of the first stage, but not higher than the initial temperature of the first stage. This gives the model a chance to jump out of the local minimum. It is also a test to determine whether the intermediate solution has been dropped in the real optimal interval during the first stage.

2. (2) At the first stage, the global perturbation model replaces the current perturbation model, because the state traversal ability of random generators is higher than the special model perturbation model of the VFSA algorithm, and the global perturbation model generated by a random number is independent of the initial temperature, which means there is no need to take the value of temperature into account.

It must be pointed out that the above improvement is only the change of the annealing scheme and perturbation model. The generalized Boltzmann–Gibbs distributed receiving probability and the Metropolis criterion adopted in the algorithm are not changed, which means the global search mechanism of the SA is not changed. The expressions of the perturbation model and annealing scheme in the two stages of MVFSA are given in Fig. 1.

Fig. 1. Perturbation model and annealing scheme in two stages of MVFSA.

To avoid the local stagnation of the traditional Misell algorithm, we combine the MVFSA and the Misell algorithm to construct the global optimization algorithm MVFSA–Misell. In the MVFSA–Misell algorithm, we apply the MVFSA to get a rough estimation of the aperture distribution near the global minimum and utilize the Misell algorithm to converge to the global minimum from the rough estimation. The flowchart of the algorithm is illustrated in Figs 2 and 3. The main steps of the algorithm can be summarized as follows:

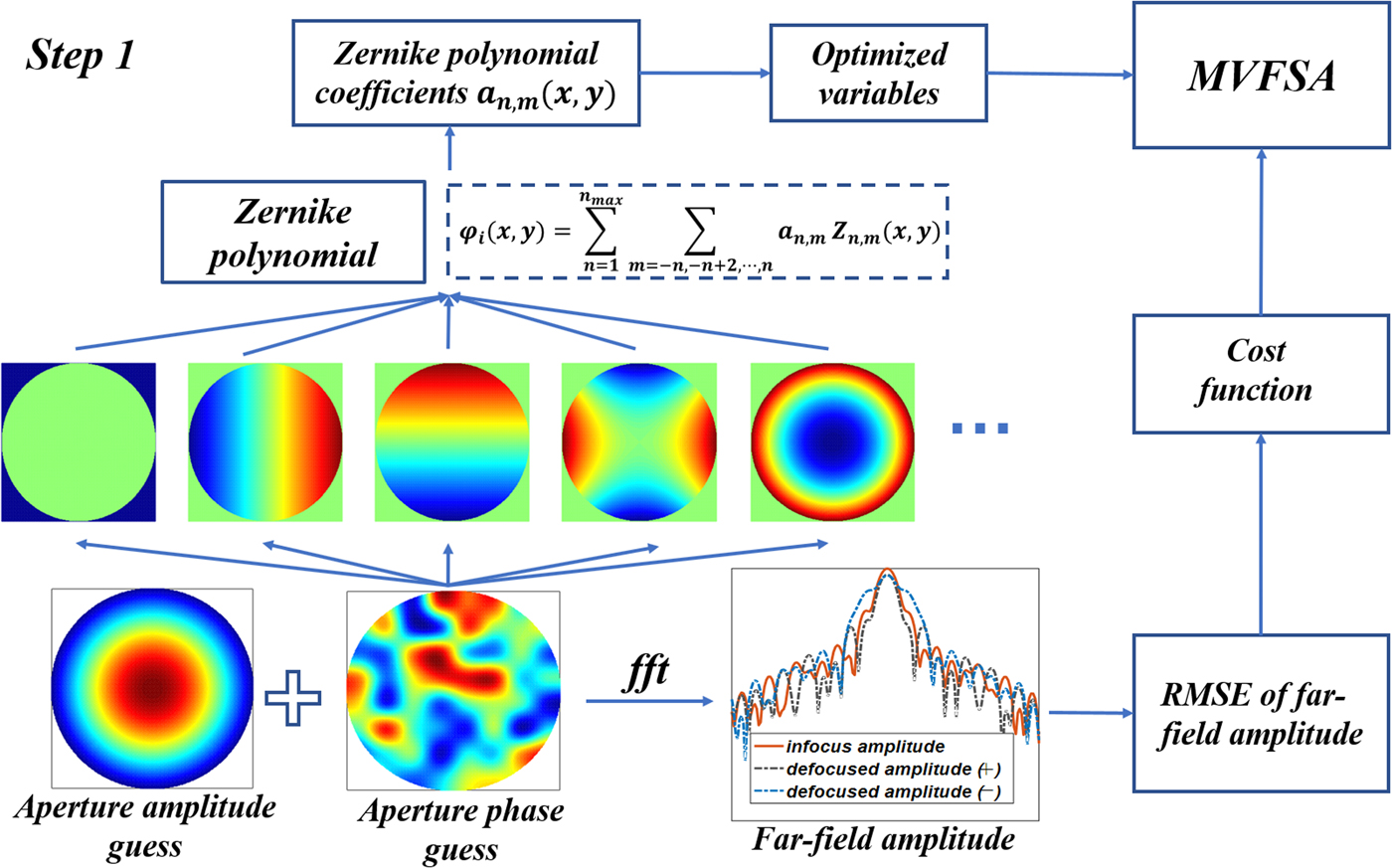
Fig. 2. Schematic diagram of step 1 of the MVFSA–Misell algorithm.

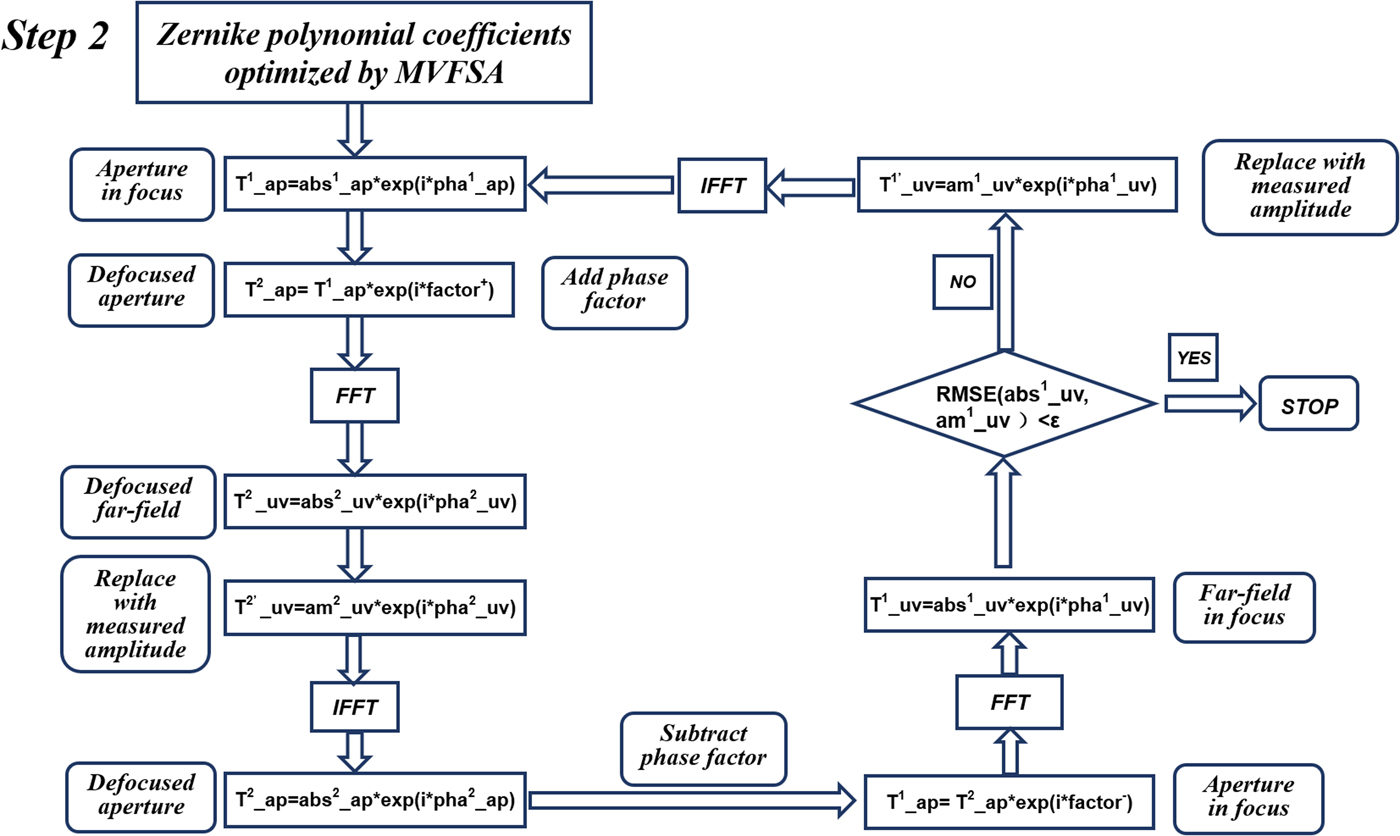
Fig. 3. Flowchart of step 2 of the MVFSA–Misell algorithm.

Step I: Achieve a rough estimation of aperture phase: To aid in the interpretation of optical test results, it is convenient to express wave-front data in the polynomial form. In this paper, we used the Zernike polynomials to parameterize the phase distributions in the aperture. In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. They can be written as

(14)$$\eqalign{ Z_n^m (r) =& \sum\limits_{k = 0}^{(n - m)/2} {{( - 1)}^k\displaystyle{{(n - k)!} \over {[(n + m - 2k)/2]![(n - m - 2k)/2]!}}} \displaystyle{{r^{n - 2k}} \over {k!}}, \cr & r \le 1,n \gt m \ge 0,n - m = {\rm even},\quad k = \displaystyle{{n - m} \over 2},} $$

where $$Z_n^m (r)$$ represents the Zernike polynomial in two positive integers, n and m, and r represents the radial radius in the circular domain. The initial Zernike polynomial coefficients can be given in different forms. Then, the Zernike polynomial coefficients are optimized by the MVFSA to minimize the cost function – the RMSE of the far-field amplitudes, which is defined as

(15)$$RMSE = \sum\limits_{k = 1}^2 {\sqrt {\displaystyle{{\sum\nolimits_N {\sum\nolimits_N {{\left( {\left \vert {F_{\,far\_k}} \right \vert - \left \vert {F_{m\_k}} \right \vert} \right)}^2}}} \over {N^2}}}}, $$

where $ \vert F_{far\_k} \vert $ is the calculated far-field amplitude, $\vert F_{m\_k}\vert$ is the measured far-field amplitude, k is the number of measured amplitudes, and N is the number of data points in the array. To save CPU time, the maximum iteration of MVFSA is set as a limited number. The goal of the MVFSA is just to achieve a rough estimation of the aperture phase instead of the final global minimum. The long subsequent iterative process of the MVFSA is replaced by the Misell algorithm in the next step due to the superior speed of the Misell algorithm.

Step II: Converge to the global minimum from the rough estimation by Misell algorithm: The step starts with a calculation of the complex infocus aperture distribution, which is composed of the optimized rough estimation of aperture phase and estimated Gaussian amplitude. Then the estimated aperture distribution is propagated into far-field by Fourier transform. There the resulting calculated far-field amplitude is replaced by the measured amplitude and the phase is retained unchanged. This modified infocus far-field amplitude and phase distribution is then propagated into aperture by inverse Fourier transform. By adding a phase factor, which connects the aperture phase error between infocus and defocused with defocusing distance, the defocused aperture pattern is solved accurately. The procedure can then iterate by propagating again to the infocus aperture plane and by repeating the cycle again and again. The convergence criterion used in this paper is defined as shown below:

(16)$$\sqrt {\displaystyle{1 \over {N^{\rm 2}}}\sum\limits_N {\sum\limits_N {{[\varphi _{in}^n (x,y) - \varphi _{in}^{n - 1} (x,y)]}^2}}} \lt 10^{ - 6},$$

where $\varphi _{in}^n (x,y)$ is the retrieved infocus phase distribution in an aperture at the nth iteration.

Reviewing the above steps, the method is convenient because only two patterns need to be observed, which is like the traditional Misell algorithm. One is an infocus far-field pattern and the other is a defocused far-field pattern. By using the MVFSA to obtain an initial phase guess in the aperture plane which is parameterized by Zernike polynomials, the proposed method can get a better solution than the traditional Misell algorithm and avoid the local stagnation of the traditional Misell algorithm. The perturbation model and annealing scheme used in the MVFSA are innovative to ensure that the MVFSA can search widely and quickly to approach a rough position near the global minimum.

Simulation

To get the amplitude of the far field as the input of the MVFSA–Misell algorithm, a simulation model is built to produce the required data firstly. A model of Shanghai Sheshan-65m-telescope aperture is used to generate infocus and defocused radiation patterns. It is a Cassegrain antenna with a 65 m main reflector and a 6.5 m sub-reflector. The amplitude distribution is the Gaussian type with a −16 dB taper and is blocked by sub-reflector, which is shown in Fig. 4(a). The phase distribution simulates two types of surface errors in this paper: one is the random surface error and the other is the gravitational surface error, which is obtained by finite element modelling at EL = 5°. The simulated aperture phase distributions are shown in Figs 4(b) and 4(c).

Fig. 4. Original distribution of aperture: (a) amplitude distribution, (b) phase distribution for random distortion, and (c) phase distribution for gravitational distortion.

The real surface deformation can be calculated from the aperture phase distribution by the following equation [Reference Rahmat-Samii1]:

(17)$$\displaystyle{{\varepsilon \left( {x,y} \right)} \over \lambda} = \displaystyle{1 \over {4\pi}} \sqrt {1 + \displaystyle{{x^2 + y^2} \over {4F^2}}} \varphi _{in}(x,y),$$

where ε(x, y) represents the surface distortion, λ is the wavelength, φ_in(x, y) represents the phase distribution in the aperture plane in focus, and F is the focal length of the antenna. The frequency used for simulation in this paper is 30 GHz in the Q band. In this paper, the mean square error of the simulated deformations is both set as 2 mm to reflect the actual situation.

The major simulation parameters are listed in Table 1. As shown in Table 1, the defocusing distance of the sub-reflector was set as 0.01 m, equal to a wavelength, to ensure more than one complete phase rotation across the aperture. The amplitudes of the infocus and defocused far-field amplitudes are shown in Fig. 5. These two amplitudes act as the input of the hybrid MVFSA–Misell algorithm. The output is the phase distribution of the aperture plane in focus. Moreover, the amplitude patterns are supposed to be oversampled by an oversampling factor to avoid the aliasing problem. In this paper, we set the oversampling factor as 0.5. All calculations were made in 64 × 64 arrays.

Fig. 5. Simulated far-field amplitudes.

Table 1. Simulation parameters

For the Misell algorithm, the convergent solution depends on the distance between the initial phase estimation and global minimum. To demonstrate the global search capability of the MVFSA–Misell algorithm, two types of initial phase estimation are used, respectively, one type is the zero plane, and the other type is seventh-order Zernike polynomials with random coefficients between −1 and 1, which are shown in Fig. 6. In the simulation, the population size of the MVFSA is set as 10, and the iterations of stage 1 and stage 2 in the MVFSA are set as 30 and 20, respectively. The convergence criterion used in this paper is defined in (16), and the maximum iterative number is set as 200.

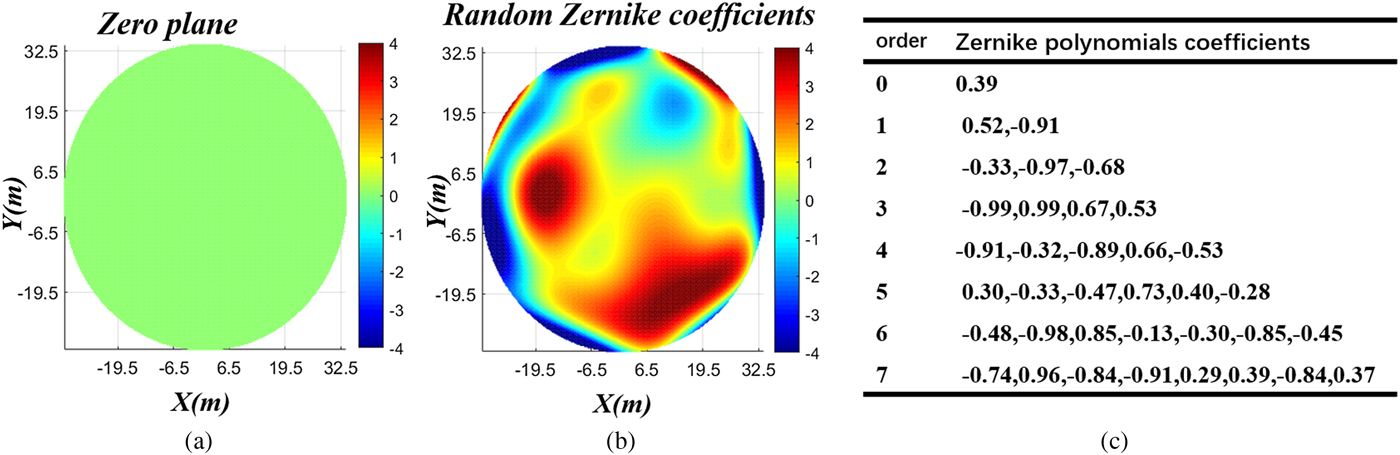
Fig. 6. Simulated initial guesses of infocus aperture phase. Note that Zernike polynomials coefficients in (c) are for phase guess in (b)

To evaluate the convergence rate and accuracy of the MVFSA–Misell algorithm, we utilize the VFSA, Misell algorithm and MVFSA–Misell algorithm, respectively, to optimize the simulated phase distribution. The convergence curves of these methods are shown in Fig. 7, and the convergent solutions of these methods are shown in Fig. 8. The RMSE of surface error is defined as follows:

(18)$$RMSE_s = \sqrt {\displaystyle{{\sum\nolimits_N {\sum\nolimits_N {{\left( {\varepsilon _{ret}(x,y) - \varepsilon _{real}(x,y)} \right)}^2}}} \over {N^2}}}, $$

where ε_ret(x, y) is the retrieved surface distortion of the reflector antenna, and ε_real(x, y) is the real surface distortion of the reflector antenna.

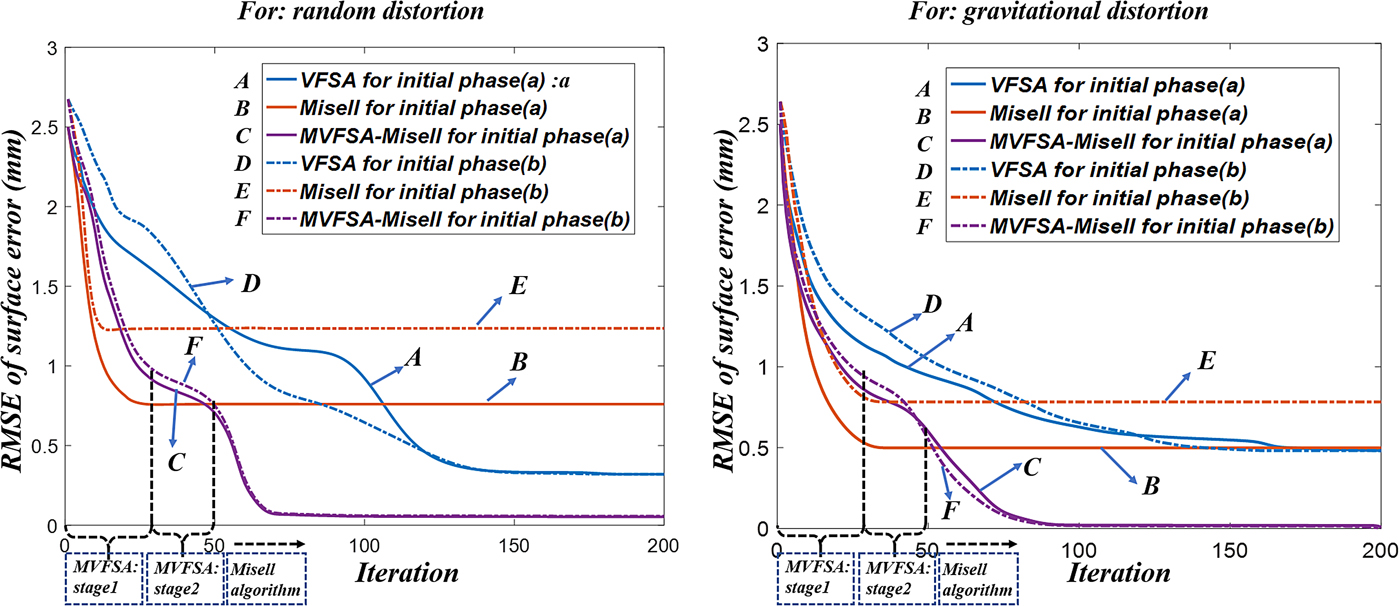
Fig. 7. Convergence curves of VFSA, Misell algorithm and MVFSA–Misell algorithm. Note that the initial phases (a) and (b) are shown in Fig. 6.

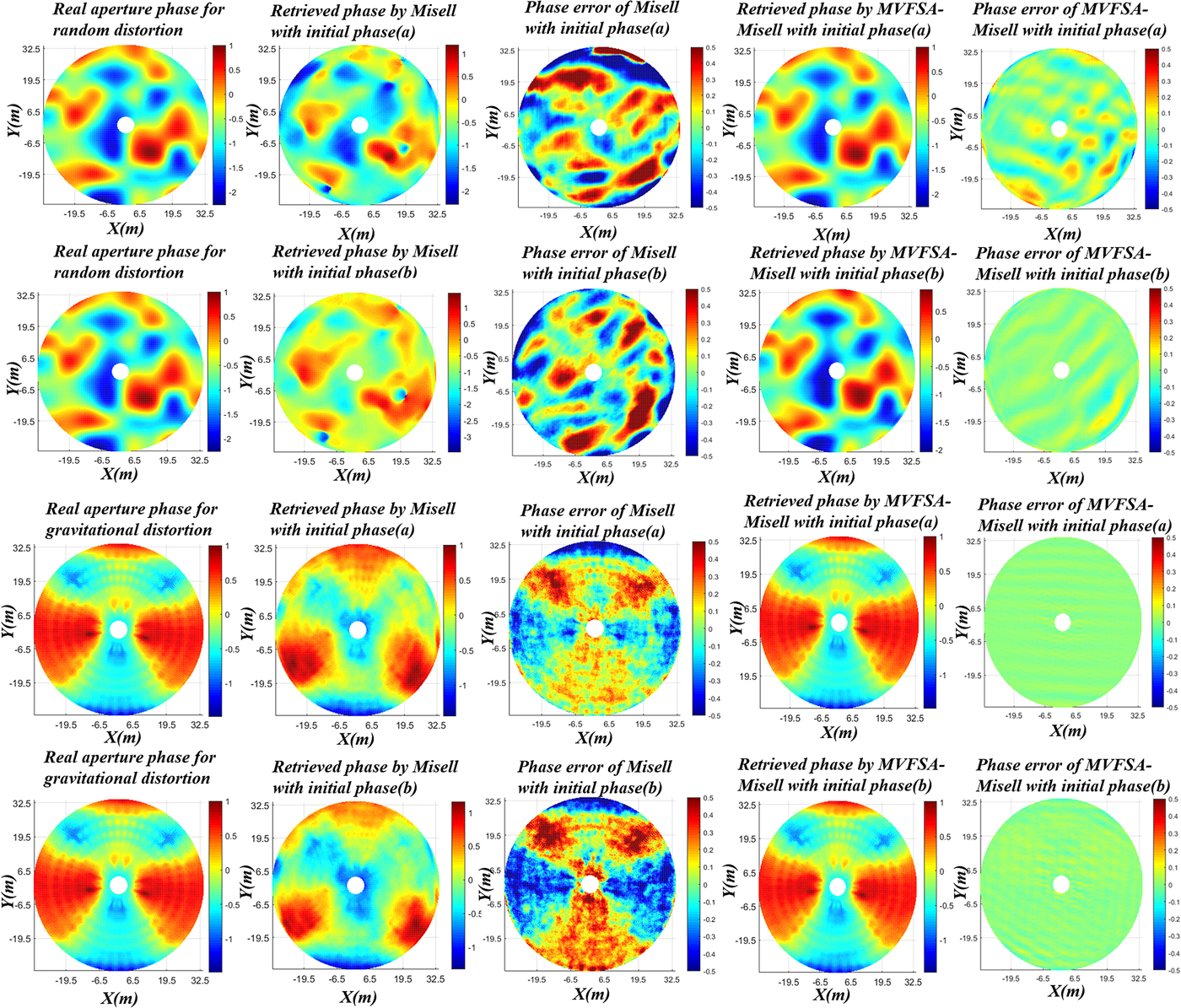
Fig. 8. Convergent solutions of the Misell algorithm and MVFSA–Misell algorithm.

The analysis of algorithm performance in convergence accuracy and speed is performed in detail according to the simulation results. The analysis is divided into two aspects as below:

1. (1) The hybrid MVFSA–Misell algorithm is able to avoid local stagnation of the traditional Misell algorithm. For the simulated random distortion, the surface distortion RMSE of the Misell algorithm is 0.76 mm (error percentage: 38%) under the initial phase (a) and is 1.23 mm (error percentage: 61.5%) under the initial phase (b), while the MVFSA–Misell algorithm converges at the same solution with 0.06 mm RMSE (error percentage: 3%) under the different initial phase estimations. Similarly, for the simulated gravitational distortion, the surface distortion RMSE of the Misell algorithm is 0.5 mm (error percentage: 25%) under the initial phase (a) and is 0.78 mm (error percentage: 39%) under the initial phase (b), while the MVFSA–Misell algorithm converges at the same solution with 0.002 mm RMSE (error percentage: 0.1%) under the different initial phase estimations. It is indicated that the Misell algorithm stagnates at different local minimums due to the difference of initial phases, while the MVFSA–Misell algorithm can converge to the global minimum under different initial guesses, which greatly improved the accuracy of the retrieved surface distortion.

2. (2) The hybrid MVFSA–Misell algorithm can greatly accelerate the speed of the traditional VFSA. For the simulated random distortion, the VFSA converges at the 183th iteration (CPU time: 1.2 h) under the initial phase (a) and converges at the 164th iteration (CPU time: 1.08 h) under the initial phase (b), while the MVFSA–Misell algorithm converges at the 72nd iteration (CPU time: 0.33 h) under the different initial phase estimations. For the simulated gravitational distortion, the VFSA converges at the 187th iteration (CPU time: 1.23 h) under the initial phase (a) and converges at the 171th iteration (CPU time: 1.12 h) under the initial phase (b), while the MVFSA–Misell algorithm converges at the 96th iteration (CPU time: 0.35 h) under the different initial phase estimations. The time consumption is decreased by more than 65% through the MVFSA–Misell algorithm. It is also shown in Fig. 7 that the global search capability of stage 1 in MVFSA is higher than that of VFSA, which means the MVFSA can approach a position with a lower cost function in finite iteration steps. In stage 2 of the MVFSA, the RMSE is decreasing continuously and the solution is getting closer to the global minimum. After the limited iteration steps of the MVFSA, the algorithm converts into the Misell algorithm immediately and converges to the final solution with a high speed.