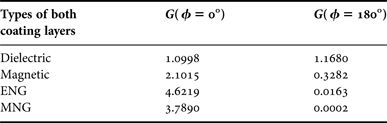I. INTRODUCTION
An axially slotted cylinder antenna is famous due to its many advantages, e.g. lightweight, design simplicity, high power capability, and greater control of its radiation pattern. It has many practical applications such as wireless communications, radar and satellite communications, and aircrafts. Its radiation and gain properties becomes more controllable when it is coated by some material [Reference Hurd1–Reference Wu and Ren11]. The radiation patterns of an axially slotted circular cylinder coated with a dielectric material have been studied by Hurd [Reference Hurd1]. He also made comparisons with experimental results. The external admittance of an axial slot on a dielectric coated metal cylinder was investigated by Knop [Reference Knop2]. Wait and Mienteka [Reference Wait and Mienteka3] have studied the fields produced by an arbitrary slot on a dielectric coated circular cylinder. They have used the saddle-point method for the derivation of the far zone field expressions. Shafai [Reference Shafai4] obtained the radiation properties of an axial slotted antenna coated with a homogenous material. Richmond [Reference Richmond5] studied the radiation properties of an axial slot on a dielectric coated elliptic cylinder. The radiation and gain properties of a slotted cylinder with two slots have been investigated by Mushref [Reference Mushref6, Reference Mushref7].
The effects of plasma coatings upon the radiation properties of an axially slotted cylinder have been studied by many authors [Reference Rusch8–Reference Marchin and Tyras10]. Wu and Ren [Reference Wu and Ren11] investigated the radiation properties of an axial slot with an anisotropic dielectric coated circular cylinder. Hamid studied the radiation properties of an axially slotted circular or elliptic cylinder coated with metamaterials [Reference Hamid12, Reference Hamid13]. He concluded that the slotted cylinder coated with metamaterials has more directive pattern with lower sidelobes as compared with the slotted cylinder coated with conventional dielectric material. Recently, Awan [Reference Awan14] has studied the effects of single negative (SNG) and single near zero background media upon the gain pattern of an axial slot coated with a single dielectric layer. The effects of different types of coating layers, SNG background media and thickness of two coating layers upon the gain pattern of an axially slotted cylinder covered with two coating layers have not been investigated previously. These effects have been studied in the present paper.
Recently, there has been a growing interest in the SNG materials [Reference Alu and Engheta15–Reference Awan22]. Such type of materials do not exist in nature but they are constructed artificially. The SNG material can be classified into two types, i.e. epsilon negative (ENG) and mu negative (MNG). An ENG material has real part of its relative permittivity as negative whereas real part of its relative permeability is positive. An MNG material is characterized by a negative real part of its relative permeability whereas real part of its relative permittivity is positive.
In this paper, an infinite axial slot is cut in a perfectly conducting cylinder and is coated with two layers. This axially slotted cylinder is embedded in a certain background medium. The effects of different types of coating layers and background medium upon the gain pattern of this slotted cylinder have been investigated. It is shown that if an axial slot is covered with both types of ENG coatings then the maximum gain in the forward direction with negligible associated sidelobes has been observed. It is also shown that if both layers are dielectric or magnetic types and embedded in a MNG medium then its gain pattern becomes more directive with maximum gain in the forward direction. The proposed theory is helpful in obtaining a directive gain from an axially slotted cylinder coated with two layers.
II. FORMULATION OF THE PROBLEM
It is considered that an infinite length hollow cylinder of perfectly conducting material is coated with two layers of homogenous, isotropic, and lossless materials. An axial slot of an infinite length which is parallel to z-axis is cut in the perfectly conducting cylinder having a narrow slot width of ϕ
o
. The radius of this cylinder is taken to be a. The geometry of the problem is shown in Fig. 1. The inner layer occupies the region 3 having radius b whereas the outer layer occupies the region 2 having radius c. This axially slotted cylinder coated with two layers is placed in a background medium which occupies region 1. The electromagnetic properties of a jth region are given by ε
j
= ε
o
εrj
and μ
j
= μ
o
μrj
with j = 1,2,3. The parameters ε
rj
and μ
rj
represent the relative permittivity and relative permeability of the jth region, respectively, with ε
o
and μ
o
as the permittivity and the permeability of the free space. Thus, propagation constant associated with the jth region can be taken as
${k_j}\, = \,{k_o}\sqrt {{\varepsilon _{rj}}{\mu _{rj}}} $
with k
o
as a free space propagation constant, i.e.
${k_o}\, = \,\omega \sqrt {{\varepsilon _o}{\mu _o}} $
. In the present study, both coating layers and background media are taken to be lossless materials. The proposed theory is also valid for the lossy materials. For this, one needs to take the parameters ε
rj
and μ
rj
as complex numbers with their imaginary parts greater than zero. This ensures the passivity condition for the assumed time convention of e−iωt
which is used in the present paper.
Fig. 1. The geometry of the problem.
An axial slot is assumed to be narrow therefore a constant distribution of an electric field, i.e. E o is maintained across it. Thus, the ϕ-component of the applied electric field is given by:
$${E_\phi} = \left\{ {\matrix{ {{E_o}} \hfill & {{\rm if}\;\vert\phi \vert \le {\phi _o}/2} \hfill \cr 0 \hfill & {{\rm Otherwise}} \hfill \cr}} \right.,$$
which can be expanded in terms of complex Fourier series as given below [Reference Chen and Cheng9]:
$${E_\phi} = \displaystyle{{{E_o}} \over \pi} \sum\limits_{n = - \infty} ^{n = + \infty} \displaystyle{{\sin \left(n{\phi _o}/2\right)} \over n}{e^{in\phi}}. $$
It is clear from equations (1)–(2) that the applied electric field generates only circumferential currents whereas there exists no axial currents for this axial slot. For this axial slot, it is reasonable to assume that slot electric field is solely E ϕ with E z = 0. This gives rise to a transverse electric (TE) mode of excitation which is associated with an axial slot. Thus, we are interested in the z-component of the magnetic field and ϕ-component of the electric field in each region because an axial slot excites TE mode.
The z-component of the radiated magnetic field
$H_z^1 $
in region 1 (ρ ≥ c) can be written as:
$$H_z^{1} = \sum\limits_{n = - \infty} ^{n = + \infty} {F_n}H_n^{(1)} \left({k_1}\rho\right){e^{in\phi}}, $$
where
$H_n^{(1)} ( \cdot )$
is the nth order Hankel function of first kind and represents an outward travelling wave solution. The factor F
n
represents an unknown coefficient. The ϕ-component of the electric field
$E_\phi ^1 $
in region 1 can be found from Maxwell's equation, i.e.
$E_\phi ^1 = \left( - i/\omega {\varepsilon _1}\right)\partial H_z^1 /\partial \rho $
which can be written as:
$$E_\phi ^1 = \displaystyle{{ - i{k_1}} \over {\omega {\varepsilon _1}}}\sum\limits_{n = - \infty} ^{n = + \infty} {F_n}H_n^{\prime(1)} \left({k_1}\rho \right){e^{in\phi}}, $$
where prime ′ denotes the derivative with respect to the argument. Likewise, the corresponding fields in region 2 (b ≤ ρ ≤ c) are given below:
$$H_z^2 = \sum\limits_{n = - \infty} ^{n = + \infty} \left[{C_n}{J_n}\left({k_2}\rho \right) + {D_n}{Y_n}\left({k_2}\rho \right)\right]{e^{in\phi}}, $$
$$E_\phi ^2 = \displaystyle{{ - i{k_2}} \over {\omega {\varepsilon _2}}}\sum\limits_{n = - \infty} ^{n = + \infty} \left[{C_n}{J_n}^{\prime}\left({k_2}\rho \right) + {D_n}{Y_n}^{\prime}\left({k_2}\rho \right)\right]{e}^{in\phi}. $$
For region 3 (a ≤ ρ ≤ b), the respective fields can be written as:
$$H_z^3 = \sum\limits_{n = - \infty} ^{n = + \infty} \left[{A_n}{J_n}\left({k_3}\rho \right) + {B_n}{Y_n}\left({k_3}\rho \right)\right]{e}^{in\phi}, $$
$$E_{\phi}^{3} = \displaystyle{{ - i{k_3}} \over {\omega {\varepsilon _3}}}\sum\limits_{n = - \infty} ^{n = + \infty} \left[{A_n}{J_n}^{\prime}\left({k_3}\rho \right) + {B_n}{Y_n}^{\prime}\left({k}_{3}\rho \right)\right]{e^{in\phi}}, $$
where J n (·) and Y n (·) are nth order Bessel's functions of first and second kinds, respectively. In equations (5)–(8), A n , Bn, Cn , and D n are unknown coefficients. Thus, all the five unknown coefficients, i.e. A n , Bn, Cn, Dn , and F n can be found by applying the tangential boundary conditions, i.e. the tangential magnetic and electric fields must be continuous at ρ = c, ρ = b, and ρ = a. These conditions can be written as follows:
$$H_z^2 = H_z^1, \quad \rho = c,\quad 0 \le \phi \le 2\pi, $$
$$E_\phi ^2 = E_\phi ^1, \quad \quad \rho = c,\quad 0 \le \phi \le 2\pi, $$
$$H_z^3 = H_z^2, \quad \rho = b,\quad 0 \le \phi \le 2\pi, $$
$$E_\phi ^3 = E_\phi ^2, \quad \rho = b,\quad 0 \le \phi \le 2\pi, $$
$$E_\phi ^3 = {E_\phi}, \quad \rho = a,\quad \vert\phi \vert \le {\phi _o}/2.$$
The unknown coefficients can be found by applying the boundary conditions given by equations (9)–(13) to the field solutions given by equations (2)–(8) and solving the resulting linear system of equations. Using this information and after some straight forward steps, the unknown coefficient F n which is of an interest for the gain in the region 1 can be written as:
$${F_n} = \displaystyle{{i\omega {\varepsilon _3}} \over {{k_3}}}\displaystyle{{4{E_o}} \over \pi} \displaystyle{{\sin \left(n{\phi _o}/2\right)} \over n}\displaystyle{1 \over {\left({k_2}c\right)\left({k_3}b\right)}}\displaystyle{1 \over {{V_n} + \left({k_2}{\varepsilon _3}/{k_3}{\varepsilon _2}\right){W_n}}},$$
where
$${V_n} = {P_n}\left[ {H_n^{(1)} \left({k_1}c\right){Q_n} + \displaystyle{{{k_1}{\varepsilon _2}} \over {{k_2}{\varepsilon _1}}}H_n^{\prime(1)} \left({k_1}c\right){R_n}} \right],$$
$${W_n} = {S_n}\left[ {H_n^{(1)} \left({k_1}c\right){T_n} + \displaystyle{{{k_1}{\varepsilon _2}} \over {{k_2}{\varepsilon _1}}}H_n^{\prime(1)} \left({k_1}c\right){U_n}} \right],$$
$${P_n} = {J_n^{\prime}}\left({k_3}a\right){Y_n^{\prime}}\left({k_3}b\right) - {J_n^{\prime}}\left({k_3}b\right){Y_n^{\prime}}\left({k_3}a\right),$$
$${Q_n} = {J_n}\left({k_2}b\right){Y_n^{\prime}}\left({k_2}c\right) - {J_n^{\prime}}\left({k_2}c\right){Y_n}\left({k_2}b\right),$$
$${R_n} = {J_n}\left({k_2}c\right){Y_n}\left({k_2}b\right) - {J_n}\left({k_2}b\right){Y_n}\left({k_2}c\right),$$
$${S_n} = {J_n^{\prime}}\left({k_3}a\right){Y_n}\left({k_3}b\right) - {J_n}\left({k_3}b\right){Y_n^{\prime}}\left({k_3}a\right),$$
$${T_n} = {J_n^{\prime}}\left({k_2}c\right){Y_n^{\prime}}\left({k_2}b\right) - {J_n^{\prime}}\left({k_2}b\right){Y_n^{\prime}}\left({k_2}c\right),$$
$${U_n} = {J_n^{\prime}}\left({k_2}b\right){Y_n}\left({k_2}c\right) - {J_n}\left({k_2}c\right){Y_n^{\prime}}\left({k_2}b\right).$$
Once the unknown coefficient F
n
is known then the z-component of radiated magnetic field and ϕ-component of radiated electric field in region 1 can be found from equations (3) and (4), respectively. As it is of an interest to find the gain pattern of an axially slotted cylinder coated with two layers in region 1. For this, one needs to find the electric and magnetic fields in the far zone in region 1. In this case, we have |k
1|ρ ≫ 1 and it is needed to use the asymptotic expressions of
$H_n^{(1)} \left({k_1}\rho \right)$
, H′(1)
n
(k
1
ρ) for large arguments which are given in [Reference Stratton23]. Using these asymptotic expressions in equations (3) and (4), the radiated electric field
$E_\phi ^1 $
and the radiated magnetic field
$H_z^1 $
in the far zone in terms of the far field patterns F(ϕ), H(ϕ) can be written as follows:
$$E_\phi ^1 = \sqrt {\displaystyle{2 \over {\pi {k_1}\rho}}} {e^{i\left({k_1}\rho - \pi /4\right)}}F(\phi ),$$
$$H_z^1 = \sqrt {\displaystyle{2 \over {\pi {k_1}\rho}}} {e^{i\left({k_1}\rho - \pi /4\right)}}H(\phi ),$$
$$\eqalign{ F(\phi ) & = i\displaystyle{{{k_1}{\varepsilon _3}} \over {{k_3}{\varepsilon _1}}}\displaystyle{{4{E_o}} \over \pi }\displaystyle{1 \over {\left( {{k_2}c} \right)\left( {{k_3}b} \right)}}\sum\limits_{n = - \infty }^{n = + \infty } \displaystyle{{\sin \left( {n{\phi _o}/2} \right)} \over n} \cr & \quad \displaystyle{{{e^{i\left( {n\phi - n\pi /2} \right)}}} \over {{V_n} + \left( {{k_2}{\varepsilon _3}/{k_3}{\varepsilon _2}} \right){W_n}}} \cr & = \sum\limits_{n = - \infty }^{n = + \infty } {{{\left( { - i} \right)}^n}} G_n^f {e^{in\phi }},} $$
with
$$\eqalign{ G_n^f & = i\displaystyle{{{k_1}{\varepsilon _3}} \over {{k_3}{\varepsilon _1}}}\displaystyle{{4{E_o}} \over \pi} \displaystyle{1 \over {\left({k_2}c\right)\left({k_3}b\right)}}\displaystyle{{\sin \left(n{\phi _o}/2\right)} \over n} \cr & \quad \displaystyle{1 \over {{V_n} + \left({k_2}{\varepsilon _3}/{k_3}{\varepsilon _2}\right){W_n}}},} $$
and F(ϕ) = η 1 H(ϕ) where η 1 is the intrinsic impedance of the background medium. The gain G(ϕ) of an axially slotted cylinder coated with two layers can be derived using the method as given by Richmond [Reference Richmond5] which is given as:
$$G(\phi ) = \displaystyle{{\left\vert F(\phi)\right\vert{^2}} \over {\sum\nolimits_{n = - \infty}^{n = + \infty} \left\vert G_n^f \right\vert{^2}}}. $$
III. NUMERICAL RESULTS
In this section, the numerical results for the gain pattern of a slotted cylinder coated with two layers are presented with different coating layer materials and background materials. The size parameters of slotted cylinder are taken to be k o c = 3, k o b = 2, and k o a = 1. For these values of k o c, kob, and k o a, after several computations, it can be shown that the summation over n for equation (27) converges rapidly for n varying from −30 to 30. Thus, the summation given in equation (27) has been truncated for n = ±30. The value of E o is taken to be unity. Likewise, the slot width of ϕ o = π/100 radians has been assumed for all the numerical results presented in this section. All the materials forming two layers and background are taken to be lossless. The background material is taken to be free space for the results presented in Figs 2–8.
Fig. 2. The gain pattern of a slotted cylinder when (a) both layers are of dielectric type with ε r3 = 4, ε r2 = 2, and μ r3 = μ r2 = 1, (b) both layers are of magnetic type with μ r3 = 4, μ r2 = 2, and ε r3 = ε r2 = 1.
Fig. 3. The gain pattern of a slotted cylinder when (a) inner layer is of magnetic type with ε r3 = 1, μ r3 = 2 with outer dielectric layer having ε r2 = 2, μ r2 = 1 (b) inner layer is of dielectric type with ε r3 = 2, μ r3 = 1 with outer layer as magnetic type having ε r2 = 1, μ r2 = 2.
Fig. 4. The inner layer is taken to be a dielectric layer with ε r3 = 2, μ r3 = 1. The outer layer is taken to be an Epsilon Negative type with μ r2 = 1. The effects of various values of ε r2 upon the gain pattern of a slotted cylinder (a) ε r2 = −0.5, (b) ε r2 = −1, and (c) ε r2 = −3.
Fig. 5. The inner layer is of dielectric type with ε r3 = 2, μ r3 = 1. The outer layer is taken to be a Mu Negative type with ε r2 = 1. The effects of various values of μ r2 upon the gain pattern of a slotted cylinder (a) μ r2 = −0.5, (b) μ r2 = −1, and (c) μ r2 = −3.
Fig. 6. The inner layer is taken to be a permeable layer with ε r3 = 1, μ r3 = 2. The outer layer is taken to be an Epsilon Negative type with μ r2 = 1. The effects of various values of ε r2 upon the gain pattern of a slotted cylinder (a) ε r2 = −0.5, (b) ε r2 = −1, and (c) ε r2 = −3.
Fig. 7. The inner layer is of magnetic type with ε r3 = 1, μ r3 = 2. The outer layer is taken to be a Mu Negative material with ε r2 = 1. The effects of various values of μ r2 upon the gain pattern of a slotted cylinder (a) μ r2 = −0.5, (b) μ r2 = −1, and (c) μ r2 = −3.
Fig. 8. The gain pattern of slotted cylinder for (a) inner layer is a mu negative (MNG) layer with ε r3 = 1, μ r3 = −2 and outer layer is of an epsilon negative (ENG) type having ε r2 = −2, μ r2 = 1 (b) inner layer is an ENG layer with ε r3 = −2, μ r3 = 1 and outer layer is of MNG type having ε r2 = 1, μ r2 = −2.
The effects of different coating layers, i.e. both layers are dielectric type or magnetic type upon gain pattern are shown in Fig. 2. For both dielectric layers, we have ε r3 = 4, ε r2 = 2 with μ r3 = μ r2 = 1. Similarly, for both magnetic type layers, we have μ r3 = 4, μ r2 = 2, and ε r3 = ε r2 = 1. It is observed that if both coating layers are dielectric type then the gain pattern has maximum value in the forward direction, i.e. ϕ = 0° which shows a considerable leakage of guided surface waves along or just above the dielectric–air interface. Likewise, it is clear from curve (a) of Fig. 2 that in backward direction, i.e. ϕ = 180° there exists a finite gain. Physically, it can be explained that the radiation from the slot travels around the periphery of the cylinder in both directions. The dielectric coating layers enhance the ripples in the gain pattern and this is due to trapped peripheral surface waves in coating layers which enhance the standing wave pattern. For the sake of completeness, it is desired to observe the effects of magnetic or permeable type coatings upon the gain pattern. For this, we have taken relative permeability of permeable layer different from unity. Such type of composite materials can be made artificially whose macroscopic permeability differs from unity. The curve (b) of Fig. 2 represents the effects of magnetic coatings upon the gain pattern. The pronounced effect of wave trapping by a magnetic type layers is striking. It is observed that ripples in the gain pattern are larger than the corresponding ones for the dielectric coating layers. Thus, it can be concluded that permeable or magnetic coatings substantially modify the gain pattern and reduces the gain in forward direction as compared with corresponding dielectric coating layers.
Figure 3 shows the gain pattern of two different types of coating layers. The curve (a) shows the gain pattern of slotted cylinder with inner layer as magnetic type with ε r3 = 1, μ r3 = 2 and outer layer as dielectric type with ε r2 = 2, μ r2 = 1. Likewise, for curve (b), the inner layer is dielectric type with ε r3 = 2, μ r3 = 1, and the outer layer is magnetic type having ε r2 = 1, μ r2 = 2. It is observed that when outer layer is dielectric type than the gain is minimum in the forward direction whereas the gain has maximum value in backward direction and at angles close to 90° and 270°. Thus, the outer dielectric layer with inner magnetic layer mainly guide the waves towards rare side of the cylinder. On the other hand, if outer layer is magnetic type with inner layer as dielectric type then gain has maximum value in the forward direction. Also an increase of the beamwidth has also been observed in this case. This is clear from curve (b) of Fig. 3. In this case, there exists a null in the backward direction.
For Figs 4 and 5, the inner layer is taken to be dielectric type with ε r3 = 2 and μ r3 = 1. In Fig. 4, the outer layer is taken to be an ENG coating with variable permittivity. On the other hand, in Fig. 5, the outer layer is a MNG type with variable permeability. It is observed from Fig. 4 that as the value of ENG coating changes from −0.5 to −1 the gain in the forward direction increases. If the value of ε r2 becomes −3, then the gain in the forward direction reduces significantly and as a result multiple side lobes and a back lobe appear in the gain pattern. Thus, it is obvious from Fig. 4 that for ε r2 = −1, the gain pattern of slotted cylinder becomes more directive with the maximum gain of approximately 4.69 in the forward direction. If the outer layer is an MNG type then gain pattern has different characteristics. As the value of permeability of the outer layer changes from −0.5 to −1 then the gain in the backward direction increases whereas the gain reduces in the forward direction. In this case, for μ r2 = −3, the gain pattern has wider beamwidth towards front side of the cylinder and loses its directional characteristics. In this case, the gain in the forward direction is greater than the corresponding gain in the backward direction. This forward gain is nearly half of the gain of ENG outer layer coating with ε r2 = −3. This can be observed by comparing curve (c) of Fig. 5 with curve (c) of Fig. 4.
For Figs 6 and 7, the inner layer is taken to be of magnetic type with ε r3 = 1 and μ r3 = 2. The outer layer is taken to be an ENG type for Fig. 6 and an MNG type for Fig. 7. It is clear from Fig. 6 that if the value of ε r2 changes from −0.5 to −1 then the gain patterns have identical shapes with the maximum gain in the forward direction and nearly zero gain in the backward direction. As the value of ε r2 becomes more negative than −1, the gain in the forward direction reduces and number of side lobes increases (not shown in Fig. 6). As the value of ε r2 becomes −3, then it is clear from Fig. 6 that gains of associated sidelobes increase and shift towards rear side of the cylinder. The directive gain characteristics of a slotted cylinder has been observed for ε r2 = −1. On the other hand, if the outer coating is an MNG type then it is observed that for μ r2 = −1, the gain has maximum value of nearly 2 in the forward direction. This maximum gain reduces to a value of nearly 1.7 in the forward direction for μ r2 = −3. In this case, the backward gain becomes 2.26.
The effects of inner and outer coatings as a SNG material have been shown in Fig. 8. For Fig. 8, the curve (a) represents the gain pattern of slotted cylinder where inner layer is an MNG type with ε r3 = 1, μ r3 = −2 and outer layer is an ENG type with ε r2 = −2, μ r2 = 1. Likewise, for curve (b), the inner layer is an ENG type with ε r3 = −2, μ r3 = 1 and the outer layer is an MNG type having ε r2 = 1, μ r2 = −2. It is clear from Fig. 8 that both gain patterns are identical in shapes having no associated sidelobes. Also they have very small contributions of guided waves towards rear side of the cylinder. Both gain patterns have directional characteristics with the maximum gain in the forward direction. This is an important result which shows that maximum of field supplied by an axial slot is guided in the forward direction.
For practical applications, we are interested in the forward and the backward gains of an axially slotted cylinder. To highlight the gains in the forward and backward directions, a comparative study is carried out for same types of both coating layers and is shown in Table 1. It is clear from Table 1 that the maximum gains in the forward direction can be obtained provided that both types of coating layers are of SNG types. The effects of inner and outer coating layer thicknesses upon the forward and backward gains with both coating layers of the same types as considered for Table 1 are given in Figs 9–12. To analyze the effects of inner coating thickness, the outer coating thickness is fixed at k o (c − b) = 1 and k o a = 1 with k o b as variable. On the other hand, for the effects of outer coating, we have taken k o a = 1, k o b = 2, and k o c is variable. It can be observed in Figs 9 and 10 that if both coating layers are either of dielectric or magnetic type then with the increase of inner coating thickness, the gains in the forward and backward directions have fluctuating behavior. This fluctuating behavior of the forward and the backward gains are more dominant for these dielectric or magnetic coatings if the outer coating thickness has been increased and is obvious in Figs 11 and 12. If both coatings are of ENG types then it can be observed in Figs 9 and 11 that with the increase of inner and outer coating thicknesses, the gains in the forward directions have fluctuating behavior and have larger gain values as compared with dielectric or magnetic coatings. These larger gains in the forward directions are associated with reduced gains in the backward directions and are obvious in Figs 10 and 12 for ENG coatings. Likewise, it is observed in Figs 9 and 11 that as the thickness of inner or outer coating increases for MNG coatings then the gains in the forward directions increase having no fluctuating behavior. For these MNG coatings, the backward gains are nearly zeros and seems to be independent of the thickness of inner and outer coatings. This is observed in Figs 10 and 12.
Fig. 9. Effects of different types of both coating layers upon the forward gain of an axially slotted cylinder covered with two coating layers as a function of ratio b/a where both layers are of same type.
Fig. 10. Effects of different types of coating layers upon the backward gain of an axially slotted cylinder covered with two coating layers as a function of ratio b/a.
Fig. 11. Effects of outer coating thickness upon the forward gain of an axially slotted cylinder covered with two coating layers for different types of both coatings.
Fig. 12. Effects of outer coating thickness upon the backward gain of an axially slotted cylinder covered with two coating layers for different types of both coatings.
Table 1. Comparative study of gains for an axially slotted cylinder with two coating layers and embedded in free space background. These two coating layers are of dielectric, magnetic, epsilon negative (ENG) and mu negative (MNG) types. For dielectric layers, we have ε r2 = ε r3 = 2, μ r2 = μ r3 = 1 and for magnetic layers we have μ r2 = μ r3 = 2, ε r2 = ε r3 = 1. Likewise, for ENG and MNG coating layers, we have ε r2 = ε r3 = −2, μ r2 = μ r3 = 1 and μ r2 = μ r3 = −2, ε r2 = ε r3 = 1 respectively.
Figures 13 and 14 show the effects of background media upon the gain pattern of a slotted cylinder when both coating layers are either of dielectric type or magnetic type. Figure 13 deals with the gain patterns of a slotted cylinder coated with two dielectric layers having same electromagnetic characteristics as given for curve (a) of Fig. 2 and embedded in free space or ENG (ε r1 = −2, μ r1 = 1) or MNG (ε r1 = 1, μ r1 = −2) background. It is observed that an ENG background reduces the forward gain significantly and shifts the gain towards the rear side of the slotted cylinder. For MNG background, the gain in the forward direction becomes maximum. This gain pattern has more directive characteristics with a pronounced gain of nearly 4.34 in the forward direction, while having very small gain in the backward direction. On the other hand, the gain pattern of a slotted cylinder, if both layers are of magnetic type, has the same electromagnetic properties as that of curve (b) of Fig. 2 and embedded in free space or ENG (ε r1 = −2, μ r1 = 1) or MNG (ε r1 = 1, μ r1 = −2), as is shown in Fig. 14. It is clear from Fig. 14 that most of the slot field is guided towards rear side of the cylinder for an ENG background. It is further observed that the gain pattern of slotted cylinder with MNG background has directional properties with the maximum gain of nearly 3.1 in the forward direction having wider beamwidth as compared with the two layered dielectric coated slotted cylinder and embedded in ENG background.
Fig. 13. The gain pattern of slotted cylinder where both the layers are dielectric type with ε r2 = 2, ε r3 = 4, and μ r2 = μ r3 = 1 and embedded in (a) free space background, (b) Epsilon Negative background with ε r1 = −2 and μ r1 = 1, and (c) Mu Negative background with ε r1 = 1 and μ r1 = −2.
Fig. 14. The gain pattern of slotted cylinder where both the layers are magnetic type with μ r2 = 2, μ r3 = 4, and ε r2 = ε r3 = 1 and embedded in (a) free space background, (b) Epsilon Negative background with ε r1 = −2 and μ r1 = 1, and (c) Mu Negative background with ε r1 = 1 and μ r1 = −2.
IV. CONCLUSION
The effects of various coating materials and background material upon the gain pattern of an axially slotted cylinder coated with two layers have been investigated. It is studied that gain pattern can be substantially modified by changing the material properties of two layers or background. It is concluded that if both layers of the slotted cylinder are of magnetic type and embedded in the free space then the gain pattern has more ripples as compared with the corresponding two layer dielectric coated slotted cylinder embedded in free space. It is also shown that if inner layer is either of dielectric or magnetic type and outer layer is an ENG layer having more negative value of its relative permittivity then the gain has directive pattern with the free space background. It is further studied that if both coating layers are either dielectric or magnetic type and embedded in an MNG background then the gain pattern is directive with the maximum gain in the forward direction.
ACKNOWLEDGEMENT
The author is thankful to the anonymous reviewers for improving the content of the manuscript.
Zeeshan Akbar Awan received a Ph.D. degree in Electronics from the Quaid-i-Azam University, Islamabad in 2013. He is presently a lecturer at the same university. He has authored more than 10 research articles. His present research interests include metamaterials, metasurfaces, and antenna theory.
