Theoretical fundamentals

TMAAs are commonly referred to as 4D arrays, because time is utilized as an additional degree of freedom for beamforming. The time modulation is typically based on fast and periodic ON/OFF keying. In result, the beamforming and beam-steering, which have been traditionally related to PAAs, can be realized without phase-shifters. Various types of TMAAs were extensively elaborated in many scientific publications [Reference Rocca, Oliveri, Mailloux and Massa4–Reference Chen, Zhang, Wu and Fang28]; therefore, only a brief introduction to this topic will be provided in this paper. Properties of the TMAA will be described in the receiving mode without losing the generality. Figure 1 shows a typical configuration of a linear TMAA with a uniform spacing between elements distributed along the x-axis and SPST (single-pole single-throw) RF switches incorporated into a feed network. Figure 2 illustrates corresponding modulating functions, which are also referred to as switching sequences.

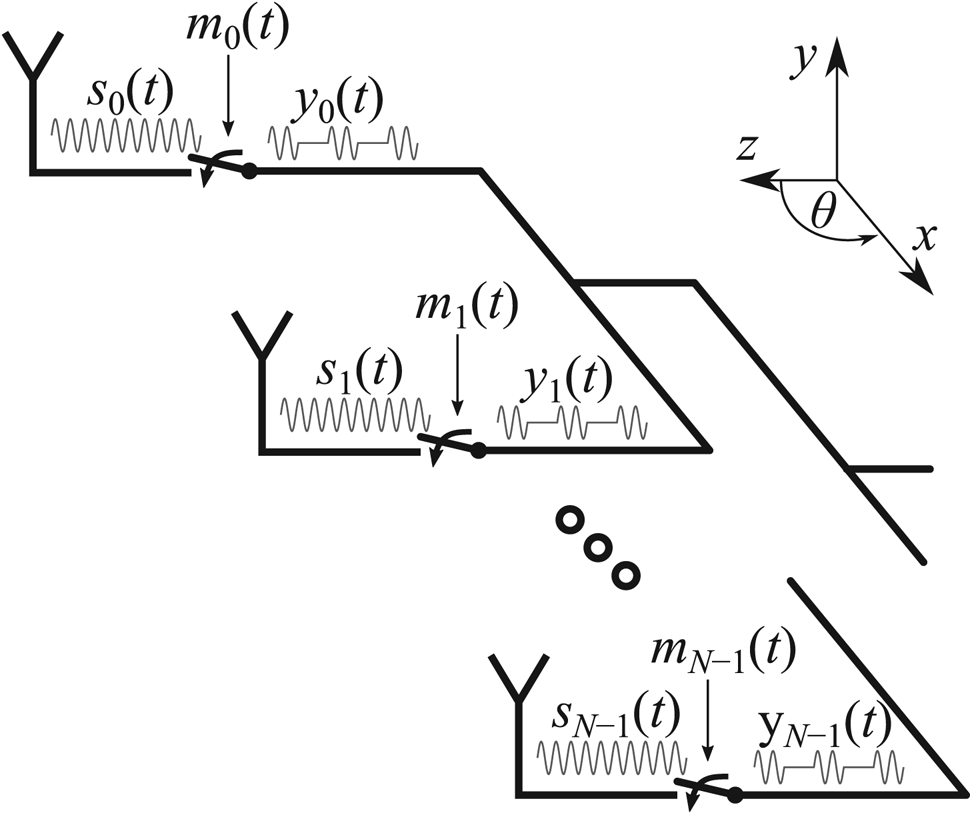
Fig. 1. Diagram of a linear TMAA with SPST switches.

Fig. 2. Unipolar switching sequences.

RF switches modulate (by means of a periodic ON/OFF keying) signals s_n(t) delivered from each antenna, where n = 0…N–1 is the index of the antenna and N is the total number of antennas in the array. Operation of each switch can be expressed as a modulation of s_n(t) by function m_n(t), which is periodic and associate value of “0” for OFF and “1” for ON. All modulating functions share the same modulation frequency f ₀ = 1/T ₀, where T ₀ is the period of modulation. Two constrains must be satisfied [Reference Maneiro-Catoira, Brégains, García-Naya and Castedo20]:

1. (1) the modulation frequency must be much smaller than the carrier frequency of an RF signal (f ₀ << f_c),

2. (2) the modulation frequency must be greater than the bandwidth of an RF signal (f ₀ > B).

The TMAA array factor can be formulated as [Reference Rocca, Oliveri, Mailloux and Massa4]:

(1)$$AF\,\lpar \theta \comma \;t\rpar = \mathop \sum \limits_{n = 0}^{N-1} m_n\,\lpar t\rpar \,S_ne^{\,jknd\sin \theta }\comma \;$$

where S_n represents the complex excitation, d is the distance between antenna elements in the array, θ is the angle, and k = 2π/λ is the wave number. Due to its periodicity, m_n(t) can be expressed in terms of a sum of complex Fourier series coefficient $M_n^{\lpar q \rpar }$:

(2)$$m_n\,\lpar t\rpar = \mathop \sum \limits_{q = {-}\infty }^\infty M_n^{\lpar q\rpar } e^{\,jq\omega _0t}$$

(3)$$M_n^{\lpar q\rpar } = \displaystyle{1 \over {T_0}}\mathop \int \limits_{{-}T_0/2}^{T_0/2} m_n\,\lpar t\rpar e^{{-}jq\omega _0t}dt\comma \;$$

where ω ₀ = 2π/T ₀ and q ∈ (-∞, ∞). After substituting (2) into (1), the time-dependency is converted to the frequency-dependency and the array factor can be formulated as follows:

(4)$$AF\lpar \theta \rpar = \mathop \sum \limits_{n = 0}^{N-1} S_nM_n^{\lpar 0 \rpar } e^{\,jknd\sin \theta } + \mathop \sum \limits_{\matrix{ {q = {-}\infty } \cr {q\ne 0} \cr } }^\infty \mathop \sum \limits_{n = 0}^{N-1} S_nM_n^{\lpar q \rpar } e^{\,jknd\sin \theta }e^{\,jq\omega _0t}.$$

According to (4), the time-modulated signal is composed of a central component (q = 0) and sideband components (q ɛ ℤ, q ≠ 0). The latter are placed on multiplies of modulation frequency around the center frequency. Figure 3 presents an example of a bandpass signal's spectrum before (Fig. 3(a)) and after (Fig. 3(b)) time modulation. It shows that the sidebands are in fact spectral replicas of the original signal; however, they demonstrate different spatial properties because each sideband carries information received at frequency f_c from a different angle [Reference Rocca, Zhu, Bekele, Yang and Massa11]. Therefore, sidebands can be utilized as diverse transmission channels [Reference Rocca, Poli, Bekele and Massa14–Reference Bogdan, Godziszewski and Yashchyshyn19].

Fig. 3. Spectrum of the signal (a) impinging upon TMAA; (b) at the output of TMAA.

Values of complex Fourier coefficients $M_n^{\lpar q \rpar }$ in (4) can be modified by adjusting the ON and OFF times of modulating functions. The beam-steering is obtained when switches are turned ON and OFF sequentially with some fixed delay with respect to the preceding one [Reference Bogdan, Bajurko and Yashchyshyn21]. Hence, operation of the n-th switch is related to the operation of the first switch in the following way:

(5)$$m_n\lpar t \rpar = m_0\lpar {t-n{\rm \Delta }t} \rpar \comma \;$$

where Δt is the delay progression. According to the time-shift property of the Fourier transform, the delay progression alters the phase of the Fourier coefficients as follows:

(6)$$m_0\lpar {t-n{\rm \Delta }t} \rpar \mathop \Leftrightarrow \limits^{\rm \Im } M_0^{\lpar q \rpar } e^{-{{\,j2\pi qn{\rm \Delta }t} \over {T_0}}}\comma \;$$

hence enables beamforming similarly to PAAs.

Design

The very first prototype of the TMAA was presented in 1963 [Reference Kummer, Villeneuve, Fong and Terrio22]. It was based on p-i-n diodes used as switches and demonstrated 10 kHz of the maximum signal bandwidth. Since then, over the last 50 years of progress in electronics and semiconductor technology, advanced switching devices with cutting edge performance have become available off-the-shelf. Moreover, more functional TMAA architectures with improved efficiency were proposed. For instance, the TMAA in [Reference Yao, Wu and Fang9] uses the I/Q channel modulator which is composed of two Wilkinson power dividers, two RF switches, two 0/π phase shifters in RF channels, and one π/2 fixed-phase shifter in the control circuit to realize a single-sideband time-modulated phase-only weighting. In [Reference Bogdan, Yashchyshyn and Jarzynka23], a less complex TMAA was presented because the 0/π phase shifters were avoided. Instead, a linear antenna array was complemented by identical, however, oppositely oriented antenna array and single-pole double-throw (SPDT) switches were used to alternate signals between elements of these two arrays as illustrated in Fig. 4. Such a design can be considered as a special case of the TMAA with bipolar squared periodic sequences [Reference Maneiro-Catoira, Brégains, García-Naya and Castedo24].

Fig. 4. Diagram of TMAA with SPDT switches connected to oppositely oriented antennas.

Each n-th pair of the oppositely oriented antennas can be treated as a single element of the linear array. Therefore, its radiation pattern in xz-plane can be calculated with equation (4). However, the Fourier coefficients $M_n^{\lpar q \rpar }$ have to be computed for the bipolar switching sequences presented in Fig. 5.

Fig. 5. Bipolar switching sequences.

The design of the TMAA used in the experiments is presented in Fig. 6. Details on the design and specification can be found in [Reference Bogdan, Godziszewski, Yashchyshyn, Kim and Hyun25]. The TMAA is composed of two layers: a superstrate with the permittivity of 2.2 (RT/duroid588) and a substrate with the permittivity of 3.66 (RO4003C). A single element of the array is composed of two oppositely oriented series-fed double-patch antennas. The elements are electromagnetically coupled with microstrip lines, which are connected to the throws of SPDT switches. The elements are designed for the center frequency of 5.6 GHz. Four elements are arranged in the form of a linear array.

Fig. 6. Design of the TMAA.

The RF switches ADRF5020 [26] are incorporated into the feed network. This particular model was selected because of its ultrashort switching time of 2 ns and a very good microwave performance at 5.6 GHz. The switching is periodic with repetition frequency f ₀ = 50 MHz, or equivalently the repetition period of 20 ns. It is also uniform, i.e. each antenna in pair is active for 0.5T ₀. The digital delay lines 3D3438 [27] are used to introduce delays between switching sequences. A step of the delay applied to switching sequences equals 60 ps which corresponds to 0.003T ₀.

The total efficiency of the TMAA (η_T) can be estimated by taking into account the radiation efficiency (η_R), the switching efficiency (η_S), and the harmonic efficiency (η_H) [Reference Chen, Zhang, Wu and Fang28]. The radiation efficiency was estimated at 0.6 by considering the radiation efficiency of the antenna structure computed with an electromagnetic simulator and the insertion loss of the switch. The switching efficiency can be estimated at 1, because the SPDT switches always connect an element of the array to the feed network. Hence, the power of an RF signal is not dissipated in the matched load during the OFF state. The harmonic efficiency depends on the switching sequence and corresponding magnitudes of harmonics, according to:

(7)$$\eta _H^{\lpar q \rpar } = \vert {M_n^{\lpar q \rpar } } \vert ^2/\mathop \sum \limits_{k = {-}\infty }^\infty \vert {M_n^{\lpar k \rpar } } \vert ^2.$$

Magnitudes of the harmonics are obtained after expressing the switching sequence in terms of the Fourier series. For example, magnitudes of the central component and the first negative harmonic for unipolar switching sequences presented in Fig. 2 equal |M_n ⁽⁰⁾| = 0.5 and |M_n ⁽⁻¹⁾| = 0.3183, respectively. In our case, the TMAA is controlled by bipolar switching sequences presented in Fig. 5; hence the opposite antennas are excited with symmetrical unipolar RF pulses. Therefore, the harmonic efficiency obtained from (7) should be multiplied by two. This yields the harmonic efficiency of η_H ⁽⁰⁾ = 0.5 and η_H ⁽⁻¹⁾ = 0.2 for the central component and the first negative harmonic, respectively. If the RF system is capable of processing multiple spectral components, then the harmonic efficiency is a sum of efficiencies calculated for each. For example, if both the central component and the first negative sideband component are processed, then the harmonic efficiency $\eta _H = \eta _H^{\lpar {-1} \rpar } + \eta _H^{\lpar 0 \rpar } = 0.7$. Therefore, the total efficiency of the TMAA for MIMO can be estimated at η _T = η _Rη _sη _H = 0.42.

Figures 7(a)–7(c) show partial antenna patterns simulated for the first negative sideband (q = –1) and different values of the delay progression Δt. The beam-steering is performed in xz-plane. Figure 7(d) shows the antenna pattern at the central component (q = 0). It is divided by a deep broadside null into two beams, which are directed toward −24° and +24° in yz-plane. Comparing Figs 7(a)–7(d) one can observe that the antenna patterns simulated over the first negative sideband and the central component are complementary.

Fig. 7. Antenna patterns of TMAA simulated for (a) q = −1 and Δt = 0, (b) q = −1 and Δt = 0.15T ₀, (c) q = −1 and Δt = 0.28T ₀, (d) q = 0.

System design

Diagram of the 2 × 2 BS-TM-MIMO concept is presented in Fig. 8. The transmitting part resembles a regular 2 × 2 MIMO transmitter, i.e. two streams of symbols x₁ and x₂ are up-converted and sent from transmitting RF chains (Tx1 and Tx2) via omnidirectional dipole antennas. Waves transmitted from omnidirectional antennas propagate inside a multipath environment. The receiving part is modified with respect to a conventional 2 × 2 MIMO receiver in two ways. Firstly, only one receiving RF chain is used instead of two. Secondly, a single TMAA with the beam-steering is used instead of two separate antennas. This modification leads to a more compact and less power consuming design; however, a wider frequency band must be processed in the receiving RF chain. These modifications are possible, because TMAA converts spatial diversity into frequency diversity, i.e. combinations of waves approaching from different directions are available on different frequencies. For instance, waves approaching from xz-plane are available on odd sidebands (q =  ±1, ±3, ±5, …) and waves approaching from yz-plane (excluding the broadside direction) are available at the center frequency (q = 0). Sidebands are demultiplexed in the baseband for further processing as diverse transmission channels.

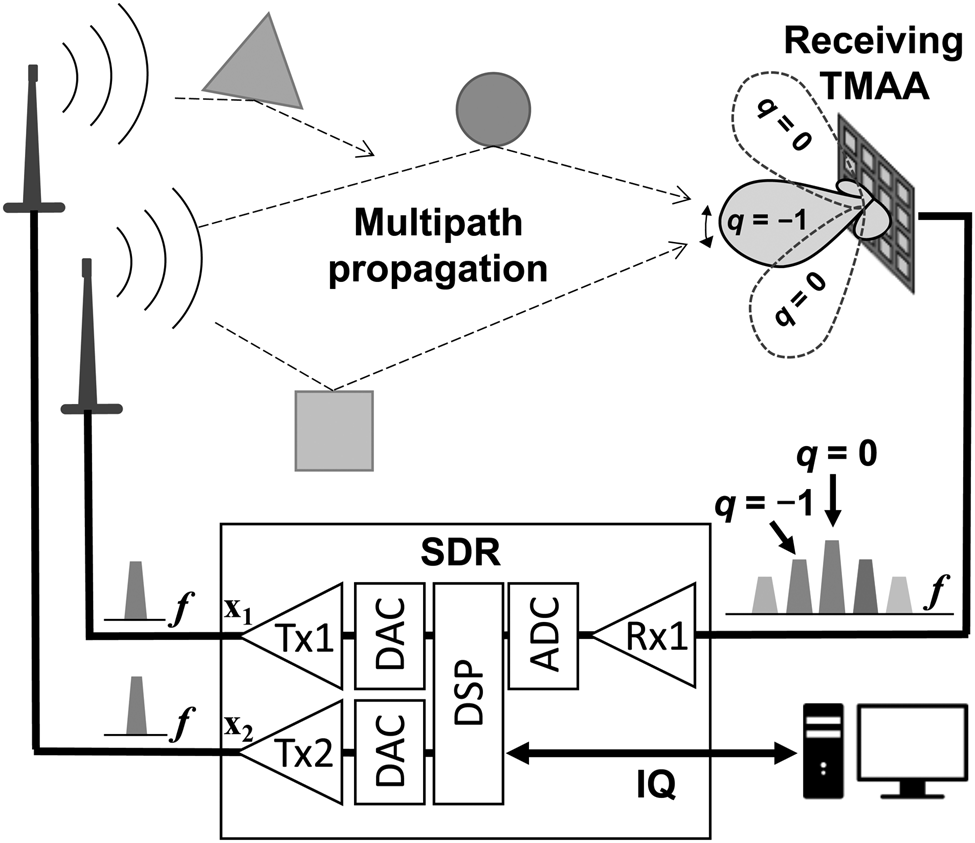
Fig. 8. Diagram of the BS-TM-MIMO.

Antenna pattern impact on MIMO performance

Two main requirements should be satisfied for an effective MIMO transmission. Firstly, a level of the signal to noise ratio (SNR) must be sufficiently high to correctly demodulate received symbols. Secondly, received signals should not be correlated. A level of the SNR can be increased by using directional antennas which provide higher gain than omnidirectional antennas, therefore can compensate for the path loss of a radio channel. Nevertheless, directional antennas reduce the angular spread of the channel, thus decrease the MIMO performance. Another solution is an adaptive antenna with a controllable pattern. Its beam can be focused toward a direction which provides a signal with high SNR and satisfactory multipath richness.

The requirement of a low correlation between spatial streams can be satisfied to some degree when antennas are dislocated on more than a quarter of the wavelength [Reference Foschini and Gans29]. Otherwise, the performance of MIMO may be significantly limited. The necessary diversity can be produced with distinct antenna patterns, i.e. highly orthogonal patterns create a low correlation, hence capacity gains are possible [Reference Jensen and Wallace30, Reference Saunders and Aragón-Zavala31]. Correlation between two antenna patterns can be expressed with an envelope correlation coefficient (ECC) [Reference Votis, Tatsis and Kostarakis32]

(8)$${\rm ECC} = \displaystyle{{{\left\vert {{\rm \int\!\!\int }\overrightarrow {F_1} ( {\theta \comma \;\varphi } ) \cdot \overrightarrow {F_{2}^{\ast} } ( {\theta \comma \;\varphi } ) d{\rm \Omega }} \right\vert }^2} \over {{\rm \int\!\!\int }{\vert {\overrightarrow {F_1} ( {\theta \comma \;\varphi } ) } \vert }^2d{\rm \Omega }{\rm \int\!\!\int }{\vert {\overrightarrow {F_2} ( {\theta \comma \;\varphi } ) } \vert }^2d{\rm \Omega }}}\comma \;$$

where $\overrightarrow {F_i} \lpar {\theta \comma \;\varphi } \rpar$ is the pattern of the i-th antenna. Value of the ECC ranges from <0.1 for low correlation to ~0.5 for the nominal, and >0.9 for the high correlation [Reference Foegelle33]. Figure 9 shows the ECC calculated for different pairs of TMAA antenna patterns. As given in Table 1, the patterns indicated with roman numbers from I to VII were simulated for the first negative sideband component (q = –1) and different Δt. Pattern VIII was simulated for the central component (q = 0). The lowest values of the ECC are obtained when pattern VIII is combined with any other, because of its divergent shape. In many applications, pattern VIII could be recognized as disadvantageous; however, in MIMO system, it can provide better diversity.

Fig. 9. ECC calculated for different pairs of TMAA antenna patterns.

Table 1. Direction of the main beam in terms of the elevation (θ) and azimuthal angles (φ) obtained for different TMAA configurations.

The ECC is a popular metric indicating the effectiveness of MIMO antennas; however, it does not consider the characteristic of a multipath environment. In practical cases, a condition number (κ) of the channel matrix is a more reliable indicator of the correlation between spatial streams. The condition number is calculated from the instantaneous channel matrix H without the need for stochastic averaging [34] according to:

(9)$$\kappa = 20\log _{10}\lpar {\hat{{\bf H}}{\hat{{\bf H}}}^{{-}1}} \rpar \;\;\;\;\lpar {{\rm dB}} \rpar $$

where ${\hat{\bf H}}$ is an estimate of the channel matrix. A well-conditioned channel matrix indicates a low correlation between received signals and yields a low value of the condition number, which facilitates MIMO communication in the high SNR regime [Reference Tse and Viswanath35]. Such a condition is usually obtained in NLOS propagation when the LOS wave is significantly attenuated.